Mathematical Modeling of Periodic Outbreaks with Waning Immunity: A Possible Long-Term Description of COVID-19
Abstract
:1. Introduction
2. The Mathematical Model
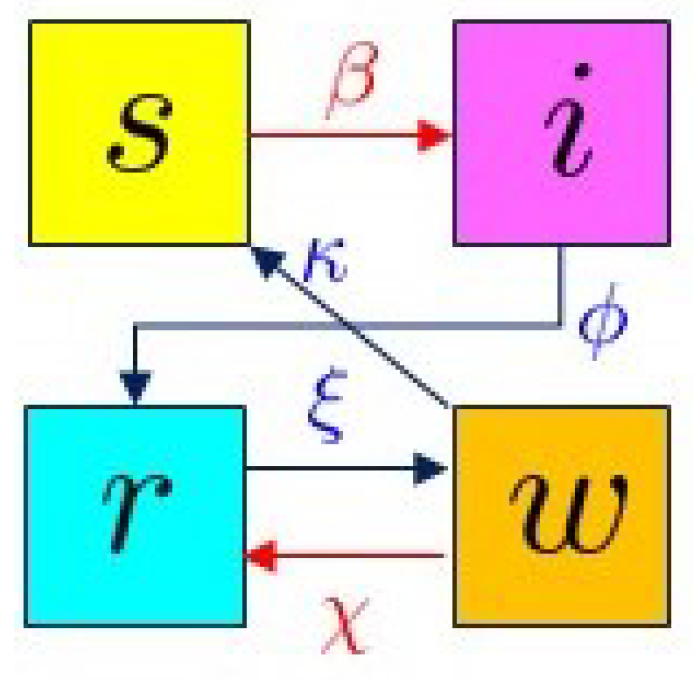
2.1. The SIRW Model
- (i)
- The waning individual can come into contact with an infected individual again, with contact rate , boosting their immunity, returning them to the r compartment; this is again described by a predator-prey term, proportional to .
- (ii)
- The waning individual loses their immunity with no additional contact with the virus and returns to the s compartment at rate .
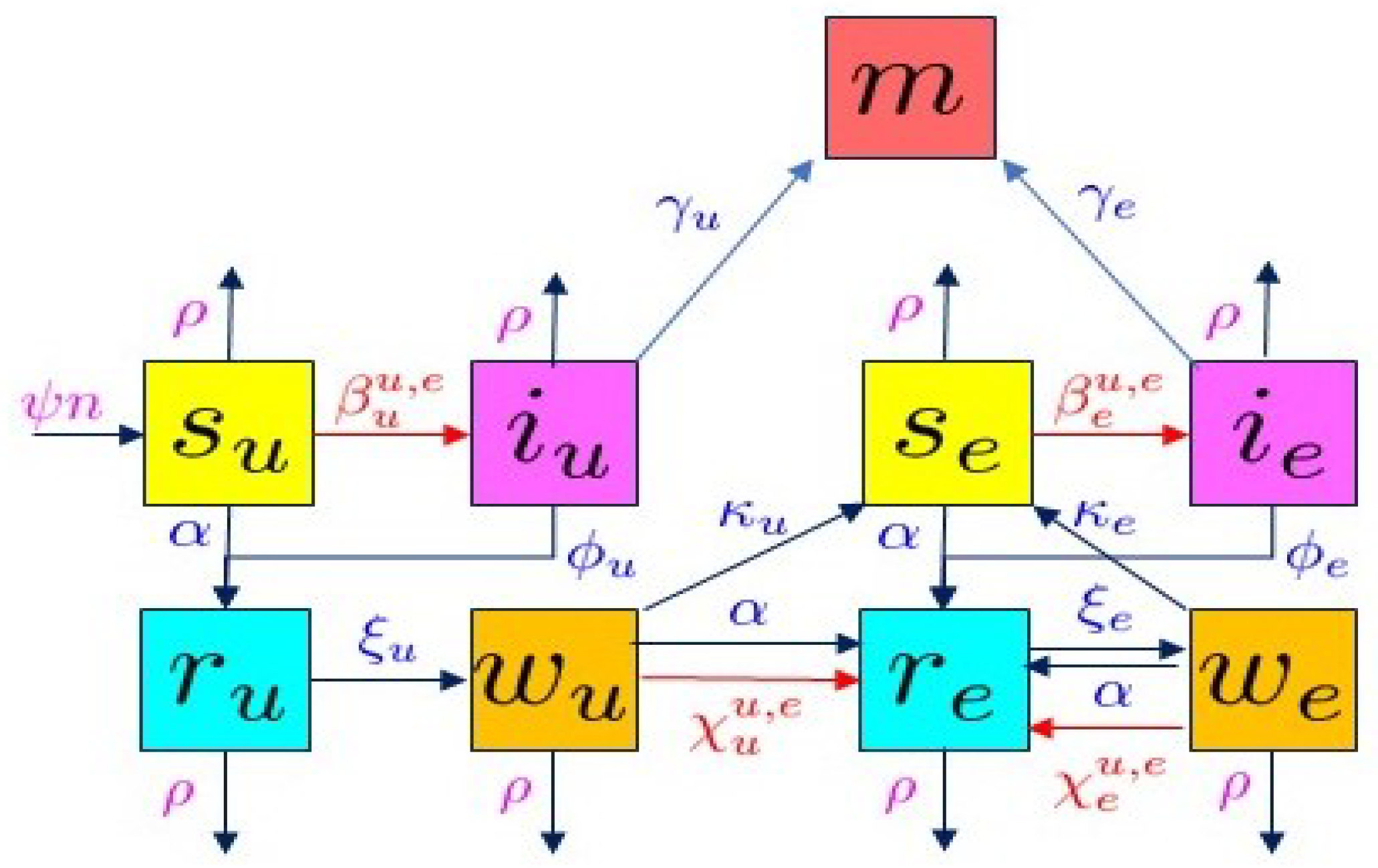
2.2. The SIRW2 Model
- (i)
- An individual can come into contact with an infected individual (either or ), with contact rate , respectively, boosting the immunity and moving directly to the compartment ;
- (ii)
- An individual can receive a vaccine booster (rate ), also boosting their immunity and moving to ;
- (iii)
- In the absence of additional contact with the virus, in the form of exposure to an infected individual or a vaccine booster, the immunity can be lost with a rate . In this case, the switch is to the compartment .
- (iv)
- The mortality rate is substantially lower: << ;
- (v)
- The recovery rate is substantially higher: >> .
- (a)
- immunity is lost more quickly after reinfection: > ;
- (b)
- however, it is also boosted more easily among those with prior immunity: , .
2.3. Basic Properties of the SIRW2 Model
2.4. Local Sensitivity Equations
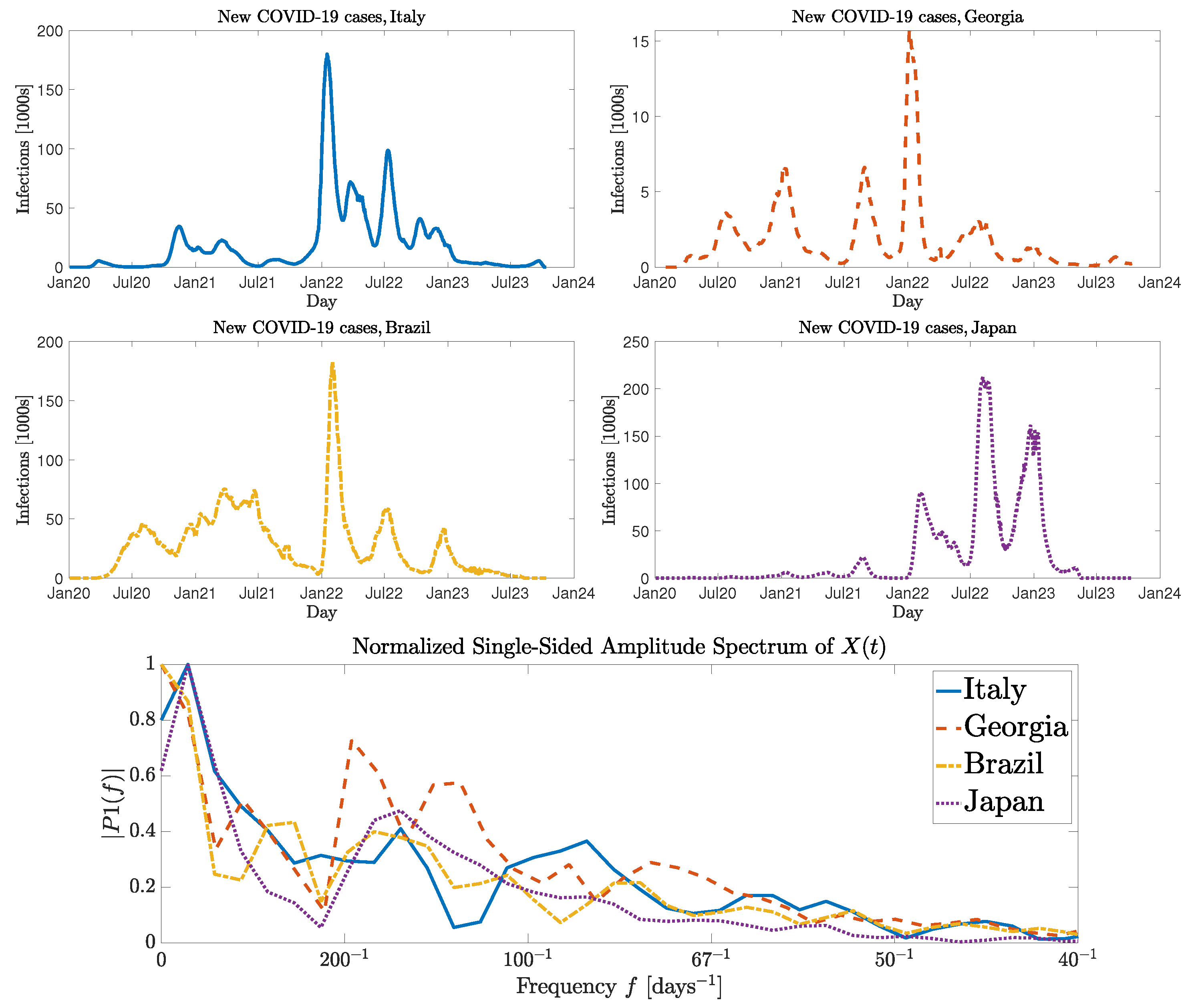
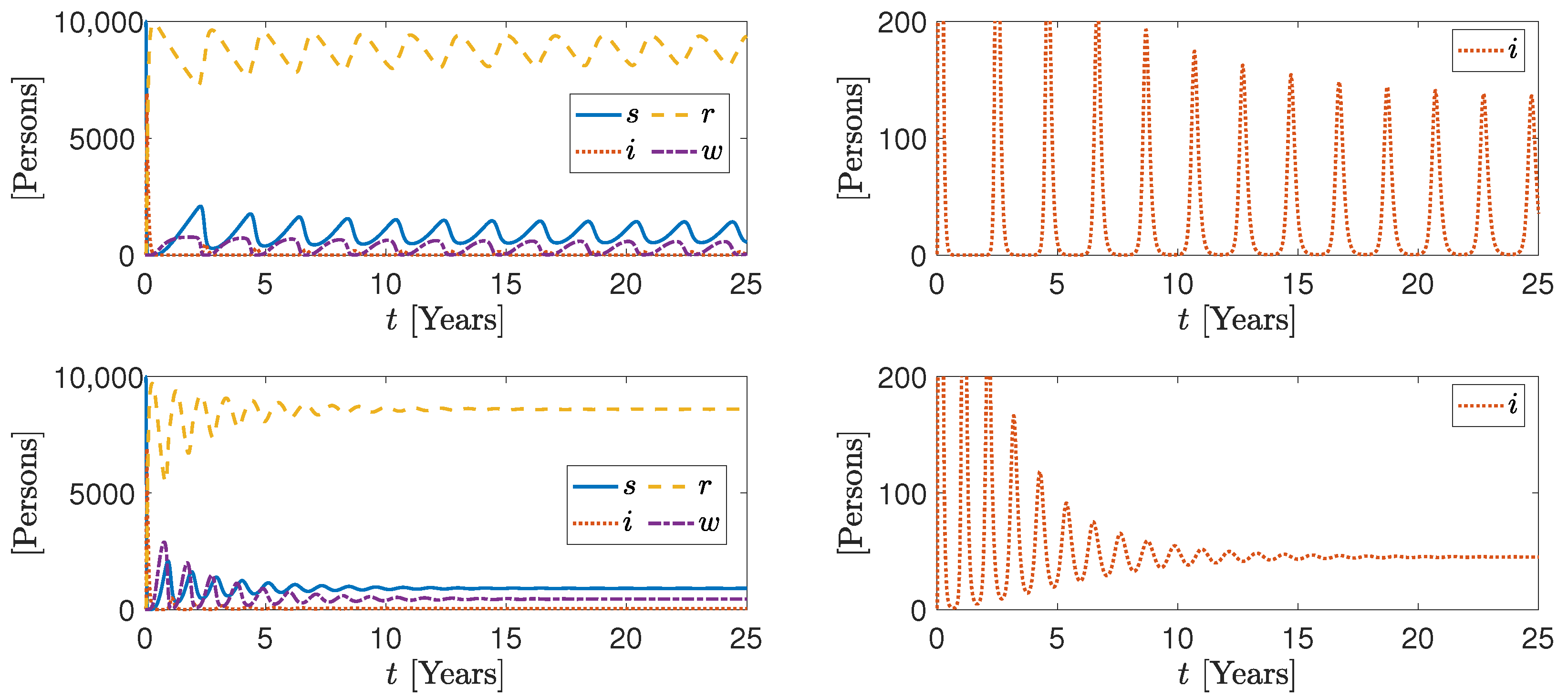
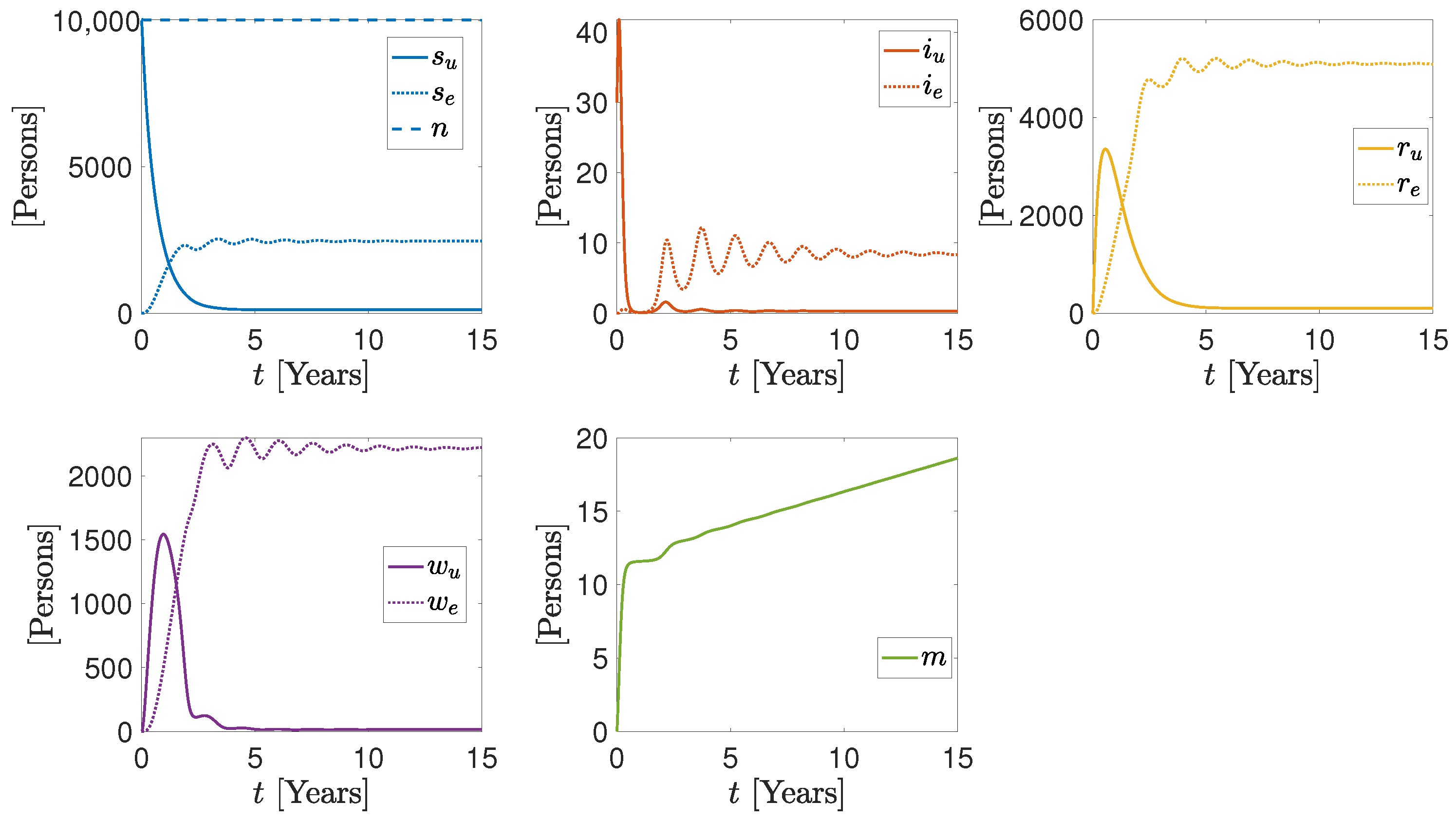
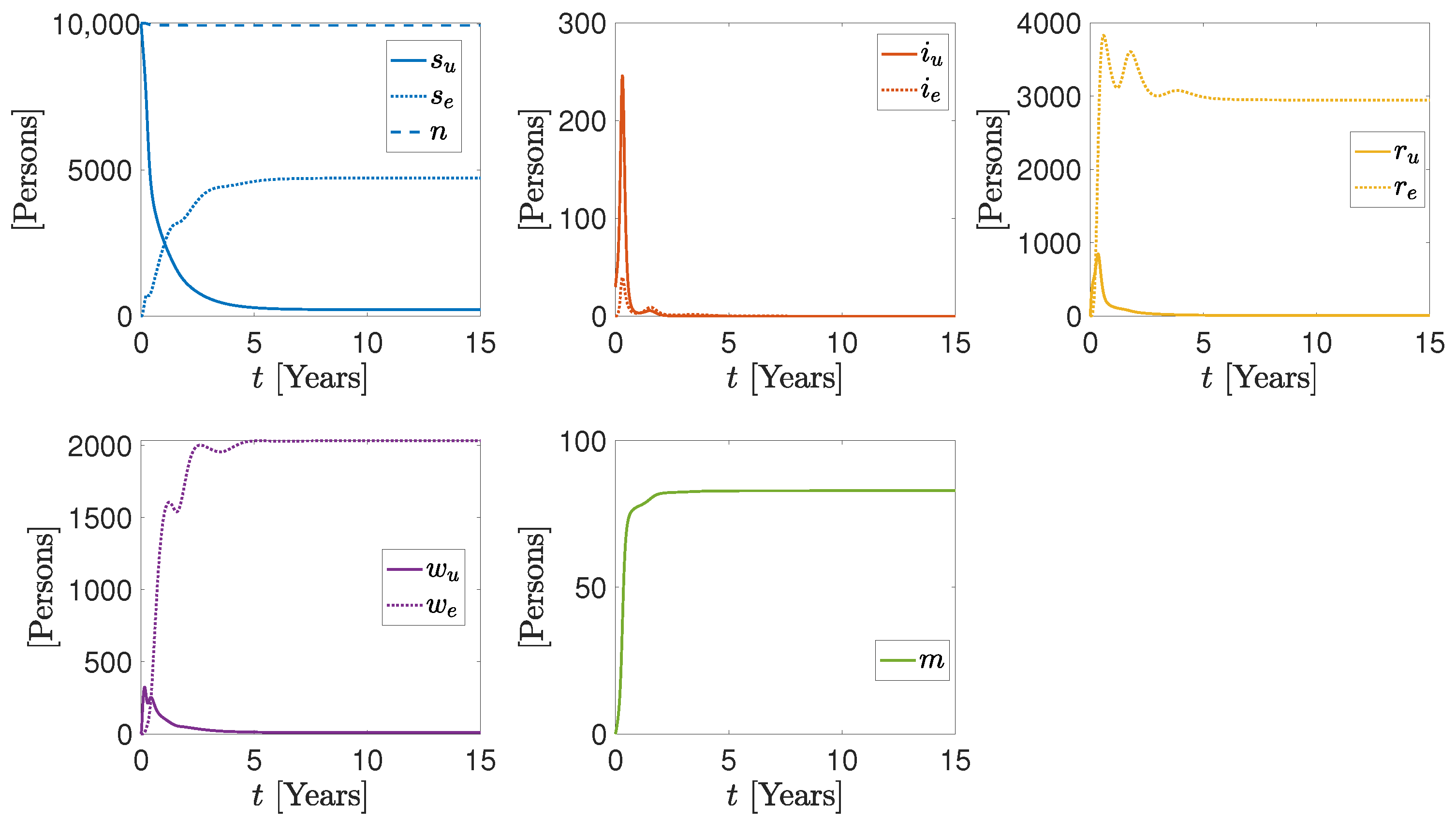
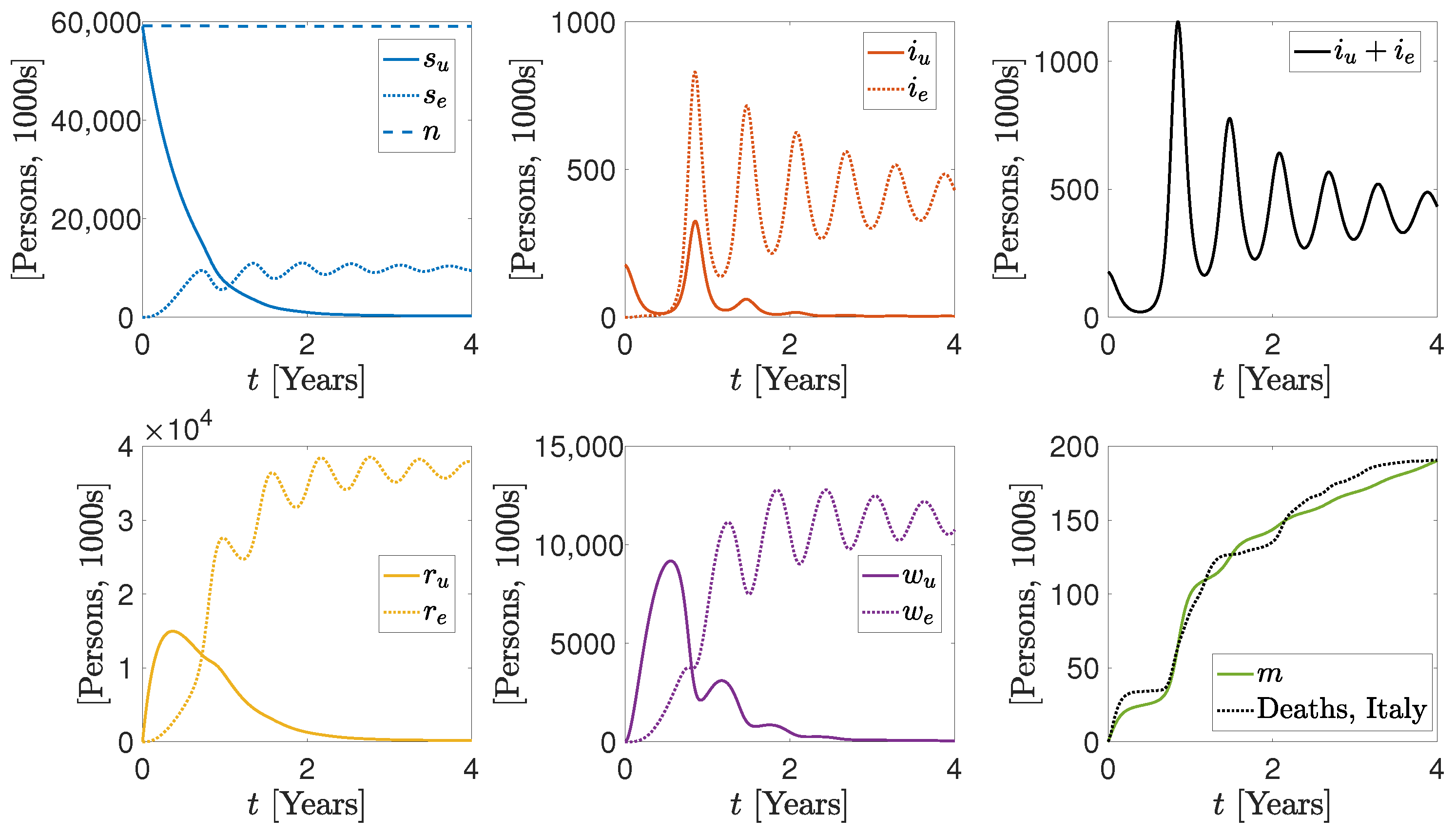
3. Numerical Results
More Realistic Cases
4. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Roser, M. Our World in Data. 2023. Available online: https://ourworldindata.org/coronavirus (accessed on 5 October 2023).
- Georgia Departent of Public Health. COVID19 Status Report. 2020. Available online: https://dph.georgia.gov/covid-19-status-report (accessed on 5 October 2023).
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar]
- Breda, D.; Diekmann, O.; De Graaf, W.; Pugliese, A.; Vermiglio, R. On the formulation of epidemic models (an appraisal of Kermack and McKendrick). J. Biol. Dyn. 2012, 6, 103–117. [Google Scholar] [CrossRef] [PubMed]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Viguerie, A.; Lorenzo, G.; Auricchio, F.; Baroli, D.; Hughes, T.J.; Patton, A.; Reali, A.; Yankeelov, T.E.; Veneziani, A. Simulating the spread of COVID-19 via a spatially-resolved susceptible–exposed–infected–recovered–deceased (SEIRD) model with heterogeneous diffusion. Appl. Math. Lett. 2021, 111, 106617. [Google Scholar] [CrossRef]
- Grave, M.; Viguerie, A.; Barros, G.F.; Reali, A.; Coutinho, A.L. Assessing the spatio-temporal spread of COVID-19 via compartmental models with diffusion in Italy, USA, and Brazil. Arch. Comput. Methods Eng. 2021, 28, 4205–4223. [Google Scholar] [CrossRef]
- Zhang, S.; Ponce, J.; Zhang, Z.; Lin, G.; Karniadakis, G. An integrated framework for building trustworthy data-driven epidemiological models: Application to the COVID-19 outbreak in New York City. PLoS Comput. Biol. 2021, 17, e1009334. [Google Scholar] [CrossRef] [PubMed]
- Parolini, N.; Dede’, L.; Antonietti, P.F.; Ardenghi, G.; Manzoni, A.; Miglio, E.; Pugliese, A.; Verani, M.; Quarteroni, A. SUIHTER: A new mathematical model for COVID-19. Application to the analysis of the second epidemic outbreak in Italy. Proc. R. Soc. A 2021, 477, 20210027. [Google Scholar] [CrossRef]
- Bhouri, M.A.; Costabal, F.S.; Wang, H.; Linka, K.; Peirlinck, M.; Kuhl, E.; Perdikaris, P. COVID-19 dynamics across the US: A deep learning study of human mobility and social behavior. Comput. Methods Appl. Mech. Eng. 2021, 382, 113891. [Google Scholar] [CrossRef]
- Jardón-Kojakhmetov, H.; Kuehn, C.; Pugliese, A.; Sensi, M. A geometric analysis of the SIS, SIRS and SIRWS epidemiological models. Nonlinear Anal. Real World Appl. 2021, 58, 103220. [Google Scholar] [CrossRef]
- Anggriani, N.; Ndii, M.Z.; Amelia, R.; Suryaningrat, W.; Pratama, M.A.A. A mathematical COVID-19 model considering asymptomatic and symptomatic classes with waning immunity. Alex. Eng. J. 2022, 61, 113–124. [Google Scholar] [CrossRef]
- Crellen, T.; Pi, L.; Davis, E.L.; Pollington, T.M.; Lucas, T.C.; Ayabina, D.; Borlase, A.; Toor, J.; Prem, K.; Medley, G.F.; et al. Dynamics of SARS-CoV-2 with waning immunity in the UK population. Philos. Trans. R. Soc. B 2021, 376, 20200274. [Google Scholar] [CrossRef] [PubMed]
- Altmann, D.M.; Boyton, R.J. Waning immunity to SARS-CoV-2: Implications for vaccine booster strategies. Lancet Respir. Med. 2021, 9, 1356–1358. [Google Scholar] [CrossRef] [PubMed]
- Dolgin, E. COVID vaccine immunity is waning-how much does that matter. Nature 2021, 597, 606–607. [Google Scholar] [CrossRef] [PubMed]
- Dafilis, M.P.; Frascoli, F.; Wood, J.G.; McCaw, J.M. The influence of increasing life expectancy on the dynamics of SIRS systems with immune boosting. ANZIAM J. 2012, 54, 50–63. [Google Scholar] [CrossRef]
- Lavine, J.S.; King, A.A.; Bjørnstad, O.N. Natural immune boosting in pertussis dynamics and the potential for long-term vaccine failure. Proc. Natl. Acad. Sci. USA 2011, 108, 7259–7264. [Google Scholar] [CrossRef]
- Wang, G.; Xiang, Z.; Wang, W.; Chen, Z. Seasonal coronaviruses and SARS-CoV-2: Effects of preexisting immunity during the COVID-19 pandemic. J. Zhejiang Univ.-Sci. B 2022, 23, 451–460. [Google Scholar] [CrossRef]
- Fillmore, N.R.; Szalat, R.E.; La, J.; Branch-Elliman, W.; Monach, P.A.; Nguyen, V.; Samur, M.K.; Brophy, M.T.; Do, N.V.; Munshi, N.C. Recent common human coronavirus infection protects against severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infection: A Veterans Affairs cohort study. Proc. Natl. Acad. Sci. USA 2022, 119, e2213783119. [Google Scholar] [CrossRef]
- Grifoni, A.; Weiskopf, D.; Ramirez, S.I.; Mateus, J.; Dan, J.M.; Moderbacher, C.R.; Rawlings, S.A.; Sutherland, A.; Premkumar, L.; Jadi, R.S.; et al. Targets of T cell responses to SARS-CoV-2 coronavirus in humans with COVID-19 disease and unexposed individuals. Cell 2020, 181, 1489–1501. [Google Scholar] [CrossRef]
- Edridge, A.W.; Kaczorowska, J.; Hoste, A.C.; Bakker, M.; Klein, M.; Loens, K.; Jebbink, M.F.; Matser, A.; Kinsella, C.M.; Rueda, P.; et al. Seasonal coronavirus protective immunity is short-lasting. Nat. Med. 2020, 26, 1691–1693. [Google Scholar] [CrossRef]
- van Boven, M.; de Melker, H.E.; Schellekens, J.F.; Kretzschmar, M. Waning immunity and sub-clinical infection in an epidemic model: Implications for pertussis in The Netherlands. Math. Biosci. 2000, 164, 161–182. [Google Scholar] [CrossRef]
- Laidlaw, B.J.; Ellebedy, A.H. The germinal centre B cell response to SARS-CoV-2. Nat. Rev. Immunol. 2022, 22, 7–18. [Google Scholar] [CrossRef] [PubMed]
- Paniskaki, K.; Anft, M.; Thieme, C.J.; Skrzypczyk, S.; Konik, M.J.; Dolff, S.; Westhoff, T.H.; Nienen, M.; Stittrich, A.; Stervbo, U.; et al. Severe acute respiratory syndrome coronavirus 2 cross-reactive b and T cell responses in kidney transplant patients. Transplant. Proc. 2022, 54, 1455–1464. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Chen, L.; Chen, J. Permanence and positive periodic solution for the single-species nonautonomous delay diffusive models. Comput. Math. Appl. 1996, 32, 109–116. [Google Scholar] [CrossRef]
- Li, H.; Guo, S. Dynamics of a SIRC epidemiological model. Electron. J. Differ. Equ. 2017, 121, 1–18. [Google Scholar]
- Roy, A.K.; Roy, P.K. Treatment of psoriasis by interleukin-10 through impulsive control strategy: A mathematical study. In Mathematical Modelling, Optimization, Analytic and Numerical Solutions; Springer: Berlin/Heidelberg, Germany, 2020; pp. 313–332. [Google Scholar]
- Roy, A.K.; Nelson, M.; Roy, P.K. A control-based mathematical study on psoriasis dynamics with special emphasis on IL-21 and IFN-γ interaction network. Math. Methods Appl. Sci. 2021, 44, 13403–13420. [Google Scholar] [CrossRef]
- Roy, A.K.; Al Basir, F.; Roy, P.K.; Chatterjee, A.N. A model analysis to measure the adherence of Etanercept and Fezakinumab therapy for the treatment of psoriasis. Nonlinear Anal. Model. Control 2022, 27, 513–533. [Google Scholar] [CrossRef]
- Birkhoff, G.; Rota, G. Ordinary Differential Equations; John Wiley& Sons: Hoboken, NJ, USA, 1978. [Google Scholar]
- Hartman, P. Ordinary Differential Equations; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- MATLAB, version R2019b; The MathWorks Inc.: Natick, MA, USA, 2019.


| Parameter/Variable | Name | Units | Periodic | Steady Equilibrium |
|---|---|---|---|---|
| s | Susceptible individuals | Persons | 9999 | 9999 |
| i | Infected individuals | Persons | 1 | 1 |
| r | Recovered individuals | Persons | 0 | 0 |
| w | Waning-immunity individuals | Persons | 0 | 0 |
| Contact rate between s and i | Persons Days | 5.5 × 10 | 5.5 × 10 | |
| Recovery rate | Days | 0.05 | 0.05 | |
| Loss-of-immunity initiation rate | Days | 5 × 10 | 0.005 | |
| Immunity boosting-contact rate | Persons Days | 2 × 10 | 2 × 10 | |
| Loss-of-immunity rate | Days | 0.005 | 0.005 |
| Parameter/Variable | Name | Units |
|---|---|---|
| Susceptible individuals (no prior immunity, prior immunity) | Persons | |
| Infected individuals (no prior immunity, prior immunity) | Persons | |
| Recovered individuals (no prior immunity, prior immunity) | Persons | |
| Waning-immunity individuals (no prior immunity, prior immunity) | Persons | |
| m | Deceased individuals | Persons |
| , | Contact rate between and , and . | Persons Days |
| Recovery rate for , | Days | |
| Loss-of-immunity initiation rate for , | Days | |
| , | Immunity boosting rates for , | Persons Days |
| Loss-of-immunity rate for , | Days | |
| Mortality rate from disease, for , | Days | |
| Vaccination rate | Days | |
| Recruitment rate | Persons · Days | |
| General mortality rate | Days |
| Parameter/Variable | Units | Sim1 | Sim2 | Sim3 |
|---|---|---|---|---|
| Persons | 9999, 0 | 9999, 0 | 9999, 0 | |
| Persons | 30, 0 | 30, 0 | 30, 0 | |
| Persons | 0, 0 | 0, 0 | 0, 0 | |
| Persons | 0, 0 | 0, 0 | 0, 0 | |
| m | Persons | 0 | 0 | 0 |
| Persons Days | 1.54 , 4 | 1.54 , 4 | 1.54 , 4 | |
| Persons Days | 5.5 , 5.5 | 5.5 , 5.5 | 5.5 , 5.5 | |
| Days | 0.13, 0.14 | 0.13, 0.14 | 0.13, 0.28 | |
| Days | 0.005, 0.005 | 0.005, 0.005 | 0.05, 0.005 | |
| Persons Days | 7.7 , 3.0 | 7.7 , 3.0 | 7.7 , 3.0 | |
| Persons Days | 2.8 , 2.8 | 2.8 , 2.8 | 2.8 , 2.8 | |
| Days | 0.005, 0.005 | 0.005, 0.005 | 0.05, 0.005 | |
| Days | 0.003, 4.4 | 0.003, 4.4 | 0.0, 0.0 | |
| Days | 0.002 | 0.004 | 0.0022 | |
| Days | 5 | 5 | 5 | |
| Days | 5 | 5 | 5 |
| Parameter/Variable | Units | Italy-Inspired Case | Brazil-Inspired Case |
|---|---|---|---|
| Persons | 59,000,000, 0 | 214,000,000, 0 | |
| Persons | 176,488, 0 | 400,488, 0 | |
| Persons | 0, 0 | 0, 0 | |
| Persons | 0, 0 | 0, 0 | |
| m | Persons | 0 | 0 |
| Persons Days | 1.9 , 3.4 | 1.9 , 3.4 | |
| Persons Days | 1.1 , 1.1 | 1.1 , 1.1 | |
| Days | 0.11, 0.11 | 0.11, 0.11 | |
| Days | 0.01, 0.01 | 0.01, 0.01 | |
| Persons Days | 1.3 , 5.1 | 1.3 , 5.1 | |
| Persons Days | 1.3 , 4.7 | 1.3 , 4.7 | |
| Days | 0.0083, 0.0083 | 0.0083, 0.0083 | |
| Days | 0.002, 0.0001 | 0.003, 0.00015 | |
| Days | 0.005 | 0.005 | |
| Days | 3 | 3 | |
| Days | 2.9 | 2.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viguerie, A.; Carletti, M.; Silvestri, G.; Veneziani, A. Mathematical Modeling of Periodic Outbreaks with Waning Immunity: A Possible Long-Term Description of COVID-19. Mathematics 2023, 11, 4918. https://doi.org/10.3390/math11244918
Viguerie A, Carletti M, Silvestri G, Veneziani A. Mathematical Modeling of Periodic Outbreaks with Waning Immunity: A Possible Long-Term Description of COVID-19. Mathematics. 2023; 11(24):4918. https://doi.org/10.3390/math11244918
Chicago/Turabian StyleViguerie, Alex, Margherita Carletti, Guido Silvestri, and Alessandro Veneziani. 2023. "Mathematical Modeling of Periodic Outbreaks with Waning Immunity: A Possible Long-Term Description of COVID-19" Mathematics 11, no. 24: 4918. https://doi.org/10.3390/math11244918





