Simultaneous Features of CC Heat Flux on Dusty Ternary Nanofluid (Graphene + Tungsten Oxide + Zirconium Oxide) through a Magnetic Field with Slippery Condition
Abstract
:1. Introduction
- What will be the influence of the magnetic parameter on fluid heat transfer rate, temperature, and velocity?
- What is the significance of the CC theory on the dusty ternary fluid model?
- What will be the impact of thermal radiation on heat transfer rate and temperature?
- What will be the influence of the velocity slip parameter on fluid velocity, temperature, and heat transfer rate?
2. Mathematical Formulation
- The dust particles are taken to be small enough and of sufficient number to be treated as a continuum and allow concepts such as density and velocity to have physical meaning.
- The dust particles are assumed to be spherical in shape, having the same radius and mass, and are undeformable.
- The Cartesian coordinate system is located in such a way that the -axis and -axis are taken along (and normal to) the surface, respectively, while the origin of the system is located at the leading edge.
- The dust particles are assumed to be uniform in size, and the density number of the dust particle is taken as constant throughout the flow.
3. Numerical Method
4. Results and Discussion
5. Conclusions
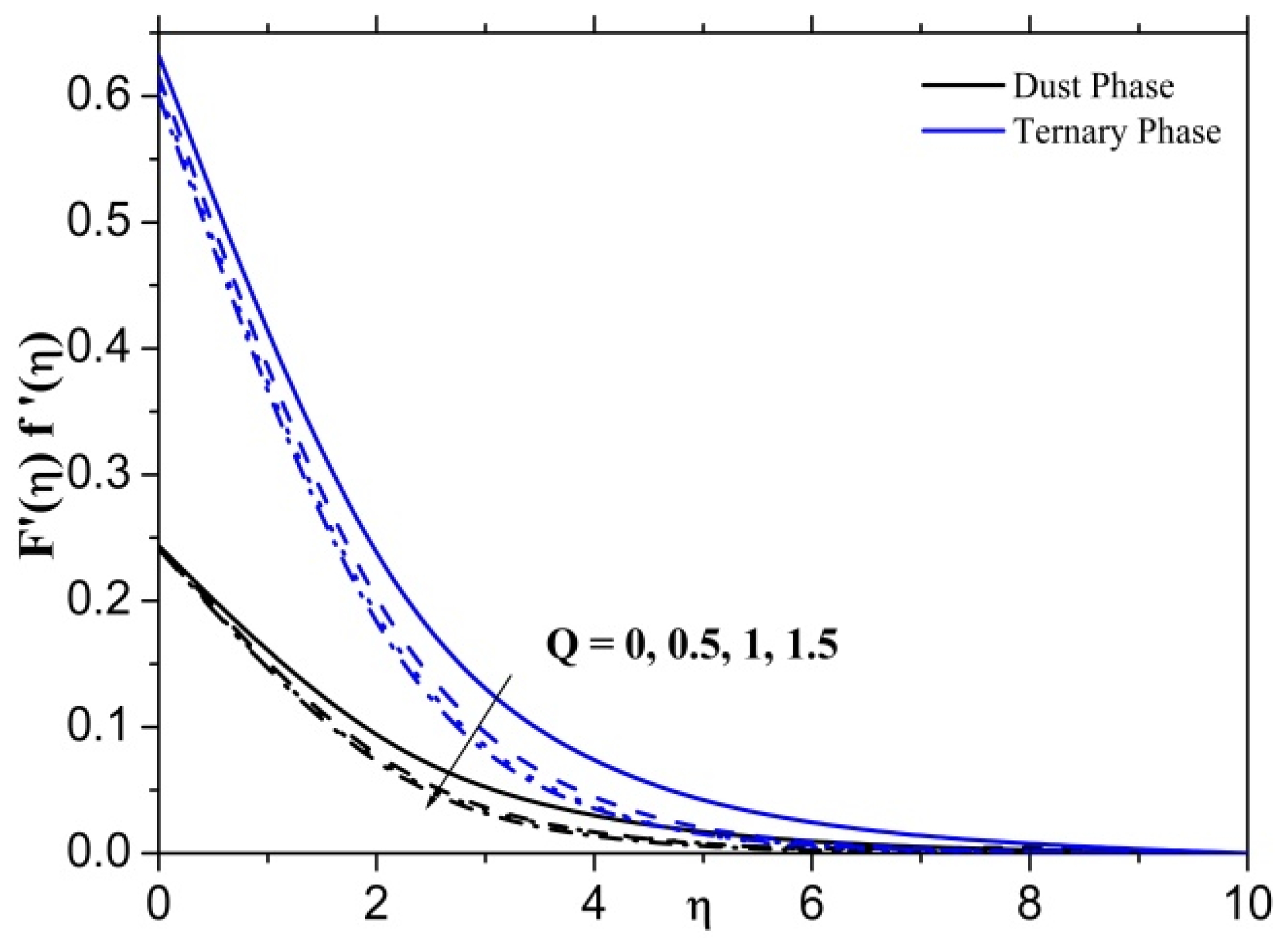
- The magnetic field depends essentially on Lorentz force, which is predominant for a larger magnetic field. Due to this, the velocity profiles decrease by further increasing the values of the magnetic parameter.
- The velocity profiles are decreasing by increasing the values of the slip parameter. However, once the slip velocity parameter is increased, the slide speed will also be decreased accordingly.
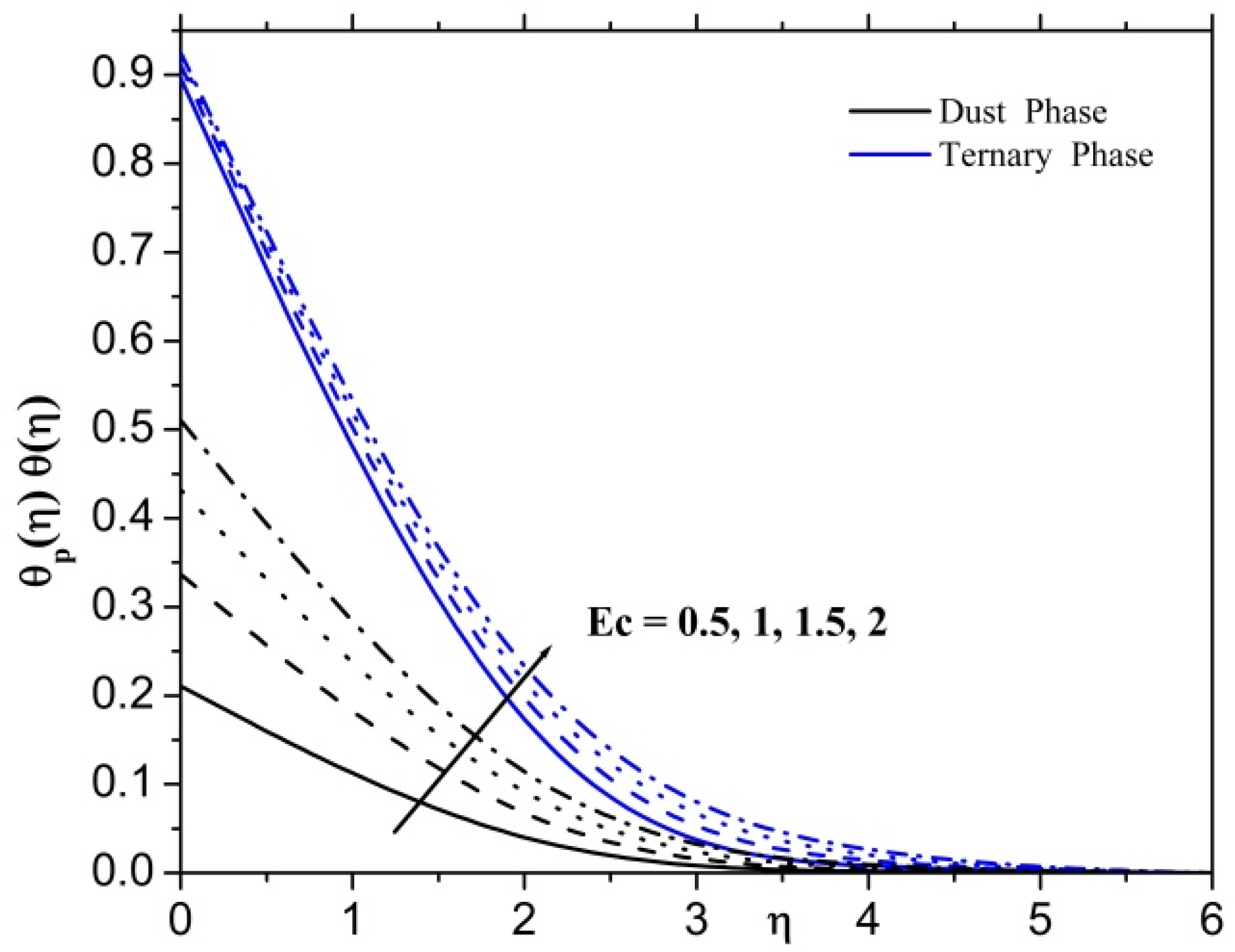
- The Eckert number is defined as the ratio between kinetic energy and the specific enthalpy difference between the wall and the fluid. Thus, increasing the Eckert number causes an increment in the temperature profile for both dusty and ternary phases.
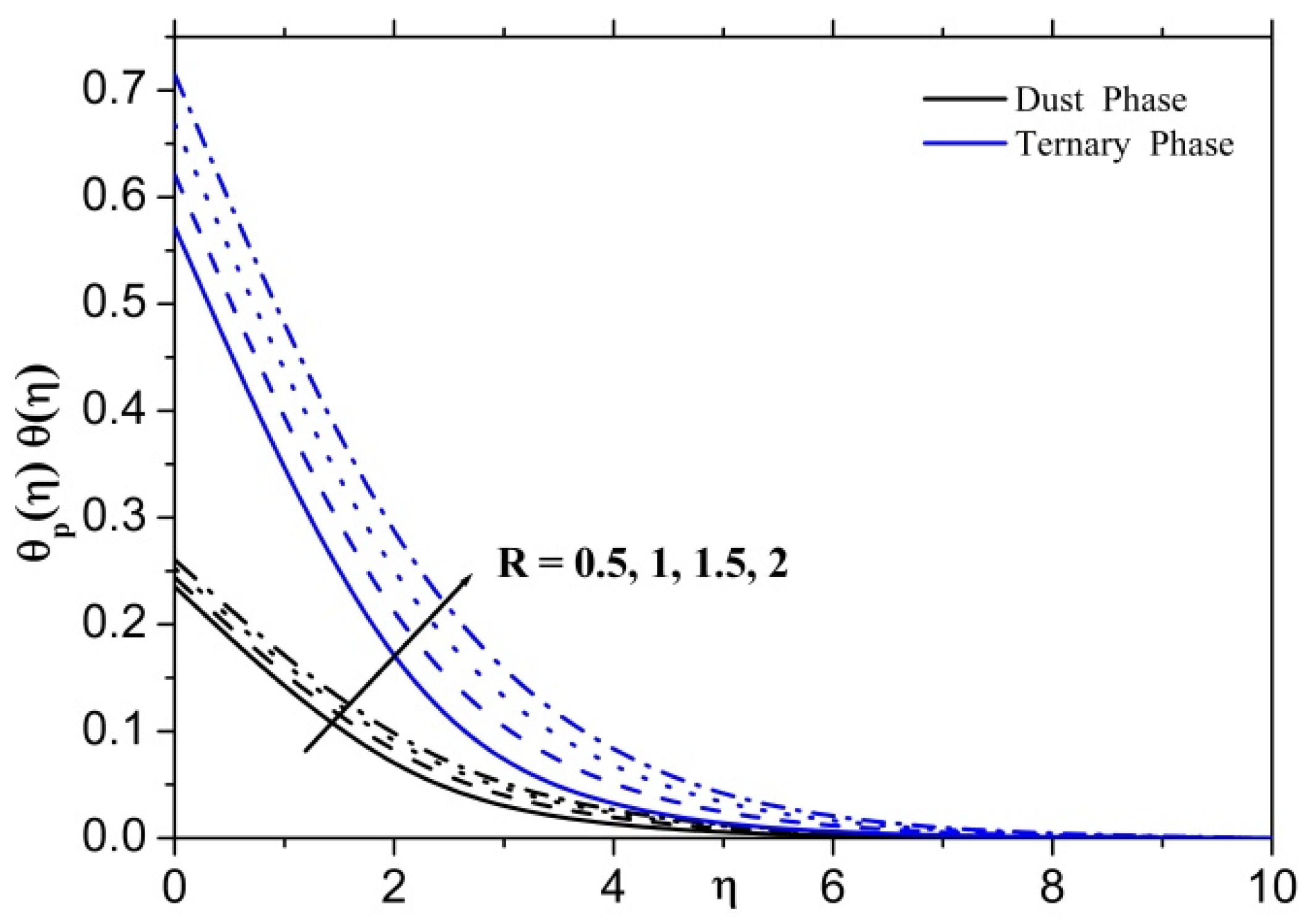
- The thermal radiation role is to boost heat transfer by enlarging the thermal radiation and thermal boundary layers for both dusty and ternary phases.
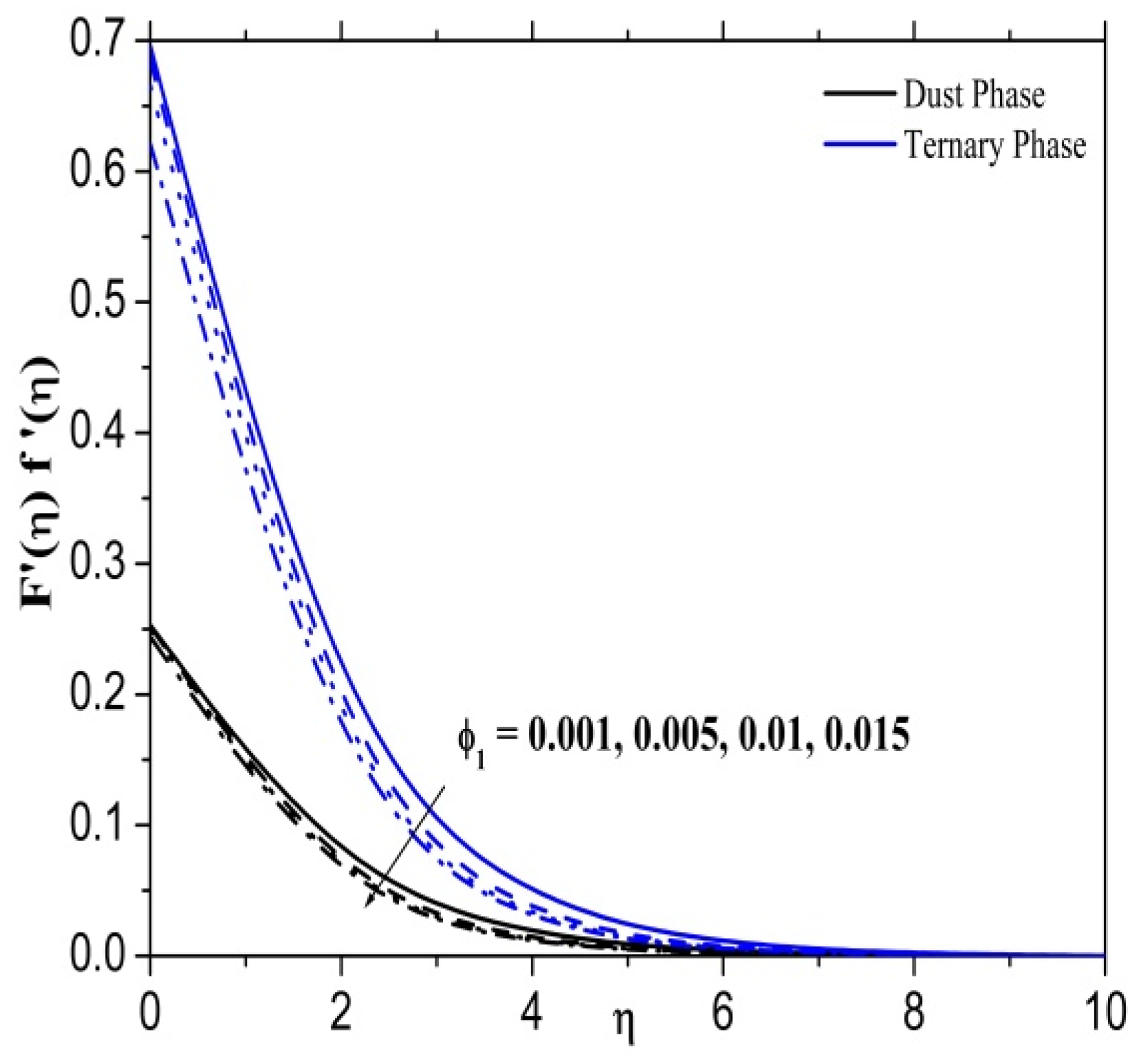
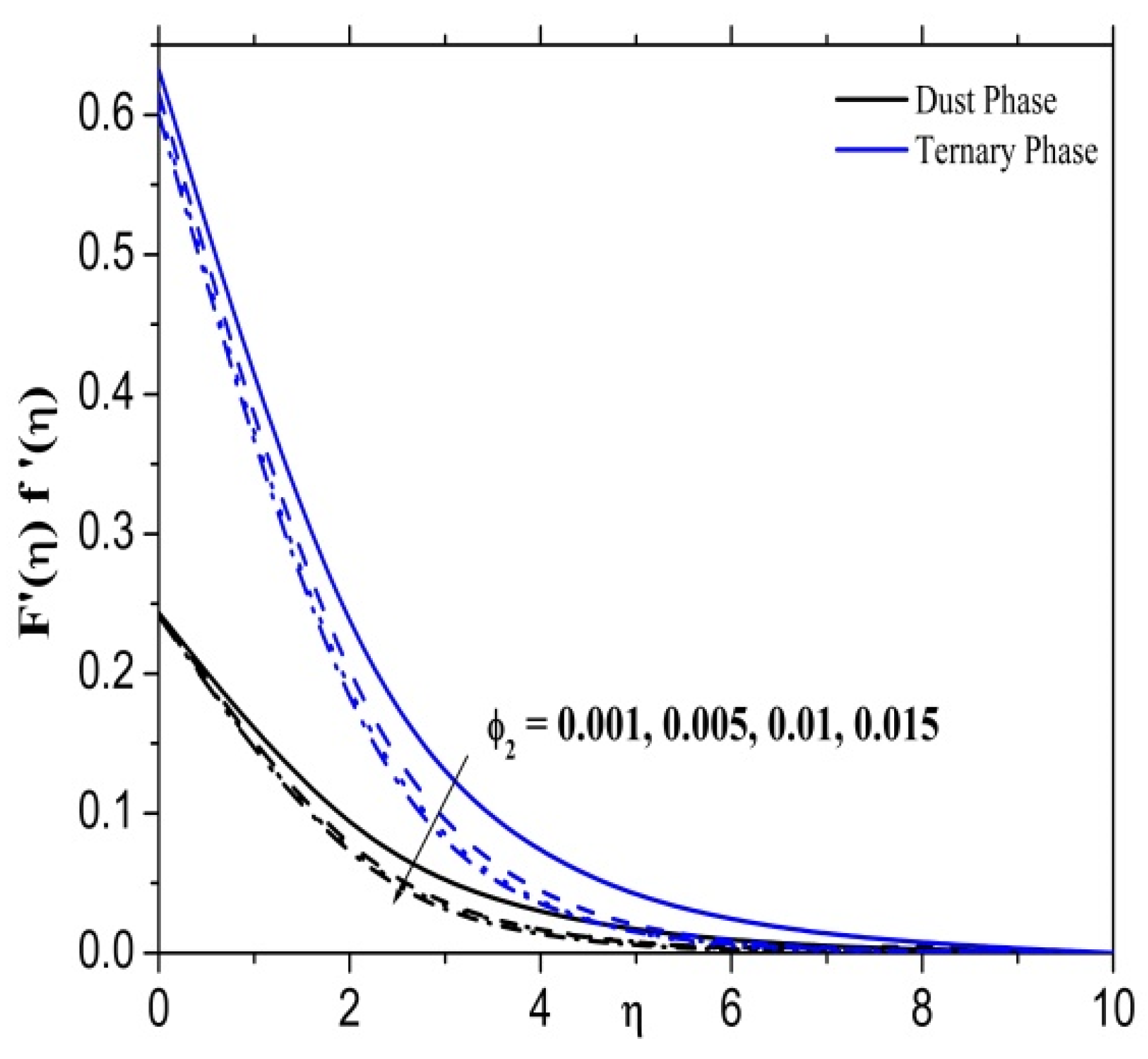
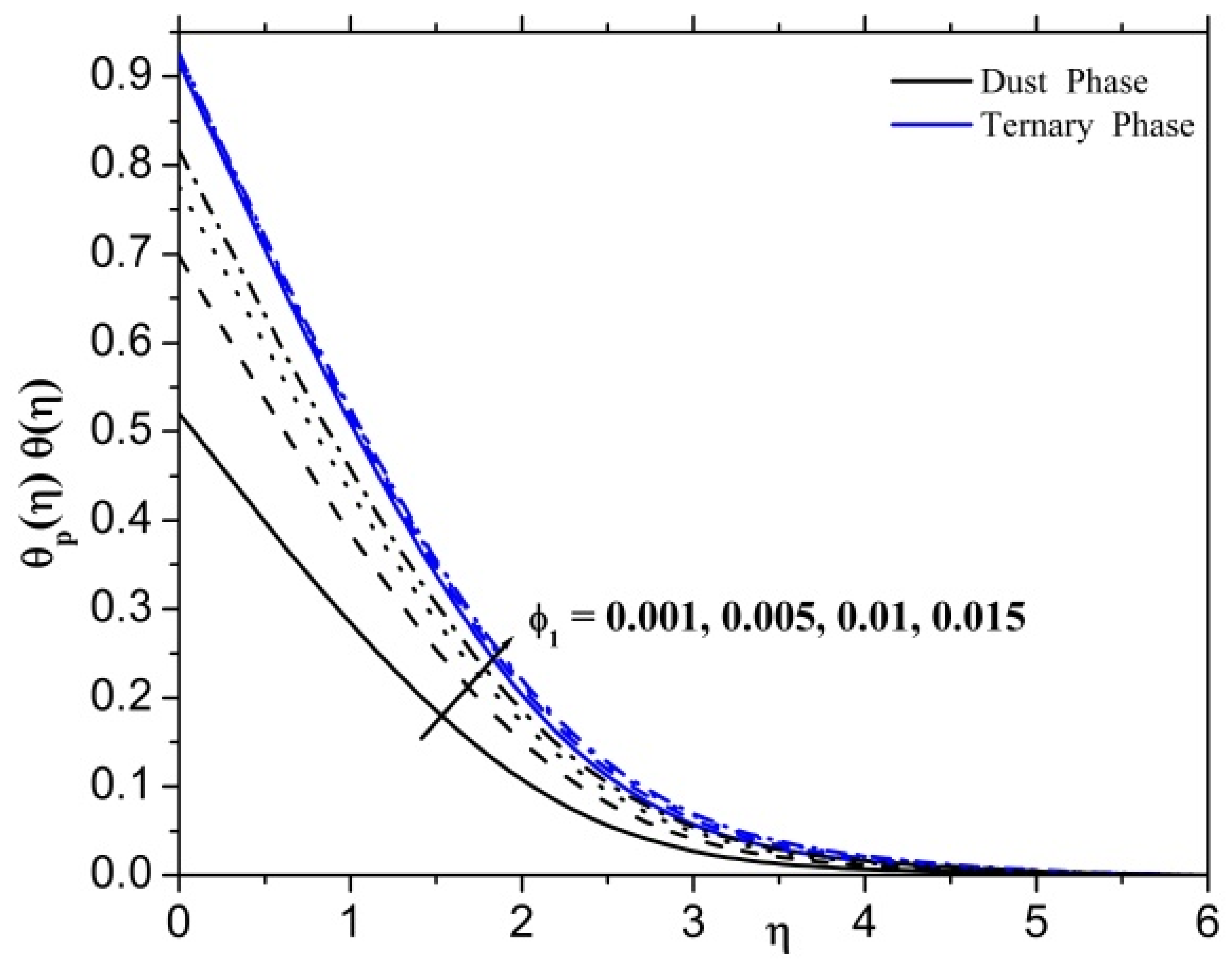
- The tiny nanoparticle effect may be deduced from the amount of heat generated by the accumulated energy. Due to this, temperature profiles are enhanced by increasing values of the nanoparticle volume friction parameter.
- An increment in the value of thermal relaxation generates a decrement in the temperature distribution.
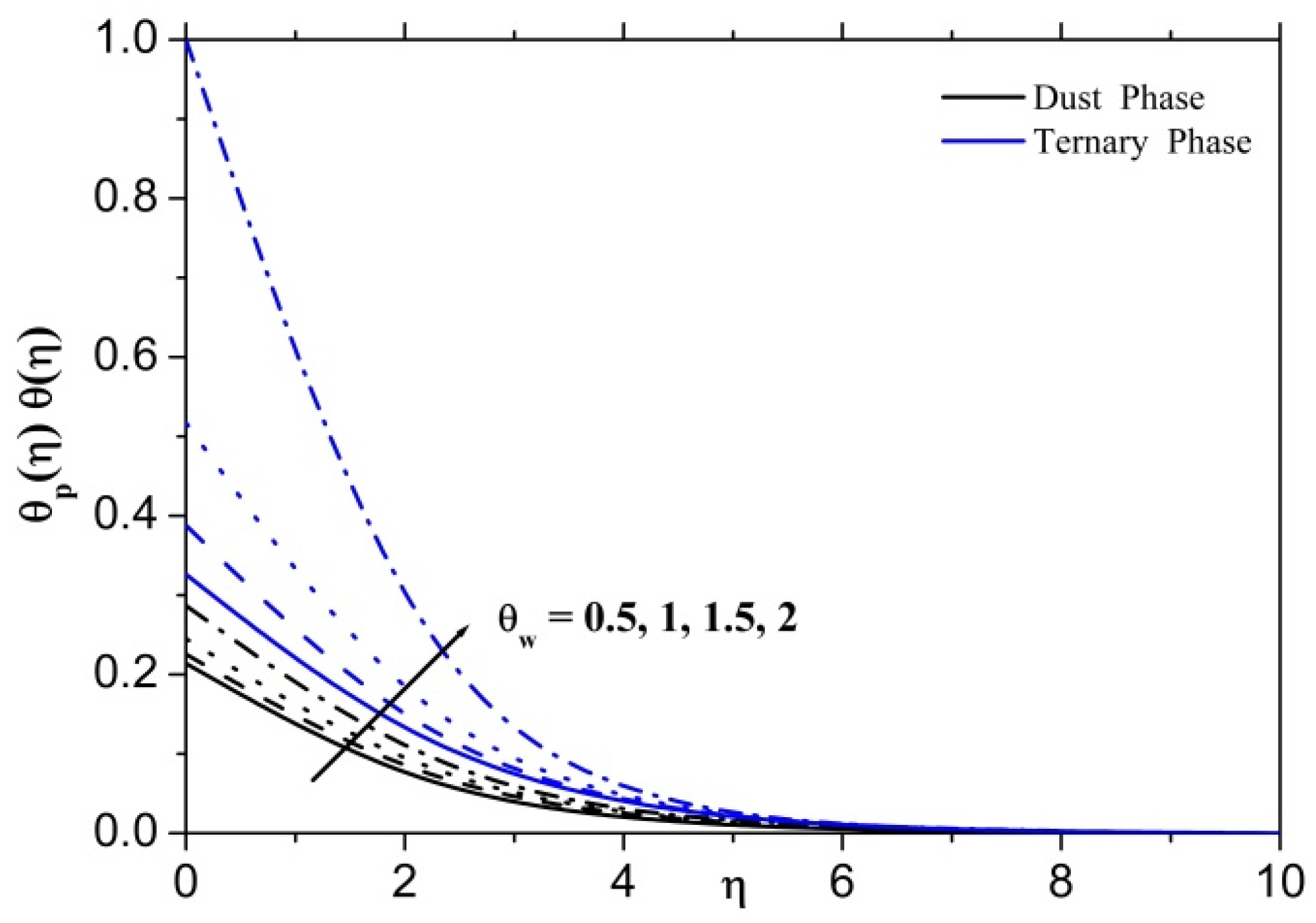
- Temperature profiles increase by increasing the values of the temperature ratio parameter.
- The performance of the dusty phase heat transfer has significantly enhanced compared to the performance of the ternary nanofluid phase.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Magnetic field | |
| Specific heat of fluid particle | |
| Specific heat of dust particle | |
| Friction factor | |
| Eckert number | |
| Stokes drag coefficient | |
| Thermal conductivity of the nano fluid | |
| Thermal conductivity of the fluid | |
| Mean absorption coefficient | |
| Mass concentration of particles | |
| Mass concentration of dust particles | |
| Magnetic parameter | |
| Number density of dust particle | |
| Nusselt number | |
| Prandtl number | |
| Radiative heat flux | |
| Radiation parameter | |
| Biot number | |
| Slip parameter | |
| Ambient fluid temperature | |
| Wall temperature | |
| Temperature of fluid and dust particle | |
| Greek letters | |
| Ratio of specific heat | |
| Fluid particle interaction parameter for velocity | |
| Fluid particle interaction parameter for temperature | |
| Thermal relaxation parameter | |
| Relaxation time of dust particle for temperature | |
| Relaxation time of dust particle for velocity | |
| Relaxation time for heat flux | |
| Electrical conductivity | |
| Volume fraction of nano particle | |
| Stefan Boltzmann constant | |
| Heat capacity of the fluid | |
| Heat capacity of the nanofluid | |
| Thermal conductivity of ternary hybrid fluid | |
| Thermal conductivity of fluid | |
References
- Choi, U.; Eastman, J. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the 1995 International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995. [Google Scholar]
- Buongiorno, J. Convective transport in nano fluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Reddy, M.; Rani, M.; Kumar, K.; Prasannakumar, B.; Lokesh, H. Hybrid dusty fluid flow through a Cattaneo–Christov heat flux model. Phys. A Stat. Mech. Its Appl. 2020, 551, 123975. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Liu, D.; Abid, M.; Imran, M.; Muhammad, T. Heat transfer analysis of hybrid nanofluid flow with thermal radiation through a stretching sheet: A comparative study. Int. Commun. Heat Mass Transf. 2022, 138, 106303. [Google Scholar] [CrossRef]
- Gürdal, M.; Pazarlıoğlu, H.K.; Tekir, M.; Arslan, K.; Gedik, E. Numerical investigation on turbulent flow and heat transfer characteristics of ferro-nanofluid flowing in dimpled tube under magnetic field effect. Appl. Therm. Eng. 2021, 200, 117655. [Google Scholar] [CrossRef]
- Ashrafi, H.; Pourmahmoud, N.; Mirzaee, I.; Ahmadi, N. Performance improvement of proton-exchange membrane fuel cells through different gas injection channel geometries. Int. J. Energy Res. 2022, 46, 8781–8792. [Google Scholar]
- Hussain, I.; Prakash, D.; Abdalla, B.; Muthtamilselvan, M. Analysis of Arrhenius activation energy and chemical reaction in nanofluid flow and heat transfer over a thin moving needle. Curr. Nanosci. 2023, 19, 39–48. [Google Scholar]
- Sadiq, M.N.; Sajid, M.; Abbas, T.; Mahmood, K.; Bashir, S.; Mahmood, W. Numerical Simulation for flow and heat transfer of a nanofluid over lubricated stretchable surface. J. Nanofluids 2023, 12, 506–513. [Google Scholar] [CrossRef]
- Prakasha, D.; Sudharani, M.; Kumar, K.G.; Chamkha, A.J. Comparative study of hybrid (graphene/magnesium oxide) and ternary hybrid (graphene/zirconium oxide/magnesium oxide) nanomaterials over a moving plate. Int. Commun. Heat Mass Transf. 2023, 140, 106557. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided liddriven differentially heated square cavity utilizing Nano fluids. Int. J. Heat Mass Transf. 2007, 52, 2002–2018. [Google Scholar]
- Khilili, S.; Dinarvand, S.; Hosseini, R.; Saber, M.; Pop, I. Magnetohydrodynamic stagnation-point flow towards stretching/shrinking permeable plate in porous medium filled with a nano fluid. J. Process Mech. Eng. 2014, 228, 309–319. [Google Scholar]
- Bakar, F.N.A.; Soid, S.K. MHD Stagnation-Point Flow and Heat Transfer Over an Exponentially Stretching/Shrinking Vertical Sheet in a Micropolar Fluid with a Buoyancy Effect. J. Adv. Res. Numer. Heat Transf. 2022, 8, 50–55. [Google Scholar]
- Ali, A.; Marwat, D.N.K.; Ali, A. Analysis of flow and heat transfer over stretching/shrinking and porous surfaces. J. Plast. Film. Sheeting 2022, 38, 21–45. [Google Scholar] [CrossRef]
- Azam, M.; Abbas, N.; Kumar, K.G.; Wali, S. Transient bioconvection and activation energy impacts on Casson nanofluid with gyrotactic microorganisms and nonlinear radiation. Waves Random Complex Media 2022, 1–20. [Google Scholar] [CrossRef]
- Reddy, M.G.; Krishnamurthy, M.R.; Praveena, M.M.; Naik, L.S.; Prakasha, D.G.; Kumar, K.G. Unsteady absorption flow and dissipation heat transfer over a non-Newtonian fluid. Waves Random Complex Media 2022, 1–15. [Google Scholar] [CrossRef]
- Reddy, M.G.; Sudharani, M.V.V.N.L.; Praveena, M.M.; Kumar, K.G. Effect of thermal conductivity on Blasius–Rayleigh–Stokes flow and heat transfer over a moving plate by considering magnetic dipole moment. Eur. Phys. J. Plus 2022, 137, 1–13. [Google Scholar]
- Gil, P. Flow and heat transfer characteristics of single and multiple synthetic jets impingement cooling. Int. J. Heat Mass Transf. 2023, 201, 123590. [Google Scholar] [CrossRef]
- Şahin, Y.S.; Toprak, B.I.; Solmaz, I.; Bayer, O. Investigation of flow and heat transfer behavior of integrated pin fin-aluminum foam heat sink. Appl. Therm. Eng. 2023, 219, 119504. [Google Scholar] [CrossRef]
- Bejawada, S.G.; Nandeppanavar, M.M. Effect of thermal radiation on magnetohydrodynamics heat transfer micropolar fluid flow over a vertical moving porous plate. Exp. Comput. Multiph. Flow 2023, 5, 149–158. [Google Scholar] [CrossRef]
- Gaur, P.K.; Jha, A.K. Heat Transfer for MHD Flow in an Inclined Channel with Heat Generation/Absorption. In Advances in Mathematical Modelling, Applied Analysis and Computation; Springer: Singapore, 2023; pp. 273–280. [Google Scholar]
- Aljaloud, A.S.M. Hybrid nanofluid mixed convection in a cavity under the impact of the magnetic field by lattice Boltzmann method: Effects of barrier temperature on heat transfer and entropy. Eng. Anal. Bound. Elem. 2023, 147, 276–291. [Google Scholar] [CrossRef]
- Yang, D.; Chen, L.; Feng, Y.; Chen, H. Comparisons of Supercritical Loop Flow and Heat Transfer Behavior Under Uniform and Nonuniform High-Flux Heat Inputs. Nucl. Sci. Eng. 2023, 197, 74–91. [Google Scholar] [CrossRef]
- Fourier, J. Théorie Analytique de Chaleur. chez Firmin Didot. Pere Et Fils; Editions Jacques Gabay: Paris, France, 1822. [Google Scholar]
- Cattaneo, C. Sulla conduzione del calore. Atti Sem. Mat. Fis. Univ. Modena 1948, 3, 83–101. [Google Scholar]
- Christov, C.I. On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Reddy, M.; Vijayakumari, P.; Kumar, K.; Shehzad, S. Zero-mass flux and Cattaneo–Christov heat flux through a Prandtl non-Newtonian nanofluid in Darcy–Forchheimer porous space. Heat Transf. 2021, 50, 220–233. [Google Scholar] [CrossRef]
- Machireddy, G.R.; Praveena, M.; Rudraswamy, N.G.; Kumar, G.K. Impact of Cattaneo–Christov heat flux on hydromagnetic flow of non-Newtonian fluids filled with Darcy–Forchheimer porous medium. Waves Random Complex Media 2021, 1–18. [Google Scholar] [CrossRef]
- Khan, S.A.; Hayat, T.; Alsaedi, A. Cattaneo Christov (CC) heat and mass fluxes in Stagnation point flow of Jeffrey nanoliquids by a stretched surface. Chin. J. Phys. 2022, 76, 205–216. [Google Scholar] [CrossRef]
- Tausif, S.M.; Das, K.; Kundu, P.K. Modified Homogeneous and Heterogeneous Chemical Reaction and Flow Performance of Maxwell Nanofluid with Cattaneo–Christov Heat Flux Law. J. Eng. Thermophys. 2022, 31, 64–77. [Google Scholar] [CrossRef]
- Hayat, T.; Fatima, A.; Muhammad, K.; Alsaedi, A. Heat transfer and entropy analysis in squeezing flow of hybrid nanofluid (Au-CuO/NaAlg) with DF (Darcy-Forchheimer) and CC (Cattaneo-Christov) heat flux. Mater. Sci. Eng. B 2023, 288, 116150. [Google Scholar] [CrossRef]
- Ullah, H.; Ullah, K.; Raja, M.A.Z.; Shoaib, M.; Nisar, K.S.; Islam, S.; Weera, W.; Al-Harbi, N. Numerical treatment of squeezed MHD Jeffrey fluid flow with Cattaneo Chrisstov heat flux in a rotating frame using Levnberg-Marquard method. Alex. Eng. J. 2023, 66, 1031–1050. [Google Scholar] [CrossRef]
- Shahzad, A.; Imran, M.; Tahir, M.; Khan, S.; Akgül; Abdullaev, S.; Yahia, I.S. Brownian motion and thermophoretic diffusion impact on Darcy-Forchheimer flow of bioconvective micropolar nanofluid between double disks with Cattaneo-Christov heat flux. Alex. Eng. J. 2023, 62, 1–15. [Google Scholar] [CrossRef]
- Muhammad, K.; Hayat, T.; Alsaedi, A.; Momani, S. Mixed convective slip flow of hybrid nanofluid (MWCNTs + Cu + Water), nanofluid (MWCNTs + Water) and base fluid (Water): A comparative investigation. J. Therm. Anal. Calorim. 2021, 143, 1523–1536. [Google Scholar] [CrossRef]
- Ghadikolaei, S.S.; Hosseinzadeh, K.; Hatami, M.; Ganji, D.D. MHD boundary layer analysis for micropolar dusty fluid containing Hybrid nanoparticles (Cu’Al2O3) over a porous medium. J. Mol. Liq. 2018, 268, 813–823. [Google Scholar] [CrossRef]
- Hosseinzadeh, K.; Alizadeh, M.; Ganji, D.D. Hydrothermal analysis on MHD squeezing nanofluid flow in parallel plates by analytical method. Int. J. Mech. Mater. Eng. 2018, 13, 4. [Google Scholar] [CrossRef] [Green Version]






| Thermophysical Properties | Base Fluid | Ternary Nanofluid | ||
|---|---|---|---|---|
| Graphene | Zirconium Oxide | Tungsten OXIDE | ||
| ) | 997.1 | 2200 | 5680 | |
| 4179 | 5000 | 502 | ||
| 0.613 | 790 | 1.7 | ||
| Ghadikolaei et al. [34] | Hosseinzadeh et al. [35] | Reddy et al. [3] | Present Results | |
|---|---|---|---|---|
| 0.7 | 0.4538 | 0.4541 | 0.4539 | 0.45415 |
| 2.0 | 0.9113 | 0.9114 | 0.9113 | 0.91133 |
| 7.0 | 1.8954 | 1.8954 | 1.8954 | 1.89545 |
| Friction Factor | ||||||
|---|---|---|---|---|---|---|
| Dusty Phase | Ternary Phase | |||||
| 0.5 | 0.785239 | 1.511657 | ||||
| 1.0 | 0.613042 | 1.447579 | ||||
| 1.5 | 0.508094 | 1.406297 | ||||
| 0.5 | 0.620207 | 1.470950 | ||||
| 1.0 | 0.541187 | 1.464362 | ||||
| 1.5 | 0.446056 | 1.453310 | ||||
| 0.005 | 0.740501 | 1.477960 | ||||
| 0.001 | 0.688252 | 1.475486 | ||||
| 0.015 | 0.640870 | 1.472762 | ||||
| 0.005 | 0.967495 | 1.480191 | ||||
| 0.001 | 0.828302 | 1.475561 | ||||
| 0.015 | 0.549498 | 1.460959 | ||||
| 0.005 | 0.740501 | 1.477961 | ||||
| 0.001 | 0.688252 | 1.475486 | ||||
| 0.015 | 0.549498 | 1.460959 | ||||
| Nusselt Number | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Dust Phase | Ternary Phase | |||||||||
| 0.5 | 1.44697 | 1.56233 | ||||||||
| 1.0 | 1.46193 | 2.69770 | ||||||||
| 1.5 | 1.48274 | 3.51973 | ||||||||
| 0.1 | 1.50243 | 1.94796 | ||||||||
| 0.3 | 1.43731 | 1.93508 | ||||||||
| 0.5 | 1.39414 | 1.92532 | ||||||||
| 0.1 | 1.51166 | 2.23259 | ||||||||
| 0.2 | 1.44758 | 1.74300 | ||||||||
| 0.3 | 1.40634 | 1.44461 | ||||||||
| 0.1 | 1.57142 | 1.97687 | ||||||||
| 0.2 | 1.84996 | 2.01510 | ||||||||
| 0.3 | 2.08391 | 2.01747 | ||||||||
| 0.5 | 1.45866 | 1.91198 | ||||||||
| 1.0 | 1.53613 | 1.88219 | ||||||||
| 1.5 | 1.57934 | 1.86686 | ||||||||
| 0.8 | 1.28682 | 1.48919 | ||||||||
| 1.2 | 1.32862 | 1.64629 | ||||||||
| 1.4 | 1.36865 | 1.79380 | ||||||||
| 0.005 | 1.06239 | 1.88550 | ||||||||
| 0.001 | 1.16455 | 1.89615 | ||||||||
| 0.015 | 1.27872 | 1.91104 | ||||||||
| 0.005 | 1.39414 | 1.92532 | ||||||||
| 0.001 | 1.43731 | 1.93508 | ||||||||
| 0.015 | 1.51166 | 2.23259 | ||||||||
| 0.005 | 1.17455 | 1.87615 | ||||||||
| 0.001 | 1.22872 | 1.89104 | ||||||||
| 0.015 | 1.30414 | 1.92532 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souayeh, B. Simultaneous Features of CC Heat Flux on Dusty Ternary Nanofluid (Graphene + Tungsten Oxide + Zirconium Oxide) through a Magnetic Field with Slippery Condition. Mathematics 2023, 11, 554. https://doi.org/10.3390/math11030554
Souayeh B. Simultaneous Features of CC Heat Flux on Dusty Ternary Nanofluid (Graphene + Tungsten Oxide + Zirconium Oxide) through a Magnetic Field with Slippery Condition. Mathematics. 2023; 11(3):554. https://doi.org/10.3390/math11030554
Chicago/Turabian StyleSouayeh, Basma. 2023. "Simultaneous Features of CC Heat Flux on Dusty Ternary Nanofluid (Graphene + Tungsten Oxide + Zirconium Oxide) through a Magnetic Field with Slippery Condition" Mathematics 11, no. 3: 554. https://doi.org/10.3390/math11030554






