Effective Incomplete Multi-View Clustering via Low-Rank Graph Tensor Completion
Abstract
1. Introduction
- By revealing the low-rank relationship within each graph and between all graphs, it is expected to restore the hidden connections between missing and available instances.
- We propose exploring the low-rank relationship of within and between views simultaneously by imposing the matrix nuclear norm regularization on each mode matrization of the third-order graph tensor that is stacked by all similarity graphs.
- The graph completion and consensus representation learning were developed to optimize jointly in a unified framework, with the goal of obtaining complete graphs for clustering. Extensive experimental results show that the proposed method outperforms other state-of-the-art IMC methods.
2. Preliminaries
2.1. Notations
2.2. Multi-View Spectral Clustering
3. The Proposed Method
3.1. Learning Model of the Proposed Method
3.2. Solution to IMC-LGC
| Algorithm 1 Incomplete multi-view clustering via low-rank graph tensor completion (IMC-LGC). |
| Require: Multi-view data , parameters . |
| Initialization: Construct the similarity graph from observable instances of each view , and then fill it into by letting its element related to the missing instances be 0. Initialize by solving (24). |
| 1: while Not converged do |
| 2: Update variable by Equation (18). |
| 3: Update by Equations (21) and (23). |
| 4: Update by solving (24). |
| 5: Update by Equation (25). |
| 6: end while |
| 7: Return . |
3.3. Computational Complexity Analysis
4. Experiments
4.1. Dataset Description and Incomplete Multi-View Data Construction
4.2. Compared Methods and Evaluation Metric
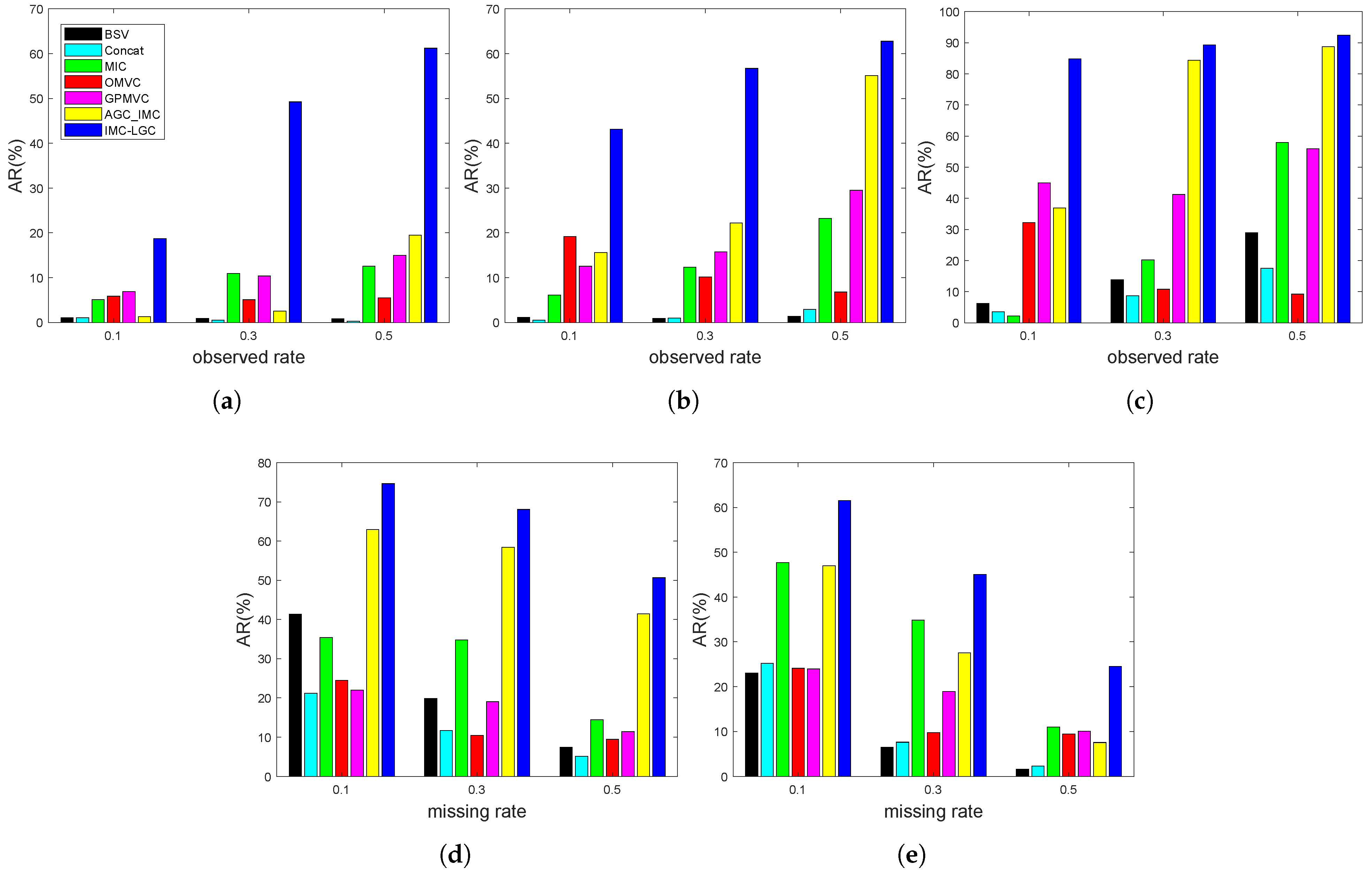
4.3. Experiment Results and Analysis
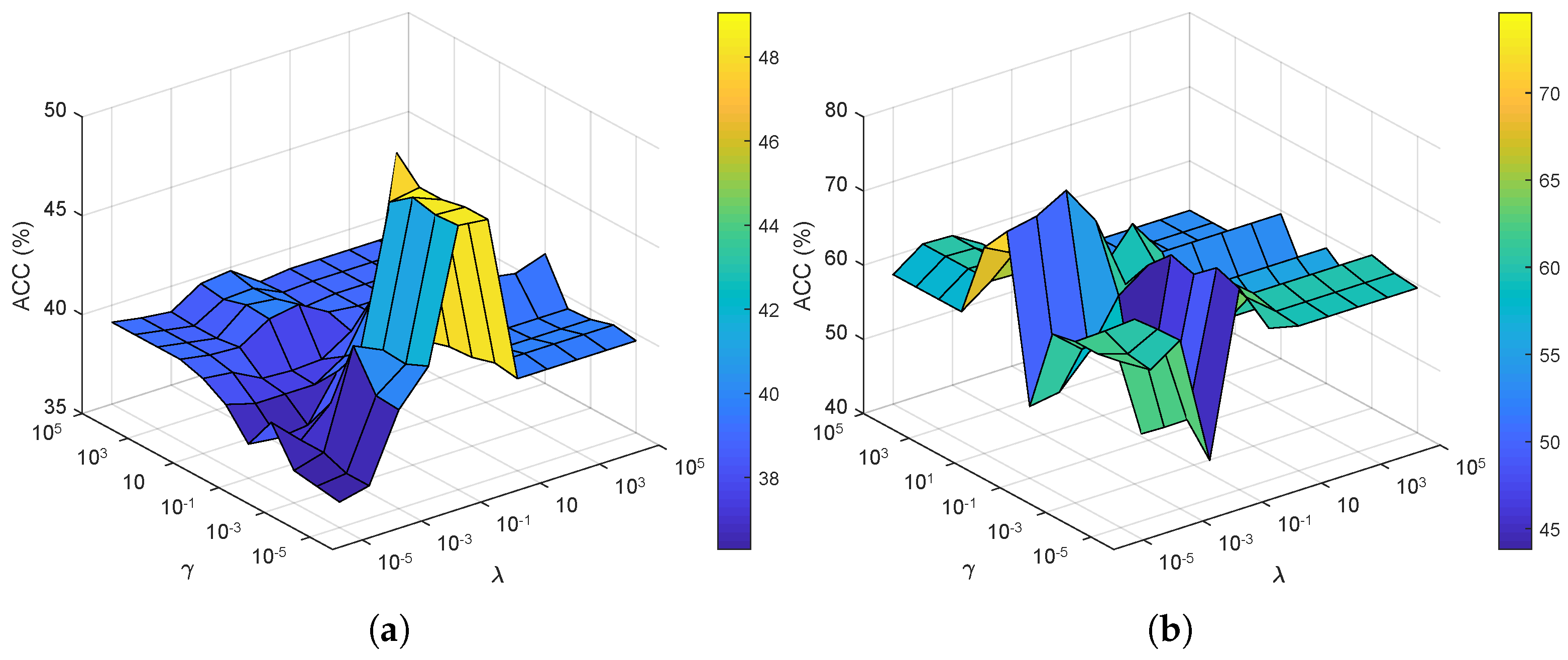
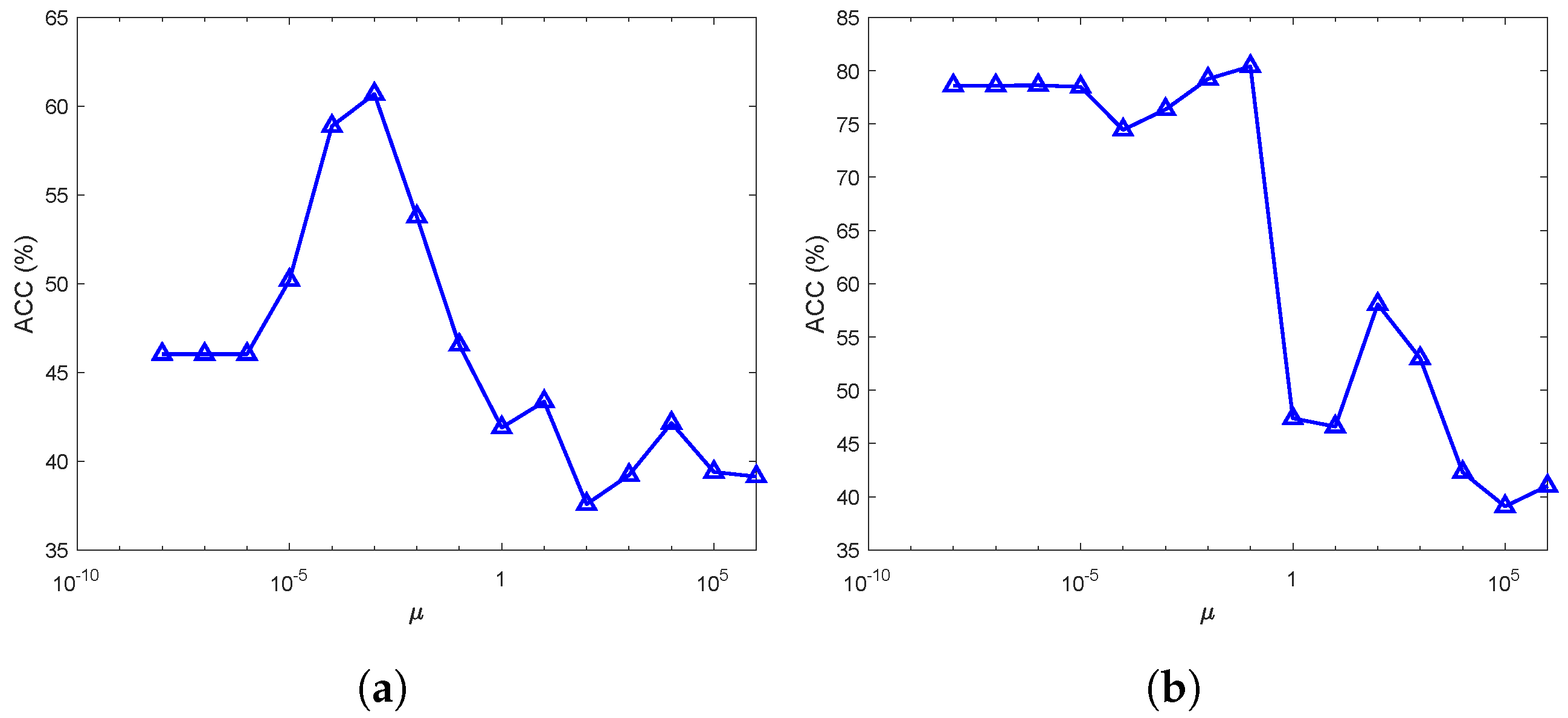
4.4. Sensitivity Analysis of the Penalty Parameters
4.4.1. Parameters and
4.4.2. Parameters
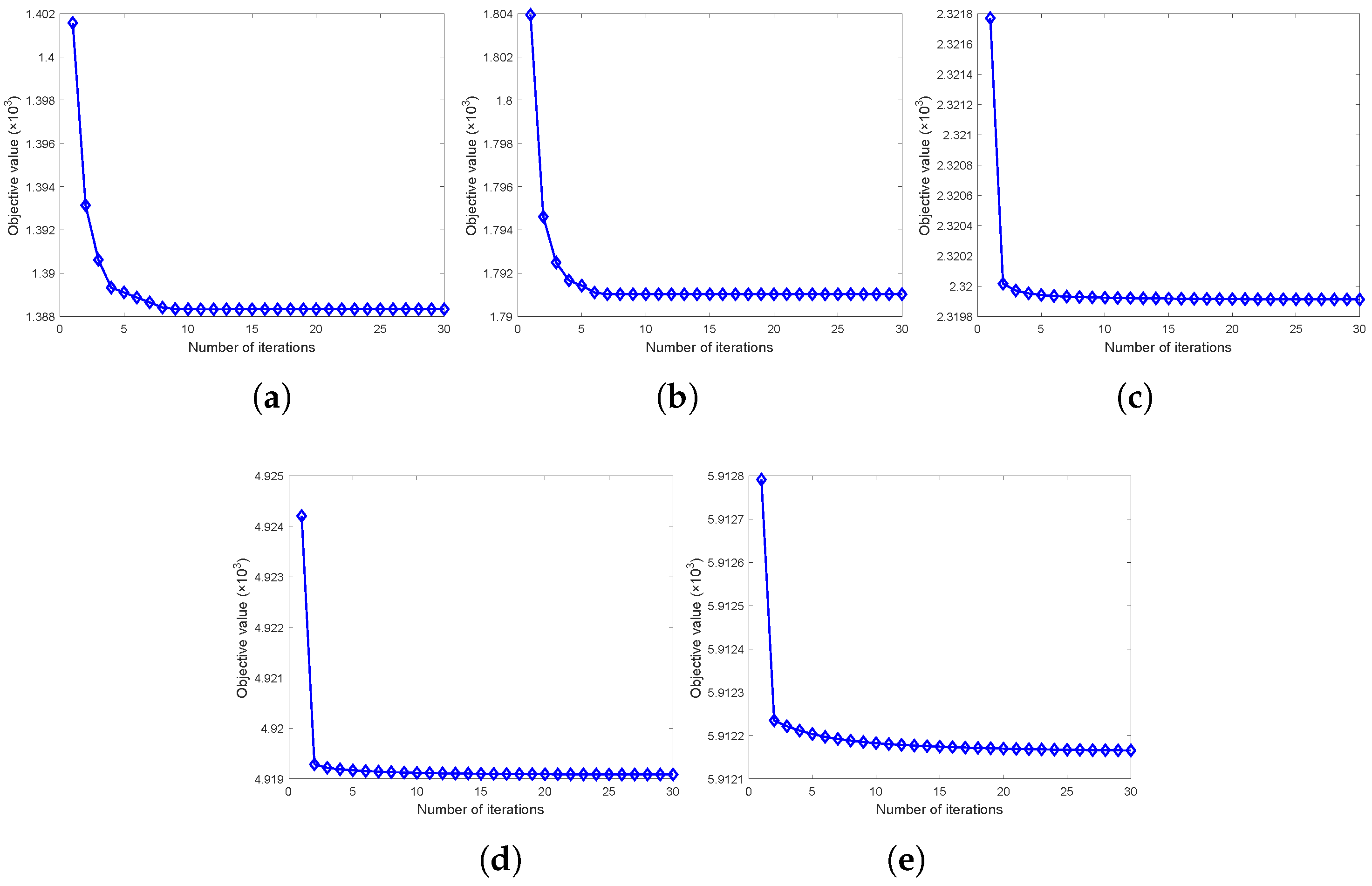
4.5. Convergence Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mari nas-Collado, I.; Sipols, A.E.; Santos-Martín, M.T.; Frutos-Bernal, E. Clustering and Forecasting Urban Bus Passenger Demand with a Combination of Time Series Models. Mathematics 2022, 10, 2670. [Google Scholar] [CrossRef]
- Lukauskas, M.; Ruzgas, T. A New Clustering Method Based on the Inversion Formula. Mathematics 2022, 10, 2559. [Google Scholar] [CrossRef]
- Sarfraz, S.; Sharma, V.; Stiefelhagen, R. Efficient parameter-free clustering using first neighbor relations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8934–8943. [Google Scholar]
- Wu, B.; Hu, B.G.; Ji, Q. A coupled hidden markov random field model for simultaneous face clustering and tracking in videos. Pattern Recognit. 2017, 64, 361–373. [Google Scholar] [CrossRef]
- Bazzica, A.; Liem, C.C.; Hanjalic, A. Exploiting scene maps and spatial relationships in quasi-static scenes for video face clustering. Image Vis. Comput. 2017, 57, 25–43. [Google Scholar] [CrossRef]
- Foggia, P.; Percannella, G.; Sansone, C.; Vento, M. Benchmarking graph-based clustering algorithms. Image Vis. Comput. 2009, 27, 979–988. [Google Scholar] [CrossRef]
- Zhao, P.; Wu, H.; Huang, S. Multi-View Graph Clustering by Adaptive Manifold Learning. Mathematics 2022, 10, 1821. [Google Scholar] [CrossRef]
- Prakoonwit, S.; Benjamin, R. 3D surface point and wireframe reconstruction from multiview photographic images. Image Vis. Comput. 2007, 25, 1509–1518. [Google Scholar] [CrossRef]
- Yin, H.; Hu, W.; Zhang, Z.; Lou, J.; Miao, M. Incremental multi-view spectral clustering with sparse and connected graph learning. Neural Netw. 2021, 144, 260–270. [Google Scholar] [CrossRef]
- Nie, F.; Li, J.; Li, X. Self-weighted Multiview Clustering with Multiple Graphs. In Proceedings of the IJCAI, Melbourne, Australia, 19–25 August 2017; pp. 2564–2570. [Google Scholar]
- Zhao, N.; Bu, J. Robust multi-view subspace clustering based on consensus representation and orthogonal diversity. Neural Netw. 2022, 150, 102–111. [Google Scholar] [CrossRef]
- Bickel, S.; Scheffer, T. Multi-view clustering. In Proceedings of the ICDM, Leipzig, Germany, 4–7 July 2004; Volume 4, pp. 19–26. [Google Scholar]
- Cai, X.; Nie, F.; Huang, H. Multi-view k-means clustering on big data. In Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013. [Google Scholar]
- Chaudhuri, K.; Kakade, S.M.; Livescu, K.; Sridharan, K. Multi-view clustering via canonical correlation analysis. In Proceedings of the 26th Annual International Conference On machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 129–136. [Google Scholar]
- Kumar, A.; Rai, P.; Daume, H. Co-regularized multi-view spectral clustering. Adv. Neural Inf. Process. Syst. 2011, 24, 1413–1421. [Google Scholar]
- Liu, J.; Wang, C.; Gao, J.; Han, J. Multi-view clustering via joint nonnegative matrix factorization. In Proceedings of the 2013 SIAM International Conference on Data Mining, SIAM, Austin, Texas, USA, 2–4 May 2013; pp. 252–260. [Google Scholar]
- Kalayeh, M.M.; Idrees, H.; Shah, M. NMF-KNN: Image annotation using weighted multi-view non-negative matrix factorization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 184–191. [Google Scholar]
- Zhao, H.; Ding, Z.; Fu, Y. Multi-view clustering via deep matrix factorization. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Huang, S.; Kang, Z.; Xu, Z. Auto-weighted multi-view clustering via deep matrix decomposition. Pattern Recognit. 2020, 97, 107015. [Google Scholar] [CrossRef]
- Li, S.Y.; Jiang, Y.; Zhou, Z.H. Partial multi-view clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014; Volume 28. [Google Scholar]
- Rai, N.; Negi, S.; Chaudhury, S.; Deshmukh, O. Partial multi-view clustering using graph regularized NMF. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 2192–2197. [Google Scholar]
- Rai, P.; Trivedi, A.; Daumé III, H.; DuVall, S.L. Multiview clustering with incomplete views. In Proceedings of the NIPS Workshop on Machine Learning for Social Computing, Whilster, BC, Canada, 11 December 2010. [Google Scholar]
- Wen, J.; Zhang, Z.; Zhang, Z.; Fei, L.; Wang, M. Generalized incomplete multiview clustering with flexible locality structure diffusion. IEEE Trans. Cybern. 2020, 51, 101–114. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Liu, H.; Fu, Y. Incomplete multi-modal visual data grouping. In Proceedings of the IJCAI, New York, NY, USA, 9–15 July 2016; pp. 2392–2398. [Google Scholar]
- Xu, N.; Guo, Y.; Zheng, X.; Wang, Q.; Luo, X. Partial multi-view subspace clustering. In Proceedings of the 26th ACM International Conference on Multimedia, Seoul, Republic of Korea, 22–26 October 2018; pp. 1794–1801. [Google Scholar]
- Shao, W.; He, L.; Philip, S.Y. Multiple incomplete views clustering via weighted nonnegative matrix factorization with l2,1 regularization. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Porto, Portugal, 7–11 September 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 318–334. [Google Scholar]
- Shao, W.; He, L.; Lu, C.t.; Philip, S.Y. Online multi-view clustering with incomplete views. In Proceedings of the 2016 IEEE International Conference on Big Data (Big Data), Washington, DC, USA, 5–8 December 2016; pp. 1012–1017. [Google Scholar]
- Hu, M.; Chen, S. Doubly aligned incomplete multi-view clustering. arXiv 2019, arXiv:1903.02785. [Google Scholar]
- Wen, J.; Xu, Y.; Liu, H. Incomplete multiview spectral clustering with adaptive graph learning. IEEE Trans. Cybern. 2018, 50, 1418–1429. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zong, L.; Liu, B.; Yang, Y.; Zhou, W. Spectral perturbation meets incomplete multi-view data. arXiv 2019, arXiv:1906.00098. [Google Scholar]
- Wu, J.; Zhuge, W.; Tao, H.; Hou, C.; Zhang, Z. Incomplete multi-view clustering via structured graph learning. In Proceedings of the Pacific Rim International Conference on Artificial Intelligence, Nanjing, China, 28–31 August 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 98–112. [Google Scholar]
- Liu, X.; Zhu, X.; Li, M.; Wang, L.; Zhu, E.; Liu, T.; Kloft, M.; Shen, D.; Yin, J.; Gao, W. Multiple kernel k k-means with incomplete kernels. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 1191–1204. [Google Scholar] [CrossRef]
- Wen, J.; Yan, K.; Zhang, Z.; Xu, Y.; Wang, J.; Fei, L.; Zhang, B. Adaptive graph completion based incomplete multi-view clustering. IEEE Trans. Multimed. 2020, 23, 2493–2504. [Google Scholar] [CrossRef]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 171–184. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor Decompositions and Applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Ng, A.Y.; Jordan, M.I.; Weiss, Y. On spectral clustering: Analysis and an algorithm. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 9–14 December 2002; pp. 849–856. [Google Scholar]
- Hagen, L.; Kahng, A.B. New spectral methods for ratio cut partitioning and clustering. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 1992, 11, 1074–1085. [Google Scholar] [CrossRef]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar]
- Gao, H.; Nie, F.; Li, X.; Huang, H. Multi-view subspace clustering. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 4238–4246. [Google Scholar]
- Nie, F.; Wang, X.; Jordan, M.; Huang, H. The constrained laplacian rank algorithm for graph-based clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Ma, S.; Goldfarb, D.; Chen, L. Fixed point and Bregman iterative methods for matrix rank minimization. Math. Program. 2011, 128, 321–353. [Google Scholar] [CrossRef]
- Cai, J.F.; Candès, E.J.; Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Naldi, M.C.; Campello, R.J.; Hruschka, E.R.; Carvalho, A. Efficiency issues of evolutionary k-means. Appl. Soft Comput. 2011, 11, 1938–1952. [Google Scholar] [CrossRef]
- Mousa, A.; El-Shorbagy, M.; Farag, M. K-means-clustering based evolutionary algorithm for multi-objective resource allocation problems. Appl. Math. Inf. Sci 2017, 11, 1681–1692. [Google Scholar] [CrossRef]
- Kwedlo, W. A clustering method combining differential evolution with the K-means algorithm. Pattern Recognit. Lett. 2011, 32, 1613–1621. [Google Scholar] [CrossRef]
- Tabatabaei, S.S.; Coates, M.; Rabbat, M. GANC: Greedy agglomerative normalized cut for graph clustering. Pattern Recognit. 2012, 45, 831–843. [Google Scholar] [CrossRef]
- Tabatabaei, S.S.; Coates, M.; Rabbat, M. Ganc: Greedy agglomerative normalized cut. arXiv 2011, arXiv:1105.0974. [Google Scholar]
- Wright, T.G.; Trefethen, L.N. Large-scale computation of pseudospectra using ARPACK and eigs. SIAM J. Sci. Comput. 2001, 23, 591–605. [Google Scholar] [CrossRef]
- Greene, D.; Cunningham, P. Practical solutions to the problem of diagonal dominance in kernel document clustering. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 377–384. [Google Scholar]
- Winn, J.; Jojic, N. Locus: Learning object classes with unsupervised segmentation. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05) Volume 1, Washington, DC, USA, 17–20 October 2005; Volume 1, pp. 756–763. [Google Scholar]
- Nie, F.; Cai, G.; Li, J.; Li, X. Auto-weighted multi-view learning for image clustering and semi-supervised classification. IEEE Trans. Image Process. 2017, 27, 1501–1511. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, H.; Liu, S.; Liu, G.; Cao, X. Low-rank tensor constrained multiview subspace clustering. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1582–1590. [Google Scholar]
- Schütze, H.; Manning, C.D.; Raghavan, P. Introduction to Information Retrieval; Cambridge University Press: Cambridge, UK, 2008; Volume 39. [Google Scholar]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]

| ACC | NMI | Purity | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Method\Rate | 0.1 | 0.3 | 0.5 | 0.1 | 0.3 | 0.5 | 0.1 | 0.3 | 0.5 |
| BSV | 34.05 | 33.71 | 33.53 | 12.19 | 11.76 | 11.50 | 34.57 | 34.40 | 34.40 |
| Concat | 32.84 | 32.50 | 32.41 | 12.68 | 11.24 | 9.68 | 34.22 | 33.97 | 34.05 |
| MIC | 40.34 | 46.64 | 47.07 | 19.54 | 28.10 | 29.04 | 44.74 | 50.17 | 49.83 |
| OMVC | 39.31 | 38.28 | 37.59 | 14.72 | 13.63 | 15.30 | 41.12 | 40.09 | 40.69 |
| GPMVC | 39.05 | 42.84 | 45.86 | 14.81 | 18.66 | 22.38 | 43.71 | 47.84 | 50.78 |
| AGC_IMC | 30.60 | 36.12 | 49.05 | 7.71 | 15.01 | 34.82 | 39.31 | 42.07 | 51.98 |
| IMC-LGC | 48.53 | 70.25 | 78.18 | 22.48 | 50.00 | 64.28 | 53.79 | 75.43 | 84.48 |
| ACC | NMI | Purity | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Method\Rate | 0.1 | 0.3 | 0.5 | 0.1 | 0.3 | 0.5 | 0.1 | 0.3 | 0.5 |
| BSV | 35.27 | 35.33 | 35.15 | 11.20 | 11.32 | 12.05 | 36.21 | 36.27 | 36.39 |
| Concat | 34.97 | 35.56 | 38.52 | 11.45 | 12.31 | 16.67 | 36.51 | 37.75 | 41.42 |
| MIC | 40.83 | 45.09 | 52.37 | 28.95 | 36.89 | 46.28 | 51.12 | 56.75 | 62.19 |
| OMVC | 45.74 | 40.89 | 38.11 | 35.13 | 27.93 | 22.76 | 58.28 | 51.89 | 47.99 |
| GPMVC | 38.76 | 42.01 | 52.07 | 20.88 | 26.24 | 34.33 | 50.36 | 54.44 | 61.48 |
| AGC_IMC | 35.15 | 45.98 | 72.84 | 31.85 | 39.69 | 61.94 | 59.76 | 62.49 | 78.05 |
| IMC-LGC | 59.82 | 79.64 | 79.34 | 49.79 | 64.65 | 65.74 | 71.24 | 80.29 | 81.24 |
| ACC | NMI | Purity | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Method\Rate | 0.1 | 0.3 | 0.5 | 0.1 | 0.3 | 0.5 | 0.1 | 0.3 | 0.5 |
| BSV | 46.30 | 56.85 | 68.65 | 29.43 | 38.16 | 49.41 | 46.45 | 56.85 | 68.65 |
| Concat | 41.70 | 48.05 | 56.80 | 28.23 | 25.61 | 34.54 | 41.70 | 48.05 | 56.80 |
| MIC | 37.15 | 47.80 | 78.75 | 17.18 | 29.75 | 61.23 | 37.30 | 48.75 | 78.80 |
| OMVC | 57.45 | 42.15 | 40.05 | 41.74 | 19.15 | 16.86 | 58.95 | 42.50 | 40.55 |
| GPMVC | 71.85 | 67.05 | 78.75 | 51.43 | 46.80 | 58.81 | 71.85 | 68.25 | 78.80 |
| AGC_IMC | 58.35 | 93.80 | 95.60 | 55.51 | 83.04 | 87.15 | 62.20 | 93.80 | 95.60 |
| IMC-LGC | 93.95 | 95.85 | 97.10 | 83.35 | 87.72 | 90.96 | 93.95 | 95.85 | 97.10 |
| ACC | NMI | Purity | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Method\Rate | 0.1 | 0.3 | 0.5 | 0.1 | 0.3 | 0.5 | 0.1 | 0.3 | 0.5 |
| BSV | 65.86 | 53.10 | 40.10 | 54.96 | 43.32 | 33.06 | 66.52 | 53.52 | 40.76 |
| Concat | 44.33 | 39.81 | 34.71 | 36.76 | 30.41 | 25.57 | 46.86 | 40.71 | 35.57 |
| MIC | 59.19 | 55.86 | 41.71 | 50.20 | 50.22 | 32.19 | 61.29 | 59.33 | 42.71 |
| OMVC | 48.81 | 35.62 | 35.57 | 37.31 | 25.22 | 24.74 | 50.05 | 36.62 | 37.14 |
| GPMVC | 46.86 | 42.48 | 35.67 | 34.42 | 31.60 | 22.66 | 48.81 | 43.33 | 37.19 |
| AGC_IMC | 75.10 | 74.33 | 66.10 | 75.20 | 69.29 | 56.23 | 78.43 | 76.90 | 66.76 |
| IMC-LGC | 87.80 | 87.80 | 77.61 | 78.91 | 77.67 | 62.89 | 87.80 | 87.80 | 77.66 |
| ACC | NMI | Purity | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Method\Rate | 0.1 | 0.3 | 0.5 | 0.1 | 0.3 | 0.5 | 0.1 | 0.3 | 0.5 |
| BSV | 48.85 | 37.25 | 26.40 | 69.10 | 56.54 | 44.92 | 54.18 | 40.98 | 30.05 |
| Concat | 49.15 | 38.63 | 28.90 | 68.76 | 57.59 | 47.73 | 53.43 | 42.25 | 32.03 |
| MIC | 61.10 | 54.45 | 30.58 | 79.13 | 73.29 | 52.94 | 65.25 | 59.23 | 33.58 |
| OMVC | 41.48 | 29.90 | 29.55 | 63.96 | 51.64 | 51.42 | 44.30 | 32.33 | 31.88 |
| GPMVC | 42.30 | 37.90 | 30.53 | 63.30 | 59.20 | 51.48 | 44.75 | 40.35 | 32.78 |
| AGC_IMC | 69.50 | 55.93 | 35.63 | 83.51 | 72.76 | 55.94 | 72.78 | 59.73 | 38.15 |
| IMC-LGC | 74.95 | 63.45 | 45.25 | 84.96 | 77.08 | 63.67 | 76.12 | 65.66 | 47.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Duan, Q.; Huang, H.; He, S.; Zou, T. Effective Incomplete Multi-View Clustering via Low-Rank Graph Tensor Completion. Mathematics 2023, 11, 652. https://doi.org/10.3390/math11030652
Yu J, Duan Q, Huang H, He S, Zou T. Effective Incomplete Multi-View Clustering via Low-Rank Graph Tensor Completion. Mathematics. 2023; 11(3):652. https://doi.org/10.3390/math11030652
Chicago/Turabian StyleYu, Jinshi, Qi Duan, Haonan Huang, Shude He, and Tao Zou. 2023. "Effective Incomplete Multi-View Clustering via Low-Rank Graph Tensor Completion" Mathematics 11, no. 3: 652. https://doi.org/10.3390/math11030652
APA StyleYu, J., Duan, Q., Huang, H., He, S., & Zou, T. (2023). Effective Incomplete Multi-View Clustering via Low-Rank Graph Tensor Completion. Mathematics, 11(3), 652. https://doi.org/10.3390/math11030652






