A Periodically Rotating Distributed Forcing of Flow over a Sphere for Drag Reduction
Abstract
1. Introduction
2. Control Strategy and Numerical Details
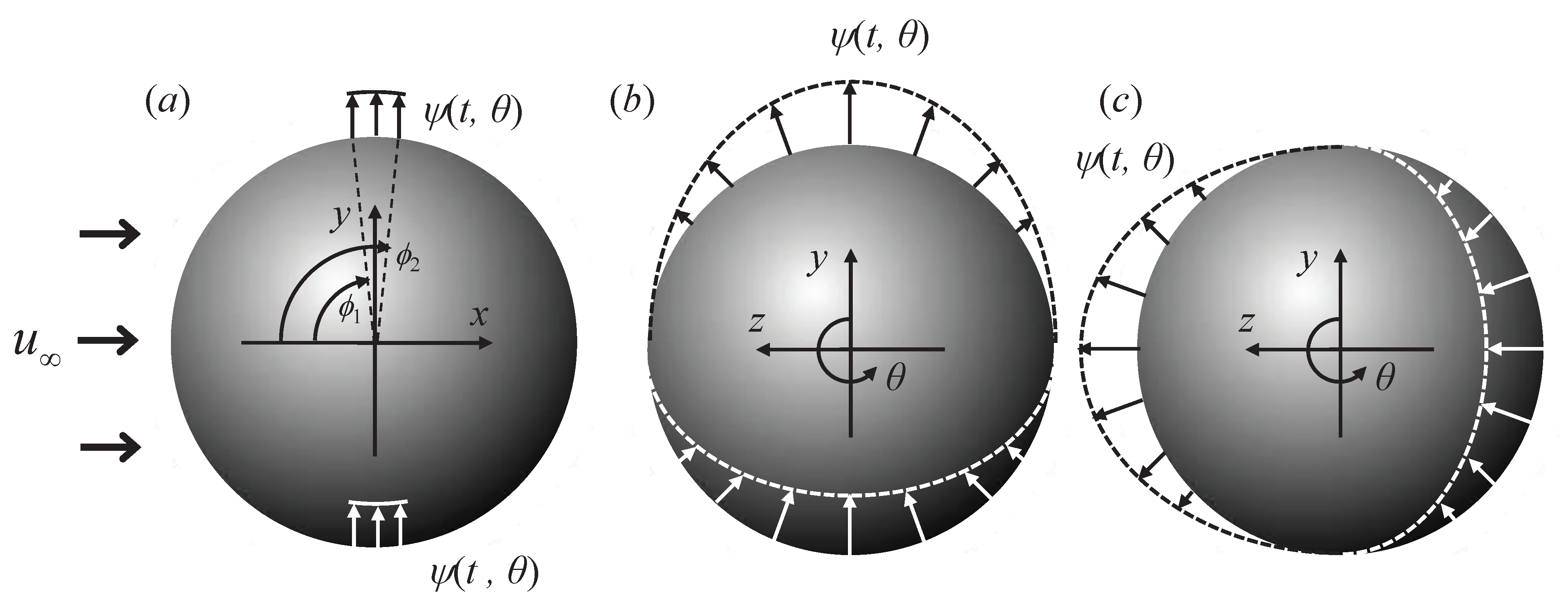
2.1. Control Strategy
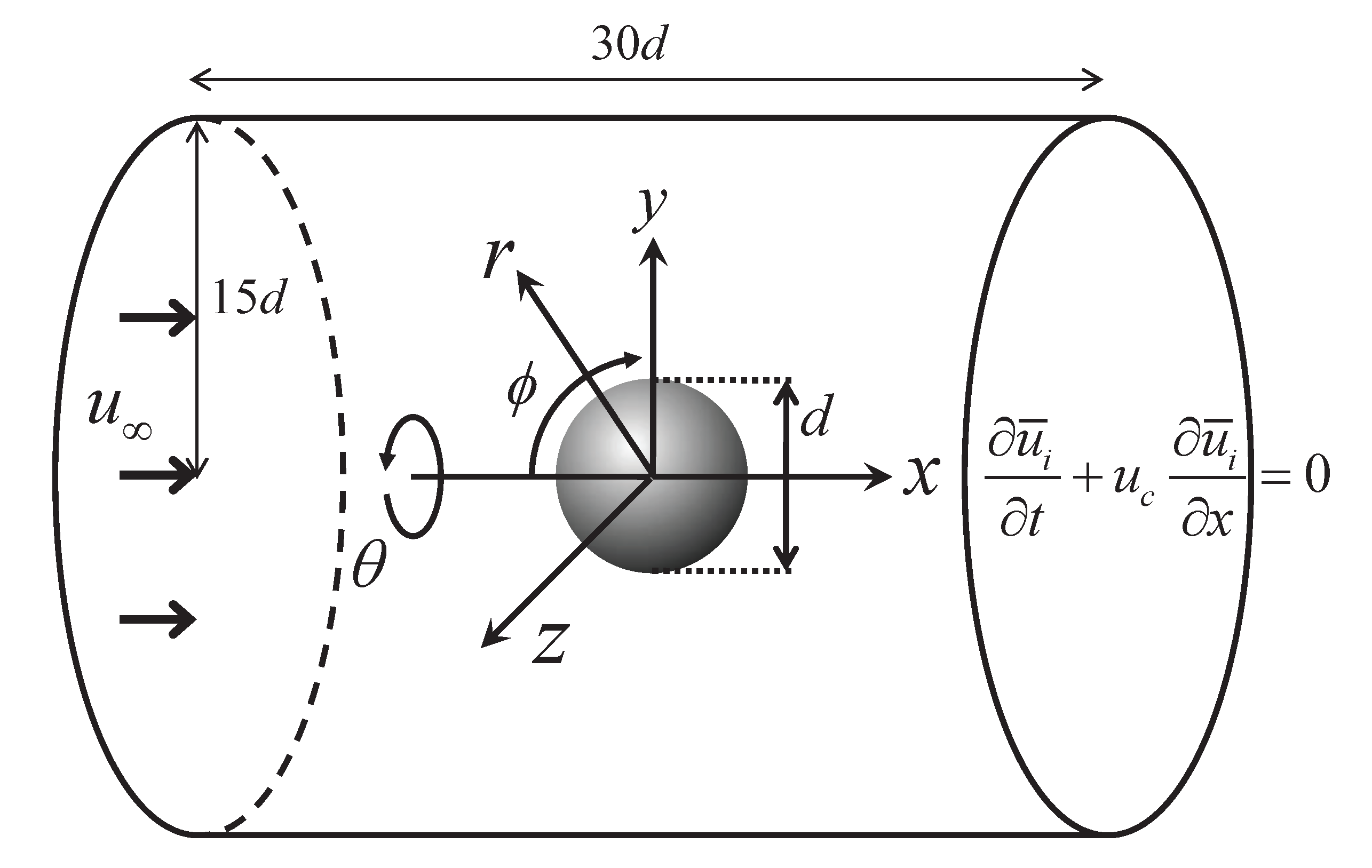
2.2. Numerical Details
3. Results and Discussion
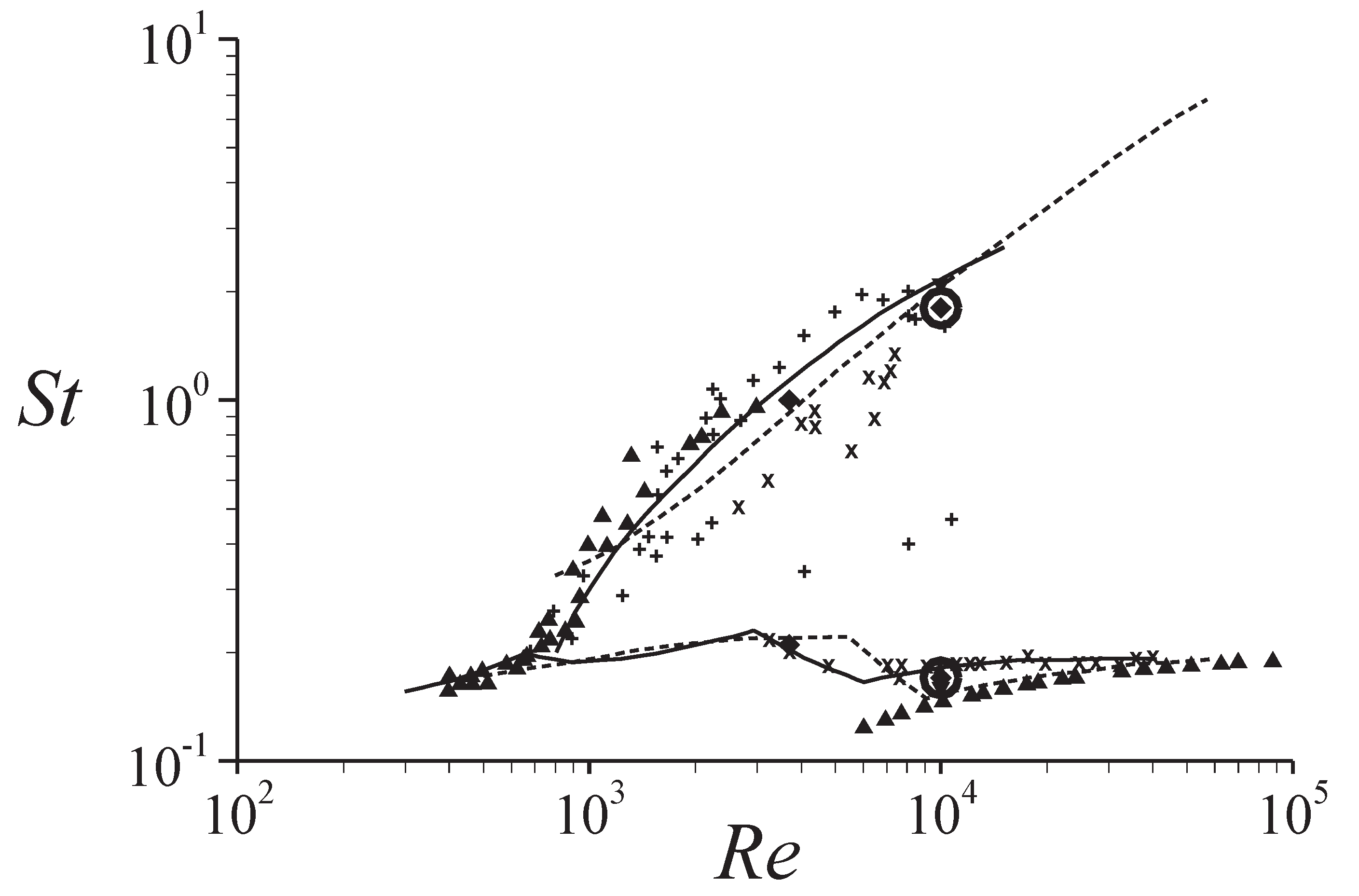
3.1. Uncontrolled Flow
3.2. Effect of Forcing Frequency f
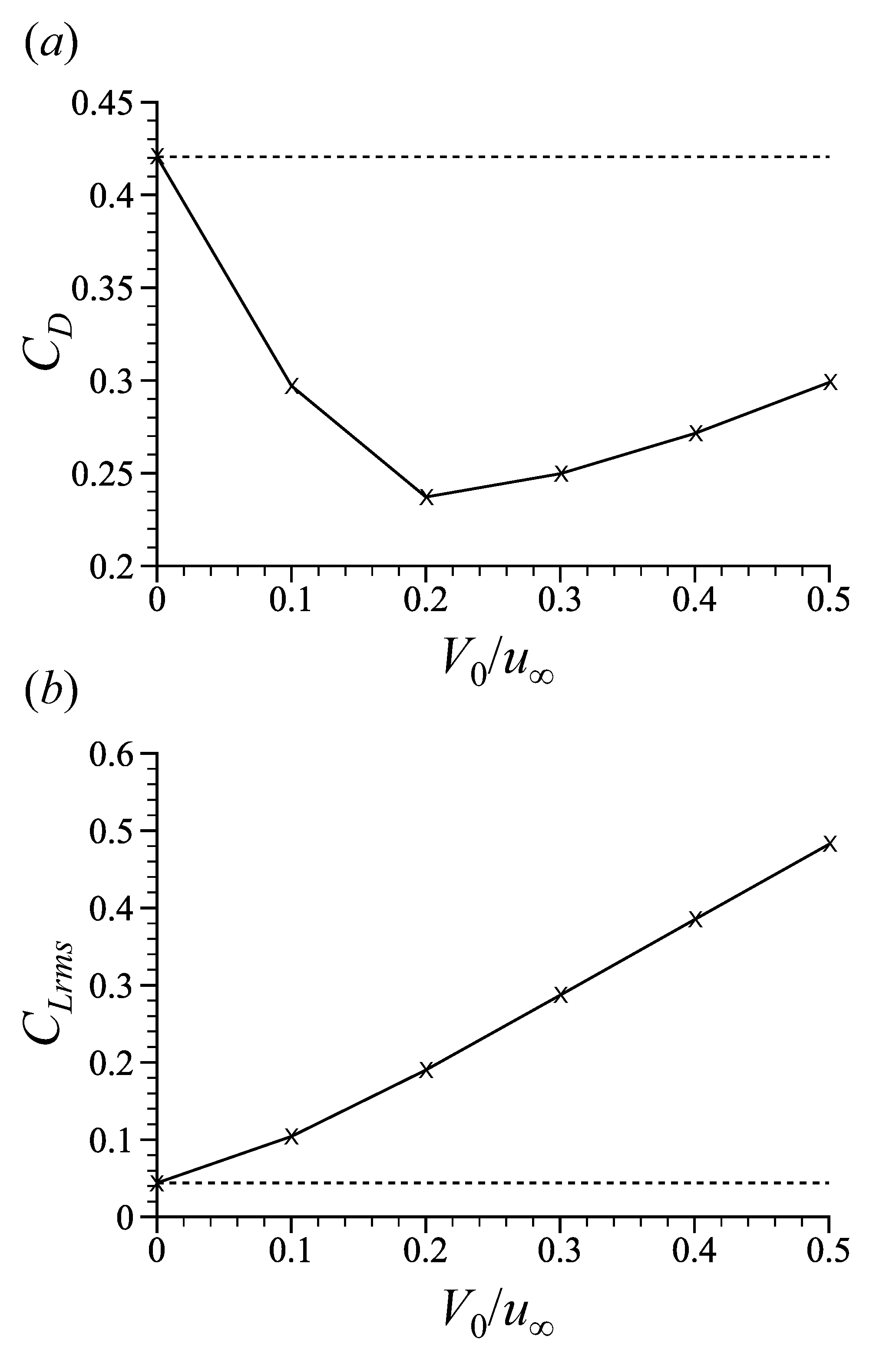
3.3. Effect of Forcing Amplitude
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| x | Streamwise direction |
| y | Transverse direction |
| z | Spanwise direction |
| r | Radial direction |
| Azimuthal direction | |
| Angle measured from the stagnation point | |
| t | Time |
| d | Sphere diameter |
| u | Fluid velocity |
| p | Pressure |
| Free stream velocity | |
| Kinematic viscosity | |
| Momentum forcing | |
| q | Mass source/sink |
| Strain rate tensor | |
| Subgrid-scale stress tensor | |
| Kronecker delta | |
| Eddy viscosity | |
| Filtered quantity | |
| Reynolds number | |
| Strouhal number | |
| Drag coefficient | |
| Lift coefficient | |
| Lift coefficient in the y direction | |
| Lift coefficient in the z direction | |
| Root-mean-square value | |
| Base pressure coefficient | |
| Separation angle | |
| Forcing amplitude | |
| f | Forcing frequency |
| Forcing velocity | |
| Streamwise distance for helical vortex |
References
- Gad-el Hak, M.; Pollard, A.; Bonnet, J.P. Flow Control: Fundamentals and Practices; Springer Science & Business Media: New York, NY, USA, 2003; Volume 53. [Google Scholar]
- Collis, S.S.; Joslin, R.D.; Seifert, A.; Theofilis, V. Issues in active flow control: Theory, control, simulation, and experiment. Prog. Aerosp. Sci. 2004, 40, 237–289. [Google Scholar] [CrossRef]
- Le, T.T.G.; Jang, K.S.; Lee, K.S.; Ryu, J. Numerical investigation of aerodynamic drag and pressure waves in hyperloop systems. Mathematics 2020, 8, 1973. [Google Scholar] [CrossRef]
- Choi, H.; Jeon, W.P.; Kim, J. Control of flow over a bluff body. Annu. Rev. Fluid Mech. 2008, 40, 113–139. [Google Scholar] [CrossRef]
- Kim, J.; Choi, H. Distributed forcing of flow over a circular cylinder. Phys. Fluids 2005, 17, 033103. [Google Scholar] [CrossRef]
- Jardin, T.; Bury, Y. Distributed forcing of the flow past a blunt-based axisymmetric bluff body. Theor. Comput. Fluid Dyn. 2014, 28, 259. [Google Scholar] [CrossRef]
- Feng, L.H.; Wang, J.J. Modification of a circular cylinder wake with synthetic jet: Vortex shedding modes and mechanism. Eur. J. Mech. B. Fluids 2014, 43, 14–32. [Google Scholar] [CrossRef]
- Naghib-Lahouti, A.; Hangan, H.; Lavoie, P. Distributed forcing flow control in the wake of a blunt trailing edge profiled body using plasma actuators. Phys. Fluids 2015, 27, 035110. [Google Scholar] [CrossRef]
- Wu, Z.; Choi, H. Modification of flow behind a circular cylinder by steady and time-periodic blowing. Phys. Fluids 2021, 33, 115126. [Google Scholar] [CrossRef]
- Lam, K.; Lin, Y. Effects of wavelength and amplitude of a wavy cylinder in cross-flow at low Reynolds numbers. J. Fluid Mech. 2009, 620, 195–220. [Google Scholar] [CrossRef]
- Kim, W.; Lee, J.; Choi, H. Flow around a helically twisted elliptic cylinder. Phys. Fluids 2016, 28, 053602. [Google Scholar] [CrossRef]
- Yoon, H.S.; Kim, M.I.; Kim, H.J. Reynolds number effects on the flow over a twisted cylinder. Phys. Fluids 2019, 31, 025119. [Google Scholar] [CrossRef]
- Yoon, J.; Kim, J.; Choi, H. Control of laminar vortex shedding behind a circular cylinder using tabs. J. Mech. Sci. Technol. 2014, 28, 1721–1725. [Google Scholar] [CrossRef]
- Kim, H.; Durbin, P. Observations of the frequencies in a sphere wake and of drag increase by acoustic excitation. Phys. Fluids 1988, 31, 3260–3265. [Google Scholar] [CrossRef]
- Jeon, S.; Choi, J.; Jeon, W.P.; Choi, H.; Park, J. Active control of flow over a sphere for drag reduction at a subcritical Reynolds number. J. Fluid Mech. 2004, 517, 113–129. [Google Scholar] [CrossRef]
- Choi, J.; Jeon, W.P.; Choi, H. Mechanism of drag reduction by dimples on a sphere. Phys. Fluids 2006, 18, 041702. [Google Scholar] [CrossRef]
- Findanis, N.; Ahmed, N. The interaction of an asymmetrical localised synthetic jet on a side-supported sphere. J. Fluids Struct. 2008, 24, 1006–1020. [Google Scholar] [CrossRef]
- Oxlade, A.R.; Morrison, J.F.; Qubain, A.; Rigas, G. High-frequency forcing of a turbulent axisymmetric wake. J. Fluid Mech. 2015, 770, 305–318. [Google Scholar] [CrossRef]
- Kim, J.; Hahn, S.; Kim, J.; Lee, D.k.; Choi, J.; Jeon, W.P.; Choi, H. Active control of turbulent flow over a model vehicle for drag reduction. J. Turbul. 2004, 5, 019. [Google Scholar] [CrossRef]
- Kim, J.; Kim, D.; Choi, H. An immersed-boundary finite-volume method for simulations of flow in complex geometries. J. Comput. Phys. 2001, 171, 132–150. [Google Scholar] [CrossRef]
- Son, D.; Jeon, S.; Choi, H. A proportional–integral–differential control of flow over a circular cylinder. Phil. Trans. R. Soc. A 2011, 369, 1540–1555. [Google Scholar] [CrossRef]
- Lee, J.; Son, D. Proportional feedback control of laminar flow over a hemisphere. J. Mech. Sci. Technol. 2016, 30, 3667–3672. [Google Scholar] [CrossRef]
- Son, D.; Choi, H. Iterative feedback tuning of the proportional-integral-differential control of flow over a circular cylinder. IEEE Trans. Control Syst. Technol. 2018, 27, 1385–1396. [Google Scholar] [CrossRef]
- Yun, J.; Lee, J. Active proportional feedback control of turbulent flow over a circular cylinder with averaged velocity sensor. Phys. Fluids 2022, 34, 095133. [Google Scholar] [CrossRef]
- Kim, J.; Moin, P. Application of a fractional-step method to incompressible Navier-Stokes equations. J. Comput. Phys. 1985, 59, 308–323. [Google Scholar] [CrossRef]
- Akselvoll, K.; Moin, P. An efficient method for temporal integration of the Navier–Stokes equations in confined axisymmetric geometries. J. Comput. Phys. 1996, 125, 454–463. [Google Scholar] [CrossRef]
- Yun, G.; Kim, D.; Choi, H. Vortical structures behind a sphere at subcritical Reynolds numbers. Phys. Fluids 2006, 18, 015102. [Google Scholar] [CrossRef]
- Mittal, R.; Iaccarino, G. Immersed boundary methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef]
- Park, N.; Lee, S.; Lee, J.; Choi, H. A dynamic subgrid-scale eddy viscosity model with a global model coefficient. Phys. Fluids 2006, 18, 125109. [Google Scholar] [CrossRef]
- Park, K.; Choi, H.; Choi, S.; Sa, Y. Effect of a casing fence on the tip-leakage flow of an axial flow fan. Int. J. Heat Fluid Flow 2019, 77, 157–170. [Google Scholar] [CrossRef]
- Song, D.; Kim, W.; Kwon, O.K.; Choi, H. Vertical and torsional vibrations before the collapse of the Tacoma Narrows Bridge in 1940. J. Fluid Mech. 2022, 949, A11. [Google Scholar] [CrossRef]
- Lee, J.; Choi, H.; Park, N. Dynamic global model for large eddy simulation of transient flow. Phys. Fluids 2010, 22, 075106. [Google Scholar] [CrossRef]
- Vreman, A. An eddy-viscosity subgrid-scale model for turbulent shear flow: Algebraic theory and applications. Phys. Fluids 2004, 16, 3670–3681. [Google Scholar] [CrossRef]
- You, D.; Moin, P. A dynamic global-coefficient subgrid-scale eddy-viscosity model for large-eddy simulation in complex geometries. Phys. Fluids 2007, 19, 065110. [Google Scholar] [CrossRef]
- Prasad, A.; Williamson, C.H. The instability of the shear layer separating from a bluff body. J. Fluid Mech. 1997, 333, 375–402. [Google Scholar] [CrossRef]
- Constantinescu, G.; Squires, K. Numerical investigations of flow over a sphere in the subcritical and supercritical regimes. Phys. Fluids 2004, 16, 1449–1466. [Google Scholar] [CrossRef]
- Muto, M.; Tsubokura, M.; Oshima, N. Negative Magnus lift on a rotating sphere at around the critical Reynolds number. Phys. Fluids 2012, 24, 014102. [Google Scholar] [CrossRef]
- Rodríguez, I.; Lehmkuhl, O.; Borrell, R.; Oliva, A. Flow dynamics in the turbulent wake of a sphere at sub-critical Reynolds numbers. Comput. Fluids 2013, 80, 233–243. [Google Scholar] [CrossRef]
- Möller, W. Experimentelle untersuchungen zur hydrodynamik der kugel. Phys. Z. 1938, 39, 57–80. [Google Scholar]
- Cometta, C. An Investigation of the Unsteady Flow Pattern in the Wake of Cylinders and Spheres Using a Hot Wire Probe; Report No. WT-21; Brown University: Providence, RI, USA, 1957. [Google Scholar]
- Achenbach, E. Vortex shedding from spheres. J. Fluid Mech. 1974, 62, 209–221. [Google Scholar] [CrossRef]
- Sakamoto, H.; Haniu, H. A study on vortex shedding from spheres in a uniform flow. J. Fluids Eng. 1990, 112, 386–392. [Google Scholar] [CrossRef]
- Mittal, R.; Najjar, F. Vortex dynamics in the sphere wake. In Proceedings of the 30th Fluid Dynamics Conference, Norfolk, VA, USA, 28 June–1 July 1999; p. 3806. [Google Scholar]
- Mittal, R. Response of the sphere wake to freestream fluctuations. Theor. Comput. Fluid Dyn. 2000, 13, 397–419. [Google Scholar] [CrossRef]
- Kim, W.; Yoo, J.Y.; Sung, J. Dynamics of vortex lock-on in a perturbed cylinder wake. Phys. Fluids 2006, 18, 074103. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]

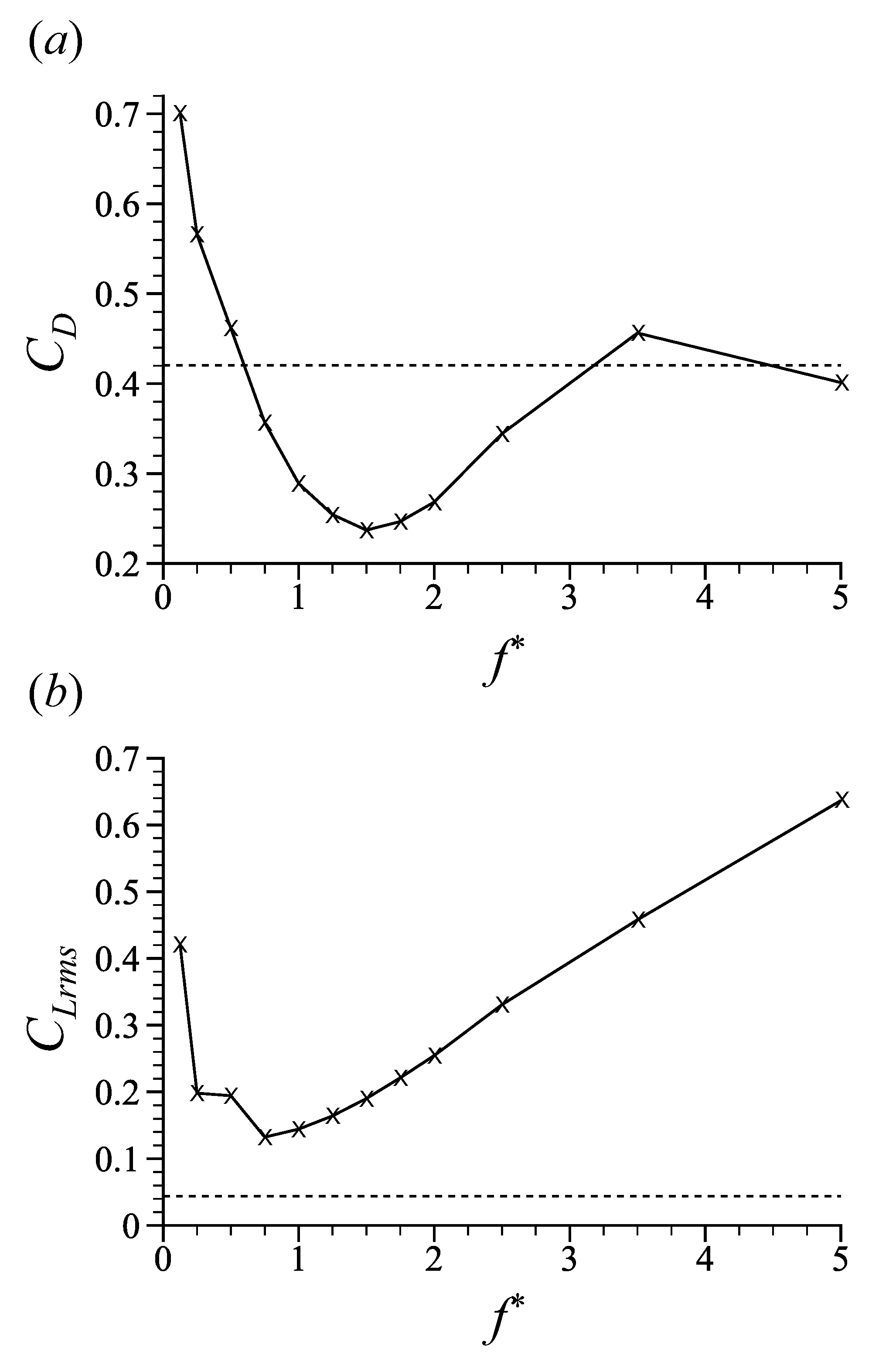
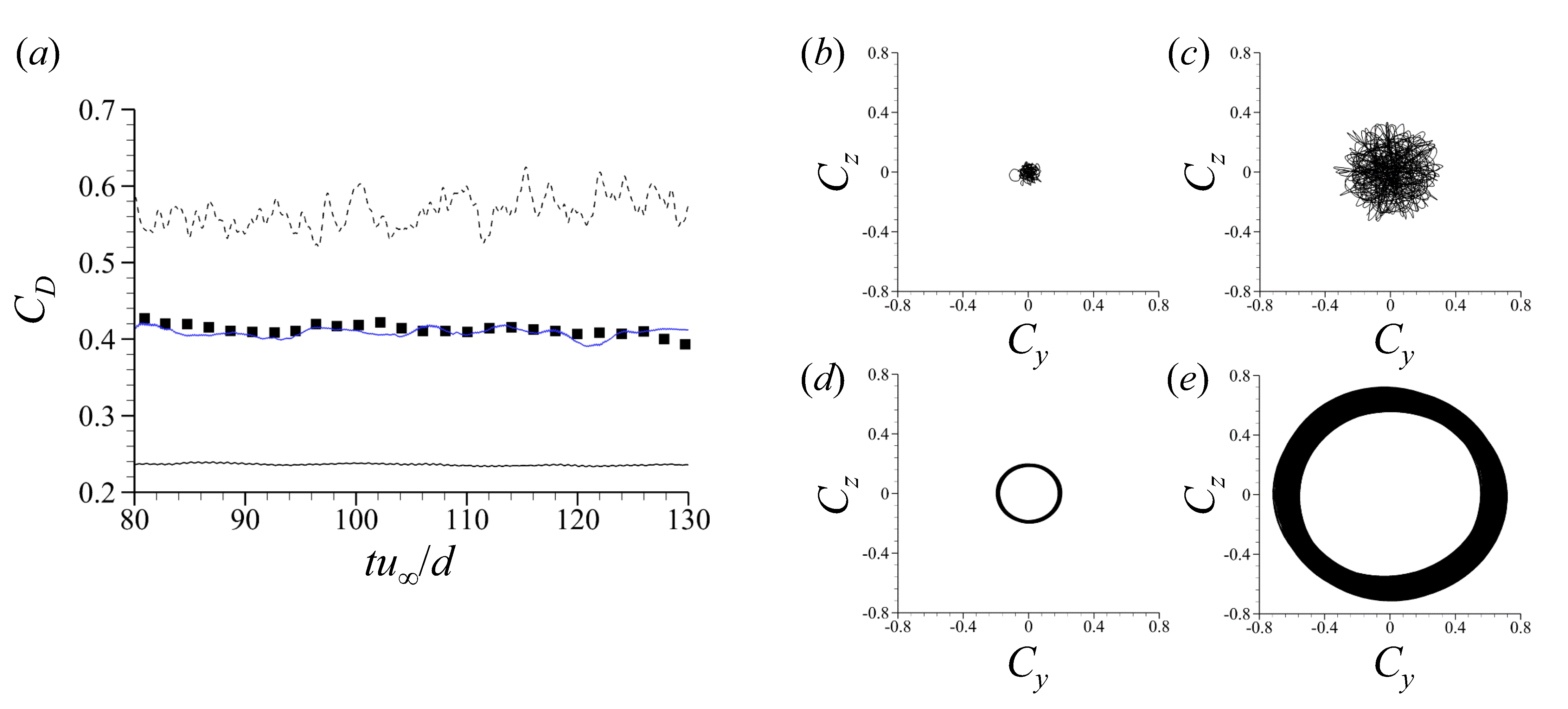
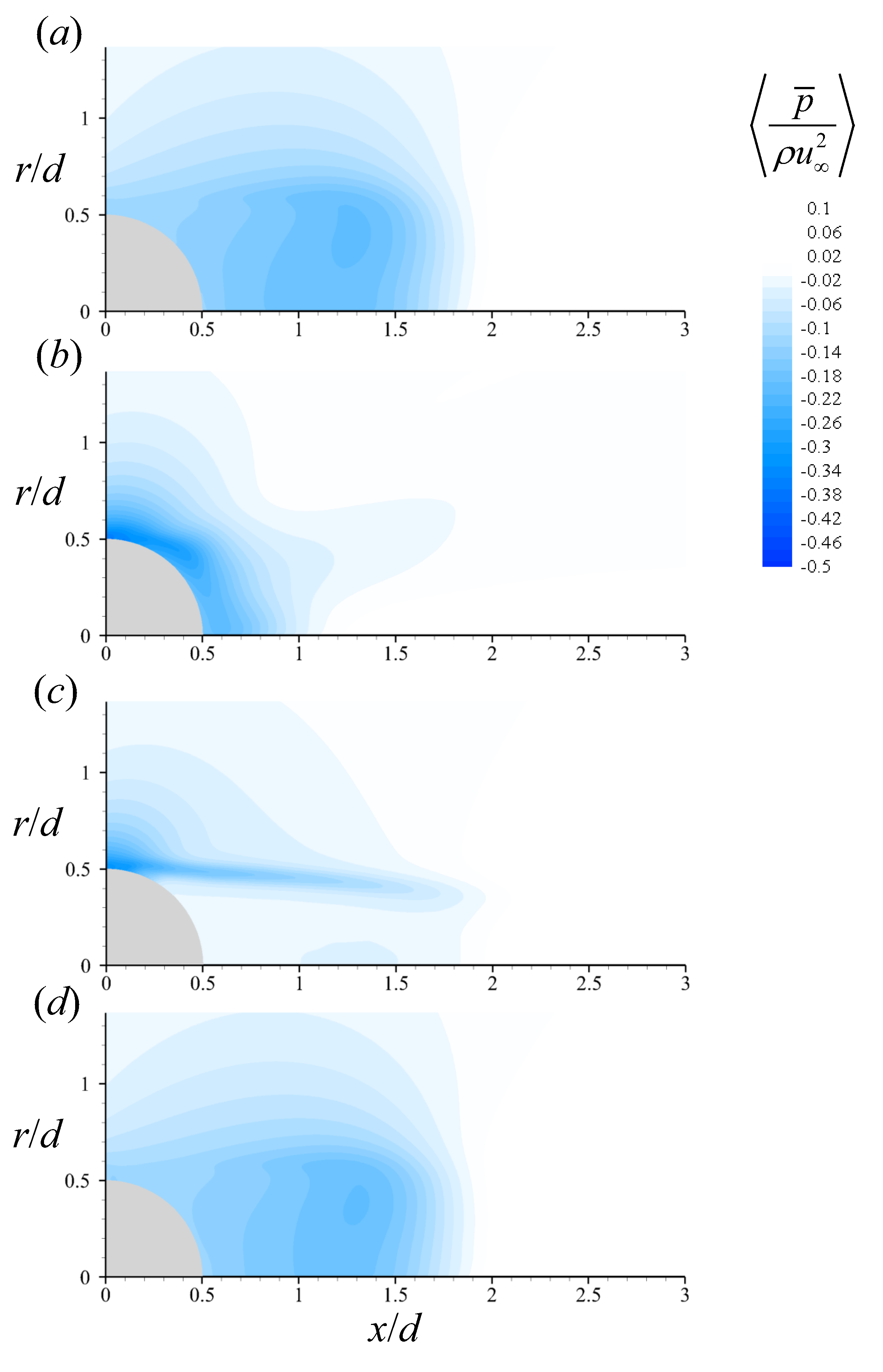
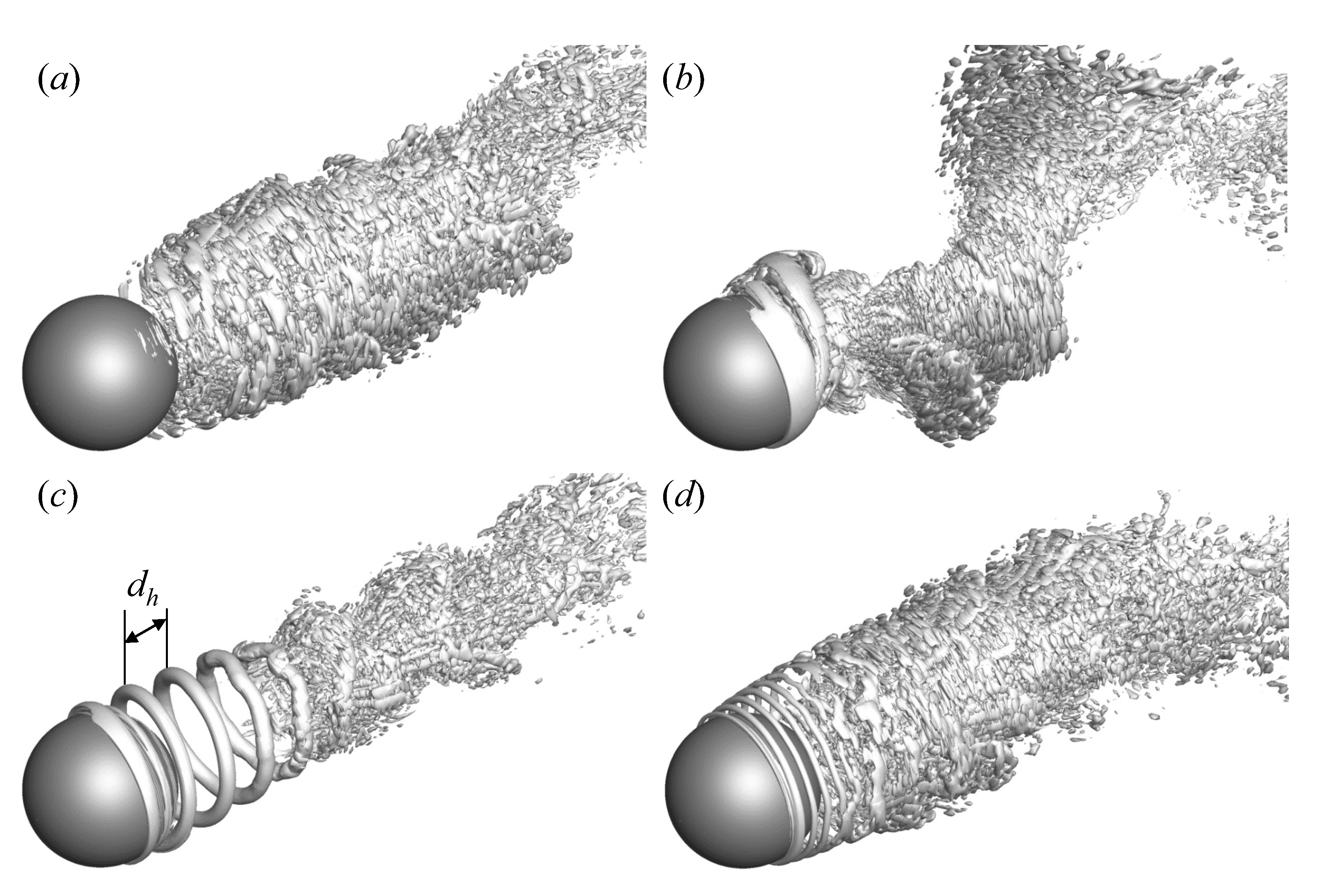
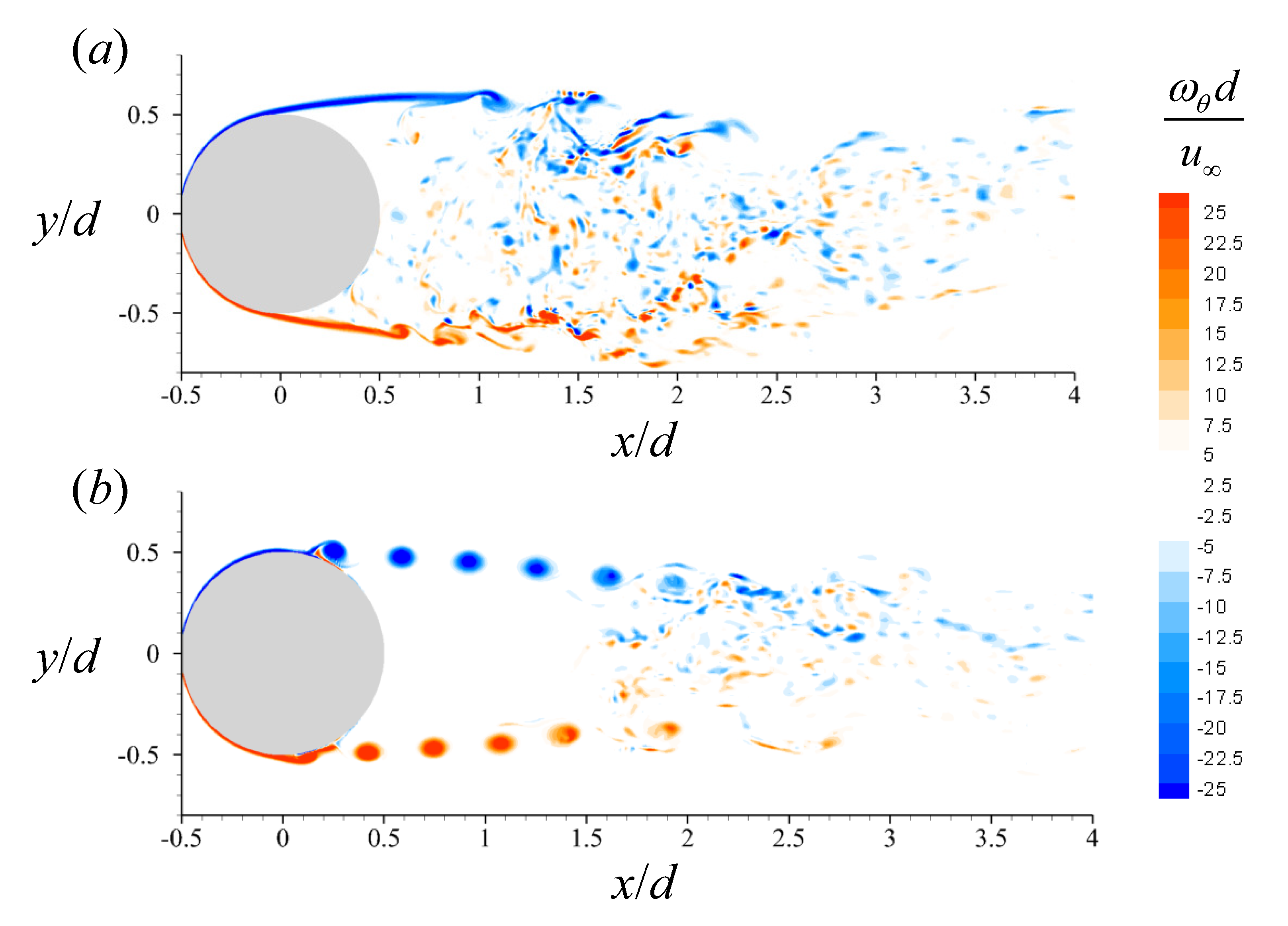

| (deg) | ||||
|---|---|---|---|---|
| Constantinescu and Squires [36] | 0.393 | −0.275 | 84 | |
| Yun et al. [27] | 0.393 | −0.274 | 90 | |
| Muto et al. [37] | 0.446 | - | - | |
| Rodríguez et al. [38] | 0.402 | −0.272 | 84.7 | |
| Present study | 0.420 | −0.274 | 88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, D.; Lee, J. A Periodically Rotating Distributed Forcing of Flow over a Sphere for Drag Reduction. Mathematics 2023, 11, 706. https://doi.org/10.3390/math11030706
Son D, Lee J. A Periodically Rotating Distributed Forcing of Flow over a Sphere for Drag Reduction. Mathematics. 2023; 11(3):706. https://doi.org/10.3390/math11030706
Chicago/Turabian StyleSon, Donggun, and Jungil Lee. 2023. "A Periodically Rotating Distributed Forcing of Flow over a Sphere for Drag Reduction" Mathematics 11, no. 3: 706. https://doi.org/10.3390/math11030706
APA StyleSon, D., & Lee, J. (2023). A Periodically Rotating Distributed Forcing of Flow over a Sphere for Drag Reduction. Mathematics, 11(3), 706. https://doi.org/10.3390/math11030706





