Compartmental Unpredictable Functions

Abstract

There is a huge family of recurrent functions, which starts with equilibria and ends with Poisson stable functions. They are fundamental in theoretical and application senses, and they admit a famous history. Recently, we have added the unpredictable functions to the family. The research has been performed in several papers and books. Obviously, theoretical and application merits of functions increase if one provides rigorously approved efficient methods of construction of concrete examples, as well as their numerical simulations. In the present study, we met the challenges for unpredictability by considering functions of two variables on diagonals. Algorithms have been created, and they are both deterministic and random. Characteristics are introduced to evaluate contributions of periodic and unpredictable components to the dynamics, and they are clearly illustrated in graphs of the functions. Definitions of non-periodic compartmental functions are provided as suggestions for the research in the future.

1. Introduction

Oscillations and recurrence play a special role in the study of dynamics of processes occurring in nature and industry. In the literature, numerous results have been obtained for periodic, quasi-periodic, and almost periodic functions due to the established valuable mathematical methods and important applications [1,2,3,4,5]. On the other hand, recurrent and Poisson stable functions are also crucial for the theory of oscillations [6,7,8,9,10]. The theory of non-linear dynamics, [1,2,6,11,12], was focused mainly on periodic motions. Functions, which can be still be considered as “periodic” and are sufficiently convenient for strict mathematical analysis, are quasi-periodic functions introduced and investigated by P. Bohl [13,14] and E. Esclangon [15], independently. The fundamental papers of H. Bohr [16,17,18] are about basics of almost periodic functions. Different theories of almost-periodicity were constructed by N.N. Bogolyubov [19], A.S. Besicovitch [20], S. Bochner [21], and V.V. Stepanov [22]. Those functions are of great importance for the development of harmonic analysis of groups, including the Fourier series. The concepts of recurrent motions and Poisson stable points are central in the qualitative theory of dynamical systems. They were considered by H.Poincare [11] and G. Birkhoff [6] as the main ingredients of complexity in celestial dynamics.

Currently, chaos theory is being widely developed, and the classical functions are not any longer sufficient to describe the dynamics of complex systems. It requires not only new models and new solutions of models, but also new functions. This is why the unpredictable and compartmental Poisson stable have been introduced in our recent papers [23,24,25,26]. Accordingly, a new method of included intervals for the existence of unpredictable and Poisson stable solutions of discrete and differential equations was suggested. Since the unpredictability leads to chaos, the role of unpredictable functions is very important in applications. The new functions are especially important for studying the dynamics of neural networks. Due to the complexity and non-linearity of neural networks, their behaviour is not confined to regular functions. In our papers, unpredictable oscillations in Hopfield-type neural networks [27], as well as shunting inhibitory cellular neural networks [28,29], were investigated.

It is indisputable that, when considering functions in applications, one should enlarge the number of methods of construction and numerical presentations of them, starting with simple algebraic operations and finalizing with Fourier series and the theory of operators. In the present study, a new way of the unpredictable function construction is suggested, which is rooted at compartmental functions. It starts with functions of two variables, which are unpredictable in one of them, and in another are either periodic, quasi-periodic, or almost-periodic and even recurrent or Poisson stable. Then, domains of the functions are narrowed to the diagonals of the coordinate spaces, where the arguments are ranged. The method of diagonals is the routine one, known, for instance, for quasi-periodic functions or almost-periodic functions [5,20], but, in the study, the diagonalization is made for dynamics, which are on essentially different new level, since the dependence on the different variables is essentially different. Correspondingly, it is an interesting problem to find such conditions that the functions on diagonals admit the unpredictability. In the present research, the problem is provided with a particular solution for the case of periodicity. So-called compartmental periodic unpredictable functions are in the focus. Beside the general problem, elements of algebra for the unpredictable functions and unpredictability of compositions have been discussed.

Working on the new types of recurrence, we have learnt, surprisingly, that, despite numerous papers on almost periodic and Poisson stable functions, there are no any prints of numerical examples and simulations, neither for the functions nor solutions of differential equations, if they are not quasi-periodic. In the same time, the needs of industry and, exceptionally, neuroscience, artificial intelligence, and other modern areas, demand numerical presentation of motions, which already have been supported seriously in theories. Our research comprehensively meets the challenges, since we have constructed samples of Poisson stable and unpredictable functions utilizing solutions of the logistic equation, as well as determining them randomly through realizations of Bernoulli schemes and Markov chains. That is, deterministic, as well as stochastic routs for the functions, have been paved. One should emphasize that, even for Poisson stable functions, which are in the research for about a century, samples of the concrete functions appeared in our papers [24,25] for the first time. The numerical experiments are advantageous, since they are accompanied with newly developed strong instruments of the functions simulations. For instance, they are suitable for synchronization of chaos, namely, Delta synchronization, which works for gas discharge-semiconductor systems [30], where even the generalized synchronization [31] is not effective. A numerical test for the unpredictable dynamics has been suggested [32], which discovers strange attractors, when conservative methods do not work [33]. Moreover, we have developed algorithms, which allow us to observe contributions of periodicity and the unpredictability for the compartmental dynamics. The algorithms are based on the concept of the degree of periodicity. We have learnt that very similar time series can be seen in several industrial experiments [34,35,36,37,38], and this is a strong argument for the application of our results. One can believe, also, that the research of the compartmental functions can give more insights into the problem of the transition from quasi-periodicity to chaos [39,40].

In Preliminaries and Definitions, one can find basic information on functions, which are in the focus of the present research. The Section 3 contains conditions on the novel parameters, sufficient to guarantee the unpredictability of compartmental functions with a periodic component. The properties are utilized in the central theoretical part of the article, Section 4, where a new class of unpredictable functions is described. The reader is invited to consider Theorem 1 as the source of weakened conditions for the unpredictability. The Section 5 contains examples of concrete compartmental periodic unpredictable functions, which are constructed by applying irregular features of dynamics in the logistic equation. The results are rigorously approved by the method of included intervals. The degree of periodicity is considered in Section 6. Its role for the analysis is carefully illustrated through several numerical simulations. The rout for construction of unpredictable functions by Markov chains is discussed in Section 7. In the final part, Miscellanea, definitions of compartmental quasi-periodic, almost periodic, recurrent, and Poisson stable functions are presented to complete the presentation. Moreover, theorems are proved on the unpredictability of functions being subdued to simple algebraic operations. The section is closed with an example of a compartmental quasi-periodic unpredictable function, which confirms potentials of the research when a diagonalized function is not necessary unpredictable.

2. Preliminaries and Definitions

Throughout the paper, $\mathbb{N},$ $\mathbb{Z},$ and $\mathbb{R}$, respectively, stand for the sets of natural numbers, integers, and real numbers. Moreover, for vectors, we use a Euclidean norm.

Definition 1. 

A bounded function $f\left(t\right):\mathbb{R}\to {\mathbb{R}}^n$ is said to be Poisson stable if there exists a sequence $t_k,$ $t_k\to \infty$ as $k\to \infty ,$ such that the sequence of functions $f(t+t_k)$ uniformly converges to $f\left(t\right)$ on each bounded interval of the real axis.

Definition 2 

([23]). A bounded function $f:\mathbb{R}\to {\mathbb{R}}^n$ is unpredictable if there exist positive numbers ${ϵ}_0,\delta$ and sequences $t_k,s_k$, both of which diverge to infinity, such that $\parallel f(t+t_k)-f\left(t\right)\parallel \to 0$ as $k\to \infty$ uniformly on compact subsets of $\mathbb{R}$ and $\parallel f(t+t_k)-f\left(t\right)\parallel >{ϵ}_0$ for each $t\in [s_k-\delta ,s_k+\delta ]$ and $k\in \mathbb{N}$.

A sequence $t_k,k=1,2,\dots ,$ in Definitions 1 and 2 is said to be the Poisson or convergence sequence of the function $f\left(t\right).$ We call the uniform convergence on compact subsets of $\mathbb{R},$the convergence property, and the existence of the sequence $s_k$ and positive numbers ${ϵ}_0,\delta$ is called the separation property.

Remark 1. 

It follows, from the last two definitions, that we consider not only continuous, but also discontinuous unpredictable and Poisson functions. The convergence and separation properties are valid regardless to the continuity. Duo to this comment, we shall use examples with continuous and discontinuous functions. The definition of continuous Poisson stable functions can be found in [7].

Definition 3. 

A bounded function $f(t,x):\mathbb{R}\times D\to {\mathbb{R}}^n,$ $D\subset {\mathbb{R}}^n$ is a domain, which is unpredictable in t, uniformly, with respect to $x\in D,$ if there exist positive numbers ${ϵ}_0$, δ and sequences $t_k$, $s_k$, both of which diverge to infinity, such that ${\displaystyle \underset{D}{sup}\parallel f(t+t_k,x)-f(t,x)\parallel \to 0}$ as $k\to \infty$ uniformly on bounded intervals of t and $x\in D,$ and ${\displaystyle \parallel f(t+t_k,x)-f(t,x)\parallel >{ϵ}_0}$ for $t\in [s_k-\delta ,s_k+\delta ],$ $x\in D$ and $k\in \mathbb{N}$.

Definition 4. 

A function $f\left(t\right):\mathbb{R}\to {\mathbb{R}}^n$ is said to be a compartmental periodic unpredictable function if $f\left(t\right)=G(t,t),$, where $G(u,v)$ is a continuous bounded function, periodic in u uniformly with respect to $v,$ and unpredictable in v uniformly with respect to $u,$, i.e., there exist positive numbers $\omega ,$ ${ϵ}_0$, δ and sequences $t_k$, $s_k$, both of which diverge to infinity, such that ${\displaystyle G(u+\omega ,v)=G(u,v)}$ for all $u,v\in \mathbb{R},$ ${\displaystyle \underset{u\in \mathbb{R}}{sup}\parallel G(u,v+t_k)-G(u,v)\parallel \to 0}$ as $k\to \infty$ uniformly on bounded intervals of $v,$ and ${\displaystyle \parallel G(u,v+t_k)-G(u,v)\parallel >{ϵ}_0}$ for $v\in [s_k-\delta ,s_k+\delta ],$ $u\in \mathbb{R}$ and $k\in \mathbb{N}$.

Definition 5. 

A function $f(t,x):\mathbb{R}\times D\to {\mathbb{R}}^n,$ $D\subset {\mathbb{R}}^n$ is a domain, which is said to be compartmental periodic unpredictable in t uniformly for $x\in D$ function, if $f(t,x)=G(t,t,x),$ where $G(u,v,x)$ is a bounded function, periodic in u uniformly with respect to $v\in \mathbb{R},$ $x\in D,$ and unpredictable in v uniformly with respect to $u\in R$ and $x\in D.$

Remark 2. 

What we use as functions on diagonals is the routine technique of multi-periodicity known for almost periodic functions [18]. If the number of periods is finite and they are incommensurate, the quasi-periodic functions as a subset of almost-periodic functions is shaped. In Definitions 3 and 4, functions differently depend on two variables since periodicity is not the unpredictability. That is, we consider a more sophisticated case of the technique this time. It is clear that the compartmental functions are already assumed to be irregular, but to clarify precisely the phenomenon as irregular, we provide conditions for the unpredictability of the functions on diagonals. The next section is devoted to the kappa property, which plays the role of the periods relation in almost-periodicity theory. The property guarantees that the unpredictability in a single variable is inherited by the function on the diagonal of the arguments space. This is why we say that the new results is a next step in application of the technique.

3. Kappa Property of Unbounded Sequences

Consider a sequence of positive real numbers $t_k,$ $t_k\to \infty$ as $k\to \infty .$ Below, the following two simple lemmas will be of use. They are rather general results adapted to the needs of the present paper.

Lemma 1. 

For an arbitrary sequence of positive real numbers $t_k,$ $k=1,2,\cdots ,$ and a positive number ω, there exist a subsequence $t_{k_l},$ $l=1,2,\cdots ,$ and a number ${\tau }_{\omega },$ $0\le {\tau }_{\omega }<\omega ,$ such that $t_{k_l}\to {\tau }_{\omega }\left(mod\omega \right)$ as $l\to \infty .$

Proof. 

Consider the sequence ${\tau }_k$, such that $t_k\equiv {\tau }_k\left(mod\omega \right),$ and $0\le {\tau }_k<\omega$ for all $k\ge 1.$ The boundedness of the sequence ${\tau }_k$ implies that there exists a subsequence ${\tau }_{k_l},$ which converges to a number ${\tau }_{\omega }$ [41].  □

For fixed $\omega >0,$ by the last lemma, there exist a subsequence $t_{k_l}$ and a number ${\tau }_{\omega }$, such that $t_{k_l}\to {\tau }_{\omega }\left(mod\omega \right)$ as $l\to \infty .$ In what follows, considering applications for unpredictable and Poisson stable functions, we shall call the number ${\tau }_{\omega }$ as the Poisson shift with respect to the $\omega .$ The set of all Poisson shifts ${\mathcal{T}}_{\omega }$ is not empty. It can consist of several or even an infinite number of elements. The number ${\kappa }_{\omega }=inf{\mathcal{T}}_{\omega },$ $0\le {\kappa }_{\omega }<\omega ,$ is said to be Poisson number with respect to the number $\omega .$ If ${\kappa }_{\omega }=0,$ then we say that the sequence $t_k$ satisfies kappa property with respect to the number $\omega .$ The following assertion is useful in the next part of the paper.

Lemma 2 

([24]). ${\kappa }_{\omega }\in {\mathcal{T}}_{\omega }.$

Proof. 

Assume on the contrary that ${\kappa }_{\omega }$ is not in ${\mathcal{T}}_{\omega }.$ Then, there exists a strictly decreasing sequence ${\tau }_m,$ $m\ge 1,$ in ${\mathcal{T}}_{\omega },$ such that ${\tau }_m\to {\kappa }_{\omega }.$ For each natural $m,$ denote by $t_i^m$ a subsequence of $t_k$, such that $t_i^m\to {\tau }_m\left(mod\omega \right)$ as $i\to \infty .$

Fix a sequence of positive numbers ${ϵ}_n,$ which converges to the zero. One can find numbers $i_n,$ $n=1,2,\dots ,$ such that $|t_{i_n}^n-{\tau }_n|<{ϵ}_n\left(mod\omega \right).$ It is clear that $t_{i_n}^n\to {\kappa }_{\omega }\left(mod\omega \right)$ as $n\to \infty .$  □

Next, examples are provided to demonstrate how rich the set of sequences is with respect to the kappa property.

Example 1. 

Let us take the unbounded sequence $t_k=\frac{(k-1)\omega }{m},$ $k\in \mathbb{N},$ where $m\in \mathbb{N},$ $\omega >0$ are fixed numbers. If $m=1$ then $t_k\equiv 0\left(mod\omega \right),$ $k\in \mathbb{N},$ and there exists a unique Poisson shift, ${\tau }_{\omega }=0.$ If $m=2$ then $t_k\equiv 0\left(mod\omega \right)$ for even numbers $k,$ and $t_k\equiv \frac{\omega }{2}\left(mod\omega \right),$ if k is an odd number. There is no other Poisson shifts, therefore, ${\mathcal{T}}_{\omega }=$ $\{0,\frac{\omega }{2}\}.$ Generally, one can find that the set of Poisson shifts is ${\mathcal{T}}_{\omega }=$ $\{0,\frac{\omega }{m},\frac{2\omega }{m},\cdots ,\frac{(m-1)\omega }{m}\}.$ Thus, we procure, for any $m=1,2,\cdots ,$ the sequence $t_k$ satisfies the kappa property with respect to $\omega .$

Example 2. 

Now, consider the sequence $t_k=k\omega +{\mu }_k,$ $0<{\mu }_k<\omega ,$ $k=1,2,\cdots ,$ ${\mu }_k,$ where the sequence ${\mu }_k$ is determined as follows,

$$\begin{array}{ccc}& & {\mu }_{2^l-l}=\frac{\omega }{2^l},{\mu }_{2^l-l+1}=\frac{2\omega }{2^l},\cdots ,{\mu }_{2^{l+1}-l-2}=\frac{(2^l-1)\omega }{2^l},l=1,2,\cdots .\hfill \end{array}$$

Thus, the sequence ${\mu }_k,$ $k=1,2,\cdots ,$ is obtained, and each element of the section $[0,\omega ]$ is a Poisson shift. So, the example when ${\mathcal{T}}_{\omega }$ is an uncountable set of numbers is considered, and the sequence $t_k$ satisfies the kappa property with respect to the number $\omega .$

4. Unpredictability of Compartmental Periodic Functions

This part is of main theoretical achievements of the paper. Theorem 1 discusses the most weak sufficient conditions for the unpredictability of compartmental functions with the periodic component, and it is more theoretical than results of the following Theorems 2–4, which are constructive to determine unpredictable functions in examples and experiments.

Theorem 1. 

Assume that $G(u,v,x):$ $\mathbb{R}\times \mathbb{R}\times D\to {\mathbb{R}}^n,$ $D\subset {\mathbb{R}}^n$ is an open and bounded set, which is a continuous function, and $\omega -$periodic in u uniformly with respect to v and $x.$ Then, the function $g(t,x)=G(t,t,x),$ is unpredictable in $t,$ uniformly with respect to $x,$ if the following conditions are valid:

(i) 

for each $ϵ>0$ there exists a positive number η such that $\parallel G(t+s,t,x)-G(t,t,x)\parallel <ϵ$ if $\left|s\right|<\eta ,t\in \mathbb{R},x\in D;$

there exist sequences $t_k,$ $s_k$ both of which diverges to infinity as $k\to \infty ,$ and positive numbers ${ϵ}_0,\delta$ such that

(ii) 

the sequence $t_k$ satisfies the kappa property with respect to the period $\omega ;$

(iii) 

${\displaystyle \underset{I\times D}{sup}\parallel G(t,t+t_k,x)-G(t,t,x)\parallel \to 0}$ on each bounded interval $I\subset R;$

(iv) 

${\displaystyle \underset{[s_k-\delta ,s_k+\delta ]\times D}{inf}\parallel G(t,t+t_k,x)-G(t,t,x)\parallel >{ϵ}_0,}$$k\in \mathbb{N}.$

Proof. 

Let us fix a positive number $ϵ,$ and a bounded interval $I\in \mathbb{R}.$ Since the sequence $t_k$ satisfies the kappa property, one can write, without loss of generality, that $t_k\to 0\left(mod\omega \right)$ as $k\to \infty .$ Therefore, by conditions $\left(i\right)$ and $\left(iii\right),$ the following inequalities are valid:

$$\begin{array}{c}\hfill \underset{\mathbb{R}\times D}{sup}\parallel G(t+t_k,t,x)-G(t,t,x)\parallel <\frac{ϵ}{2}\end{array}$$

(1)

and

$$\begin{array}{c}\hfill \underset{I\times D}{sup}\parallel G(t,t+t_k,x)-G(t,t,x)\parallel <\frac{ϵ}{2},\end{array}$$

(2)

for sufficiently large $k.$

Using inequalities (1) and (2), we obtain:

$$\begin{array}{ccc}& & \parallel g(t+t_k,x)-g(t,x)\parallel =\parallel G(t+t_k,t+t_k,x)-G(t,t,x)\parallel \le \hfill \\ & & \parallel G(t+t_k,t+t_k,x)-G(t,t+t_k,x)\parallel +\parallel G(t,t+t_k,x)-G(t,t,x)\parallel <\hfill \\ & & \frac{ϵ}{2}+\frac{ϵ}{2}=ϵ,\hfill \end{array}$$

for all $t\in I,$ $x\in D.$ That is, $g(t+t_k,x)$ converges to $g(t,x)$ on each arbitrary bounded time interval uniformly for $x\in D.$ Moreover, conditions $\left(i\right)$ and $\left(ii\right)$ imply that ${\displaystyle \underset{\mathbb{R}\times D}{sup}\parallel G(t+t_k,t,x)-G(t,t,x)\parallel <\frac{{ϵ}_0}{2}}$ for sufficiently large $k.$ Applying assumption $\left(iv\right),$ one can obtain:

$$\begin{array}{ccc}& & \parallel g(t+t_k,x)-g(t,x)\parallel =\parallel G(t+t_k,t+t_k,x)-G(t,t,x)\parallel \ge \hfill \\ & & \parallel G(t+t_k,t+t_k,x)-G(t+t_k,t,x)\parallel -\parallel G(t+t_k,t,x)-G(t,t,x)\parallel >\hfill \\ & & {ϵ}_0-\frac{{ϵ}_0}{2}=\frac{{ϵ}_0}{2},\hfill \end{array}$$

for all $t\in [s_k-\delta ,s_k+\delta ],$ $x\in D,$ $k\in \mathbb{N}.$ The lemma is proved.  □

The following assertion is a corollary of the Theorem 1.

Theorem 2. 

Assume that a continuous and bounded function $G(u,v):\mathbb{R}\times \mathbb{R}\to {\mathbb{R}}^n,$ is $\omega -$periodic in $u.$ The function $f\left(t\right)=G(t,t)$ is unpredictable if the following conditions are valid,

(i) 

for each $ϵ>0$ there exists a positive number η such that $\parallel G(t+s,t)-G(t,t)\parallel <ϵ$ if $\left|s\right|<\eta ,t\in \mathbb{R};$

there exist sequences $t_k,$ $s_k$ both of which diverges to infinity as $k\to \infty ,$ and positive numbers ${ϵ}_0,\delta$, such that

(ii) 

the sequence $t_k$ satisfies kappa property with respect to the period $\omega ;$

(iii) 

$\parallel G(t,t+t_k)-G(t,t)\parallel \to 0,$ uniformly on each bounded interval $I\subset R$ of $t;$

(iv) 

${\displaystyle \underset{[s_k-\delta ,s_k+\delta ]}{inf}\parallel G(t,t+t_k)-G(t,t)\parallel >{ϵ}_0,}$$k\in \mathbb{N}.$

Remark 3. 

Conditions $\left(iii\right)$ and $\left(iv\right)$ in the Theorem 2 are satisfied if $G(t,u)$ is unpredictable in the second argument by Definition 4.

Theorem 3. 

Assume that a function $G(t,u):\mathbb{R}\times D\to {\mathbb{R}}^n,D\subseteq {\mathbb{R}}^n,$ is $\omega -$periodic in t and satisfies the inequalities $L_1∥u_1-u_2∥\le ∥G(t,u_1)-G(t,u_2)∥\le L_2∥u_1-u_2∥,$ where $L_1,L_2$ are positive constants, for all $t\in \mathbb{R},u_1,u_2\in D.$ If $\upsilon \left(t\right):\mathbb{R}\to D$ is an unpredictable function, such that the convergence sequence $t_k$ admits the kappa property with respect to period ω, then $G(t,\upsilon (t\left)\right)$ is an unpredictable function.

Proof. 

Consider the function $F(t,u)=G(t,\upsilon (u\left)\right).$ We shall prove that $F(t,u)$ is unpredictable in $u.$ Let us fix positive number $ϵ$ and a bounded interval $I.$ Since of the kappa property, for a sufficiently large number k, we have ${\displaystyle \parallel \upsilon (u+t_k)-\upsilon \left(u\right)\parallel <\frac{ϵ}{L_2}}$ for $u\in I.$ That is why,

$$\begin{array}{ccc}& & \parallel F(t,u+t_k)-F(t,u)\parallel =\parallel G(t,\upsilon (u+t_k))-G(t,\upsilon \left(u\right))\parallel \hfill \\ & & \le L_2\parallel \upsilon (u+t_k)-\upsilon \left(u\right)\parallel \le L_2\frac{ϵ}{L_2}\le ϵ,\hfill \end{array}$$

for all $t\in \mathbb{R},$ and $u\in I.$ On the other hand, there exist a sequence $s_k$ and positive numbers ${ϵ}_0,\delta$ such that $\parallel \upsilon (u+t_k)-\upsilon \left(u\right)\parallel >{ϵ}_0$ for $t\in [s_k-\delta ,s_k+\delta ].$ Therefore, we have:

$$\begin{array}{ccc}& & \parallel F(t,u+t_k)-F(t,u)\parallel =\parallel G(t,\upsilon (u+t_k))-G(t,\upsilon \left(u\right))\parallel \hfill \\ & & \ge L_1\parallel \upsilon (u+t_k)-\upsilon \left(u\right)\parallel >L_1{ϵ}_0,\hfill \end{array}$$

for each $t\in [s_k-\delta ,s_k+\delta ].$ Thus, one can conclude that the function $G(t,\upsilon (t\left)\right)$ is unpredictable.  □

Theorem 4. 

Assume that a function $G(t,u):\mathbb{R}\times D\to {\mathbb{R}}^n,D\subseteq {\mathbb{R}}^n,$ is a domain, it is unpredictable in t uniformly with respect to $u,$ and it satisfies the inequality $∥G(t,u_1)-G(t,u_2)∥\le L∥u_1-u_2∥,$ $t\in \mathbb{R},u_1,u_2\in D,$ where L is positive constant. If $\upsilon \left(t\right):\mathbb{R}\to D$ is a Poisson stable function with the Poisson sequence $t_k$ common with that for $G(t,u),$ and $2L{sup}_{t\in \mathbb{R}}\parallel \upsilon \left(t\right)\parallel <{ϵ}_0,$ where ${ϵ}_0$ is a separation constant for $G(t,u)$ then the composition $G(t,\upsilon (t\left)\right)$ is an unpredictable function.

Proof. 

Let us fix a positive number $ϵ,$ and a bounded interval $I.$ Since $G(t,\upsilon (t\left)\right)$ is unpredictable in $t,$ and $\upsilon \left(t\right)$ is a Poisson stable function, there exists sufficiently large $k,$ such that: ${\displaystyle \parallel G(t+t_k,\upsilon (t+t_k))-G(t,\upsilon (t+t_k))\parallel <\frac{ϵ}{2},}$ and ${\displaystyle \parallel \upsilon (t+t_k)-\upsilon \left(t\right)\parallel <\frac{ϵ}{2L}}$ for $t\in I.$ That is,

$$\begin{array}{ccc}& & \parallel G(t+t_k,\upsilon (t+t_k))-G(t,\upsilon \left(t\right))\parallel \le \parallel G(t+t_k,\upsilon (t+t_k))-G(t,\upsilon (t+t_k))\parallel +\hfill \\ & & \parallel G(t,\upsilon (t+t_k))-G(t,\upsilon \left(t\right))\parallel \le \parallel G(t+t_k,\upsilon (t+t_k))-G(t,\upsilon (t+t_k))\parallel +\hfill \\ & & L\parallel \upsilon (t+t_k)-\upsilon \left(t\right)\parallel \le \frac{ϵ}{2}+L\frac{ϵ}{2L}\le ϵ,\hfill \end{array}$$

for all $t\in I.$ Thus, $G(t+t_k,\upsilon (t+t_k))\to G(t,\upsilon \left(t\right))$ uniformly on each bounded interval of the real axis. Under assumptions of the theorem, we have that there exists a sequence $s_k$ and positive numbers ${ϵ}_0,\delta$ such that ${\displaystyle \parallel G(t+t_k,\upsilon (t+t_k))-G(t,\upsilon (t+t_k))\parallel >{ϵ}_0}$ for $t\in [s_k-\delta ,s_k+\delta ].$ We obtain:

$$\begin{array}{ccc}& & \parallel G(t+t_k,\upsilon (t+t_k))-G(t,\upsilon \left(t\right))\parallel \ge \parallel G(t+t_k,\upsilon (t+t_k))-G(t,\upsilon (t+t_k))\parallel -\hfill \\ & & \parallel G(t,\upsilon (t+t_k))-G(t,\upsilon \left(t\right))\parallel \ge \parallel G(t+t_k,\upsilon (t+t_k))-G(t,\upsilon (t+t_k))\parallel -\hfill \\ & & L\parallel \upsilon (t+t_k)-\upsilon \left(t\right)\parallel >{ϵ}_0-2L\underset{t\in \mathbb{R}}{sup}\parallel \upsilon \left(t\right)\parallel >0,\hfill \end{array}$$

for $t\in [s_k-\delta ,s_k+\delta ],$ and the function $G(t,\upsilon (t\left)\right)$ is unpredictable.  □

5. Unpredictable Functions Related to the Logistic Equation

In this part of the paper, examples of two unpredictable functions are presented. They have the unpredictability, and additional constructive properties, which significantly increase the use of the functions. Lemmas 3–6 make strong theoretical basis for future research in industrial and neuroscience problems. The approach covers both deterministic and stochastic potentials.

Let us consider the logistic map:

$${\lambda }_{i+1}=\nu {\lambda }_i(1-{\lambda }_i),i\in \mathbb{Z}.$$

(3)

In [23], it was proved that, for each $\nu \in [3+{(2/3)}^{1/2},4]$, the Equation (3) admits an unpredictable solution ${\mu }_i,$ $i\in \mathbb{Z}.$ That is, there exist a positive number ${ϵ}_0,$ and the sequences ${\zeta }_k,{\eta }_k,$ $k\in \mathbb{N},$ of positive integers, both of which diverge to infinity, such that $|{\mu }_{i+{\zeta }_k}-{\mu }_i|\to 0$ as $k\to \infty$ for each i in a bounded interval of integers and $|{\mu }_{{\zeta }_k+{\eta }_k}-{\mu }_{{\eta }_k}|>{ϵ}_0$ for each $k\in \mathbb{N}.$

Lemma 3. 

Assume that $\xi \left(t\right):(0,h]\to {\mathbb{R}}^n,$ where h is a positive number, is a bounded function. Then, the function $\pi \left(t\right)={\mu }_i\xi (t-ih),$ $t\in (ih,(i+1\left)h\right],$ $i\in \mathbb{Z},$ is Poisson stable in the sense of Definition 2.

Proof. 

Let us fix an interval of real numbers $(\alpha ,\beta )$ and a number $i\in \mathbb{Z}$ such that $(\alpha ,\beta )\subset \left[\right(i-1)h,(i+s+1\left)h\right],$ where s is a natural number. Then, for $t_k={\zeta }_{k}h,$ $k\in \mathbb{N},$ and $t\in (jh,(j+1\left)h\right],$ $i-1\le j\le i+s,$, we have $t+{\zeta }_{k}h\in ((j+{\zeta }_k)h,(j+{\zeta }_k+1)h],$ and $\xi (t-(j+{\zeta }_k)h)=\xi (t-jh).$

Denote $M={sup}_{t\in (0,h]}\parallel \xi \left(t\right)\parallel .$ For a fixed positive number $ϵ,$ and sufficiently large number k, it is true that $|{\mu }_{j+{\zeta }_k}-{\mu }_j|<\frac{ϵ}{M},$ $i-1\le j\le i+s.$ Therefore, for $t\in (lh,(l+1\left)h\right],$ where l is a fixed integer number from $i-1$ to $i+s,$ one can obtain that

$$\begin{array}{ccc}\hfill & & \parallel \pi (t+t_k)-\pi \left(t\right)\parallel =\parallel \pi (t+{\zeta }_{k}h)-\pi \left(t\right)\parallel =\parallel {\mu }_{l+{\zeta }_k}\xi (t-(l+{\zeta }_k)h)-{\mu }_l\xi (t-lh)\parallel =\hfill \\ & & |{\mu }_{l+{\zeta }_k}-{\mu }_j|\parallel \xi (t-lh)\parallel \le |{\mu }_{l+{\zeta }_k}-{\mu }_l|M<ϵ.\hfill \end{array}$$

The last inequality is valid for all $i-1\le l\le i+s.$ Consequently, $\parallel \pi (t+t_k)-\pi \left(t\right)\parallel <ϵ$ if $t\in (\alpha ,\beta ).$ Thus, the function $\pi \left(t\right)$ is Poisson stable.  □

Lemma 4. 

The function $\pi \left(t\right)={\mu }_i\xi (t-ih),$ $t\in (ih,(i+1\left)h\right],$ $i\in \mathbb{Z},$ is unpredictable if the following condition is satisfied,

(A) 

there exists a positive number ${ϵ}_1$ such that $\parallel \xi \left(t\right)\parallel >{ϵ}_1$ for each $t\in (0,h].$

Proof. 

By Lemma 3, the sequence of functions $\pi (t+t_k)$ uniformly converges to $\pi \left(t\right)$ on compact subsets of $\mathbb{R}.$ It remains to show that the function $\pi \left(t\right)$ satisfies the separation property. Due to the unpredictability of the sequence ${\mu }_i,$ there exist a positive number ${ϵ}_0,$ and the sequence ${\eta }_k,$ ${\eta }_k\to \infty$ as $k\to \infty ,$ such that $|{\mu }_{{\zeta }_k+{\eta }_k}-{\mu }_{{\eta }_k}|>{ϵ}_0$ for each $k\in \mathbb{N}.$

For $t_k={\zeta }_{k}h,$ $k=1,2,\cdots ,$ and $t\in ({\eta }_{k}h,({\eta }_k+1)h]$ we have that $t+t_k=t+{\zeta }_{k}h\in (({\zeta }_k+{\eta }_k)h,({\zeta }_k+{\eta }_k+1)h].$ That is why $\xi (t+t_k)=\xi (t-({\zeta }_k+{\eta }_k)h)=\xi (t-{\zeta }_{k}h)$ for all $t\in ({\eta }_{k}h,({\eta }_k+1)h].$ So, by using condition (A), we obtain:

$$\begin{array}{ccc}\hfill & & \parallel \pi (t+t_k)-\pi \left(t\right)\parallel =\parallel {\mu }_{{\zeta }_k+{\eta }_k}\xi (t-({\zeta }_k+{\eta }_k)h)-{\mu }_{{\eta }_k}\xi (t-{\zeta }_{k}h)\parallel =\hfill \\ & & |{\mu }_{{\zeta }_k+{\eta }_k}-{\mu }_{{\eta }_k}|\parallel \xi (t-{\zeta }_{k}h)\parallel >{ϵ}_0{ϵ}_1>0,\hfill \end{array}$$

(4)

for all $t\in ({\eta }_{k}h,({\eta }_k+1)h],$ $k=1,2,\cdots .$ Thus, the function $\pi \left(t\right)$ is unpredictable with with positive numbers ${ϵ}^{*}={ϵ}_0{ϵ}_1,$ $\delta =\frac{h}{2},$ and sequences $t_k={\zeta }_{k}h,$ $s_k={\eta }_{k}h+\frac{h}{2},$ $k\in \mathbb{N}.$  □

Lemma 5. 

The function $\pi \left(t\right)={\mu }_i\xi (t-ih),$ $t\in (ih,(i+1\left)h\right],$ $i\in \mathbb{Z},$ is unpredictable if the following condition is valid,

(B) 

there exist positive numbers $\delta ,s$ and ${ϵ}_1$ such that $[s-\delta ,s+\delta ]\subset (0,h]$ and $\parallel \xi \left(t\right)\parallel >{ϵ}_1$ for each $t\in [s-\delta ,s+\delta ].$

Proof. 

The convergence property of the function $\pi \left(t\right)$ is proved in Lemma 3. Let us show that the function $\pi \left(t\right)$ satisfies the separation property. There exist a positive number ${ϵ}_0,$ and the sequence ${\eta }_k,$ ${\eta }_k\to \infty$ as $k\to \infty ,$ such that $|{\mu }_{{\zeta }_k+{\eta }_k}-{\mu }_{{\eta }_k}|>{ϵ}_0$ for each $k\in \mathbb{N}.$

From $t_k={\zeta }_{k}h,$ $k=1,2,\cdots ,$ and $t\in ({\eta }_{k}h+s-\delta ,{\eta }_{k}h+s+\delta ]$ it follows that $t+t_k=t+{\zeta }_{k}h\in (({\zeta }_k+{\eta }_k)h+s-\delta ,({\zeta }_k+{\eta }_k)h+s+\delta ].$ Therefore, $\xi (t+t_k)=\xi (t-({\zeta }_k+{\eta }_k)h)=\xi (t-{\eta }_{k}h),$ $k=1,2,\cdots .$ Applying condition (B), we obtain:

$$\begin{array}{ccc}\hfill & & \parallel \pi (t+t_k)-\pi \left(t\right)\parallel =\parallel {\mu }_{{\zeta }_k+{\eta }_k}\xi (t-({\zeta }_k+{\eta }_k)h)-{\mu }_{{\eta }_k}\xi (t-{\zeta }_{k}h)\parallel =\hfill \\ & & |{\mu }_{{\zeta }_k+{\eta }_k}-{\mu }_{{\eta }_k}|\parallel \xi (t-{\eta }_{k}h)\parallel >{ϵ}_0{ϵ}_1>0,\hfill \end{array}$$

(5)

for all $t\in ({\eta }_{k}h+s-\delta ,{\eta }_{k}h+s+\delta ],$ $k=1,2,\cdots .$ So, one can conclude that the function $\pi \left(t\right)$ is unpredictable with positive numbers ${ϵ}^{*}={ϵ}_0{ϵ}_1,$ $\delta ,$ and sequences $t_k={\zeta }_{k}h,$ $s_k={\eta }_{k}h+s,$ $k=1,2,\cdots .$  □

Now, let us define a continuous function $\Xi \left(t\right):\mathbb{R}\to {\mathbb{R}}^n,$ such that:

$$\begin{array}{c}\hfill \Xi \left(t\right)={\int }_{-\infty }^t{e}^{-\alpha (t-s)}\pi \left(s\right)ds,\end{array}$$

(6)

where $\alpha$ is a positive real number, and $\pi \left(t\right)$ is the unpredictable function, which satisfies one of the conditions (A) or (B). The function $\Xi \left(t\right)$ is bounded on the whole real axis, such that ${sup}_{t\in \mathbb{R}}\parallel \Xi \left(t\right)\parallel \le \frac{M_{\pi }}{\alpha },$ where $M_{\pi }={sup}_{t\in \mathbb{R}}\parallel \pi \left(t\right)\parallel .$ By applying the unpredictability of the function $\pi \left(t\right)$ with condition (B), we will prove the following lemma. One can see that the condition (B) implies the condition (A).

Lemma 6. 

The function $\Xi \left(t\right)$ is unpredictable.

Proof. 

Consider a fixed bounded and closed interval $[a,b],$ of the axis and a positive number $ϵ$. Now, applying the method of included intervals [24], we will show that the sequence $\Xi (t+t_k)$ uniformly converges to $\Xi \left(t\right)$ on $[a,b].$ Let us fix a positive number $\xi$ and a number $c<a,$ which satisfy the following inequalities $\frac{2M_{\pi }}{\alpha }{e}^{-\alpha (a-c)}<\frac{ϵ}{2}$ and $\frac{\xi }{\alpha }[1-e^{-\alpha (b-c)}]<\frac{ϵ}{2}.$ Let k be a large enough number, such that ${\displaystyle \parallel \pi (t+t_k)-\pi \left(t\right)\parallel <\xi }$ on $[c,b].$ Then, for all $t\in [a,b]$, we obtain:

$$\begin{array}{ccc}& & \parallel \Xi (t+t_k)-\Xi \left(t\right)\parallel =\parallel {\int }_{-\infty }^t{e}^{-\alpha (t-s)}(\pi (s+t_k)-\pi \left(s\right))ds\parallel =\hfill \\ & & \parallel {\int }_{-\infty }^c{e}^{-\alpha (t-s)}(\pi (s+t_k)-\pi \left(s\right))ds+{\int }_c^t{e}^{-\alpha (t-s)}(\pi (s+t_k)-\pi \left(s\right))ds\parallel \le \hfill \\ & & {\int }_{-\infty }^c{e}^{-\alpha (t-s)}2M_{\pi }ds+{\int }_c^t{e}^{-\alpha (t-s)}\xi ds\hfill \\ & & \le \frac{2M_{\pi }}{\alpha }{e}^{-\alpha (a-c)}+\frac{\xi }{\alpha }[1-e^{-\alpha (b-c)}]<\frac{ϵ}{2}+\frac{ϵ}{2}=ϵ.\hfill \end{array}$$

Thus, $\parallel \Xi (t+t_k)-\Xi \left(t\right)\parallel \to 0$ as $k\to \infty$ uniformly on the interval $[a,b].$

According Lemma 5, we have $\parallel \pi (t+t_k)-\pi \left(t\right)\parallel >{ϵ}^{*}$ for $t\in [s_k-\delta ,s_k+\delta ].$ Fix a natural number k and positive ${\delta }_1<\delta$, such that $\frac{2M_{\pi }{\delta }_1}{\alpha }[1-e^{-\alpha {\delta }_1}]<\frac{{ϵ}^{*}}{3\alpha }.$ Consider two alternative cases: (i) $\parallel \Xi (t_k+s_k)-\Xi \left(s_k\right)\parallel <\frac{2{\delta }_1{ϵ}^{*}}{3\alpha },$ (ii) $\parallel \Xi (t_k+s_k)-\Xi \left(s_k\right)\parallel \ge \frac{2{\delta }_1{ϵ}^{*}}{3\alpha }.$

It is easily seen that the following relation holds:

$$\begin{array}{ccc}\hfill & & {\displaystyle \Xi (t+t_k)-\Xi \left(t\right)=\Xi (t_k+s_k)-\Xi \left(s_k\right)+{\int }_{s_k}^t{e}^{-\alpha (t-s)}(\pi (s+t_k)-\pi \left(s\right))ds.}\hfill \end{array}$$

(7)

(i)

From the last relation, we obtain:

$$\begin{array}{ccc}\hfill & & {\displaystyle \parallel \Xi (t+t_k)-\Xi \left(t\right)\parallel \ge \parallel {\int }_{s_k}^t{e}^{-\alpha (t-s)}(\pi (s+t_k)-\pi \left(s\right))ds\parallel -\parallel \Xi (t_k+s_k)-\Xi \left(s_k\right)\parallel >}\hfill \\ & & {\int }_{s_k}^t{e}^{-\alpha (t-s)}{ϵ}^{*}ds-\frac{2{\delta }_1{ϵ}^{*}}{3\alpha }\ge \frac{{\delta }_1{ϵ}^{*}}{\alpha }-\frac{2{\delta }_1{ϵ}^{*}}{3\alpha }=\frac{{\delta }_1{ϵ}^{*}}{3\alpha }\hfill \end{array}$$

(8)

for $t\in [s_k-{\delta }_1,s_k+{\delta }_1].$

(ii)

Using the relation (7) we get that

$$\begin{array}{ccc}\hfill & & {\displaystyle \parallel \Xi (t+t_k)-\Xi \left(t\right)\parallel \ge \parallel \Xi (t_k+s_k)-\Xi \left(s_k\right)\parallel -\parallel {\int }_{s_k}^t{e}^{-\alpha (t-s)}(\pi (s+t_k)-\pi \left(s\right))ds\parallel >}\hfill \\ & & \frac{2{\delta }_1{ϵ}^{*}}{3\alpha }-{\int }_{s_k}^t{e}^{-\alpha (t-s)}2M_{\pi }ds\ge \frac{2{\delta }_1{ϵ}^{*}}{3\alpha }-\frac{2M_{\pi }{\delta }_1}{\alpha }[1-e^{-\alpha {\delta }_1}]>\frac{{\delta }_1{ϵ}^{*}}{3\alpha }\hfill \end{array}$$

(9)

for $t\in [s_k-{\delta }_1,s_k+{\delta }_1].$ Thus, the inequalities (8) and (9) prove finally that the function $\Xi \left(t\right)$ is unpredictable with positive numbers ${ϵ}_1=\frac{{\delta }_1{ϵ}^{*}}{3\alpha },$ ${\delta }_1$ and sequences $t_k,$ $s_k.$  □

6. Degree of Periodicity and Numerical Simulations

In this part of the paper, a quantitative characteristic, the degree of periodicity, is introduced for functions with the kappa property. Examples with graphs of compartmental unpredictable functions related to the logistic equation are presented. The dependence of their trajectories on the degree of periodicity is discussed.

To illustrate the dynamics of the compartmental unpredictable function, we will use the function $\Xi \left(t\right),$ which is defined by (6), with $\alpha =-3,$ and the function $\pi \left(t\right)={\mu }_i\xi (t-ih),$ $t\in (ih,(i+1\left)h\right],$ $i\in \mathbb{N},$ where $\xi \left(t\right)\equiv 1.$ The function $\Xi \left(t\right)$ is bounded, such that ${sup}_{t\in \mathbb{R}}|\Xi \left(t\right)|\le \frac{1}{3},$ and is the exponentially stable unpredictable solution of the differential equation ${\Xi }^{\prime }=-3\Xi +\pi \left(t\right).$ This is why, for the numerical simulations of the function, we will use solutions of the equation.

The number h is said to be the length of step of the functions $\pi \left(t\right)$ and $\Xi \left(t\right).$ For compartmental unpredictable functions, the ratio of the period and the length of step, $\nabla =\omega /h,$ is called the degree of periodicity.

Next, we shall construct the function, which is a compartmental one and unpredictable due to the kappa property.

Consider the following function, $G(t,u)=(5{sin}^2\left(0.1t\right)+0.1)arctan(\Xi \left(u\right))+0.5\Xi {\left(u\right)}^3,$, which is $10\pi -$periodic in $t,$ uniformly with respect to $u.$ The function $arctan\left(u\right)$ satisfies Lipschitz conditions with $L_1=3/4$ and $L_2=1,$ if $\left|u\right|\le \frac{1}{3}.$ This is why, according Theorems 6 and 7, the component-functions $arctan(\Xi (u\left)\right)$ and $0.5{\Xi }^3\left(u\right)$ are unpredictable.

Consider the function

$$\begin{array}{c}\hfill f_1\left(t\right)=G(t,t)=(5{sin}^2\left(0.1t\right)+0.1)arctan(\Xi \left(t\right))+0.5{\Xi }^3\left(t\right).\end{array}$$

(10)

where h—the length of step is a parameter.

We will show that the assumptions of Theorem 2 are valid for the function $f_1\left(t\right).$ The uniform continuity of $G(t,u)$ implies the condition (i) Since of $\omega =10\pi ,$ one can consider the function $\Xi \left(t\right)$ with the convergence sequence and separation sequences $t_k={\zeta }_{k}h,$ $s_k={\eta }_{k}h+s,$ $k=1,2,\cdots .$ such that condition (ii) is valid. Let us fix a bounded interval $I\subset \mathbb{R}.$ The sequence $\Xi (t+t_k)$ uniformly converges to $\Xi \left(t\right)$ on the interval. This is why,

$$\begin{array}{ccc}& & |G(t,t+t_k)-G(t,t)|\le |5{sin}^2\left(0.1t\right)+0.1\left|\right|arctan(\Xi (t+t_k))-arctan(\Xi \left(t\right))|+\hfill \\ & & 0.5|\Xi (t+t_k)-\Xi \left(t\right)\left|\right|{\Xi }^2(t+t_k)+\Xi (t+t_k)\Xi \left(t\right)+|{\Xi }^2\left(t\right)|\le 5.27|\Xi (t+t_k)-\Xi \left(t\right)|,\hfill \end{array}$$

and the sequence of functions $G(t,t+t_k)$ converges to $G(t,t)$ uniformly on $I.$ That is, condition $\left(iii\right)$ is satisfied.

According Lemma 6, for $t\in [s_k-{\delta }_1,s_k+{\delta }_1]$, we have $|\Xi (t+t_k)-\Xi \left(t\right)|>{ϵ}_1,k=1,2,\dots$ That is,

$$\begin{array}{ccc}& & |G(t,t+t_k)-G(t,t)|=|(5{sin}^2\left(0.1t\right)+0.1)arctan(\Xi (t+t_k))+0.5\Xi (t+t_k)-\hfill \\ & & {sin}^2\left(0.1t\right)arctan(\Xi \left(t\right))-0.5\Xi \left(t\right)|\ge |5{sin}^2\left(0.1t\right)+0.1|L_1|\Xi (t+t_k)-\Xi \left(t\right)|-\hfill \\ & & 0.5|{\Xi }^2(t+t_k)+\Xi (t+t_k)\Xi \left(t\right)+|{\Xi }^2\left(t\right)\left|\right|\Xi (t+t_k)-\Xi \left(t\right)|\ge \hfill \\ & & (5.1L_1-\frac{0.5}{3})|\Xi (t+t_k)-\Xi \left(t\right)|>3.65|\Xi (t+t_k)-\Xi \left(t\right)|>3.65{ϵ}_1.\hfill \end{array}$$

The last inequality implies that condition $\left(iv\right)$ is valid. Thus, all conditions of Theorem 2 are correct, and the function $f_1\left(t\right)$ is unpredictable. Moreover, the arguments of Theorem 2 indicates that $f_1\left(t\right)$ is a compartmental unpredictable function.

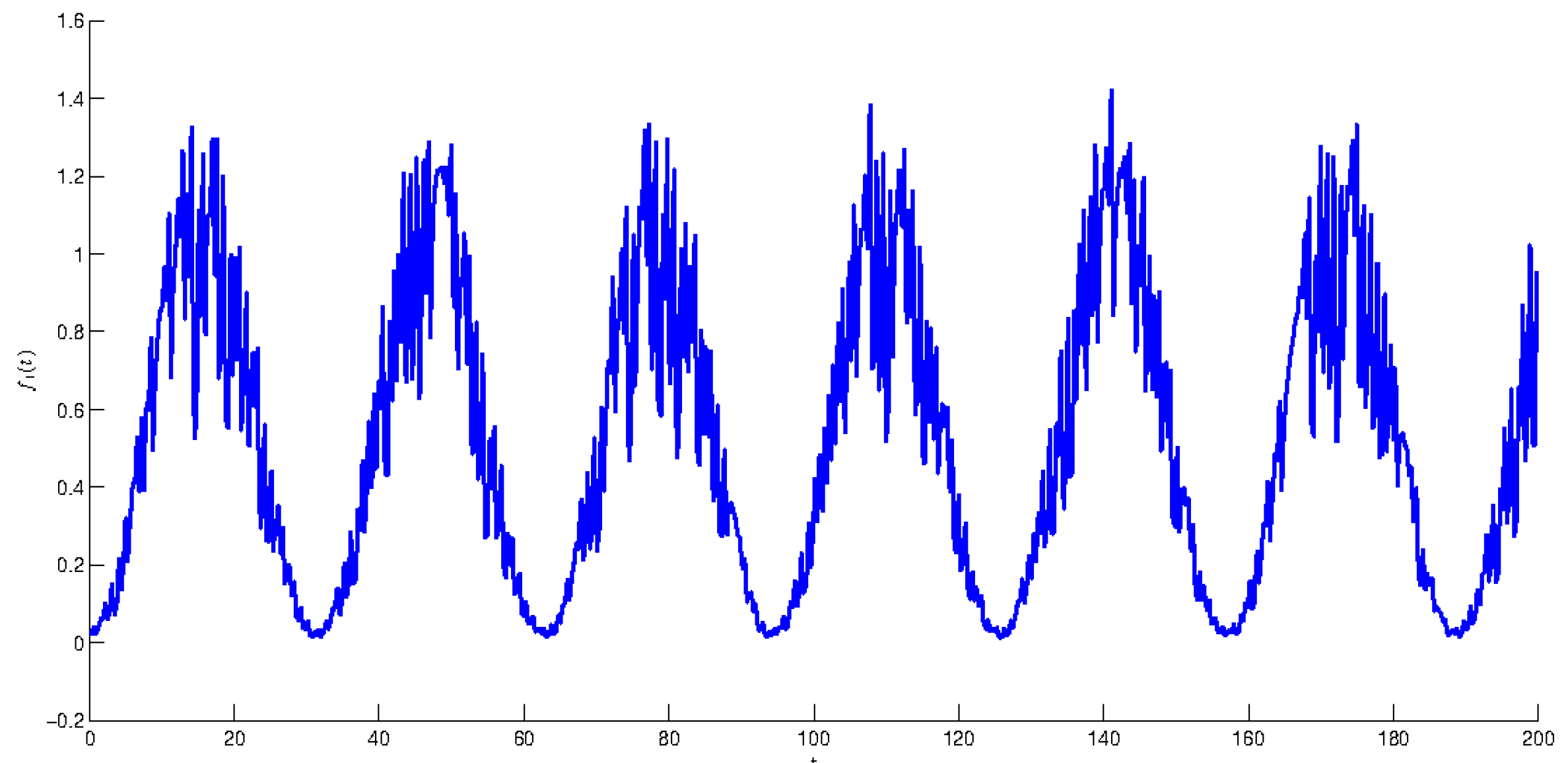
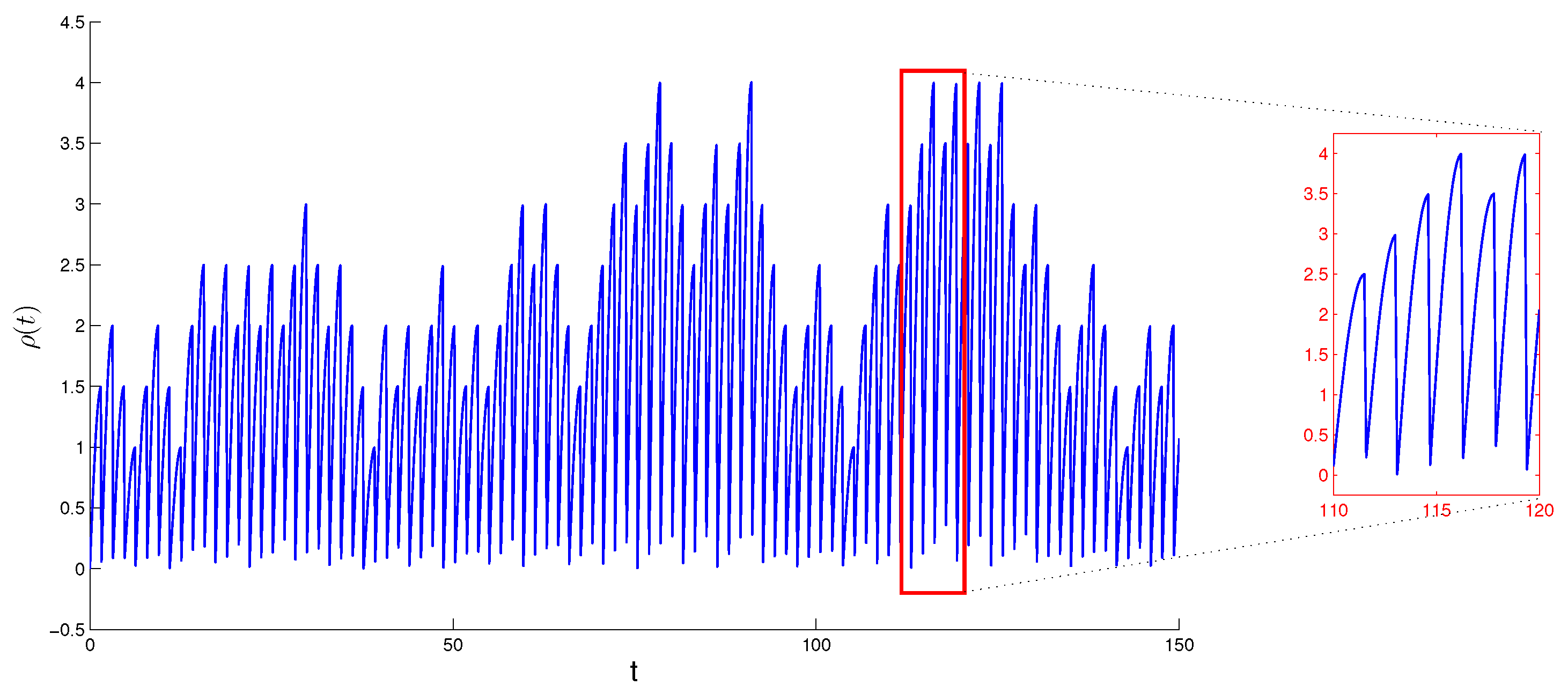
In Figure 1 the graph of function $f_1\left(t\right),$ where the length of step $h=0.1\pi ,$ and degree of periodicity $\nabla =200$, is shown.

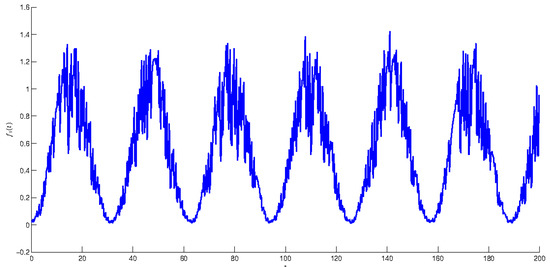
Figure 1. The graph of compartmental periodic unpredictable function $f_1\left(t\right).$ The length of step $h=0.1\pi ,$ and degree of periodicity $\nabla =200$.

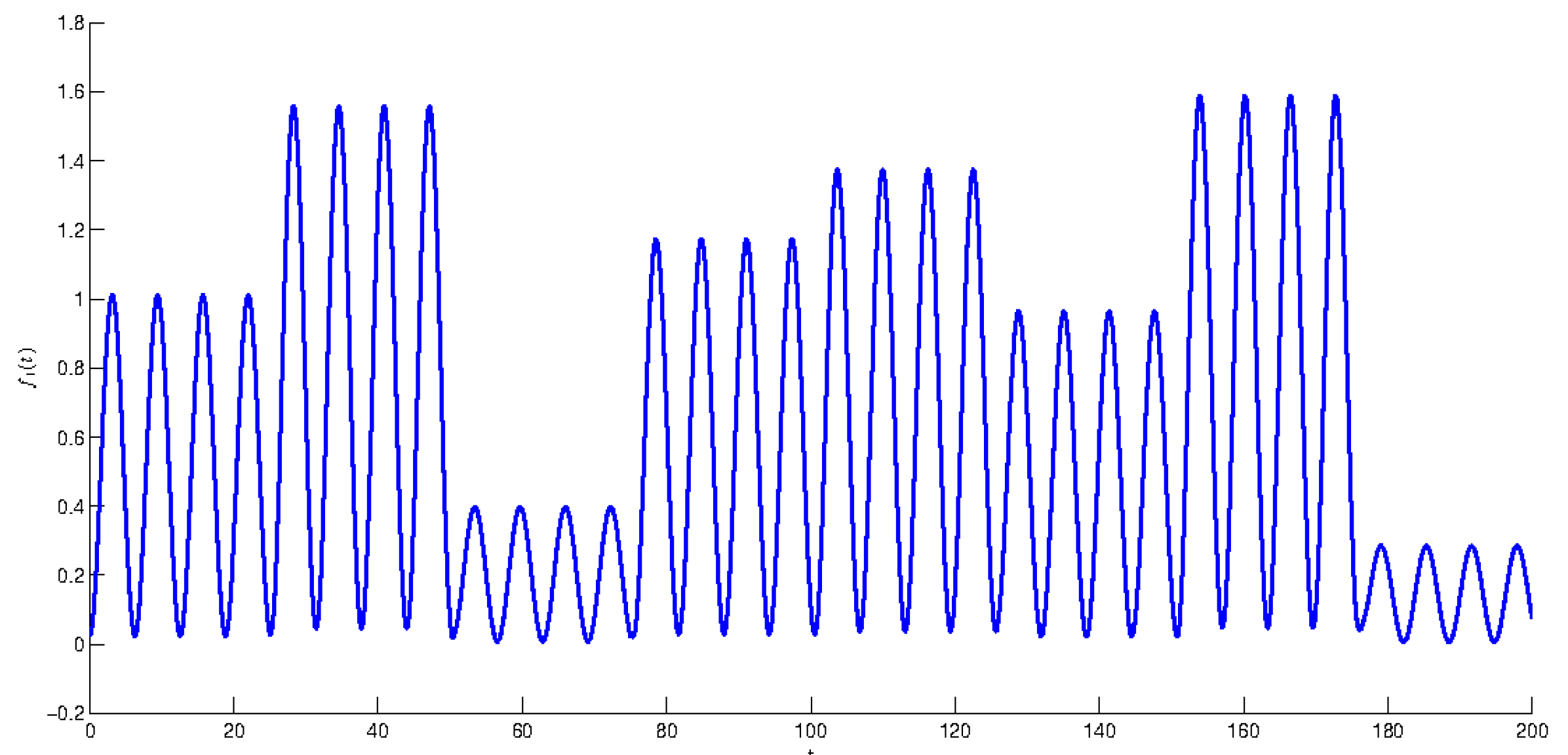
Similarly to the function $f_1\left(t\right),$ it can be shown that the compartmental periodic unpredictable function, $f_2\left(t\right)=G(t,t),$ where $G(t,u)=(5{sin}^2\left(0.5t\right)+0.1)arctan\left(u\right)+0.5u^3,$ and $u=\Xi \left(t\right),$ is unpredictable. The function $G(t,u)$ is $2\pi -$ periodic in $t,$ uniformly with respect to $u.$ Figure 2 depicts the graph of function $f_2\left(t\right)$ with length of step $h=8\pi ,$ so that the degree of periodicity $\nabla =0.25.$

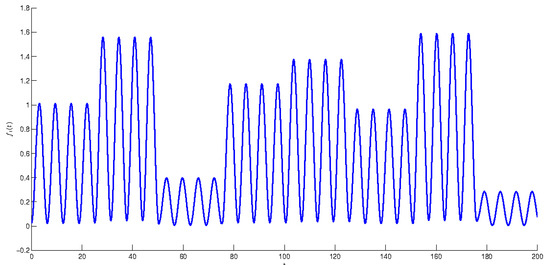
Figure 2. The graph of function $f_2\left(t\right)$ with the length of step $h=8\pi ,$ and the degree of periodicity $\nabla =0.25$.

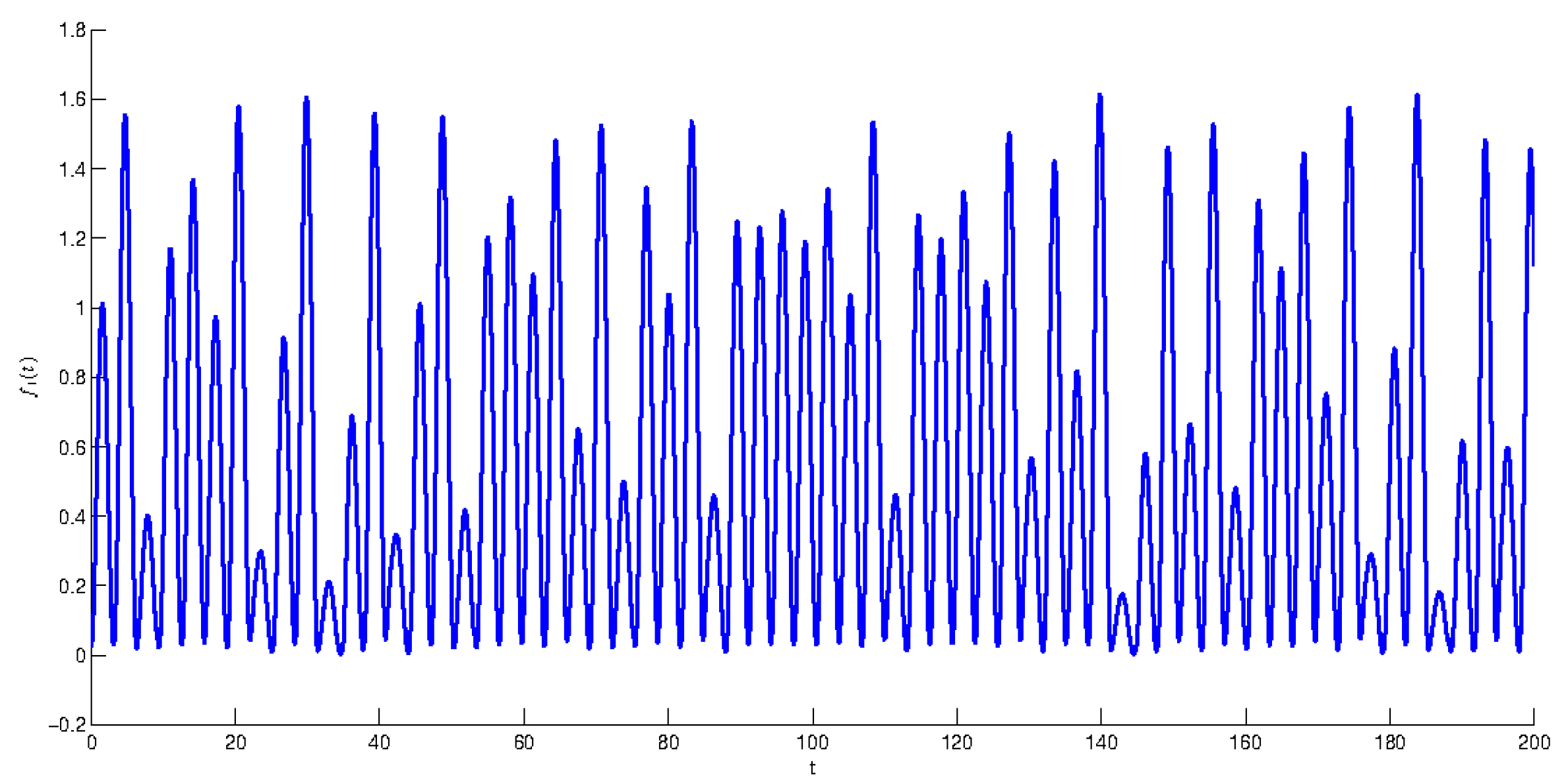
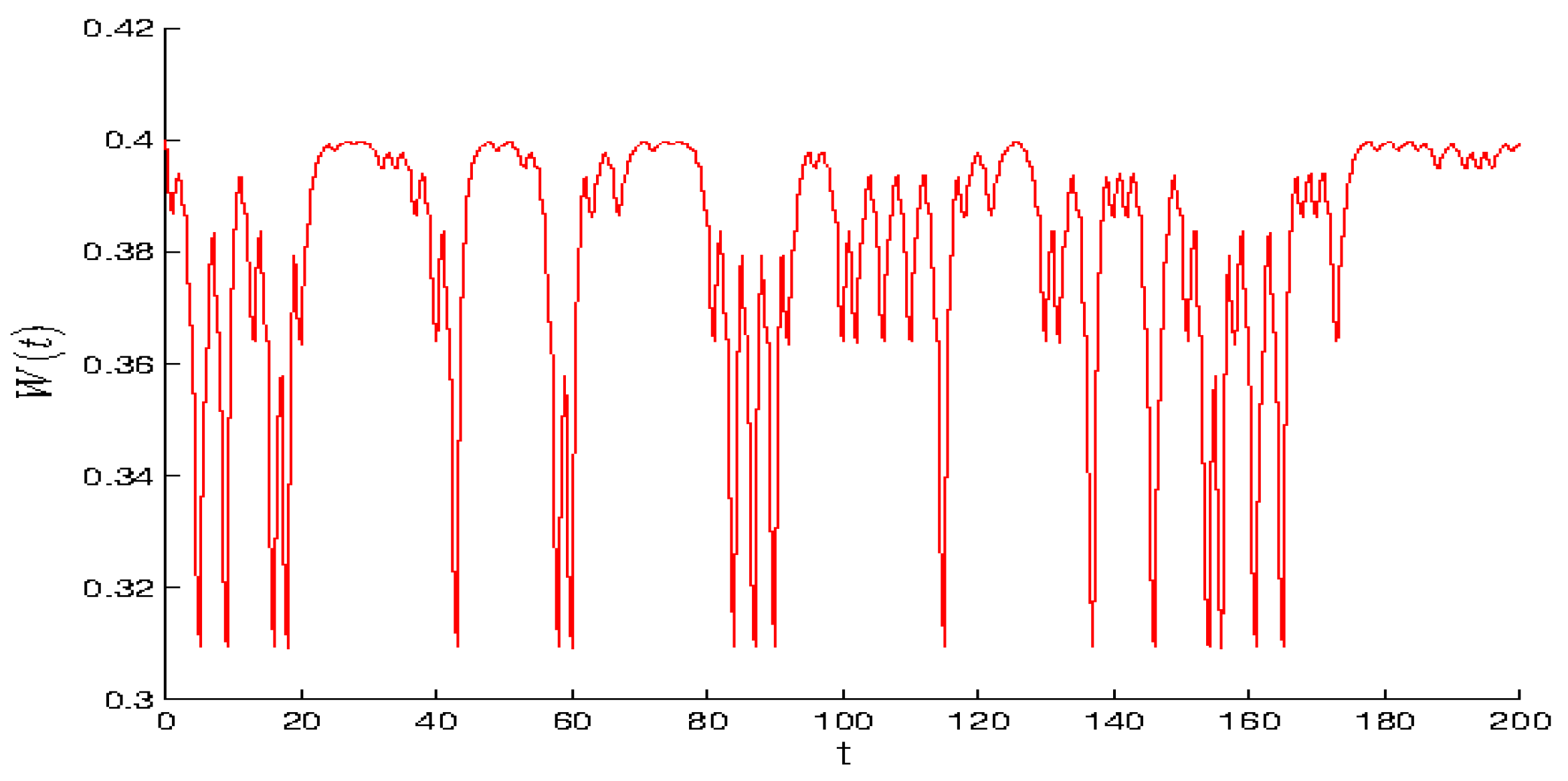
Compartmental periodic unpredictable function $f_3\left(t\right)=(5{sin}^2\left(t\right)+0.1)arctan(\Xi \left(t\right))+0.5{\Xi }^3\left(t\right),$ with the period $\pi$ and the length of step $h=\pi$ is presented in Figure 3. According Theorem 2, the function $f_3\left(t\right)$ is unpredictable.

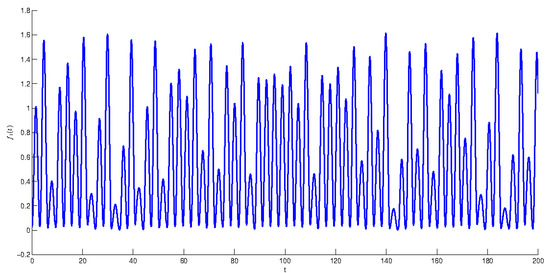
Figure 3. The graph of compartmental periodic unpredictable function $f_3\left(t\right).$ The degree of periodicity $\nabla =1$.

Issuing from the results of the last three simulations, let us make observations how the value of the degree of periodicity effects the shape of graphs of compartmental periodic unpredictable functions. Observing the graphs in Figure 1, when $\nabla >1,$ we see that the solution admits clear periodic shape, which is enveloped by the irregularity with small amplitude. Oppositely, if $\nabla \le 1,$ one can see in Figure 2 and Figure 3 that the periodicity lost its dominance and unpredictability prevails. More precisely, periodicity appears only locally on separated intervals, if $\nabla <1.$ That is, the periodicity envelopes the unpredictability this time. The periodicity is not seen at all for $\nabla =1$ in Figure 3. So, the unit is the boundary value between dominance of regularity and irregularity, which are present with periodicity and the unpredictability respectively. The conclusions can be useful for analysis of experiments [34,35,36,37,38].

7. Randomly Determined Compartmental Unpredictable Functions

In this section, we demonstrate algorithms how to construct unpredictable functions by using Markov chains with finite state spaces. They will be used in the Miscellanea for compartmental quasi-periodic unpredictable functions.

A Markov chain is a stochastic model, which describes a sequence of possible events, such that the probability of each event depends only on the state attained in the previous one [42,43,44].

Since we expect for the unpredictable dynamics realizations to be bounded, the special Markov chain with boundaries is constructed below. Let the real-valued scalar dynamics be:

$$\begin{array}{c}\hfill X_{n+1}=X_n+Y_n,n\ge 0,\end{array}$$

(11)

be given such that $Y_n=\{-0.5;0.5\}$ is a random variable. The probability distribution $P\left(0.5\right)=P(-0.5)=1/2,$ if $X_n\ne 1,4,$ and certain events $Y_n=-0.5,$ if $X_n=4,$ and $Y_n=0.5,$ if $X_n=1.$ To satisfy the construction of the present research, we will make the following agreements. First of all, denote $s_0=1,$ $s_1=1.5,$ $s_2=2,$ $s_3=2.5,$ $s_4=3,$ $s_5=3.5,$ $s_6=4.$ Consider the state space of the process $S=\{s_0,s_1,s_2,s_3,s_4,s_5,s_6\},$ and the value $X_n\in S$ is the state of the process at time $n.$ The Markov chain is a random process, which satisfies the property $P\{X_{n+1}=s_j|X_0,\dots ,X_n\}=P\{X_{n+1}=s_j|X_n\}$ for all $s_i,s_j\in S$ and $n\ge 0.$ Moreover, $P\{X_{n+1}=s_j|X_n=s_i\}=p_{ij},$ where $p_{ij}$ is the transition probability that the chain jumps from state i to state $j.$ It is clear that ${\sum }_{j=0}^6{p}_{ij}=1$ for all $i=0,\dots ,6.$ The unpredictability of infinite realizations of the dynamics is approved by Theorem 2.2 [45].

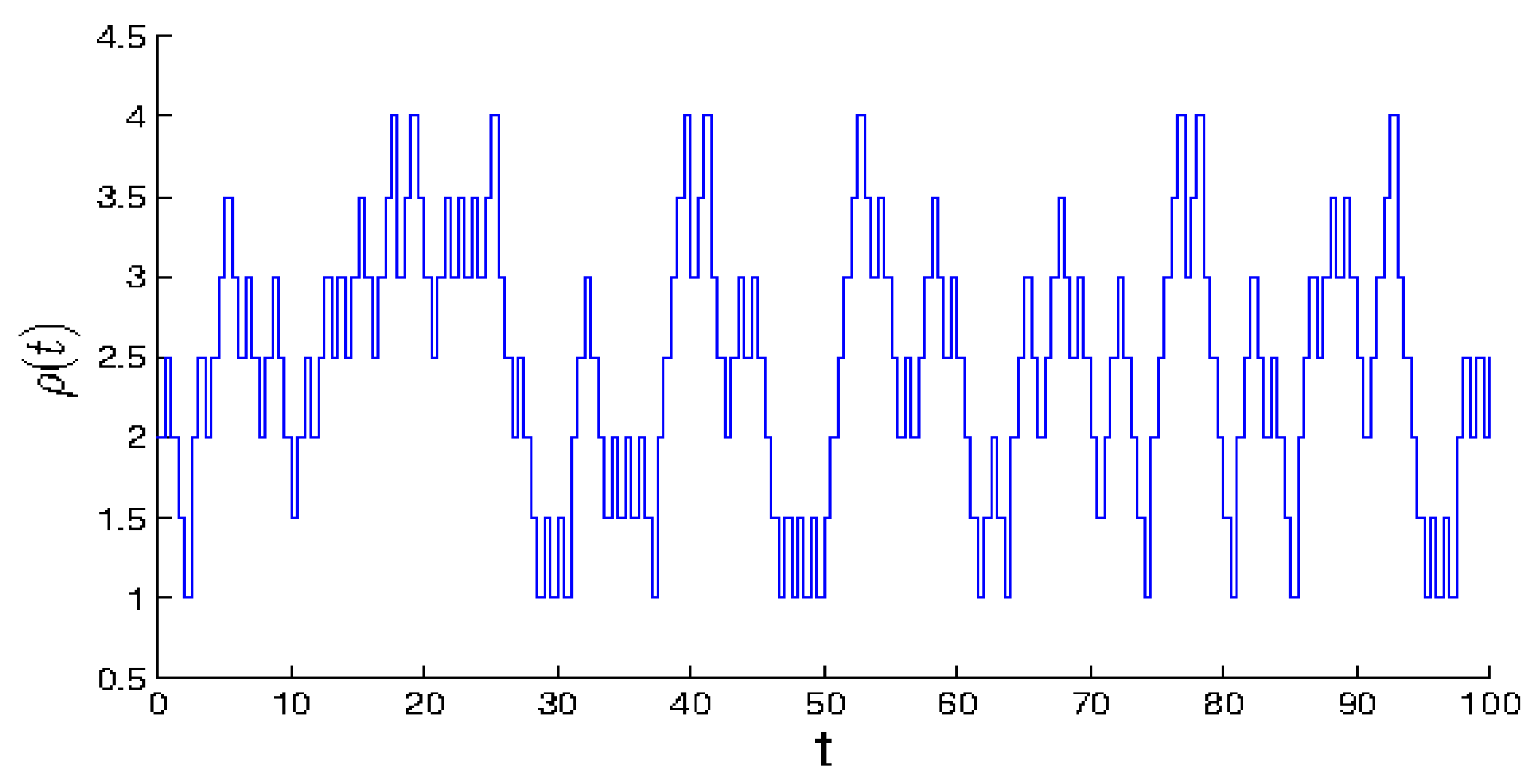
Next, we shall introduce randomly determined unpredictable function $\rho \left(t\right)=X_n\xi (t-nh),$ if $t\in [hn,h(n+1\left)\right),$ where $\xi \left(t\right):(0,h]\to \mathbb{R},$ is a bounded function. In Figure 4 and Figure 5, the graph of the function $\rho \left(t\right)$ with $\xi \left(t\right)\equiv 1$ and $\xi \left(t\right)=sin(t-0.5n\pi ),$ respectively, for all $t\in [hn,h(n+1\left)\right),$ is drawn.

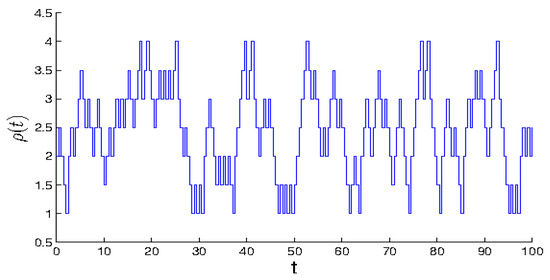
Figure 4. The graph of the piecewise constant unpredictable function $\rho \left(t\right)=X_n\xi (t-nh),t\in [hn,h(n+1)),n=0,1,2,\dots$ The vertical lines are drawn for better visibility.

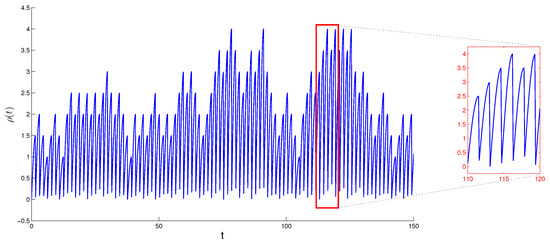
Figure 5. The graph of the piecewise continuous unpredictable function $\rho \left(t\right)=X_{n}sin(t$-$0.5n\pi ),$ $t\in [hn,h(n+1\left)\right),n=0,1,2,\dots$ The vertical lines are drawn for better visibility.

Now, let us show construction of continuous unpredictable functions through the Markov process. Consider the ordinary differential equation:

$$W^{\prime }\left(t\right)=\alpha W\left(t\right)+tanh\left(\rho \left(t\right)\right),$$

(12)

where $\alpha$ is a negative number. The Equation (12) admits a unique exponentially stable unpredictable solution [45]. It is impossible to specify the initial value of the solution, but, by applying the property of exponential stability, one can consider any solution as arbitrarily close. In Figure 6, the graph of the solution, $W\left(t\right),$ $W\left(0\right)=0.4$ of Equation (12), where the parameter $\alpha$ is equal to −2.5, and $\rho \left(t\right)=X_n$ for $t\in [n,n+1),$ is shown.

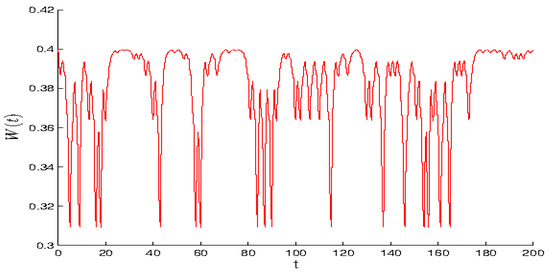
Figure 6. The solution $W\left(t\right)$ of Equation (12) with initial value $W\left(0\right)=0.4$ exponentially approaches the unpredictable Markovian function.

8. Miscellanea

In the beginning of this part, two theorems are provided for construction of the unpredictable functions by using simple algebraic operations. The assertion of unpredictability of a composition is another result of the section. To provide information for next development of the study, several new definitions of compartmental unpredictable functions are presented. One can be invited to use the definitions to find conditions, which imply that the functions on diagonals are unpredictable in the sense of Definition 2. The irregular behaviour is demonstrated with numerical simulation in an example for a compartmental quasi-periodic unpredictable function.

Theorem 5. 

If the function $\psi \left(t\right):\mathbb{R}\to {\mathbb{R}}^n$ is unpredictable, then the sum $\psi \left(t\right)+C$, where C is a constant, is also unpredictable.

Proof. 

Denote $f\left(t\right)=\psi \left(t\right)+C.$ We have that $\parallel f(t+t_k)-f\left(t\right)\parallel =\parallel \psi (t+t_k)-\psi \left(t\right)\parallel ,$ this is why, $f(t+t_k)\to f\left(t\right),$ as $k\to \infty$ uniformly on compact subsets of $\mathbb{R}$ and $\parallel f(t+t_k)-f\left(t\right)\parallel >{ϵ}_0$ for each $t\in [s_k-\delta ,s_k+\delta ]$ and $k\in \mathbb{N}$.  □

Theorem 6. 

Assume that $\psi \left(t\right):\mathbb{R}\to {\mathbb{R}}^n$ is an unpredictable function. Then, the function ${\psi }^{2m+1}\left(t\right),$ $m\in \mathbb{N},$ is unpredictable.

Proof. 

There exists numbers ${ϵ}_0,$ $\delta >0$ and sequences $t_k,$ $s_k$, both of which diverge to infinity, such that $\psi (t+t_k)$ converges to $\psi \left(t\right)$ as $k\to \infty$ uniformly on compact subsets of $\mathbb{R}$ and $\parallel \psi (t+t_k)-\psi \left(t\right)\parallel >{ϵ}_0$ for each $[s_k-\delta ,s_k+\delta ]$ and $k\in \mathbb{N}.$ The proof of the Poisson stability of ${\psi }^{2m+1}\left(t\right)$ is not difficult, since it follows from uniformly continuity of ${\psi }^{2m+1}\left(t\right)$ on a compact set. Now, we will show that $\parallel {\psi }^{2m+1}(t+t_k)-{\psi }^{2m+1}\left(t\right)\parallel >ϵ\left({ϵ}_0\right)$ for some positive number $ϵ\left({ϵ}_0\right)$ and $t\in [s_k-\delta ,s_k+\delta ].$ Fix a natural number $m.$ Consider the function $F(x,y)=x^{2m+1}-y^{2m+1}$ for $|x-y|\ge {ϵ}_0.$ By using the method of Lagrange multipliers, one can find that the minimum of $F(x,y)$ occurs at the points $x_0,y_0$ with $|x_0|=|y_0|=\frac{{ϵ}_0}{2}.$ Therefore, $\parallel {\psi }^{2m+1}(t+t_k)-{\psi }^{2m+1}\left(t\right)\parallel \ge \frac{{ϵ}_0^{2m+1}}{2^{2m}}$ for $m\in \mathbb{N},$ $t\in [s_k-\delta ,s_k+\delta ].$ Thus, the function ${\psi }^{2m+1}\left(t\right)$ is unpredictable with sequences $t_k,s_k$ and positive numbers $\delta$ and $ϵ<\frac{{ϵ}_0^{2m+1}}{2^{2m}}.$  □

Remark 4. 

An unpredictable function to an even degree is not necessary unpredictable. This can be shown by considering the function $G(x,y)=x^{2m}-y^{2m},$ $m=1,2,\cdots .$ Let us write the function $G(x,y)$ in the form $G(x,y)=(x-y)(x+y)g(x,y).$ Despite $|x-y|\ge {ϵ}_0,$ the sum $x+y$ may be arbitrary small, and the separation property will not be satisfied.

Theorem 7. 

Assume that bounded function $f\left(u\right):{\mathbb{R}}^n\to {\mathbb{R}}^n,$ satisfies the inequalities $L_1∥u_1-u_2∥\le ∥f\left(u_1\right)-f\left(u_2\right)∥\le L_2∥u_1-u_2∥,$ where $L_1,L_2$ are positive constants, for all $u_1,u_2\in {\mathbb{R}}^n.$ Then, the function $f\left(\psi \right(t\left)\right)$ is unpredictable, provided that $\psi \left(t\right):\mathbb{R}\to {\mathbb{R}}^n$ is an unpredictable function.

Proof. 

Consider the function $g\left(t\right)=f\left(\psi \right(t\left)\right).$ Let us fix positive number $ϵ$ and a bounded interval $I.$ One can find sufficiently large k it is true that $\parallel \psi (t+t_k)-\psi \left(t\right)\parallel <\frac{ϵ}{L_2}$ for $t\in I.$ This is why,

$$\parallel g(t+t_k)-g\left(t\right)\parallel =\parallel f\left(\psi (t+t_k)\right)-f\left(\psi \left(t\right)\right)\parallel \le L_2\parallel \psi (t+t_k)-\psi \left(t\right)\parallel <ϵ,$$

for all $t\in I.$ Moreover, there exist a sequence $s_k$ and positive numbers ${ϵ}_0,$ $\delta$, such that $\parallel \psi (t+t_k)-\psi \left(t\right)\parallel >{ϵ}_0$ for $t\in [s_k-\delta ,s_k+\delta ].$ Then, we obtain:

$$\parallel g(t+t_k)-g\left(t\right)\parallel =\parallel f\left(\psi (t+t_k)\right)-f\left(\psi \left(t\right)\right)\parallel \ge L_1\parallel \psi (t+t_k)-\psi \left(t\right)\parallel >L_1{ϵ}_0,$$

for all $t\in [s_k-\delta ,s_k+\delta ].$  □

For further researches, it is important to consider the most general definitions of a Poisson stable and unpredictable functions, excluding their continuity.

Definition 6 

([3]). A continuous function $f\left(t\right):\mathbb{R}\to {\mathbb{R}}^n$ is called quasi-periodic with periods $2\pi /{\omega }_1,2\pi /{\omega }_2,\cdots ,2\pi /{\omega }_m$ if for every positive ϵ there exists a positive number δ such that a number ρ satisfies the inequality ${sup}_{t\in \mathbb{R}}\parallel f(t+\rho )-f\left(t\right)\parallel <ϵ,$ provided that $|{\omega }_k\rho |<\delta \left(mod2\pi \right),$ $k=1,2,\cdots ,m.$

Definition 7. 

A function $f\left(t\right):\mathbb{R}\to {\mathbb{R}}^n$ is said to be compartmental quasi-periodic unpredictable, if $f\left(t\right)=G(t,t),$ where $G(u,v)$ is a continuous bounded function, quasi-periodic in u uniformly with respect to $v\in \mathbb{R},$ and unpredictable in v uniformly with respect to $u\in \mathbb{R}.$

Definition 8 

([4]). A continuous function $f\left(t\right):\mathbb{R}\to {\mathbb{R}}^n$ is said to be almost periodic if, for any positive ϵ, the set $S(f,ϵ)=\{\omega :\parallel f(t+\omega )-f(t)\parallel <ϵ$ for all $t\in \mathbb{R}\}$ is relatively dense.

Definition 9. 

A function $f\left(t\right):\mathbb{R}\to {\mathbb{R}}^n$ is said to be compartmental almost periodic unpredictable, if $f\left(t\right)=G(t,t),$ where $G(u,v)$ is a continuous bounded function, almost periodic in u uniformly with respect to $v\in \mathbb{R},$ and unpredictable in v uniformly with respect to $u\in \mathbb{R}.$

Definition 10 

([46]). A continuous function $f\left(t\right):\mathbb{R}\to {\mathbb{R}}^n$ is called recurrent if for any positive ϵ there can be found a positive number L, such that for each real number t and any interval I of length L there exists a number $\tau \in I,$ which satisfies $\parallel f(t+\tau )-f\left(t\right)\parallel <ϵ.$

Definition 11. 

A function $f\left(t\right):\mathbb{R}\to {\mathbb{R}}^n$ is said to be compartmental recurrent unpredictable, if $f\left(t\right)=G(t,t),$ where $G(u,v)$ is a function recurrent in u uniformly with respect to $v\in \mathbb{R},$ and unpredictable in v uniformly with respect to $u\in \mathbb{R}.$

Definition 12. 

A function $f\left(t\right):\mathbb{R}\to {\mathbb{R}}^n$ is said to be compartmental Poisson stable unpredictable, if $f\left(t\right)=G(t,t),$ where $G(u,v)$ is a Poisson stable in u uniformly with respect to $v\in \mathbb{R},$ and unpredictable in v uniformly with respect to $u\in \mathbb{R}.$

Next, we formulate definitions of specific compartmental functions.

Definition 13. 

A sum $\varphi \left(t\right)+\psi \left(t\right)$ is said to be modulo periodic (quasi-periodic, almost-periodic, recurrent, Poisson stable) unpredictable function, if $\varphi \left(t\right)$ is a continuous periodic (quasi-periodic, almost-periodic, recurrent, Poisson stable) function and $\psi \left(t\right)$ is an unpredictable function.

Definition 14. 

A product $\varphi \left(t\right)\psi \left(t\right)$ is said to be factor periodic (quasi-periodic, almost-periodic, recurrent, Poisson stable) unpredictable function, if $\varphi \left(t\right)$ is a continuous periodic (quasi-periodic, almost-periodic, recurrent, Poisson stable) and $\psi \left(t\right)$ is an unpredictable functions.

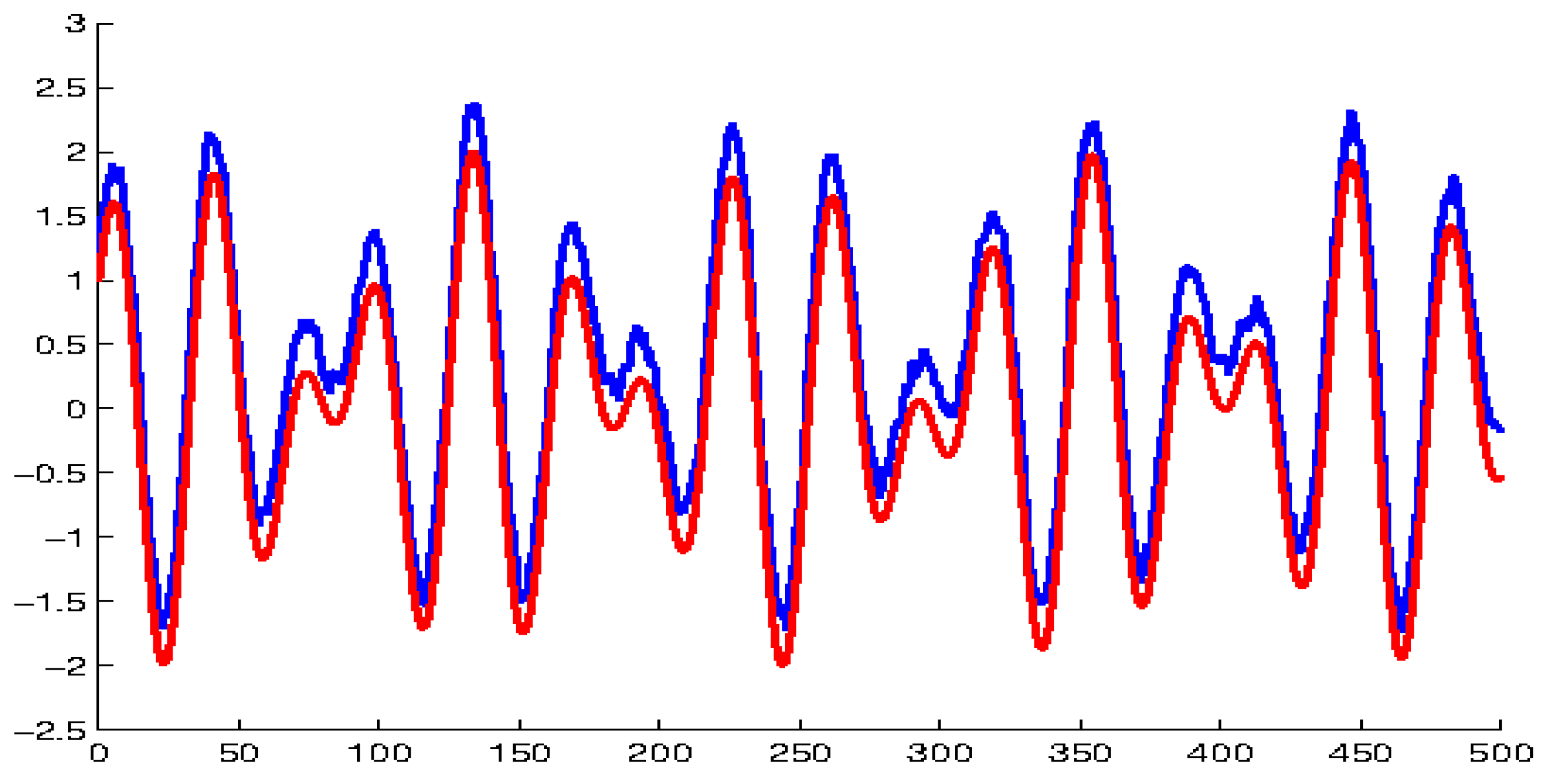
It is important to remark that the Definitions 7, 9, 11 and 12, are provided without any theoretical consequences within the present research. We consider them as a reason for open problems, such that conditions can be looked for the unpredictability of the functions, similar to the kappa property. Nevertheless, this time, we suggest the next simulation result to illustrate the irregularity as well possibility to see contribution of quasi-periodic and the unpredictable components to the composed dynamics. The graphs of quasi-periodic and compartmental quasi-periodic unpredictable function are shown in Figure 7. According to Theorem 7, the component $0.5tanh\left(W\right(t\left)\right)$ is unpredictable with Lipschitz constants $L_1=0.43$ and $L_2=0.5,$ since ${sup}_{t\in \mathbb{R}}\left|W\left(t\right)\right|<\frac{2}{5}.$ Thus, $f\left(t\right)=sin\left(0.2t\right)+cos\left(0.1\sqrt{2}t\right)+0.5tanh\left(W\left(t\right)\right)$ can be accepted as modulo quasi-periodic unpredictable function. One can see that the irregular graph of the unpredictable function $f\left(t\right)$ envelopes the graph of the quasi-periodic function $g\left(t\right)=sin\left(0.2t\right)+cos\left(0.1\sqrt{2}t\right),$ such that contribution of both quasi-periodicity and irregularity are clearly seen in the dynamics of compartmental function. Obviously, an analogue of the degree of periodicity can be looked for the quasi-periodicity, and the contributions of the components are discussed more deeply.

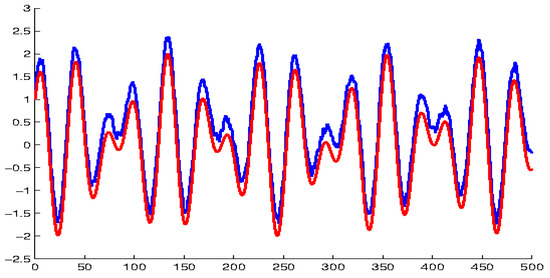
Figure 7. The red curve is the graph of quasi−periodic function $g\left(t\right)=sin\left(0.2t\right)+cos\left(0.1\sqrt{2}t\right),$ and the blue curve is the graph of the randomly determined compartmental quasi−periodic unpredictable function $f\left(t\right)=sin\left(0.2t\right)+cos\left(0.1\sqrt{2}t\right)+0.5tanh\left(W\left(t\right)\right)$.