Local Property of Depth Information in 3D Images and Its Application in Feature Matching
Abstract
:1. Introduction
- We explore the local property of the depth information of image pairs taken before and after the camera movements.
- We prove the local property of the depth information: the ratio of the depth difference of a keypoint and its neighbor pixels before and after the camera movement approximates to a constant.
- Based on the local property, a local depth-based feature descriptor is proposed, which can be used as a supplement of the traditional feature.
2. Related Work
2.1. Image Matching
2.2. Depth Information Estimation
3. The SIFT Key Features
- Scale space and Gaussian difference space
- Gaussian difference pyramid
- Keypoint positioning
- Keypoint offset correction
- Key feature descriptors
4. False matching Based on SIFT Feature Descriptors
5. Local Property of Depth Information under the Camera Movement
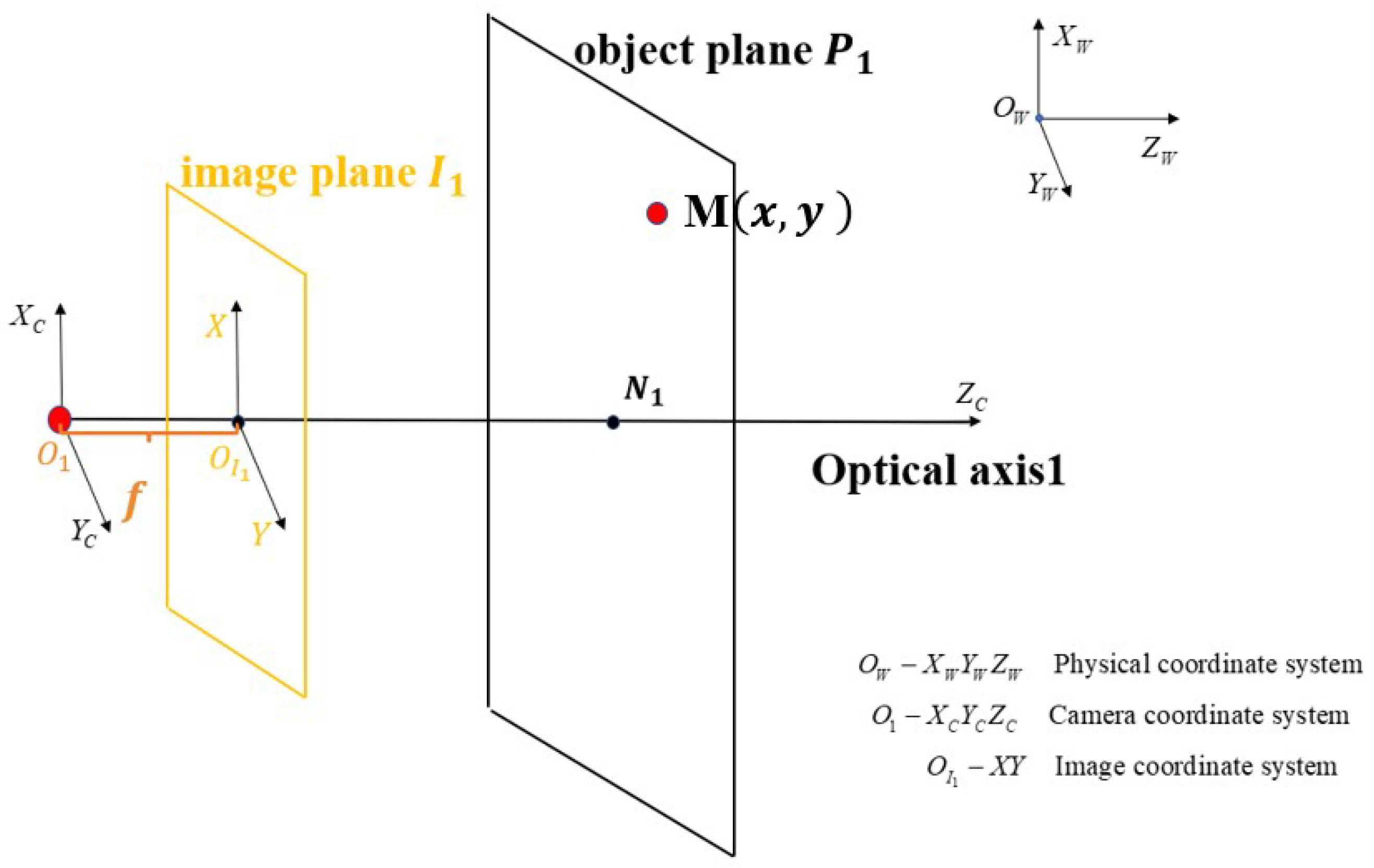
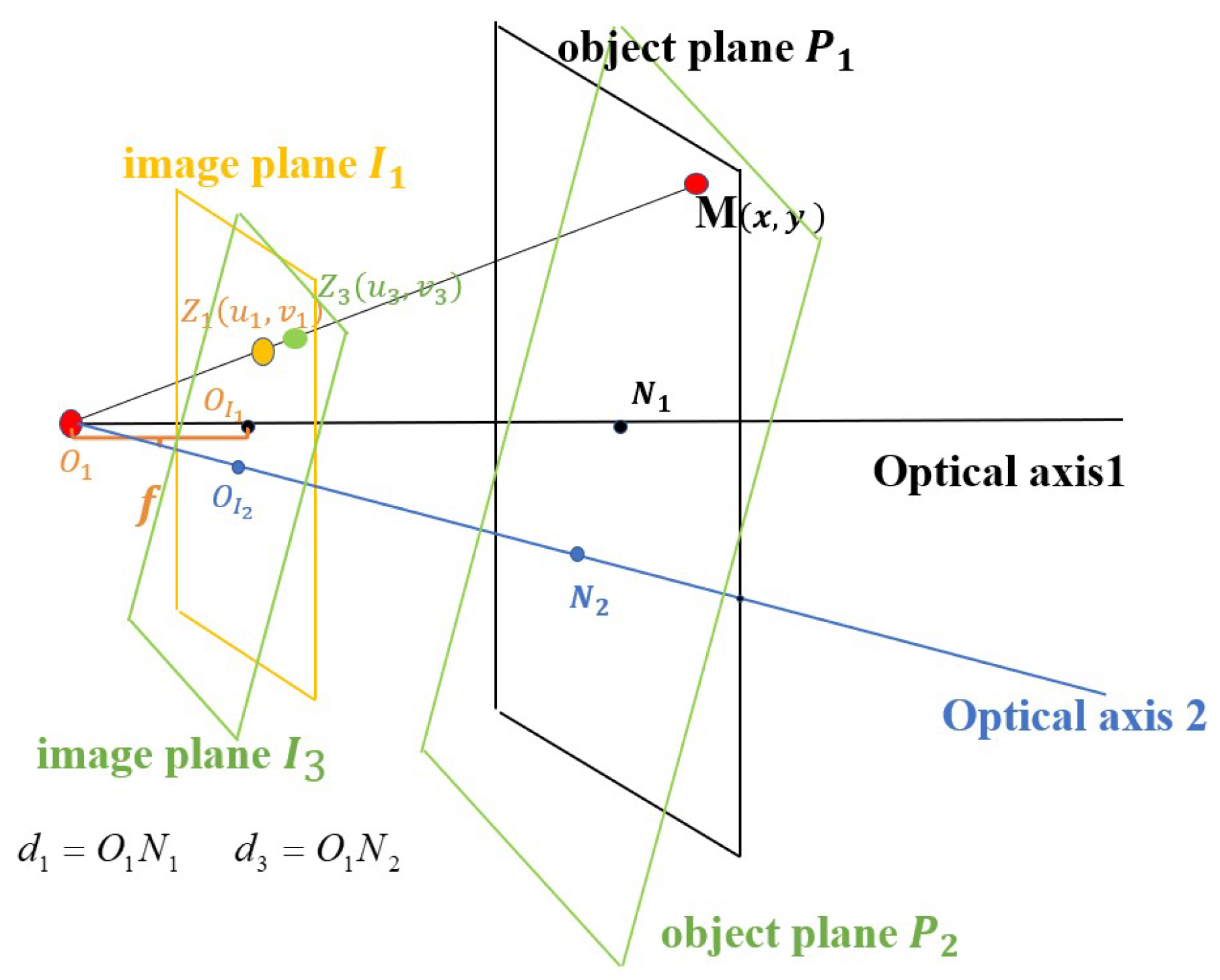
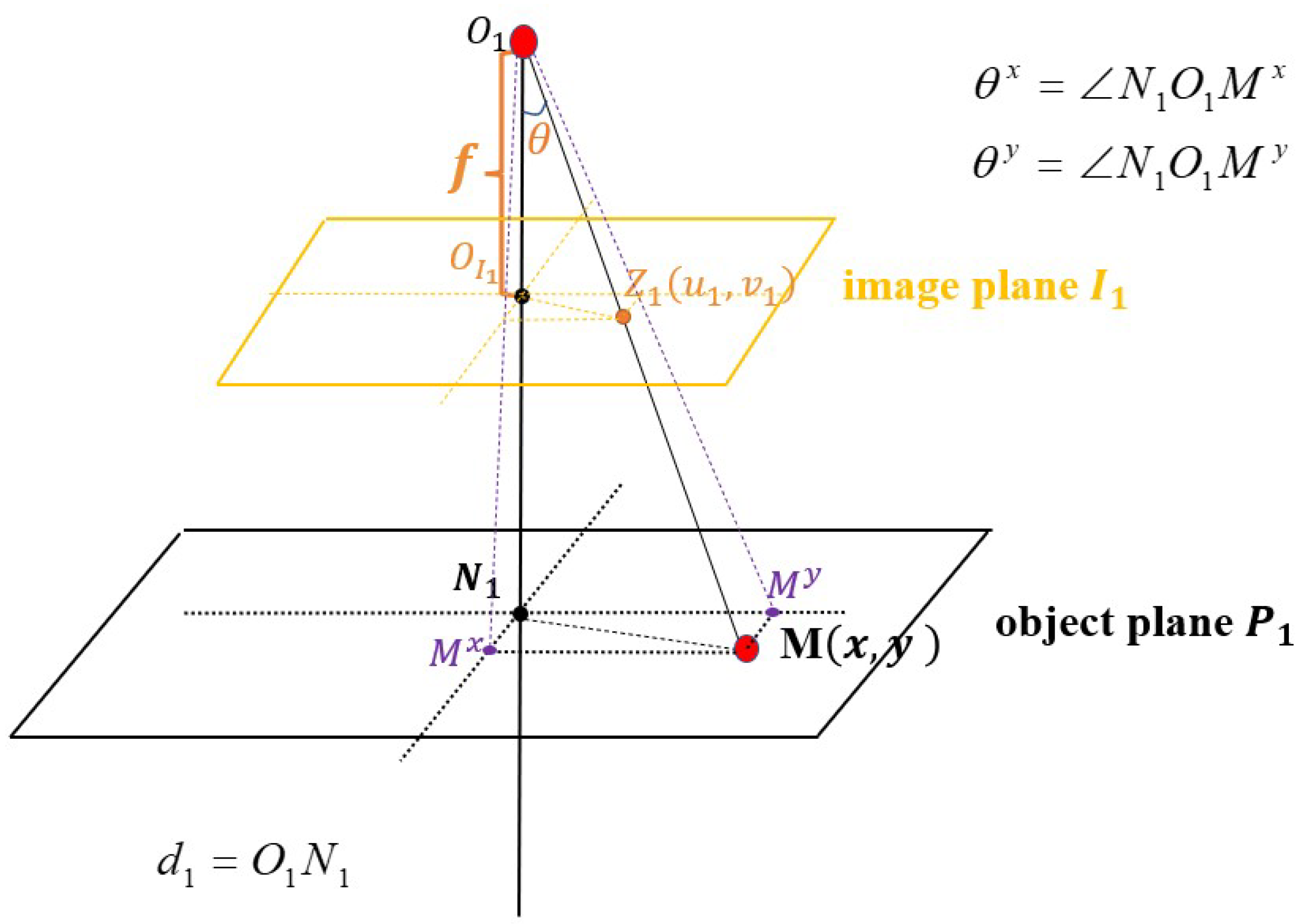
5.1. The Movement of the Camera Center along the Optic Axis

5.2. The Rotation of the Camera’s Optical Axis
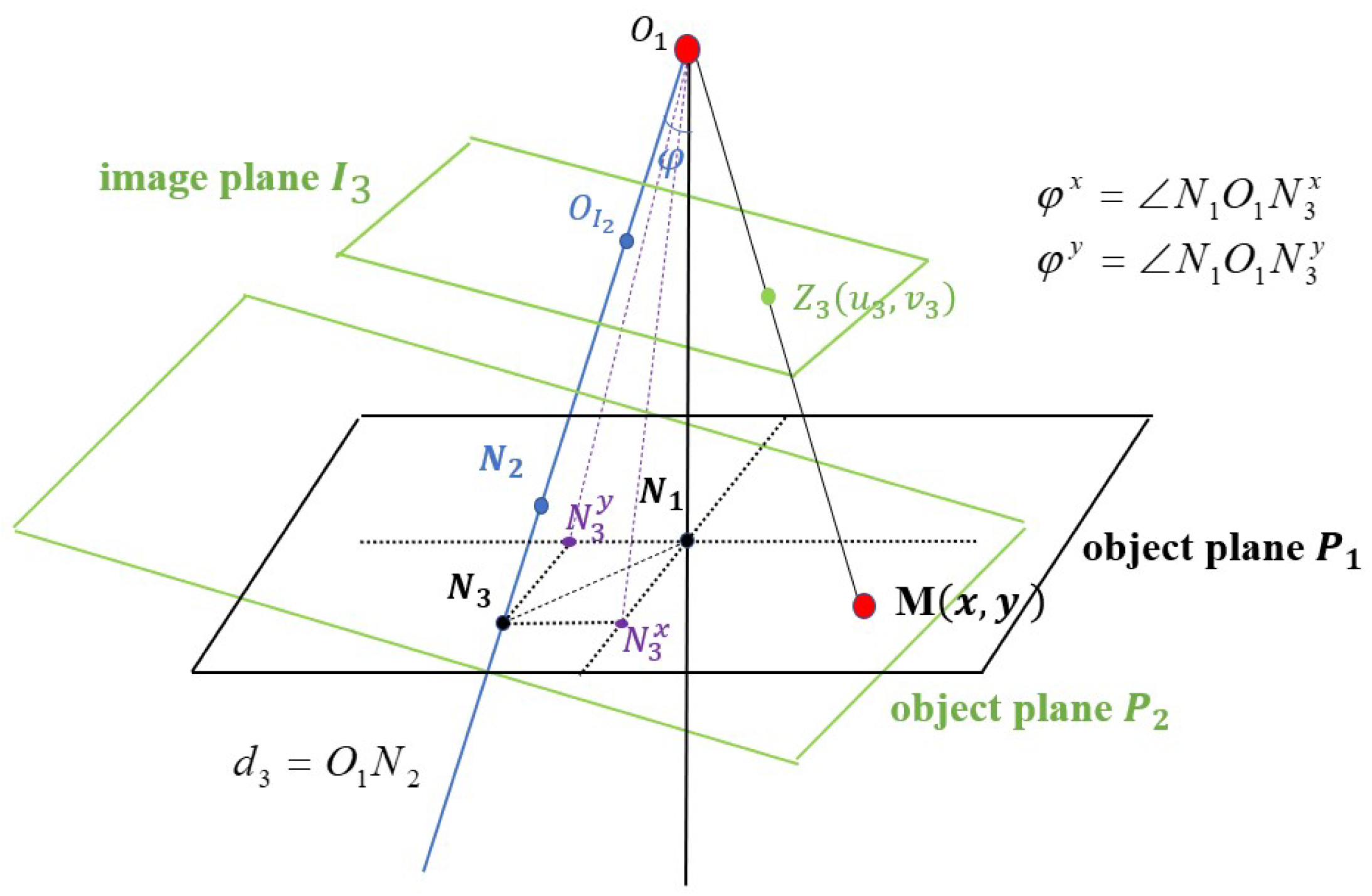

5.3. The Local Property of Depth Information Irrelevant to Camera Movements
6. Depth-Based Supplemental Vector of the SIFT Feature Descriptor
7. Experiments
7.1. Experimental Data
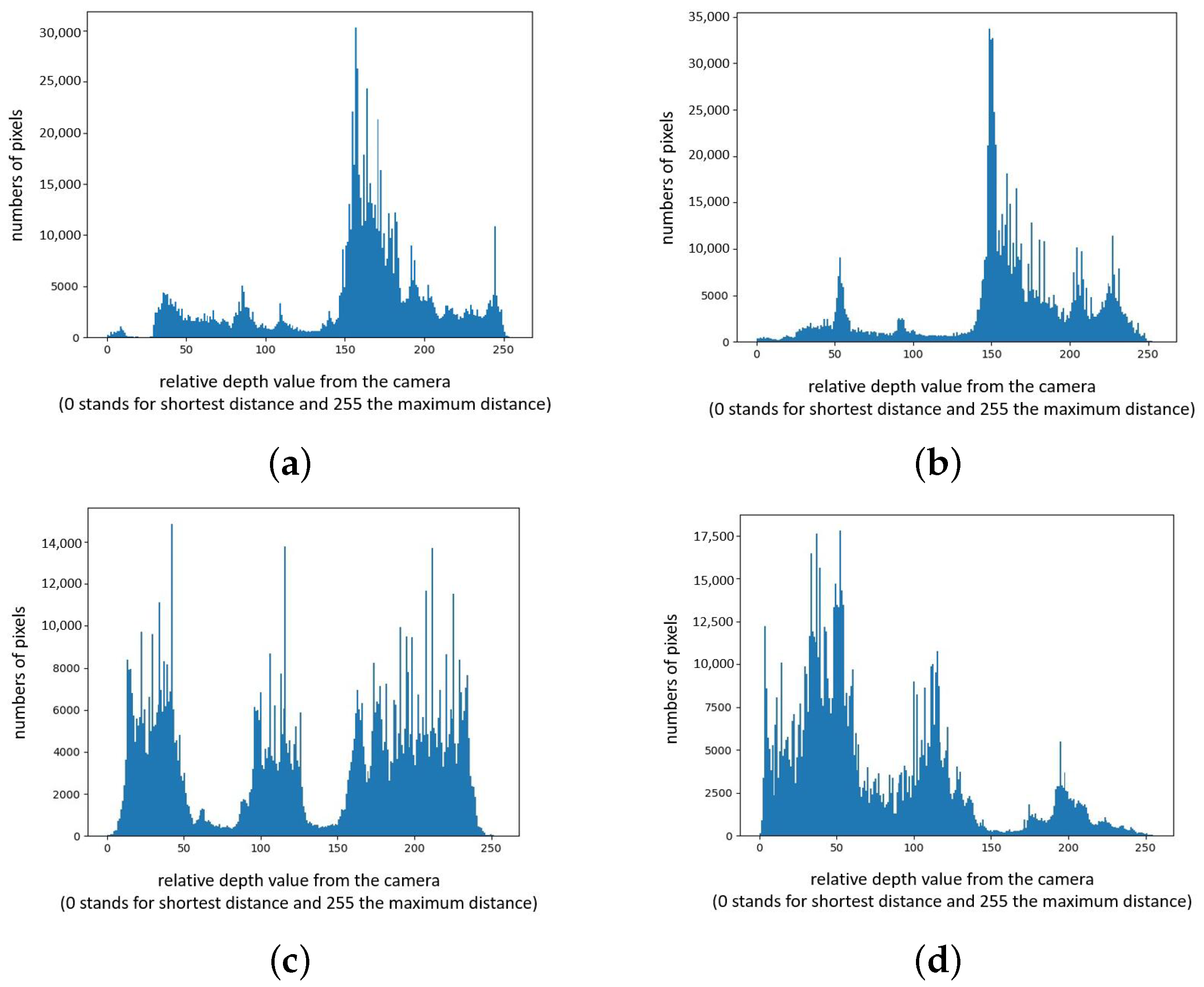
7.2. Pixel Pre-Classification
7.3. Experimental Results
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, J.; Jiang, X.; Fan, A.; Jiang, J.; Yan, J. Image Matching from Handcrafted to Deep Features: A Survey. Int. J. Comput. Vis. 2020, 1, 23–79. [Google Scholar] [CrossRef]
- Zitová, B.; Flusser, J. Image Registration Methods: A Survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef] [Green Version]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Gool, L.V. SURF: Speeded up robust features. In Proceedings of the 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006. [Google Scholar]
- Alahi, A.; Ortiz, R.; Vandergheynst, P. FREAK: Fast Retina Keypoint. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Bellavia, F. SIFT Matching by Context Exposed. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 2445–2457. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Wang, Y.; Chen, J.; Guo, J.; Lu, Y. A completely affine invariant image-matching method based on perspective projection. Mach. Vis. Appl. 2012, 23, 231–242. [Google Scholar] [CrossRef]
- Mishkin, D.; Matas, J.; Perdoch, M. MODS: Fast and robust method for two-view matching. Comput. Vis. Image Underst. 2015, 141, 81–93. [Google Scholar] [CrossRef] [Green Version]
- Morel, J.M.; Yu, G. Asift: A new framework for fully affine invariant image comparison. SIAM J. Imaging Sci. 2009, 2, 438–469. [Google Scholar] [CrossRef] [Green Version]
- Pang, Y.; Li, W.; Yuan, Y.; Pan, J. Fully affine invariant surf for image matching. Neurocomputing 2012, 85, 6–10. [Google Scholar] [CrossRef]
- Toft, C.; Turmukhambetov, D.; Sattler, T.; Kahl, F.; Brostow, G.J. Single-Image Depth Prediction Makes Feature Matching Easier. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Chen, Y.; Wang, G.; Wu, L. Research on feature point matching algorithm improvement using depth prediction. J. Eng. 2019, 2019, 8905–8909. [Google Scholar] [CrossRef]
- Schuon, S.; Theobalt, C.; Davis, J.; Thrun, S. LidarBoost: Depth superresolution for ToF 3D shape scanning. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 343–350. [Google Scholar]
- Liu, C.; Kim, K.; Gu, J.; Furukawa, Y.; Kautz, J. Planercnn: 3d plane detection and reconstruction from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4450–4459. [Google Scholar]
- Liu, C.; Yang, J.; Ceylan, D.; Yumer, E.; Furukawa, Y. Planenet: Piece-wise planar reconstruction from a single rgb image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2579–2588. [Google Scholar]
- Li, Z.; Snavely, N. Megadepth: Learning single-view depth prediction from internet photos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Li, J.; He, L.; Ren, G. A feature point matching method for binocular stereo vision images based on deep learning. Autom. Instrum. 2022, 2, 57–60. [Google Scholar]
- Zhang, Z.; Huo, W.; Lian, M.; Yang, L. Research on fast binocular stereo vision ranging based on Yolov5. J. Qingdao Univ. Eng. Technol. Ed. 2021, 36, 20–27. [Google Scholar]
- Chen, W.; Fu, Z.; Yang, D.; Deng, J. Single-image depth perception in the wild. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 730–738. [Google Scholar]
- Ummenhofer, B.; Zhou, H.; Uhrig, J.; Mayer, N.; Ilg, E.; Dosovitskiy, A.; Brox, T. DeMoN: Depth and Motion Network for Learning Monocular Stereo. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Facil, J.M.; Ummenhofer, B.; Zhou, H.; Montesano, L.; Brox, T.; Civera, J. CAM-Convs: Camera-Aware Multi-Scale Convolutions for Single-View Depth. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Zhou, H.; Ummenhofer, B.; Brox, T. DeepTAM: Deep Tracking and Mapping with Convolutional Neural Networks. Int. J. Comput. Vis. 2020, 128, 756–769. [Google Scholar] [CrossRef]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor Segmentation and Support Inference from RGBD Images; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Abdel-Hakim, A.E.; Farag, A. CSIFT: A SIFT Descriptor with Color Invariant Characteristics. In Proceedings of the IEEE Computer Society Conference on Computer Vision Pattern Recognition, New York, NY, USA, 17–22 June 2006. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Rosten, E.; Porter, R.; Drummond, T. Faster and better: A machine learning approach to corner detection. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 105–119. [Google Scholar] [CrossRef] [Green Version]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. Brief: Binary robust independent elementary features. In Proceedings of the European Conference on Computer Vision, Crete, Greece, 5–11 September 2010; pp. 778–792. [Google Scholar]
- Balammal Geetha, S.; Muthukkumar, R.; Seenivasagam, V. Enhancing Scalability of Image Retrieval Using Visual Fusion of Feature Descriptors. Intell. Autom. Soft Comput. 2022, 31, 1737–1752. [Google Scholar] [CrossRef]
- Csurka, G.; Dance, R.; Fan, L.; Willamowski, J.; Bray, C. Visual categorization with bags of keypoints. In Proceedings of the Workshop on Statistical Learning in Computer Vision, Prague, Czech Republic, May 2004; pp. 1–22. [Google Scholar]
- Tang, L.; Ma, S.; Ma, X.; You, H. Research on Image Matching of Improved SIFT Algorithm Based on Stability Factor and Feature Descriptor Simplification. Appl. Sci. 2022, 12, 8448. [Google Scholar] [CrossRef]
- Feng, Q.; Tao, S.; Liu, C.; Qu, H.; Xu, W. IFRAD: A Fast Feature Descriptor for Remote Sensing Images. Remote Sens. 2021, 13, 3774. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Chung, K.L.; Tseng, Y.C.; Chen, H.Y. A Novel and Effective Cooperative RANSAC Image Matching Method Using Geometry Histogram-Based Constructed Reduced Correspondence Set. Remote Sens. 2022, 14, 3256. [Google Scholar] [CrossRef]
- Tombari, F.; Salti, S.; Stefano, L.D. Unique signatures of histograms for local surface description. In Proceedings of the European Conference on Computer Vision, Crete, Greece, 5–11 September 2010; pp. 356–369. [Google Scholar]
- Salti, S.; Tombari, F.; Di Stefano, L. SHOT: Unique Signatures of Histograms for Surface and Texture Description. Comput. Vis. Image Underst. 2014, 125, 251–264. [Google Scholar] [CrossRef]
- Prakhya, S.M.; Liu, B.; Lin, W. B-SHOT: A binary feature descriptor for fast and efficient keypoint matching on 3D point clouds. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1929–1934. [Google Scholar]
- Steder, B.; Rusu, R.B.; Konolige, K.; Burgard, W. NARF: 3D range image features for object recognition. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010. [Google Scholar]
- Johnston, A.; Carneiro, G. Self-supervised monocular trained depth estimation using self-attention and discrete disparity volume. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Zhou, T.; Brown, M.; Snavely, N.; Lowe, D.G. Unsupervised learning of depth and ego-motion from video. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 21–26. [Google Scholar]
- Ranjan, A.; Jampani, V.; Balles, L.; Kim, K.; Sun, D.; Wulff, J.; Black, M.J. Competitive collaboration: Joint unsupervised learning of depth, camera motion, optical flow and motion segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 15–20. [Google Scholar]
- Mahjourian, R.; Wicke, M.; Angelova, A. Unsupervised Learning of Depth and Ego-Motion from Monocular Video Using 3D Geometric Constraints. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 5667–5675. [Google Scholar]
- Wang, J.; Liu, P.; Wen, F. Self-supervised learning for RGB-guided depth enhancement by exploiting the dependency between RGB and depth. IEEE Trans. Image Process. 2023, 32, 159–174. [Google Scholar] [CrossRef]
- Marr, D.; Hildreth, E. Theory of Edge Detection. Proc. R. Soc. Biol. Sci. 1980, 207, 187–217. [Google Scholar]
- Olkkonen, H.; Pesola, P. Gaussian Pyramid Wavelet Transform for Multiresolution Analysis of Images. Graph. Model. Image Process. 1996, 58, 394–398. [Google Scholar] [CrossRef]
- Lindeberg, T. Feature Detection with Automatic Scale Selection. Int. J. Comput. Vis. 1998, 30, 79–116. [Google Scholar] [CrossRef]
- Wang, M.; Lai, C.H. A Concise Introduction to Image Processing using C++; Chapman and Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Ram, P.; Sinha, K. Revisiting kd-tree for nearest neighbor search. In Proceedings of the 25th Acm Sigkdd International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1378–1388. [Google Scholar]



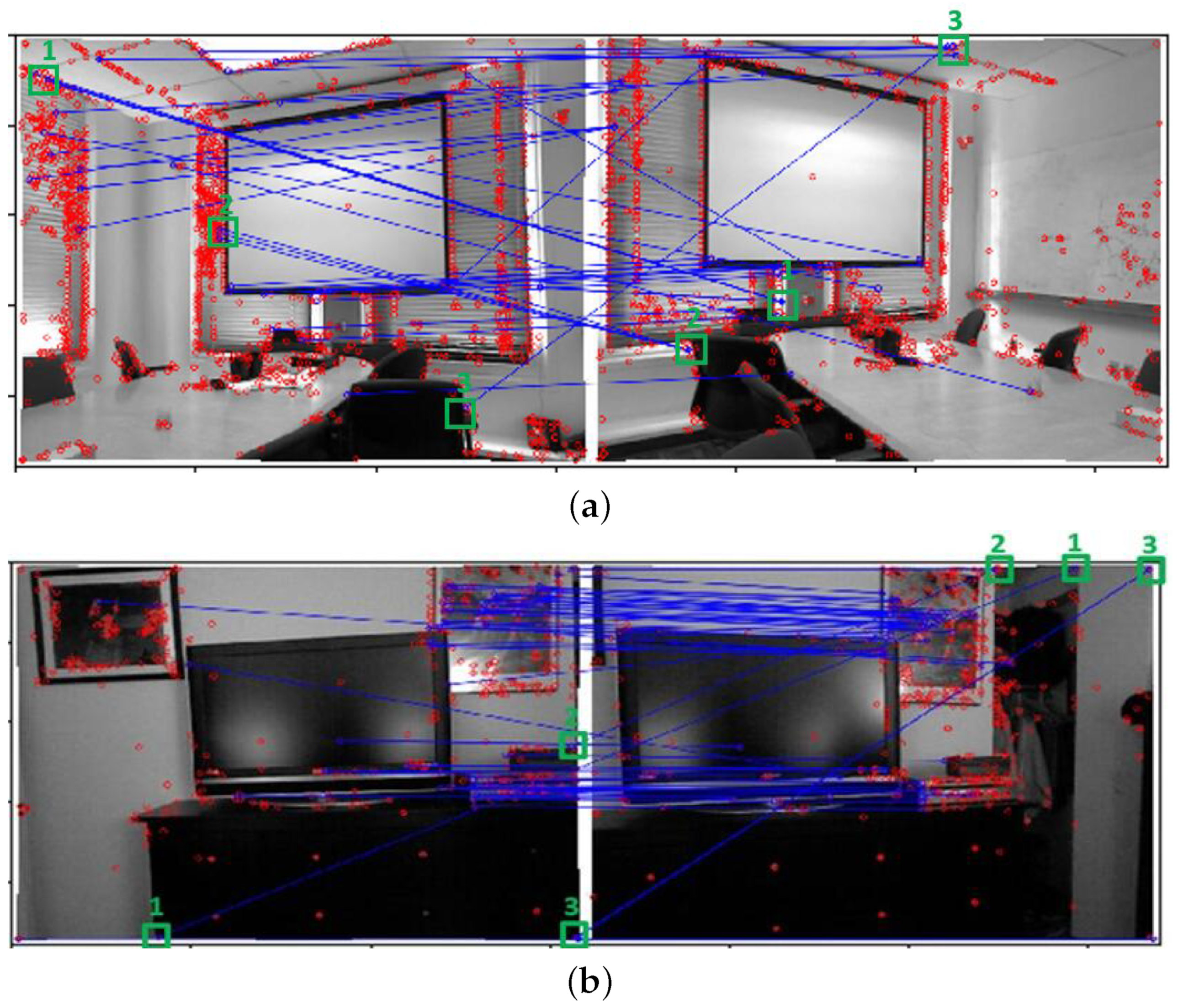

| Image Pair | Total Number of Keypoints | Number of SIFT Matching Pairs | Accuracy Rate | Number of Matching Pairs after Improvement | Accuracy Rate |
|---|---|---|---|---|---|
| 1(18,19) | 629 | 28 | 67.86% | 14 | 78.57% |
| 2(25,26) | 2756 | 41 | 36.59% | 9 | 88.89% |
| 3(69,70) | 2038 | 28 | 96.43% | 13 | 100.00% |
| 4(124,125) | 2800 | 514 | 77.43% | 375 | 90.13% |
| 5(131,132) | 2424 | 378 | 89.15% | 280 | 96.43% |
| 6(191,192) | 1101 | 66 | 80.30% | 22 | 100.00% |
| 7(411,412) | 1282 | 46 | 89.13% | 19 | 94.74% |
| 8(510,511) | 1065 | 39 | 84.62% | 16 | 93.75% |
| 9(568,569) | 2238 | 84 | 83.33% | 43 | 93.02% |
| 10(975,976) | 1681 | 52 | 82.69% | 24 | 91.67% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, E.; Chen, F.; Wang, M.; Cheng, H.; Liu, R. Local Property of Depth Information in 3D Images and Its Application in Feature Matching. Mathematics 2023, 11, 1154. https://doi.org/10.3390/math11051154
Yang E, Chen F, Wang M, Cheng H, Liu R. Local Property of Depth Information in 3D Images and Its Application in Feature Matching. Mathematics. 2023; 11(5):1154. https://doi.org/10.3390/math11051154
Chicago/Turabian StyleYang, Erbing, Fei Chen, Meiqing Wang, Hang Cheng, and Rong Liu. 2023. "Local Property of Depth Information in 3D Images and Its Application in Feature Matching" Mathematics 11, no. 5: 1154. https://doi.org/10.3390/math11051154
APA StyleYang, E., Chen, F., Wang, M., Cheng, H., & Liu, R. (2023). Local Property of Depth Information in 3D Images and Its Application in Feature Matching. Mathematics, 11(5), 1154. https://doi.org/10.3390/math11051154






