New Results on Finite-Time Synchronization of Complex-Valued BAM Neural Networks with Time Delays by the Quadratic Analysis Approach
Abstract
:1. Introduction
- (1)
- A type of research approach to CVBAMNNs with time delays is introduced in our paper: quadratic analysis approach.
- (2)
- Two novel inequalities are proposed in our paper to analyze the FTS of delayed CVBAMNNs.
- (3)
- New controllers are designed.
- (4)
- Through using quadratic analysis approach, inequality techniques and designing novel controllers, two new sufficient conditions are achieved to assure the FTS between the master system and the slave system.
2. Preliminaries
3. Main Results
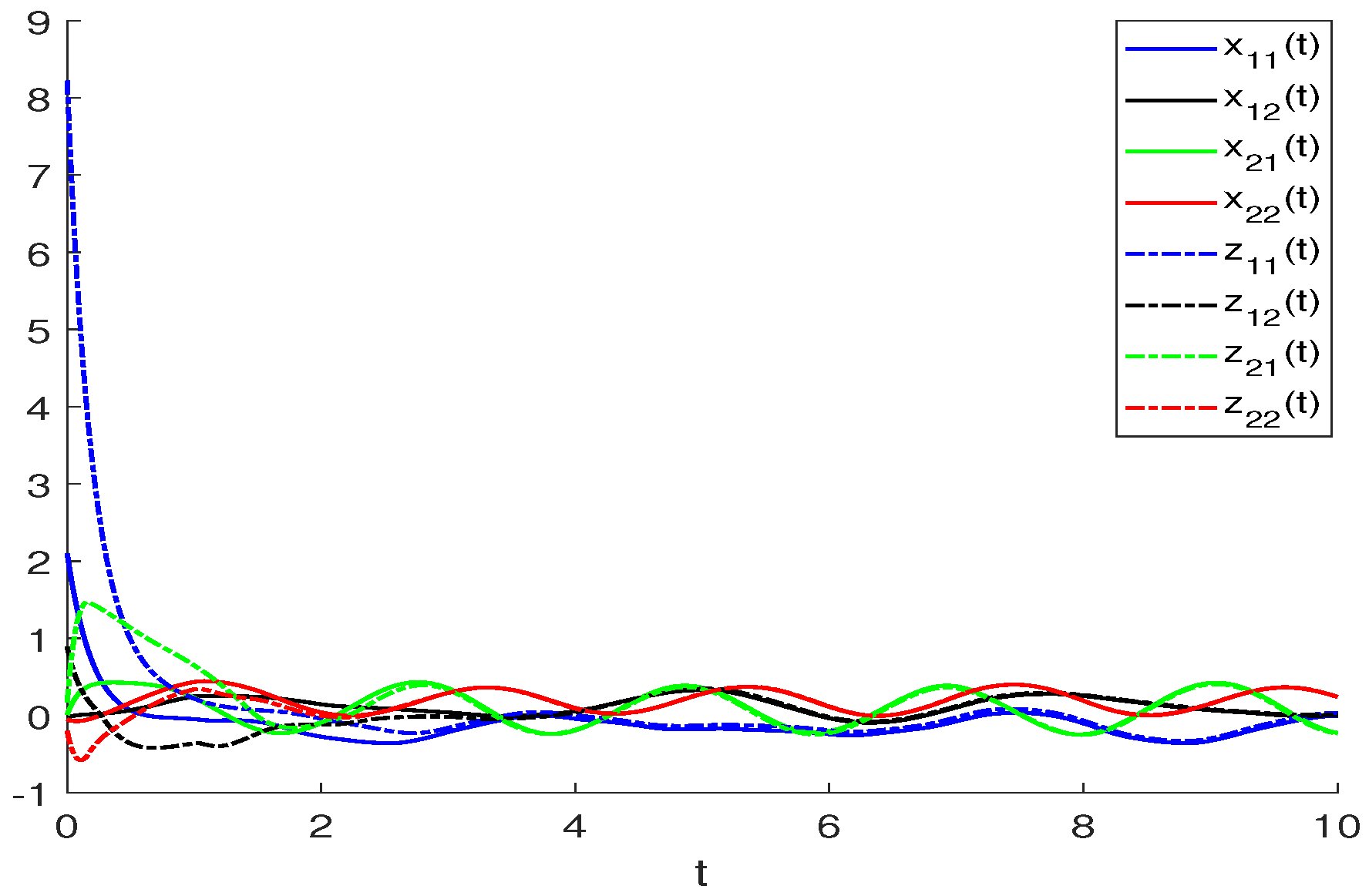
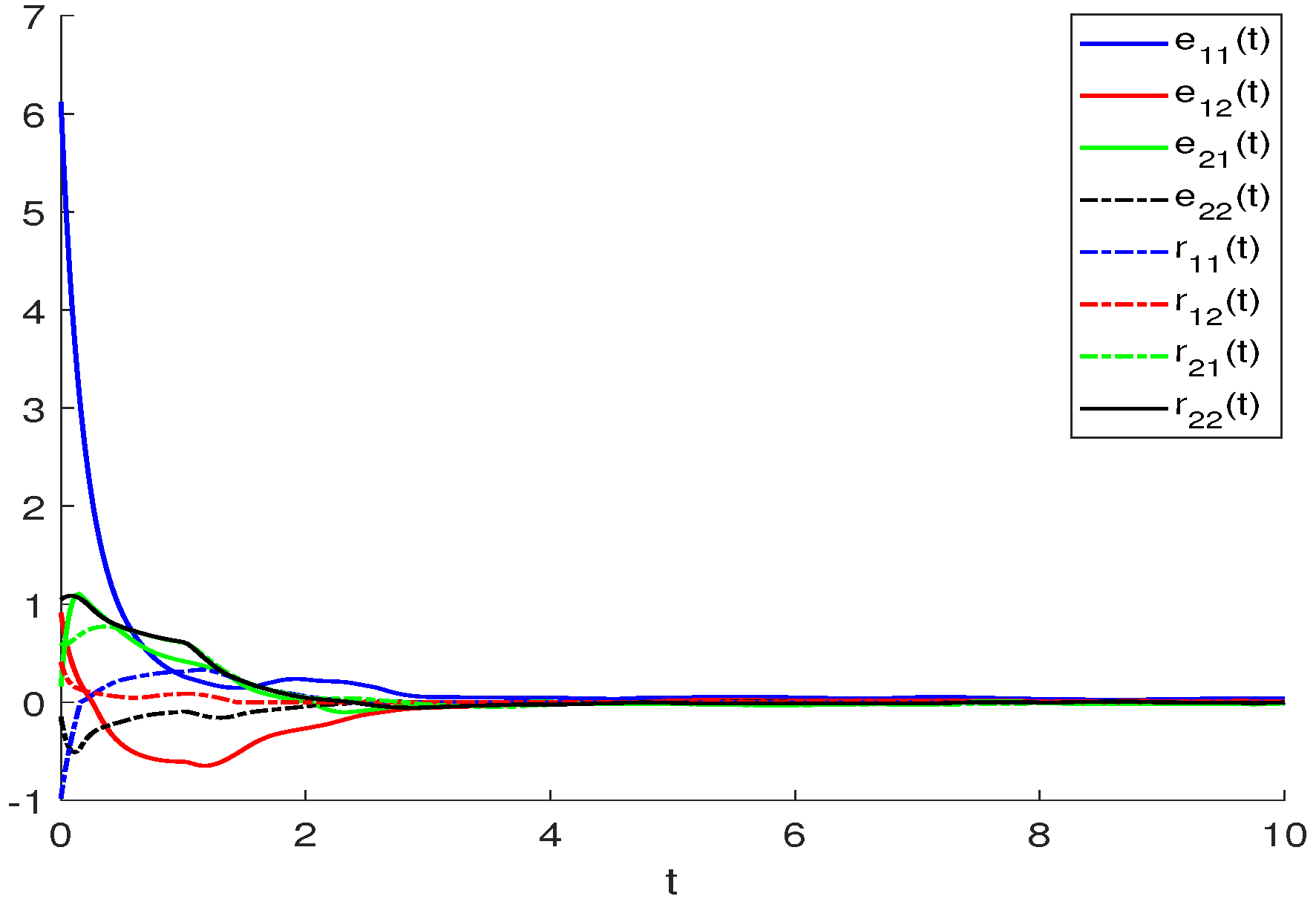
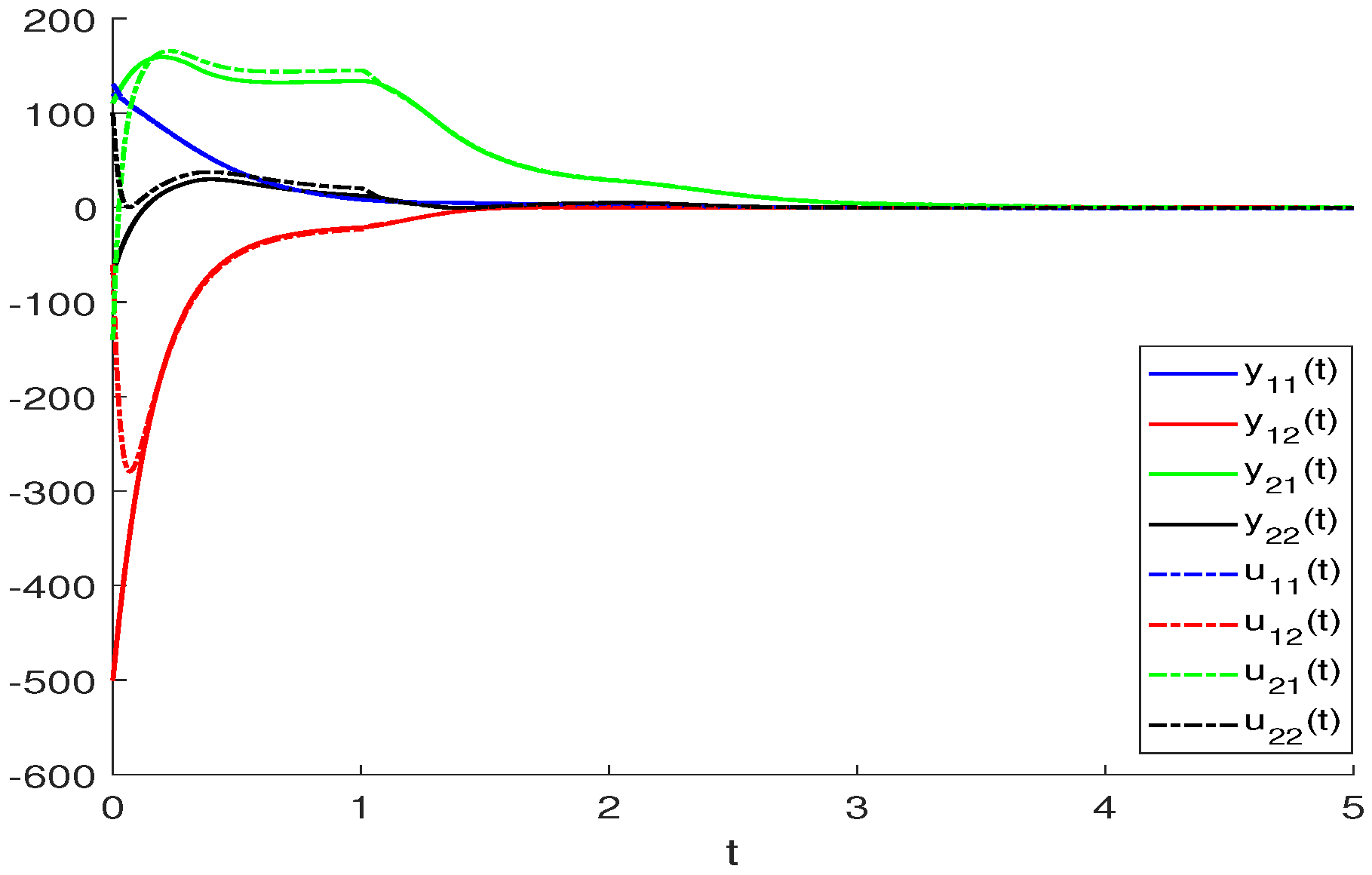
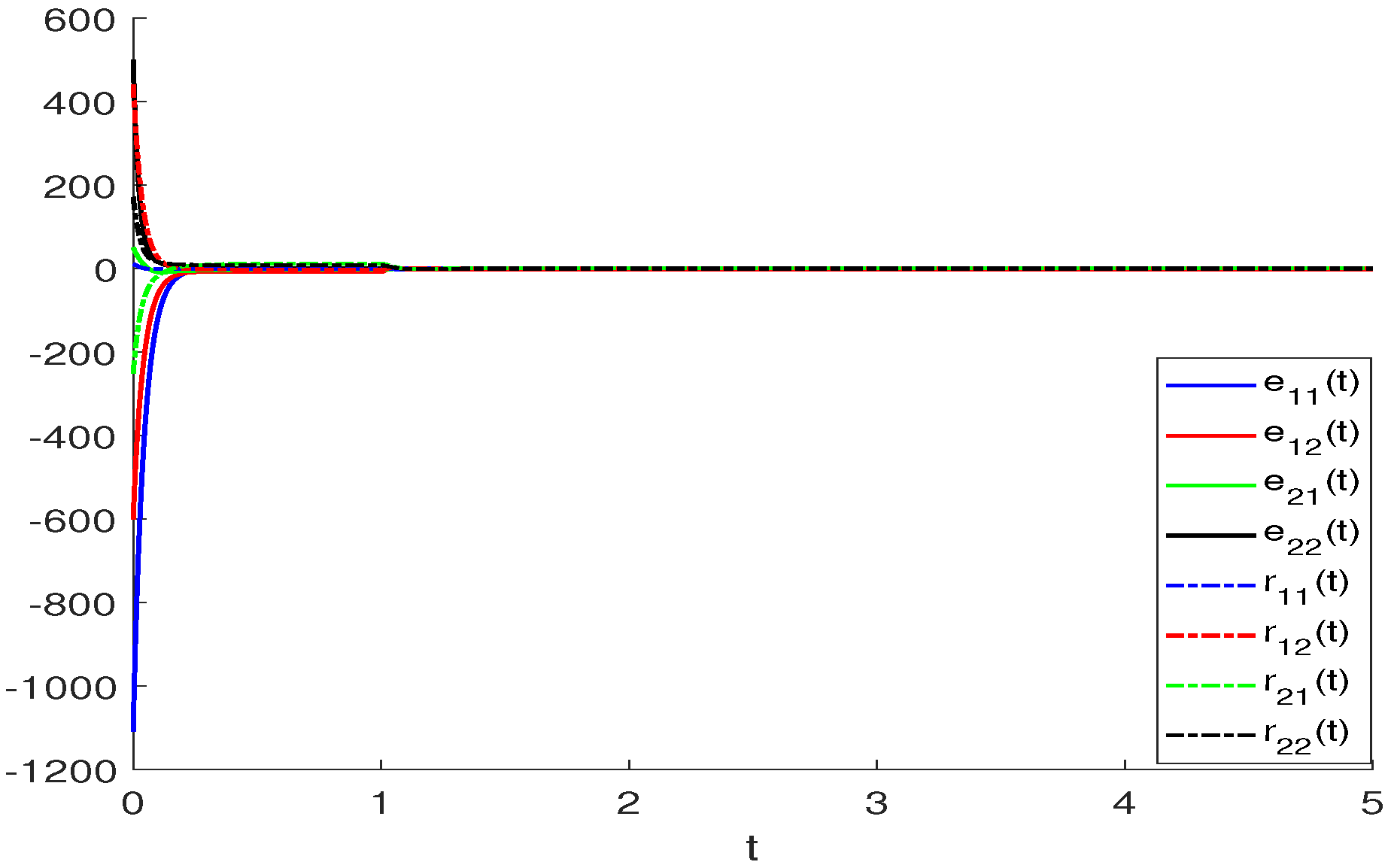
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duan, L.; Shi, M.; Huang, C.X.; Fang, X.W. Synchronization in finite-/fixed-time of delayed diffusive complex-valued neural networks with discontinuous activations. Chaos Solitons Fractals 2021, 142, 110386. [Google Scholar] [CrossRef]
- Zhang, J.M.; Bao, H. Synchronization of fractional-order three-neuron complex-valued BAM neural networks with multiple time delays via discontinuous neuron activations. In Proceedings of the 2018 Chinese Control Furthermore, Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 1093–1098. [Google Scholar]
- Kumar, A.; Das, S.; Rajeev; Yadav, V.K. Global exponential synchronization of complex-valued recurrent neural networks in presence of uncertainty along with time-varying bounded and unbounded delay terms. Int. J. Dyn. Control 2021, 10, 902–916. [Google Scholar] [CrossRef]
- Li, L.; Chen, W.S.; Wu, J. Global Exponential stability and synchronization for novel complex-valued neural networks with proportional delays and inhibitory factors. IEEE Trans. Cybern. 2021, 51, 2142–2152. [Google Scholar] [CrossRef]
- Yuan, M.M.; Wang, W.P.; Wang, Z.; Luo, X.; Kurths, J. Exponential synchronization of delayed memristor-based uncertain complex-valued neural networks for image protection. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 151–165. [Google Scholar] [CrossRef]
- Zhu, S.; Liu, D.; Yang, C.Y.; Fu, J. Synchronization of memristive complex-valued neural networks with time delays via pinning control method. IEEE Trans. Cybern. 2020, 50, 3806–3815. [Google Scholar] [CrossRef]
- Liu, M.; Li, Z.F.; Jiang, H.J.; Hu, C.; Yu, Z.Y. Exponential synchronization of complex-valued neural networks via average impulsive interval strategy. Neural Process. Lett. 2020, 52, 1377–1394. [Google Scholar] [CrossRef]
- Zhang, W.W.; Zhang, H.; Cao, J.D.; Zhang, H.M.; Chen, D.Y. Synchronization of delayed fractional-order complex-valued neural networks with leakage delay. Phys. A Stat. Mech. Its Appl. 2020, 556, 124710. [Google Scholar] [CrossRef]
- Pan, C.N.; Bao, H.B. Exponential synchronization of complex-valued memristor-based delayed neural networks via quantized intermittent control. Neurocomputing 2020, 404, 317–328. [Google Scholar] [CrossRef]
- Yu, J.; Hua, C.; Jiang, H.J.; Wang, L.M. Exponential and adaptive synchronization of inertial complex-valued neural networks: A non-reduced order and non-separation approach. Neural Netw. 2020, 124, 50–59. [Google Scholar] [CrossRef]
- Liu, M.J.; Wang, X.R.; Zhang, Z.Y.; Wang, Z. Global synchronization of complex-valued neural networks with stochastic disturbances and time-varying delay. IEEE Access 2019, 7, 182600–182610. [Google Scholar] [CrossRef]
- Wang, P.F.; Zou, W.Q.; Su, H.; Feng, J.Q. Exponential synchronization of complex-valued delayed coupled systems on networks with aperiodically on-off coupling. Neurocomputing 2019, 369, 155–165. [Google Scholar] [CrossRef]
- Pan, J.S.; Zhang, Z.Q. Finite-time synchronization for delayed complex-valued neural networks via the exponential-type controllers of time variable. Chaos Solitons Fractals 2021, 146, 110897. [Google Scholar] [CrossRef]
- Aouiti, C.; Bessifi, M. Sliding mode control for finite-time and fixed-time synchronization of delayed complex-value d recurrent neural networks with discontinuous activation functions and nonidentical parameters. Eur. J. Control 2021, 59, 109–122. [Google Scholar] [CrossRef]
- Yu, T.H.; Cao, J.D.; Rutkowski, L.; Luo, Y.P. Finite-time synchronization of complex-valued memristive-based neural networks via hybrid control. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 3938–3947. [Google Scholar] [CrossRef]
- Luo, F.; Xiang, Y.; Wu, E.L. Finite-time synchronization of coupled complex-valued chaotic systems with time-delays and bounded perturbations. Mod. Phys. Lett. B 2021, 35, 2150130. [Google Scholar] [CrossRef]
- Song, X.N.; Man, J.T.; Song, S.; Zhang, Y.J.; Ning, Z.K. Finite/fixed-time synchronization for Markovian complex-valued memristive neural networks with reaction-diffusion terms and its application. Neurocomputing 2020, 414, 131–142. [Google Scholar] [CrossRef]
- Xiong, K.L.; Yu, J.; Hua, C.; Wen, S.P.; Jiang, H.J. Finite-time synchronization of fully complex-valued networks with or without time-varying delays via intermittent control. Neurocomputing 2020, 413, 173–184. [Google Scholar] [CrossRef]
- Aouiti, C.; Bessifi, M.; Li, X.D. Finite-time and fixed-time synchronization of complex-valued recurrent neural networks with discontinuous activations and time-varying delays. Circuits Syst. Signal Process. 2020, 39, 5406–5428. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.Z.; Li, W.X. Adaptive finite-time synchronization control for fractional-order complex-valued dynamical networks with multiple weights. Commun. Nonlinear Sci. Numer. Simul. 2020, 85, 105239. [Google Scholar] [CrossRef]
- Xiong, K.L.; Yu, J.; Hu, C.; Jiang, H.J. Synchronization in finite/fixed time of fully complex-valued dynamical networks via nonseparation approach. J. Frankl. Inst. 2021, 358, 2367–2381. [Google Scholar] [CrossRef]
- Xu, Y.; Li, W.X. Finite-time synchronization of fractional-order complex-valued coupled systems. Phys. A 2020, 549, 123903. [Google Scholar] [CrossRef]
- Zheng, B.B.; Hu, C.; Yu, J.; Jiang, H.J. Finite-time synchronization of fully complex-valued neural networks with fractional-order. Neurocomputing 2020, 373, 70–80. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Cao, J.D.; Cai, Z.W.; Huang, L.H. Periodicity and finite-time periodic synchronization of discontinuous complex-valued neural networks. Neural Netw. 2019, 119, 249–260. [Google Scholar] [CrossRef]
- Liu, Y.J.; Huang, J.J.; Qin, Y.; Yang, X.B. Finite-time synchronization of complex-valued neural networks with finite-time distributed delays. Neurocomputing 2020, 416, 152–157. [Google Scholar] [CrossRef]
- Sun, K.L.; Zhu, S.; Wei, Y.C.; Zhang, X.K.; Gao, F. Finite-time synchronization of memristor-based complex-valued neural networks with time delays. Phys. Lett. A 2019, 383, 2255–2263. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Liu, X.P.; Lin, C.; Chen, B. Finite-time synchronization for complex-valued recurrent neural networks with time delays. Hindawi Complex. 2018, 2018, 8456737. [Google Scholar] [CrossRef] [Green Version]
- Wu, E.L.; Yang, X.S.; Xu, C.; Alsaadi, F.E.; Hayat, T. Finite-time synchronization of complex-valued delayed neural networks with discontinuous activations. Asian J. Control. 2018, 20, 2237–2247. [Google Scholar] [CrossRef]
- Liu, Y.J.; Qin, Y.; Huang, J.J.; Huang, T.W.; Yang, X.B. Finite-time synchronization of complex-valued neural networks with multiple time-varying delays and infinite distributed delays. Neural Process. Lett. 2019, 50, 1773–1787. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Li, A.L.; Yu, S.H. Finite-time synchronization for delayed complex-valued neural networks via integrating inequality method. Neurocomputing 2018, 318, 248–260. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.Y.; Wang, S.B.; Zhou, W.J.; Xia, Z.Q. Finite-time synchronization for a class of fully complex-valued networks with coupling delay. IEEE Access 2018, 6, 17923–17932. [Google Scholar] [CrossRef]
- Guo, R.N.; Zhang, Z.Y.; Chen, J.; Lin, C.; Liu, Y. Finite-time synchronization for delayed complex-valued BAM neural networks. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 872–877. [Google Scholar]
- Zhou, C.; Zhang, W.L.; Yang, X.S.; Xu, C.; Feng, J.W. Finite-time synchronization of complex-valued neural networks with mixed delays and uncertain perturbations. Neural Process. Lett. 2017, 46, 271–291. [Google Scholar] [CrossRef]
- Manikandan, M.; Ratnavelu, K.; Balasubramaniam, P.; Ong, S.H. Synchronization of BAM Cohen-Grossberg FCNNs with mixed time delays. Iran. J. Fuzzy Syst. 2021, 18, 159–173. [Google Scholar]
- Li, L.C.; Xu, R.; Gan, Q.T.; Lin, J.Z. A switching control for finite-time synchronization of memristor-based BAM neural networks with stochastic disturbances. Nonlinear Anal. Model. Control 2020, 25, 958–979. [Google Scholar] [CrossRef]
- Zhang, L.Z.; Yang, Y.Q. Finite time impulsive synchronization of fractional order memristive BAM neural networks. Neurocomputing 2020, 384, 213–224. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Li, J.W.; Niu, Y.Q. Finite-time stabilization of fractional-order delayed bidirectional associative memory neural networks. Sci. Asia 2019, 45, 589–596. [Google Scholar] [CrossRef] [Green Version]
- Tang, R.Q.; Yang, X.S.; Wan, X.X.; Zou, Y.; Cheng, Z.S.; Fardoun, H.M. Finite-time synchronization of nonidentical BAM discontinuous fuzzy neural networks with delays and impulsive effects via non-chattering quantized control. Commun. Nonlinear Sci. Numer. Simul. 2019, 78, 104893. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Rajchakit, G.; Cao, J.D.; Bagdasar, O. Mittag–Leffler state estimator design and synchronization analysis for fractional-order BAM neural networks with time delays. Int. J. Adapt. Control. Signal Process. 2019, 33, 855–874. [Google Scholar] [CrossRef]
- Aouiti, C.; Li, X.D.; Miaadi, F. A new LMI approach to finite and fixed time stabilization of high-order class of BAM neural networks with time-varying delays. Neural Process. Lett. 2019, 50, 815–838. [Google Scholar] [CrossRef]
- Wang, W.P.; Wang, X.; Luo, X.; Yuan, M.M. Finite-time projective synchronization of memristor-based BAM neural networks and applications in image encryption. IEEE Access 2018, 6, 56457–56476. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Li, L.X.; Peng, H.P.; Xiao, J.H.; Yang, Y.X.; Zheng, M.W.; Zhao, H. Finite-time synchronization for memristor-based BAM neural networks with stochastic perturbations and time-varying delays. Int. J. Robust Nonlinear Control 2018, 28, 5118–5139. [Google Scholar] [CrossRef]
- Sader, M.; Abdurahman, A.; Jiang, H.J. General decay synchronization of delayed BAM neural networks via nonlinear feedback control. Appl. Math. Comput. 2018, 337, 302–314. [Google Scholar] [CrossRef]
- Chen, C.; Li, L.X.; Peng, H.P.; Yang, Y.X. Adaptive synchronization of memristor-based BAM neural networks with mixed delays. Appl. Math. Comput. 2018, 322, 100–110. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Liu, X.P.; Guo, R.N.; Lin, C. Finite-time stability for delayed complex-valued BAM neural networks. Neural Process. Lett. 2018, 48, 179–193. [Google Scholar] [CrossRef]
- Xu, C.J.; Li, P.L.; Pang, Y.C. Finite-time stability for fractional-order bidirectional associative memory neural networks with time delays. Commun. Theor. Phys. 2017, 67, 137–142. [Google Scholar] [CrossRef]
- Rajivganthi, C.; Rihan, F.; Lakshmanan, S.; Muthukumar, P. Finite-time stability analysis for fractional-order Cohen–Grossberg BAM neural networks with time delays. Neural Comput. Appl. 2018, 29, 1309–1320. [Google Scholar] [CrossRef]
- Xiao, J.Y.; Zhong, S.M.; Li, Y.T.; Xu, F. Finite-time Mittag–Leffler synchronization of fractional-order memristive BAM neural networks with time delays. Neurocomputing 2017, 219, 431–439. [Google Scholar] [CrossRef]
- Chen, Z.W.; Zhang, R.J.; Wang, L.S. Finite-time stochastic synchronization for a class of BAM neural networks with uncertain parameters. Commun. Appl. Anal. 2016, 20, 263–276. [Google Scholar]
- Zhang, Z.Q.; Cao, J.D. Novel finite-time synchronization criteria for inertial neural networks with time delays via integral inequality method. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1476–1485. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Cao, J.D. Finite-time synchronization for fuzzy inertial neural networks by maximum value approach. IEEE Trans. Fuzzy Syst. 2022, 30, 1436–1446. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Chen, M.; Li, A.L. Further study on finite-time synchronization for delayed inertial neural networks via inequality skills. Neurocomputing 2020, 373, 15–23. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Z. Finite-time synchronization analysis for BAM neural networks with time-varying delays by applying the maximum-value approach with new inequalities. Mathematics 2022, 10, 835. [Google Scholar] [CrossRef]
- Wang, J.; Tian, Y.; Hua, L.; Shi, K.; Zhong, S.; Wen, S. New results on finite-time synchronization control of Chaotic memristor-based inertial neural networks with time-varying delays. Mathematics. Mathematics 2023, 11, 684. [Google Scholar] [CrossRef]
- Yang, W.; Xiao, L.; Huang, J.; Yang, J. Fixed-time synchronization of neural networks based on quantized intermittent control for image protection. Mathematics 2021, 9, 3086. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, H.; Zhang, W.; Zhang, H. Finite-time projective synchronization of Caputo type fractional complex-valued delayed neural networks. Mathematics 2021, 9, 1406. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Zhang, Z. New Results on Finite-Time Synchronization of Complex-Valued BAM Neural Networks with Time Delays by the Quadratic Analysis Approach. Mathematics 2023, 11, 1378. https://doi.org/10.3390/math11061378
Yang Z, Zhang Z. New Results on Finite-Time Synchronization of Complex-Valued BAM Neural Networks with Time Delays by the Quadratic Analysis Approach. Mathematics. 2023; 11(6):1378. https://doi.org/10.3390/math11061378
Chicago/Turabian StyleYang, Zhen, and Zhengqiu Zhang. 2023. "New Results on Finite-Time Synchronization of Complex-Valued BAM Neural Networks with Time Delays by the Quadratic Analysis Approach" Mathematics 11, no. 6: 1378. https://doi.org/10.3390/math11061378
APA StyleYang, Z., & Zhang, Z. (2023). New Results on Finite-Time Synchronization of Complex-Valued BAM Neural Networks with Time Delays by the Quadratic Analysis Approach. Mathematics, 11(6), 1378. https://doi.org/10.3390/math11061378




