A Generalized Mathematical Model of Toxoplasmosis with an Intermediate Host and the Definitive Cat Host
Abstract
:1. Introduction
2. Mathematical Model
- Cats can be susceptible (S), infected (I), or recovered/vaccinated ().
- The mouse population is divided into two classes, namely, susceptible () and infectious ().
- Oocysts (O) denotes the amount of T. gondii oocysts.
- The mouse and cat populations are assumed to be constant.
- A susceptible mouse or cat moves to the infectious class after contact with T. gondii oocysts (at rates and , respectively).
- A susceptible cat flows to the recovered/vaccinated class at a rate . An infectious cat flows to the vaccinated/recovered subpopulation at a rate .
- T. gondii oocysts are generated by infectious cats .
- is the degradation/removal rate of T. gondii oocysts in the environment.
- represents the birth and death rate for cats.
- represents the birth and death rate of mice.
- A proportion q of vertical transmittal is assumed in the cat population.
- A proportion p of vertical transmittal is assumed in the mouse population.
3. Stability Analysis
4. Mathematical Model with Full Vertical Transmission in the Mouse Population
4.1. Toxoplasmosis-Free Steady State Considering Full Vertical Transmission in Mice
4.2. Global Stability of Toxoplasmosis-Free Equilibrium Points
4.3. Toxoplasmosis-Endemic Steady State
4.4. Global Stability of the Toxoplasmosis-Endemic Equilibrium Point
5. Mathematical Model without Full Vertical Transmission in the Mouse Population
5.1. Stability Analysis of the Toxoplasmosis-Free Equilibrium Point
5.2. Stability Analysis of the Toxoplasmosis Endemic Equilibrium Point
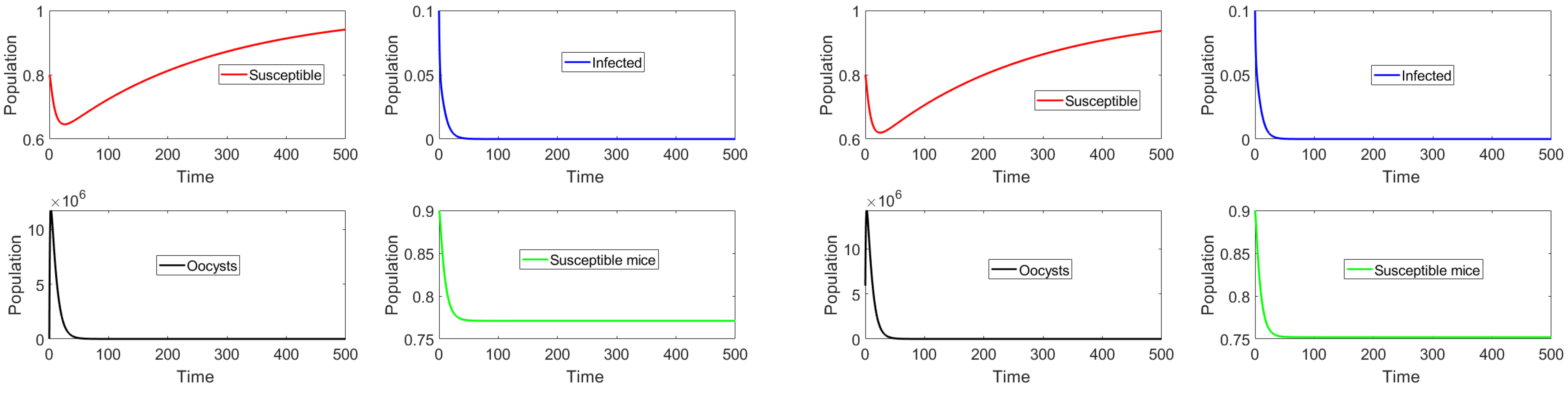
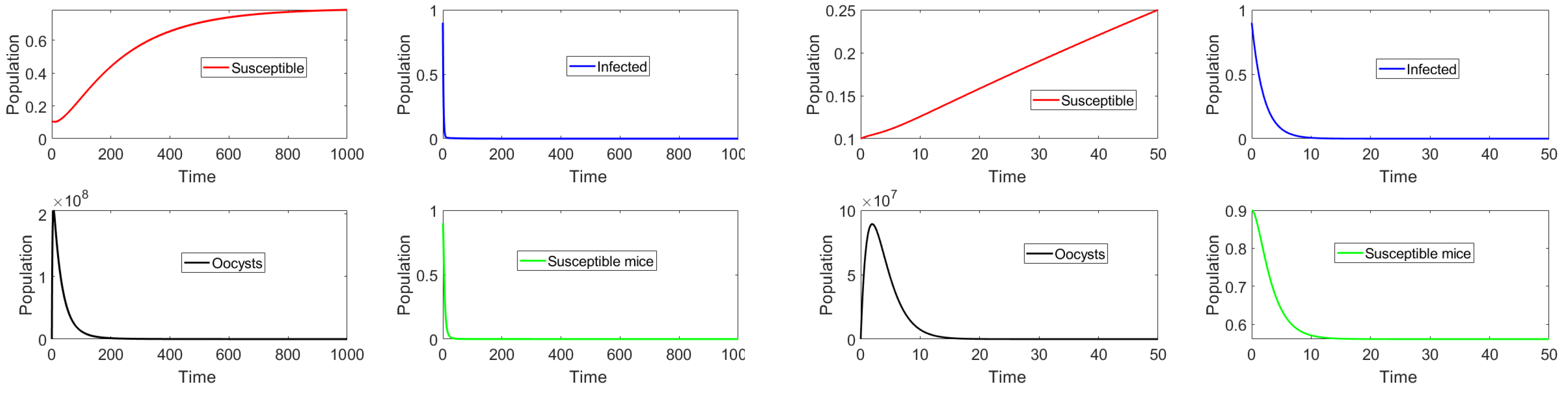
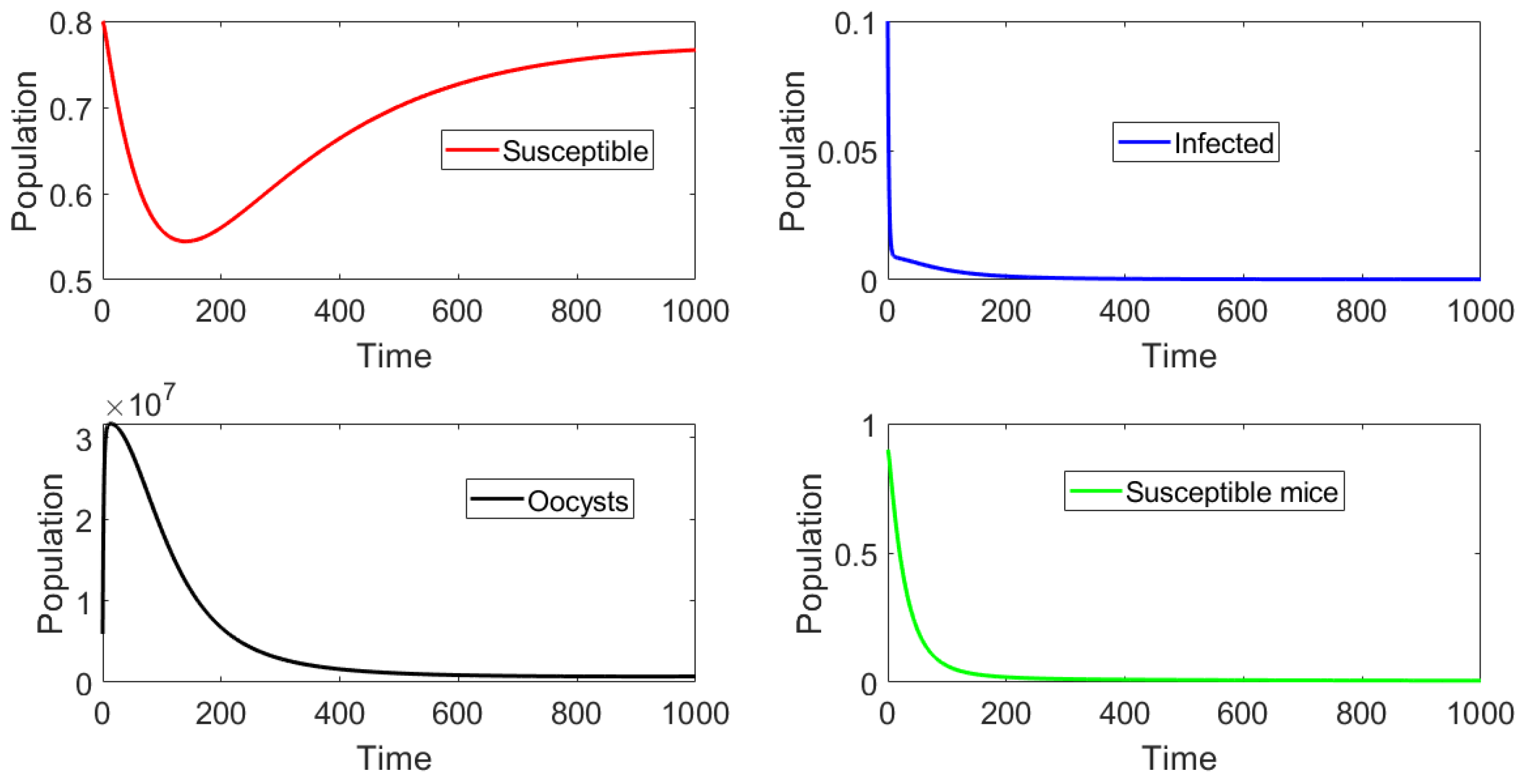
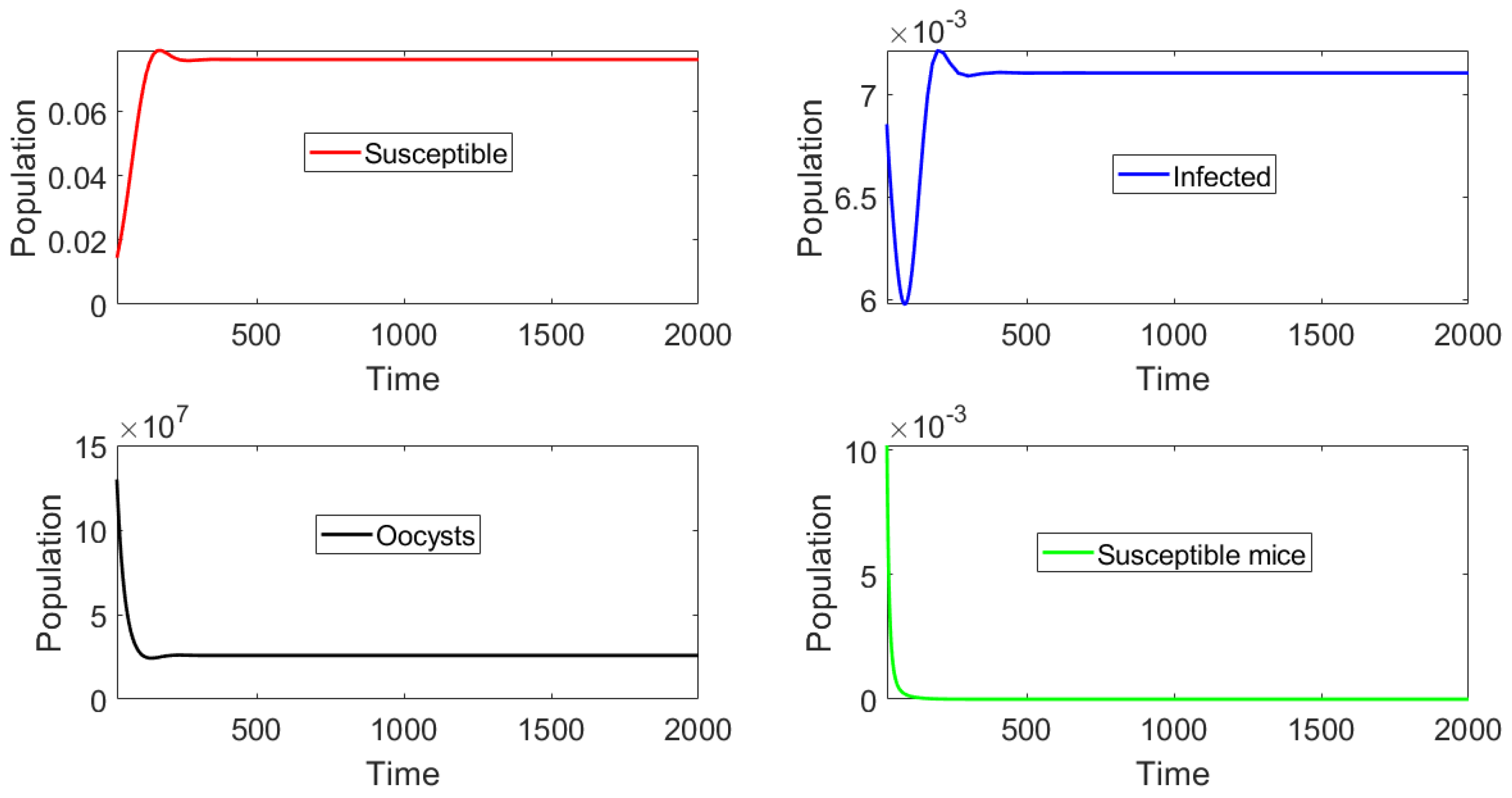
6. Numerical Simulations of Different Scenarios
6.1. Toxoplasmosis-Free Scenario ()
6.2. Toxoplasmosis Endemic Scenario ()
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reyes-Lizano, L.; Chinchilla-Carmona, M.; Guerrero-Bermúdez, O.; Arias-Echandi, M.; Castro-Castillo, A. Trasmisión de Toxoplasma gondii en Costa Rica: Un concepto actualizado. Acta Méd. Costarric. 2001, 43, 36–38. (In Spanish) [Google Scholar] [CrossRef]
- Beaver, P.; Jung, R.; Cupp, E. Clinical Parasitology, 9th ed.; Lea & Febiger: Philadelphia, PA, USA, 1984. [Google Scholar]
- Markell, E.; Voge, M.; David, J. Parasitología Médica; Mc Graw-Hill: Madrid, Spain, 1990. (In Spanish) [Google Scholar]
- Dubey, J. Duration of Immunity to Shedding of Toxoplasma gondii Oocysts by Cats. J. Parasitol. 1995, 81, 410–415. [Google Scholar] [CrossRef]
- Sibley, L.; Boothroyd, J. Virulent strains of Toxoplasma gondii comprise a single clonal lineage. Nature 1992, 359, 82–85. [Google Scholar] [CrossRef]
- Sunquist, M.; Sunquist, F. Wild Cats of the World; University of Chicago Press: Chicago, IL, USA, 2002. [Google Scholar]
- CDC. Center for Disease Control and Prevention, Toxoplasmosis. 2022. Available online: https://www.cdc.gov/parasites/toxoplasmosis/ (accessed on 10 March 2022).
- Dubey, J.P. The history of Toxoplasma gondii—The first 100 years. J. Eukaryot. Microbiol. 2008, 55, 467–475. [Google Scholar] [CrossRef]
- Lappin, M. Feline toxoplasmosis. Practice 1999, 21, 578–589. [Google Scholar] [CrossRef]
- Aramini, J.; Stephen, C.; Dubey, J.P.; Engelstoft, C.; Schwantje, H.; Ribble, C.S. Potential contamination of drinking water with Toxoplasma gondii oocysts. Epidemiol. Infect. Camb. Univ. Press 1999, 122, 305–315. [Google Scholar] [CrossRef]
- Dubey, J.P.; Thayer, D.W.; Speer, C.A.; Shen, S.K. Effect of gamma irradiation on unsporulated and sporulated Toxoplasma gondii oocysts. Int. J. Parasitol. 1998, 28, 369–375. [Google Scholar] [CrossRef]
- Mead, P.; Slutsker, L.; Dietz, V.; McCaig, L.; Bresee, J.S.; Shapiro, C.; Griffin, P.; Tauxe, R. Food-related illness and death in the United States. Emerg. Infect. Dis. 1999, 5, 607–625. [Google Scholar] [CrossRef]
- Dubey, J.; Frenkel, J. Feline toxoplasmosis from acutely infected mice and the development of Toxoplasma cysts. J. Protozool. 1976, 23, 537–546. [Google Scholar] [CrossRef]
- Dabritz, H.; Conrad, P.A. Cats and Toxoplasma: Implications for public health. Zoonoses Public Health 2010, 57, 34–52. [Google Scholar] [CrossRef]
- Torda, A. Toxoplasmosis. Are cats really the source? Aust. Fam. Physician 2001, 30, 743–747. [Google Scholar]
- Turner, M.; Lenhart, S.; Rosenthal, B.; Zhao, X. Modeling effective transmission pathways and control of the world’s most successful parasite. Theor. Popul. Biol. 2013, 86, 50–61. [Google Scholar] [CrossRef]
- Deng, H.; Cummins, R.; Schares, G.; Trevisan, C.; Enemark, H.; Waap, H.; Srbljanovic, J.; Djurkovic-Djakovic, O.; Pires, S.M.; van der Giessen, J.W.; et al. Mathematical modelling of Toxoplasma gondii transmission: A systematic review. Food Waterborne Parasitol. 2021, 22, e00102. [Google Scholar] [CrossRef]
- Robert-Gangneux, F.; Murat, J.B.; Fricker-Hidalgo, H.; Brenier-Pinchart, M.P.; Gangneux, J.P.; Pelloux, H. The placenta: A main role in congenital toxoplasmosis? Trends Parasitol. 2011, 27, 530–536. [Google Scholar] [CrossRef]
- Vargas-Villavicencio, J.A.; Cedillo-Peláez, C.; Rico-Torres, C.; Besne-Merida, A.; Garcia-Vazquez, F.; Saldana, J.; Correa, D. Mouse model of congenital infection with a non-virulent Toxoplasma gondii strain: Vertical transmission, “sterile” fetal damage, or both? Exp. Parasitol. 2016, 166, 116–123. [Google Scholar] [CrossRef]
- Shiono, Y.; Mun, H.S.; He, N.; Nakazaki, Y.; Fang, H.; Furuya, M.; Aosai, F.; Yano, A. Maternal–fetal transmission of Toxoplasma gondii in interferon-γ deficient pregnant mice. Parasitol. Int. 2007, 56, 141–148. [Google Scholar] [CrossRef]
- Darcy, F.; Zenner, L. Experimental models of toxoplasmosis. Res. Immunol. 1993, 144, 16–23. [Google Scholar] [CrossRef]
- Pezerico, S.B.; Langoni, H.; Da Silva, A.V.; Da Silva, R.C. Evaluation of Toxoplasma gondii placental transmission in BALB/c mice model. Exp. Parasitol. 2009, 123, 168–172. [Google Scholar] [CrossRef]
- Rejmanek, D.; Vanwormer, E.; Mazet, J.A.; Packham, A.E.; Aguilar, B.; Conrad, P.A. Congenital transmission of Toxoplasma gondii in deer mice (Peromyscus maniculatus) after oral oocyst infection. J. Parasitol. 2010, 96, 516–520. [Google Scholar] [CrossRef]
- Araujo, F.G.; Hunter, C.A.; Remington, J.S. Treatment with interleukin 12 in combination with atovaquone or clindamycin significantly increases survival of mice with acute toxoplasmosis. Antimicrob. Agents Chemother. 1997, 41, 188–190. [Google Scholar] [CrossRef] [Green Version]
- Hide, G. Role of vertical transmission of Toxoplasma gondii in prevalence of infection. Expert Rev. Anti-Infect. Ther. 2016, 14, 335–344. [Google Scholar] [CrossRef]
- Marshall, P.; Hughes, J.; Williams, R.; Smith, J.; Murphy, R.; Hide, G. Detection of high levels of congenital transmission of Toxoplasma gondii in natural urban populations of Mus domesticus. Parasitology 2004, 128, 39–42. [Google Scholar] [CrossRef] [Green Version]
- Murphy, R.G.; Williams, R.H.; Hughes, J.M.; Hide, G.; Ford, N.J.; Oldbury, D.J. The urban house mouse (Mus domesticus) as a reservoir of infection for the human parasite Toxoplasma gondii: An unrecognised public health issue? Int. J. Environ. Health Res. 2008, 18, 177–185. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo-Chavez, C.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: New York, NY, USA, 2012; Volume 2. [Google Scholar]
- Iqbal, M.S.; Ahmed, N.; Akgül, A.; Raza, A.; Shahzad, M.; Iqbal, Z.; Rafiq, M.; Jarad, F. Analysis of the fractional diarrhea model with Mittag-Leffler kernel. AIMS Math 2022, 7, 13000–13018. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.; Roberts, M. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef] [Green Version]
- Hethcote, H. Mathematics of infectious diseases. SIAM Rev. 2005, 42, 599–653. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, J.D.; Echeverry, L.M.; Rincon, C.A.P. Stability and bifurcation in epidemic models describing the transmission of toxoplasmosis in human and cat populations. Math. Methods Appl. Sci. 2017, 40, 5575–5592. [Google Scholar] [CrossRef]
- González-Parra, G.C.; Arenas, A.J.; Aranda, D.F.; Villanueva, R.J.; Jódar, L. Dynamics of a model of Toxoplasmosis disease in human and cat populations. Comput. Math. Appl. 2009, 57, 1692–1700. [Google Scholar] [CrossRef] [Green Version]
- Arenas, A.J.; González-Parra, G.; Micó, R.J.V. Modeling toxoplasmosis spread in cat populations under vaccination. Theor. Popul. Biol. 2010, 77, 227–237. [Google Scholar] [CrossRef]
- Lélu, M.; Langlais, M.; Poulle, M.L.; Gilot-Fromont, E. Transmission dynamics of Toxoplasma gondii along an urban–rural gradient. Theor. Popul. Biol. 2010, 78, 139–147. [Google Scholar] [CrossRef]
- Mateus-Pinilla, N.; Hannon, B.; Weigel, R. A computer simulation of the prevention of the transmission of Toxoplasma gondii on swine farms using a feline T. gondii vaccine. Prev. Vet. Med. 2002, 55, 17–36. [Google Scholar] [CrossRef] [PubMed]
- Marinović, A.A.B.; Opsteegh, M.; Deng, H.; Suijkerbuijk, A.W.; van Gils, P.F.; Van Der Giessen, J. Prospects of toxoplasmosis control by cat vaccination. Epidemics 2020, 30, 100380. [Google Scholar] [CrossRef]
- Innes, E.A.; Hamilton, C.; Garcia, J.L.; Chryssafidis, A.; Smith, D. A one health approach to vaccines against Toxoplasma gondii. Food Waterborne Parasitol. 2019, 15, e00053. [Google Scholar] [CrossRef]
- Freyre, A.; Choromanski, L.; Fishback, J.; Popiel, I. Immunization of cats with tissue cysts, bradyzoites, and tachyzoites of the T-263 strain of Toxoplasma gondii. J. Parasitol. 1993, 79, 716–719. [Google Scholar] [CrossRef]
- Frenkel, J. Transmission of toxoplasmosis and the role of immunity in limiting transmission and illness. J. Am. Vet. Med. Assoc. 1990, 196, 233–240. [Google Scholar]
- Sullivan, A.; Agusto, F.; Bewick, S.; Su, C.; Lenhart, S.; Zhao, X. A mathematical model for within-host Toxoplasma gondii invasion dynamics. Math. Biosci. Eng. 2012, 9, 647. [Google Scholar]
- González-Parra, G.; Sultana, S.; Arenas, A.J. Mathematical Modeling of Toxoplasmosis Considering a Time Delay in the Infectivity of Oocysts. Mathematics 2022, 10, 354. [Google Scholar] [CrossRef]
- Sultana, S.; González-Parra, G.; Arenas, A.J. Dynamics of toxoplasmosis in the cat’s population with an exposed stage and a time delay. Math. Biosci. Eng. 2022, 19, 12655–12676. [Google Scholar] [CrossRef]
- González-Parra, G.; Arenas, A.J.; Chen-Charpentier, B.; Sultana, S. Mathematical modeling of toxoplasmosis with multiple hosts, vertical transmission and cat vaccination. Comput. Appl. Math. 2023, 42, 88. [Google Scholar] [CrossRef]
- Ahmed, N.; Macías-Díaz, J.E.; Shahid, N.; Raza, A.; Rafiq, M. A dynamically consistent computational method to solve numerically a mathematical model of polio propagation with spatial diffusion. Comput. Methods Programs Biomed. 2022, 218, 106709. [Google Scholar] [CrossRef]
- Korobeinikov, A.; Wake, G.C. Lyapunov functions and global stability for SIR, SIRS, and SIS epidemiological models. Appl. Math. Lett. 2002, 15, 955–960. [Google Scholar] [CrossRef] [Green Version]
- Korobeinikov, A. Lyapunov functions and global stability for SIR and SIRS epidemiological models with non-linear transmission. Bull. Math. Biol. 2006, 68, 615–626. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shuai, Z.; van den Driessche, P. Global stability of infectious disease models using Lyapunov functions. SIAM J. Appl. Math. 2013, 73, 1513–1532. [Google Scholar] [CrossRef] [Green Version]
- Williams, R.; Morley, E.; Hughes, J.; Duncanson, P.; Terry, R.; Smith, J.; Hide, G. High levels of congenital transmission of Toxoplasma gondii in longitudinal and cross-sectional studies on sheep farms provides evidence of vertical transmission in ovine hosts. Parasitology 2005, 130, 301–307. [Google Scholar] [CrossRef] [Green Version]
- Lakshmikantham, V.; Leela, S.; Martynyuk, A. Stability Analysis of Nonlinear Systems; Marcel Dekker, Inc.: New York City, NY, USA, 1989. [Google Scholar]
- Routh, E.J. A Treatise on the Stability of a Given State of Motion: Particularly Steady Motion. Being the Essay to which the Adams Prize Was Adjudged in 1877, in the University of Cambridge; Macmillan and Company: London, UK, 1877. [Google Scholar]
- Berthier, K.; Langlais, M.; Auger, P.; Pontier, D. Dynamics of a feline virus with two transmission modes within exponentially growing host populations. Proc. R. Soc. B Biol. Sci. 2000, 267, 2049–2056. [Google Scholar] [CrossRef]
- Fayer, R. Toxoplasma gondii: Transmission, diagnosis and prevention. Can. Vet. 1981, 22, 344–352. [Google Scholar]
- Dubey, J.; Beattie, C. Toxoplasmosis of Animals and Man; CRC Press: Boca Raton, FL, USA, 1988. [Google Scholar]
- Dubey, J.P.; Graham, D.H.; Blackston, C.R.; Lehmann, T.; Gennari, S.M.; Ragozo, A.M.A.; Nishi, S.M.; Shen, S.K.; Kwok, O.C.H.; Hill, D.E.; et al. Biological and genetic characterisation of Toxoplasma gondii isolates from chickens (Gallus domesticus) from São Paulo, Brazil: Unexpected findings. Int. J. Parasitol. 2002, 32, 99–105. [Google Scholar] [CrossRef]

| Parameter | Description | Value |
|---|---|---|
| Death and birth rates (cats) | (1/weeks) [52] | |
| Shedding period | (1/weeks) [4] | |
| Clearance rate | (1/day) [4,36] | |
| k | Oocysts per day (cat) | (1/day) [53] |
| Transmission rate | varying | |
| Transmission rate | ||
| Vaccination rate | varying | |
| Subpopulations | Description | Initial values |
| S | Susceptible cats | 0.45 [36,54,55] |
| I | Infected cats | 1/130 [36,54,55] |
| Vaccinated/Recovered | ||
| O | Occysts | |
| Susceptible mice (proportion) | 0.9 | |
| Infected mice (proportion) | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sultana, S.; González-Parra, G.; Arenas, A.J. A Generalized Mathematical Model of Toxoplasmosis with an Intermediate Host and the Definitive Cat Host. Mathematics 2023, 11, 1642. https://doi.org/10.3390/math11071642
Sultana S, González-Parra G, Arenas AJ. A Generalized Mathematical Model of Toxoplasmosis with an Intermediate Host and the Definitive Cat Host. Mathematics. 2023; 11(7):1642. https://doi.org/10.3390/math11071642
Chicago/Turabian StyleSultana, Sharmin, Gilberto González-Parra, and Abraham J. Arenas. 2023. "A Generalized Mathematical Model of Toxoplasmosis with an Intermediate Host and the Definitive Cat Host" Mathematics 11, no. 7: 1642. https://doi.org/10.3390/math11071642
APA StyleSultana, S., González-Parra, G., & Arenas, A. J. (2023). A Generalized Mathematical Model of Toxoplasmosis with an Intermediate Host and the Definitive Cat Host. Mathematics, 11(7), 1642. https://doi.org/10.3390/math11071642








