Evolutionary Padé Approximation for Heat and Mass Transfer Analysis of Falkner–Skan Flow of a Bio-Convective Casson Fluid
Abstract
:1. Introduction
- (i)
- This study presents the analysis of heat and mass transfer in the Falkner–Skan flow of a bio-convective Casson fluid past a wedge by an artificial-intelligence-based paradigm. To the best of the authors’ knowledge, this is the first application of the EPA scheme to analyze the Falkner–Skan flow of bio-convective Casson fluid over a wedge.
- (ii)
- This work introduces the usage of Padé rational functions to handle asymptotic boundary conditions. This aspect is an interesting new direction in hybridizing convention-based semi-analytic methods to obtain a rationally tailed approximate solution to the model.
- (iii)
- As far as the authors’ intentions are concerned, the current script can be viewed as the first step towards the development of an artificial intelligence-assisted code for analyzing heat and mass transfer in fluid dynamics.
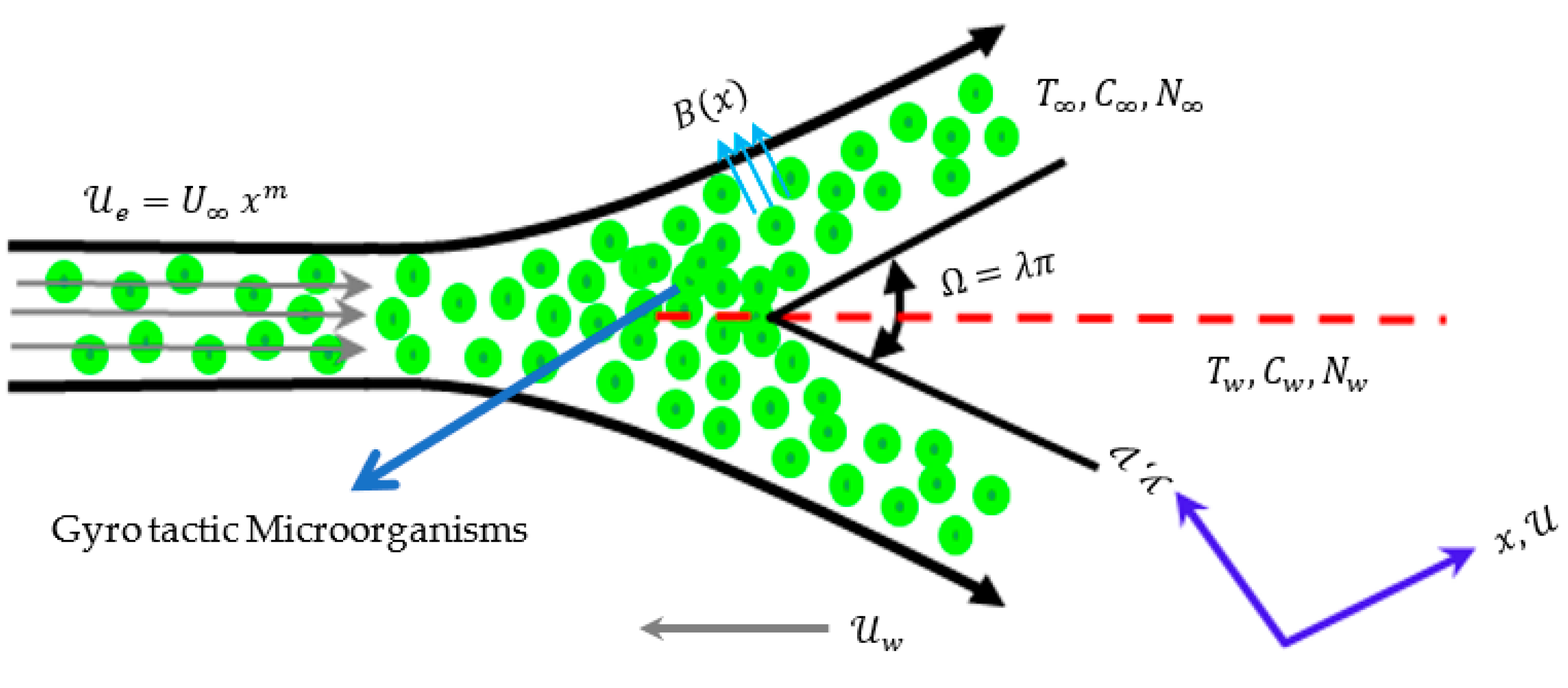
2. Problem Statement
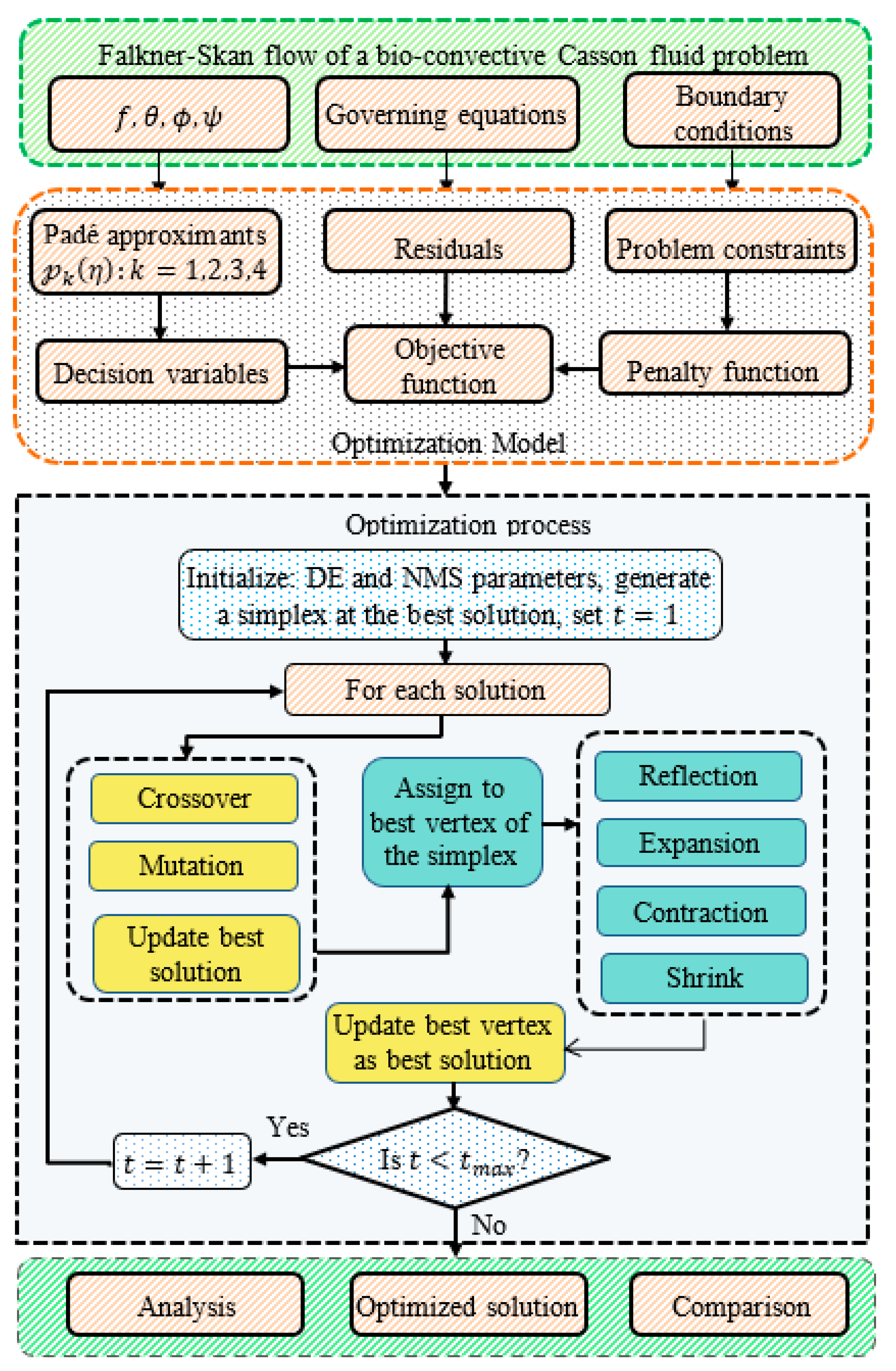
3. Evolutionary Padé Approximation (EPA) Framework
3.1. Formulation of Equivalent Optimization Problem
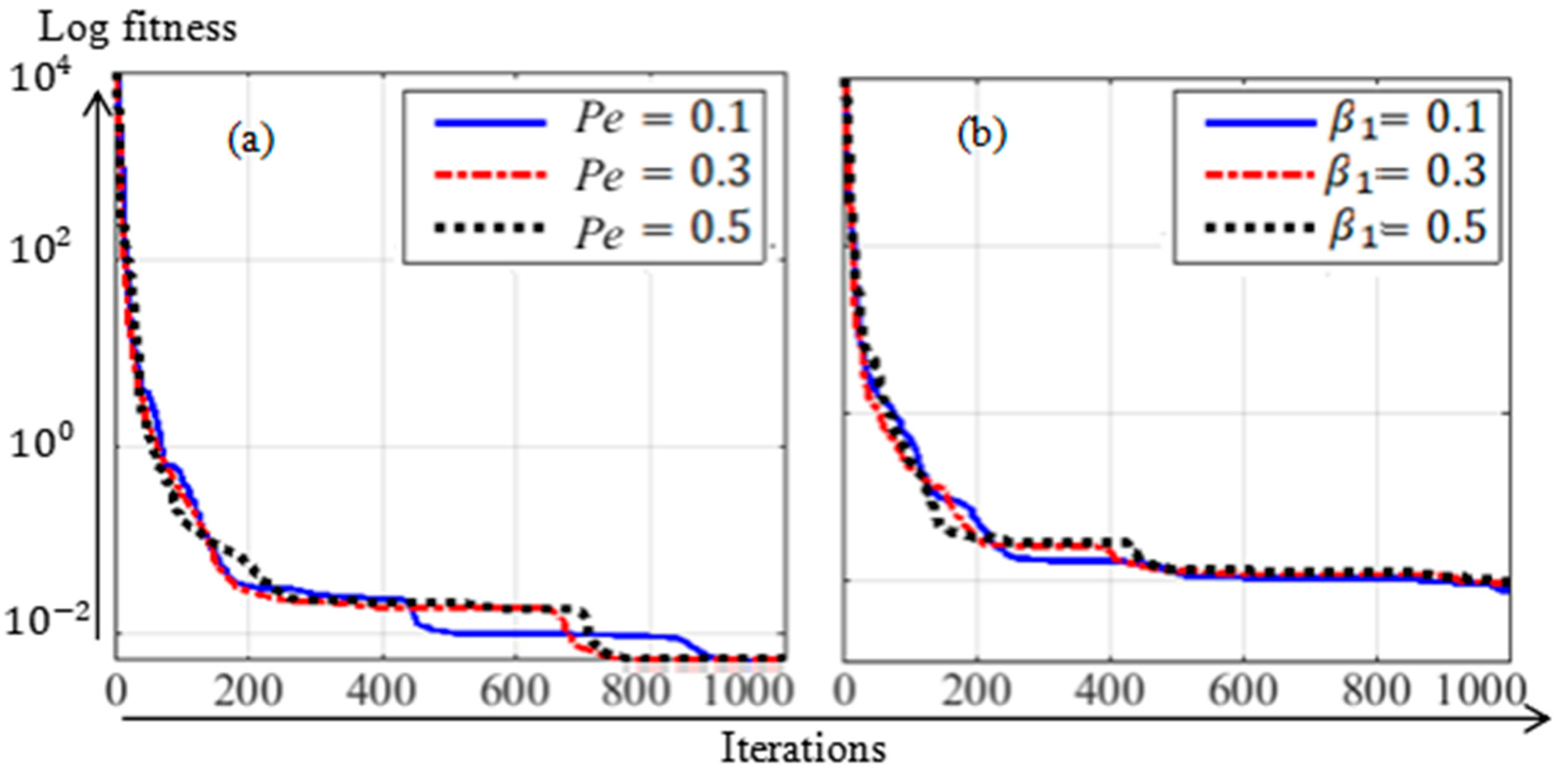
3.2. Hybrid of Differential Evolution (DE) and Nelder-Mead Simplex (NMS) Algorithms
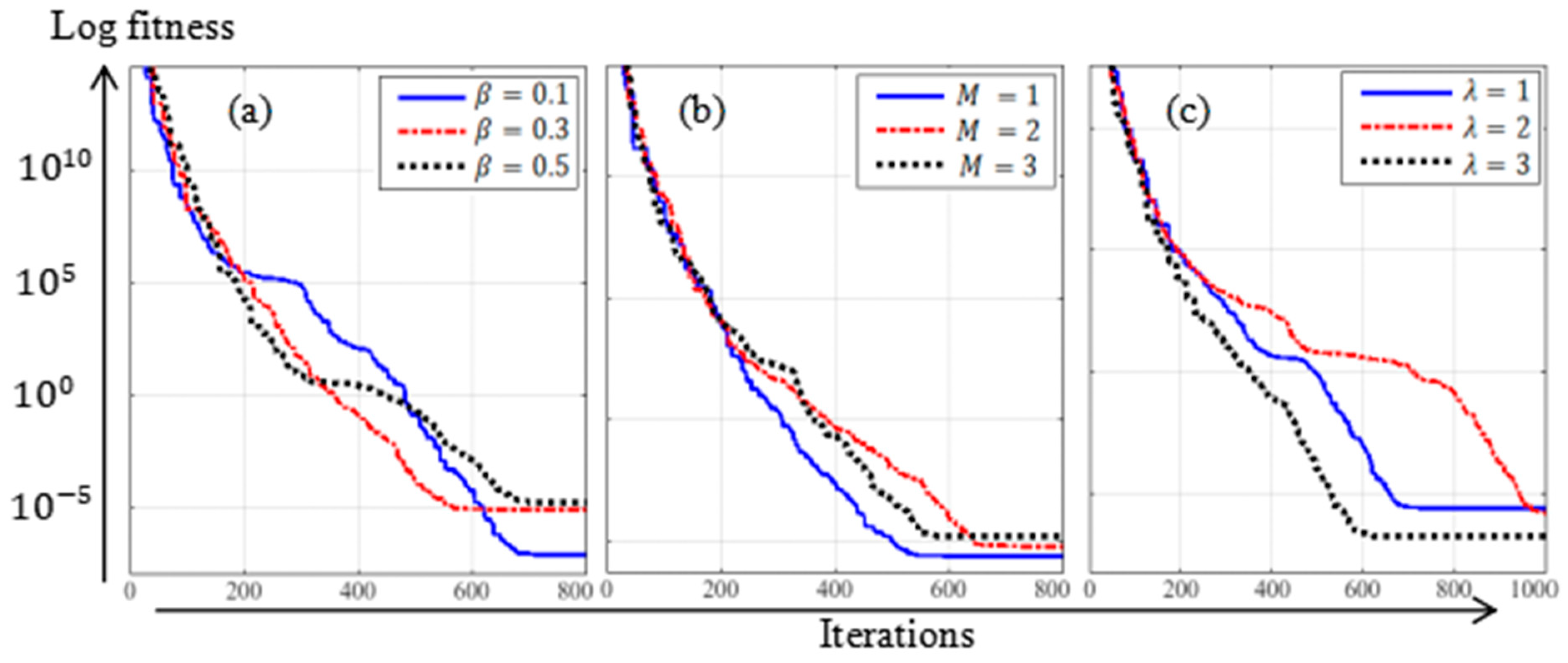
4. Results and Discussion
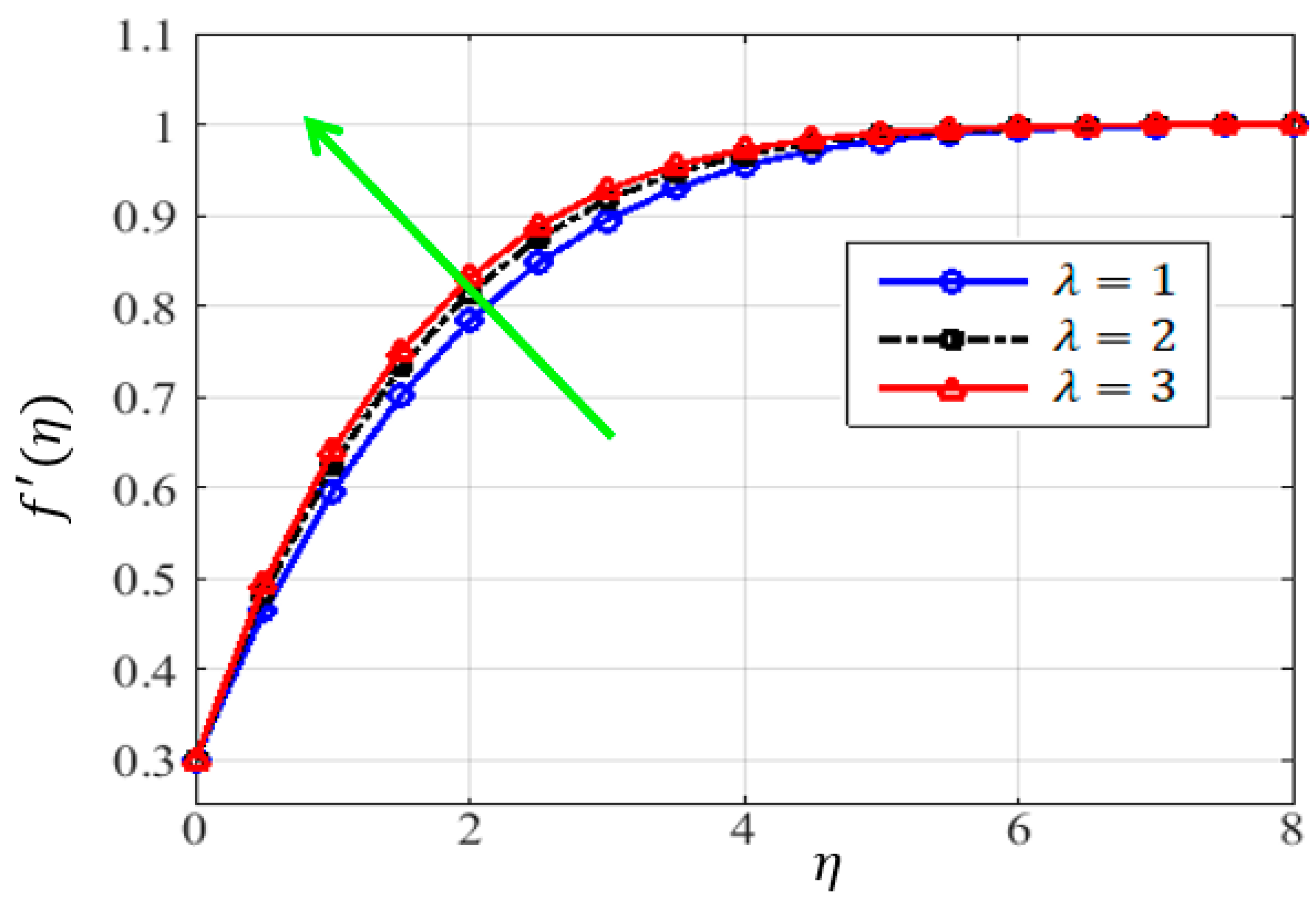
4.1. Dynamics of Velocity Profiles
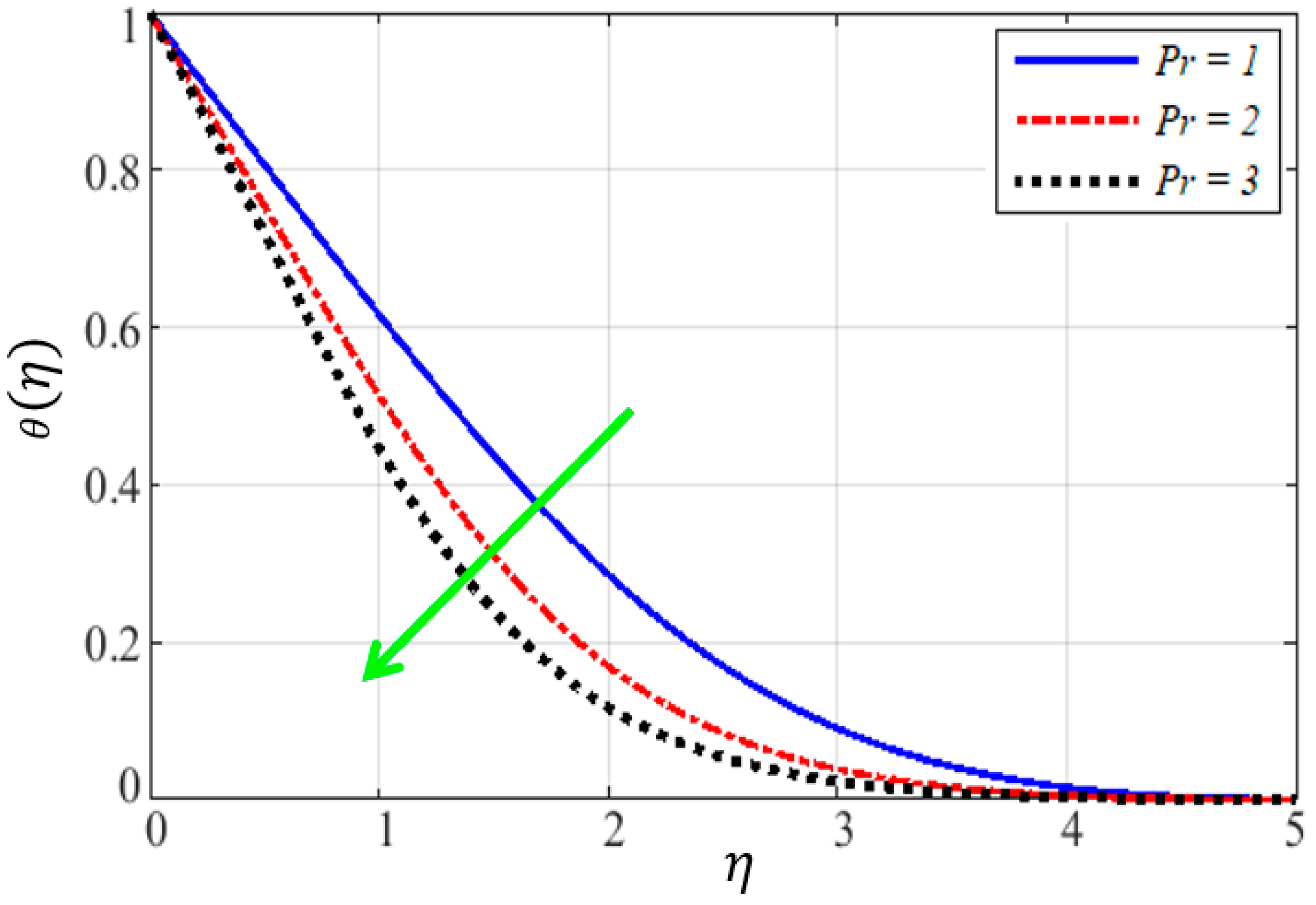
4.2. Dynamics of Temperature Field
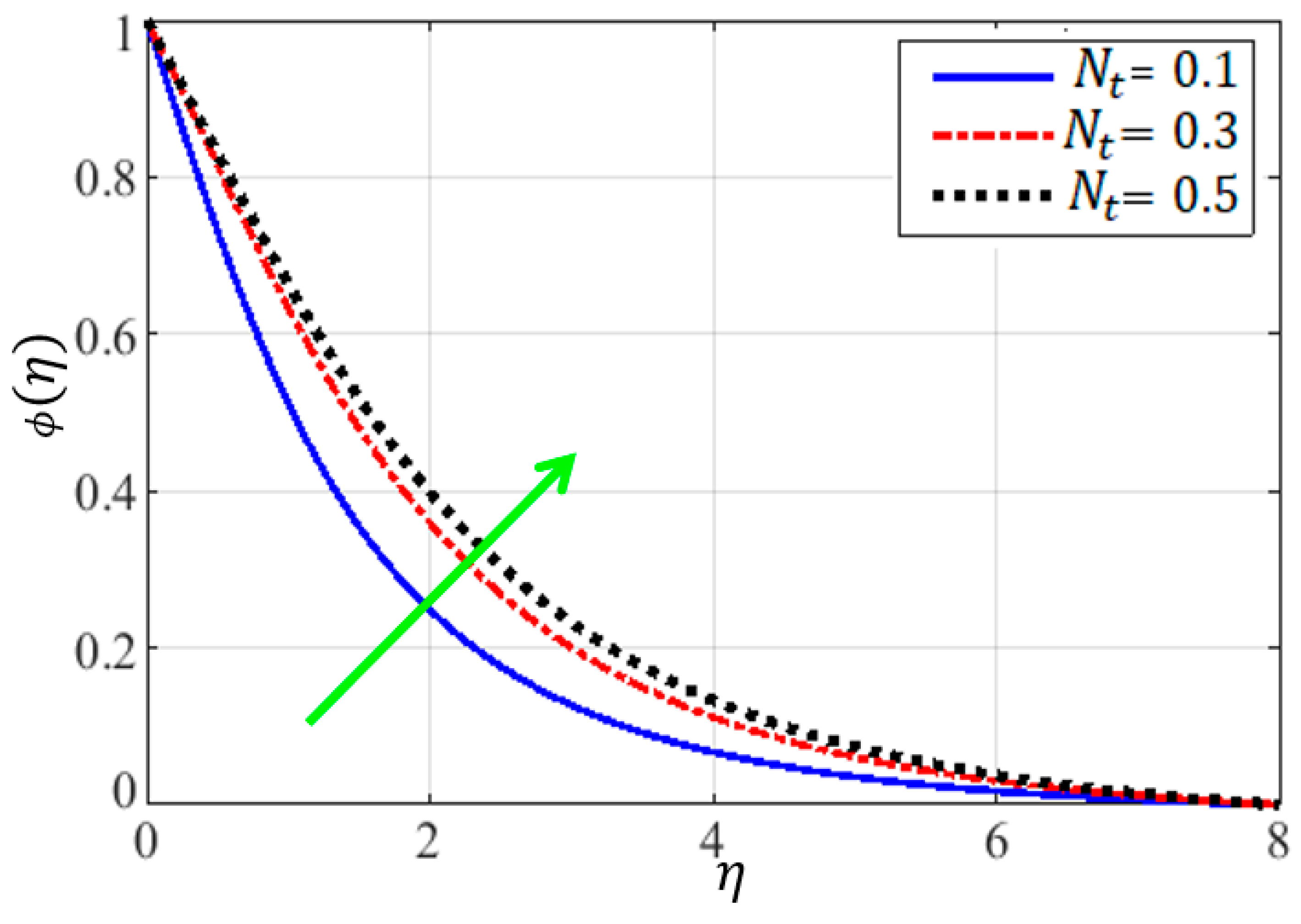
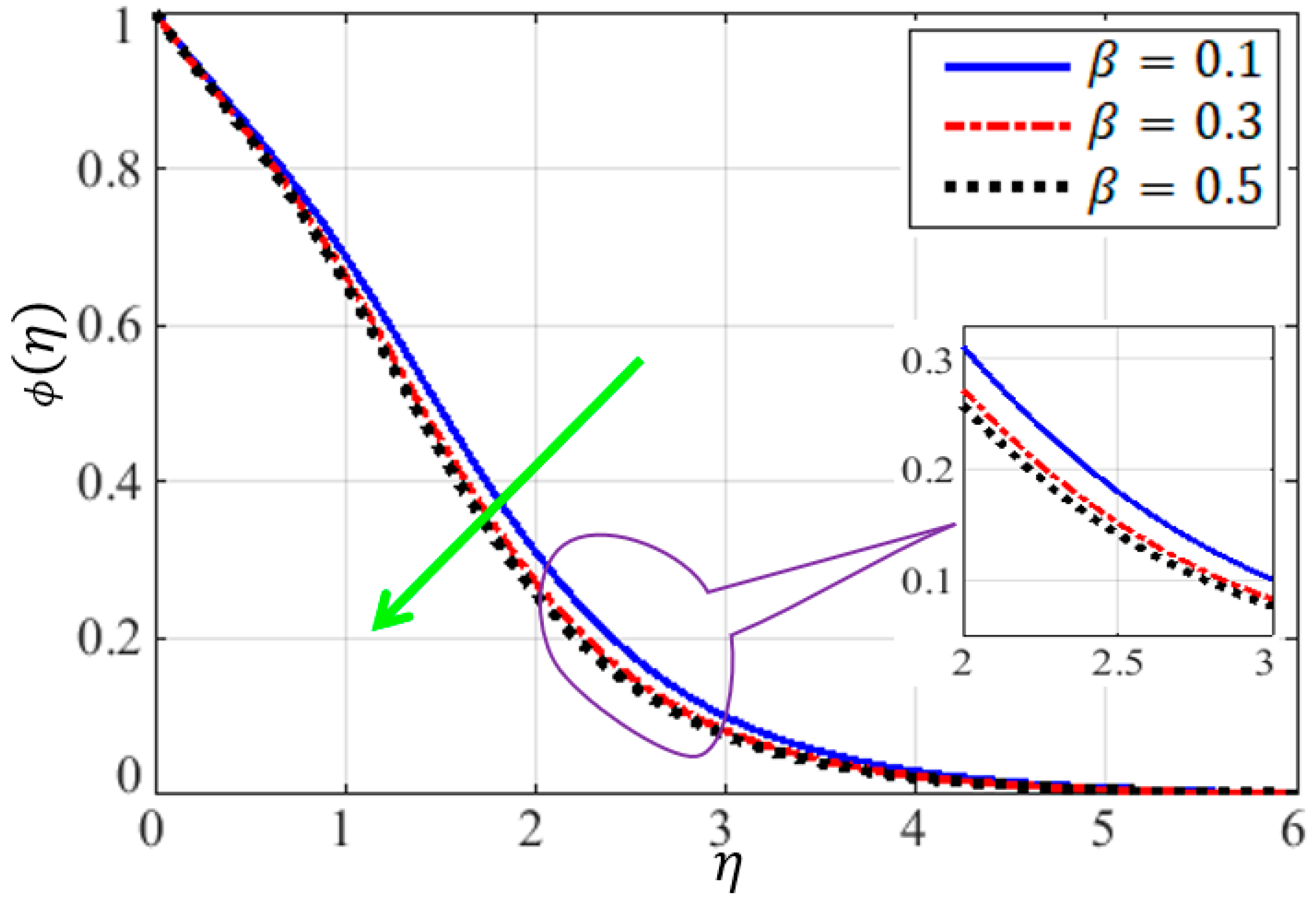
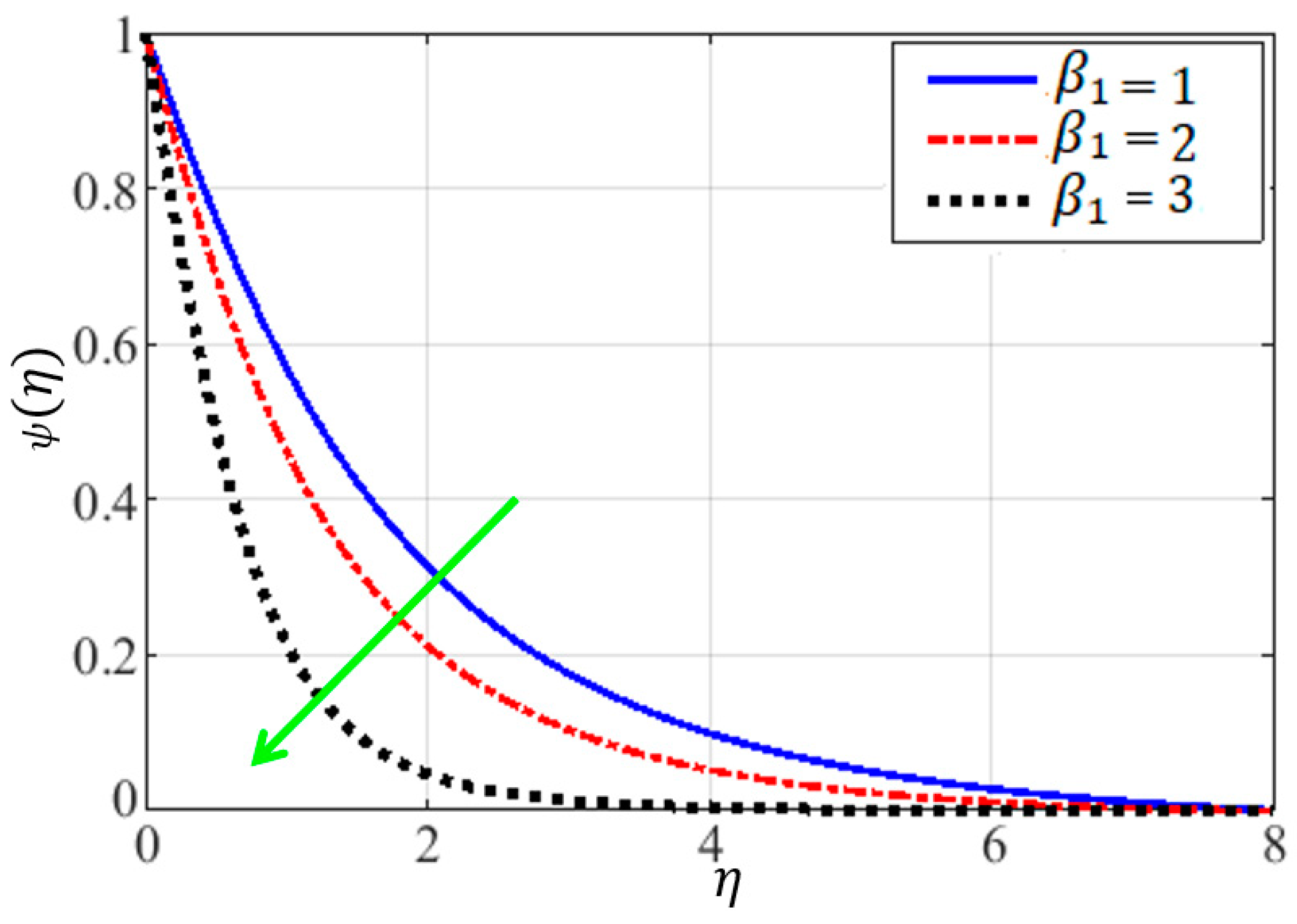
4.3. Dynamics of Fluid Concentration Fields
4.4. Dynamics of Density of Motile Organisms
5. Conclusions
- The governing equation of the velocity profile involves three physical parameters: Casson fluid viscosity force parameter (), magnetic field parameter (), and fluid flow parameter (). The velocity profile increases when each of these parameters is increased.
- Heat transfer rate increases with the increasing values of the radiation parameter () and thermophoresis parameter (), whereas it decreases with the increasing values of the Prandtl number ().
- When the magnetic field parameter () and Casson fluid viscosity force parameter () are increased, the fluid concentration field drops. On the other hand, when the thermophoresis parameter () is increased, the fluid concentration field increases.
- Finally, when the Péclet number () increases, the density field of motile microorganisms decreases; however, as the radiation parameter () and Prandl number () increase, the density field continues to increase as well.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Velocity components (m/s). | |
| Temperature of the fluid (K) | |
| Concentration of the fluid (Moles/kg) | |
| Density of motile micro organisms | |
| , | Space coordinates (m). |
| , | Specific heat capacity at constant pressure (J/Kg K) |
| Velocity component of the fluid at the wedge | |
| Temperature of the fluid at the wedge | |
| Concentration of the fluid at the wedge | |
| Velocity component of the fluid at the free stream | |
| Temperature of the fluid at the free stream | |
| Concentration of the fluid at the free stream | |
| Free stream velocity | |
| Coefficient of thermophoresis diffusion | |
| Coefficient of thermophoretic diffusion | |
| Varying magnetic field | |
| Magnetic induction parameter | |
| Density of coefficient of diffusion | |
| Maximum swimming speed of the cell | |
| Chemotaxis coefficient | |
| Acceleration due to gravity (m/s2) | |
| Electrical conductivity () | |
| Fluid heat capacity (Kg/m3K) | |
| Effective heat capacity of particle (Kg/m3K) | |
| Density of the fluid (kg/m3) | |
| Thermal conductivity of the fluid | |
| Subscripts | |
| ,y | Partial derivatives |
| Conditions at the wedge and free stream, respectively. | |
| All other subscripts denote physical constants. | |
| Dimensionless parameters | |
| Péclet number | |
| Prandtl number | |
| Lewis number | |
| Brownian motion parameter | |
| Thermophoresis parameter | |
| Radiation parameter | |
| Magnetic field parameter | |
| Parameter of Falkner–Skan power law | |
| Hartree pressure gradient parameter | |
| Casson fluid viscosity force parameter | |
| Fluid parameter | |
| Wedge parameter | |
| Dimensionless variables | |
| Similarity variable | |
| Velocity profile | |
| Temperature profile | |
| Fluid concentration profile | |
| Motile microorganism density | |
| Others | |
| Kinematic viscosity of the fluid | |
| Specific heat capacitance | |
| Effective heat capacity of the fluid phase with respect to the particle | |
| Base fluid’s density | |
| Aggregate absorption coefficient | |
| Stefan-Boltzmann coefficient | |
| Dynamic viscosity of base fluid | |
| Derivative with respect to similarity variable | |
Appendix A
| Pseudo code of DE-NMS algorithm |
| Step I: Initialization |
|
| , , store the best solution as . |
|
| Step II: //DE phase // |
| For each , choose distinct integers . Set . |
|
| Step III: // NMS phase// |
|
| Step IV: Display results: Display as optimum solution of problem (38) and Stop. |
References
- Harris, J. Rheology and Non-Newtonian Flow; Longman: New York, NY, USA, 1977; pp. 28–33. [Google Scholar]
- Bird, R.B.; Curtis, C.F.; Armstrong, R.C.; Hassager, O. Dynamics of Polyometric Liquids; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Batchelor, B.G.K. The effect of Brownian motion on the bulk stress in a suspension of spherical particles. J. Fluid Mech. 1977, 83, 97–117. [Google Scholar] [CrossRef]
- Hillesdon, A.J.; Pedley, T.J.; Kessler, J.O. The development of concentration gradients in a suspension of chemotactic bacteria. Bull. Math. Biol. 1995, 57, 299. [Google Scholar] [CrossRef]
- Guell, D.C.; Brenner, H.; Frankel, R.B.; Hartman, H. Hydrodynamic forces and band formation in swimming magnetotactic bacteria. J. Theor. Biol. 1988, 135, 525. [Google Scholar] [CrossRef] [Green Version]
- Alloui, Z.; Nguyen, T.H.; Bilgen, E. Bioconvection of gravitactic microorganisms in a vertical cylinder. Int. Commun. Heat Mass Transf. 2005, 32, 739–747. [Google Scholar] [CrossRef]
- Ishikawa, T.; Pedley, T.J. The rheology of a semi-dilute suspension of swimming model micro-organisms. J. Fluid Mech. 2007, 588, 399–435. [Google Scholar] [CrossRef]
- Mehandia, V.; Nott, P.R. The collective dynamics of self-propelled particles. J. Fluid Mech. 2008, 595, 239–264. [Google Scholar] [CrossRef] [Green Version]
- Pedley, T.J. Instability of uniform micro-organism suspensions revisited. J. Fluid Mech. 2010, 647, 335–359. [Google Scholar] [CrossRef]
- Nguyen-quang, T.R.I.; Guichard, F. The role of bioconvection in plankton population with thermal stratification. Int. J. Bifurc. Chaos 2010, 20, 1761–1778. [Google Scholar] [CrossRef]
- Ghorai, S.; Panda, M.K.; Hill, N.A. Bioconvection in a suspension of isotropically scattering phototactic algae. Phys. Fluids 2010, 22, 071901. [Google Scholar] [CrossRef]
- Kuznetsov, A.V. Bio-thermal convection induced by two different species of microorganisms. Int. Commun. Heat Mass Transf. 2011, 38, 548–553. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, M.; Nadeem, S.; Mesloub, S. Falkner–Skan wedge flow of a power-law fluid with mixed convection and porous medium. Comp. Fluids 2011, 49, 22–28. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Rastegari, M.T.; Asadi, M.; Bég, O.A. A study of non-Newtonian flow and heat transfer over a non-isothermal wedge using the homotopy analysis method. Chem. Eng. Commun. 2011, 199, 231–256. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary layer flow past a wedge moving in a nanofluid. Math. Probl. Eng. 2013, 2013, 637285. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Akbar, N.S. MHD three-dimensional boundary layer flow of Casson nanofluid past a linearly stretching sheet with convective boundary condition. IEEE Trans. Nanotechnol. 2014, 13, 109–115. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Sandeep, N. Heat and mass transfer in MHD non-Newtonian bio-convection flow over a rotating cone/plate with cross diffusion. J. Mol. Liq. 2016, 215, 115–126. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Mondal, I.C.; Chamkha, A.J. Casson fluid flow and heat transfer past a symmetric wedge. Heat Transf. Asian Res. 2013, 42, 665–675. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Raju, C.S.K.; Sandeep, N. Unequal diffusivities case of homogeneous–heterogeneous reactions within viscoelastic fluid flow in the presence of induced magnetic-field and nonlinear thermal radiation. Alex. Eng. J. 2016, 55, 1595–1606. [Google Scholar] [CrossRef] [Green Version]
- Raju, C.S.K.; Sandeep, N. Unsteady three-dimensional flow of Casson–Carreau fluids past a stretching surface. Alex. Eng. J. 2016, 55, 1115–1126. [Google Scholar] [CrossRef] [Green Version]
- Uddin, M.J.; Kabir, M.N.; Bég, O.A. Computational investigation of Stefan blowing and multiple-slip effects on buoyancy-driven bio-convection nanofluid flow with microorganisms. Int. J. Heat Mass Transf. 2016, 95, 116–130. [Google Scholar] [CrossRef]
- Dhanai, R.; Rana, P.; Kumar, L. Lie group analysis for bio-convection MHD slip flow and heat transfer of nanofluid over an inclined sheet: Multiple solutions. J. Taiwan Inst. Chem. Eng. 2016, 66, 283–296. [Google Scholar] [CrossRef]
- Coelho, P.M.; Pinho, F.T.; Oliveira, P.J. Fully developed forced convection of the Phan-Thien–Tanner fluid in ducts with a constant wall temperature. Int. J. Heat Mass Trans. 2002, 45, 1413–1423. [Google Scholar] [CrossRef] [Green Version]
- Francisca, J.S.; Tso, C.P.; Hung, Y.M.; Rilling, D. Heat transfer on asymmetric thermal viscous dissipative Couette–Poiseuille flow of pseudo-plastic fluids. J. Non-Newton. Fluid Mech. 2012, 169–170, 42–53. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Rashad, A.M.; Kameswaran, P.K.; Abdou, M.M.M. Radiation effects on natural bioconvection flow of a nanofluid containing gyrotactic microorganisms past a vertical plate with streamwise temperature variation. J. Nanofluids 2017, 6, 587–595. [Google Scholar] [CrossRef]
- Rashad, A.M.; Chamkha, A.; Mallikarjuna, B.; Abdou, M.M.M. Mixed bioconvection flow of a nanofluid containing gyrotactic microorganisms past a vertical slender cylinder. Front. Heat Mass Transf. 2018, 10, 21. [Google Scholar]
- Rashad, A.M.; Nabwey, H.A. Gyrotactic mixed bioconvection flow of a nanofluid past a circular cylinder with convective boundary condition. J. Taiwan Inst. Chem. Eng. 2019, 99, 9–17. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Sandeep, N. A comparative study on heat and mass transfer of the Blasius and Falkner–Skan flow of a bio-convective Casson fluid past a wedge. Eur. Phys. J. Plus 2016, 131, 405. [Google Scholar] [CrossRef]
- Falkner, V.M.; Skan, S.W. Some approximate solutions of the boundary layer equations. Philos. Mag. 1931, 12, 865–896. [Google Scholar] [CrossRef]
- Thomas, J.W. Numerical Partial Differential Equations: Finite Difference Methods; Springer: New York, NY, USA, 1995. [Google Scholar]
- Hartley, T.; Wanner, T. A semi-implicit spectral method for stochastic nonlocal phase-field models. Discrete Contin. Dyn. Syst. A 2009, 25, 399–429. [Google Scholar] [CrossRef]
- Guo, B.Y.; Shen, J.; Wang, Z.Q. Chebyshev rational spectral and pseudo spectral methods on a semi-infinite interval. Int. J. Numer. Methods Eng. 2002, 53, 65–84. [Google Scholar] [CrossRef]
- Inayat, U.; Iqbal, S.; Manzoor, T. Theoretical investigation of two-dimensional nonlinear radiative thermionics in Nano-MHD for solar insolation: A semi-empirical approach. Comput. Model. Eng. Sci. 2022, 130, 751–776. [Google Scholar] [CrossRef]
- Khan, K.A.; Seadawy, A.R.; Raza, N. The homotopy simulation of MHD time dependent three dimensional shear thinning fluid flow over a stretching plate. Chaos Solitons Fractals 2022, 157, 111888. [Google Scholar] [CrossRef]
- Abdullah, M.; Butt, A.R.; Raza, N.; Haque, E.U. Semi-analytical technique for the solution of fractional Maxwell fluid. Can. J. Phys. 2018, 95, 472–478. [Google Scholar] [CrossRef]
- Abdullah, M.; Butt, A.R.; Raza, N.; Alshomrani, A.S.; Alzahrani, A.K. Analysis of blood flow with nanoparticles induced by uniform magnetic field through a circular cylinder with fractional Caputo derivatives. J. Magn. Magn. Mater. 2018, 446, 28–36. [Google Scholar] [CrossRef]
- Razzaq, A.; Seadawy, A.R.; Raza, N. Heat transfer analysis of viscoelastic fluid flow with fractional Maxwell model in the cylindrical geometry. Phys. Scr. 2020, 95, 115220. [Google Scholar] [CrossRef]
- Babaei, M. A general approach to approximate solutions of nonlinear differential equations using particle swarm optimization. Appl. Soft Comput. 2013, 13, 3354–3365. [Google Scholar] [CrossRef]
- Mastorakis, N.E. Unstable ordinary differential equations: Solution via genetic algorithms and the method of Nelder-Mead. WSEAS Trans. Math. 2006, 5, 1276–1281. [Google Scholar]
- Cao, H.; Kang, L.; Chen, Y. Evolutionary modelling of systems of ordinary differential equations with genetic programming. Genet. Program. Evolvable Mach. 2000, 1, 309–337. [Google Scholar] [CrossRef]
- Panagant, N.; Bureerat, S. Solving partial differential equations using a new differential evolution algorithm. Math. Probl. Eng. 2014, 10, 747490. [Google Scholar] [CrossRef] [Green Version]
- Ali, J.; Saeed, M.; Rafiq, M.; Iqbal, S. Numerical treatment of nonlinear model of virus propagation in computer networks: An innovative evolutionary Padé approximation scheme. Adv. Differ. Equ. 2018, 2018, 214. [Google Scholar] [CrossRef] [Green Version]
- Ali, J.; Raza, A.; Ahmed, N.; Ahmadian, A.; Rafiq, M.; Ferrara, M. Evolutionary optimized Padé approximation scheme for analysis of covid-19 model with crowding effect. Oper. Res. Perspect. 2021, 100207. [Google Scholar] [CrossRef]
- Nisar, K.S.; Ali, J.; Mahmood, M.K.; Ahmad, D.; Ali, S. Hybrid evolutionary Padé approximation approach for numerical treatment of nonlinear partial differential equations. Alex. Eng. J. 2021, 60, 4411–4421. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Ali, J.; Saeed, M.; Chaudhry, N.A.; Tabassum, M.F.; Luqman, M. Low cost efficient remedial strategy for stagnated Nelder-Mead simplex method. Pak. J. Sci. 2017, 69, 119–126. [Google Scholar]
- Kuo, B.L. Heat transfer analysis for the Falkner–Skan wedge flow by the differential transformation method. Int. J. Heat Mass Transf. 2005, 48, 5036–5046. [Google Scholar] [CrossRef]
- Yih, K.A. MHD forced convection flow adjacent to a non-isothermal wedge. Int. Commun. Heat Mass Transf. 1999, 26, 819–827. [Google Scholar] [CrossRef]
- Escandón, J.; Santiago, F.; Bautista, O.; Méndez, F. Hydrodynamics and thermal analysis of a mixed electro magneto hydrodynamic pressure driven flow for Phan–Thien–Tanner fluids in a microchannel. Int. J. Therm. Sci. 2014, 86, 246–257. [Google Scholar] [CrossRef]









| Kuo [48] | Raju and Sandeep [28] | Present Study | ||||
|---|---|---|---|---|---|---|
| λ = 0 | λ = 2 | λ = 0 | λ = 2 | λ = 0 | λ = 2 | |
| 0.72 | 0.41809 | 0.5298 | 0.41886 | 0.5296 | 0.41821 | 0.5298 |
| 1.0 | 0.46960 | 0.60541 | 0.46960 | 0.6052 | 0.46960 | 0.60551 |
| 10 | 1.02974 | 1.4561 | 1.02974 | 1.4588 | 1.02974 | 1.4593 |
| 30 | 1.4873 | 2.1582 | 1.4873 | 2.1580 | 1.4873 | 2.1580 |
| 100 | 2.2229 | 3.2869 | 2.2229 | 3.2873 | 2.2229 | 3.2870 |
| 1000 | 4.7901 | 7.2225 | 4.7901 | 7.2334 | 4.7901 | 7.2298 |
| Yih [49] | Mukhophaday et al. [18] | Raju and Sandeep [28] | Present Study | |
|---|---|---|---|---|
| −0.05 | 0.21348 | 0.21380 | 0.21375 | 0.21351 |
| 0.0 | 0.33323 | 0.33220 | 0.33221 | 0.33226 |
| 1/3 | 0.75745 | 0.75758 | 0.75757 | 0.75758 |
| 1.0 | 1.232588 | 1.23271 | 1.23270 | 1.23272 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basendwah, G.A.; Raza, N.; Ali, J. Evolutionary Padé Approximation for Heat and Mass Transfer Analysis of Falkner–Skan Flow of a Bio-Convective Casson Fluid. Mathematics 2023, 11, 1688. https://doi.org/10.3390/math11071688
Basendwah GA, Raza N, Ali J. Evolutionary Padé Approximation for Heat and Mass Transfer Analysis of Falkner–Skan Flow of a Bio-Convective Casson Fluid. Mathematics. 2023; 11(7):1688. https://doi.org/10.3390/math11071688
Chicago/Turabian StyleBasendwah, Ghada Ali, Nauman Raza, and Javaid Ali. 2023. "Evolutionary Padé Approximation for Heat and Mass Transfer Analysis of Falkner–Skan Flow of a Bio-Convective Casson Fluid" Mathematics 11, no. 7: 1688. https://doi.org/10.3390/math11071688







