A New Discretization Scheme for the Non-Isotropic Stockwell Transform

Abstract

To avoid the undesired angular expansion of the sampling grid in the discrete non-isotropic Stockwell transform, in this communication we propose a scale-dependent discretization scheme that controls both the radial and angular expansions in unison. Based on the new discretization scheme, we derive a sufficient condition for the construction of Stockwell frames in ${\displaystyle L^2\left({\mathbb{R}}^2\right)}$.

1. Introduction

For an efficient representation of non-transient signals, R.G. Stockwell [1] introduced a hybrid time-frequency tool by combining the merits of the classical short-time Fourier and wavelet transforms. For any finite energy signal ${\displaystyle f\in L^2\left(\mathbb{R}\right)}$, the Stockwell transform with respect to a window function ${\displaystyle \psi \in L^2\left(\mathbb{R}\right)}$ is defined by

$$\begin{array}{c}\hfill {\mathcal{S}}_{\psi }\left[f\right](\omega ,b)=\left|\omega \right|{\int }_{\mathbb{R}}f\left(t\right)\overline{\psi \left(\omega (t-b)\right)}{e}^{-2\pi it\omega }dt,b\in \mathbb{R},\omega \in \mathbb{R}\setminus \left\{0\right\},\end{array}$$

(1)

where ${\displaystyle b}$ and ${\displaystyle \omega }$ denote the time and spectral localization parameters, respectively. The Stockwell transform (1) offers the absolutely referenced phase information of the given signal ${\displaystyle f}$ by fixing the modulating sinusoids with respect to the time axis while translating and dilating the window function ${\displaystyle \psi }$. Thus, the Stockwell transform provides a frequency-dependent resolution while maintaining a direct relationship with the Fourier spectrum [2,3,4,5]. These unique features of the Stockwell transform are apt for diversified applications to different branches of science and engineering, including geophysics, optics, quantum mechanics, signal and image processing, and so on [5,6,7,8,9,10,11,12].

To harness the merits of the Stockwell transform in higher dimensions, we have recently introduced the notion of non-isotropic angular Stockwell transform in [11]. The essence of such a non-isotropic Stockwell transform lies in the fact that the underlying window functions are directionally tunable, which enhances the potency for resolving geometric features in two-dimensional signals. For any ${\displaystyle f\in L^2\left({\mathbb{R}}^2\right)}$, the non-isotropic angular Stockwell transform with respect to the window function ${\displaystyle \mathrm{\Psi }\in L^2\left({\mathbb{R}}^2\right)}$ is defined as

$$\begin{array}{c}\hfill {\mathcal{S}}_{\mathrm{\Psi }}\left[f\right](\mathbf{w},\mathbf{b},\theta )=|det{A}_{\mathbf{w}}|{\int }_{{\mathbb{R}}^2}f\left(\mathbf{t}\right)\overline{\mathrm{\Psi }\left(R_{\theta }{A}_{\mathbf{w}}(\mathbf{t}-\mathbf{b})\right)}{e}^{-2\pi i{\mathbf{t}}^T\mathbf{w}}d\mathbf{t},\end{array}$$

(2)

where ${\displaystyle \mathbf{t}={(t_1,t_2)}^T\in {\mathbb{R}}^2}$, ${\displaystyle \mathbf{b}={(b_1,b_2)}^T\in {\mathbb{R}}^2}$, ${\displaystyle \mathbf{w}={({\omega }_1,{\omega }_2)}^T\in {\mathbb{R}}^2}$ with ${\displaystyle {\omega }_1,{\omega }_2\ne 0}$ and ${\displaystyle \theta \in [0,2\pi )}$. The matrix ${\displaystyle A_{\mathbf{w}}\in GL(2,\mathbb{R})}$ and the rotation matrix ${\displaystyle R_{\theta }}$ appearing in (2) are given by

$$A_{\mathbf{w}}=\left(\begin{array}{cc}{\omega }_1& 0\\ 0& {\omega }_2\end{array}\right)\mathrm{and}{R}_{\theta }=\left(\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & \phantom{-}cos\theta \end{array}\right),$$

(3)

respectively. Furthermore, in the same article [11], we have also presented a discrete analogue of (2) by adopting the following procedure:

(i).

The frequency variable ${\displaystyle \mathbf{w}={({\omega }_1,{\omega }_2)}^T}$ is discretized by choosing ${\displaystyle {\mathbf{w}}_j={({\lambda }^j,{\lambda }^j)}^T}$, where ${\displaystyle \lambda >1}$ and ${\displaystyle j\in \mathbb{Z}}$. Consequently, the matrix ${\displaystyle A_{\mathbf{w}}}$ given by (3) takes the form:

$$\begin{array}{c}\hfill A_j=\left(\begin{array}{cc}{\lambda }^j& 0\\ 0& {\lambda }^j\end{array}\right).\end{array}$$

(ii).

The angular parameter ${\displaystyle \theta }$ is discretized by sub-dividing the interval ${\displaystyle [0,2\pi )}$ into ${\displaystyle L}$-equally spaced angles by taking ${\displaystyle {\theta }_{\ell }=\ell {\theta }_0}$, where ${\displaystyle {\theta }_0=2\pi /L}$ and ${\displaystyle \ell \in {\mathbb{Z}}_L=\left\{0,1,2,\cdots ,L-1\right\}}$.

(iii).

For ${\displaystyle \mathbf{m}={(m_0,m_1)}^T\in {\mathbb{Z}}^2}$ and ${\displaystyle {\alpha }_0,{\alpha }_1>0}$, the translation parameter ${\displaystyle \mathbf{b}}$ is discretized by taking into consideration both of the preceding discretizations of ${\displaystyle \mathbf{w}}$ and ${\displaystyle \theta }$ and choosing ${\displaystyle {\mathbf{b}}_{\mathbf{m}}^{j,\ell }=A_{-j}{R}_{-{\theta }_{\ell }}\left(m_0{\alpha }_0,m_1{\alpha }_1\right)}$.

However, much to the dismay, the aforementioned discretization process suffers from a couple of severe limitations: first, the discretization of the frequency variable ${\displaystyle \mathbf{w}}$ is non-parabolic in nature; second, the discretization of the angular variable ${\displaystyle \theta }$ is completely independent of the scale ${\displaystyle \lambda }$, which results in an uncontrollable angular expansion of the grid at higher values of ${\displaystyle j}$ (see Figure 1), thereby limiting the directional selectivity at higher frequencies. In this communication, our goal is to circumvent these limitations by proposing a new scale-dependent discretization scheme for the discrete non-isotropic angular Stockwell transform. Under the new discretization scheme, the frequency dilation is always doubly effective in one fixed direction as in the orthogonal direction. Moreover, at each higher level of resolution, the split in the angular region is increased proportionally, thereby preventing the undesired angular expansion of the sampling grid and enhancing the directional selectivity at high frequencies.

The rest of the article is organized as follows: Section 2 serves as the pedestal and deals with the formal aspects of the novel discretization scheme. In Section 3, we derive a sufficient condition for the non-isotropic Stockwell frames in ${\displaystyle L^2\left({\mathbb{R}}^2\right)}$. Finally, a conclusion together with an impetus to the future research work is extracted in Section 4.

2. Discourse on the New Discretization Scheme

This section is solely devoted to the formulation of a new discretization scheme for the non-isotropic angular Stockwell transform (2). We reiterate that the proposed discretization scheme is not only based on the parabolic scaling law but also prevents the undesired angular expansion of the underlying sampling grid. A detailed exposition of the formal discrete scheme is given below:

(i).

The discretization of the frequency variable ${\displaystyle \mathbf{w}={({\omega }_1,{\omega }_2)}^T}$ is achieved via the parabolic scaling law by choosing ${\displaystyle {\mathbf{w}}_j={({\lambda }^j,{\lambda }^{j/2})}^T}$, where ${\displaystyle \lambda >1}$ is a fixed integer and ${\displaystyle j\in \mathbb{Z}}$ determines the level of resolution. Consequently, the anisotropy matrix is given by

$$\begin{array}{c}\hfill A_j=\left(\begin{array}{cc}{\lambda }^j& 0\\ 0& {\lambda }^{j/2}\end{array}\right),\end{array}$$

(4)

and the discretized frequency variable ${\displaystyle {\mathbf{w}}_j}$ can be expressed via the matrix ${\displaystyle A_j}$ as

$$\begin{array}{c}\hfill {\mathbf{w}}_j={({\lambda }^j,{\lambda }^{j/2})}^T=A_j{(1,1)}^T.\end{array}$$

(5)

(ii)

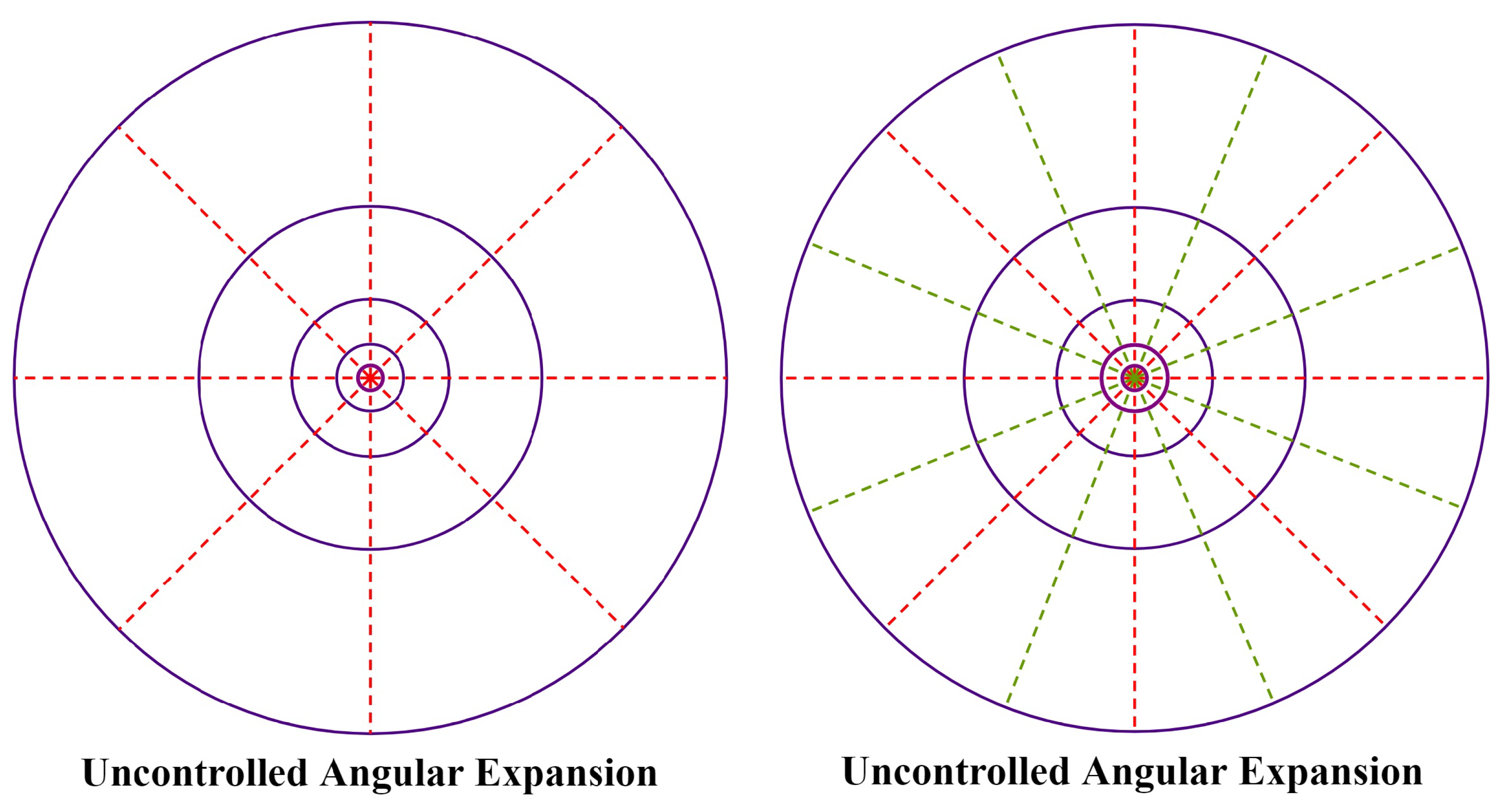
For fixed ${\displaystyle L_0\in \mathbb{Z}}$, the rotation parameter ${\displaystyle \theta }$ is sampled into ${\displaystyle L_0}$ equi-spaced pieces as

$$\begin{array}{c}\hfill {\theta }_{\ell }={\displaystyle \frac{2\pi \ell }{L_0}},\mathrm{where}\ell \in {\mathbb{Z}}_{L_0}=\left\{0,1,2,\cdots ,L_0-1\right\}.\end{array}$$

(6)

To prevent the expansion of the angular region at higher values of ${\displaystyle j}$, it is desirable to make the spacing between the consecutive angles scale-dependent. As such, we choose ${\displaystyle L_0={\lambda }^{\lfloor j/2\rfloor }}$, where ${\displaystyle \lfloor j/2\rfloor }$ denotes the integral part of ${\displaystyle j/2}$. Consequently, the scale-dependent angular discretization is given below:

$$\begin{array}{c}\hfill {\theta }_{{\ell }_j}={\displaystyle \frac{2\pi \ell }{{\lambda }^{\lfloor j/2\rfloor }}},\mathrm{where}\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}=\left\{0,1,2,\cdots ,{\lambda }^{\lfloor j/2\rfloor }-1\right\}.\end{array}$$

(7)

(iii)

The discretization of the spatial variable ${\displaystyle \mathbf{b}}$ is carried out by taking into consideration both the previous discretizations of frequency and angular variables. For ${\displaystyle \mathbf{m}={(m_1,m_2)}^T\in {\mathbb{Z}}^2}$ and ${\displaystyle \beta >0}$, the spatial variable ${\displaystyle \mathbf{b}}$ is sampled as

$$\begin{array}{c}\hfill {\mathbf{b}}_{\mathbf{m}}^{j,\ell }:=\left(A_{-j}{R}_{-{\theta }_{{\ell }_j}}\right)\left(\beta \mathbf{m}\right).\end{array}$$

(8)

In view of the above discretization scheme, the novel sampling grid associated with the discrete non-isotropic angular Stockwell transform takes the following form:

$$\begin{array}{c}\hfill \mathrm{\Lambda }=\left\{\left(A_j{(1,1)}^T,\left(A_{-j}{R}_{-{\theta }_{{\ell }_j}}\right)\left(\beta \mathbf{m}\right),{\theta }_{{\ell }_j}\right):j\in \mathbb{Z},\mathbf{m}\in {\mathbb{Z}}^2,\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }},{\theta }_{{\ell }_j}={\displaystyle \frac{2\pi \ell }{{\lambda }^{\lfloor j/2\rfloor }}}\right\}.\end{array}$$

(9)

In order to appreciate the nuances between the existing and the newly proposed discretization schemes, we depict the respective sampling grids separately in Figure 1 and Figure 2. For plotting the sampling grid associated with the discretization scheme proposed in [11], we choose ${\displaystyle \lambda =2}$, ${\displaystyle \mathbf{m}={(1,1)}^T}$ and then partition the angular variable ${\displaystyle \theta =2\pi \ell /L}$, ${\displaystyle \ell \in {\mathbb{Z}}_{\ell }}$ in two ways by taking ${\displaystyle L=8}$ and ${\displaystyle L=16}$. Since the existing discretization is not scale-dependent in the angular variable, with increased levels of resolution the angular expansion is uncontrollable, as shown in Figure 1.

Figure 1. Basic discrete sampling grid for ${\displaystyle j=0,2,4,6,8}$ with ${\displaystyle L=8}$ (left) and ${\displaystyle L=16}$ (right) [11].

Figure 1. Basic discrete sampling grid for ${\displaystyle j=0,2,4,6,8}$ with ${\displaystyle L=8}$ (left) and ${\displaystyle L=16}$ (right) [11].

In contrast to this, the sampling grid (9) efficiently prevents the angular expansion at higher scales because the new discretization scheme is completely scale-dependent, and the split in the angular region is increased at each next level of resolution. For a pictorial illustration of the aforementioned fact, we choose ${\displaystyle \lambda =2}$, ${\displaystyle \beta =1}$ in (9) and vary the level of resolution ${\displaystyle j}$ over the set ${\displaystyle \{0,2,4,6,8,10,\cdots \}}$. Then, we observe that for ${\displaystyle j=0}$, there is no partition in the angular region. Additionally, for ${\displaystyle j=2}$ there are two partitions in the angular region determined by the points ${\displaystyle {\theta }_{0_2}=0}$ and ${\displaystyle {\theta }_{1_2}=\pi }$, and the corresponding partition in the spatial variable is determined by the points ${\displaystyle {\mathbf{b}}_{\mathbf{m}}^{2,0}=\left(A_{-2}{R}_{-{\theta }_{0_2}}\right)\mathbf{m}}$ and ${\displaystyle {\mathbf{b}}_{\mathbf{m}}^{2,1}=\left(A_{-2}{R}_{-{\theta }_{1_2}}\right)\mathbf{m}}$. Furthermore, for ${\displaystyle j=4}$ the angular region attains quadruple partition at the points ${\displaystyle {\theta }_{0_4}=0}$, ${\displaystyle {\theta }_{1_4}=\pi /2}$, ${\displaystyle {\theta }_{2_4}=\pi }$, and ${\displaystyle {\theta }_{3_4}=3\pi /2}$, and consequently the spatial region is partitioned at ${\displaystyle {\mathbf{b}}_{\mathbf{m}}^{4,0}=\left(A_{-4}{R}_{-{\theta }_{0_4}}\right)\mathbf{m}}$, ${\displaystyle {\mathbf{b}}_{\mathbf{m}}^{4,1}=\left(A_{-4}{R}_{-{\theta }_{1_4}}\right)\mathbf{m}}$, ${\displaystyle {\mathbf{b}}_{\mathbf{m}}^{4,2}=\left(A_{-4}{R}_{-{\theta }_{2_4}}\right)\mathbf{m}}$ and ${\displaystyle {\mathbf{b}}_{\mathbf{m}}^{4,3}=\left(A_{-4}{R}_{-{\theta }_{3_4}}\right)\mathbf{m}}$. In a similar fashion, we can show that for ${\displaystyle j=6,8,10,\cdots }$ both the angular and spatial regions are partitioned into ${\displaystyle 8,16,32,\cdots }$ equispaced regions. Thus, we infer that at higher values of ${\displaystyle j}$, the partition points of the angular region are increased proportionally; as such, the angular expansion of sampling grid (9) can be efficiently controlled, as shown in Figure 2.

Figure 2. Refined discrete sampling grid (9) at ${\displaystyle j=0,2,4,6,8,10}$.

Figure 2. Refined discrete sampling grid (9) at ${\displaystyle j=0,2,4,6,8,10}$.

3. The Non-Isotropic Stockwell Frames

This section is completely devoted to demonstrating that the new discretization scheme proposed in Section 2 is also helpful for the construction of Stockwell frames in ${\displaystyle L^2\left({\mathbb{R}}^2\right)}$. For ${\displaystyle \left(A_j{(1,1)}^T,\left(A_{-j}{R}_{-{\theta }_{{\ell }_j}}\right)\left(\beta \mathbf{m}\right),{\theta }_{{\ell }_j}\right)\in \mathrm{\Lambda }}$, we define a quadruple of fundamental operators, viz, translation (${\displaystyle {\mathcal{T}}_{\left(A_{-j}{R}_{-{\theta }_{{\ell }_j}}\right)\left(\beta \mathbf{m}\right)}}$), dilation (${\displaystyle {\mathcal{D}}_{A_j}}$), rotation (${\displaystyle R_{{\theta }_{{\ell }_j}}}$), and modulation (${\displaystyle {\mathcal{M}}_{A_j{(1,1)}^T}}$) operators acting on ${\displaystyle \mathrm{\Psi }\in L^2\left({\mathbb{R}}^2\right)}$ as:

$$\begin{array}{c}{\mathcal{T}}_{\left(A_{-j}{R}_{-{\theta }_{{\ell }_j}}\right)\left(\beta \mathbf{m}\right)}\mathrm{\Psi }\left(\mathbf{t}\right)=\mathrm{\Psi }(\mathbf{t}-\left(A_{-j}{R}_{-{\theta }_{{\ell }_j}}\right)\left(\beta \mathbf{m}\right))\hfill \\ {\mathcal{D}}_{A_j}\mathrm{\Psi }\left(\mathbf{t}\right)=\left|det{A}_j\right|\mathrm{\Psi }\left(A_j\mathbf{t}\right)\hfill \\ R_{{\theta }_{{\ell }_j}}\mathrm{\Psi }\left(\mathbf{t}\right)={\mathrm{\Psi }}_{{\ell }_j}\left(\mathbf{t}\right):=\mathrm{\Psi }\left(R_{{\theta }_{{\ell }_j}}\mathbf{t}\right)\hfill \\ {\mathcal{M}}_{A_j{(1,1)}^T}\mathrm{\Psi }\left(\mathbf{t}\right)=\mathrm{\Psi }\left(\mathbf{t}\right)exp\left\{2\pi i{\mathbf{t}}^T\left(A_j{(1,1)}^T\right)\right\}\hfill \end{array}\}.$$

(10)

Upon joint application of the elementary operators defined in (10), we obtain a discrete collection of analyzing functions ${\displaystyle {\mathrm{\Psi }}_{j,\mathbf{m},\ell }\left(\mathbf{t}\right)}$ as

$$\begin{array}{cc}\hfill {\mathrm{\Psi }}_{j,\mathbf{m},\ell }\left(\mathbf{t}\right)& ={\mathcal{M}}_{A_j{(1,1)}^T}{R}_{{\theta }_{{\ell }_j}}{\mathcal{T}}_{\left(A_{-j}{R}_{-{\theta }_{{\ell }_j}}\right)\left(\beta \mathbf{m}\right)}{\mathcal{D}}_{A_j}\mathrm{\Psi }\left(\mathbf{t}\right)\hfill \\ \hfill & =\left|det{A}_j\right|{\mathrm{\Psi }}_{{\ell }_j}\left(A_j\left(\mathbf{t}-A_{-j}{R}_{-{\theta }_{{\ell }_j}}\beta \mathbf{m}\right)\right)exp\left\{2\pi i{\mathbf{t}}^T\left(A_j{(1,1)}^T\right)\right\}\hfill \\ \hfill & =\left|det{A}_j\right|{\mathrm{\Psi }}_{{\ell }_j}\left(A_j\mathbf{t}-R_{-{\theta }_{{\ell }_j}}\beta \mathbf{m}\right)exp\left\{2\pi i{\mathbf{t}}^T\left(A_j{(1,1)}^T\right)\right\}.\hfill \end{array}$$

(11)

Moreover, the two-dimensional Fourier transform of the analyzing functions (11) can be computed as follows:

$$\begin{array}{cc}\hfill \mathcal{F}\left[{\mathrm{\Psi }}_{j,\mathbf{m},\ell }\right]\left(\mathbf{w}\right)& ={\int }_{{\mathbb{R}}^2}{\mathrm{\Psi }}_{j,\mathbf{m},\ell }\left(\mathbf{t}\right)e^{-2\pi i{\mathbf{t}}^T\mathbf{w}}d\mathbf{t}\hfill \\ \hfill & =\left|det{A}_j\right|{\int }_{{\mathbb{R}}^2}{\mathrm{\Psi }}_{{\ell }_j}\left(A_j\mathbf{t}-R_{-{\theta }_{{\ell }_j}}\beta \mathbf{m}\right)exp\left\{2\pi i{\mathbf{t}}^T\left(A_j{(1,1)}^T\right)\right\}{e}^{-2\pi i{\mathbf{t}}^T\mathbf{w}}d\mathbf{t}\hfill \\ \hfill & ={\int }_{{\mathbb{R}}^2}{\mathrm{\Psi }}_{{\ell }_j}\left(\mathbf{z}\right)exp\left\{2\pi i{\left(A_{-j}\mathbf{z}+A_{-j}{R}_{-{\theta }_{{\ell }_j}}\beta \mathbf{m}\right)}^T{A}_j{(1,1)}^T\right\}exp\left\{-2\pi i{\left(A_{-j}\mathbf{z}+A_{-j}{R}_{-{\theta }_{{\ell }_j}}\beta \mathbf{m}\right)}^T\mathbf{w}\right\}d\mathbf{z}\hfill \\ \hfill & =exp\left\{2\pi i{\left(\beta \mathbf{m}\right)}^T{R}_{{\theta }_{{\ell }_j}}\left({(1,1)}^T-A_{-j}\mathbf{w}\right)\right\}{\int }_{{\mathbb{R}}^2}{\mathrm{\Psi }}_{{\ell }_j}\left(\mathbf{z}\right)exp\left\{2\pi i{\mathbf{z}}^T{(1,1)}^T\right\}exp\left\{-2\pi i{\mathbf{z}}^T\left(A_{-j}\mathbf{w}\right)\right\}d\mathbf{z}\hfill \\ \hfill & =exp\left\{2\pi i{\left(\beta \mathbf{m}\right)}^T{R}_{{\theta }_{{\ell }_j}}\left({(1,1)}^T-A_{-j}\mathbf{w}\right)\right\}\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left(A_{-j}\mathbf{w}\right),\hfill \end{array}$$

where ${\displaystyle \mathrm{\Phi }}$ is the modulated version of the given window function ${\displaystyle \mathrm{\Psi }}$ and is given by

$$\begin{array}{c}\hfill {\mathrm{\Phi }}_{{\ell }_j}\left(\mathbf{t}\right)={\mathrm{\Psi }}_{{\ell }_j}\left(\mathbf{t}\right)exp\left\{2\pi i{\mathbf{t}}^T{(1,1)}^T\right\}.\end{array}$$

(12)

Based on the refined sampling grid (9) and the family of analyzing functions constructed in (11), we define the novel discrete non-isotropic Stockwell system ${\displaystyle \mathrm{\Gamma }(\mathrm{\Psi },\mathrm{\Lambda })}$ as

$$\begin{array}{c}\hfill \mathrm{\Gamma }(\mathrm{\Psi },\mathrm{\Lambda }):=\left\{{\mathrm{\Psi }}_{j,\mathbf{m},\ell }\left(\mathbf{t}\right)={\mathcal{M}}_{A_j{(1,1)}^T}{R}_{{\theta }_{{\ell }_j}}{\mathcal{T}}_{\left(A_{-j}{R}_{-{\theta }_{{\ell }_j}}\right)\left(\beta \mathbf{m}\right)}{\mathcal{D}}_{A_j}\mathrm{\Psi }\left(\mathbf{t}\right):j\in \mathbb{Z},\mathbf{m}\in {\mathbb{Z}}^2,\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}\right\}.\end{array}$$

(13)

Then, our main goal is to demonstrate that the system ${\displaystyle \mathrm{\Gamma }(\mathrm{\Psi },\mathrm{\Lambda })}$ constitutes a frame for ${\displaystyle L^2\left({\mathbb{R}}^2\right)}$. To facilitate the motive, below we recall the fundamental notion of a frame in a separable Hilbert space [3]:

Definition 1.

Given a separable Hilbert space ${\displaystyle \mathcal{H}}$, a sequence of elements ${\displaystyle \left\{f_i\right\}}$ in ${\displaystyle \mathcal{H}}$ is said to be a frame for ${\displaystyle \mathcal{H}}$, if there exists constants ${\displaystyle 0<C_1\le C_2<\infty }$, such that

$$\begin{array}{c}\hfill C_1\parallel f{\parallel }_{\mathcal{H}}\le \sum _i{\left|{〈f,f_i〉}_2\right|}^2\le C_2\parallel f{\parallel }_{\mathcal{H}},\forall f\in \mathcal{H}.\end{array}$$

(14)

The constants ${\displaystyle C_1}$ and ${\displaystyle C_2}$ appearing in (14) are called as the lower and upper frame bounds, respectively. In case ${\displaystyle C_1=C_2=C>1}$, the frame is said to be tight, and if ${\displaystyle C=1}$, the frame is called a Parseval’s frame.

In the following theorem, we shall derive a sufficient condition for the system ${\displaystyle \mathrm{\Gamma }(\mathrm{\Psi },\mathrm{\Lambda })}$ to be a frame for ${\displaystyle L^2\left({\mathbb{R}}^2\right)}$. Prior to that, for any ${\displaystyle \mathrm{\Phi }\left(\mathbf{t}\right)}$ as given by (12), we set

$$\begin{array}{c}\hfill H({\xi }_1,{\xi }_2)=\mathrm{ess}.\underset{{\omega }_1,{\omega }_2\in \mathbb{R}}{sup}\left(\sum _{j\in \mathbb{Z}}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}\left|\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1,{\lambda }^{-j/2}{\omega }_2\right)\right|\left|\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1+{\xi }_1,{\lambda }^{-j/2}{\omega }_2+{\xi }_2\right)\right|\right).\end{array}$$

(15)

Theorem 1.

Let ${\displaystyle \mathrm{\Psi }\in L^2\left({\mathbb{R}}^2\right)}$ be any window function and ${\displaystyle \mathrm{\Phi }}$ be the corresponding modulated version given by (12) such that

$$\begin{array}{c}\hfill C_1\le \sum _{j\in \mathbb{Z}}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}{\left|\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1,{\lambda }^{-j/2}{\omega }_2\right)\right|}^2\le C_2,\end{array}$$

(16)

almost everywhere ${\displaystyle {\omega }_1,{\omega }_2\in \mathbb{R}}$, with ${\displaystyle 0<C_1\le C_2<\infty }$. Then, for fixed ${\displaystyle \beta >0}$ the system (13) constitutes a frame for ${\displaystyle L^2\left({\mathbb{R}}^2\right)}$ if the function ${\displaystyle H(x,y)}$ given by (15) satisfies:

$$\begin{array}{c}\hfill \sum _{0\ne r\in \mathbb{Z}}\sum _{0\ne s\in \mathbb{Z}}{\left[H\left({\beta }^{-1}r,{\beta }^{-1}s\right)H\left(-{\beta }^{-1}r,-{\beta }^{-1}s\right)\right]}^{1/2}=C_3<C_1.\end{array}$$

(17)

Moreover, in that case the lower and upper frame bounds are given by ${\displaystyle \left(\frac{C_1-C_3}{{\beta }^2}\right)}$ and ${\displaystyle \left(\frac{C_2+C_3}{{\beta }^2}\right)}$, respectively.

Proof. 

For any ${\displaystyle f\in L^2\left({\mathbb{R}}^2\right)}$, the implication of Plancheral theorem for the two-dimensional Fourier transform yields

$$\begin{array}{cc}\hfill & \sum _{j\in \mathbb{Z}}\sum _{\mathbf{m}\in {\mathbb{Z}}^2}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}{\left|{〈f,{\mathrm{\Psi }}_{j,\mathbf{m},\ell }〉}_2\right|}^2\hfill \\ \hfill & =\sum _{j\in \mathbb{Z}}\sum _{\mathbf{m}\in {\mathbb{Z}}^2}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}{\left|{\int }_{{\mathbb{R}}^2}\mathcal{F}\left[f\right]\left(\mathbf{w}\right)\overline{\mathcal{F}\left[{\mathrm{\Psi }}_{j,\mathbf{m},\ell }\right]\left(\mathbf{w}\right)}d\mathbf{w}\right|}^2\hfill \\ \hfill & =\sum _{j\in \mathbb{Z}}\sum _{\mathbf{m}\in {\mathbb{Z}}^2}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}|{\int }_{{\mathbb{R}}^2}\mathcal{F}\left[f\right]\left(\mathbf{w}\right)\overline{\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left(A_{-j}\mathbf{w}\right)}exp\left\{-2\pi i{\left(\beta \mathbf{m}\right)}^T{R}_{{\theta }_{{\ell }_j}}\left({(1,1)}^T-A_{-j}\mathbf{w}\right)\right\}d\mathbf{w}{|}^2\hfill \\ \hfill & =\sum _{j\in \mathbb{Z}}\sum _{\mathbf{m}\in {\mathbb{Z}}^2}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}{\lambda }^{3j/2}|{\int }_0^{{\beta }^{-1}{\lambda }^j}{\int }_0^{{\beta }^{-1}{\lambda }^{j/2}}exp\left\{-2\pi i{\left(\beta \mathbf{m}\right)}^T{R}_{{\theta }_{{\ell }_j}}\left({(1,1)}^T-A_{-j}\mathbf{w}\right)\right\}\hfill \\ \hfill & \times \left(\sum _{n_1\in \mathbb{Z}}\sum _{n_2\in \mathbb{Z}}\mathcal{F}\left[f\right]\left({\omega }_1+{\beta }^{-1}{\lambda }^j{n}_1,{\omega }_2+{\beta }^{-1}{\lambda }^{j/2}{n}_2\right)\overline{\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1+{\beta }^{-1}{n}_1,{\lambda }^{-j/2}{\omega }_2+{\beta }^{-1}{n}_2\right)}\right)d{\omega }_{1}d{\omega }_2{|}^2\hfill \\ \hfill & ={\displaystyle \frac{1}{{\beta }^2}}\sum _{j\in \mathbb{Z}}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}{\int }_0^{{\beta }^{-1}{\lambda }^j}{\int }_0^{{\beta }^{-1}{\lambda }^{j/2}}\left|\sum _{n_1\in \mathbb{Z}}\sum _{n_2\in \mathbb{Z}}\right[\mathcal{F}\left[f\right]\left({\omega }_1+{\beta }^{-1}{n}_1,{\omega }_2+{\beta }^{-1}{n}_2\right)\hfill \\ \hfill & \times \overline{\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1+{\beta }^{-1}{\lambda }^j{n}_1,{\lambda }^{-j/2}{\omega }_2+{\beta }^{-1}{\lambda }^{j/2}{n}_2\right)}]{|}^{2}d{\omega }_{1}d{\omega }_2\hfill \\ \hfill & ={\displaystyle \frac{1}{{\beta }^2}}\sum _{j\in \mathbb{Z}}\sum _{r\in \mathbb{Z}}\sum _{s\in \mathbb{Z}}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }[\mathcal{F}\left[f\right]\left({\omega }_1,{\omega }_2\right)\overline{\mathcal{F}\left[f\right]\left({\omega }_1+{\beta }^{-1}{\lambda }^{j}r,{\omega }_2+{\beta }^{-1}{\lambda }^{j/2}s\right)}\hfill \\ \hfill & \times \overline{\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1,{\lambda }^{-j/2}{\omega }_2\right)}\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1+{\beta }^{-1}r,{\lambda }^{-j/2}{\omega }_2+{\beta }^{-1}s\right)]d{\omega }_{1}d{\omega }_2\hfill \\ \hfill & ={\displaystyle \frac{1}{{\beta }^2}}{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\left|\mathcal{F}\left[f\right]\left({\omega }_1,{\omega }_2\right)\right|}^2\left\{\sum _{j\in \mathbb{Z}}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}{\left|\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1,{\lambda }^{-j/2}{\omega }_2\right)\right|}^2\right\}d{\omega }_{1}d{\omega }_2\hfill \\ \hfill & +{\displaystyle \frac{1}{{\beta }^2}}\sum _{j\in \mathbb{Z}}\sum _{0\ne r\in \mathbb{Z}}\sum _{0\ne s\in \mathbb{Z}}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }[\mathcal{F}\left[f\right]\left({\omega }_1,{\omega }_2\right)\overline{\mathcal{F}\left[f\right]\left({\omega }_1+{\beta }^{-1}{\lambda }^{j}r,{\omega }_2+{\beta }^{-1}{\lambda }^{j/2}s\right)}\hfill \\ \hfill & \times \overline{\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1,{\lambda }^{-j/2}{\omega }_2\right)}\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1+{\beta }^{-1}r,{\lambda }^{-j/2}{\omega }_2+{\beta }^{-1}s\right)]d{\omega }_{1}d{\omega }_2\hfill \\ \hfill & =P\left(\mathrm{principle}\mathrm{term}\right)+R\left(\mathrm{residue}\mathrm{term}\right).\hfill \end{array}$$

(18)

Note that the principle term is the product between the power of the input function and the sum of the spectral powers of the analyzers. Therefore, in view of (16), it follows that the lower and upper bounds for the principal term are given by

$$\begin{array}{c}\hfill \left({\displaystyle \frac{C_1}{{\beta }^2}}\right)\parallel f{\parallel }_2^2\le P\le \left({\displaystyle \frac{C_2}{{\beta }^2}}\right)\parallel f{\parallel }_2^2.\end{array}$$

(19)

The residue term captures the interference effect among the analyzing functions and can be computed by invoking the Cauchy–Schwarz inequality twice successively in the following fashion:

$$\begin{array}{cc}\hfill R& =\left|{\displaystyle \frac{1}{{\beta }^2}}\sum _{j\in \mathbb{Z}}\sum _{0\ne r\in \mathbb{Z}}\sum _{0\ne s\in \mathbb{Z}}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\right[\mathcal{F}\left[f\right]\left({\omega }_1,{\omega }_2\right)\overline{\mathcal{F}\left[f\right]\left({\omega }_1+{\beta }^{-1}{\lambda }^{j}r,{\omega }_2+{\beta }^{-1}{\lambda }^{j/2}s\right)}\hfill \\ \hfill & \times \overline{\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1,{\lambda }^{-j/2}{\omega }_2\right)}\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1+{\beta }^{-1}r,{\lambda }^{-j/2}{\omega }_2+{\beta }^{-1}s\right)\left]d{\omega }_{1}d{\omega }_2\right|\hfill \\ \hfill & \le {\displaystyle \frac{1}{{\beta }^2}}\sum _{j\in \mathbb{Z}}\sum _{0\ne r\in \mathbb{Z}}\sum _{0\ne s\in \mathbb{Z}}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}[{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\left|\mathcal{F}\left[f\right]\left({\omega }_1,{\omega }_2\right)\right|}^2\left|\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1,{\lambda }^{-j/2}{\omega }_2\right)\right|\hfill \\ \hfill & \times \left|\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1+{\beta }^{-1}r,{\lambda }^{-j/2}{\omega }_2+{\beta }^{-1}s\right)\right|d{\omega }_{1}d{\omega }_2{]}^{1/2}\hfill \\ \hfill & [{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\left|\mathcal{F}\left[f\right]\left({\omega }_1+{\beta }^{-1}{\lambda }^{j}r,{\omega }_2+{\beta }^{-1}{\lambda }^{j/2}s\right)\right|}^2\left|\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1,{\lambda }^{-j/2}{\omega }_2\right)\right|\hfill \\ \hfill & \times \left|\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1+{\beta }^{-1}r,{\lambda }^{-j/2}{\omega }_2+{\beta }^{-1}s\right)\right|d{\omega }_{1}d{\omega }_2{]}^{1/2}.\hfill \end{array}$$

(20)

Making use of the substitutions ${\displaystyle {\omega }_1+{\beta }^{-1}{\lambda }^{j}r={\xi }_1}$ and ${\displaystyle {\omega }_2+{\beta }^{-1}{\lambda }^{j/2}s={\xi }_2}$ in the post-factor on the R.H.S of inequality (20), we obtain

$$\begin{array}{cc}\hfill R& \le {\displaystyle \frac{1}{{\beta }^2}}\sum _{0\ne r\in \mathbb{Z}}\sum _{0\ne s\in \mathbb{Z}}\left[{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\left|\mathcal{F}\left[f\right]\left({\omega }_1,{\omega }_2\right)\right|}^2\right(\sum _{j\in \mathbb{Z}}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}\left|\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1,{\lambda }^{-j/2}{\omega }_2\right)\right|\hfill \\ \hfill & \times \left|\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1+{\beta }^{-1}r,{\lambda }^{-j/2}{\omega }_2+{\beta }^{-1}s\right)\right|)d{\omega }_{1}d{\omega }_2{]}^{1/2}\hfill \\ \hfill & \left[{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\left|\mathcal{F}\left[f\right]\left({\xi }_1,{\xi }_2\right)\right|}^2\right(\sum _{j\in \mathbb{Z}}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}\left|\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\xi }_1,{\lambda }^{-j/2}{\xi }_2\right)\right|\hfill \\ \hfill & \times \left|\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\xi }_1-{\beta }^{-1}r,{\lambda }^{-j/2}{\xi }_2-{\beta }^{-1}s\right)\right|)d{\xi }_{1}d{\xi }_2{]}^{1/2}\hfill \\ \hfill & \le {\displaystyle \frac{1}{{\beta }^2}}\parallel f{\parallel }_2^2\left(\sum _{0\ne r\in \mathbb{Z}}\sum _{0\ne s\in \mathbb{Z}}{\left[H\left({\beta }^{-1}r,{\beta }^{-1}s\right)H\left(-{\beta }^{-1}r,-{\beta }^{-1}s\right)\right]}^{1/2}\right),\hfill \end{array}$$

(21)

Consequently, the infimum and supremum of the power output are given by

$$\begin{array}{cc}\hfill & \underset{f\in L^2\left({\mathbb{R}}^2\right),f\ne 0}{inf}\left(\parallel f{\parallel }_2^{-2}\sum _{j\in \mathbb{Z}}\sum _{\mathbf{m}\in {\mathbb{Z}}^2}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}{\left|{〈f,{\mathrm{\Psi }}_{j,\mathbf{m},\ell }〉}_2\right|}^2\right)\ge {\displaystyle \frac{1}{{\beta }^2}}\{\underset{{\omega }_1,{\omega }_2\in S}{inf}\left(\sum _{j\in \mathbb{Z}}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}{\left|\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1,{\lambda }^{-j/2}{\omega }_2\right)\right|}^2\right)\hfill \\ \hfill & -\sum _{0\ne r\in \mathbb{Z}}\sum _{0\ne s\in \mathbb{Z}}{\left[H\left({\beta }^{-1}r,{\beta }^{-1}s\right)H\left(-{\beta }^{-1}r,-{\beta }^{-1}s\right)\right]}^{1/2}\}.\hfill \end{array}$$

(22)

and

$$\begin{array}{cc}\hfill & \underset{f\in L^2\left({\mathbb{R}}^2\right),f\ne 0}{sup}\left(\parallel f{\parallel }_2^{-2}\sum _{j\in \mathbb{Z}}\sum _{\mathbf{m}\in {\mathbb{Z}}^2}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}{\left|{〈f,{\mathrm{\Psi }}_{j,\mathbf{m},\ell }〉}_2\right|}^2\right)\ge {\displaystyle \frac{1}{{\beta }^2}}\{\underset{{\omega }_1,{\omega }_2\in \mathbb{R}}{sup}\left(\sum _{j\in \mathbb{Z}}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}{\left|\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1,{\lambda }^{-j/2}{\omega }_2\right)\right|}^2\right)\hfill \\ \hfill & +\sum _{0\ne r\in \mathbb{Z}}\sum _{0\ne s\in \mathbb{Z}}{\left[H\left({\beta }^{-1}r,{\beta }^{-1}s\right)H\left(-{\beta }^{-1}r,-{\beta }^{-1}s\right)\right]}^{1/2}\}.\hfill \end{array}$$

(23)

By virtue of the estimates (22) and (23), it follows that

$$\begin{array}{c}\hfill \left({\displaystyle \frac{C_1-C_3}{{\beta }^2}}\right)\parallel f{\parallel }_2^2\le \sum _{j\in \mathbb{Z}}\sum _{\mathbf{m}\in {\mathbb{Z}}^2}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}{\left|{〈f,{\mathrm{\Psi }}_{j,\mathbf{m},\ell }〉}_2\right|}^2\le \left({\displaystyle \frac{C_2+C_3}{{\beta }^2}}\right)\parallel f{\parallel }_2^2.\end{array}$$

This completes the proof of Theorem 1. ${\displaystyle \square }$

Towards the end of the ongoing section, we aim to formulate a simple condition under which the hypothesis (17) is satisfied. More explicitly, we shall demonstrate that if the function (12) is band-limited to a certain closed ball ${\displaystyle {\mathfrak{B}}_{\infty }({\mathbf{t}}_0,r)}$ centered at ${\displaystyle {\mathbf{t}}_0\in {\mathbb{R}}^2}$ with radius ${\displaystyle r>0}$, then the system (13) constitutes a frame for ${\displaystyle L^2\left({\mathbb{R}}^2\right)}$ provided the sampling constant ${\displaystyle \beta >0}$ is chosen to be small enough.

Corollary 1.

Let ${\displaystyle \mathrm{\Phi }\in L^2\left({\mathbb{R}}^2\right)}$ be as given in (12) and ${\displaystyle 0<\beta <1/2r}$. If ${\displaystyle \mathit{supp}\left(\mathcal{F}\left[\mathrm{\Phi }\right]\left(\mathbf{w}\right)\right)\subset {\mathfrak{B}}_{\infty }(\mathbf{0},r)}$, the closed ball centered about ${\displaystyle \mathbf{0}={(0,0)}^T\in {\mathbb{R}}^2}$ having radius ${\displaystyle r}$, and

$$\begin{array}{c}\hfill C_1\le \sum _{j\in \mathbb{Z}}\sum _{\ell \in {\mathbb{Z}}_{{\lambda }^{\lfloor j/2\rfloor }}}{\left|\mathcal{F}\left[{\mathrm{\Phi }}_{{\ell }_j}\right]\left({\lambda }^{-j}{\omega }_1,{\lambda }^{-j/2}{\omega }_2\right)\right|}^2\le C_2,\end{array}$$

(24)

almost everywhere ${\displaystyle {\omega }_1,{\omega }_2\in \mathbb{R}}$, with ${\displaystyle 0<C_1\le C_2<\infty }$, then the system (13) constitutes a frame for ${\displaystyle L^2\left({\mathbb{R}}^2\right)}$ with the lower and upper frame bounds as ${\displaystyle {\beta }^{-2}{C}_1}$ and ${\displaystyle {\beta }^{-2}{C}_2}$, respectively. In particular, if ${\displaystyle C_1=C_2=C}$, then the system (13) turns to be a tight frame with the frame bound as ${\displaystyle {\beta }^{-2}C}$.

Proof. 

According to the hypothesis, the window function ${\displaystyle \mathrm{\Psi }}$ is so chosen that the corresponding modulated version ${\displaystyle \mathrm{\Phi }}$ given by (12) is band-limited in the sense that ${\displaystyle \mathcal{F}\left[\mathrm{\Phi }\right]\left(\mathbf{w}\right)\subset {\mathfrak{B}}_{\infty }(\mathbf{0},r)}$. Therefore, we have ${\displaystyle \mathcal{F}\left[\mathrm{\Phi }\right]\left(R_{{\theta }_{{\ell }_j}}{A}_{-j}\mathbf{w}\right)\ne 0}$ if and only if ${\displaystyle R_{{\theta }_{{\ell }_j}}{A}_{-j}\mathbf{w}\in {\mathfrak{B}}_{\infty }(\mathbf{0},r)}$. Consequently, for ${\displaystyle \xi ={({\xi }_1,{\xi }_2)}^T\in {\mathbb{R}}^2}$ we obtain

$$\begin{array}{c}\hfill \left|\mathcal{F}\left[\mathrm{\Phi }\right]\left(R_{{\theta }_{{\ell }_j}}{A}_{-j}\mathbf{w}+\xi \right)\right|\ne 0⟺R_{{\theta }_{{\ell }_j}}{A}_{-j}\mathbf{w}\in {\mathfrak{B}}_{\infty }(-\xi ,r).\end{array}$$

(25)

Clearly, if ${\displaystyle \xi \in {\mathbb{R}}^2}$ is such that ${\displaystyle {\mathfrak{B}}_{\infty }(\mathbf{0},r)\cap {\mathfrak{B}}_{\infty }(-\xi ,r)=\phi }$, then in view of (15) we have ${\displaystyle H\left(\xi \right)=0}$. Indeed, this is the case if ${\displaystyle \parallel \xi {\parallel }_{\infty }>2r}$. Hence, we conclude that

$$\begin{array}{c}\hfill \sum _{0\ne r\in \mathbb{Z}}\sum _{0\ne s\in \mathbb{Z}}{\left[H\left({\beta }^{-1}r,{\beta }^{-1}s\right)H\left(-{\beta }^{-1}r,-{\beta }^{-1}s\right)\right]}^{1/2}=0,\forall \beta <1/2r.\end{array}$$

(26)

This evidently completes the proof of Corollary 1. ${\displaystyle \square }$

Remark 1.

Since modulation in the spatial domain corresponds to a simple shift in the frequency domain; therefore, in view of (12) it suffices to verify the conditions (16) and (17) for the function ${\displaystyle {\mathrm{\Psi }}_{{\ell }_j}\left(\mathbf{t}\right)}$ instead of the modulated version ${\displaystyle {\mathrm{\Phi }}_{{\ell }_j}\left(\mathbf{t}\right)={\mathrm{\Psi }}_{{\ell }_j}\left(\mathbf{t}\right)exp\left\{2\pi i{\mathbf{t}}^T{(1,1)}^T\right\}}$. Moreover, it is also quite conspicuous that the argument of Corollary 1 holds in case the function ${\displaystyle \mathrm{\Psi }}$ is band-limited to the closed ball centered about ${\displaystyle \mathbf{1}={(1,1)}^T\in {\mathbb{R}}^2}$ and having radius ${\displaystyle r}$; that is, ${\displaystyle \mathcal{F}\left[\mathrm{\Psi }\right]\left(\mathbf{w}\right)\subset {\mathfrak{B}}_{\infty }(\mathbf{1},r)}$.

4. Conclusions and Future Work

In this communication, we introduced a scale-dependent discretization scheme for the non-isotropic Stockwell transform. Under the refined discretization procedure, one can efficiently control both the radial and angular expansions simultaneously. As an endorsement to the undertaken problem, we also demonstrated that the novel discretization scheme allows for the construction of Stockwell frames in ${\displaystyle L^2\left({\mathbb{R}}^2\right)}$. Nevertheless, as a future research aspect, it is lucrative to numerically compute the frame bounds for several classes of two-dimensional functions, particularly the Gabor functions, so that general results can be made regarding tightness of the frame with an increase in the number of frequency, spatial, and orientation sampling steps. Based on the numerical outcomes, certain experimental results concerning the image representation and reconstruction processes can be executed. Moreover, in view of the fact that the two-dimensional Gabor functions play an important role in many computer vision applications and modelling biological vision, the study can further be extended in that direction.