Connectivity Status of Intuitionistic Fuzzy Graph and Its Application to Merging of Banks

Abstract

Intuitionistic fuzzy graph theory is used to represent ambiguous networks, such as financial and social networks. The connectivity of such networks has a significant role in analyzing the network characteristics. This study investigates the connectivity status of vertices in an intuitionistic fuzzy graph. Few properties have been established. Some areas of applications are shown for merging different banks and finding the central affected nodes by any infectious diseases.

1. Introduction

The online network is one of the most used items in our daily life. Additionally, by using graph theory, a network can be easily presented and visualized. We can use the vertices and edges of a graph to represent nodes and links between network nodes. Using this uncertainty with a graph, one can develop a fuzzy graph. Fuzzy graph theory has applications in neural networks, artificial intelligence, etc. The connectivity status of a fuzzy graph was introduced in [1]. This paper examines a connection metric called connectivity status, which may be viewed as a gauge of the whole system’s average flow and systems vertex flow via each vertex should be represented by an indicator called connectivity status of vertices, which will help us to understand the identification and change of nodes and links in their required areas. However, here, we simply looked at the membership values. To make it more precise we will use membership values as well as non-membership values. In this paper, we introduce the connectivity status (C.S.) on an intuitionistic fuzzy graph, an extension of connectivity status (C.S.) on a fuzzy graph. This will help us understand the perfect identification and change of nodes and links in their required areas, and one can develop a proper network system. By using this, we have made some applications on infectious diseases and bank merging. By connectivity status (C.S.) on an intuitionistic fuzzy graph on contagious diseases, we can easily identify the person who is more or less infected. Applying bank merging will help us influence consumers, boost sales, and boost profitability. Additionally, clients will have access to their location from any amalgamated bank branch nearby. The fundamental idea behind fuzzy graphs was first introduced by Kauffmann [2] in 1973. Based on “paper sets” from Zadeh’s lecture [3], Rosenfeld presented fuzzy graphs in 1975 [4]. That year, fuzzy graphs were also mentioned in some work by Yeh et al. [5]. The expanded form of graph theory known as fuzzy graph theory can be thought of as including the ambiguity of both the nature of the links between the objects and their qualities. Sheeba et al. [6] introduced strong paths, extra strong paths, the connectedness of strength k between two unique vertices of a fuzzy network, the weight matrix of a fuzzy graph, the strength of a fuzzy graph, and the strength of connectivity of a fuzzy graph. Bhutani et al. [7] proposed that if the weight of an arc equals the strength of connectedness of its end nodes, then the arc is considered strong.

Banerjee [8] discovered the degree of connectivity between all pairs of unique vertices in the graph using an ideal $O\left(n^2\right)$ approach. Binu et al. [9] explained the concepts of connectivity index and average connectivity index for fuzzy graphs. Mathew et al. [10] proposed fuzzy node connectivity and fuzzy arc connectivity as two additional connectivity factors in fuzzy graphs and an innovative new clustering method based on fuzzy arc connection. Ma et al. [11] introduced fuzzy edge connectivity, fuzzy local edge connectivity, and several strategies to compute fuzzy edge connectivity and fuzzy local edge connectivity of certain graphs.

Sebastian et al. [12] introduced theorems for fuzzy graphs with arbitrary connectivity values and computations of fuzzy edge connectivity parameters for a few unique subcategories of fuzzy graphs, such as saturated and β-saturated cycles, and complements of fuzzy graphs. Mathew et al. [13] discussed the idea of a fuzzy graph’s cycle connectivity. Binu et al. [14] introduced the cyclic connectivity index (CCI) and average CCI (ACCI) of fuzzy graphs. Mathew et al. [15] introduced the connectivity ideas in fuzzy incidence graphs. Fang et al. [16] introduced the connectivity index (CI), average connectivity index (ACI), and Wiener index (WI) of fuzzy incidence graphs. Binu et al. [1] introduced the connectivity status of vertices in a fuzzy graph. In the study, the fuzzy graph’s vertices are divided into connectivity status promoting vertices, connectivity status decreasing vertices, and connectivity status neutral vertices. Here, we observed only the membership value of vertices and edges, but the corresponding non-membership value is also useful for much accuracy.

Atanassov [17] introduced an intuitionistic fuzzy set (IFS), which is a generalization of the term”fuzzy set”. Chakraborty et al. [18] presented the idea of intuitionistic fuzzy graphs and some of their fundamental characteristics. Dhavudh et al. [19] defined path, bridge, and cut–vertex on intuitionistic fuzzy graphs of the second type. Karunambigai et al. [20] introduced the strong arc, weakest arc, strong path, strongest path, α-strong arc, β-strong arc, δ-weak arc, and strength of connectedness between two nodes on intuitionistic fuzzy graphs. Naeem et al. [21] introduced the connectivity index (CI), and average connectivity index (ACI) on intuitionistic fuzzy graphs. Nazeeret al. [22] proposed the notion of intuitionistic fuzzy incidence graphs (IFIGs) with connectivity ideas. Alzoubi et al. [23] introduced some concepts of connectivity in an intuitionistic fuzzy graph and connectivity in complete intuitionistic fuzzy graphs. Fallatah et al. [24] discussed intuitionistic fuzzy soft graphs, the intersection of two intuitionistic fuzzy soft graphs, the union of two intuitionistic fuzzy soft graphs, strong, complete path, gain path, loss path, and gain-loss matrix in an intuitionistic fuzzy soft graph. Nazeer et al. [25] introduced cyclic connectivity, cyclic connectivity index, and average cyclic connectivity index on fuzzy incidence graph. For further studies, readers can read [26,27].

Motivation: In the literature, connectivity status is defined for fuzzy graphs. In this definition, the connectivity status of a node captures the measurement of connecting with other nodes. For a node in a social network (any society), the connectedness with other members depends on the willingness of others too. Thus only membership values (willingness for the relationship) are not enough to measure such connectivity status. Some other factors may be obstacles to the connectedness (relationship), but certain factors may assure the non-connectedness (unwillingness for the relationship). These factors must be included in the calculation. This motivates us to define the connectivity status in an intuitionistic environment. Additionally, some methods are available for merging banking sectors in different countries. All these methods are based on statistical data (crisp data). Data in the form of intuitionistic fuzzy graphs will lead to different results/different scenarios of connectedness. If we consider all banks as nodes and their relationship as edges, then the connectivity status of nodes (banks) can be calculated. This application also motivates this study.

Main Contribution: This article gave some formulas for the connectivity status of some vertices based on an ordering of membership values and non-membership values. Some algorithms and related real-life applications on infectious diseases and bank merging are also included in this paper.

The organization of the article:

• Section 1: Introduction
• Section 2: Basic concepts
• Section 3: Connectivity status of an intuitionistic fuzzy graph
• Section 4: Application of connectivity status
• Section 5: Conclusions

2. Basic Concepts

Intuitionistic fuzzy set [17]: An intuitionistic fuzzy set of a set E is $A=\left\{\left(x,\mu \left(x\right),\nu \left(x\right)\right) | x\in E\right\}$ where $\mu :E\to \left[0,1\right]$ and $\upsilon : E\to \left[0,1\right]$ represent the membership and non-membership functions with the condition 0 $\le \mu \left(x\right)+\upsilon \left(x\right)\le 1 \forall x\in E$.

Intuitionistic fuzzy Graph [18]: An intuitionistic fuzzy graph (IFG) is of the form $G=\left(V,E\right),$ where

i.

$V=\left\{a_1,a_2,\dots ,a_n\right\}$ be a vertex set such that $\mu :V\to \left[0,1\right]$ and $\upsilon :V\to \left[0,1\right]$ represent the membership and non-membership functions (for vertices) with the condition $0\le \mu \left(a_i\right)+\upsilon \left(a_i\right)\le 1$ for all $a_i\in V\left(i=1,2,\dots .,n\right).$

ii.

$E\subset V\times V$ be an edge set such that $\sigma :V\times V\to \left[0,1\right]$ and $\eta :V\times V\to \left[0,1\right]$ represent the membership and non-membership functions (for the edges) with the condition $\sigma \left(a_i,a_j\right)\le min\left[\mu \left(a_i\right),\mu \left(a_j\right)\right],$ $\eta \left(a_i,a_j\right)\le max\left[\upsilon \left(a_i\right),\upsilon \left(a_j\right)\right]$ and $0\le \sigma \left(a_i,a_j\right)+\eta \left(a_i,a_j\right)\le 1$ for every $\left(a_i,a_j\right)\in E$.

The degrees of membership and non-membership are shown in this case by the triple $\left(a_i,{\mu }_i,{\upsilon }_i\right)$ of the vertex $a_i,$ and the degrees of membership and non-membership are shown in this case by the triple $\left(e_{ij},{\sigma }_{ij},{\eta }_{ij}\right)$ of the edge relation $e_{ij}=\left(a_i , a_j\right)$.

Complete intuitionistic fuzzy Graph (CIFG) [20]: An IFG $\mathrm{G}=\left(\mathrm{V},\mathrm{E}\right)$ is said to be a complete IFG if ${\sigma }_{ij}=min\left({\mu }_i , {\mu }_j\right) and {\eta }_{ij}=max\left({\upsilon }_i , {\upsilon }_{j }\right)$ for every ${\mathrm{a}}_{\mathrm{i}},{\mathrm{a}}_{\mathrm{j}}\in \mathrm{V}$.

Path [20]: A path P of an IFG is a collection of distinct vertices $a_1,a_2,\dots ,a_n$ that satisfies either one of the following conditions

(a)

${\sigma }_{ij}>0$ and ${\eta }_{ij}>0$

(b)

${\sigma }_{ij}=0$ and ${\eta }_{ij}>0$

(c)

${\sigma }_{ij}>0and{\eta }_{ij}=0forsomeiandj\left(i,j=1,2,\dots ,n\right)$.

Strength of the path with respect to the membership value of IFG [20]:

The strength of the path with respect to the membership value is the minimum membership value on the edges in P.

Strength of the path with respect to the non-membership value of IFG [20]:

The strength of the path with respect to the non-membership value is the maximum non-membership value on the edges in P.

Strength of the path of IFG [20]:

The strength of the path is the minimum membership value on the edges in P and the maximum non-membership value on the edges in P can be represented as a $\left(x,y\right)$.

Strength of connectedness between ‘a’ and ‘b’ in G [20]:

The strength of connectedness between ‘a’ and ‘b’ is the maximum strength $\left\{CONN G^1\left(a,b\right)\right\}$ among all possible paths connecting $a$ and $b$ with respect to the membership value and minimum strength $\left\{CONN G^2\left(a,b\right)\right\}$ among all possible paths, and connecting $a$ and $b$ with respect to the non-membership value can be represented by $(\left\{CONN G^1\left(a,b\right)\right\},\{CONN G^2(a,b$)$\})$.

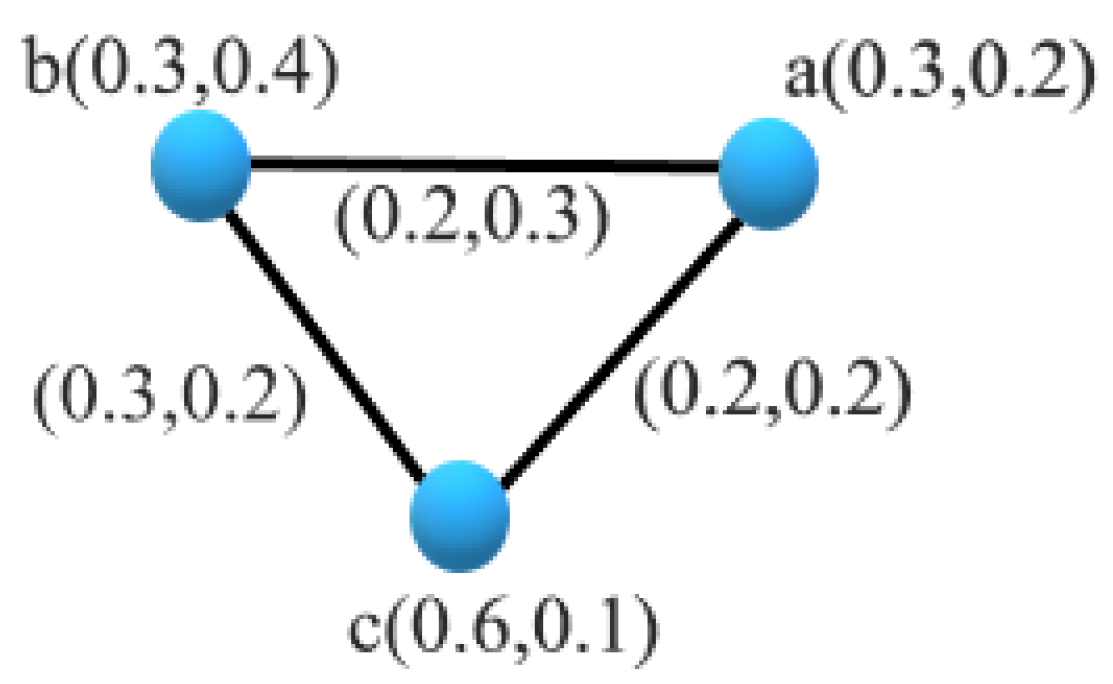
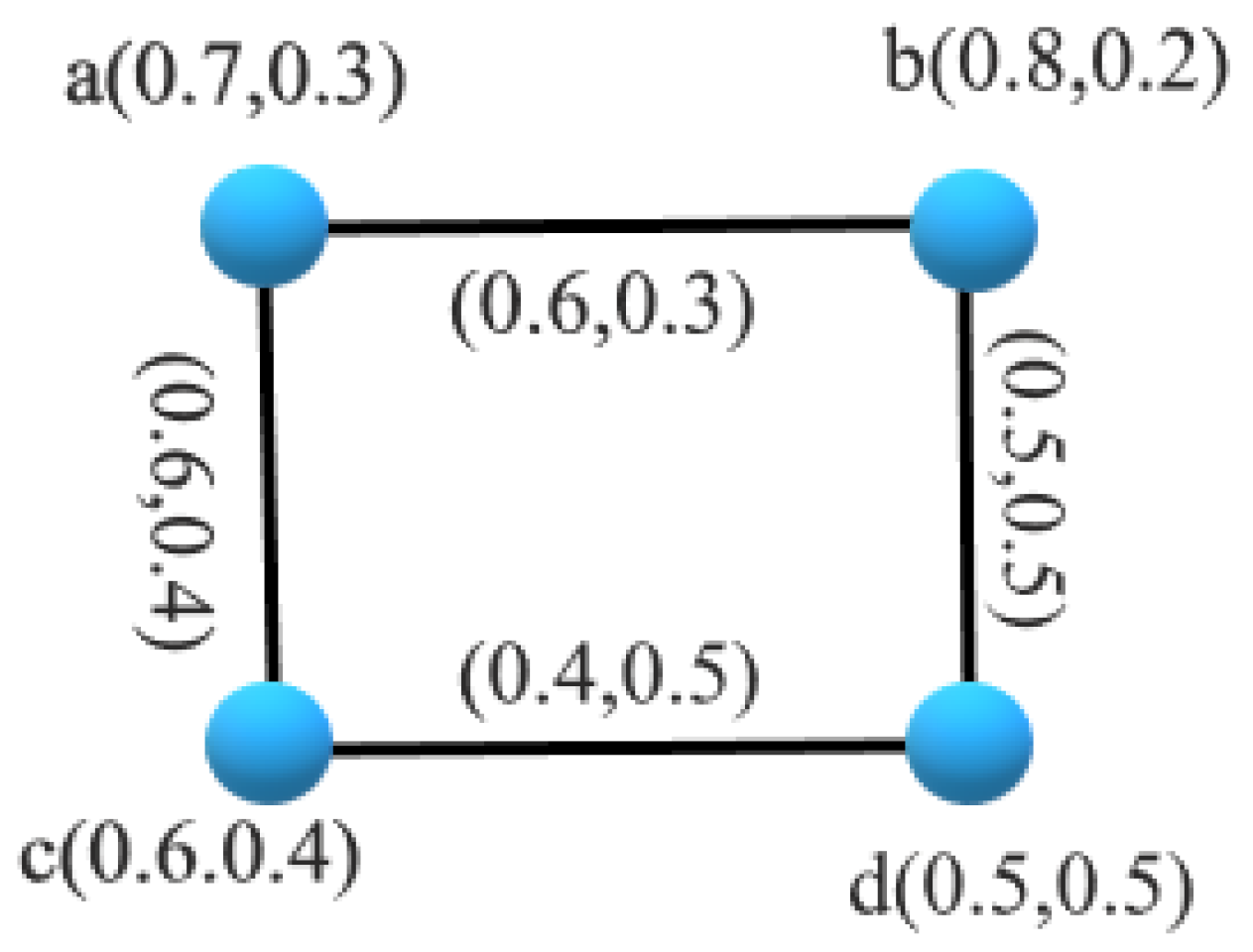
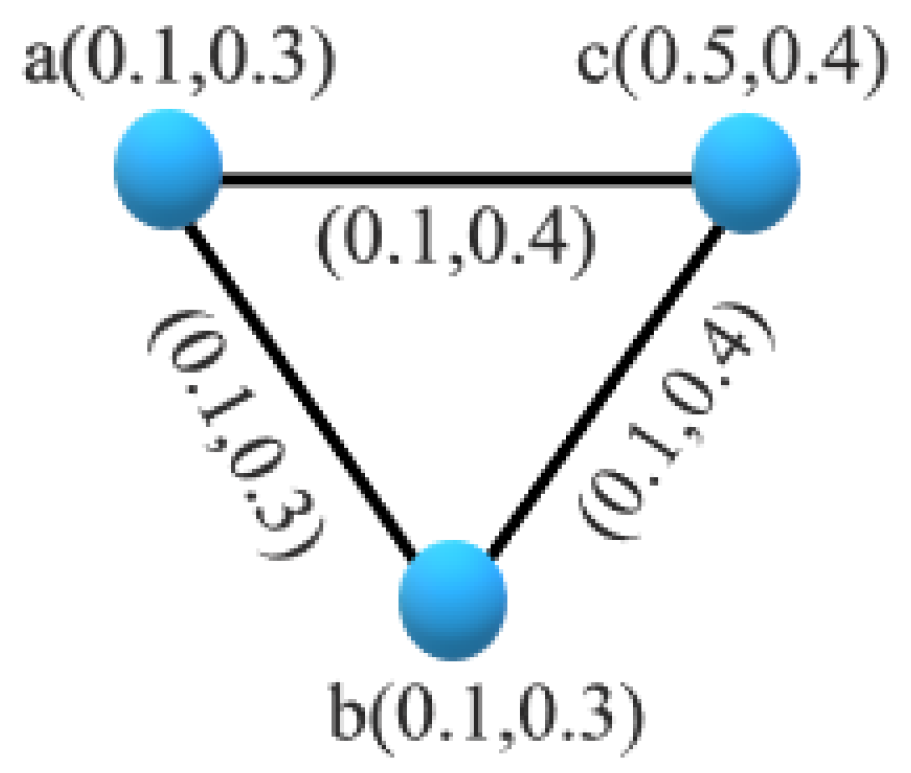
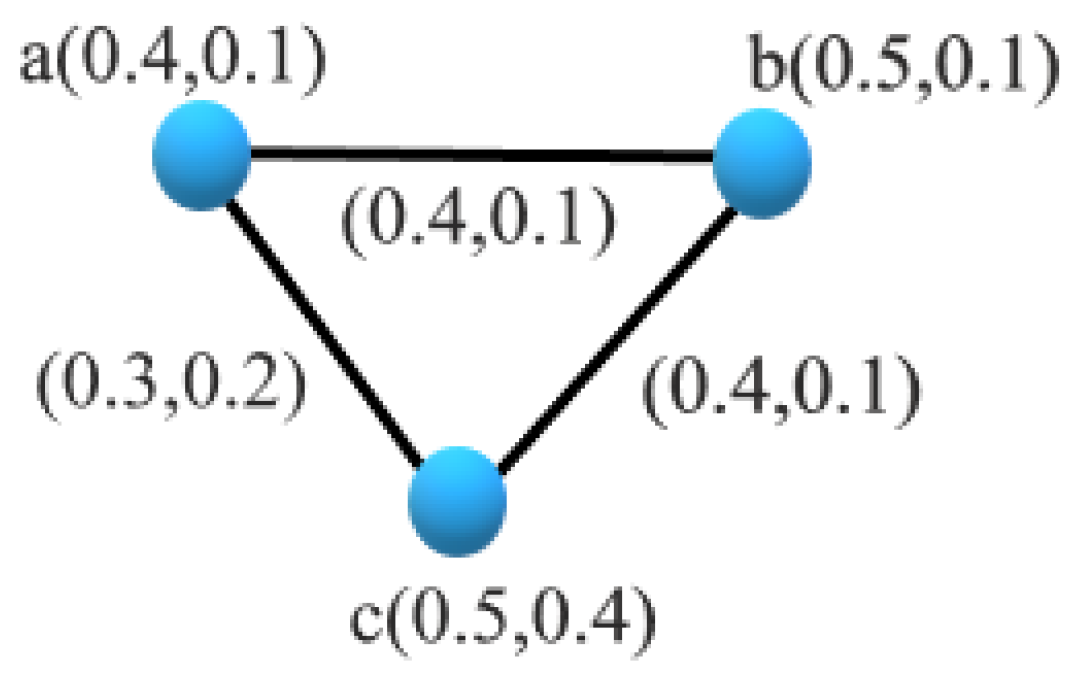
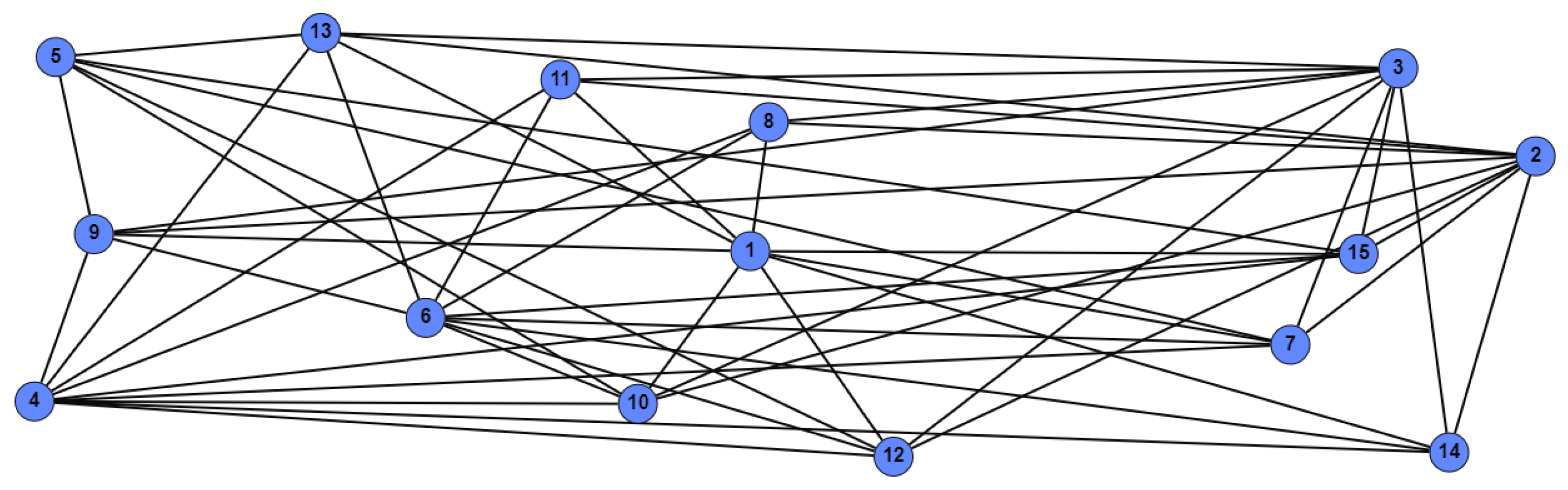
3. Connectivity Status in an Intuitionistic Fuzzy Graph:

The definition of connectivity status is given as follows.

Definition 1. 

Let $V=\left\{a_1,a_2,\dots ,a_n \right\}$ be an ordered vertex set of intuitionistic fuzzy graph $G=\left(V, E\right).$The connectivity status of a vertex $a\in V$ is defined by $C{S}_G\left(a\right)=\frac{1}{n-1}({\displaystyle \sum }_{\begin{array}{c}k=1\\ a\ne a_k\end{array}}^{n}CON{N}_G^1\left(a,a_{\mathrm{k}}\right),{\displaystyle \sum }_{\begin{array}{c}k=1\\ a\ne a_k\end{array}}^{n}CON{N}_G^2\left(a,a_{\mathrm{k}}\right))=(\frac{1}{n-1}{\displaystyle \sum }_{\begin{array}{c}k=1\\ a\ne a_k\end{array}}^{n}CON{N}_G^1\left(a,a_{\mathrm{k}}\right),\frac{1}{n-1}{\displaystyle \sum }_{\begin{array}{c}k=1\\ a\ne a_k\end{array}}^{n}CON{N}_G^2\left(a,a_{\mathrm{k}}\right))$ = $\left( C{S}_G^1\left(a\right), C{S}_G^2\left(a\right)\right)$.

Connectivity status of $G=\left(V,E\right)$ is defined as $CS\left(G\right)$ = $\frac{1}{n}{\displaystyle \sum }_{k=1}^{n}CS\left(a_k\right)$.

Example 1. 

An intuitionistic fuzzy graph $G\left(V,E\right)$ is shown in Figure 1. Here, $CON{N}_G^1\left(a,b\right)=0.2, CON{N}_G^2$($a,b)=0.2,$$CON{N}_G^1\left(a,c\right)=$0.2$, CON{N}_G^2$($a,c)=0.2,$ $CON{N}_G^1$($b,a)=0.2, CON{N}_G^2\left(b,a\right)=0.2,$ $CON{N}_G^1\left(b,c\right)=0.3, CON{N}_G^2$($b,c)=0.2,$ $CON{N}_G^1\left(c, a\right)=0.2, CON{N}_G^2\left(c,a\right)=0.2, CON{N}_G^1\left(c,b\right)=0.3,CON{N}_G^2$($c,b)=0.2$.

Therefore, $C{S}_G\left(a\right)=\frac{1}{2}\left(\left(0.2+0.2\right),\left(0.2+0.2\right)\right)=\left(0.2,0.2\right)$ [Using Definition 1],

similarly, $C{S}_G\left(b\right)=\left(0.25,0.2\right),C{S}_G\left(C\right)=\left(0.25,0.2\right)$

$CS\left(G\right)=\frac{1}{3}(\left(0.2+0.25+0.25\right),$ (0.2 + 0.2 + 0.2)) = (0.233, 0.2) [Using Definition 1].

Definition 2. 

(Minimum C.S. of IFG). Let $V=\left\{a_1,a_2,\dots ,a_n \right\}$ be an ordered vertex set of an intuitionistic fuzzy graph $G=\left(V, E\right)$. The connectivity status of the vertex set is$\left\{b_1,b_2,\dots , b_n\right\}$where $b_i=\left( C{S}_G^1\left(a_i\right), C{S}_G^2\left(a_i\right)\right)=\left(x_i,y_i\right)=CS\left(a_i\right) i=1,2,\dots ,n$.

Let us consider a function $f:R^2\to R$ such that

$$f\left(x,y\right)=2x-\frac{y}{2}$$

We now define a relation on the set $\left\{b_1,b_2,\dots ,b_n\right\}$ defined by $b_r\le b_t$ if and only if $f\left(b_r\right)\le f\left(b_t\right)$.

Where the relation$‘\le ’$ on the set $\left\{b_1,b_2,\dots ,b_n\right\}$implies that$b_t\left(C.S.of{a}_t\right)$is better than of $b_r(C.S.of{a}_r$) if and only if $f\left(b_r\right)\le f\left(b_t\right).$

Then, the connectivity status of a vertex$a_j \in V$ of IFG $G\left(V, E\right)$ will be minimum if $f\left(b_j\right)$ is minimum on the set $\left\{b_1,b_2,\dots , b_n\right\}$.

Definition 3. 

(Maximum C.S. of IFG). Let $V=\left\{a_1,a_2,\dots ,a_n \right\}$ be an ordered vertex set of intuitionistic fuzzy graph $G=\left(V, E\right)$. The connectivity status of the vertex set is $\left\{b_1,b_2,\dots , b_n\right\}$where $b_i=\left( C{S}_G^1\left(a_i\right), C{S}_G^2\left(a_i\right)\right)=\left(x_i,y_i\right)=CS\left(a_i\right) i=1,2,\dots ,n$.

Let us consider a function $f:R^2\to R$such that $f\left(x,y\right)=2x-\frac{y}{2}$

We now define a relation on the set $\left\{b_1,b_2,\dots , b_n\right\}$ defined by $b_r\le b_t$ if and only if $f\left(b_r\right) \le f\left(b_t\right)$.

Where the relation$‘\le ’$ on the set $\left\{b_1,b_2,\dots , b_n\right\}$ implies that$b_t \left(C.S. of a_t \right)$is better than of $b_r (C.S. of a_r$ ) if and only if $f\left(b_r\right)\le f\left(b_t\right).$

Then, the connectivity status of a vertex$a_j \in V$ of IFG $G\left(V, E\right)$ will be maximum if $f\left(b_j\right)$ is maximum on the set $\left\{b_1,b_2,\dots , b_n\right\}$.

Definition 4. 

(Connectivity status of a vertex of CIFG). Let $V=\left\{a_1,a_2,\dots ,a_n \right\}$ be an ordered vertex set of intuitionistic fuzzy graph $G=\left(V, E\right).$The connectivity status of a vertex $a\in V$is defined by $C{S}_G\left(a\right)=\frac{1}{n-1}({\displaystyle \sum }_{a^{*}є V \backslash a}\sigma \left(a,a^{*}\right),$ ${\displaystyle \sum }_{a^{*}є V \backslash a}\eta \left(a,a^{*}\right)$) = $(\frac{1}{n-1}{\displaystyle \sum }_{a^{*}є V \backslash a}\sigma \left(a,a^{*}\right),$ $\frac{1}{n-1}{\displaystyle \sum }_{a^{*}є V \backslash a}\eta \left(a,a^{*}\right))$ = $\left( C{S}_G^1\left(a\right), C{S}_G^2\left(a\right)\right)$.

The following formula provides the connectivity status of some vertices if some order is found for membership values and non-membership values.

Theorem 1. 

In a CIFG$\mathrm{G}=\left(\mathrm{V},\mathrm{E}\right),$ if $V=\left\{a_1,a_2,\dots ,a_n\right\}$has an ordering such that$\mu \left(a_1\right)\le \mu \left(a_2\right)\le$…$\le \mu (a_n)$and$\upsilon \left(a_1\right)\ge \upsilon \left(a_2\right)\ge \dots \ge \upsilon \left(a_n\right)$then$CS\left(a_1\right)=\left(\mu \left(a_1\right),\upsilon \left(a_1\right)\right)$ and $CS\left(a_j\right)=\left(\frac{1}{n-1}\left\{{\displaystyle \sum }_{p=1}^{j-1}\mu \left(a_p\right)+\left(n-j\right)\mu \left(a_j\right)\right\}, \frac{1}{n-1}\left\{{\displaystyle \sum }_{p=1}^{j-1}\upsilon \left(a_p\right)+\left(n-j\right)\upsilon \left(a_j\right)\right\}\right)$ for$2 \le j \le n$.

Proof. 

In a CIFG, $G=\left(V,E\right),V=\left\{a_1,a_2,\dots ,a_n \right\}$ has an ordering $\mu \left(a_1\right)\le \mu \left(a_2\right)\le \dots \le \mu (a_n)$ and $\upsilon \left(a_1\right)\ge \upsilon \left(a_2\right)\ge \dots \ge \upsilon \left(a_n\right)$.

So, $\sigma \left(a_1,a_p\right)=\mu \left(a_1\right)$ for $p=2,3,\dots ,n,$ $\eta \left(a_1,a_p\right)=\upsilon \left(a_1\right)$ for $p=2,3,\dots ,n$

Now, $CS\left(a_1\right)=\frac{1}{n-1}\left({\displaystyle \sum }_{p=2}^n\sigma \left(a_1,a_p\right),{\displaystyle \sum }_{p=2}^n\eta \left(a_1,a_p\right)\right)=\frac{1}{n-1} \left(n-1\right)\left(\mu \left(a_1\right),\upsilon \left(a_1\right)\right)$ $=\left(\mu \left(a_1\right),\upsilon \left(a_1\right)\right)$

$a_j є V and 1<j \le n$

$\sigma \left(a_p,a_j\right)=\mu \left(a_p\right)$ for $p=1,2,3,\dots , \left(j-1\right)$

$\eta \left(a_p,a_j\right)=\upsilon \left(a_p\right)$ for $p=1,2,3,\dots , \left(j-1\right)$

$\sigma \left(a_p,a_j\right)=\mu \left(a_j\right)$ for $p=\left(j+1\right),\left(j+2\right),\dots ,n$

$\eta \left(a_p,a_j\right)=\upsilon \left(a_j\right)$ for $p=\left(j+1\right),\left(j+2\right),\dots ,n$

Thus, $CS\left(a_j\right)=\frac{1}{n-1}\left(\left({\displaystyle \sum }_{p=1}^{j-1}\sigma \left(a_j{a}_P\right),{\displaystyle \sum }_{p=1}^{j-1}\eta \left(a_j{a}_P\right)\right)+\left({\displaystyle \sum }_{p=j+1}^n\sigma \left(a_j{a}_P\right),{\displaystyle \sum }_{p=j+1}^n\eta \left(a_j{a}_P\right)\right)\right)$= $\frac{1}{n-1}\left(\left({\displaystyle \sum }_{p=1}^{j-1}\mu \left(a_p\right),{\displaystyle \sum }_{p=1}^{j-1}\upsilon \left(a_p\right)\right)+\left(n-j\right)\left(\mu \left(a_j\right),\upsilon \left(a_j\right)\right)\right)$ $=(\frac{1}{n-1}\left\{{\displaystyle \sum }_{p=1}^{j-1}\mu \left(a_p\right)+\left(n-j\right)\mu \left(a_j\right)\right\},$ $\frac{1}{n-1}\left\{{\displaystyle \sum }_{p=1}^{j-1}\upsilon \left(a_p\right)+\left(n-j\right)\upsilon \left(a_j\right)\right\})$ for $2 \le j \le n$. □

Theorem 2. 

In a CIFG$G=\left(V,E\right),\mathrm{if}V=\left\{a_1,a_2,\dots ,a_n \right\}$ has an ordering$\mu \left(a_1\right)\le \mu \left(a_2\right)\le \dots \le \mu (a_n)$ and $\upsilon \left(a_1\right)\ge \upsilon \left(a_2\right)\ge \dots \ge \upsilon \left(a_n\right),$then there exist at least two same connectivity status vertices in G.

Proof. 

In a CIFG $G=\left(V,E\right),V=\left\{a_1,a_2,\dots ,a_n \right\}$ has an ordering $\mu \left(a_1\right)\le \mu \left(a_2\right)\le \dots \le \mu (a_n)$ and $\upsilon \left(a_1\right)\ge \upsilon \left(a_2\right)\ge \dots \ge \upsilon \left(a_n\right)$ Now, $CS \left(a_{n-1}\right)=\frac{1}{n-1}\left(\left({\displaystyle \sum }_{p=1}^{n-2}\sigma \left(a_{n-1}{a}_P\right),{\displaystyle \sum }_{p=1}^{n-2}\eta \left(a_{n-1}{a}_P\right)\right)+\left(\sigma \left(a_{n-1,}{a}_n\right), \eta \left(a_{n-1,}{a}_n\right)\right)\right)$ $=\frac{1}{n-1} \left(\left({\displaystyle \sum }_{p=1}^{n-2}\mu \left(a_P\right),{\displaystyle \sum }_{p=1}^{n-2}\upsilon \left(a_P\right)\right)+\left(\mu \left(a_{n-1}\right),\upsilon \left(a_{n-1}\right)\right)\right)$= $\frac{1}{n-1}\left({\displaystyle \sum }_{p=1}^{n-1}\mu \left(a_P\right),{\displaystyle \sum }_{p=1}^{n-1}\upsilon \left(a_P\right)\right)$=$CS\left(a_n\right)$. □

Theorem 3. 

In a CIFG$G=\left(V,E\right),$ $\mathrm{if}V=\left\{a_1,a_2,\dots ,a_n\right\}$ has an ordering $\mu \left(a_1\right)\le \mu \left(a_2\right)\le \dots \le \mu (a_n)$and $\upsilon \left(a_1\right)\ge \upsilon \left(a_2\right)\ge \dots \ge \upsilon \left(a_n\right),$ then $CS\left(a_1\right)\le \dots \le CS\left(a_n\right)$ and$mi{n}_{CS}\left(G\right)=CS\left(a_1\right)$and$ma{x}_{CS}\left(G\right)=CS\left(a_n\right)$.

Proof. 

In a CIFG $G=\left(V,E\right),$ we have $\mu \left(a_1\right)\le \mu \left(a_2\right)\le \dots \le \mu (a_n)$.

This implies that $\left(n-1\right)\mu \left(a_1\right)\le \mu \left(a_1\right)+\left(n-2\right)\mu \left(a_2\right)\le \mu \left(a_1\right)+\mu \left(a_2\right)+\left(n-3\right)\mu \left(a_3\right)\le \dots \le {\displaystyle \sum }_{p=1}^{j-1}\mu \left(a_P\right)+\left(n-j\right)\mu \left(a_J\right)\le \dots \le {\displaystyle \sum }_{p=1}^{n-1}\mu \left(a_P\right)$

Thus, $\frac{1}{n-1}\left\{\left(n-1\right)\mu \left(a_1\right)\right\}\le \frac{1}{n-1}\left\{\mu \left(a_1\right)+\left(n-2\right)\mu \left(a_2\right)\right\}\le \frac{1}{n-1}\left\{\mu \left(a_1\right)+\mu \left(a_2\right)+\left(n-3\right)\mu \left(a_3\right)\right\}\le \dots \le \frac{1}{n-1}\left\{{\displaystyle \sum }_{p=1}^{j-1}\mu \left(a_P\right)+\left(n-j\right)\mu \left(a_J\right)\right\}\le \dots \le \frac{1}{n-1}\left\{{\displaystyle \sum }_{p=1}^{n-1}\mu \left(a_P\right)\right\}$

Hence, $C{S}_G^1\left(a_1\right)\le C{S}_G^1\left(a_2\right)\le \dots \le C{S}_G^1\left(a_n\right)$

Using the condition, $\upsilon \left(a_1\right)\ge \upsilon \left(a_2\right)\ge \dots \ge \upsilon \left(a_n\right),$ we get

$$\begin{gathered} \left(n-1\right)\upsilon \left(a_1\right)\ge \upsilon \left(a_1\right)+\left(n-2\right)\upsilon \left(a_2\right)\ge \upsilon \left(a_1\right)+\upsilon \left(a_2\right)+\left(n-3\right)\upsilon \left(a_3\right)\ge \dots \\ \ge {\displaystyle \sum }_{p=1}^j\upsilon \left(a_p\right)+\left(n-j\right)\upsilon \left(a_j\right)\ge \dots \ge {\displaystyle \sum }_{p=1}^{n-1}\upsilon \left(a_p\right) \end{gathered}$$

Hence, $\frac{1}{n-1}\left\{\left(n-1\right)\upsilon \left(a_1\right)\right\}\ge \frac{1}{n-1}\left\{\upsilon \left(a_1\right)+\left(n-2\right)\upsilon \left(a_2\right)\right\}\ge \frac{1}{n-1}\left\{\upsilon \left(a_1\right)+\upsilon \left(a_2\right)+\left(n-3\right)\upsilon \left(a_3\right)\right\}\ge \dots \ge \frac{1}{n-1}\left\{{\displaystyle \sum }_{p=1}^j\upsilon \left(a_p\right)+\left(n-j\right)\upsilon \left(a_j\right)\right\}\ge \dots \ge \frac{1}{n-1}\left\{{\displaystyle \sum }_{p=1}^{n-1}\upsilon \left(a_p\right)\right\}$

Thus, $C{S}_G^2\left(a_1\right)\ge C{S}_G^2\left(a_2\right)\ge \dots \ge C{S}_G^2\left(a_n\right).$

Since, $C{S}_G^1\left(a_1\right)\le C{S}_G^1\left(a_2\right)\le \dots \le C{S}_G^1\left(a_n\right)$ and $C{S}_G^2\left(a_1\right)\ge C{S}_G^2\left(a_2\right)\ge \dots \ge C{S}_G^2\left(a_n\right)$.

Thus,

$$CS\left(a_1\right)\le \dots \le \mathrm{C}S\left(a_n\right)\left[\mathrm{Referred\; to\; Definition}2\right]$$

(1)

It could be written directly from $\left(i\right)$ that $mi{n}_{CS}\left(G\right)=CS\left(a_1\right),$ $ma{x}_{CS}\left(G\right)=CS\left(a_n\right)$. □

Theorem 4. 

In a CIFG$, G=\left(V,E\right),$ if $V=\left\{a_1,a_2,\dots ,a_n\right\}$ has an ordering $\mu \left(a_1\right)\le \mu \left(a_2\right)\le \dots \le \mu (a_n)$ and $\upsilon \left(a_1\right)\ge \upsilon \left(a_2\right)\ge \dots \ge \upsilon \left(a_n\right).$If two vertices have equal membership and non-membership values, they have the same connectivity status.

Proof. 

In a CIFG $G=\left(V,E\right),V=\left\{a_1,a_2,\dots ,a_n \right\}$ has an ordering $\mu \left(a_1\right)\le \mu \left(a_2\right)\le \dots \le \mu (a_n)$ and $\upsilon \left(a_1\right)\ge \upsilon \left(a_2\right)\ge \dots \ge \upsilon \left(a_n\right)$.

Assume that two vertices have equal membership and non-membership values; let they are $a_{p}and{a}_{p+1}.$

If p $=1, \mu \left(a_1\right)=\mu \left(a_2\right)$

$\upsilon \left(a_1\right)=\upsilon \left(a_2\right)$

Now,

$$\begin{gathered} CS\left(a_2\right)=\frac{1}{n-1}\left(\left(\mu \left(a_1\right)+\left(n-2\right)\mu \left(a_2\right)\right),\left(\upsilon \left(a_1\right)+\left(n-2\right)\upsilon \left(a_2\right)\right)\right) \\ =\frac{1}{n-1}\left(\left(\mu \left(a_1\right)+\left(n-2\right)\mu \left(a_1\right)\right),\left(\upsilon \left(a_1\right)+\left(n-2\right)\upsilon \left(a_1\right)\right)\right) \\ =\frac{1}{n-1} \left(n-1\right)\left(\mu \left(a_1\right),\upsilon \left(a_1\right)\right) \\ =\left(\mu \left(a_1\right),\upsilon \left(a_1\right)\right) \\ =CS\left(a_1\right) \end{gathered}$$

For $2\le p\le \left(n-1\right)$ let, $\mu \left(a_p\right)=\mu \left(a_{p+1}\right)$

$$\upsilon \left(a_p\right)=\upsilon \left(a_{p+1}\right)$$

$$\begin{gathered} CS\left(a_p\right)=\frac{1}{n-1}\left(\left({\displaystyle \sum }_{k=1}^{p-1}\mu \left(a_k\right)+\left(n-p\right)\mu \left(a_p\right)\right),\left({\displaystyle \sum }_{k=1}^{p-1}\upsilon \left(a_k\right)+\left(n-p\right)\upsilon \left(a_p\right)\right)\right) \\ =\frac{1}{n-1}(\left({\displaystyle \sum }_{k=1}^{p-1}\mu \left(a_k\right)+\mu \left(a_p\right)+\left(n-\left(p+1\right)\right)\mu \left(a_p\right)\right),\left({\displaystyle \sum }_{k=1}^{p-1}\upsilon \left(a_k\right)+\upsilon \left(a_p\right)+\left(n-\left(p+1\right)\right)\upsilon \left(a_p\right)\right)) \\ =\frac{1}{n-1}\left(\left({\displaystyle \sum }_{k=1}^p\mu \left(a_k\right)+\left(n-\left(p+1\right)\right)\mu \left(a_{p+1}\right)\right),\left({\displaystyle \sum }_{k=1}^p\upsilon \left(a_k\right)+\left(n-\left(p+1\right)\right)\upsilon \left(a_{p+1}\right)\right)\right)=CS\left(a_{p+1}\right) \end{gathered}$$

□

4. Application

Application of C.S. in an IFG in the spreading of infectious diseases:

Let us discuss the chance of being infected or non-infected by COVID-19 virus by the knowledge of intuitionistic fuzzy graphs using the connectivity status.

For this, we take a group of $n$ persons (these persons contact and meet themselves every day).

Let these persons (vertices) be named as $v_1,v_2,\dots v_n.$ The edges between them represent the meeting and connection. The chance of spreading the virus is taken as the edge membership value, and the edge non-membership value is represented by the chance of not spreading the virus. It is known that all viruses may infect everyone by contacting or touching the chance of being affected or not affected. Here, Vertex’s membership and non-membership values are represented by the chance of affected and non-affected.

To justify a person as infected (in the sense of a spreading virus) or safe.

Step 1: First, calculate the connectivity status of each of the vertices (n persons). Step 2: If $C{S}_G(w)$ equals to (x, y) where $wєV$ then define a function $f:R^2\to R$ such that $\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)=2\mathrm{x}-\frac{\mathrm{y}}{2}$. Step 3: Mark the vertices (persons) having the largest functional value for the connectivity status (x,y) of vertices. Step 4: Mark the vertices (persons) having the lowest functional value for the connectivity status (x,y) of vertices. Step 5: We call the vertex or vertices (person or persons) obtained from Step 3 the most infected vertex or vertices (person or persons) and denoted it by Vmif. Step 6: We call the vertex or vertices (person or persons) obtained from Step 4 as the safest vertex or vertices (person or persons) and denoted it by Vsaf.

Example 2. 

The adjacency matrix of IFG (see Figure 2) with respect to membership values is given below.

$$\left[\begin{array}{cc}0& \begin{array}{cc}0.6& \begin{array}{cc}0.6& 0\end{array}\end{array}\\ \begin{array}{c}0.6\\ \begin{array}{c}0.6\\ 0\end{array}\end{array}& \begin{array}{c}\begin{array}{cc}0& \begin{array}{cc}0& 0.5\end{array}\end{array}\\ \begin{array}{c}\begin{array}{cc}0& \begin{array}{cc}0& 0.4\end{array}\end{array}\\ \begin{array}{cc}0.5& \begin{array}{cc}0.4& 0\end{array}\end{array}\end{array}\end{array}\end{array}\right]$$

The adjacency matrix of IFG (see Figure 2) with respect to non-membership values is given below.

$$\left[\begin{array}{cc}0& \begin{array}{cc}0.3& \begin{array}{cc}0.4& 0\end{array}\end{array}\\ \begin{array}{c}0.3\\ \begin{array}{c}0.4\\ 0\end{array}\end{array}& \begin{array}{c}\begin{array}{cc}0& \begin{array}{cc}0& 0.5\end{array}\end{array}\\ \begin{array}{c}\begin{array}{cc}0& \begin{array}{cc}0& 0.5\end{array}\end{array}\\ \begin{array}{cc}0.5& \begin{array}{cc}0.5& 0\end{array}\end{array}\end{array}\end{array}\end{array}\right]$$

Using Algorithm $1,$ we get the first component of the strength of connectedness in the form of an adjacency matrix.

$$\left[\begin{array}{cc}0& \begin{array}{cc}0.6& \begin{array}{cc}0.6& 0.5\end{array}\end{array}\\ \begin{array}{c}0.6\\ \begin{array}{c}0.6\\ 0.5\end{array}\end{array}& \begin{array}{c}\begin{array}{cc}0& \begin{array}{cc}0.6& 0.5\end{array}\end{array}\\ \begin{array}{c}\begin{array}{cc}0.6& \begin{array}{cc}0& 0.5\end{array}\end{array}\\ \begin{array}{cc}0.5& \begin{array}{cc}0.5& 0\end{array}\end{array}\end{array}\end{array}\end{array}\right]$$

Similarly, we get the last component of the strength of connectedness in the form of an adjacency matrix using Algorithm 2.

$$\left[\begin{array}{cc}0& \begin{array}{cc}0.3& \begin{array}{cc}0.4& 0.5\end{array}\end{array}\\ \begin{array}{c}0.3\\ \begin{array}{c}0.4\\ 0.5\end{array}\end{array}& \begin{array}{c}\begin{array}{cc}0& \begin{array}{cc}0.4& 0.5\end{array}\end{array}\\ \begin{array}{c}\begin{array}{cc}0.4& \begin{array}{cc}0& 0.5\end{array}\end{array}\\ \begin{array}{cc}0.5& \begin{array}{cc}0.5& 0\end{array}\end{array}\end{array}\end{array}\end{array}\right]$$

Hence, using Algorithm 3, we get

$$\begin{gathered} C{S}_G\left(a\right)=\left(0.566,0.4\right) \\ C{S}_G\left(b\right)=\left(0.566,0.4\right) \\ C{S}_G\left(c\right)=\left(0.566,0.433\right) \\ C{S}_G\left(d\right)=\left(0.5,0.5\right) \end{gathered}$$

Here,$a,b$ are the most infected vertices (persons).

For most infected vertex, we need to take necessary action.

Here,$d$ is the safest vertex (person).

Algorithm 1: Algorithm to find the 1st component of the strength of connectedness between pair of vertices in the form of an adjacency matrix of an IFG $G=\left(V,E\right)$.

Input: A weighted undirected Graph $G\prime =\left(V,E\prime \right)$ with respect to the membership value of an IFG $G=\left(V,E\right)$ with |V|= n and $n\times n$ matrix of weight on the edge membership weight[w(x,y)] of IFG.  Output: A matrix 1st component of the strength of connectedness between pair of vertices in the form of an adjacency matrix named strength[][]. The steps are given as follows. $Q$ ← $V$ for each u ∈ $Q$: for each v ∈ $Q$: if u == v: then do strength [u][v] ← 0 else strength[u][v] ← GETMAXOF (u,v) Procedure GETMAXOF (u,v): $Q$ ← $V$ for u ∈ $Q:$ do visited [u] ← false maxwt ← 0 DFS(u,v) return maxwt End Procedure Procedure DFS(u,v) visited[u] ← true store u in path if u == v minwt ← MININPATH (path) if minwt$>$maxwt: do maxwt ← minwt else for each t ∈ adj [u]: if not visited [t]: DFS(t,v) remove u from path visited [u] ← false End Procedure Procedure MININPATH (path): weight ← 0 length ← number of nodes stored in path for i in range length: u ← path[i] v ← path[j] weight ← w(u,v) store weight in value sort value in ascending order return value[0] End Procedure

For detailed pseudocode of Algorithm 1, see Appendix A and for output for Appendix C.

$\mathrm{Algorithm}2:\mathrm{Algorithm}\mathrm{to}\mathrm{find}\mathrm{the}\mathrm{last}\mathrm{component}\mathrm{of}\mathrm{the}\mathrm{strength}\mathrm{of}\mathrm{connectedness}\mathrm{between}\mathrm{pair}\mathrm{of}\mathrm{vertices}\mathrm{in}\mathrm{the}\mathrm{form}\mathrm{of}\mathrm{an}\mathrm{adjacency}\mathrm{matrix}\mathrm{of}\mathrm{an}\mathrm{IFG}G=\left(V,E\right)$.

$\mathrm{Input}:\mathrm{A}\mathrm{weighted}\mathrm{undirected}\mathrm{Graph}G\prime \left(V,E\prime \right)$ $\mathrm{with}\mathrm{respect}\mathrm{to}\mathrm{non}-\mathrm{membership}\mathrm{value}\mathrm{of}\mathrm{an}\mathrm{IFG}G=\left(V,E\right)$ $\mathrm{with} |$ $\mathrm{V}$ $=\mathrm{n}\mathrm{and}n\times n$ $\mathrm{matrix}\mathrm{of}\mathrm{weight}\mathrm{on}\mathrm{the}\mathrm{edge}\mathrm{non}-\mathrm{membership}\mathrm{weight}\left[w\left(x,y\right)\right]$ of IFG.  Output: A matrix last component of the strength of connectedness between pair of vertices in the form of an adjacency matrix named strength [][] $Q$$\text{←} V$ for each u $\text{∈} Q$: for each v $\text{∈} Q:$ if u == v: then do strength [u][v] ← 0 else strength[u][v] ← GETMINOF (u,v) Procedure GETMINOF (u,v): $Q$$\text{←} V$ for u ∈ $Q$: do visited [u] ← false minwt ← 1 DFS(u,v) return minwt End Procedure $\mathrm{Procedure}DFS\left(u,v\right)$ visited[u] ← true store u in path if u == v maxwt ← MAXINPATH (path) if maxwt < minwt: do minwt ← maxwt else for each t ∈adj [u]: if not visited [t]: DFS(t,v) remove u from path visited [u] ← false End Procedure Procedure MAXINPATH (path): weight ← 0 length ← number of nodes stored in path for i in range length: u ← path[i] v ← path[j] weight ← w(u,v) store weight in value sort value in descending order return value[0] End Procedure

For detailed pseudocode of v 1, see Appendix B

Algorithm 3: Algorithm to find the connectivity status of an IFG.

$\mathrm{Step}1:\mathrm{Find}CON{N}_G^1\left(a,b\right) \forall a,b\in V$$\mathrm{using}\mathrm{above}Algorithm 1$$\mathrm{in}\mathrm{the}\mathrm{form}\mathrm{of}n\times n$ adjacency matrix, say M. $\mathrm{Step}2:\mathrm{Find} CON{N}_G^2\left(a,b\right) \forall a,b\in V$ $\mathrm{using}\mathrm{above}Algorithm 2$ $\mathrm{in}\mathrm{the}\mathrm{form}\mathrm{of}n\times n$ $\mathrm{adjacency}$ matrix, say N. $\mathrm{Step}3:\mathrm{For}1\le i\le n$ $\mathrm{compute}C{S}_G^1\left(a_i\right)=\frac{1}{n-1}{\displaystyle \sum }_{r=1}^n{P}_{ir};P_{ir}$ $\mathrm{is}$ $\mathrm{and}\mathrm{column}r$ $\mathrm{in}M.$ $\mathrm{Step}4:\mathrm{For}1\le i\le n$ $\mathrm{compute}C{S}_G^2\left(a_i\right)=\frac{1}{n-1}{\displaystyle \sum }_{\mathrm{r}=1}^{\mathrm{n}}{\mathrm{Q}}_{\mathrm{ir}}$$;{\mathrm{Q}}_{\mathrm{ir}}$ $\mathrm{is}$ $\mathrm{and}$ $\mathrm{in}N.$ $\mathrm{Step}5:\mathrm{Compute}C{S}_G\left(a_i\right)=\left(C{S}_G^1\left(a_i\right),C{S}_G^2\left(a_i\right)\right)$ $\mathrm{Step}6:\mathrm{Compute} CS\left(G\right)=\frac{1}{n}{\displaystyle \sum }_{i=1}^{n}CS\left(a_i\right)$

Let us consider a group of friends $a,b,c,d$ from a COVID-19-affected region. Each friend may be affected by COVID-19 by themselves or anyone else.

Let us find the connectivity status of the system (IFG) using the connectivity status of vertices (friends). Now we find the differences between non-membership values from the membership values of the C.S. in this graph.

An algorithm may be proposed to determine whether a system (IFG) is the most infected or safest.

Step 1: If the difference $\le$0, then we call the system (IFG) the safest and neutralized.

Step 2: If the difference $>0,$ then we call the system (IFG) the most infected.

Example 3. 

From Example 2, we found

$$CS\left(G\right)=\left(0.549,0.433\right)$$

Here, the system (IFG) is the most infected, so this system (IFG) needs necessary action.

Definition 5. 

(Reducibility and inducibility of connectivity status under some influence).

The connectivity status of an intuitionistic fuzzy graph (system) will be reduced if the first component of it is reduced and the last component of it is induced.

Similarly, the connectivity status of an intuitionistic fuzzy graph (system) will be induced if the first component of it is induced and the last component of it is reduced.

To illustrate this definition, a methodology and an algorithm may be proposed.

(1)

$First$ calculate the C.S. of the given intuitionistic fuzzy graph (system) under no influence (this may be maintaining social distance, sanitizing, immunity increasing, vaccinizing, etc.), and this is denoted by $CSNI\left(G\right)$.

(2)

Now calculate the new C.S. under some influence of the IFG (system) denoted by$CSI \left(G\right)$.

(3)

If the $firstcomponentofCSNI\left(G\right)-firstcomponentofCSI\left(G\right)>$ $0$ and the $second component of CSNI\left(G\right)-second component ofCSI\left(G\right) \le 0,$ then the connectivity status is reduced.

(4)

If the $firstcomponentofCSNI\left(G\right)-firstcomponentofCSI\left(G\right)\le$ $0$ and the $second component of CSNI\left(G\right)-second component of CSI\left(G\right)>0,$ then the connectivity status is induced.

Example 4. 

First, we take the IFG (system) under no influence (see  Figure 1).

Using Algorithm 1, we get the first component of the strength of connectedness in the form of an adjacency matrix

$${\left[\begin{array}{ccc}0& 0.2& 0.2\\ 0.2& 0& 0.3\\ 0.2& 0.3& 0\end{array}\right]}_{3\times 3}$$

Similarly, we get the last component of the strength of connectedness in the form of an adjacency matrix using Algorithm $2$

$${\left[\begin{array}{ccc}0& 0.2& 0.2\\ 0.2& 0& 0.2\\ 0.2& 0.2& 0\end{array}\right]}_{3\times 3}$$

Hence, using Algorithm 3, we get

$$\begin{gathered} C{S}_G\left(a\right)=\left(0.2,0.2\right) \\ C{S}_G\left(b\right)=\left(0.25,0.2\right) \\ C{S}_G\left(C\right)=\left(0.25,0.2\right) \\ CS\left(G\right)=\left(0.233,0.2\right) \end{gathered}$$

Now we take the IFG (system) (see  Figure 3) under some influence on  Figure 1

Using Algorithm 1, we get the first component of the strength of connectedness in the form of an adjacency matrix

$${\left[\begin{array}{ccc}0& 0.1& 0.1\\ 0.1& 0& 0.1\\ 0.1& 0.1& 0\end{array}\right]}_{3\times 3}$$

(2)

Similarly, we get the last component of the strength of connectedness in the form of an adjacency matrix using Algorithm 2.

$${\left[\begin{array}{ccc}0& 0.3& 0.4\\ 0.3& 0& 0.4\\ 0.4& 0.4& 0\end{array}\right]}_{3\times 3}$$

Hence, using Algorithm 3, we get

$$\begin{gathered} C{S}_G\left(a\right)=\left(0.1,0.35\right) \\ C{S}_G\left(b\right)=\left(0.1,0.35\right) \\ C{S}_G\left(C\right)=\left(0.1,0.4\right) \\ CS\left(G\right)=\left(0.1,0.36\right) \end{gathered}$$

Here, C.S of IFG (system) is reduced

Example 5. 

Again we take the IFG [see Figure 4] under some influence on the Figure 1.

Using Algorithm 1, we get the first component of the strength of connectedness in the form of an adjacency matrix

$${\left[\begin{array}{ccc}0& 0.4& 0.4\\ 0.4& 0& 0.4\\ 0.4& 0.4& 0\end{array}\right]}_{3\times 3}$$

Similarly, we get the last component of the strength of connectedness in the form of an adjacency matrix using Algorithm 2.

$${\left[\begin{array}{ccc}0& 0.1& 0.1\\ 0.1& 0& 0.1\\ 0.1& 0.1& 0\end{array}\right]}_{3\times 3}$$

Hence, using Algorithm 3, we get

$$\begin{gathered} C{S}_G\left(a\right)=\left(0.4,0.1\right) \\ C{S}_G\left(b\right)=\left(0.4,0.1\right) \\ C{S}_G\left(C\right)=\left(0.4,0.1\right) \\ CS\left(G\right)=\left(0.4,0.1\right) \end{gathered}$$

Here, the C.S of the IFG (system) is induced. So, a change of influence is required.

Sometimes it may be observed that the C.S is neither reduced nor induced by an IFG (system) under some influence.

Then, a change of influence is required.

Area of Applications of Connectivity Status (C.S.)

The merger of banks means greater financial strength for banks involved in the transaction.

Having greater economic power can lead to a higher market share. More influence over customers, grow revenues and increase profits. Additionally, customers will get access from any merged bank branch nearby to his/her location.

Let us discuss the chance of merging between two banks by using the connectivity status of intuitionistic fuzzy graphs.

The stability of a bank depends on the year of service, number of branches, sufficient growth rate, and other minor parameters. However, it is impossible for us to collect all data because it is very time-consuming and costly. We consider the chance of stability of the bank by using the number of branches (as a major parameter).

The chance of instability of a bank depends on the number of customers (as the number of branches depends on the number of customers), year of service, sufficient growth rate, and other minor parameters. Here, we consider the chance of the instability of the bank by using the number of customers (as a major parameter).

Suppose we want to find a chance of merging between two banks. In that case, we need to check the correlation coefficient between the two banks with respect to return type data (closed to closed) on the bank share price, the number of branches in the same city, joined by the number of the same projects, and other minor parameters. However, it is impossible to collect all data because it is very time-consuming. So here, we consider the chance of merging between two banks by using the correlation coefficient between the two banks with respect to return type data (closed to closed) on the bank share price (as a major parameter).

Suppose we want to find a chance of non-merge between two banks. In that case, we need to check the profit of the two banks (as the rate of return on equity depends on the net profit), the number of branches in the same city, joined by the number of the same projects, and other minor parameters. However, it is impossible to collect all data because it is very time-consuming. So here, we consider the chance of non-merging between two banks by using the profit of the two banks (as a major parameter).

Here, we take some private banks to contract a network system depending on the chance of stability of the bank and the chance of merging between stable and non-stable banks.

If the chance of stability $\ge \alpha ,$ then the bank is considered a stable bank; else, it is an unstable bank.

We create a link to connect a stable and unstable bank with respect to the chance of merging and non-merging. However, there will be no connection between the two same kinds of banks. Additionally, there will be no connection between a stable and unstable bank if both bank rate of return is depraved.

Let these banks (vertices) be named as $v_1,v_2,\dots v_n$. The edges between them represent the merging and connection. Now the chance of merging between two banks is taken as the edge membership value, and the edge non-membership value is represented by the chance of non-merging between two banks. Vertex’s membership and non-membership values are represented by the bank’s chance of stability and instability. See Algorithm 4 for generalised version of bank merging.

Algorithm 4: Algorithm for bank merging

$\mathrm{Step}1:\mathrm{First},\mathrm{calculate}\mathrm{the}\mathrm{connectivity}\mathrm{status}C{S}_G\left(a\right)=\left(x,y\right)$ $\mathrm{where}a\left(a bank\right)\in V\left(set of banks\right)$ $\mathrm{of}\mathrm{an}\mathrm{IFG}G\left(V,E\right)$. $\mathrm{Step}2:\mathrm{We}\mathrm{define}\mathrm{a}\mathrm{function}f:R^2\to R$ $\mathrm{such}\mathrm{that} f\left(x,y\right)=2x-\frac{y}{2}$  $\mathrm{Step}3:\mathrm{Enlist}\mathrm{the}\mathrm{banks}\mathrm{from}\mathrm{the}\mathrm{list}\mathrm{of}\mathrm{stable}\mathrm{banks}\mathrm{in}\mathrm{such}\mathrm{a}\mathrm{way}\mathrm{that}\mathrm{has}\mathrm{the}\mathrm{largest}\mathrm{functional}\mathrm{value}\mathrm{for}\mathrm{the}\mathrm{connectivity}\mathrm{status}\left(x,y\right)$ of banks.  $\mathrm{Step}4:\mathrm{Enlist}\mathrm{the}\mathrm{banks}\mathrm{from}\mathrm{the}\mathrm{list}\mathrm{of}\mathrm{unstable}\mathrm{banks}\mathrm{in}\mathrm{a}\mathrm{way}\mathrm{with}\mathrm{the}\mathrm{largest}\mathrm{functional}\mathrm{value}\mathrm{for}\mathrm{the}\mathrm{connectivity}\mathrm{status}\left(x,y\right)$ of banks.  Step 5: Now we merge the bank from the 1st position of the stable bank with the 1st position of the unstable bank.  Step 6: Now delete 1st position of the stable bank and 1st position of the unstable bank. Then, continue the same process on the remaining system (IFG) until the number of stable banks vanishes.

Let us take the banks, namely ICICI $\mathrm{BANK},$ AXIS $\mathrm{BANK},$ BANK OF BARODA (BOB), INDIAN $\mathrm{BANK},$ HDFC BANK, UNION BANK OF INDIA (UBI), FEDERAL BANK, BANDHAN BANK, CSB BANK, INDUSIND BANK, KOTAK MAHINDRA BANK (KMB), DCB BANK, IDFC BANK, JAMMU&KASHMIR BANK (J&K), KARNATAKA BANK. Now we find the stable or unstable banks using the chance of stability. Now we evaluate the chance of stability (see

Table 1. List of banks with parameters (number of branches and stability).

Bank Name	Number of Branches	Chance of Stability
ICICI	$5614$	0.57
AXIS	$4758$	$0.49$
B0B	$9683$	$1$
INDIAN	$5721$	$0.59$
HDFC	$6499$	$0.67$
UBI	$8700$	$0.89$
FEDERAL	$1282$	$0.13$
BANDHAN	$1190$	$0.12$
CSB	$654$	$0.067$
INDUSIND	$2320$	$0.23$
KMB	$1702$	$0.17$
DCB	$415$	$0.04$
IDFC	$641$	$0.066$
J&K	$964$	$0.099$
KARNATAKA	$922$	$0.095$

) with the help of the number of branches (see Table 1).

We assume the chance of stability is 1 when it has the maximum number of branches. The following process will evaluate the chance of stability of the other banks.

$X$ is a bank, $Y$ is the number of branches of $X,$ and $W$ is the maximum number of branches in the list of given banks.

If $U$ is the chance of stability of $X,$ then $U=Y/W$

We illustrate the number of branches and the chance of stability in the following table.

Here, we fix $\alpha =0.4$ so that we can easily calculate, using Table 1, which is stable or unstable (see

Table 2. List of stable and unstable banks.

Stable Bank Name	Unstable Bank Name
ICICI	FEDERAL
AXIS	BANDHAN
BOB	CSB
INDIAN	INDUSIND
HDFC	KMB
UBI	DCB
	IDFC
	J&K
	KARNATAKA

).

Now we evaluate the chance of instability (see

Table 3. List of banks with parameters(Number of Branches, Number of Customers).

Bank Name	Number of Branches as per the Report 2022	Chance of Stability	Number of Customers (Crore) as per Report 2022	Chance of Instability
ICICI	5614	0.57	1.85	0.37
AXIS	4758	0.49	2.85	0.41
BOB	9683	1	13.2	0
INDIAN	5721	0.59	10	0.15
HDFC	6499	0.67	6.80	0.19
UBI	8700	0.89	16.1	0
FEDERAL	1282	0.13	1	0.815
BANDHAN	1190	0.12	2.77	0.72
CSB	654	0.067	0.15	0.92
INDUSIND	2320	0.23	2.5	0.65
KMB	1702	0.17	3.66	0.64
DCB	415	0.04	0.10	0.95
IDFC	641	0.066	0.73	0.89
J&K	964	0.099	1.83	0.79
KARNATAKA	922	0.095	1.1	0.84

) of the banks with the help of the number of customers (see Table 3). Now the process is given below.

Let us assume that $X$ is a bank, $Y$ is the chance of stability of $X,Z$ is the number of customers of $X,$ and $W$ is the maximum number of customers in the list of given banks.

If $U$ is the chance of instability of $X$ then $U=\left(1-Y\right)\ast \left(W-Z\right)/W$

Now we evaluate the chance of merging between a stable and non-stable bank with the help of the correlation coefficient with respect to return type data (closed to closed) on the bank share price of those banks. Now the process is given below.

Suppose $X$ is a stable bank, $Y$ is an unstable bank, $Z$ is a correlation coefficient between $X$ and $Y$ with respect to return type data (closed to closed) on the bank share price, $W$ is a chance of stability of $X,U$ is a chance of stability of $Y$.

If $T$ is a chance of merging between $X$ and $Y,$ then $T=Z\ast min\left\{U,W\right\}.$

Now we evaluate the chance of non-merging between a stable and unstable bank with the help of those banks’ net profit (see

Table 4. List of banks with parameters (net profit, rate of return).

Bank Name	Net Profit (Crore) during the Period (July to September)	Rate of Return on Eequity during the Period (July to September)
ICICI	7558	22.46
AXIS	5330	13.85
BOB	3313	36.63
INDIAN	1225	31.62
HDFC	10,605	4.99
UBI	1848	29.42
FEDERAL	703.71	26.8
BANDHAN	209.3	0.66
CSB	121	16.23
INDUSIND	1805	46.82
KMB	3608	9.08
DCB	112	36.79
IDFC	556	54.57
J&K	243.49	9.7
KARNATAKA	411.47	20.39

). Now the process is given below.

Suppose $X$ is a stable bank, $Y$ is an unstable bank, $Z$ is the largest net profit among the profits of the given banks, $R$ is an average net profit of $X$ and $Y,$ $W$ is a chance of instability of $X,$ $U$ is a chance of instability of $Y$.

If T is a chance of non-merging (see

Table 5. List of banks with correlation coefficients.

Banks Name	Correlation Coefficient with Respect to Return TYPE data (Closed to Closed) between Two Banks during the Period (July to September 2022)	Chance of Merging between Two Banks	Chance of Non-Merging between Two Banks
ICICI&FEDERAL	$0.524245$	$0.0681$	$0.4636$
ICICI & BANDHAN	$0.49593$	$0.0595$	$0.4339$
ICICI & CSB	$0.145379$	$0.0097$	$0.5837$
ICICI & INDUSIND	$0.554577$	$0.1275$	$0.3167$
ICICI & KMB	$0.597856$	$0.1016$	$0.2727$
ICICI & DCB	$0.366598$	$0.0146$	$0.6001$
ICICI & IDFC	$0.457479$	$0.0301$	$0.5335$
ICICI & (J&K)	0.515209	0.051	0.4787
ICICI & KARNATAKA	0.399523	0.0379	0.5063
AXIS & FEDERAL	0.5551	0.0721	0.5411
AXIS & BANDHAN	0.5244	0.0629	0.5040
AXIS & CSB	0.3228	0.0216	0.6717
AXIS & INDUSIND	0.5184	0.1192	0.3799
AXIS & KMB	0.5382	0.0914	0.3369
AXIS & DCB	0.3568	0.0142	0.6991
AXIS& IDFC	0.4359	0.0287	0.6252
AXIS & (J&K)	0.3686	0.0364	0.5668
AXIS & KARNATAKA	0.4149	0.0394	0.5905
BOB & FEDERAL	0.642981	0.0835	0.6054
BOB &BANDHAN	0.501459	0.0601	0.5706
BOB & CSB	0.329027	0.022	0.7573
BOB & INDUSIND	0.454136	$0.1044$	0.4416
BOB & KMB	0.400756	$0.0681$	$0.4024$
BOB & DCB	0.392867	$0.0157$	$0.7873$
BOB & IDFC	$0.520839$	$0.0343$	$0.7034$
BOB & (J&K)	$0.553853$	$0.0548$	$0.6277$
BOB & KARNATAKA	$0.518468$	$0.0492$	$0.6607$
INDIAN & FEDERAL	0.393396	$0.0511$	$0.7030$
INDIAN & BANDHAN	$0.49638$	0.0595	0.6383
INDIAN & CSB	$0.185665$	0.0124	0.8546
INDIAN & INDUSIND	$0.221698$	$0.0509$	$0.5287$
INDIAN & KMB	$0.254946$	$0.0433$	$0.4735$
INDIAN & DCB	$0.463412$	$0.0185$	$0.8773$
INDIAN & IDFC	$0.355061$	$0.0234$	$0.7970$
INDIAN & (J&K)	$0.449315$	$0.0444$	$0.7097$
INDIAN & KARNATAKA	$0.457658$	$0.0434$	$0.7441$
HDFC & FEDERAL	$0.4038$	$0.0524$	$0.3605$
HDFC & BANDHAN	$0.4644$	$0$	$0$
HDFC & CSB	$0.0588$	$0.0039$	$0.4549$
HDFC & INDUSIND	$0.4969$	$0.1142$	$0.2388$
HDFC & KMB	$0.5176$	$0$	$0$
HDFC & DCB	$0.2293$	$0.0091$	$0.4676$
HDFC & IDFC	$0.3666$	$0.0242$	$0.4119$
HDFC & (J&K)	$0.3420$	$0$	$0$
HDFC & KARNATAKA	$0.3715$	$0.0352$	$0.3908$
UBI & FEDERAL	$0.6502$	$0.0845$	$0.6563$
UBI & BANDHAN	$0.5740$	$0.0688$	$0.6121$
UBI & CSB	$0.3067$	0.0205[M1]	$0.8210$
UBI & INDUSIND	$0.4781$	$0.1099$	$0.4789$
UBI & KMB	$0.4513$	$0.0767$	$0.4395$
UBI & DCB	$0.5022$	$0.02$	$0.8485$
UBI & IDFC	$0.5131$	$0.0338$	$0.7633$
UBI & (J&K)	$0.5150$	$0$.0509	$0.6826$
UBI &KARNATAKA	$0.5435$	$0.0516$	$0.7143$

) between $X$ and $Y,$ then $T=max\left\{U,W\right\}\ast \left(Z-R\right)/Z$.

If the rate of return (see Table 4) of $X$ and $Y$ is $\mathrm{less}\mathrm{than}$β, then there will be no connection between them.

The net profit and rate of return of the banks in given below.

For a smooth calculation, we fixed $\beta =10$.

So, we can easily see (Table 4) that the rate of return of the banks, such as HDFC, BANDHAN, KMB, and J & K are less than 10. However, we know HDFC is stable, and the others three are unstable.

So, there will be no connection between HDFC and the others three banks.

By using the chance of stability (Table 3), the chance of instability (Table 3), net profit (Table 4), and correlation coefficient (see Table 5), with respect to return type data (closed to closed) on the bank share price between two banks, we construct a new table regarding the chance of merging and the chance of non-merging between the two banks.

An intuitionistic fuzzy graph is drawn (see Figure 5) from Table 3 and Table 5. Here, banks are considered as vertices. The chance of merging between two banks is taken as the edge membership value, and the edge non-membership value is represented by the chance of non-merging between two banks. Vertex’s membership and non-membership values are represented by the bank’s chance of stability and instability.

Using Algorithm 1, we get the first component of the strength of connectedness of the IFG (see Figure 5) in the form of an adjacency matrix (see

Table 6. Adjacency matrix of the strength of connectedness (1st component).

	ICICI	AXIS	BOB	INDIAN	HDFC	UBI	FEDERAL	BANDHAN	CSB	INDUSIND	KMB	DCB	IDFC	J&K	KARNATAKA
ICICI	0	0.1192	0.1044	0.0595	0.1142	0.1099	0.0845	0.0688	0.022	0.1275	0.1016	0.02	0.0343	0.0548	0.0516
AXIS	0.1192	0	0.1044	0.0595	0.1142	0.1099	0.0845	0.0688	0.022	0.1192	0.1016	0.02	0.0343	0.0548	0.0516
BOB	0.1044	0.1044	0	0.0595	0.1044	0.1044	0.0845	0.0688	0.022	0.1044	0.1016	0.02	0.0343	0.0548	0.0516
INDIAN	0.0595	0.0595	0.0595	0	0.0595	0.0595	0.0595	0.0595	0.022	0.0595	0.0595	0.02	0.0343	0.0548	0.0516
HDFC	0.1142	0.1142	0.1044	0.0595	0	0.1099	0.0845	0.0688	0.022	0.1142	0.1016	0.02	0.0343	0.0548	0.0516
UBI	0.1099	0.1099	0.1044	0.0595	0.1099	0	0.0845	0.0688	0.022	0.1099	0.1016	0.02	0.0343	0.0548	0.0516
FEDERAL	0.0845	0.0845	0.0845	0.0595	0.0845	0.0845	0	0.0688	0.022	0.0845	0.0845	0.02	0.0343	0.0548	0.0516
BANDHAN	0.0688	0.0688	0.0688	0.0595	0.0688	0.0688	0.0688	0	0.022	0.0688	0.0688	0.02	0.0343	0.0548	0.0516
CSB	0.022	0.022	0.022	0.022	0.022	0.022	0.022	0.022	0	0.022	0.022	0.02	0.022	0.022	0.022
INDUSIND	0.1275	0.1192	0.1044	0.0595	0.1142	0.1099	0.0845	0.0688	0.022	0	0.1016	0.02	0.0343	0.0548	0.0516
KMB	0.1016	0.1016	0.1016	0.0595	0.1016	0.1016	0.0845	0.0688	0.022	0.1016	0	0.02	0.0343	0.0548	0.0516
DCB	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0	0.02	0.02	0.02
IDFC	0.0343	0.0343	0.0343	0.0343	0.0343	0.0343	0.0343	0.0343	0.022	0.0343	0.0343	0.02	0	0.0343	0.0343
J&K	0.0548	0.0548	0.0548	0.0548	0.0548	0.0548	0.0548	0.0548	0.022	0.0548	0.0548	0.02	0.0343	0	0.0516
KARNATAKA	0.0516	0.0516	0.0516	0.0516	0.0516	0.0516	0.0516	0.0516	0.022	0.0516	0.0516	0.02	0.0343	0.0516	0

).

Similarly, we get the last component of the strength of connectedness in the form of an adjacency matrix using Algorithm 2 (see

Table 7. Adjacency matrix of the strength of connectedness (last component).

	ICICI	AXIS	BOB	INDIAN	HDFC	UBI	FEDERAL	BANDHAN	CSB	INDUSIND	KMB	DCB	IDFC	J&K	KARNATAKA
ICICI	0	0.3369	0.4024	0.4735	0.3167	0.4395	0.3605	0.4339	0.4549	0.3167	0.2727	0.4676	0.4119	0.4787	0.3908
AXIS	0.3369	0	0.4024	0.4735	0.3369	0.4395	0.3605	0.4339	0.4549	0.3369	0.3369	0.4676	0.4119	0.4787	0.3908
BOB	0.4024	0.4024	0	0.4735	0.4024	0.4395	0.4024	0.4339	0.4549	0.4024	0.4024	0.4676	0.4119	0.4787	0.4024
INDIAN	0.4735	0.4735	0.4735	0	0.4735	0.4735	0.4735	0.4735	0.4735	0.4735	0.4735	0.4735	0.4735	0.4787	0.4735
HDFC	0.3167	0.3369	0.4024	0.4735	0	0.4395	0.3605	0.4339	0.4549	0.2388	0.3167	0.4676	0.4119	0.4787	0.3908
UBI	0.4395	0.4395	0.4395	0.4735	0.4395	0	0.4395	0.4395	0.4549	0.4395	0.4395	0.4676	0.4395	0.4787	0.4395
FEDERAL	0.3605	0.3605	0.4024	0.4735	0.3605	0.4395	0	0.4339	0.4549	0.3605	0.3605	0.4676	0.4119	0.4787	0.3908
BANDHAN	0.4339	0.4339	0.4339	0.4735	0.4339	0.4395	0.4339	0	0.4549	0.4339	0.4339	0.4676	0.4339	0.4787	0.4339
CSB	0.4549	0.4549	0.4549	0.4735	0.4549	0.4549	0.4549	0.4549	0	0.4549	0.4549	0.4676	0.4549	0.4787	0.4549
INDUSIND	0.3167	0.3369	0.4024	0.4735	0.2388	0.4395	0.3605	0.4339	0.4549	0	0.3167	0.4676	0.4119	0.4787	0.3908
KMB	0.2727	0.3369	0.4024	0.4735	0.3167	0.4395	0.3605	0.4339	0.4549	0.3167	0	0.4676	0.4119	0.4787	0.3908
DCB	0.4676	0.4676	0.4676	0.4735	0.4676	0.4676	0.4676	0.4676	0.4676	0.4676	0.4676	0	0.4676	0.4787	0.4676
IDFC	0.4119	0.4119	0.4119	0.4735	0.4119	0.4395	0.4119	0.4339	0.4549	0.4119	0.4119	0.4676	0	0.4787	0.4119
J&K	0.4787	0.4787	0.4787	0.4787	0.4787	0.4787	0.4787	0.4787	0.4787	0.4787	0.4787	0.4787	0.4787	0	0.4787
KARNATAKA	0.3908	0.3908	0.4024	0.4735	0.3908	0.4395	0.3908	0.4339	0.4549	0.3908	0.3908	0.4676	0.4119	0.4787	0

).

Hence, using Algorithm 3, we get

$C{S}_G($ ICICIBANK $)=\left(0.07659286,0.3969\right)$

$C{S}_G($ AXISBANK $)=\left(0.076,0.4043\right)$

$C{S}_G($ BANK OF BARODA $)=\left(0.07279286,0.4269\right)$

$C{S}_G($ INDIANBANK $)=\left(0.0513,0.4738\right)$

$C{S}_G($ HDFCBANK $)=\left(0.07528571,0.3944\right)$

$C{S}_G($ UNION BANK OF INDIA $)=\left(0.07436429,0.4478\right)$

$C{S}_G($ FEDERAL BANK $)=\left(0.06446429,0.4111\right)$

$C{S}_G($ BANDHANBANK $)=\left(0.05661429,0.4442\right)$

$C{S}_G($ CSBBANK $)=\left(0.021857143,0.4588\right)$

$C{S}_G($ INDUSINDBANK $)=\left(0.07659286,0.3944\right)$

$C{S}_G($ KOTAK MAHINDRA BANK $)=\left(0.07179286,0.3969\right)$

$C{S}_G($ DCBBANK $)=\left(0.02,0.4688\right)$

$C{S}_G($ IDFCBANK $)=\left(0.0324,0.4316\right)$

$C{S}_G($ JAMMU&KASHMIR BANK $)=\left(0.04827857,0.4787\right)$

$C{S}_G($ KARNATAKA BANK $)=\left(0.04599286,0.4219\right)$

From Algorithm 4 (Step 2), conclude the list of stable banks in a way that has the largest functional value.

• HDFC BANK
• ICICI BANK
• AXIS BANK
• BANK OF BARODA
• UNION BANK OF INDIA
• INDIAN BANK

From Algorithm 4 (Step 2), conclude the list of non-stable banks in a way that has the largest functional value

• INDUSIND BANK
• KOTAK MAHINDRA BANK
• FEDERAL BANK
• KARNATAKA BANK
• BANDHAN BANK
• IDFC BANK
• JAMMU&KASHMIR BANK
• CSB BANK
• DCB BANK

From Algorithm 4 (Step 5), we get HDFC BANK will merge with INDUSIND BANK

Now delete HDFC and INDUSIND banks, then continue the same process.

Using Algorithm 1, we get the first component of the strength of connectedness in the form of an adjacency matrix (see

Table 8. Adjacency matrix of the strength of connectedness (1st component): reduced list of 13 banks.

	ICICI	AXIS	BOB	INDIAN	UBI	FEDERAL	BANDHAN	CSB	KMB	DCB	IDFC	J&K	KARNATAKA
ICICI	0	0.0914	0.0767	0.0595	0.0767	0.0767	0.0688	0.022	0.1016	0.02	0.0343	0.0548	0.0516
AXIS	0.0914	0	0.0767	0.0595	0.0767	0.0767	0.0688	0.022	0.0914	0.02	0.0343	0.0548	0.0516
BOB	0.0767	0.0767	0	0.0595	0.0835	0.0835	0.0688	0.022	0.0767	0.02	0.0343	0.0548	0.0516
INDIAN	0.0595	0.0595	0.0595	0	0.0595	0.0595	0.0595	0.022	0.0595	0.02	0.0343	0.0548	0.0516
UBI	0.0767	0.0767	0.0835	0.0595	0	0.0845	0.0688	0.022	0.0767	0.02	0.0343	0.0548	0.0516
FEDERAL	0.0767	0.0767	0.0835	0.0595	0.0845	0	0.0688	0.022	0.0767	0.02	0.0343	0.0548	0.0516
BANDHAN	0.0688	0.0688	0.0688	0.0595	0.0688	0.0688	0	0.022	0.0688	0.02	0.0343	0.0548	0.0516
CSB	0.022	0.022	0.022	0.022	0.022	0.022	0.022	0	0.022	0.02	0.022	0.022	0.022
KMB	0.1016	0.0914	0.0767	0.0595	0.0767	0.0767	0.0688	0.022	0	0.02	0.0343	0.0548	0.0516
DCB	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0	0.02	0.02	0.02
IDFC	0.0343	0.0343	0.0343	0.0343	0.0343	0.0343	0.0343	0.022	0.0343	0.02	0	0.0343	0.0343
J&K	0.0548	0.0548	0.0548	0.0548	0.0548	0.0548	0.0548	0.022	0.0548	0.02	0.0343	0	0.0516
KARNATAKA	0.0516	0.0516	0.0516	0.0516	0.0516	0.0516	0.0516	0.022	0.0516	0.02	0.0343	0.0516	0

).

Similarly, we get the last component of the strength of connectedness in the form of an adjacency matrix using Algorithm 2 (see

Table 9. Adjacency matrix of the strength of connectedness (last component) (row and column headers are same as Table 8).

	ICICI	AXIS	BOB	INDIAN	UBI	FEDERAL	BANDHAN	CSB	KMB	DCB	IDFC	J&K	KARNATAKA
ICICI	0	0.3369	0.4024	0.4735	0.4395	0.4636	0.4339	0.5837	0.2727	0.6001	0.5335	0.4787	0.5063
AXIS	0.3369	0	0.4024	0.4735	0.4395	0.4636	0.4339	0.5837	0.3369	0.6001	0.5335	0.4787	0.5063
BOB	0.4024	0.4024	0	0.4735	0.4395	0.4636	0.4339	0.5837	0.4024	0.6001	0.5335	0.4787	0.5063
INDIAN	0.4735	0.4735	0.4735	0	0.4735	0.4735	0.4735	0.5837	0.4735	0.6001	0.5335	0.4787	0.5063
UBI	0.4395	0.4395	0.4395	0.4735	0	0.4636	0.4395	0.5837	0.4395	0.6001	0.5335	0.4787	0.5063
FEDERAL	0.4636	0.4636	0.4636	0.4735	0.4636	0	0.4636	0.5837	0.4636	0.6001	0.5335	0.4787	0.5063
BANDHAN	0.4339	0.4339	0.4339	0.4735	0.4395	0.4636	0	0.5837	0.4339	0.6001	0.5335	0.4787	0.5063
CSB	0.5837	0.5837	0.5837	0.5837	0.5837	0.5837	0.5837	0	0.5837	0.6001	0.5837	0.5837	0.5837
KMB	0.2727	0.3369	0.4024	0.4735	0.4395	0.4636	0.4339	0.5837	0	0.6001	0.5335	0.4787	0.5063
DCB	0.6001	0.6001	0.6001	0.6001	0.6001	0.6001	0.6001	0.6001	0.6001	0	0.6001	0.6001	0.6001
IDFC	0.5335	0.5335	0.5335	0.5335	0.5335	0.5335	0.5335	0.5837	0.5335	0.6001	0	0.5335	0.5335
J&K	0.4787	0.4787	0.4787	0.4787	0.4787	0.4787	0.4787	0.5837	0.4787	0.6001	0.5335	0	0.5063
KARNATAKA	0.5063	0.5063	0.5063	0.5063	0.5063	0.5063	0.5063	0.5837	0.5063	0.6001	0.5335	0.5063	0

).

Using the previous way, we get ICICI BANK will merge with KOTAK MAHINDRA BANK.

Now delete ICICI and KOTAK MAHINDRA banks, then continue the same process.

Using Algorithm 1, we get the first component of the strength of connectedness in the form of an adjacency matrix (see

Table 10. Adjacency matrix of the strength of connectedness (1st component) reduced list of 11 banks.

	AXIS	BOB	INDIAN	UBI	FEDERAL	BANDHAN	CSB	DCB	IDFC	J&K	KARNATAKA
AXIS	0	0.0721	0.0595	0.0721	0.0721	0.0688	0.022	0.02	0.0343	0.0548	0.0516
BOB	0.0721	0	0.0595	0.0835	0.0835	0.0688	0.022	0.02	0.0343	0.0548	0.0516
INDIAN	0.0595	0.0595	0	0.0595	0.0595	0.0595	0.022	0.02	0.0343	0.0548	0.0516
UBI	0.0721	0.0835	0.0595	0	0.0845	0.0688	0.022	0.02	0.0343	0.0548	0.0516
FEDERAL	0.0721	0.0835	0.0595	0.0845	0	0.0688	0.022	0.02	0.0343	0.0548	0.0516
BANDHAN	0.0688	0.0688	0.0595	0.0688	0.0688	0	0.022	0.02	0.0343	0.0548	0.0516
CSB	0.022	0.022	0.022	0.022	0.022	0.022	0	0.02	0.022	0.022	0.022
DCB	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0	0.02	0.02	0.02
IDFC	0.0343	0.0343	0.0343	0.0343	0.0343	0.0343	0.022	0.02	0	0.0343	0.0343
J&K	0.0548	0.0548	0.0548	0.0548	0.0548	0.0548	0.022	0.02	0.0343	0	0.0516
KARNATAKA	0.0516	0.0516	0.0516	0.0516	0.0516	0.0516	0.022	0.02	0.0343	0.0516	0

).

Similarly, we get the last component of the strength of connectedness in the form of an adjacency matrix using Algorithm 2 (see

Table 11. Adjacency matrix of the strength of connectedness (last component): reduced list of 11 banks.

	AXIS	BOB	INDIAN	UBI	FEDERAL	BANDHAN	CSB	DCB	IDFC	J&K	KARNATAKA
AXIS	0	0.5706	0.6383	0.6121	0.5411	0.504	0.6717	0.6991	0.6252	0.5668	0.5905
BOB	0.5706	0	0.6383	0.6121	0.5706	0.5706	0.6717	0.6991	0.6252	0.5706	0.5905
INDIAN	0.6383	0.6383	0	0.6383	0.6383	0.6383	0.6717	0.6991	0.6383	0.6383	0.6383
UBI	0.6121	0.6121	0.6383	0	0.6121	0.6121	0.6717	0.6991	0.6252	0.6121	0.6121
FEDERAL	0.5411	0.5706	0.6383	0.6121	0	0.5411	0.6717	0.6991	0.6252	0.5668	0.5905
BANDHAN	0.504	0.5706	0.6383	0.6121	0.5411	0	0.6717	0.6991	0.6252	0.5668	0.5905
CSB	0.6717	0.6717	0.6717	0.6717	0.6717	0.6717	0	0.6991	0.6717	0.6717	0.6717
DCB	0.6991	0.6991	0.6991	0.6991	0.6991	0.6991	0.6991	0	0.6991	0.6991	0.6991
IDFC	0.6252	0.6252	0.6383	0.6252	0.6252	0.6252	0.6717	0.6991	0	0.6252	0.6252
J&K	0.5668	0.5706	0.6383	0.6121	0.5668	0.5668	0.6717	0.6991	0.6252	0	0.5905
KARNATAKA	0.5905	0.5905	0.6383	0.6121	0.5905	0.5905	0.6717	0.6991	0.6252	0.5905	0

).

Using the previous way, we get AXIS BANK will merge with BANDHAN BANK.

Now delete AXIS and BANDHAN banks, then continue the same process.

Using Algorithm 1, we get the first component of the strength of connectedness in the form of an adjacency matrix (see

Table 12. Adjacency matrix of the strength of connectedness (1st component): reduced list of 9 banks.

	BOB	INDIAN	UBI	FEDERAL	CSB	DCB	IDFC	J&K	KARNATAKA
BOB	0	0.0511	0.0835	0.0835	0.022	0.02	0.0343	0.0548	0.0516
INDIAN	0.0511	0	0.0511	0.0511	0.022	0.02	0.0343	0.0511	0.0511
UBI	0.0835	0.0511	0	0.0845	0.022	0.02	0.0343	0.0548	0.0516
FEDERAL	0.0835	0.0511	0.0845	0	0.022	0.02	0.0343	0.0548	0.0516
CSB	0.022	0.022	0.022	0.022	0	0.02	0.022	0.022	0.022
DCB	0.02	0.02	0.02	0.02	0.02	0	0.02	0.02	0.02
IDFC	0.0343	0.0343	0.0343	0.0343	0.022	0.02	0	0.0343	0.0343
J&K	0.0548	0.0511	0.0548	0.0548	0.022	0.02	0.0343	0	0.0516
KARNATAKA	0.0516	0.0511	0.0516	0.0516	0.022	0.02	0.0343	0.0516	0

).

Similarly, we get the last component of the strength of connectedness in the form of an adjacency matrix using Algorithm 2 (see

Table 13. Adjacency matrix of the strength of connectedness (last component): reduced list of 9 banks.

	BOB	INDIAN	UBI	FEDERAL	CSB	DCB	IDFC	J&K	KARNATAKA
BOB	0	0.703	0.6563	0.6054	0.7573	0.7873	0.7034	0.6277	0.6607
INDIAN	0.703	0	0.703	0.703	0.7573	0.7873	0.7034	0.703	0.703
UBI	0.6563	0.703	0	0.6563	0.7573	0.7873	0.7034	0.6563	0.6607
FEDERAL	0.6054	0.703	0.6563	0	0.7573	0.7873	0.7034	0.6277	0.6607
CSB	0.7573	0.7573	0.7573	0.7573	0	0.7873	0.7573	0.7573	0.7573
DCB	0.7873	0.7873	0.7873	0.7873	0.7873	0	0.7873	0.7873	0.7873
IDFC	0.7034	0.7034	0.7034	0.7034	0.7573	0.7873	0	0.7034	0.7034
J&K	0.6277	0.703	0.6563	0.6277	0.7573	0.7873	0.7034	0	0.6607
KARNATAKA	0.6607	0.703	0.6607	0.6607	0.7573	0.7873	0.7034	0.6607	0

).

Using the previous way, we get BANK OF BARODA will merge with FEDERAL BANK.

Now delete BANK OF BARODA and FEDERAL banks, then continue the same process.

Using Algorithm 1, we get the first component of the strength of connectedness in the form of an adjacency matrix (see

Table 14. Adjacency matrix of the strength of connectedness (1st component): reduced list of 7 banks.

	INDIAN	UBI	CSB	DCB	IDFC	J&K	KARNATAKA
INDIAN	0	0.0444	0.0205	0.02	0.0338	0.0444	0.0444
UBI	0.0444	0	0.0205	0.02	0.0338	0.0509	0.0516
CSB	0.0205	0.0205	0	0.02	0.0205	0.0205	0.0205
DCB	0.02	0.02	0.02	0	0.02	0.02	0.02
IDFC	0.0338	0.0338	0.0205	0.02	0	0.0338	0.0338
J&K	0.0444	0.0509	0.0205	0.02	0.0338	0	0.0509
KARNATAKA	0.0444	0.0516	0.0205	0.02	0.0338	0.0509	0

).

Similarly, we get the last component of the strength of connectedness in the form of an adjacency matrix using Algorithm 2 (see

Table 15. Adjacency matrix of the strength of connectedness (last component): reduced list of 7 banks.

	INDIAN	UBI	CSB	DCB	IDFC	J&K	KARNATAKA
INDIAN	0	0.7097	0.821	0.8485	0.7633	0.7097	0.7143
UBI	0.7097	0	0.821	0.8485	0.7633	0.6826	0.7143
CSB	0.821	0.821	0	0.8485	0.821	0.821	0.821
DCB	0.8485	0.8485	0.8485	0	0.8485	0.8485	0.8485
IDFC	0.7633	0.7633	0.821	0.8485	0	0.7633	0.7633
J&K	0.7097	0.6826	0.821	0.8485	0.7633	0	0.7143
KARNATAKA	0.7143	0.7143	0.821	0.8485	0.7633	0.7143	0

).

Using the previous way we get UNION BANK OF INDIA will merge with JAMMU&KASHMIR BANK.

Now delete UNION BANK OF INDIA and JAMMU & KASHMIR banks, then continue the same process.

Using Algorithm 1, we get the first component of the strength of connectedness in the form of an adjacency matrix (see

Table 16. Adjacency matrix of the strength of connectedness (1st component): reduced list of 5 banks.

	INDIAN	CSB	DCB	IDFC	KARNATAKA
INDIAN	0	0.0124	0.0185	0.0234	0.0434
CSB	0.0124	0	0.0124	0.0124	0.0124
DCB	0.0185	0.0124	0	0.0185	0.0185
IDFC	0.0234	0.0124	0.0185	0	0.0234
KARNATAKA	0.0434	0.0124	0.0185	0.0234	0

).

Similarly, we get the last component of the strength of connectedness in the form of an adjacency matrix using Algorithm 2 (see

Table 17. Adjacency matrix of the strength of connectedness (last component): reduced list of 5 banks.

	INDIAN	CSB	DCB	IDFC	KARNATAKA
INDIAN	0	0.8546	0.8773	0.797	0.7441
CSB	0.8546	0	0.8773	0.8546	0.8546
DCB	0.8773	0.8773	0	0.8773	0.8773
IDFC	0.797	0.8546	0.8773	0	0.797
KARNATAKA	0.7441	0.8546	0.8773	0.797	0

).

Using the previous way, we get INDIAN BANK will merge with KARNATAKA BANK.

So, finally, we get.

HDFC BANK will merge with INDUSIND BANK

ICICI BANK will merge with KOTAK MAHINDRA BANK.

AXIS BANK will merge with BANDHAN BANK.

BANK OF BARODA will merge with FEDERAL BANK.

UNION BANK OF INDIA will merge with JAMMU&KASHMIR BANK.

INDIAN BANK will merge with KARNATAKA BANK.

5. Conclusions

This study introduced a connectivity parameter known as connectivity status in an intuitionistic fuzzy graph. This division helps identify and predict the average flow through the system. A vertex’s connectivity status of an IFG serves as a gauge for the average flow via that specific vertex. This paper provided some formulas regarding the connectivity status of some vertices depending on some ordering of membership values and non-membership values. Additionally, this paper introduced an algorithm to evaluate the connectivity status of vertices and the connectivity status of the system easily. Algorithms and related real-life applications on infectious diseases and bank merging are also included in this paper. This area will influence future researchers to think about this and develop software for designing appropriate networks without hesitation. It will be easy to get a highly technical and powerful smart power grid system using the concept of connectivity status. Additionally, this study can be extended to other generalizations of IFSs to study the connectivity of graphs, such as (2,1)-fuzzy sets and $\left(m,n\right)$-fuzzy sets. These are left as future scope of the study.