Global Dynamics of a Social Hierarchy-Stratified Malaria Model: Insight from Fractional Calculus
Abstract
:1. Introduction
2. Fractional-Order Social Hierarchy-Stratified Model
- (i)
- If ∀, then is nondecreasing for each .
- (ii)
- If ∀, then is nonincreasing for each .
2.1. Basic Properties of the Fractional Model
2.1.1. Positivity and Boundedness of Solution
2.1.2. Existence and Uniqueness of Solution
2.2. Basic Reproduction Number
3. Global Asymptotic Dynamics of the Model
3.1. Global Asymptotic Stability of DFE
- (N1):
- For , is globally asymptotically stable;
- (N2):
- , , for .
3.2. Global Asymptotic Stability of EE
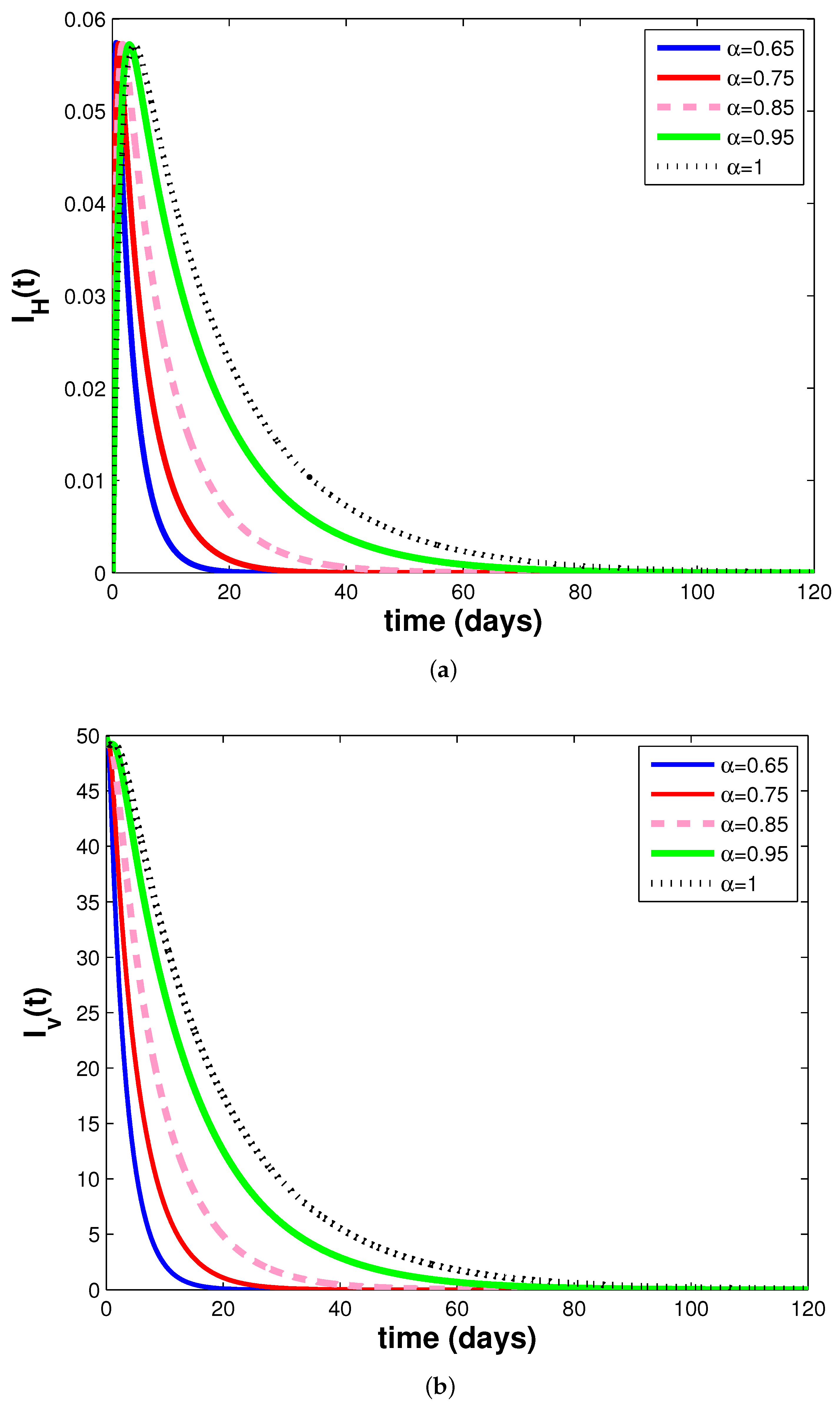
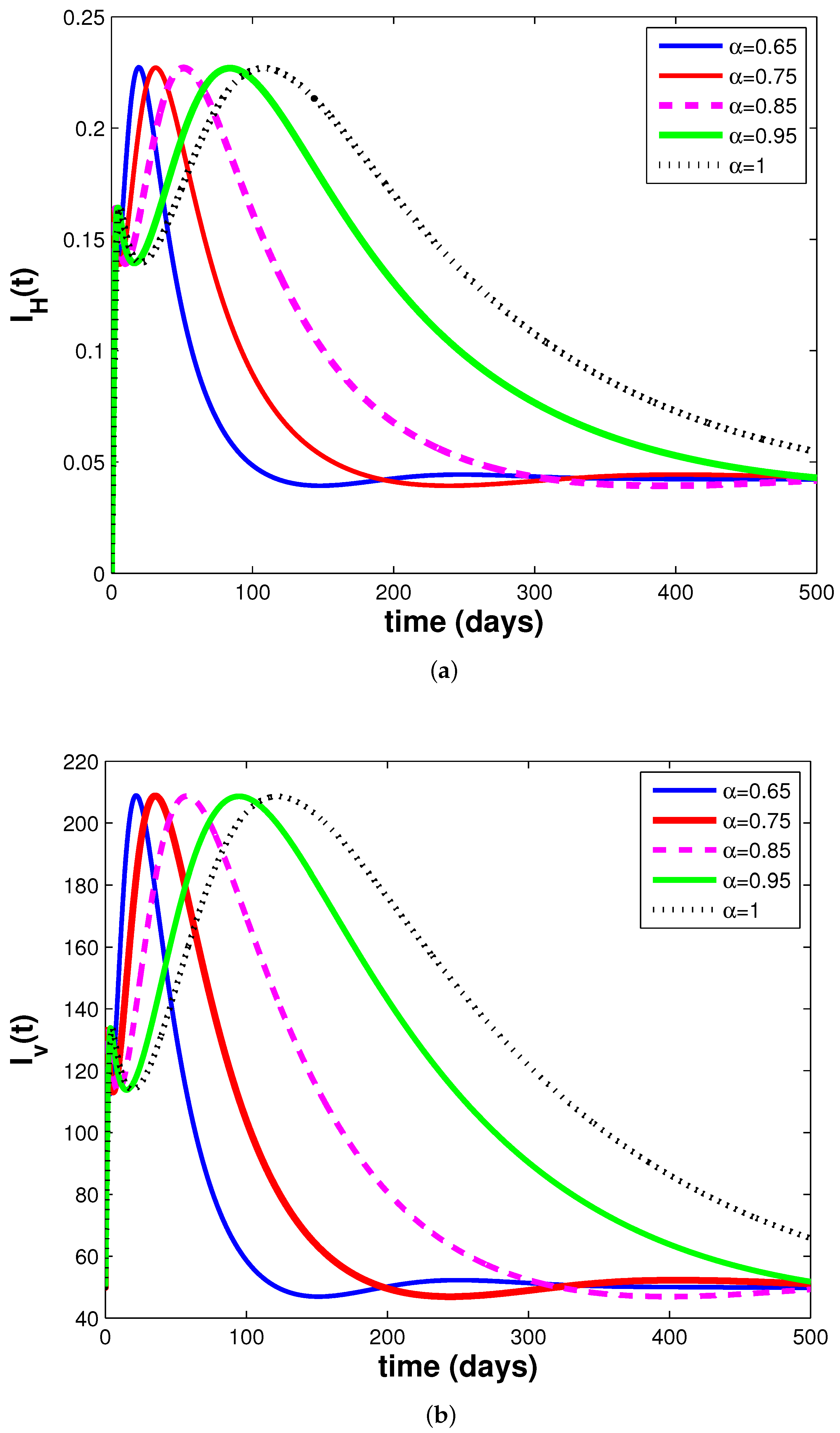
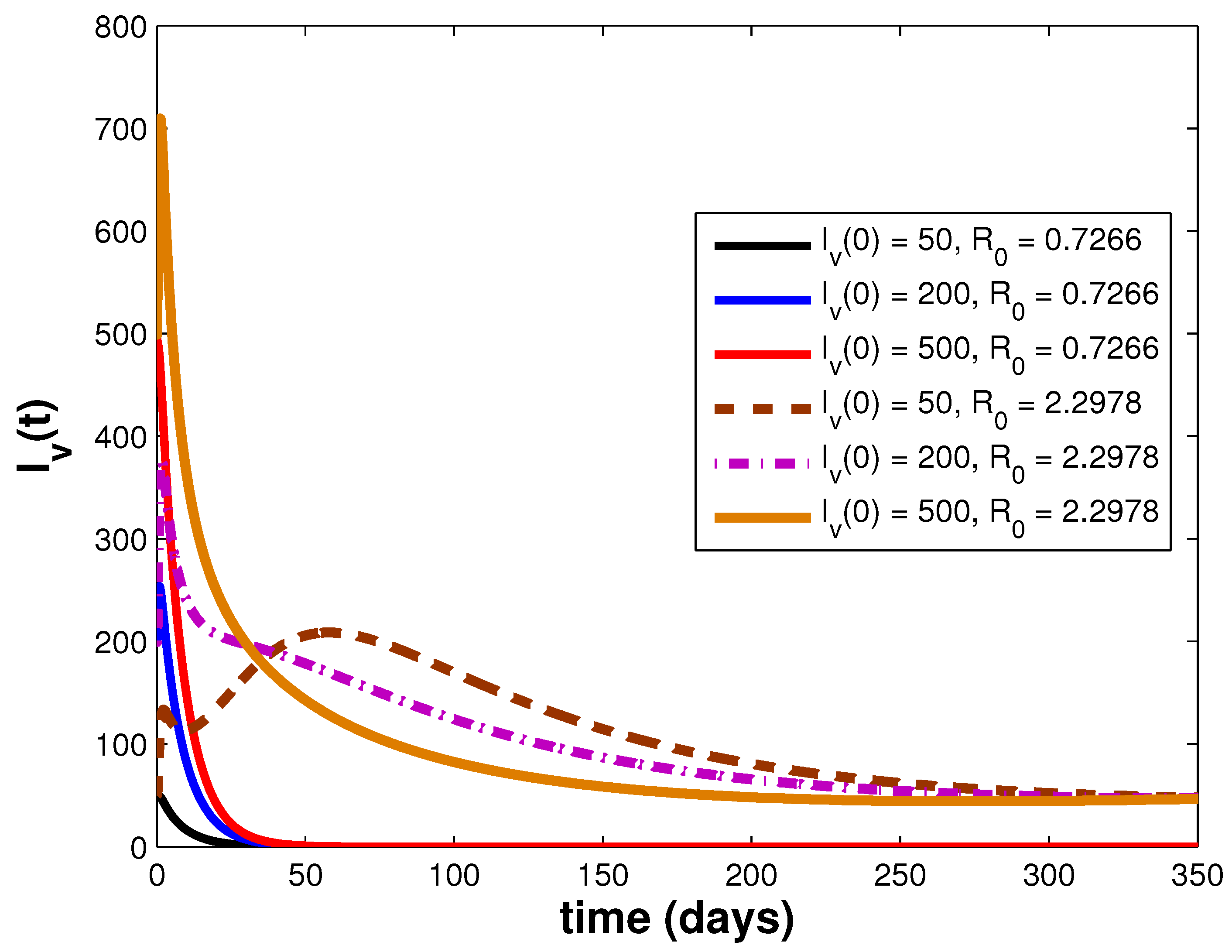
3.3. Simulations and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Johnson, N.P.; Muella, J. Updating the accounts: Global mortality of the 1918–1920 “Spanish” influenza pandemic. Bull. Hist. Med. 2002, 76, 105–115. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization (WHO). World Malaria Report; WHO: Geneva, Switzerland, 2021; Available online: https://www.who.int/teams/global-malaria-programme/ (accessed on 27 February 2024).
- Olaniyi, S.; Alade, T.O.; Chuma, F.M.; Ogunsola, A.W.; Aderele, O.R.; Abimbade, S.F. A fractional-order nonlinear model for a within-host chikungunya virus dynamics with adaptive immunity using Caputo derivative operator. Healthc. Anal. 2023, 4, 100205. [Google Scholar] [CrossRef]
- Centres for Diseases Control and Prevention (CDC). Malaria. Available online: http://www.cdc.gov/malaria/ (accessed on 27 February 2024).
- Abimbade, S.F.; Olaniyi, S.; Ajala, O.A. Recurrent malaria dynamics: Insight from mathematical modelling. Eur. Phys. J. Plus 2022, 137, 292. [Google Scholar] [CrossRef]
- Tasman, H.; Aldila, D.; Dumbela, P.A.; Ndii, M.Z.; Fatmawati; Herdicho, F.F.; Chukwu, C.W. Assessing the impact of relapse, reinfection and recrudescence on malaria eradication policy: A bifurcation and optimal control analysis. Trop. Med. Infect. Dis. 2022, 7, 263. [Google Scholar] [CrossRef] [PubMed]
- Keno, T.D.; Obsu, L.L.; Makinde, O.D. Modeling and Optimal analysis of malaria epidemic in the presence of temperature variability. Asian-Eur. J. Math. 2022, 15, 2250005. [Google Scholar] [CrossRef]
- Bakare, E.A.; Hoskova-Mayerova, S. Numerical treatment of optimal control theory applied to malaria transmission dynamic model. Qual. Quant. 2023, 57, 409–431. [Google Scholar] [CrossRef]
- Traore, B.; Barro, M.; Sangare, B.; Traore, S. A temperature-dependent mathematical model of malaria transmission with stage-structured mosquito population dynamics. Nonauton. Dyn. Syst. 2021, 8, 267–296. [Google Scholar] [CrossRef]
- Fatmawati; Herdicho, F.F.; Windarto; Chukwu, W.; Tasman, H. An optimal control of malaria transmission model with mosquito seasonal factor. Results Phys. 2021, 25, 104238. [Google Scholar] [CrossRef]
- Olaniyi, S.; Okosun, K.O.; Adesanya, S.O.; Lebelo, R.S. Modelling malaria dynamics with partial immunity and protected travellers: Optimal control and cost-effectiveness analysis. J. Biol. Dynam. 2020, 14, 90–115. [Google Scholar] [CrossRef]
- Layaka, A.M.; Abbo, B.; Haggar, D.M.S.; Youssouf, P. Optimal control analysis of intra-host dynamics of malaria with immune response. Adv. Dyn. Syst. Appl. 2021, 16, 1097–1115. [Google Scholar]
- Ndii, M.Z.; Adi, Y.A. Understanding the effects of individual awareness and vector controls on malaria transmission dynamics using multiple optimal control. Chaos Solitons Fractals 2021, 153, 111476. [Google Scholar] [CrossRef]
- Keno, T.D.; Dano, L.B.; Ganati, G.A. Optimal control and cost-effectiveness strategies of malaria transmission with impact of climate variability. J. Math. 2022, 5924549. [Google Scholar] [CrossRef]
- Ukawuba, I.; Shaman, J. Inference and dynamic simulation of malaria using a simple climate-driven entomological model of malaria transmission. PLoS Comput. Biol. 2022, 18, e1010161. [Google Scholar] [CrossRef] [PubMed]
- Mangongo, T.T.; Bukweli, J.K.; Kampempe, J.D.B.; Mabela, R.M.; Munganga, J.M.W. Stability and global sensitivity analysis of the transmission dynamics of malaria with relapse and ignorant infected humans. Phys. Scr. 2022, 97, 024002. [Google Scholar] [CrossRef]
- Olaniyi, S.; Falowo, O.D.; Okosun, K.O.; Mukamuri, M.; Obabiyi, O.S. Effect of saturated treatment on malaria spread with optimal intervention. Alex. Eng. J. 2023, 6, 443–459. [Google Scholar] [CrossRef]
- Kuddus, M.A.; Rahman, A. Modelling and analysis of human-mosquito malaria transmission dynamics in Bangladesh. Math. Comput. Simul. 2022, 193, 123–138. [Google Scholar] [CrossRef]
- Anwar, M.N.; Smith, L.; Devine, A.; Mehra, S.; Walker, C.R.; Ivory, E.; Conway, E.; Mueller, I.; McCaw, J.M.; Flegg, J.A.; et al. Mathematical models of Plasmodium vivax transmission: A scoping review. PLoS Comput. Biol. 2024, 20, e1011931. [Google Scholar] [CrossRef]
- Olaniyi, S.; Ajala, O.A.; Abimbade, S.F. Optimal control analysis of a mathematical model for recurrent malaria dynamics. Oper. Res. Forum. 2023, 4, 14. [Google Scholar] [CrossRef]
- Olaniyi, S.; Abimbade, S.F.; Ajala, O.A.; Chuma, F.M. Efficiency and economic analysis of intervention strategies for recurrent malaria transmission. Qual. Quanty 2024, 58, 627–645. [Google Scholar] [CrossRef]
- Olaniyi, S.; Mukamuri, M.; Okosun, K.O.; Adepoju, O.A. Mathematical analysis of a social hierarchy-structured model for malaria transmission dynamics. Results Phys. 2022, 34, 104991. [Google Scholar] [CrossRef]
- Vellappandi, M.; Kumar, P.; Govindaraj, V. Role of fractional derivatives in the mathematical modeling of the transmission of Chlamydia in the United States from 1989 to 2019. Nonlinear Dyn. 2023, 111, 4915–4929. [Google Scholar] [CrossRef] [PubMed]
- Nisar, K.S.; Farman, M.; Abdel-Aty, M.; Cao, J. A review on epidemic models in sight of fractional calculus. Alex. Eng. J. 2023, 75, 81–113. [Google Scholar] [CrossRef]
- Bonyah, E. A malaria status model: The perspective of Mittag-Leffler function with stochastic component. Commun. Biomath. Sci. 2022, 5, 40–62. [Google Scholar] [CrossRef]
- Aldwoah, K.A.; Almalahi, M.A.; Abdulwasaa, M.A.; Shah, K.; Kawale, S.V.; Awadalla, M.; Alahmadi, J. Mathematical analysis and numerical simulations of the piecewise dynamics model of malaria transmission: A case study in Yemen. AIMS Math. 2024, 9, 4376–4408. [Google Scholar] [CrossRef]
- Diethelm, K.; Garrapa, R.; Giusti, A.; Stynes, M. Why fractional derivatives with nonsingular kernels should not be used. Fract. Calc. Appl. Anal. 2020, 23, 610–634. [Google Scholar] [CrossRef]
- Atangana, A.; Qureshi, S. Mathematical modeling of an autonomous nonlinear dynamical system for malaria transmission using Caputo derivative. In Fractional Order Analysis: Theory, Methods and Applications; Dutta, H., Akdemir, A.O., Atangana, A., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Boukhouima, A.; Hattaf, K.; Lotfi, E.M.; Mahrouf, M.; Torres, D.F.M.; Yousfi, N. Lyapunov functions for fractional-order systems in biology: Methods and applications. Chaos Soliton Fractals 2020, 140, 110224. [Google Scholar] [CrossRef]
- Omame, A.; Okuonghae, D.; Nwajeri, U.K.; Onyenegecha, C.P. A fractional-order multi-vaccination model for COVID-19 with non-singular kernel. Alex. Eng. J. 2022, 61, 6089–6104. [Google Scholar] [CrossRef]
- Paul, A.K.; Basak, N.; Kuddus, M.A. A mathematical model for simulating the transmission dynamics of COVID-19 using the Caputo-Fabrizio fractional-order derivative with nonsingular kernel. Inf. Med. Unlocked 2023, 43, 101416. [Google Scholar] [CrossRef]
- Olaniyi, S.; Abimbade, S.F.; Chuma, F.M.; Adepoju, O.A.; Falowo, O.D. A fractional-order tuberculosis model with efficient and cost-effective optimal control interventions. Decis. Anal. J. 2023, 8, 100324. [Google Scholar] [CrossRef]
- Abidemi, A.; Owolabi, K.M. Unravelling the dynamics of Lassa Fever transmission with nosocomial infections via non-fractional and fractional mathematical models. Eur. Phys. J. Plus 2024, 139, 108. [Google Scholar] [CrossRef]
- Boukhouima, A.; Lotfi, E.M.; Mahrouf, M.; Rosa, S.; Torres, D.F.M.; Yousfi, N. Stability analysis and optimal control of a fractional HIV-AIDS epidemic model with memory and general incidence rate. Eur. Phys. J. Plus 2021, 136, 103. [Google Scholar] [CrossRef]
- Ghosh, U.; Thirthar, A.A.; Mondal, B.; Majumdar, P. Effect of fear, treatment, and hunting cooperation on an eco-epidemiological model: Memory effect in terms of fractional derivative. Iran. J. Sci. Technol. Trans. Electr. Eng. 2022, 46, 1541–1554. [Google Scholar] [CrossRef] [PubMed]
- Asamoah, J.K.K.; Addai, E.; Arthur, Y.D.; Okyere, E. A fractional mathematical model for listeriosis infection using two kernels. Decis. Anal. J. 2023, 6, 100191. [Google Scholar] [CrossRef]
- Owolabi, K.; Pindza, E. A nonlinear epidemic model for tuberculosis with Caputo operator and fixed point theory. Healthcare Anal. 2022, 2, 100111. [Google Scholar] [CrossRef]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Castillo-Chavez, C.; Blower, P.; Driessche, P.V.D.; Kirschner, W.; Yakubu, A. Mathematical Approaches for Emerging and Re-Emerging Infectious Diseases: Models, Methods and Theory; Springer: New York, NY, USA, 2002. [Google Scholar]
- Sulayman, F.; Abdullah, F.A. Dynamical behaviour of a modified tuberculosis model with impact of public health eductaion and hospital treatment. Axioms 2022, 11, 723. [Google Scholar] [CrossRef]
- Wangari, I.M.; Olaniyi, S.; Lebelo, R.S.; Okosun, K.O. Transmission of COVID-19 in the presence of single-dose and double-dose vaccines with hesitancy: Mathematical modeling ad optimal control analysis. Front. Appl. Math. Stat. 2023, 9, 1292443. [Google Scholar] [CrossRef]
- Olaniyi, S.; Kareem, G.G.; Abimbade, S.F.; Chuma, F.M.; Sangoniyi, S.O. Mathematical modelling and analysis of autonomous HIV/AIDS dynamics with vertical transmission and nonlinear treatment. Iran J. Sci. 2024, 48, 181–192. [Google Scholar] [CrossRef]
- Vargas-De-León, C. Constructions of Lyapunov functions for classic SIS, SIR and SIRS epidemic models with variable population size. Foro-Red-Mat Rev. Electr. Cont. Mat. 2009, 26. [Google Scholar]
- Goswami, N.K.; Olaniyi, S.; Abimbade, S.F.; Chuma, F.M. A mathematical model for investigating the effect of media awareness programs on the spread of COVID-19 with optimal control. Healthc. Anal. 2024, 5, 100300. [Google Scholar] [CrossRef]
- Lasalle, J.P. The Stability of Dynamical Systems; SIAM: Philadelphia, PA, USA, 1976. [Google Scholar]
- Odibat, Z.M.; Momami, S. An algorithm for the numerical solution of differential equations of fractional order. J. Appl. Math. Inform. 2008, 26, 15–27. [Google Scholar]
- Ahmed, N.; Macías-Díaz, J.E.; Raza, A.; Baleanu, D.; Rafiq, M.; Iqbal, Z.; Ahmad, M.O. Design, analysis and comparison of a nonstandard computational method for the solution of a general stochastic fractional epidemic model. Axioms 2022, 11, 10. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abimbade, S.F.; Chuma, F.M.; Sangoniyi, S.O.; Lebelo, R.S.; Okosun, K.O.; Olaniyi, S. Global Dynamics of a Social Hierarchy-Stratified Malaria Model: Insight from Fractional Calculus. Mathematics 2024, 12, 1593. https://doi.org/10.3390/math12101593
Abimbade SF, Chuma FM, Sangoniyi SO, Lebelo RS, Okosun KO, Olaniyi S. Global Dynamics of a Social Hierarchy-Stratified Malaria Model: Insight from Fractional Calculus. Mathematics. 2024; 12(10):1593. https://doi.org/10.3390/math12101593
Chicago/Turabian StyleAbimbade, Sulaimon F., Furaha M. Chuma, Sunday O. Sangoniyi, Ramoshweu S. Lebelo, Kazeem O. Okosun, and Samson Olaniyi. 2024. "Global Dynamics of a Social Hierarchy-Stratified Malaria Model: Insight from Fractional Calculus" Mathematics 12, no. 10: 1593. https://doi.org/10.3390/math12101593
APA StyleAbimbade, S. F., Chuma, F. M., Sangoniyi, S. O., Lebelo, R. S., Okosun, K. O., & Olaniyi, S. (2024). Global Dynamics of a Social Hierarchy-Stratified Malaria Model: Insight from Fractional Calculus. Mathematics, 12(10), 1593. https://doi.org/10.3390/math12101593






