Painlevé Analysis of the Traveling Wave Reduction of the Third-Order Derivative Nonlinear Schrödinger Equation
Abstract
:1. Introduction
2. Reduction to the System of Nonlinear Ordinary Differential Equations
3. Painlevé Test for the System of Ordinary Differential Equations Obtained
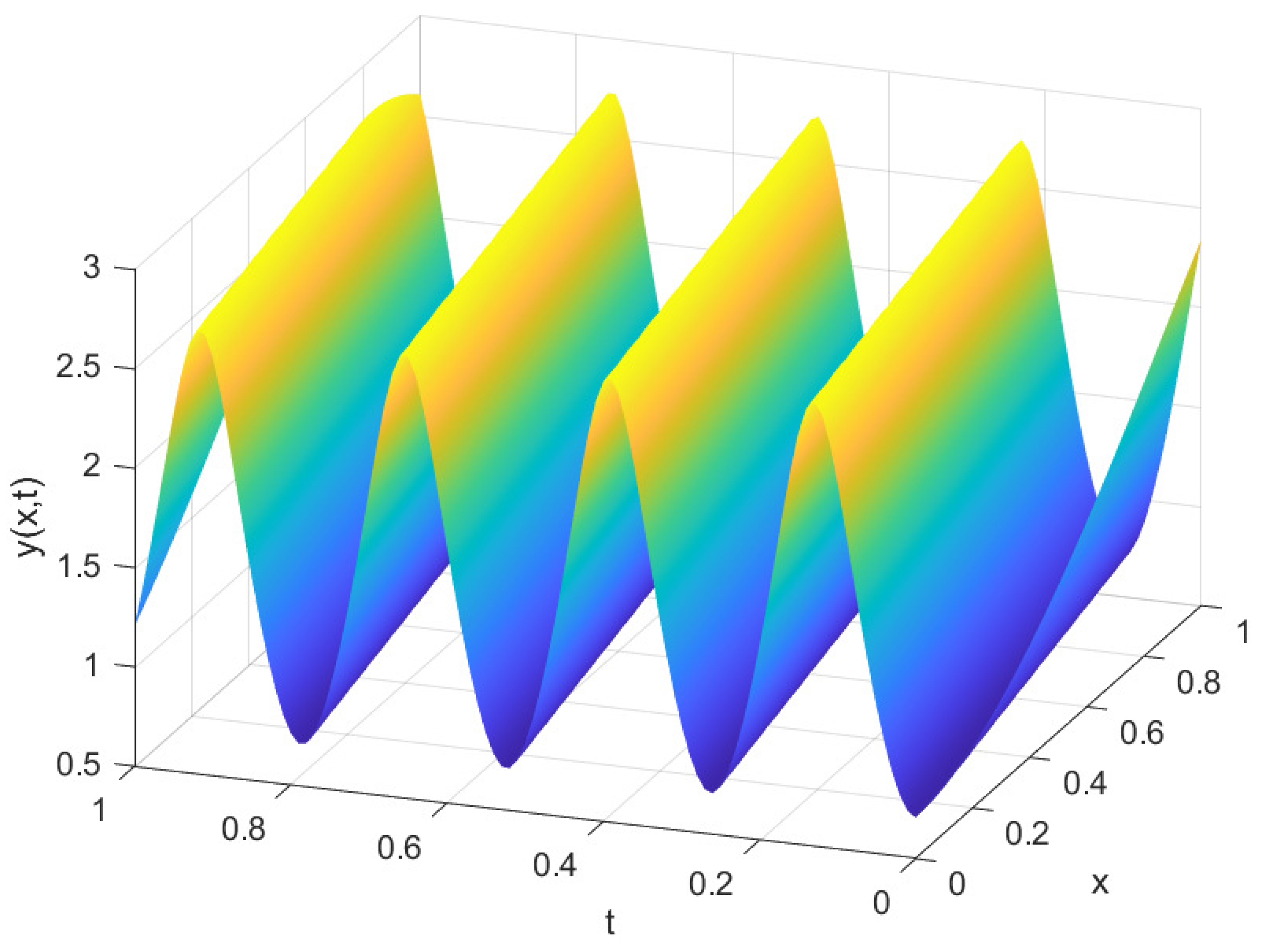
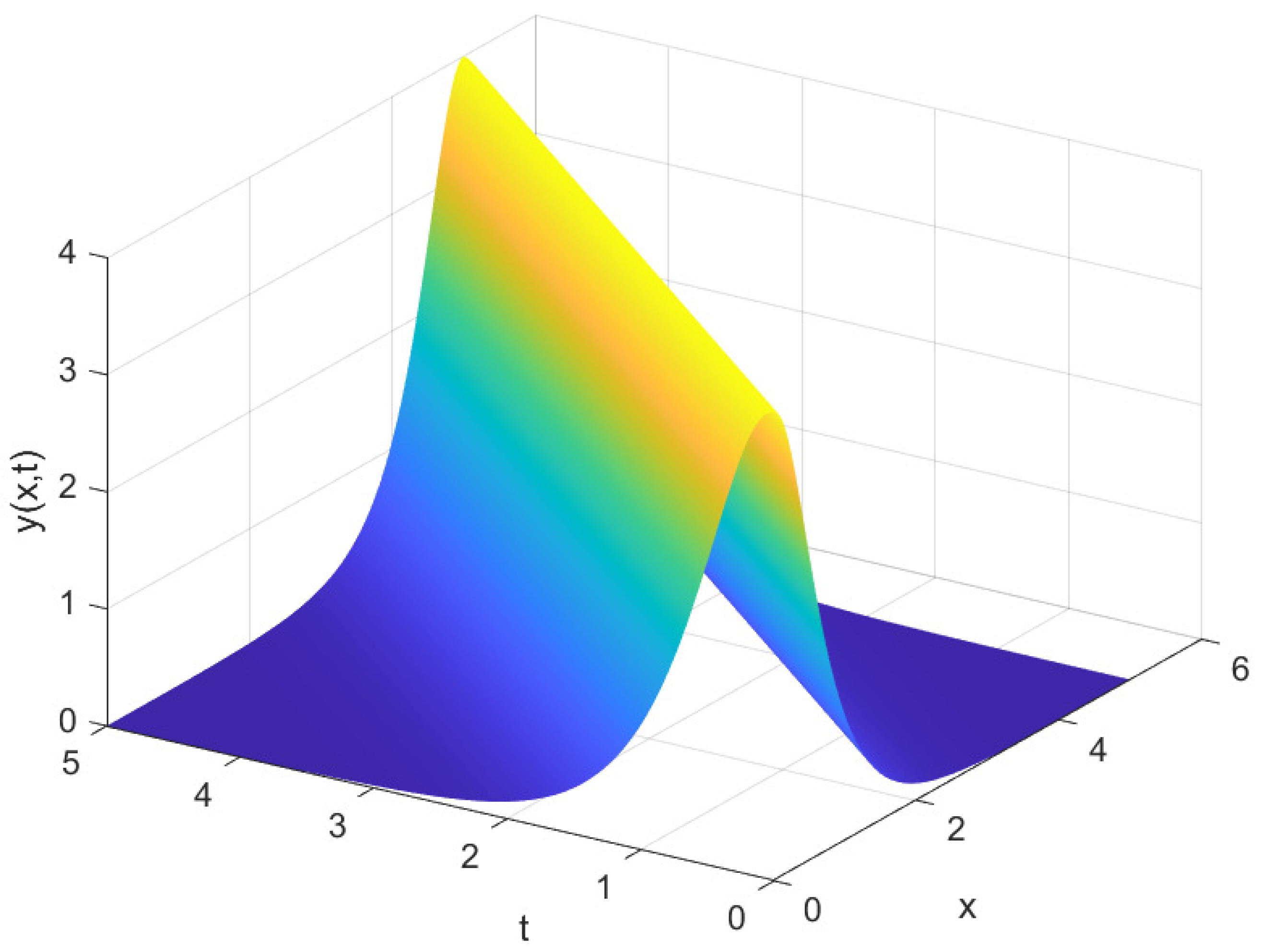
4. Periodic and Solitary Wave Solutions of the System of Ordinary Differential Equations Obtained
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jawad, A.J.A.M.; Al Azzawi, F.J.I.; Biswas, A.; Khan, S.; Zhou, Q.; Moshokoa, S.P.; Belic, M.R. Bright and singular optical solitons for Kaup–Newell equation with two fundamental integration norms. Optik 2019, 182, 594–597. [Google Scholar] [CrossRef]
- Biswas, A.; Ekici, M.; Sonmezoglu, A.; Alqahtani, R.T. Sub-pico-second chirped optical solitons in mono-mode fibers with Kaup–Newell equation by extended trial function method. Optik 2018, 168, 208–216. [Google Scholar] [CrossRef]
- Wang, K.L. Novel solitary wave and periodic solutions for the nonlinear Kaup–Newell equation in optical fibers. Opt. Quant. Electron. 2024, 56, 514. [Google Scholar] [CrossRef]
- Salas, A.H.; El-Tantawy, S.A.; Youssef, A.A.A.R. New solutions for chirped optical solitons related to Kaup-Newell equation: Application to plasma physics. Optik 2020, 218, 165203. [Google Scholar] [CrossRef]
- Yıldırım, Y.; Biswas, A.; Zhou, Q.; Alshomrani, A.S.; Belic, M.R. Sub pico-second optical pulses in birefringent fibers for Kaup–Newell equation with cutting-edge integration technologies. Results Phys. 2019, 15, 102660. [Google Scholar] [CrossRef]
- Ahmed, H.M.; Rabie, W.B.; Ragusa, M.A. Optical solitons and other solutions to Kaup–Newell equation with Jacobi elliptic function expansion method. Anal. Mat. Phys. 2021, 11, 1–16. [Google Scholar] [CrossRef]
- Zayed, E.M.; El-Horbaty, M.; Gepreel, K.A. Dispersive optical soliton solutions in birefringent fibers with stochastic Kaup–Newell equation having multiplicative white noise. Math. Method. Appl. Sci. 2024, 47, 352–370. [Google Scholar] [CrossRef]
- Kaup, D.J.; Newell, A.C. An exact solution for a derivative Schrödinger equation. J. Math. Phys. 1979, 19, 798. [Google Scholar] [CrossRef]
- Imai, K. Generalization of the Kaup-Newell inverse scattering formulation and Darboux transformation. J. Phys. Soc. Jpn. 1999, 68, 355–359. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. The inverse scattering transform-Fourier analysis for nonlinear problems. Stud. Appl. Math 1974, 53, 249–315. [Google Scholar] [CrossRef]
- Grosse, H. New solitons connected to the Dirac equation. Phys. Rep. 1986, 134, 297–304. [Google Scholar] [CrossRef]
- Solli, D.R.; Ropers, C.; Koonath, P.; Jalali, B. Optical rogue waves. Nature 2007, 450, 1054–1057. [Google Scholar] [CrossRef]
- He, J.; Wang, L.; Li, L.; Porsezian, K.; Erdélyi, R. Few-cycle optical rogue waves: Complex modified Korteweg–de Vries equation. Phys. Rev. E 2014, 89, 062917. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Chen, Y. A new form of general soliton solutions and multiple zeros solutions for a higher-order Kaup–Newell equation. J. Math. Phys. 2021, 62, 12. [Google Scholar] [CrossRef]
- Lin, H.; He, J.; Wang, L.; Mihalache, D. Several categories of exact solutions of the third-order flow equation of the Kaup–Newell system. Nonlinear Dynam. 2020, 100, 2839–2858. [Google Scholar] [CrossRef]
- Clarkson, P.A.; Cosgrove, C.M. Painleve analysis of the non-linear Schrodinger family of equations. J. Phys. A Math. Gen. 1987, 2, 2003. [Google Scholar] [CrossRef]
- Lü, X.; Peng, M. Painlevé-integrability and explicit solutions of the general two-coupled nonlinear Schrödinger system in the optical fiber communications. Nonlinear Dynam. 2013, 73, 405–410. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Safonova, D.V.; Biswas, A. Painlevé analysis and a solution to the traveling wave reduction of the Radhakrishnan—Kundu—Lakshmanan equation. Regul. Chaotic Dyn. 2019, 24, 607–614. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Safonova, D.V. Painlevé analysis and traveling wave solutions of the fourth-order differential equation for pulse with non-local nonlinearity. Optik 2021, 227, 166019. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Safonova, D.V. Nonautonomous first integrals and general solutions of the KdV-Burgers and mKdV-Burgers equations with the source. Math. Meth. Appl. Sci. 2019, 42, 4627–4636. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Painlevé analysis and exact solutions of the Korteweg–de Vries equation with a source. Appl. Math. Lett. 2015, 41, 41–45. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Ramani, A.; Segur, H. A connection between nonlinear evolution equations and ordinary differential equations of P-type. I. J. Math Phys. 1980, 21, 715–721. [Google Scholar] [CrossRef]
- Goriely, A. Integrability and Nonintegrability of Dynamical Systems; World Scientific: Singapore, 2001; Volume 19. [Google Scholar]
- Tabor, M.; Weiss, J. Analytic structure of the Lorenz system. Phys. Rev. A 1981, 24, 2157. [Google Scholar] [CrossRef]
- Rañada, A.F.; Ramani, A.; Dorizzi, B.; Grammaticos, B. The weak-Painlevé property as a criterion for the integrability of dynamical systems. J. Math. Phys. 1985, 26, 708–710. [Google Scholar] [CrossRef]
- Ramani, A.; Dorizzi, B.; Grammaticos, B. Painlevé conjecture revisited. Phys. Rev. Lett. 1982, 49, 1539–1541. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Simplest equation method to look for exact solutions of nonlinear differential equations. Chaos. Soliton. Fract. 2005, 24, 1217–1231. [Google Scholar] [CrossRef]
- Zayed, E.M.; Shohib, R.M. Optical solitons and other solutions to Biswas–Arshed equation using the extended simplest equation method. Optik 2019, 185, 626–635. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Method for finding highly dispersive optical solitons of nonlinear differential equations. Optik 2020, 206, 163550. [Google Scholar] [CrossRef]
- Rasheed, N.M.; Al-Amr, M.O.; Az-Zo’bi, E.A.; Tashtoush, M.A.; Akinyemi, L. Stable optical solitons for the Higher-order Non-Kerr NLSE via the modified simple equation method. Mathematics 2021, 9, 1986. [Google Scholar] [CrossRef]
- Jawad, A.J.A.M.; Petković, M.D.; Biswas, A. Modified simple equation method for nonlinear evolution equations. Appl. Math. Comput. 2010, 217, 869–877. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kudryashov, N.A.; Lavrova, S.F. Painlevé Analysis of the Traveling Wave Reduction of the Third-Order Derivative Nonlinear Schrödinger Equation. Mathematics 2024, 12, 1632. https://doi.org/10.3390/math12111632
Kudryashov NA, Lavrova SF. Painlevé Analysis of the Traveling Wave Reduction of the Third-Order Derivative Nonlinear Schrödinger Equation. Mathematics. 2024; 12(11):1632. https://doi.org/10.3390/math12111632
Chicago/Turabian StyleKudryashov, Nikolay A., and Sofia F. Lavrova. 2024. "Painlevé Analysis of the Traveling Wave Reduction of the Third-Order Derivative Nonlinear Schrödinger Equation" Mathematics 12, no. 11: 1632. https://doi.org/10.3390/math12111632




