Kelly Criterion Extension: Advanced Gambling Strategy
Abstract
1. Introduction
2. Kelly Criterion Basics
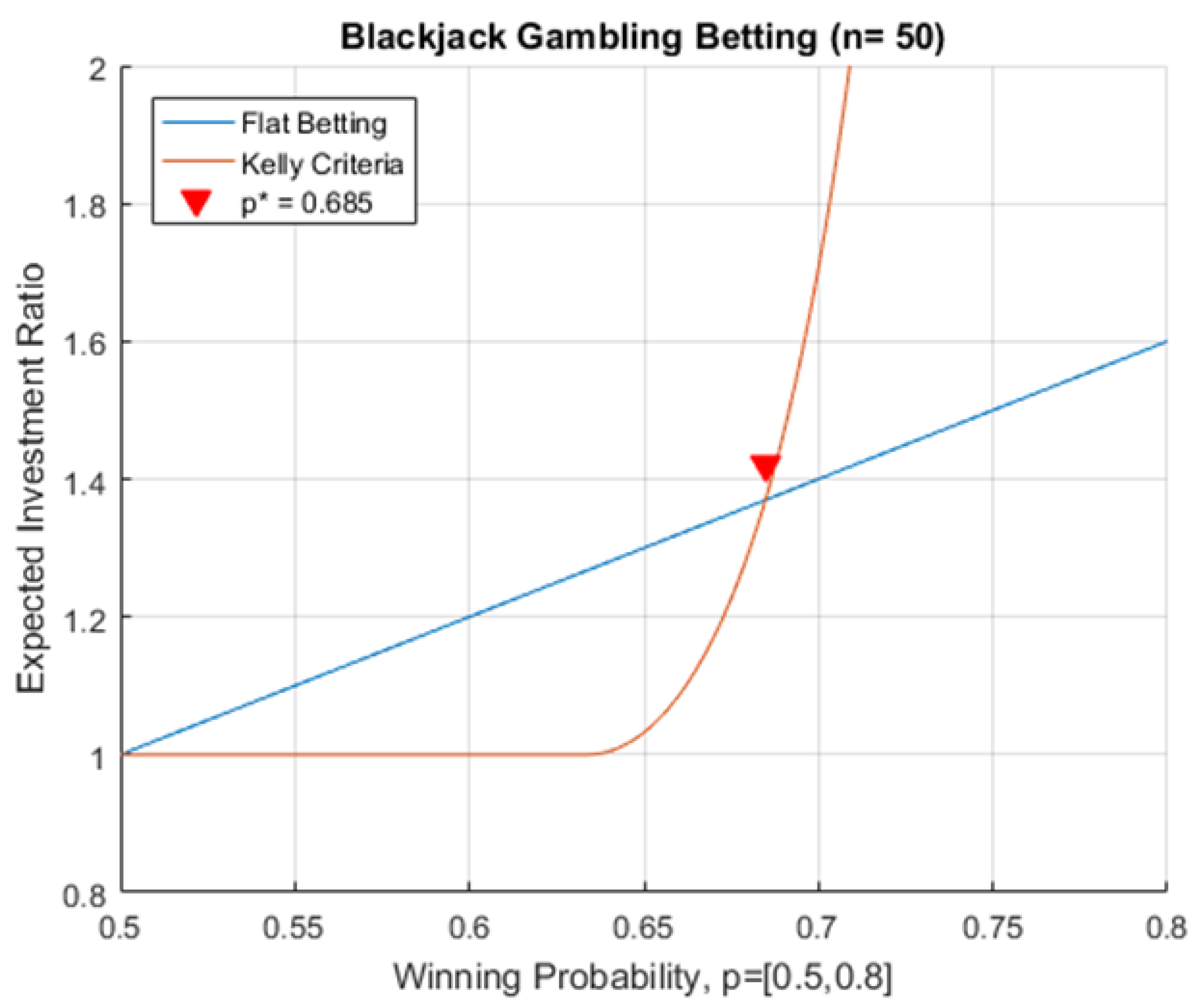
2.1. Optimizing Blackjack Betting
2.2. Optimizing Winning Reward Rate
3. Kelly Criterion Extension
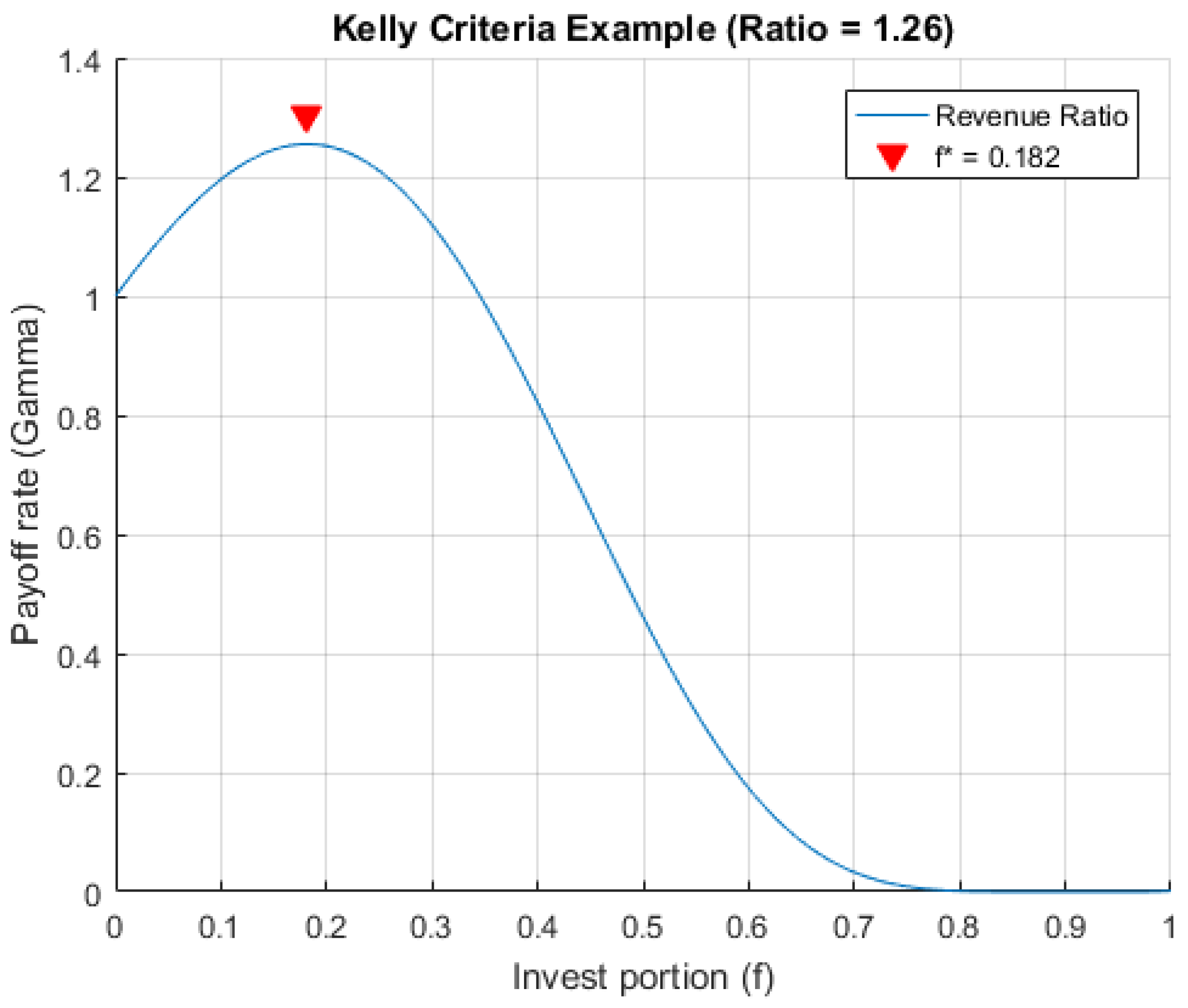
Gambling the Mutual Fund Investment
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kelly, J.L. A New Interpretation of Information Rate. Bell Syst. Tech. J. 1956, 35, 917–926. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Nekrasov, V. Kelly Criterion for Multivariate Portfolios: A Model-Free Approach. 2014. Available online: https://ssrn.com/abstract=2259133 (accessed on 16 November 2023).
- Bellman, R.; Kalaba, R. On the role of dynamic programming in statistical communication theory. IRE Trans. Inf. Theory 1957, 3, 197–203. [Google Scholar] [CrossRef]
- Mossin, J. Optimal multiperiod portfolio policies. J. Bus. 1968, 41, 215–229. [Google Scholar] [CrossRef]
- Cover, T.M. An algorithm for maximizing expected log investment return. IEEE Trans. Inf. Theory 1984, 30, 369–373. [Google Scholar] [CrossRef]
- Browne, S. Risk-constrained dynamic active portfolio management. Manag. Sci. 2000, 46, 1188–1199. [Google Scholar] [CrossRef]
- Wu, M.E.; Hung, P.J. A Framework of Option Buy-Side Strategy with Simple Index Futures Trading Based on Kelly Criterion. In Proceedings of the 2018 5th International Conference on Behavioral, Economic, and Socio-Cultural Computing (BESC), Kaohsiung, Taiwan, 12–14 November 2018; pp. 210–212. [Google Scholar]
- Wu, M.E.; Wang, C.H.; Chung, W.H.; Tso, R.; Yang, I.H. An Empirical Comparison between Kelly Criterion and Vince’s Optimal F. In Proceedings of the 2015 IEEE International Conference on Smart City/SocialCom/SustainCom (SmartCity), Chengdu, China, 19–21 December 2015; pp. 806–810. [Google Scholar]
- Park, C.H.; Irwin, S.H. What do we know about the profitability of techincal analysis? J. Econ. Surv. 2007, 21, 786–826. [Google Scholar] [CrossRef]
- Basu, S. Investment Performance of Common Stocks in Relation To Their Price-earnings Ratios: A Test of The Efficeint Market Hypothesis. J. Financ. 1977, 32, 663–682. [Google Scholar]
- Thorp, E.O. Chaper 9—The kelly criterion in blackjack sports betting, and the stock market. In Handbook of Asset and Liability Management; Zenios, S., Ziemba, W., Eds.; North-Holland: San Diego, CA, USA, 2008; pp. 385–428. [Google Scholar]
- Hsieh, C.H.; Barmish, B.R. On Kelly Betting: Some Limitations. arXiv 2017, arXiv:1710.01787. [Google Scholar]
- Hsieh, C.H.; Barmish, B.R.; Gubner, J.A. Kelly betting can be too conservative. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 3695–3701. [Google Scholar]
- Hsieh, C.H.; Barmish, B.R. On Drawdown-Modulated Feedback Control in Stock Trading. IFAC-PapersOnLine 2017, 50, 952–958. [Google Scholar] [CrossRef]
- Vince, R. The Leverage Space Trading Model: Reconciling Portfolio Management Strategies and Economic Theory, 1st ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Ansari, V.A.; Khan, S. Momentum anomaly: Evidence from India. Manag. Financ. 2012, 38, 206–223. [Google Scholar] [CrossRef]
- Brown, B.M. Martingale Central Limit Theorems. Ann. Math. Stat. 1971, 42, 59–66. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley and Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Thorp, E.O. Optimal Gambling Systems for Favorable Games. Rev. Int. Stat. Inst. 1969, 37, 273–293. [Google Scholar] [CrossRef]
- Peter Smoczynski, D.T. An Explicit Solution of the Problem of Optimizing the Allocations of a Bettor’s Wealth when Wagering on Horse Races. Math. Sci. 2010, 35, 10–17. [Google Scholar]
- Weide, J.; Peterson, D.W.; Maier, S.F. A Strategy Which Maximizes the Geometric Mean Return on Portfolio Investments. Manag. Sci. 2010, 23, 1117–1123. [Google Scholar] [CrossRef]
- Securities, U.; Commission, E. Mutual Funds and ETFs: A Guide for Investors. 2017. Available online: https://www.sec.gov/investor/pubs/sec-guide-to-mutual-funds.pdf (accessed on 16 November 2023).
- Fernando, D.; Klapper, L.F.; Sulla, V.; Vittas, D. World Bank Policy Research Working Paper; World Bank Group: Washington, DC, USA, 2003; p. 3055. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-K. Kelly Criterion Extension: Advanced Gambling Strategy. Mathematics 2024, 12, 1725. https://doi.org/10.3390/math12111725
Kim S-K. Kelly Criterion Extension: Advanced Gambling Strategy. Mathematics. 2024; 12(11):1725. https://doi.org/10.3390/math12111725
Chicago/Turabian StyleKim, Song-Kyoo (Amang). 2024. "Kelly Criterion Extension: Advanced Gambling Strategy" Mathematics 12, no. 11: 1725. https://doi.org/10.3390/math12111725
APA StyleKim, S.-K. (2024). Kelly Criterion Extension: Advanced Gambling Strategy. Mathematics, 12(11), 1725. https://doi.org/10.3390/math12111725





