Mathematical Modeling and Transmission Dynamics Analysis of the African Swine Fever Virus in Benin
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Formulation
2.2. Model Fitting and Parameters Estimation
3. Results
3.1. Analytical Results
3.1.1. Basic Properties
- Non-negativity and boundedness of the solution
- Existence and uniqueness of a solution
3.1.2. Disease-Free Equilibrium, Computation of the Control and Basic Reproduction Numbers
- Disease-free equilibrium
- Computation of the Control Reproduction Number,
- Computation of the basic reproduction number,
3.1.3. Local and Global Stabilities of the Disease-Free Equilibrium
- Local stability of the disease-free equilibrium
- If , then each infected animal (pig) generates, on average, less than one new infected animal (pig) during his period of infectiousness. In this case, we can expect the disease to disappear in the community.
- If , then each infected animal (pig) generates, on average, more than one new infected animal. In this case, the disease could persist in the community.
- Global stability of the disease-free equilibrium
3.1.4. The Endemic Equilibrium Point and Its Stability
3.2. Numerical Simulations
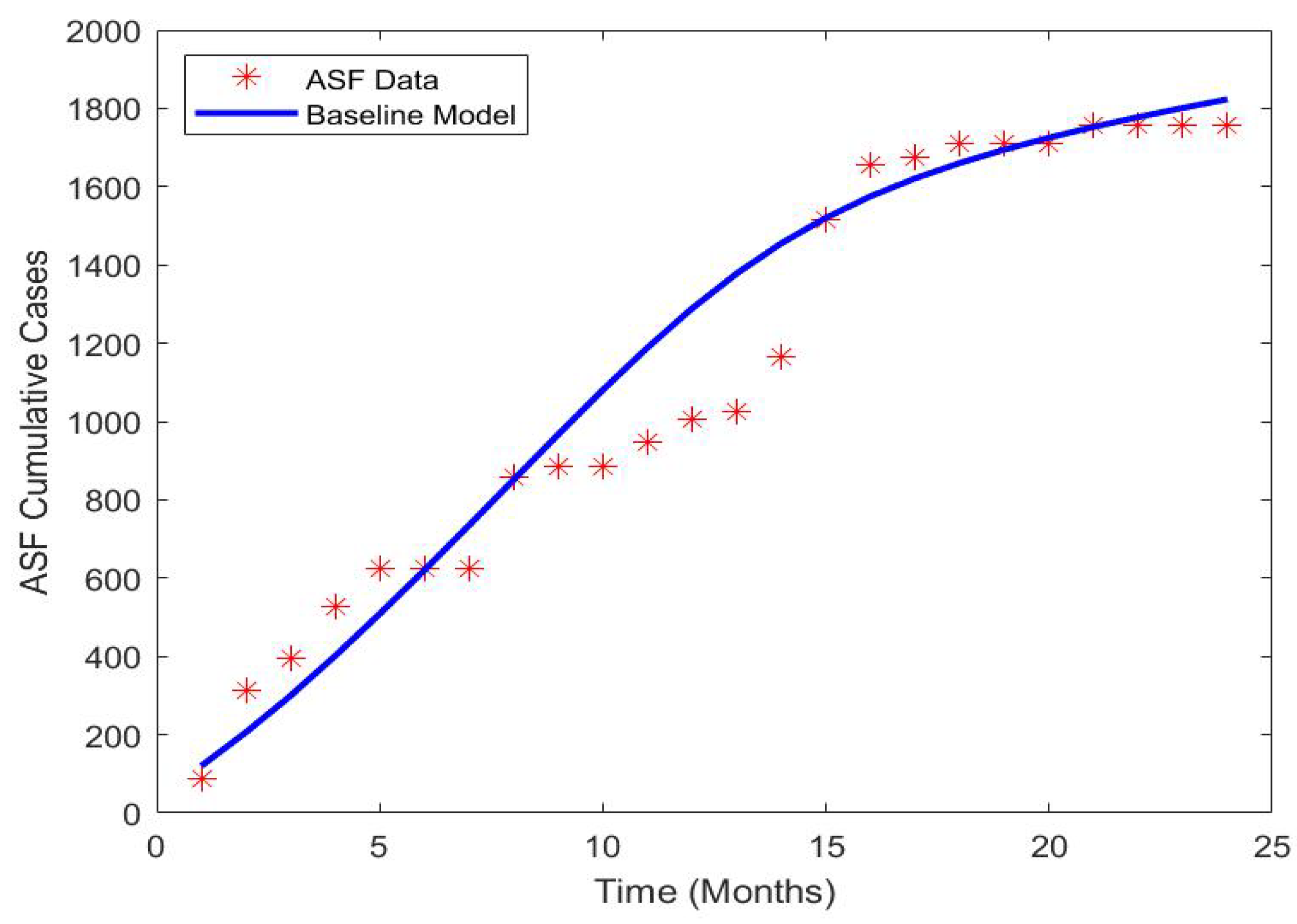
3.2.1. Model Fitting and Parameter Estimation
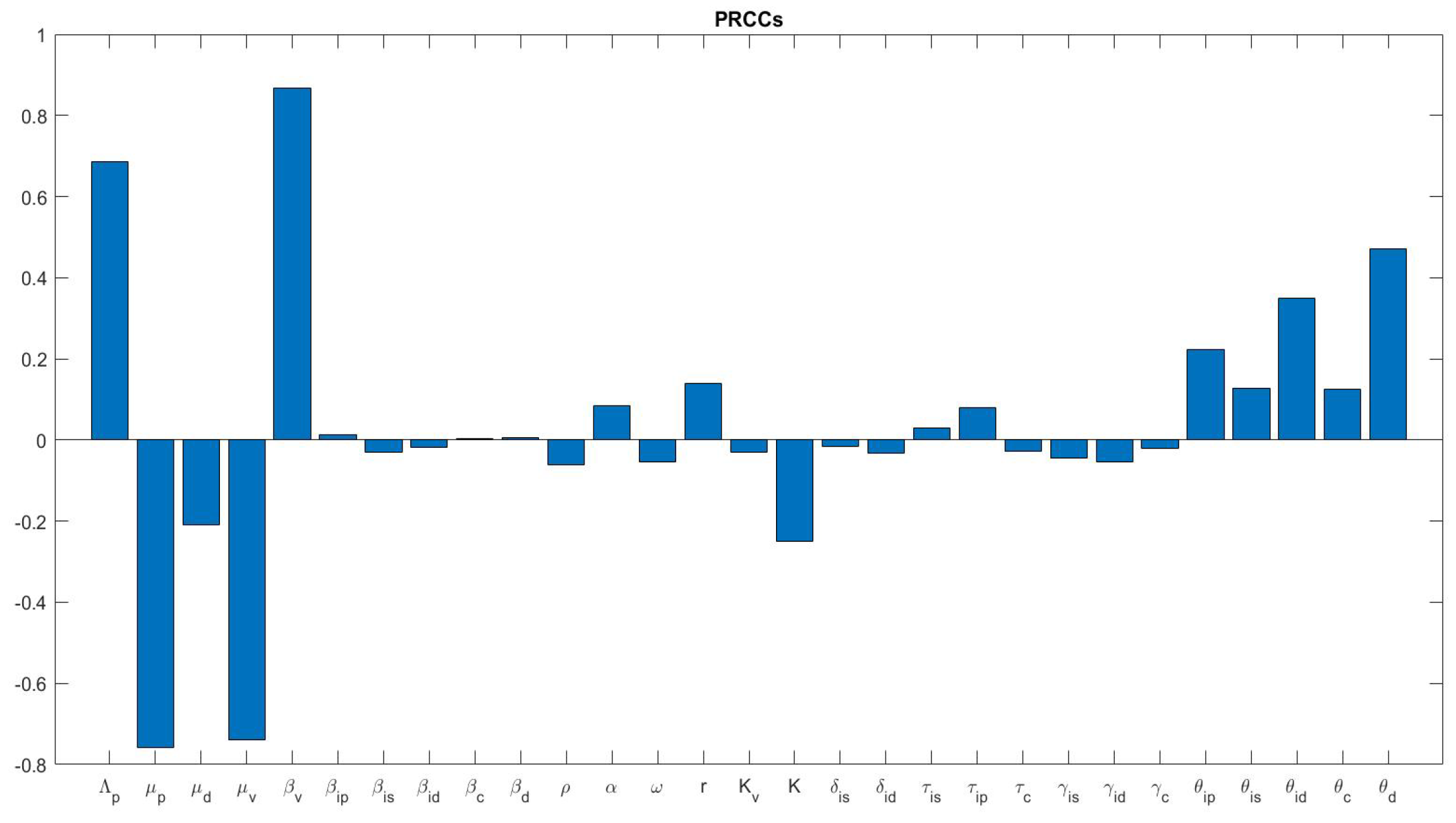
3.2.2. Global Sensitivity Analysis of
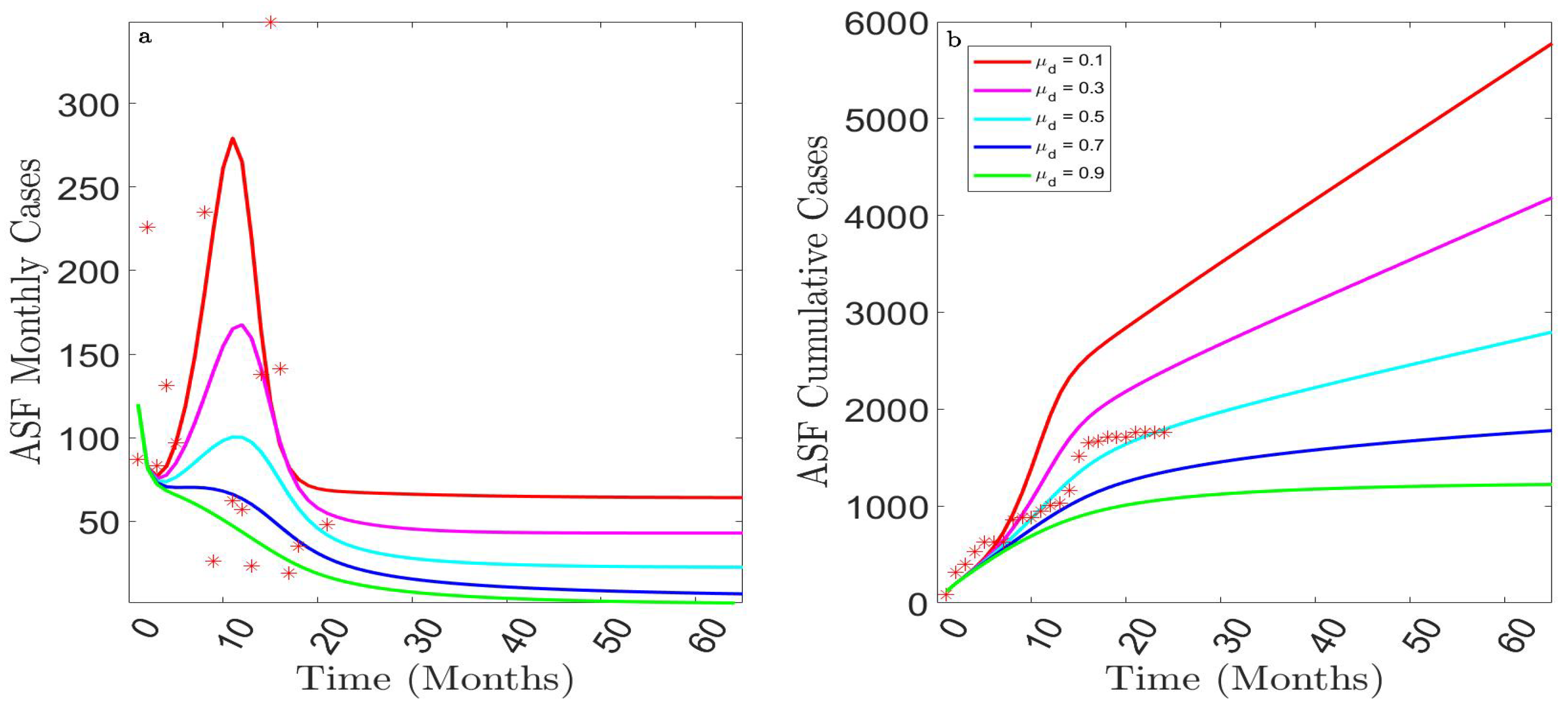
3.2.3. Assessing the Impact of the Burying or Cremation Rate of ASFV-Infected Dead Pigs,
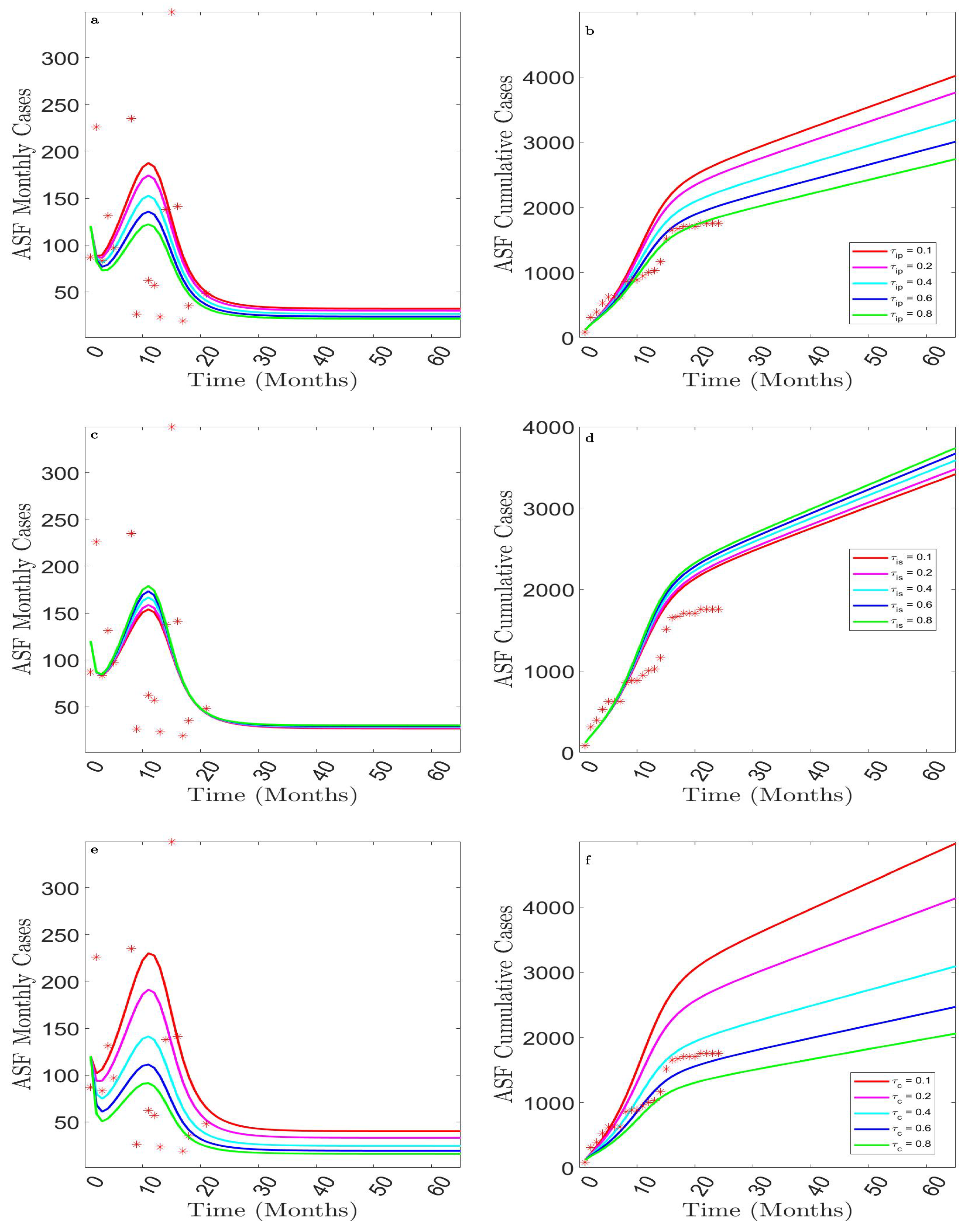
3.2.4. Assessing the Impact of Detecting Presymptomatic, Symptomatic, and Asymptomatic Cases
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Basic Reproduction Rate
- , , and
- If , then , because nothing comes out of an empty compartment.
- for because the infected are in the first m compartments.
- If , then for .
- If , then all the eigenvalues of the Jacobian matrix on point , are of the negative real part.
References
- Chenais, E.; Depner, K.; Guberti, V.; Dietze, K.; Viltrop, A.; Ståhl, K. Epidemiological considerations on African swine fever in Europe 2014–2018. Porc. Health Manag. 2019, 5, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Galindo, I.; Alonso, C. African swine fever virus: A review. Viruses 2017, 9, 103. [Google Scholar] [CrossRef] [PubMed]
- Quembo, C.J.; Jori, F.; Vosloo, W.; Heath, L. Genetic characterization of african swine fever virus isolates from soft ticks at the wildlife/domestic interface in mozambique and identification of a novel genotype. Transbound. Emerg. Dis. 2018, 65, 420–431. [Google Scholar] [CrossRef] [PubMed]
- Dixon, L.K.; Stahl, K.; Jori, F.; Vial, L.; Pfeiffer, D.U. African swine fever epidemiology and control. Annu. Rev. Anim. Biosci. 2020, 8, 221–246. [Google Scholar] [CrossRef] [PubMed]
- Jurado, C.; Mur, L.; PérezAguirreburualde, M.S.; Cadenas-Fernández, E.; Martínez-López, B.; Sánchez-Vizcaíno, J.M.; Perez, A. Risk of african swine fever virus introduction into the united states through smuggling of pork in air passenger luggage. Sci. Rep. 2019, 9, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, R.E. On a form of swine fever occurring in british east africa (kenya colony). J. Comp. Pathol. Ther. 1921, 34, 159–191. [Google Scholar] [CrossRef]
- Penrith, M.-L.; Vosloo, W.; Jori, F.; Bastos, A.D. African swine fever virus eradication in africa. Virus Res. 2013, 173, 228–246. [Google Scholar] [CrossRef] [PubMed]
- Mulumba-Mfumu, L.K.; Saegerman, C.; Dixon, L.K.; Madimba, K.C.; Kazadi, E.; Mukalakata, N.T.; Oura, C.A.; Chenais, E.; Masembe, C.; Ståhl, K.; et al. African swine fever: Update on eastern, central and southern africa. Transbound. Emerg. Dis. 2019, 66, 1462–1480. [Google Scholar] [CrossRef] [PubMed]
- Arias, M.; Jurado, C.; Gallardo, C.; Fernández-Pinero, J.; Sánchez-Vizcaíno, J. Gaps in african swine fever: Analysis and priorities. Transbound. Emerg. Dis. 2018, 65, 235–247. [Google Scholar] [CrossRef]
- Beltran-Alcrudo, D.; Falco, J.R.; Raizman, E.; Dietze, K. Transboundary spread of pig diseases: The role of international trade and travel. BMC Vet. Res. 2019, 15, 64. [Google Scholar] [CrossRef]
- Fasina, F.O.; Kissinga, H.; Mlowe, F.; Mshang’a, S.; Matogo, B.; Mrema, A.; Mhagama, A.; Makungu, S.; Mtui-Malamsha, N.; Sallu, R.; et al. Drivers, risk factors and dynamics of african swine fever outbreaks, southern highlands, tanzania. Pathogens 2020, 9, 155. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Cordón, P.; Montoya, M.; Reis, A.; Dixon, L. African swine fever: A re-emerging viral disease threatening the global pig industry. Vet. J. 2018, 233, 41–48. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Zhao, D.; Wang, J.; Zhang, Y.; Wang, M.; Gao, Y.; Li, F.; Wang, J.; Bu, Z.; Rao, Z.; et al. Architecture of african swine fever virus and implications for viral assembly. Science 2019, 526, 110798. [Google Scholar] [CrossRef] [PubMed]
- Calkins, C.M.; Scasta, J.D. Transboundary animal diseases (tads) affecting domestic and wild African ungulates: African swine fever, foot and mouth disease, rift valley fever (1996–2018). Res. Vet. Sci. 2020, 131, 69–77. [Google Scholar] [CrossRef] [PubMed]
- Arias, M.; Sánchez-Vizcaíno, J.M.; Morilla, A.; Yoon, K.; Zimmerman, J. African swine fever. In Trends in Emerging Viral Infections of Swine; Wiley: Hoboken, NJ, USA, 2002; pp. 119–124. [Google Scholar]
- Barasona, J.A.; Gallardo, C.; Cadenas-Fernández, E.; Jurado, C.; Rivera, B.; Rodríguez-Bertos, A.; Arias, M.; Sánchez-Vizcaíno, J.M. First oral vaccination of eurasian wild boar against African swine fever virus genotype ii. Front. Vet. Sci. 2019, 6, 137. [Google Scholar] [CrossRef] [PubMed]
- Morilla, A.; Yoon, K.-J.; Zimmerman, J.J. Trends in Emerging Viral Infections of Swine; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Sánchez, E.G.; Pérez-Núñez, D.; Revilla, Y. Development of vaccines against african swine fever virus. Virus Res. 2019, 265, 150–155. [Google Scholar] [CrossRef] [PubMed]
- de Carvalho Ferreira, H.; Backer, J.; Weesendorp, E.; Klinkenberg, D.; Stegeman, J.; Loeffen, W. Transmission rate of african swine fever virus under experimental conditions. Vet. Microbiol. 2013, 165, 296–304. [Google Scholar] [CrossRef] [PubMed]
- Gulenkin, V.; Korennoy, F.; Karaulov, A.; Dudnikov, S. Cartographical analysis of african swine fever outbreaks in the territory of the russian federation and computer modeling of the basic reproduction ratio. Prev. Vet. Med. 2011, 102, 167–174. [Google Scholar] [CrossRef]
- Lange, M.; Guberti, V.; Thulke, H.-H. Understanding asf spread and emergency control concepts in wild boar populations using individual-based modelling and spatio-temporal surveillance data. EFSA Support. Publ. 2018, 15, 1521E. [Google Scholar] [CrossRef]
- Loi, F.; Cappai, S.; Laddomada, A.; Feliziani, F.; Oggiano, A.; Franzoni, G.; Rolesu, S.; Guberti, V. Mathematical approach to estimating the main epidemiological parameters of african swine fever in wild boar. Vaccines 2020, 8, 521. [Google Scholar] [CrossRef]
- Pietschmann, J.; Guinat, C.; Beer, M.; Pronin, V.; Tauscher, K.; Petrov, A.; Keil, G.; Blome, S. Course and transmission characteristics of oral low-dose infection of domestic pigs and european wild boar with a caucasian african swine fever virus isolate. Arch. Virol. 2015, 160, 1657–1667. [Google Scholar] [CrossRef]
- Barongo, M.B.; Bishop, R.P.; Fèvre, E.M.; Knobel, D.L.; Ssematimba, A. A mathematical model that simulates control options for African swine fever virus (asfv). PLoS ONE 2016, 11, e0158658. [Google Scholar] [CrossRef] [PubMed]
- Gervasi, V.; Marcon, A.; Bellini, S.; Guberti, V. Evaluation of the efficiency of active and passive surveillance in the detection of african swine fever in wild boar. Vet. Sci. 2019, 7, 5. [Google Scholar] [CrossRef]
- Halasa, T.; Bøtner, A.; Mortensen, S.; Christensen, H.; Toft, N.; Boklund, A. Simulating the epidemiological and economic effects of an african swine fever epidemic in industrialized swine populations. Vet. Microbiol. 2016, 193, 7–16. [Google Scholar] [CrossRef]
- EFSA Panel on Animal Health and Welfare (AHAW); More, S.; Miranda, M.A.; Bicout, D.; Bøtner, A.; Butterworth, A.; Calistri, P.; Edwards, S.; Garin-Bastuji, B.; Good, M.; et al. African swine fever in wild boar. EFSA J. 2018, 16, e05344. [Google Scholar]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Bani-Yaghoub, M.; Gautam, R.; Shuai, Z.; Van DenDriessche, P.; Ivanek, R. Reproduction numbers for infections with free-living pathogens growing in the environment. J. Biol. Dyn. 2012, 6, 923–940. [Google Scholar] [CrossRef]
- Li, M.Y.; Graef, J.R.; Wang, L.; Karsai, J. Global dynamics of a seir model with varying total population size. Math. Biosci. 1999, 160, 191–213. [Google Scholar] [CrossRef] [PubMed]
- Kamgang, J.C.; Sallet, G. Computation of threshold conditions for epidemiological models and global stability of the disease-free equilibrium (dfe). Math. Biosci. 2008, 213, 1–12. [Google Scholar] [CrossRef]
- Lakshmikantham, V.; Leela, S.; Martynyuk, A.A. Stability Analysis of Nonlinear Systems; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Smith, H.L. Monotone Dynamical Systems: An Introduction to the Theory of Competitive and Cooperative Systems: An Introduction to the Theory of Competitive and Cooperative Systems; Number 41; American Mathematical Society: Ann Arbor, MI, USA, 2008. [Google Scholar]
- Castillo-Chavez, C.; Thieme, H. Asymptotically autonomous epidemic models. In Mathematical Population Dynamics: Analysis of Heterogeneity; Wuerz Publishing Ltd.: Winnipeg, MB, Canada, 1994. [Google Scholar]
- Castillo-Chavez, C.; Song, B. Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 2004, 1, 361. [Google Scholar] [CrossRef]
- Carr, J. Applications of Center Manifold Theory; Springer: New York, NY, USA; Heidelberg/Berlin, Germany, 1981. [Google Scholar]
- Song, H.; Li, J.; Jin, Z. Nonlinear dynamic modeling and analysis of african swine fever with culling in china. Commun. Nonlinear Sci. Numer. Simul. 2023, 117, 106915. [Google Scholar] [CrossRef]
- Zhang, X.; Rong, X.; Li, J.; Fan, M.; Wang, Y.; Sun, X.; Huang, B.; Zhu, H. Modeling the outbreak and control of african swine fever virus in large-scale pig farms. J. Theor. Biol. 2021, 526, 110798. [Google Scholar] [CrossRef] [PubMed]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [PubMed]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Blower, S.M.; Dowlatabadi, H. Sensitivity and uncertainty analysis of complex models of disease transmission: An HIV model, as an example. In International Statistical Review/Revue Internationale de Statistique; Wiley: Hoboken, NJ, USA, 1994; pp. 229–243. [Google Scholar]

| Variables | Description | Unit |
|---|---|---|
| S | Number of susceptible pigs. | Head |
| Number of presymptomatic infectious pigs. | Head | |
| Number of symptomatic infectious pigs. | Head | |
| Number of detected pigs (confirmed cases). | Head | |
| C | Number of asymptomatic infectious pigs (carrier). | Head |
| R | Number of recovered pigs. | Head |
| D | Number of dead pigs (due to ASFV). | Head |
| V | The viral load of free-living ASFV in the pig farm (environment). | Cells· |
| N | Total number of pigs (active population). . | Head |
| Parameters | Description | Unit |
|---|---|---|
| Total birth rate of pigs. | Head· | |
| Per capita death rate of pigs (natural death of pigs). | ||
| Rate at which ASFV pig carcasses are disposed of via burial or cremation (Burying or cremation rate of ASFV-infected dead pigs). | ||
| Natural decay rate of ASFV. | ||
| Transmission rate of free-living ASFV in pig farm to susceptible ones (Transmission rate from contact with fomites such as premises, vehicles, clothes, consumption of contaminated feed). | ||
| Presymptomatic period (average duration of animals (pigs) in the presymptomatic infectious class). | ||
| ASFV reactivation rate of carrier pigs (transition from carrier to symptomatic infectious class). | ||
| r | ASFV growth rate. | |
| ASFV carrying capacity. | Cell· | |
| K | ASFV concentration capacity. | Cell· |
| () | Per capita ASF-specific death rate of animals (pigs) from the symptomatic (detected) infectious class | |
| (, ) | Per capita rate at which symptomatic (presymptomatic, asymptomatic) infected pigs are detected positive to ASFV. | |
| (, ) | Recovery rate of symptomatic (detected, asymptomatic) pigs. | |
| (, , , ) | Effective transmission rate of ASFV for animals (pigs) from the presymptomatic (symptomatic, detected, asymptomatic, death) class. | |
| (, , , ) | Infection intensity (average contribution) of animals (pigs) from the presymptomatic (symptomatic, detected, asymptomatic, death) class. |
| Conditions for | Possible Positive Solutions | |||||
|---|---|---|---|---|---|---|
| < 1 | − | − | − | − | − | No solution |
| − | − | − | + | − | More than one solution | |
| − | − | + | − | − | More than one solution | |
| − | + | − | − | − | More than one solution | |
| − | − | + | + | − | More than one solution | |
| − | + | + | − | − | More than one solution | |
| − | + | − | + | − | More than one solution | |
| − | + | + | + | − | More than one solution | |
| + | − | − | − | − | One solution | |
| + | + | − | − | − | One solution | |
| + | − | + | − | − | More than one solution | |
| + | − | − | + | − | More than one solution | |
| + | + | + | − | − | One solution | |
| + | − | + | + | − | More than one solution | |
| + | + | − | + | − | More than one solution | |
| + | + | + | + | − | One solution | |
| > 1 | − | − | − | − | + | One solution |
| State Variables | S | C | R | D | V | |||
|---|---|---|---|---|---|---|---|---|
| Value | 200,000 | 200 | 30 | 50 | 120 | 50 | 50 | 500,000 |
| Parameters | Value | Source | Parameters | Value (CI) | Source |
|---|---|---|---|---|---|
| 500 | Assumed | 0.6549 | Estimated | ||
| 0.35 | Assumed | [0.4369, 0.8999] | |||
| 0.50 | Assumed | Estimated | |||
| 0.225 | Assumed | [, 0.8999] | |||
| 0.0714 | Adapted | 0.4603 | Estimated | ||
| 0.0714 | Adapted | [, 0.8988] | |||
| 0.0714 | Adapted | 0.8863 | Estimated | ||
| 0.3 | Assumed | [, 0.8999] | |||
| 0.3 | Assumed | 0.8998 | Estimated | ||
| 0.3 | Assumed | [0.0735, 0.8999] | |||
| r | 0.01 | Assumed | 0.0049 | Estimated | |
| K | 2,000,000 | Assumed | [, 0.0213] | ||
| 3,000,000 | Assumed | 0.8999 | Estimated | ||
| 0.7899 | [37] | [0.1486, 0.8999] | |||
| 0.0060 | [38] | 0.0056 | Estimated | ||
| 0.0065 | [38] | [, 0.7146] | |||
| 0.0065 | [38] | 0.8949 | Estimated | ||
| 0.0065 | [38] | [0.3774, 0.8999] | |||
| 0.0076 | [38] | 0.8999 | Estimated | ||
| [0.4687, 0.8999] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayihou, S.Y.; Doumatè, T.J.; Hameni Nkwayep, C.; Bowong Tsakou, S.; Glèlè Kakai, R. Mathematical Modeling and Transmission Dynamics Analysis of the African Swine Fever Virus in Benin. Mathematics 2024, 12, 1749. https://doi.org/10.3390/math12111749
Ayihou SY, Doumatè TJ, Hameni Nkwayep C, Bowong Tsakou S, Glèlè Kakai R. Mathematical Modeling and Transmission Dynamics Analysis of the African Swine Fever Virus in Benin. Mathematics. 2024; 12(11):1749. https://doi.org/10.3390/math12111749
Chicago/Turabian StyleAyihou, Sèna Yannick, Têlé Jonas Doumatè, Cedric Hameni Nkwayep, Samuel Bowong Tsakou, and Romain Glèlè Kakai. 2024. "Mathematical Modeling and Transmission Dynamics Analysis of the African Swine Fever Virus in Benin" Mathematics 12, no. 11: 1749. https://doi.org/10.3390/math12111749






