Three-Step Iterative Algorithm for the Extended Cayley–Yosida Inclusion Problem in 2-Uniformly Smooth Banach Spaces: Convergence and Stability Analysis
Abstract
:1. Introduction
2. Background and Problem Formulation
- (i)
- Uniformly Smooth if ;
- (ii)
- 2-uniformly smooth if there exists a positive real constant such that
- (i)
- , for all ;
- (ii)
- , where and
- (i)
- α-strongly accretive with regard to if there is a constant such that
- (ii)
- β-relaxed strongly accretive with regard to if there is a constant such that
- (iii)
- -symmetric accretive with regard to , if is α-strongly accretive, and is β-relaxed accretive with if and only if .
- (i)
- -Lipschitz continuous, where ;
- (ii)
- -strongly accretive, where .
Problem Formulation
3. Fixed-Point Equation and Three-Step Iterative Algorithm
3.1. Existence Result
3.2. Three-Step Iterative Algorithm
- (I)
- The sequence produced by Algorithm 1 converges strongly to the unique solution of problem (9).
- (II)
- Additionally, the sequence produced by Algorithm 1 is stable with respect to
| Algorithm 1 Three-Step Iterative Algorithm |
| Let , be a single-valued mapping, and be a multi-valued mapping. Let and be the generalized Cayley and Yosida approximation operators defined in (3) and (4), respectively. Then, we develop the following iterative scheme: Let be a sequence and define by where , . Here, are sequences in considered to accommodate possible computational inaccuracies. |
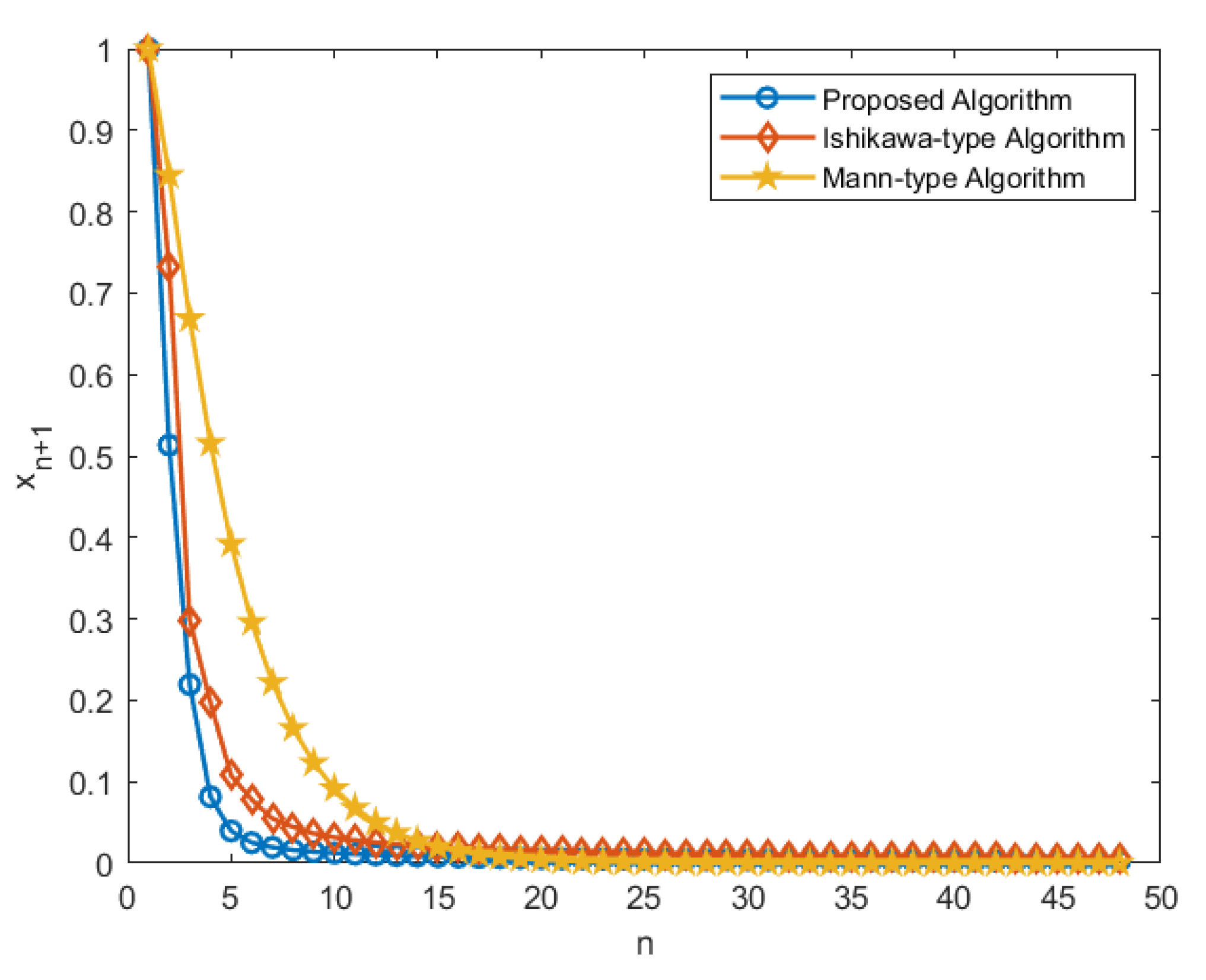
4. Numerical Example
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ansari, Q.H.; Yao, J.C. A fixed point theorem and its applications to system of variational inequalities. Bull. Aust. Math. Soc. 1999, 59, 433–442. [Google Scholar] [CrossRef]
- Pang, J.S. Asymmetric variational inequality problems over product of sets: Applications and iterative methods. Math. Program. 1985, 31, 206–219. [Google Scholar] [CrossRef]
- Yan, W.Y.; Fang, Y.P.; Huang, N.J. A new system of set-valued variational inclusions with H-monotone operators. Math. Inequal. Appl. 2005, 8, 537–546. [Google Scholar] [CrossRef]
- Abubakar, J.; Kumam, P.; Deepho, J. Multistep hybrid viscosity method for split monotone variational inclusion and fixed point problems in Hilbert spaces. AIMS Math. 2020, 5, 5969–5992. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Verma, R.U. Generalized system of (A, η)-maximal relaxed monotone variational inclusion problems based on generalized hybrid algorithms. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 238–251. [Google Scholar] [CrossRef]
- Rockafellar, R.T. On the maximality of sums ofnonlinear monotone operators. Trans. Am. Math. Soc. 1970, 149, 75–88. [Google Scholar] [CrossRef]
- Lan, H.Y.; Kim, J.H.; Cho, Y.J. On a new system of nonlinear A-monotone multivalued variational inclusions. J. Math. Anal. Appl. 2007, 327, 481–493. [Google Scholar] [CrossRef]
- De, A. Hille-Yosida Theorem and Some Applications. Ph.D. Thesis, Department of Mathematics and its Applications, Central European University, Budapest, Hungary, 2015. [Google Scholar]
- Balooee, J. Resolvent algorithms for system of generalized nonlinear variational inclusions and fxed point problems. Afr. Mat. 2014, 25, 1023–1042. [Google Scholar] [CrossRef]
- Cao, H.W. Yosida approximation equations technique for system of generalized set-valued variational inclusions. J. Inequal. Appl. 2013, 2013, 455. [Google Scholar] [CrossRef]
- Lan, H.Y. Generalized Yosida approximation based on relatively A-maximal m-relaxed monotonicity frameworks. Abs. Appl. Anal. 2013, 2013, 157190. [Google Scholar]
- Hassouni, A.; Moudafi, A. A perturbed algorithm for variational inclusions. J. Math. Anal. Appl. 1994, 183, 706–712. [Google Scholar] [CrossRef]
- Douglas, J.; Rachford, H.H. On the numerical solution of heat conduction problems in two and three space variables. Trans. Am. Math. Soc. 1956, 82, 421–439. [Google Scholar] [CrossRef]
- Peaceman, D.W.; Rachford, H.H., Jr. The numerical solution of parabolic and elliptic differential equations. J. Appl. Ind. Math. 1955, 3, 28–41. [Google Scholar] [CrossRef]
- Tseng, P. A modified forward-backward splitting method for maximal monotone mappings. SIAM J. Control Optim. 2000, 38, 431–446. [Google Scholar] [CrossRef]
- Gibali, A.; Thong, D.V. Tseng type methods for solving inclusion problems and its applications. Calcolo 2018, 55, 49. [Google Scholar] [CrossRef]
- Ahmad, I.; Rahaman, M.; Ahmad, R.; Ali, I. Convergence analysis and stability of perturbed three-step iterative algorithm for generalized mixed ordered quasi-variational inclusion involving XOR operator. Optimization 2020, 69, 821–845. [Google Scholar] [CrossRef]
- Glowinski, G.; Tallec, P.L. Augmented Lagrangian and Operator Spliting Methods in Nonlinear Mechanics; SIAM: Philadelphia, PA, USA, 1989. [Google Scholar]
- Helmberg, G. Introduction to Spectral Theory in Hilbert Space: The Cayley Transform; North-Holland Series in Applied Mathematics and Mechanics, Applied Mathematics and Mechanics #6; North-Holland Publishing Company: Amsterdam, The Netherlands, 1969. [Google Scholar]
- Fang, Y.P.; Huang, N.J. H-accretive operator and resolvent operator technique for variational inclusions in Banach spaces. Appl. Math. Lett. 2004, 17, 647–653. [Google Scholar] [CrossRef]
- Agarwal, R.P.; O’Regan, D.; Sahu, D.R. Fixed Point Theory for Lipschitzian-Type Mappings with Applications; Springer: New York, NY, USA, 2009; Volume 6. [Google Scholar]
- Xu, H.K. Inequalities in Banach spaces with applications. Nonlinear Anal. Theory Methods Appl. 1991, 16, 1127–1138. [Google Scholar] [CrossRef]
- Kazmi, K.R.; Khan, F.A.; Shahzad, M. A system of generalized variational inclusions involving generalized H(·, ·)-accretive mapping in real q-uniformly smooth Banach spaces. Appl. Math. Comput. 2011, 217, 9679–9688. [Google Scholar] [CrossRef]
- Osilike, M.O. Stability results for the Ishikawa fixed point iteration procedure. Ind. J. Pure Appl. Math. 1995, 26, 937–945. [Google Scholar]
- Weng, X.L. Fixed point iteration for local srictly pseudocontractive mapping. Proc.Am.Math.Soc. 1991, 113, 727–731. [Google Scholar] [CrossRef]
- Ahmad, R.; Ali, I.; Rahaman, M.; Ishtyak, M.; Yao, J.C. Cayley inclusion problem with its corresponding generalized resolvent equation problem in uniformly smooth Banach spaces. Appl. Anal. 2022, 101, 1354–1368. [Google Scholar] [CrossRef]
- Rajpoot, A.K.; Ishtyak, M.; Ahmad, R.; Wang, Y.; Yao, J.C. Convergence analysis for Yosida variational inclusion problem with its corresponding Yosida resolvent equation problem through inertial extrapolation scheme. Mathematics 2023, 11, 763. [Google Scholar] [CrossRef]
- Akram, M.; Dilshad, M.; Rajpoot, A.K.; Babu, F.; Ahmad, R.; Yao, J.C. Modified Iterative Schemes for a Fixed-Point Problem and a Split Variational Inclusion Problem. Mathematics 2022, 10, 2098. [Google Scholar] [CrossRef]
- Zhao, X.; Sahu, D.R.; Wen, C.F. Iterative methods for system of variational inclusions involving accretive operators and applications. Fixed Point Theory 2018, 19, 801–822. [Google Scholar] [CrossRef]
- Iqbal, J.; Ali, I.; Arora, P.K.; Mir, W.A. Set-valued variational inclusion problem with fuzzy mappings involving XOR-operation. AIMS Math. 2021, 6, 3288–3304. [Google Scholar] [CrossRef]

| No. of Iterations | For | For .
| For |
|---|---|---|---|
| n = 1 | −0.5 | 0.2 | 1 |
| n = 2 | 0.398825035 | 0.961323961 | 1.139101739 |
| n = 3 | 0.269533992 | 0.498765092 | 0.557440987 |
| n = 4 | 0.132297719 | 0.205800419 | 0.221155261 |
| n = 5 | 0.050226267 | 0.054881135 | 0.055909079 |
| n = 10 | 0.022189534 | 0.022190736 | 0.022191014 |
| n = 15 | 0.01479883 | 0.01479883 | 0.01479883 |
| n = 20 | 0.011134277 | 0.011134277 | 0.011134277 |
| n = 25 | 0.008932186 | 0.008932186 | 0.008932186 |
| n = 30 | 0.007222087 | 0.007222087 | 0.007222087 |
| n = 35 | 0.006062878 | 0.006062878 | 0.006062878 |
| n = 40 | 0.005224884 | 0.005224884 | 0.005224884 |
| n = 45 | 0.004499671 | 0.004412204 | 0.004412204 |
| n = 55 | 0.003818503 | 0.003755349 | 0.003755349 |
| n = 70 | 0.003268839 | 0.003268839 | 0.003268839 |
| No. of Iterations | Algorithm 1 | Algorithm
(32) | Algorithm (33) |
|---|---|---|---|
| n = 1 | 1 | 1 | 1 |
| n = 2 | 0.513406206 | 0.732158368 | 0.844808005 |
| n = 3 | 0.219329442 | 0.298731566 | 0.668676662 |
| n = 4 | 0.081548826 | 0.197299587 | 0.515703683 |
| n = 5 | 0.039620365 | 0.107807382 | 0.392252818 |
| n = 10 | 0.012456521 | 0.031819764 | 0.091455223 |
| n = 15 | 0.007980668 | 0.020022186 | 0.020119998 |
| n = 20 | 0.004324994 | 0.005890604 | 0.014881626 |
| n = 25 | 0.000918114 | 0.004672308 | 0.011861738 |
| n = 30 | 0.000193369 | 0.00387296 | 0.009864815 |
| n = 35 | 4.05 | 0.00844483 | 0.003307718 |
| n = 40 | 8.45 | 0.007382855 | 0.002886711 |
| n = 45 | 1.76 | 0.006558468 | 0.002560908 |
| n = 50 | 3.65 | 3.65 | 3.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, I.; Wang, Y.; Ahmad, R. Three-Step Iterative Algorithm for the Extended Cayley–Yosida Inclusion Problem in 2-Uniformly Smooth Banach Spaces: Convergence and Stability Analysis. Mathematics 2024, 12, 1977. https://doi.org/10.3390/math12131977
Ali I, Wang Y, Ahmad R. Three-Step Iterative Algorithm for the Extended Cayley–Yosida Inclusion Problem in 2-Uniformly Smooth Banach Spaces: Convergence and Stability Analysis. Mathematics. 2024; 12(13):1977. https://doi.org/10.3390/math12131977
Chicago/Turabian StyleAli, Imran, Yuanheng Wang, and Rais Ahmad. 2024. "Three-Step Iterative Algorithm for the Extended Cayley–Yosida Inclusion Problem in 2-Uniformly Smooth Banach Spaces: Convergence and Stability Analysis" Mathematics 12, no. 13: 1977. https://doi.org/10.3390/math12131977
APA StyleAli, I., Wang, Y., & Ahmad, R. (2024). Three-Step Iterative Algorithm for the Extended Cayley–Yosida Inclusion Problem in 2-Uniformly Smooth Banach Spaces: Convergence and Stability Analysis. Mathematics, 12(13), 1977. https://doi.org/10.3390/math12131977






