Robust Constrained Cooperative Control for Multiple Trains
Abstract
:1. Introduction
2. Problem Description
2.1. Graph Theory
2.2. Model
3. Main Results
3.1. Robust Constrained Cooperative Control Algorithm
3.2. Model Transformations
3.2.1. Constraint Set Transformations
3.2.2. Model Transformations
3.3. Convergence Analysis
3.4. The Effects of External Disturbances
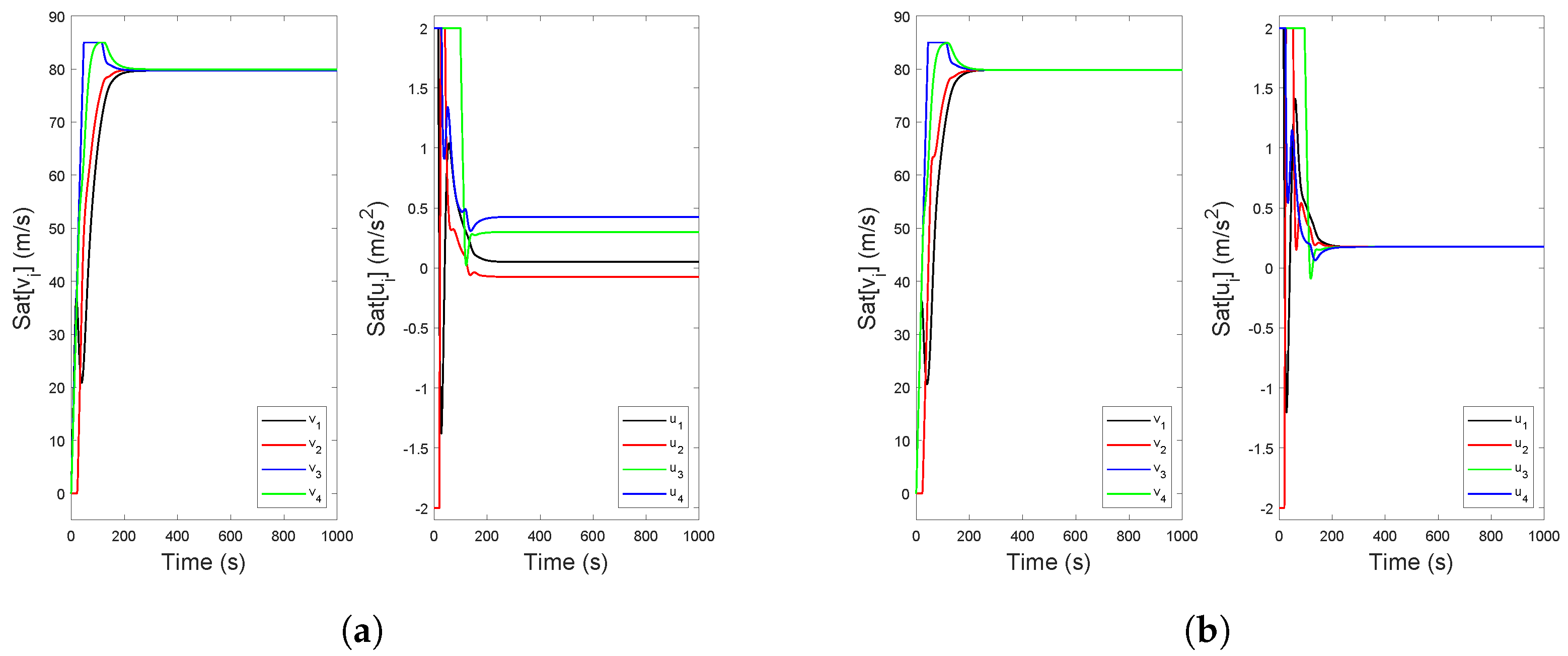
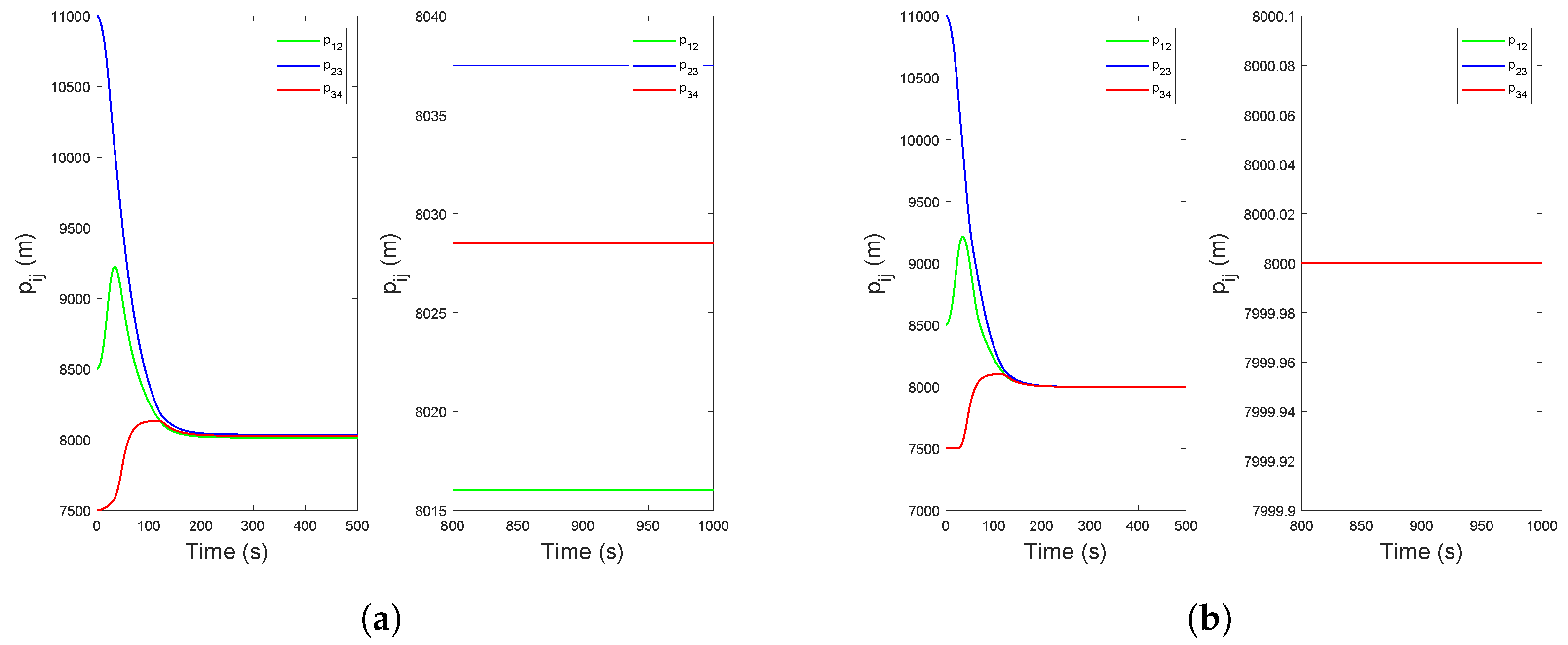
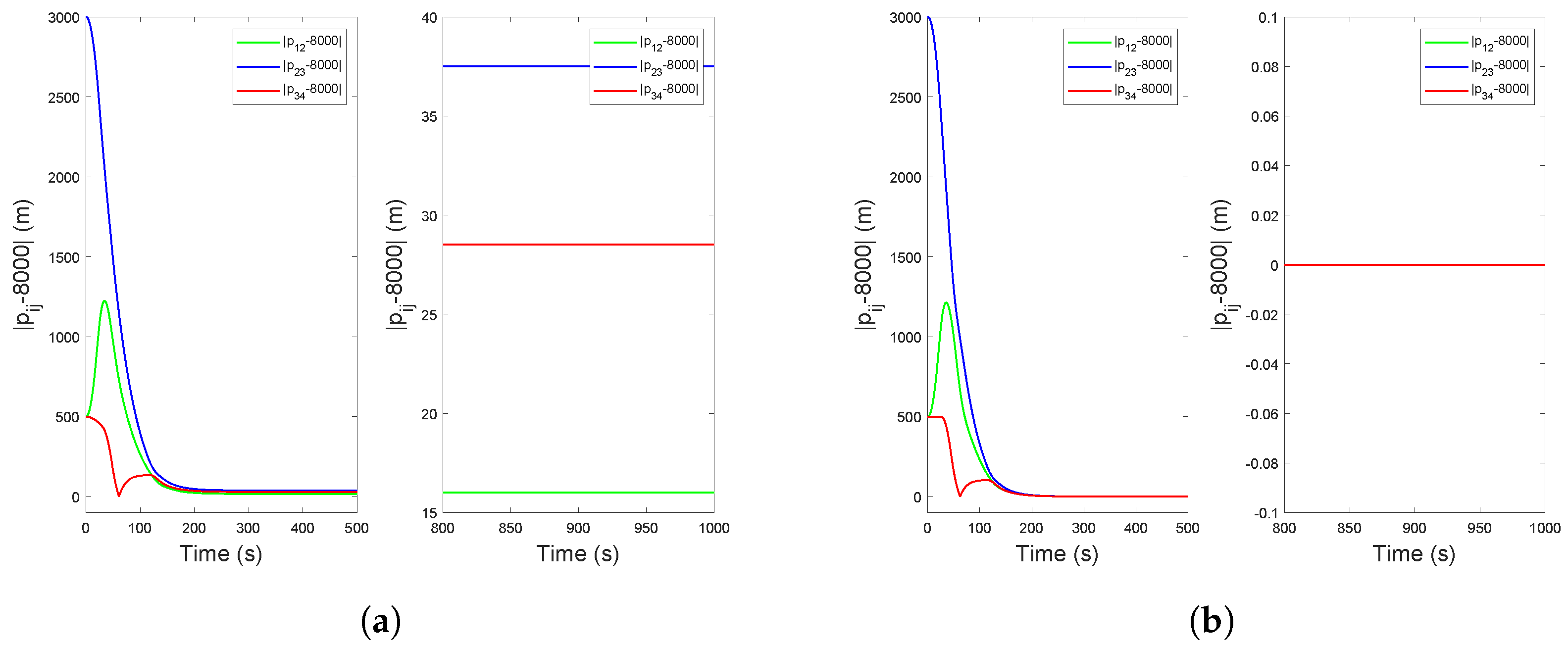
4. Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, P.; Tian, Y.; Gui, G.; Yang, C. Cooperative control for multiple train systems: Self-adjusting zones, collision avoidance and constraints. Automatica 2022, 144, 110470. [Google Scholar] [CrossRef]
- Yang, C.D.; Sun, Y.P. Mixed H2/H∞ cruise controller design for high speed train. Int. J. Control 2001, 74, 905–920. [Google Scholar] [CrossRef]
- Song, Q.; Song, Y.D.; Tang, T.; Ning, B. Computationally inexpensive tracking control of high-speed trains with traction/braking saturation. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1116–1125. [Google Scholar] [CrossRef]
- Ji, H.; Hou, Z.; Zhang, R. Adaptive iterative learning control for high-speed trains with unknown speed delays and input saturations. IEEE Trans. Autom. Sci. Eng. 2016, 13, 260–273. [Google Scholar] [CrossRef]
- Pan, D.; Zheng, Y.; Qiu, J.; Zhao, L. Synchronous control of vehicle following behavior and distance under the safe and efficient steady-following state: Two case studies of high-Speed train following control. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1445–1456. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Gao, Z. Coordinated cruise control for high-speed train movements based on a multi-agent model. Transp. Res. C Emerg. Technol. 2015, 56, 281–292. [Google Scholar] [CrossRef]
- Bai, W.; Lin, Z.; Dong, H.; Ning, B. Distributed cooperative cruise control of multiple high-Speed trains under a state-dependent information transmission topology. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2750–2763. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, T.; Karimi, H.R. Distributed cruise control of high-speed trains. J. Frankl. Inst. 2017, 354, 6044–6061. [Google Scholar] [CrossRef]
- Bai, W.; Dong, H.; Lü, J.; Li, Y. Event-triggering communication based distributed coordinated control of multiple high-speed trains. IEEE Trans. Veh. Technol. 2021, 70, 8556–8566. [Google Scholar] [CrossRef]
- Dong, H.; Gao, S.; Ning, B. Cooperative control synthesis and stability analysis of multiple trains under moving signaling systems. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2730–2738. [Google Scholar] [CrossRef]
- Gao, S.; Dong, H.; Ning, B.; Zhang, Q. Cooperative prescribed performance tracking control for multiple high-speed trains in moving block signaling system. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2740–2749. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Gao, Z. Distributed optimal control for multiple high-speed train movement: An alternating direction method of multipliers. Automatica 2020, 112, 108646. [Google Scholar] [CrossRef]
- Tian, Y.; Lin, P. Cooperative control for multiple high-speed trains with constraints and acceleration zone under moving block system. Int. J. Robust Nonlinear Control 2022, 32, 3662–3673. [Google Scholar] [CrossRef]
- Yan, X.; Cai, B.; Ning, B.; ShangGuan, W. Online distributed cooperative model predictive control of energy-saving trajectory planning for multiple high-speed train movements. Transp. Res. C Emerg. Technol. 2016, 69, 60–78. [Google Scholar] [CrossRef]
- Su, S.; Tang, T.; Roberts, C. A cooperative train control model for energy saving. IEEE Trans. Intell. Transp. Syst. 2015, 16, 622–631. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, H.; Wang, H.; Wang, X.; Dong, H. Cooperative multi-scenario departure control for virtual coupling trains: A fixed-time approach. IEEE Trans. Veh. Technol. 2021, 70, 8545–8555. [Google Scholar] [CrossRef]
- Lin, P.; Huang, Y.; Zhang, Q.; Yuan, Z. Distributed velocity and input constrained tracking control of high-speed train systems. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7882–7888. [Google Scholar] [CrossRef]
- Sun, X.; Zeng, M.; Lin, P. Distributed constrained control for multi-train systems with multiple cars. Int. J. Robust. Nonlinear Control 2024, 34, 2315–2332. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, L.; Wang, H.; Tang, T.; Li, K. Robust distributed cruise control of multiple high-speed trains based on disturbance observer. IEEE Trans. Intell. Transp. Syst. 2021, 22, 267–279. [Google Scholar] [CrossRef]
- Yao, X.; Wu, L.; Guo, L. Disturbance-observer-based fault tolerant control of high-speed trains: A Markovian jump system model approach. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 1476–1485. [Google Scholar] [CrossRef]
- Tang, H.; Wang, Q.; Feng, X. Robust stochastic control for high-speed trains with nonlinearity, parametric uncertainty, and multiple time-varying delays. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1027–1037. [Google Scholar] [CrossRef]
- Xi, W.; Hu, M.; Wang, H.; Dong, H.; Ying, Z. Formation control for virtual coupling trains with parametric uncertainty and unknown disturbances. IEEE Trans. Circuits Syst. II-Express Briefs 2023, 70, 3429–3433. [Google Scholar] [CrossRef]
- Wang, D.; Su, S.; Han, L.; Li, D. Finite-time distributed adaptive coordinated control for multiple traction units of high-speed trains. IEEE Trans. Intell. Transp. Syst. 2024, 1–15. [Google Scholar] [CrossRef]
- Godsil, C.; Royle, G.F. Algebraic Graph Theory; Springer: Berlin/Heidelberg, Germany, 2001; Volume 207. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Davis, W.J. The tractive resistance of electric locomotives and cars. Gen. Electr. Rev. 1926, 29, 685–707. [Google Scholar]
- Lin, P.; Ren, W.; Yang, C.; Gui, W. Distributed consensus of second-order multiagent systems with nonconvex velocity and control input constraints. IEEE Trans. Autom. Control 2018, 63, 1171–1176. [Google Scholar] [CrossRef]
- Lin, P.; Ren, W.; Gao, H. Distributed velocity-constrained consensus of discrete-time multi-agent systems with nonconvex constraints, switching topologies, and delays. IEEE Trans. Autom. Control 2017, 62, 5788–5794. [Google Scholar] [CrossRef]
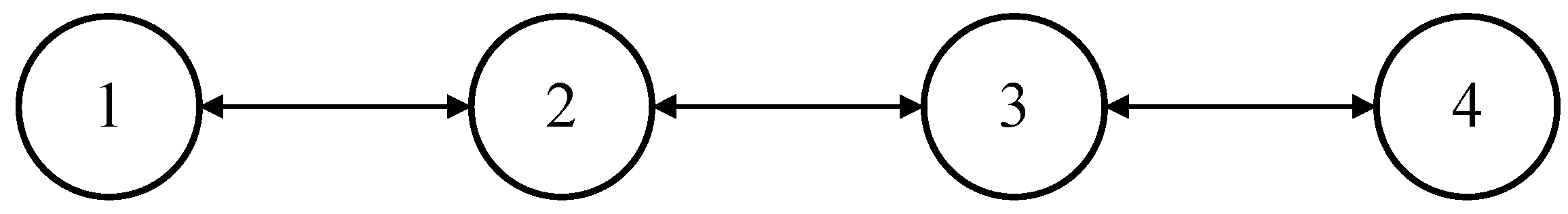

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.; Fan, X.; Wei, Y. Robust Constrained Cooperative Control for Multiple Trains. Mathematics 2024, 12, 2003. https://doi.org/10.3390/math12132003
Hu Q, Fan X, Wei Y. Robust Constrained Cooperative Control for Multiple Trains. Mathematics. 2024; 12(13):2003. https://doi.org/10.3390/math12132003
Chicago/Turabian StyleHu, Qijie, Xinyu Fan, and Yue Wei. 2024. "Robust Constrained Cooperative Control for Multiple Trains" Mathematics 12, no. 13: 2003. https://doi.org/10.3390/math12132003






