A Rate of Change and Center of Gravity Approach to Calculating Composite Indicator Thresholds: Moving from an Empirical to a Theoretical Perspective

Abstract

A composite indicator (CI) is the mathematical aggregation of sub-dimension (local) indicators used to provide an overall score for the multidimensional concept being measured. CIs are widely used to assess the benefits or risks in human endeavors, such as by creating life satisfaction indices or disaster risk indicators. One important aspect of the development of CIs is setting up value thresholds for taking action, such as in determining the minimum acceptable level of life satisfaction in a community or the maximum acceptable flood risk value beyond which people should be ordered to evacuate from the area in danger. The analytic hierarchy/network process (AHNP) is widely used for the development of CIs. In a review of 111 AHP/ANP CI studies, fewer than 10% discussed any threshold. This means that about 90% of the developed CIs were theoretically sound but lacked the actionable thresholds necessary to be of practical use. Furthermore, for the few studies that set thresholds, the values were typically set arbitrarily or using inadequate statistical approaches. To address this important concern, this study first discusses the most commonly used approaches to setting up thresholds, as well as their inadequacies, and proposes the development of AHP/ANP CI thresholds using a mathematical approach based on the rate of change and center of gravity (RCCG) concepts. Using this approach, a virtual reference alternative, i.e., a threshold profile (TP) made up of the local thresholds of each indicator, is calculated. The key advantage of the proposed method is that it not only provides a non-arbitrary way to set up a CI threshold; more importantly, it is independent of the data and/or alternatives to be evaluated; that is, a threshold calculated with the proposed approach constitutes an absolute reference value, outside the dataset.

1. Introduction

A composite indicator is a compilation of a set of individual indicators which, in turn, represent different dimensions (also called sub-dimensions) of a concept (the main dimension) being measured [1,2]. Composite indicators can be used, for example, to compare countries and organizations in terms of benefits (e.g., life satisfaction) and risks (e.g., disaster risks). They have been widely discussed in the literature [1,2]. In a nutshell, composite indicators consist of the weighted aggregation of multiple indicators (local indicators) to obtain a single (global) indicator. For example, the well-known human development index (HDI) is a composite indicator which consists of the summary measure of achievements in three key dimensions of human development, including a long and healthy life (with the measuring indicator being life expectancy at birth), education (measured in terms of expected years of schooling for children and mean years of schooling for adults), and standard of living (measured in terms of gross national income per capita) [3]. In turn, these dimensions are also measured using their own local indicators. In general, composite indicators have a hierarchical structure with the top (global) index being constituted by the aggregation of multiple (local) indicators, which may also have different weights. The HDI was created without weighting any of its three dimensions, and the convenience of weighting the dimensions differently has been debated. Should the dimensions have different weights, the HDI composite indicator would become the weighted addition of the local indicator values [4].

One question that comes to mind when using composite indicators is “what are the threshold settings?” For example, considering the HDI, a long and healthy life is measured in terms of life expectancy at birth. Therefore, the question would be “what threshold level of life expectancy in a country is unacceptably low and requires decisive government action?” Or in a disaster risks model, the question would be “what is the maximum tolerable risk to a given population?” Decision makers and planners need to set a threshold to trigger action as needed (e.g., If the risk is above the established permissible threshold). These threshold decisions need to be made at local and global indicator levels when using composite indicators. Since composite indicators can be used to assess aspects, such as benefits or risks, threshold-related questions that arise can be those such as “what is the minimum acceptable level of a benefit?” Or “what is the maximum acceptable level of a risk?” In practice, these thresholds are set quite arbitrarily and with no theoretical support, as will be shown in the present study.

For the purpose of this study, a threshold can be defined as a level, point, or value above which (for risk models) or below which (for benefits models) something is true or will take place and below which it is not or will not [5]. Thresholds are very important in composite indicators because they allow for a line to be drawn to separate a good from a bad situation. Crossing an indicator threshold can be used, for example, to monitor and provide alerts when territories come under non tolerable risks of disaster such as severe droughts [6] or to define minimum acceptable levels of gender participation in academic events [7].

This line of separation between good and bad situations, the indicator threshold, can be made in relative or absolute terms. The relative approach is easy because the indicator threshold is set up in relation to a reference (e.g., the country is expected to have a life expectancy not lower than a neighboring country). However, it is important to ask several questions about setting an indicator threshold in absolute terms. How it should be calculated, and what are its rationality, validity, and limits of application?

This study proposes a rigorous approach to threshold calculations in composite indicators that are developed in the context of the widely used analytic hierarchy process (AHP) or its generalization, the analytic network process (ANP), in absolute measurement models [8,9]. For this purpose, the extant literature on AHP/ANP composite indicators and threshold setting is reviewed, and the different approaches are discussed. Next, necessary conditions for threshold calculations are suggested, and a mathematically rigorous approach that meets these conditions is proposed and demonstrated with an example.

2. Literature Review

To explore the extant literature on the current state of threshold calculations when using composite indicators based on AHP/ANP, a systematic literature review was conducted. The search was conducted in the Web of Science database, given that it is recognized as the repository of the highest-quality research articles. Several searches were tried, with mixed results. For example, in the medical field, the acronyms “AHP” and “ANP” stand for “Acute hepatic porphyria” and “Atrial natriuretic peptide”, respectively. Therefore, no acronyms were used in the search. Similarly, one of the preliminary search terms included “index” (in addition to “indicator”), and this provided an excessive number of unrelated papers due to the large number of studies on the AHP compatibility index. Finally, the search term “(Composite indicator) AND ((analytic hierarchy process) OR (Analytic network process))” in any of the fields was found to be the most suitable. This search led to a total of 111 articles (see Appendix A). These articles were examined in two rounds. First, the abstracts were read to exclude any article that did not deal with the topic at hand or that was unavailable to examine in detail (for example, some foreign journals). This decreased the pool of selected articles to 97. In the second round, a content analysis of the articles was conducted to determine if the studies discussed (even briefly) threshold settings for the developed composite indicators (10 articles) or if they developed the composite indicators without discussing thresholds or their calculations (87 articles).

A review of the extant literature showed that, in general, the use of composite indicators is widely used for the measurement of benefits or risks in many different areas, such as water quality assessment, sustainability evaluation, drought risk measurement, and others [6,10,11,12]. On the other hand, the discussion and setting up of thresholds (e.g., the minimum accepted benefit; the maximum accepted risk) to trigger proper action was rarely discussed; only about 10% of the studied articles did this, and some only in a vague or indirect way. These studies are listed in

Table 1. List of composite indicator studies where threshold setting is addressed.

Item	Source	Title	Contribution
1	Molinos-Senante et al. (2019) [10] Journal of Env. Management	Assessing the sustainability of small wastewater treatment systems: A composite indicator approach.	Quality of service for drinking water is assessed. If the max. quality CI score of 1 threshold is not reached, corrective action suggested.
2	Chung, et al. (2014) [13] World Journal of Gastroenterology	Can composite performance measures predict survival of patients with colorectal cancer?	Life expectancy evaluation composite indicator is based on its correlation of colon rectal cancer with life expectation.
3	Abdar et al. (2022) [14] Env. Sci. & Pollution Research	A composite index for assessment of agricultural sustainability: the case of Iran	The interval of standard meviation from the mean (ISDM) was applied for CI thresholds, e.g., unsustainable: CI < mean-standard deviation.
4	Corona-Sobrino et al. (2020) [7] PLOS One	Closing the gender gap at academic conferences: A tool for monitoring and assessing academic events	They use European Union gender set parameters as thresholds to create an action semaphore red/orange/green.
5	Bravo et al. (2023) [6] Natural Hazards	DRAI: a risk-based drought monitoring and alerting system in Brazil	The DRAI system generates alerts from statistical analysis based on the hazard, vulnerability, and risk indices following a normal distribution. An alert is generated whenever an index exceeds the value of the average of its historical series plus two SD.
6	Go, D. et al. [15] PLOS One	Development of the Korean Community Health Determinants Index (K-CHDI)	Authors develop a CI for health determinant index and validated it based on its correlation with life expectation data various communities.
7	Aguilar-Rivera, N. (2019) [11] Socio-Econ. Planning Sciences	A framework for the analysis of socio-economic and geographic sugarcane agro- industry sustainability	In this study, the normalized CI scale (0–1) is divided in four parts corresponding to the anchors high (1), medium (0.75), low (0.5), and very low (0.25).
8	Boggia et al. [16] Intl. Trans. in Oper. Research	Using accounting dataset for agricultural sustainability assessment through a multi-criteria approach: an Italian case study	Authors use the multiple reference point weak-strong composite indicators (MRP-WSCI) method, which allows decision-makers to set various reference levels for the indicators, such as aspiration levels (what is admissible) and aspiration levels (what is desirable), for each indicator.
9	Wang, et al. [17] Ecological Indicators	Vulnerability of mariculture areas to oil-spill stress in waters north of the Shandong Peninsula, China	To describe the spatial variations in vulnerability, the normalized values were divided into five classes by quartile distribution: extremely low, relatively low, medium, relative high, and extremely high.
10	Bansal, et al. [18] Modeling Earth Syst. and Env.	Evaluating urban flood hazard index (UFHI) of Dehradun city using GIS and multi-criteria decision analysis.	Authors use the natural breaks (or Jenks) classification method to identify very high, high, medium, and low flow hazard. Note: This method is best used with unevenly distributed data but not skewed toward either end of the distribution.

.

2.1. Common Threshold Setting Approaches

Even in studies where thresholds were discussed, the way they were set was rather arbitrary. For example, on a typical 0-to-1 scale (the reason we call this scale “typical” is because it is common practice to normalize the different dimension scales of a common scale in a 0-to-1 scale for comparison purposes and facilitate their aggregation), a risk indicator must have a threshold above 0.5 to be considered dangerous, or an overall benefit index of no less than 0.8 to be considered attractive. This kind of practical approach has two serious weaknesses: first, it implicitly assumes that the risk increases linearly; and second, it assumes that all risk levels are equally important. The same logic applies to benefits indicators. Next, we review the most common practices used to calculate thresholds and discuss their limitations.

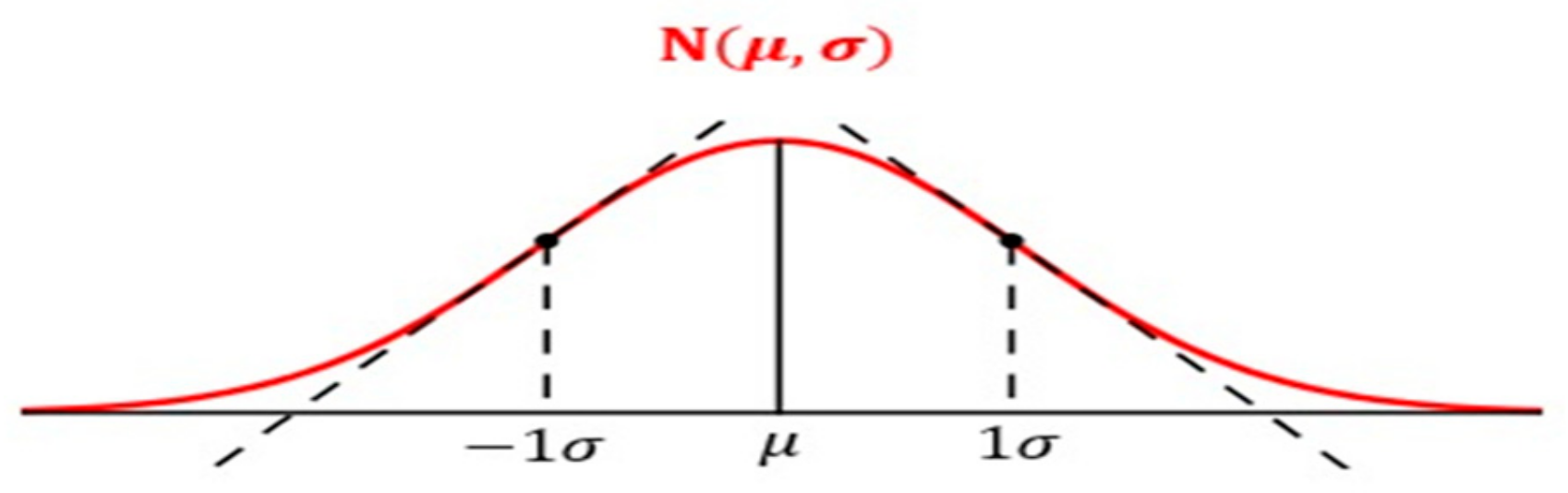
• Empirical–Statistical Approach

In an empirical–statistical approach, where there is a Gaussian (normal) distribution of the indicator values of the evaluated alternatives, some evaluators divide the distribution according to its mean and standard deviation into two extremes and a center zone for low (below −1σ), high (above 1σ), and medium (between −1σ and σ from μ), respectively, as shown in Figure 1.

An example of this approach, also called an interval of standard deviation from the mean (ISDM), is given by Abdar, Amirtaimoori, Mehrjedi, and Boshrabadi [14], who developed a composite index for the assessment of agricultural sustainability and used this approach for threshold setting, following similar studies [19,20].

Another example of this kind of statistical approach is the Z scoring method, which is a method originally used to normalize different scales to make them comparable but is now applied to obtain thresholds.

• The Z equation is defined as Z = (X − μ)/σ,

where:

• Z = transformed value (measured in standard deviation units);
• X = value to be transformed (from the original dataset);
• μ = arithmetic average of the distribution;
• σ = standard deviation of the distribution.

In summary, the empirical statistical approach is a kind of normalization for an interval scale using the mean value as the origin of the coordinate system. As usual, it is assumed for this statistical approach that the data distribution is normal, which is not always the case. The main problem with this type of statistical method is that the threshold value depends on the dataset, which means that the threshold value is a relative value that will change every time the dataset changes. Moreover, this way of building the threshold may have an inadvertent bias due to the dataset characteristics. Therefore, this is not the best way to calculate the threshold value. It is better for a threshold to be an absolute value independent of the dataset, in other words, a value outside of the dataset and not susceptible to changes from the flux of data, or even to its quantity and/or quality.

In particular, what is defined or recognized as acceptable or unacceptable in a risk assessment model should not be dependent on the dataset. In general, the value or level of what is acceptable or not should be an absolute cardinal value, totally independent of the dataset. For example, the performance of a student should not automatically be considered good just because it represents the best data in the sample or, vice versa, it should not be considered bad just because it represents the worst data point in the sample. In a good (absolute) threshold value, it is the threshold that judges the data, not the data the threshold.

This difference in calculation based on the use of a relative or absolute mode is more relevant in a disaster risk assessment model. In this model, the threshold of tolerability should not be calculated in a relative mode (linked to a dataset) because this dependency may leave the threshold blind to impact values that can have serious consequences for the stakeholders. For example, for a model that assesses territorial natural disaster risks, the threshold of tolerance should be calculated using an absolute value that is linked to the tolerable degree of impact or destruction in that territory, a degree that, in general, will not only depend on the collected set of data but also on the characteristics of the territory.

• Trisect Method

Another commonly used approach involves simply trisecting the scale (from 0 to 1 or 0 to 100 or 0 to 1000) in an approximately equidistant form. For the 0 to 1000 cases, the trisect would be as follows: ≤300, 300–600, and >600, (1/3 for each zone) for low, medium, and high, respectively. For example,

Table 2. Application of a trisect approach.

Levels of Risk Exposition According to BESIAK
Reference point (Thresholds)	Risk Level
BESIAK total ≤ 300	Low
300 < BESIAK total ≤ 600	Moderate
BESIAK total > 600	High

below shows this approach, taken from the Manual for the Evaluation of Rotating Shift Systems in Mining Operations (BESIAK), which is based on the classic work by [21].

In this case, each third of the distribution is arbitrarily imposed, which is not compatible with how thresholds are actually distributed in reality. Risk does not normally follow such a linear distribution, or present as a balanced, equidistant, or equivalent type. On impact measurement scales, a “Low” unit is normally not equivalent to a “Medium-impact” unit or a “High-impact” unit. It is necessary to determine these cut-off points analytically by measuring the true exchange value (exchange ratio) between the risk levels, which is what is proposed in this study.

• Max–Min Method

To set up the threshold, this method simply averages the maximum and minimum value of the data or the set of alternatives as follows: (Max + Min)/2, as illustrated in Figure 2. It assumes linearity regarding the rate of change between a low and a high threshold; that is, this method considers that one point in the high zone is equally as important as a point in the medium or low zone. When this method is used in risk models, another error that occurs is that it considers the maximum as intrinsically risky (will always be above the threshold) and the minimum as intrinsically not risky (will always be below the threshold), which, of course, is not true.

A variant of this method applies normalization with respect to the difference between the maximum and minimum value alternatives. This normalization approach is commonly used for interval scales. Its expression is

$$\frac{(Max\left(Ai\right) –A\left(i\right)) }{(Max(Ai) –Min(Ai))}.$$

Here, we estimate the distance of an alternative “i” and normalize it within the range {Max(Ai) – Min(Ai)} of the set of alternatives.

However, this distance does not necessarily correspond to a cut-off point (even if it is a distance to the maximum value of the set), and its normalization is not appropriate either since the normalized vector is altered in one of its basal elements, which is the proportion between its components. For example, if, initially, the first element of the vector is double the second element, after normalization, this scenario may not be maintained; therefore, relevant information is altered (this does not happen within a ratio scale standard normalization). Notice that this normalization will depend on the dataset, which makes the threshold value also dependent (relative) on the dataset; as previously discussed, this is not a good idea. This method is mainly used because it is relatively simple to understand. For example, Gonzalez-Urango et al. [22] used this approach to set up a value of 0.5 as a threshold to identify major concerns in the challenges to virtual instruction.

• Union of Minima

This method is the most conservative and simply uses the minimum values (not null) of the scale for all indicators and generates a “warning” to the user if any of them is exceeded. Needless to say, given its extreme degree of conservatism, this threshold calculation procedure can result in a high-cost design. However, in some applications, such as those in medical care, this approach, also called “All or None”, is usually chosen because accepting anything less than complete care would not be compatible with pursuing excellence [23,24]. For example, Molinos-Senante et al. (2019) [10] stated that given that only two 2 of the 40 rural drinking water supply systems (RDWSS) had obtained a perfect quality of service score, there was room for the other 38 systems to improve. This conclusion was made because since attaining a perfect score was possible, anything less should be addressed.

In conclusion, none of the available threshold setting approaches discussed above are compliant with the following expected properties that, in our opinion, must exist for threshold values.

2.2. Proposed Principles for Composite Indicators Thresholds

a.

Thresholds must be independent of the data and/or alternatives to be evaluated.

A threshold, by definition, is an element associated with the capacity of the surrounding environment; that is, the value of the risk or benefit threshold is an element external to the system. Therefore, it is not proper that the threshold values be dependent on the set of data that belongs to the same system. The threshold should be an absolute reference value, outside the dataset.

b.

Thresholds must take into consideration the equivalence value of the elements that make up the measurement scale (its transformation function) to determine their rate of change at the equilibrium point and, from there, determine the best value for the scale threshold.

Assigning threshold values arbitrarily or simply dividing the global scale into arbitrary segments is not a correct threshold setting method because this procedure disregards the fact that the global scale is a weighted composite of the local scales of the indicators. If the composition form has to be respected, then the composite threshold (the global threshold) has to be built in the same way. For instance, if a criterion has a greater weight, that criterion should more greatly affect the global threshold than the rest of the criteria set.

While the above arguments could apply to any approach to the development of thresholds for composite indicators, this study focuses on the case of composite indicators developed with the AHP/ANP methodology. The reason for this is that the AHP constitutes a widely used methodology for the development of composite indicators, and its use is also officially promoted by international organizations focused on developing global indicators [25]. However, given the absence of a mathematically grounded calculation of threshold indicator values, the usefulness of AHP/ANP composite indicators as an important decision making tool is greatly diminished.

Improper threshold calculations have more serious consequences in the case of multicriteria evaluation models in which each criterion has a measurement scale with a local threshold for the different indicators (e.g., return on investment, cost, risk), and the overall phenomenon evaluated (e.g., an investment portfolio suitability) requires the calculation of a global measurement value (calculated as the combination of the local values weighted and aggregated) and its corresponding global threshold (e.g., what is the minimum value to consider the portfolio suitable?).

In summary, our literature review exposes a gap in the extant literature at two levels: firs, there is a lack of reporting on setting up CI thresholds (only about 10% of the reviewed papers did it—Table 1); and second, there is a lack of a proper process by which to calculate valid AHP/ANP CI thresholds (many thresholds settings in studies listed in Table 1 were either arbitrary or data-dependent). The present study addresses the identified gap in the CI thresholds literature (reporting and calculation) by proposing a solid mathematical approach based on the rate of change and center of gravity (RCCG) concepts, which will be explained next.

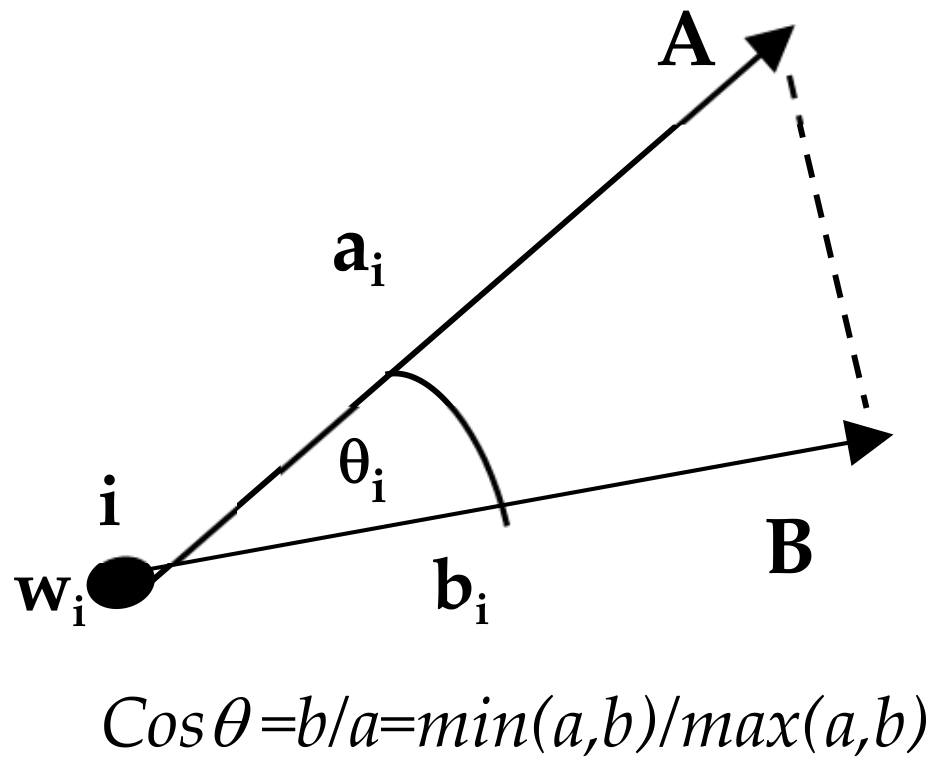
2.3. An RCCG Approach to Local Threshold Calculation: A Geometric Explanation

Next, a geometric explanation of why the center of gravity and the rate of change are used to calculate the local threshold of an absolute measurement scale.

There are two points that represent two consecutive levels of a scale. Without losing generality, it is possible to say that these tow points of the scale are L (low) and M (moderate). In a risk model, L represents a lower risk level and therefore the expert’s comfort zone (where he feels comfortable), while M represents a higher risk level or the expert’s discomfort zone. Note: In a benefits model, exactly the opposite happens.

The aim is to determine the border or frontier between both zones, that is, the threshold where one passes from the comfortable zone to the uncomfortable zone, corresponding to the balance or equilibrium line between both zones.

Graphically, this can be depicted as in Figure 3.

In a risk model, the left zone of the graph (L) is preferable to the right zone (M) since the expert feels more comfortable facing a lower risk (L < M).

The formula for the center of gravity (CG) helps us to find the equilibrium line (the threshold) between both zones since points M and L have different weights, namely, w1 and w2, respectively, with w2 being greater than w1.

$$\mathrm{CG}=\frac{(w1\ast M+w2\ast L)}{(w1+w2)}$$

If we assign value 1 to w1 (the unit), then it is necessary to determine w2. This value is given by the ratio of change between M and L; that is, M/L. This is equivalent to saying that the area with the greatest weight is the comfort zone of the expert and that the comfort zone in a risks model is point L (the lower level of the scale). Since w2 should be greater than w1, then w2 = M/L (>1).

If it should be conducted in reverse, that is, w2 = 1 (now, w2 is the unit), the result would be the same assuming that w1 = L/M (<1); the rate of change is inverted to maintain the concept of the most weighted zone in a risk model (w2 > w1). This leads to

$$\begin{gathered} \mathrm{CG} (L \mathrm{to} M)=(1\ast M+(M/L)\ast L)/(1+M/L)=2ML/\left(M+L\right)\mathrm{or} \\ \mathrm{CG} (M \mathrm{to} L)=(M\ast (L/M)+1\ast L)/(L/M+1)=2ML/(L+M). \end{gathered}$$

This symmetry is very interesting because it is telling us something that is expected (and valuable), i.e., that no matter what the starting point is (L or M), the result is always the same; applying the ratio of change is inverted when the direction of calculation is inverted (i.e., the direction of rate of change L to M is changed to M to L).

For the benefits model, we have to invert the L and M points (the levels of the scale) of Figure 3 since now the comfortable zone for the expert is located in the higher-level M (M > L), which represents more benefits.

Graphically, this can be depicted as in Figure 4.

In this case, the formula for CG (the local threshold of the scale) is

$$\begin{gathered} \mathrm{CG} (M \mathrm{to} L)=(M\ast (M/L)+1\ast L)/(M/L+1)=(L^2+M^2)/(L+M)\mathrm{or} \\ \mathrm{CG} (L \mathrm{to} M)=(1\ast M+(L/M)\ast L)/(1+L/M)=(L^2+M^2)/(M+L). \end{gathered}$$

Again, the symmetry appears no matter what the point starting is; the result is the same.

Summary

It is through rate of change and center of gravity that we know the threshold’s value. Due to the levels of the scale having different values, they need to be balanced (find the equivalence between them); for example, how many “Lows” of the scale make one “Moderate” within the same scale of measurement? Once this issue is solved, then it is possible to apply the center of gravity formula to find the geometric equilibrium point between both consecutive levels; this point represents the local threshold value of the scale.

3. Theoretical Framework

AHP decision-making modeling involves the setting of a goal at the top of the decision hierarchy, followed by a decision criteria level, which, in turn, may have a sub-criteria level, and so forth until we reach the final level of the alternatives to be evaluated. The criteria are weighted based on their relative comparisons. The alternatives may be evaluated using pairwise comparisons (relative mode) or by developing evaluation scales for the alternatives (absolute mode).

The typical AHP structure for composite indicators is a hierarchical distribution in which a single composite index sits at the top of the hierarchy and is composed of dimension variables at the immediate level below which, in turn, there may be sub-dimensions at the next lower level, and so forth. However, if the elements at any level influence each other, or if there is a feedback influence from the lower-level elements to the upper ones, then the structure is that of a network, and the ANP, which is a generalization of AHP, is required. In both cases, an absolute measurement model with suitable indicators is used to assess the dimension variables.

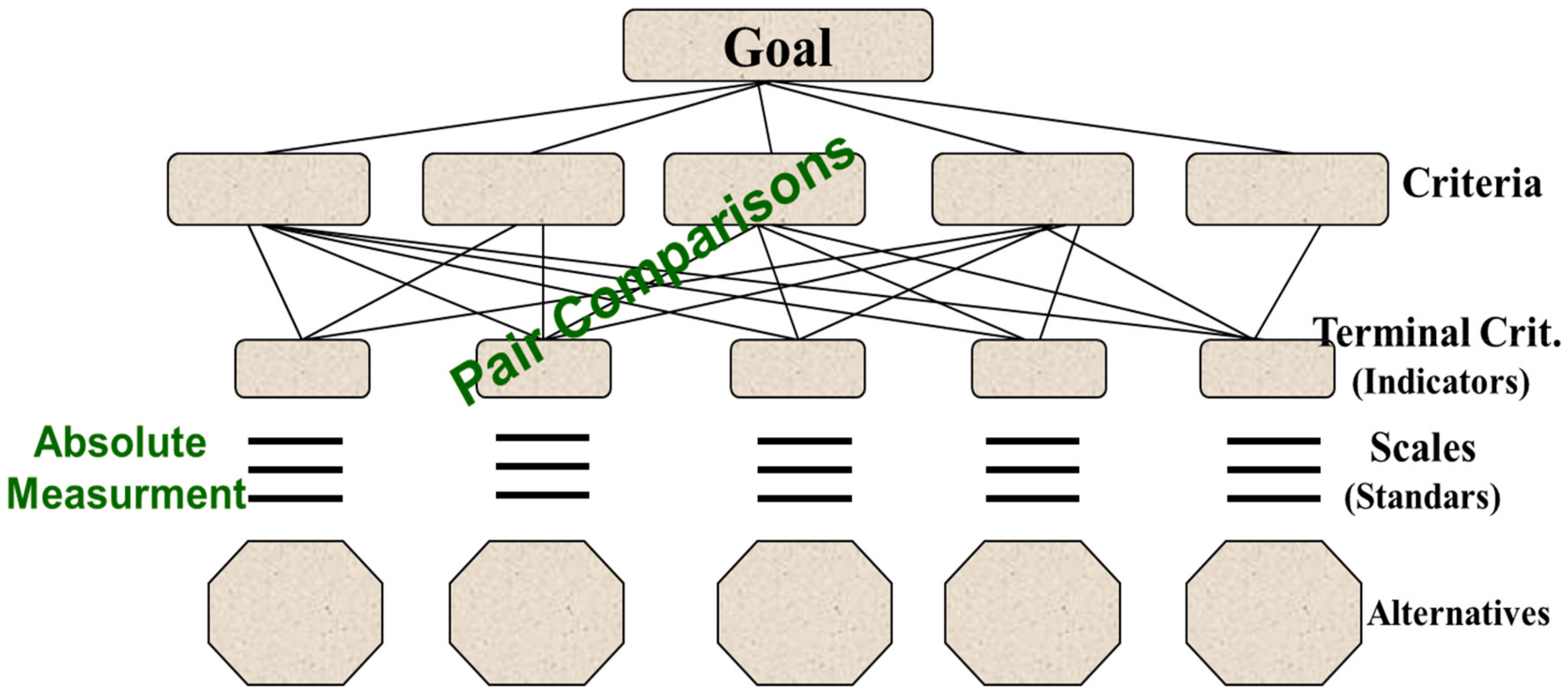
3.1. Brief Mathematical Discussion of AHP/ANP Absolute Models and Their Use for Composite Indicators

The AHP/ANP is not a technique or method but rather a methodology. In other words, the AHP/ANP goes beyond being used as a tool with a guided approach but also has a strong theoretical framework that must be understood for its correct application. Moreover, it has been said that any worthwhile scientific method requires axioms and theory to support it. Therefore, it is necessary to review the AHP axioms, which include the superposition principle and the eigenvector operator. These theoretical elements have been formally discussed in the AHP/ANP literature [26,27], and the reader is invited to review them there. They are presented here in a way that is more suitable for the purpose of the present discussion, which is a different approach to the same material.

3.1.1. AHP Hierarchical Superposition Principle

This principle makes it possible to approach complex (non-linear) problems through a superposition of lines, in the same way that we can approach a higher degree curve through a series of small tangent lines, where each approximation line can be assimilated to a level of the hierarchy.

The superposition equation used to obtain the priority of any alternative is given by the vertical multiplication of the weights of the criteria of each level “i” of each branch “j” of the hierarchy (w(i,j)). Then, the horizontal weighted sum is performed at its lower level, weighting the local relative value of the alternative “Al(j,k)” terminal criterion to the terminal criterion of the hierarchy, which results in the global relative value (with respect to the objective global or goal) of alternative “k”, defined as “Ag(k)”, in relative or absolute measures.

In this way, the global evaluation of an alternative is given by the following expression:

Ag^k = ∑_j ((∏_iw_ij) ∗ S_j(Al^k)),

where:

• i = number of levels of the hierarchy;
• j = number of terminal criteria of the hierarchy (the measurement indicators);
• k = alternative number;
• w_ij = weight of criterion j at the level I;
• S_j(Al^k) = local evaluation of alternative k in the scale belonging to the terminal criteria j (the measurement indicator j); the evaluation is made with a rating scale (the transformation function) in the absolute measurement mode;
• Ag^k = global evaluation of alternative k, evaluated in all terminal criteria (the measurement indicators).

These functions are known as “multilinear functions”; they are the simplest form of nonlinear functions whose density in the Banach spaces ensures our ability to represent the problem at the scale or depth that the user requires. One can imagine that each level of the hierarchy may represent one tangent of the curve, as shown in Figure 5.

It is interesting to note that if the hierarchy has a single level of criteria (i.e., i = 1), it corresponds to the simplest case of a hierarchy. In this case, the AHP model will effectively be a simple linear function (∑_j w_j ∗ Al_j) consisting of a single hierarchy level with a low ability to represent complex problems.

The concept of multilinear form plays a special role in capturing and consolidating the meaning of judgments in hierarchical structures (AHP) and networks (ANP) in such a way that, with a step-by-step scheme, it allows us to approach and deepen our understanding of the problem and its complexity as much as necessary. Every connected graph that represents a decision-making problem, regardless of its complexity, can be approximated (covered) by a multilinear form.

3.1.2. Eigenvector Operator (Calculating the Weights)

The weights of the criteria w(i) are calculated from the pairwise comparison matrices (PCM) of each level of the hierarchy. This is undertaken through the systemic eigenvector operator accompanied by the statistical consistency index that is calculated from the largest eigenvalue of the matrix associated with the eigenvector, which defines the stable equilibrium point of the PCM. A physical representation of the eigenvector is shown in Figure 6.

Figure 6 represents the vibration mode of a physical structure subjected to an external force or stimulus, for example, an earthquake, and it is used in seismic structural analysis. Depending on its construction material and geometry, each structure has different vibration modes. Still, one of these modes will be the dominant one and will concentrate the maximum information about the structure reaction to the stimulus. This information will be used to calculate the final equilibrium state. Each of the vibration modes corresponds to one of the eigenvectors of the matrix, and the dominant mode corresponds to the main eigenvector. This mode will be the dominant eigenvector and will best represent the final equilibrium point of the whole system.

By having a dominant or main eigenvector, that is, one of the vibrating modes accumulates most of the information of the system within itself, this mode will be the dominant eigenvector and will best represent the final equilibrium of the system (it could be defined in terms analogous to a center of gravity of the information at the equilibrium point).

The two equations used to determine the stable equilibrium point with acceptable consistency are as follows:

$$\mathrm{W}(\mathrm{i})=\underset{\mathrm{n}\to \infty }{\lim }\{\frac{{\left(A\right)}^{n}e}{(e{\left(A\right)}^{n}e)}\},$$

where:

• e = unitary vector {1,…,1};
• (A) = pairwise comparison matrix;
• W(i) = eigenvector, i.e., an absolute metric scale for complex systems;

and

$$\begin{gathered} {\mathsf{\lambda }}_{\max }=\underset{\mathrm{n}\to \infty }{\lim }(\mathrm{Trace}[\mathrm{A}{]}^{\mathrm{n}}{)}^{1/\mathrm{n}}, \\ \mathrm{IC}=\{({\mathsf{\lambda }}_{\max }-\mathrm{n})/(\mathrm{n}-1)\}, \\ \mathrm{CR}=\mathrm{CI}/\mathrm{RI}, \end{gathered}$$

where:

Largest eigenvalue λ_max: a measure of consistency of the constructed metric;

• CI = consistency index (one wants to be as close as possible to the “n” value);
• RI = random consistency index (one wants to be as far away as possible to this value);
• CR = consistency ratio (CR ≤ 10% is considered an acceptable consistency ratio);
• N = dimension of the PCM.

In summary, the preferred evaluation process captures the priorities of judgments through a pairwise comparison of the elements. These comparisons are arranged in a matrix, and the priorities are derived from the largest eigenvector of the matrix, which defines an absolute ratio scale.

The background mathematical theory (vector algebra, graph theory, perturbation theory, and Perron–Frobenius theorem) ensures the validity of the results and measures the inconsistency of judgments. Priorities derived in this way satisfy the properties of a ratio scale just like weight and length satisfy the properties of physical scales.

3.2. AHP/ANP Relative and Absolute Measurement

In the physical world, objects can be measured relatively (comparing them to each other) or absolutely (comparing them against a standard). Absolute measurement is a very different concept from relative measurement. For example, using a yardstick to measure the length of a room is an example of absolute measurement. An important property of absolute measurements is that each measurement is independent (this is the most important characteristic when we are looking for the threshold behavior) of the others; that is, they are not modified by measuring other elements with the same yardstick. In multicriteria theory, absolute measurement is the extension of the yardstick idea, although different yardsticks may be used for the different criteria.

There are two ways to evaluate the alternatives in the AHP: relative and absolute measurement. With relative measurement (RM), the alternatives are compared to each other, and with absolute measurement (AM), the scale is constructed for each terminal criterion (normally a unique scale). The AM mode is very useful in engineering, particularly for the construction of standards and of analytical thresholds and their applications [28].

The threshold in a scale is an indispensable element in the construction of standards in decision-making. For example, the maximum level of tolerable risk or minimum level of benefit required for an action or project to be effective is necessary to determine. These values or standards may exist (e.g., legal regulations) or they may be constructed through analysis and stakeholder agreement. The threshold corresponds to a cut-off point or change in intensity in the scale where the new impact value acquires a different meaning, for example, going from a tolerable risk to a non-tolerable one. This cut-off point can occur both at a local level (in a particular indicator or terminal criterion) and at a global level (for the entire evaluation model) and, in many cases, determines an important decision or course of action. Figure 7 illustrates the difference of the absolute measurement in AHP.

Only alternatives are measured in an absolute mode. The alternatives are measured against the standards in each criterion. Each terminal criterion (indicator) has an associated intensity scale through which each alternative is evaluated in absolute terms. An example of work experience level criterion is shown in

Table 3. Example of work experience level scale.

Qualitative Scale	Quantitative Scale	Absolute Ratio Scale
Exceptional	15 or more years of experience	1.0000
A lot	Between 8 to 14 years of experience	0.5815
Average	Between 4 and 7 years of experience	0.2792
Some	Between 1 and 3 years of experience	0.1163
Very little	Less than 1 year of experience	0.0698

.

In both cases (qualitative and quantitative), the ordinal scale must be transformed into a normalized absolute ratio scale through a transformation function (explained later) coming from the pairwise comparison matrix (PCM), as shown in

Table 4. Pairwise comparison matrix (PCM): work experience indicator.

Work Experience	Outstanding	A Lot	Average	Some	Very Little	Absolute Ratio Scale
Outstanding > 14	1	a12	a13	a14	a15	1
A Lot (8–14)		1	a23	a24	a25	0.5815
Average (4–7)			1	a34	a35	0.2792
Some (1–3)				1	a45	0.1163
Very little < 1					1	0.0698

.

In Table 4, a₁₂ represents the comparison of the importance scale of the level Outstanding work experience (over 14 years of experience) with respect to the level A Lot of work experience (8 to 14 years), using the fundamental scale (Saaty’s scale); a₁₃ represents the same comparison but with respect to the level of Average work experience (4 to 7 years), and so on. When all the comparisons of the matrix are completed, it is possible to calculate the main eigenvector (normalized using the ideal norm). This vector is shown in the last column at the right in Table 4 and represents the numerical value of the different levels of the scale at its equilibrium point (limit of the matrix).

3.3. Scales, Invariants and Thresholds

To properly understand the meaning and calculation of the threshold of a scale, it is essential to understand the concepts of measurement and measurement scales. A threshold can belong to any type of scale: nominal, ordinal, interval, ratio, absolute ratio, semi-log, and log. Depending on the scale that is used, different things can be achieved (or not achieved) with the elements of the scale.

3.3.1. Scales

Knowledge about scales of measurement, their capacities, and their scope is not very well understood or disseminated among the people who build indicators. It is painfully common to find ordinal scales (such as the Likert scale) or interval scales used as if they were ratio scales or absolute ratio scales. This confusion can invalidate all the work conducted, including the calculation of the threshold. For this reason, it is strongly suggested that ratio or absolute ratio scales be used. In this work, we will use absolute ratio scales in line with the AHP method in its absolute measurement mode. It is useful to review the most-used scales and their properties.

• Types of most used scales

• Nominal Scale: Invariant under one-to-one correspondence (bijective function).

This scale is used to identify elements, for example, a checking account number, telephone number, identity card, etc. The numbers on the scale do not provide any additional information. No valid arithmetic operations can be performed on these numbers because they do not constitute a measure.

• Ordinal Scale: Invariant against monotonic transformations.

This scale orders the elements of the scale. The numbers on the scale only explain the order from lowest to highest or from highest to lowest. No valid arithmetic operations can be performed on these numbers because they do not constitute a measure. The most common use of this scale is to determine the statistical mode and (in some cases) the median of the set. Here, we can also locate the Likert scale in its basic form.

• Interval Scale: Invariant against the transformation Y = a * X + b, with positive a and b.

With this scale, it is possible to subtract values from the same scale or make a weighted sum of values from the same scale but not to add or multiply values from the same or different scale. This is due to the invariant that this scale presents (Y = aX + b, equation of the line that passes through b with b > 0). By adding two elements of the scale, we obtain Y = a(X1 + X2) + 2b, whose form is of the type aX + 2b, losing its invariant since the constant in the Y axis is 2b and not b. However, subtraction is allowed since in that case, the constant “b” is eliminated and Y = aX remains, which corresponds to a ratio scale which has greater properties than the interval scale. Sometimes, the interval scale is also called a ratio difference scale since when making the difference, the value obtained belongs to a ratio scale which, in theory, allows us to make ratios between intervals, i.e., ΔY/ΔX. However, this procedure introduces certain dangers, especially when normalizing the vectors. (In this author’s opinion, it is always preferable to use the original over the adjusted copy.) Some examples of interval scales are temperature scales and the utility function.

• Ratio Scale: Invariant against the transformation Y = a * X, with “a” positive.

This scale makes it possible to add and subtract values from the same scale and to multiply and divide values from the same or different scales. This includes all the physical scales of measurement (distance, area, time, speed, etc.) that are normally understood as measurement. Note that this scale is a dimensional scale; that is, it presents units (kg, km, seconds, etc.), allowing its combination with other scales. For example, speed = distance/time and requires a known (non-arbitrary) zero.

• Absolute Ratio Scale: Invariant against the transformation Y = X (identity function).

The absolute ratio scale is a particular case of the ratio scale and therefore exhibits all its properties. This scale differs from the ratio scale because it is normalized by the “a” constant (the slope), which represents the unit of the scale, leaving the identity function Y = X as its invariant. Therefore, this is an absolute dimensionless scale; it does not require a known zero, and its neutral value is the number one and not zero.

Examples of this scale include the Reynolds number, the Mach number, the π number, the “e” number, the numbers of the Saaty’s fundamental scale, and all the numbers that we use on a daily basis. A great advantage of this scale is that it does not require a definition of the type of number. If one says a = 3 * b, one does not need to know if 3 is 3 kilos or 3 Ll; it simply represents the ratio or proportion of one element to the other; it is an absolute number.

Also, the absolute scale does not require the presence of zero in its construction. Furthermore, when A = B in an absolute scale, it means that A/B = 1 and not necessarily that A − B = 0.

In fact, the neutral of this scale is one not zero. This is best understood on a logarithmic scale, where if A = B, then log(A/B) = 0 and log(A − B) is not defined. Zero on the absolute scale is not required. Therefore, the “standard” metric (ratio scale) that we know that includes zero will not necessarily correspond to our ability to feel and perceive our experiences and therefore adequately represent the systems that surround us (what is the zero of beauty or the zero of joy?). If we cannot adequately represent a system (in terms of feeling and perceiving), how can we make accurate decisions about the world around us?

In general, we can say that

0 = traditional neutral, belonging to ratio scale appropriate for known physical scales;

1 = neutral of the absolute ratio scale (sensations and perceptions scales), which can be defined as an appropriate scale for the scope of decision making.

It is interesting to note that in physical scales, the evaluation comes first and then the interpretation of what is evaluated, while in decision scales, the understanding and/or knowledge of the topic comes first and then its evaluation or the construction of the number that represents it, normally through the construction of an absolute scale of measurement. It is also interesting to remember that our brain perceives intensity changes better under a logarithmic scale, as demonstrated by the psychologists Weber and Fechner in their famous Weber–Fechner law [29]. More-recent findings have shown support for this law based on a deeper understanding of the brain’s neuron function [30,31]. This is most likely the main reason that the scale constructed by experts under the PCM method takes an exponential form.

All these characteristics make the absolute ratio scale ideal to work with; it makes it possible to operationally manipulate and combine it with multiple indicators in a mathematically correct and appropriate way to represent our sensations and perceptions, which provides the ability to build standards and thresholds (local and global) in a natural way.

It is worth briefly discussing invariance and examples of thresholds in scales, which are two important concepts for this study. An invariant is something that does not vary under a transformation. For example, if we move a 3 m rigid bar by a distance d, its length will not be altered; that is, the measurement of the bar is invariant to a coordinate translation. The invariance is relevant because it is the element that defines the category of scale we are using (not the existence of a zero in the scale).

3.3.2. Examples of Thresholds in Scale Types

A threshold is an essential element in any decision-making process, particularly in risk-assessment models. In these models, it is very important to be able to answer the question “if the risk is inevitable, what is the maximum tolerable level of risk?” This level of tolerable risk must be calculated analytically, including an analytical formulation that explains where the cut-off values come from, their method of calculation, and their relationship with the measurement scale used. The threshold can belong to any type of scale: nominal, ordinal, interval, proportional, absolute proportional. The arithmetic operation capabilities of the scale elements depend on the scale type.

Table 5. Types of scale, invariants, and examples.

Scale Type	Invariant	Scale Threshold Example
Nominal	Bijective Function (one to one correspondence)	Car license plates ending in 3 and 4 (excluded from traffic circulation)
Ordinal	Monotone Function (increasing or decreasing)	Minimum grade: 4.0. (minimum grade for course approval)
Intervals (arbitrary zero)	Y = aX + b. (a, b > 0) (Straight line equation passing by b)	Temperature: 37 °C (maximum acceptable temperature to allow entry into a facility)
Ratio (dimensional, requires a known zero)	Y = aX. (a > 0) (Straight line equation passing by 0)	Speed: 50 km/h (maximum allowed speed)
Absolute Ratio (dimensionless, does not require a known zero)	Y = X (Identity Function)	Risk: 0.2485 (24.85%); maximum acceptable risk to implement a project in a given territory

Note that in the case of an absolute ratio scale, the existence or nonexistence of zero on the scale is not a necessary condition. It is common to think that it is the zero that makes the difference in the type of scale; however, zero is rather a consequence of the type of scale. The scale is mathematically defined by its invariant.

shows a summary of the most common types of scale, their invariants, and an example of each.

3.3.3. Representativeness of the Measurement Scale

The representativeness of a measurement scale is the ability of the numbers that belong to the scale to represent the sensations and emotions captured from the acquired experiences, which, ultimately, can (or cannot) be transformed into acquired knowledge; in this way, we incorporate it into the decision-making process of the actors.

In a “raw” quantitative ratio scale, the numbers that make it up do not necessarily represent, in themselves, the measure of the intensity of preference that should be captured in a measurement scale. It is necessary to transform this scale, even if it is a ratio scale. A simple example of the latter is the measure of the dangerousness of the speed of a vehicle. Although 80 km/hr is proportionally double that of 40 km/hr, its hazard ratio in the event of an accident is not 1:2; it is much greater (which is a product of the energy involved). Therefore, it is necessary to capture these differences or rather their reasons or intensities of preference. This is achieved through the ratios or proportions between the sensations (aij = si/sj), which are ordered in a pairwise comparison matrix (PCM) whose balance point is given by the largest eigenvector of the PCM. The measurement scale generated corresponds to an absolute ratio scale and is deeply incorporated in the AHP and ANP method in its absolute measurement mode. In general, the number of comparisons required in a reciprocal matrix is n * (n − 1)/2, with “n” being the dimension or size of the matrix. Below is an example of a 3 × 3 matrix (three comparisons required). Also, the consistency ratio (CR) in a 3 × 3 matrix shows the calculation to be consistent if it is lower than or equal to 5%.

$$\mathrm{A}=\begin{array}{ccc}1& a12& a13\\ a21& 1& a23& \mathrm{aij}=1/\mathrm{aji} (\mathrm{positive}\mathrm{reciprocal}\mathrm{matrix})\\ a31& a32& 1\end{array}$$

where:

aij = comparison of element “i” with element “j” (sensation/experience/knowledge of element “i” with respect to element “j”).

3.4. PCM as a Transformation Function

The coordinates of the eigenvector of the PCM can be visualized as the transformation function in a coordinate plane, transforming the ordinal (or other) scale on the abscissa axis (X axis) into an absolute ratio scale on the ordinates (Y axis) with a range from 0 to 1. Its objective is to capture the preference intensities between the elements (the levels) to be compared in the matrix at its equilibrium point (the matrix principal eigenvector).

Figure 8 illustrates a transformation function from an ordinal scale (X axis) to a cardinal scale (Y axis) for the “Experience Level” example.

Note the nonlinearity of the curve, especially in the lower area, adjusting, in this case, more to a quadratic function. If we realize that every indicator of the model follows an exponential trend, it is easy to understand the cumulative error that can be made when using ordinal scales.

It is also possible to obtain measurement scales from field data, but this requires that the indicator be quantitative, which is often not possible, and that there be sufficient data to validate it. Furthermore, it always requires the interpretation of the expert regarding the data captured (data do not carry an interpretation in itself). This interpretation must be carefully made considering the expert’s experience regarding the behavior and meaning of the variable. The interpretation must be captured methodologically and analytically. In general, simple surveys (normally based on ordinal scales) are not fully useful since they do not reflect changes in intensity on the scale.

As mentioned, the final objective of the transformation function is to capture the preference intensities between the elements that make up the scale at their equilibrium point with the help of the expert. The final scale should include the expert’s interpretation of the data based on his/her experience and knowledge regarding the topic. The transformation function of a scale is the first step or requirement in determining the local threshold value of the scale analytically.

3.5. Conclusions about Scales

• The complexity of the problem to be solved normally leads to the use of a large number of variables and indicators, aimed at analyzing the available alternatives.
• These indicators and scales must be specific to the problem and independent of their qualitative or quantitative nature.
• The AHP/ANP provides a mechanism with which to construct measurement and cardinal scales for all types of intensity scales. Only scales that constitute a measure have the arithmetic properties necessary to synthetize the many scales present in an AHP/ANP model, combine results from and to other methods, and perform sensitivity and stability analyses.
• The coordinates of a PCM eigenvector can be visualized as a transformation function, from ordinal to cardinal, in a coordinate plane.
• It is important to understand the nature and properties of the scales used by each methodology to use them appropriately (this is the responsibility of the professional user).
• Technological development has created an extensive number of figures and data. The challenge is to determine the relevant variables of a problem and find the necessary data and its representativeness or importance to evaluate the alternatives within the context of the problem.
• Numbers are important, but knowledge is even more important. Numbers, by themselves, may be totally invalid, useless, or irrelevant.

As AHP creator Thomas L. Saaty stated, “it is essential to obtain the scales from measurements, rather than measurements from scales” [32].

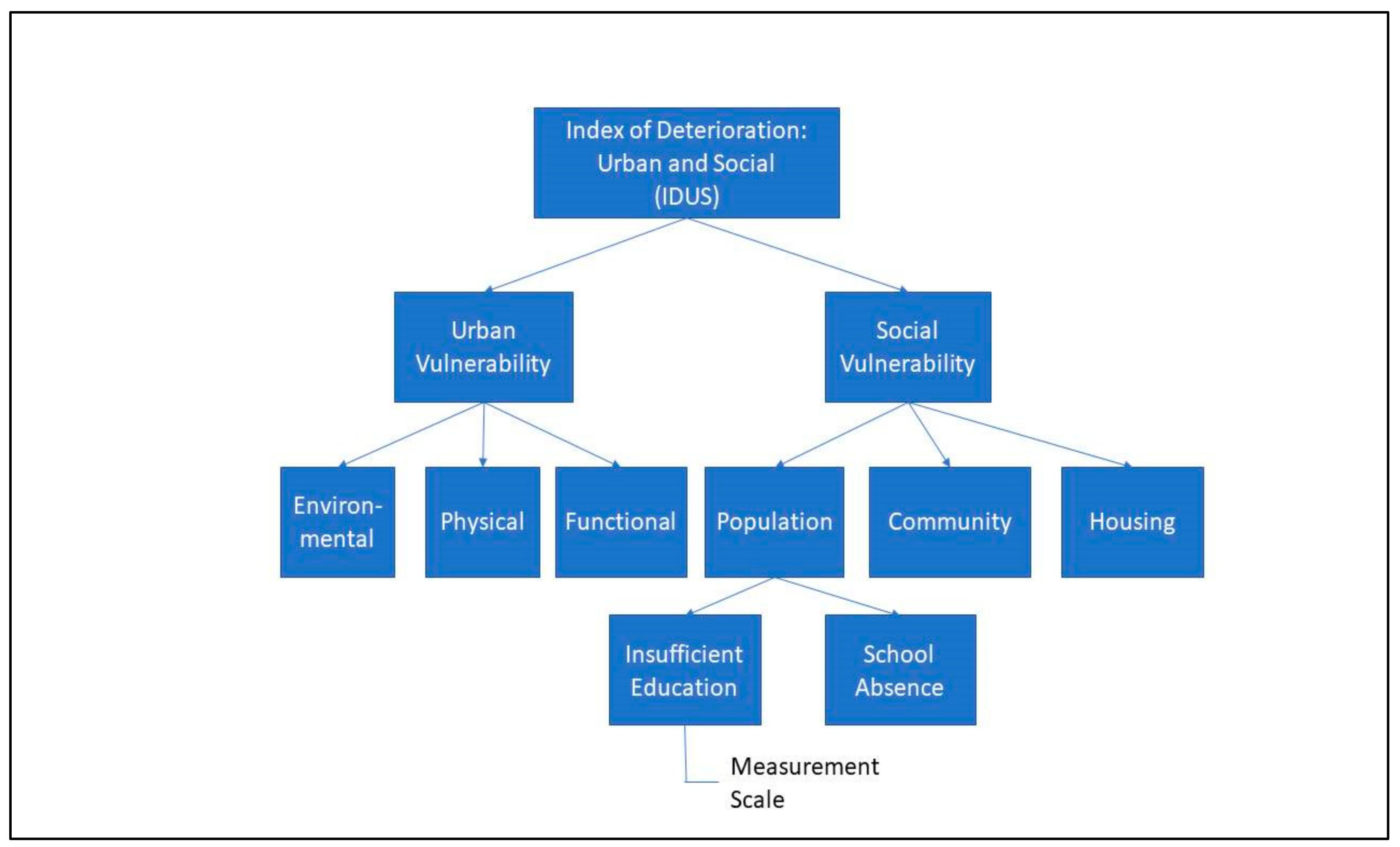
4. Calculation of the Local Threshold of a Scale

The local threshold (LT) calculation is carried out based on three concepts:

• Transformation function (vector of priorities of the scale at the equilibrium point);
• Rate of change (at the equilibrium point);
• Center of gravity (at the equilibrium point).

The local thresholds of the scales are obtained from the functions that transform the ordinal scales into cardinal scales, also known as transformation functions.

The transformation function represents the preference intensity ratios of the values described in the ordinal scale and transforms them to a cardinal scale of absolute ratios.

The properties of the absolute ratio scales allow the scales to operate directly with their values allows us to combine various scales with each other and, from this, to calculate local and global thresholds.

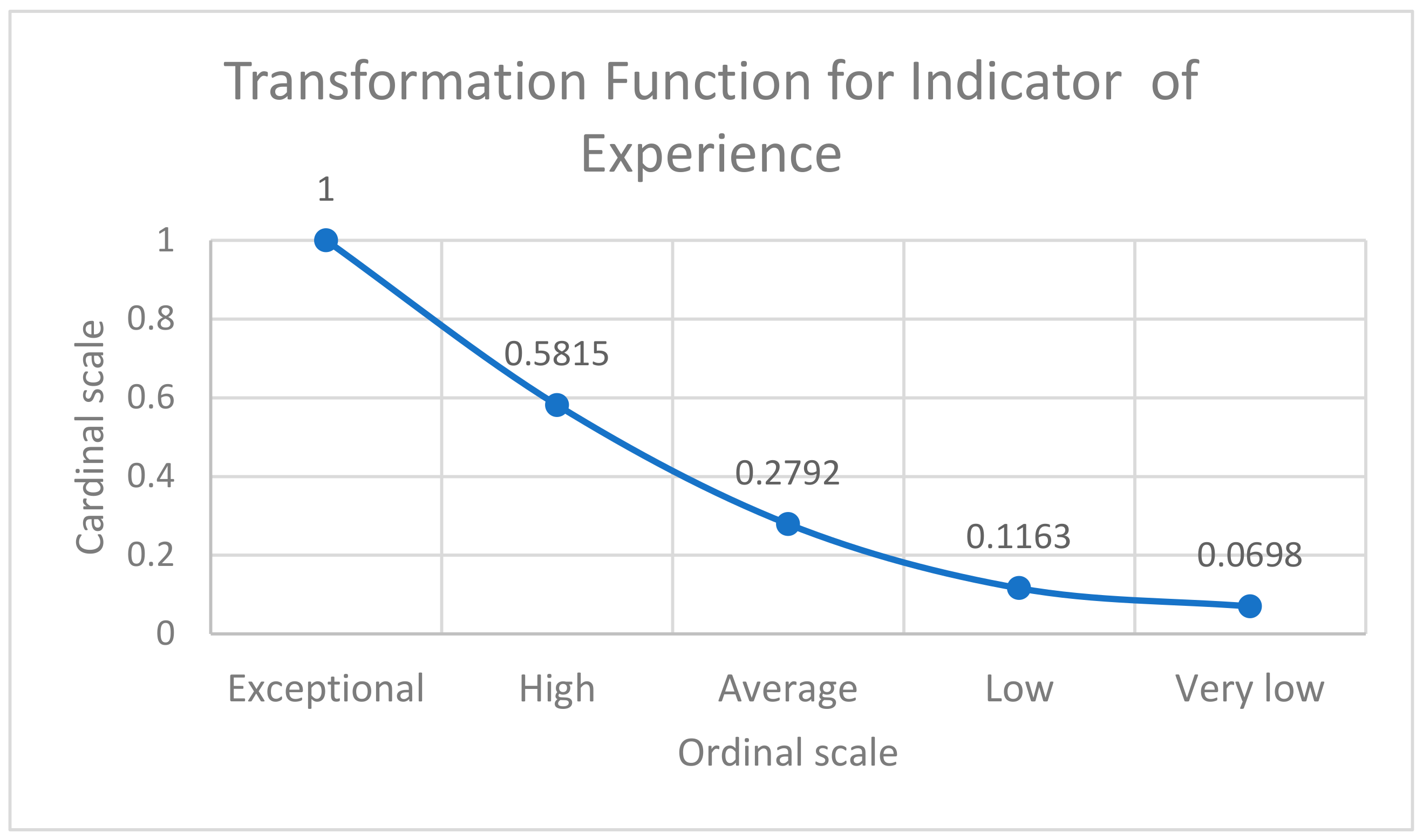
4.1. Transformation Function

The transformation function allows for the transformation of ordinal values into cardinal values on an absolute ratio scale so that they can be used arithmetically, capturing the differences in intensity between the different levels of the scale. To accomplish this, a PCM is constructed which, with the help of the expert, allows for the priorities to be determined (preference intensities) between the different levels of the scale.

Table 6. Pairwise comparison of scale intensities with their cardinal priorities.

Ordinal Scale of Insufficient Education Level	High	Moderate	Low	Very Low	Cardinal Scale of Insufficient Education Level
High	1	2	7	9	1
Moderate	1/2	1	4	6	0.5524
Low	1/7	1/4	1	3	0.1736
Very Low	1/9	1/6	1/3	1	0.0847
Ordinal					Cardinal

shows a PCM of scale intensities with the cardinal priorities (indicator extracted from a risk model).

A typical question for this PCM would be “Regarding the indicator “insufficient level of education”, which is riskier, High or Low?” The answer is that high is riskier than low. The next question would be “how much riskier?” The answer is very strongly riskier, which, on Saaty’s fundamental 1–9 scale, corresponds to the value 7 (description of element a₁₃ of the PCM) [26,27]. Graphically, the function is as shown in Figure 9. The “null” level has been added to this scale for practical reasons (it is not a requirement).

Indicator: Insufficient Level of Education
Level	High	Moderate	Low	Very Low	Null
Value	1	0.5524	0.1736	0.0847	0

In this way, the scale of five ordinal descriptive levels on the X axis is transformed into a scale with numerical levels whose values belong to a scale with absolute ratios that reflect the intensities of preference (cardinal scale on Y axis). This is the first step in determining the local threshold (LT) value in the scale. The next step is to determine the rate of change embedded in this function.

4.2. Rate of Change

The rate or ratio of change is the extent to which one variable changes with respect to another, which can also be expressed as the change value of one variable with respect to another [34]. Once the scale transformation function (the vector of indicator intensities) has been obtained, it is necessary to calculate the rate of change of the expert with respect to the components of the vector. The question here is “what is the expert’s rate of change with respect to moving from one level to an adjacent level of the scale?” Or in plain words: how many “Lows” are worth a “Moderate” for the expert?

The first step in this rate of change approach is to identify the type of evaluation model being used. Is it one assessing disadvantages (risks or costs model) or a framework assessing advantages (opportunities or benefits model)? Both cases will be discussed since there are different expressions for calculating the threshold depending on whether the model is about risks or benefits.

4.3. Center of Gravity

The center of gravity is defined as the geometric point where the structure or system is balanced, that is, where the structure can be laid in a point that keeps its global balance. The relevance of the center of gravity is that it is the point where one level precisely equals the next adjacent level, which makes it possible to answer the question “how many ‘Lows’ make one ‘Moderate’ at the equilibrium point?” This concept will be further explained in Section 4.5.

The center of gravity is given by the following formula:

$$\mathrm{C}\mathrm{G}=\frac{\sum (wi\ast Yi)}{\sum (wi)}.$$

(1)

Equation (1) shows that every piece of the system moves the center of gravity (CG) based on its own importance (wi) and distance from the origin (Yi) divided (normalized) by the total weight of the system.

4.4. Application of an RCCG Approach in a Risk Model

Based on the above rationale, the following function, which focuses on the rate of change from a moderate-risk to a low-risk level, is proposed as a measure of the local threshold (LT) between the adjacent moderate (M) and low (L) levels of an indicator scale for the case of a risk model.

$$\mathrm{LT}=\frac{(1\ast M+(M/L)\ast L)}{(1+\frac{M}{L})}=\frac{2ML}{(M+L)},$$

(2)

where the ratio (M/L) corresponds to the rate of change when moving from moderate to low.

It is important to note that all the values described here belong to an absolute ratio scale and vary in a range from 0 to 1. Also, note the similarity of the form of Equation (2) with the center of gravity formula Equation (1). The values 1 and (M/L) of Equation (2) correspond to the weights w₁ and w₂ of Equation (1), and the values of M and L correspond to the coordinates Yi of the priority vector plotted in the transformation function. The sum of (w₁ + w₂) = (1 + M/L) represents the total weight of the system. This correspondence between Equations (1) and (2) is not a coincidence and is explained below.

4.5. Construction of LT Calculation Function

There are several explanations for the choice of the LT local threshold calculation function and how to construct it. But first, we must remember that we are looking for a threshold, that is, a cut-off point, a limit, or balance point, where a little more or a little less removes us from the maximum efficiency value (whether this is a risk or a benefit). The breakeven point should lie between two adjacent values of the scale; therefore, it is possible to approach it using a weighted linear function such as the center of gravity function (Equation (2)).

Then, the threshold calculation function must have a weighted linear form, as in Equation (3):

LT = w1 ∗ Y1 + w2 ∗ Y2.

(3)

The function has two elements since the threshold considers only two adjacent points (levels) of the transformation function.

Equation (3) is a good approximation for two reasons:

• It considers balance in terms of the parameters of the function; that is, if one parameter is changed, the other will also change to compensate (concept of center of gravity).
• It is always possible to interpolate a nonlinear function constructed by points using a weighted linear function as long as it is between two adjacent points of the function to be approximated (Taylor application).

If we assume that these two adjacent points of the LT function (they could be any two adjacent points) are the moderate “M” and low “L” levels, then the position values Y1 and Y2 will be M and L, respectively, as in Equation (4):

LT = w1∗M + w2∗L.

(4)

Now, it is necessary to define the values of w₁ and w₂ for LT (note that w₁ + w₂ = 1).

By construction, w₁ and w₂ correspond to the weights or relative importance of M and L; therefore, it is possible to obtain these values by applying the same concept of the PCM for a two-level matrix to compare M and L elements. The general priority vector of a 2 × 2 matrix with a comparison parameter k is given by the pair w₁ = k/(k + 1) and w₂ = 1/(k + 1).

This is because the 2 × 2 matrix M = $\begin{array}{cc}1& k\\ 1/k& 1\end{array}$ is 100% consistent since its initial state.

Therefore, its priority vector at the equilibrium point is any normalized column. By normalizing column 2, the priority vector {k/(k + 1), 1/(k + 1)} is obtained.

As previously mentioned, the interpolation of two adjacent points of a scale transformation function can be adequately approximated by a weighted linear function, such as the LT calculation function. If we consider that the two points to be interpolated are M “Moderate” and L “Low”, then the weights of these points correspond to the priority vector at the balanced point, where it is interesting to calculate LT (at the limit or equilibrium point). Then, w₁ = 1/(k + 1) and w₂ = k/(k + 1), with k > 1.

In a risk model, the low level or L point is considered a reference point; that is, it is more important or with more weight than the M point. Then, the weight of L will be w₁ = k/(k + 1), the weight with the highest value; while the weight of M will be w₂ = 1/(k + 1), the weight with the lowest value. It is called a reference point because in a risk model, the starting point needed to estimate the maximum limit of tolerance of the expert is the lower adjacent level (low).

If a benefits model was being used, then the location of the reference point would be reversed, assigning w₁ to M and w₂ to L since the starting point needed to estimate the minimum limit of tolerance for the benefit by the expert is M.

Therefore, when replacing the values of w₁ and w₂ in the initial LT expression, it becomes Equation (5):

LT = 1/(k + 1) ∗ M + k ∗ (k + 1) ∗ L.

(5)

Rearranging the terms, LT takes the most defined form of Equation (6):

$$\mathrm{LT}=\frac{(1\ast M+\mathrm{k}\ast L)}{(1+\mathrm{k})}.$$

(6)

In this way, all that remains is to determine the value of “k”, which represents the number of units of L required to “balance” one unit of M (i.e., how many Ls make one M at the limit or the equilibrium point). In other words, “k” corresponds to the rate of change between M and L at the equilibrium point. Therefore, k = M/L.

Replacing “k” in Equation (1) gives the final expression for the local threshold as a function of the values of M and L:

$$\mathrm{LT}=\frac{(1\ast M+(M/L)\ast L)}{(1+\frac{M}{L})}.$$

(7)

This simplifies to

$$\mathrm{LT}=\frac{2ML}{(M+L)}.$$

(8)

Figure 10 allows for a graphic appreciation of what has been previously described for a numerical case of a risk model.

4.6. Rate of Change and Center of Gravity in a Benefits Model

The following function is proposed as a measure of the LT between the adjacent moderate (M) and low (L) levels of a scale for a benefits model. Notice that the formula is deduced via the same process applied for a risk model. The difference is the new location for the rate of change (M/L). This rate represents the importance or weight of M before L.

$$\mathrm{LT}=\frac{\left(\frac{M}{L}\right)\ast M+1\ast L}{\left(\frac{M}{L}\right)+1}=\frac{(M^2+L^2)}{(M+L)}$$

(9)

Again, note the similarity with the formula for the center of gravity seen in Equation (1). In this case, the ratio of change weights the largest element (M); this is because being a benefits model, the threshold defines the minimum tolerable benefit, which implies taking the highest value as a reference point and going down through the transformation function until reaching the point of maximum stress or minimum acceptable benefit. It is important to note that all the values described here belong to an absolute ratio scale and vary in a range from 0 to 1. Some reference points and extreme values that Equations (2)–(9) can take are described below.

Three important considerations:

1.

It is supposed that LT is located between the adjacent levels M and L. Although this is the general case, sometimes, the adjacent levels may be others. For example, LT could lie between the levels M = moderate and H = high, which would be strange in a risk model but not impossible. In this case, it is enough to replace “M” with “H” and “L” with “M” in Equation (9).

2.

In a risks model, the aim is to stress the risk (maximum tolerable risk); while in a benefits model, the aim is to stress the benefit (minimum acceptable or tolerable benefit).

3.

In a benefits model, the treatment is the same, but the reference point is changed to the highest level and the direction of the arrow is going down (reversed with respect to Figure 10). In this example, we take the reference point (RP) on M and go down through the transformation function. This is because in a profit model, one must start from the highest level and look for the minimum tolerable profit (profit threshold of the scale).

4.7. Some Singular and Reference Points for Risks and Benefits Models

Next, we discuss some concepts that show how the equilibrium point compares with some classic analytic points like the average and extreme values of minimum and maximum.

• The Average point:

The arithmetic average of adjacent values of a scale will always be greater than LT in a risks model and lower than LT in a benefits model:

$$\mathrm{LT}=\frac{2ML}{(M+L)} \le \frac{(M+L)}{2} \le \frac{(M^2+L^2)}{(M+L)}$$

(10)

It is interesting to note that both for the case of maximum risk and minimum benefit, the arithmetic average is not a good predictor of the threshold value. This, in general, is in accordance with reality. The scale transformation functions are generally exponential functions and do not follow a linear equation as the arithmetic average does.

• Binary Scales:

A binary scale (0, 1) is a particular type of scale with only two levels, where the cardinal scale coincides with the ordinal scale at the limit. On a scale with only two levels, the limit of a ratio scale is an ordinal scale. As can be seen in the generic coordinate vector for a 2 × 2 matrix: {1/(k + 1), k/(k + 1)}, when “k” tends to infinity, it becomes the binary scale (ordinal scale) 0–1. Therefore, the limit of a cardinal scale is an ordinal scale.

In a binary scale of a risk model, the maximum acceptable risk is zero; that is, a risk greater than the minimum possible is not allowed in a binary variable. This occurs because the next value on the scale is one which is the maximum value (an unacceptable value in a risk model). Replacing the values of the binary scale in Equation (8) (M = 1 and L = 0), LT = 0 is obtained, which corresponds to the expected value for the local threshold on a binary scale

In a binary scale of a benefits model, the minimum acceptable benefit is the maximum of the scale. That is, a benefit less than the maximum possible value in a binary scale is not allowed (this occurs because the next value on the scale is zero). Replacing the values of the binary scale in Equation (9) (M = 1 and L = 0), LT = 1 is obtained, which corresponds to the expected value for the local threshold on a binary scale. Notice that the average formula does not return the expected value of 0 for the local threshold in the risk model or the expected value of 1 in the benefits model.

• Special situations:

Extreme values are given in special situations and particularly selected by the expert.

• Extreme Values in a Risk Model:

If the expert decides that the threshold is between low (L) and very low (VL) on a scale with very high, high, moderate, low, and very low levels, the LT value is given by

$$\mathrm{LT}=\frac{2L(VL)}{L+(VL)}.$$

(11)

Or, if the expert considers the threshold to be between high (H) and moderate (M), the LT value is given by

$$\mathrm{LT}=\frac{2HM}{H+M}.$$

(12)

• Extreme Values in a Benefits Model:

If the expert decides that the threshold is between moderate (M) and high (H) on a scale with low, moderate, high, and very high levels, the LT value will be given by

$$\mathrm{LT}=\frac{H^2+M^2}{(H+M)}.$$

(13)

Notice that one must use only the adjacent levels of the scale to calculate LT. The more levels the scale has, the more precise the scale is, and the better the LT calculation will be.

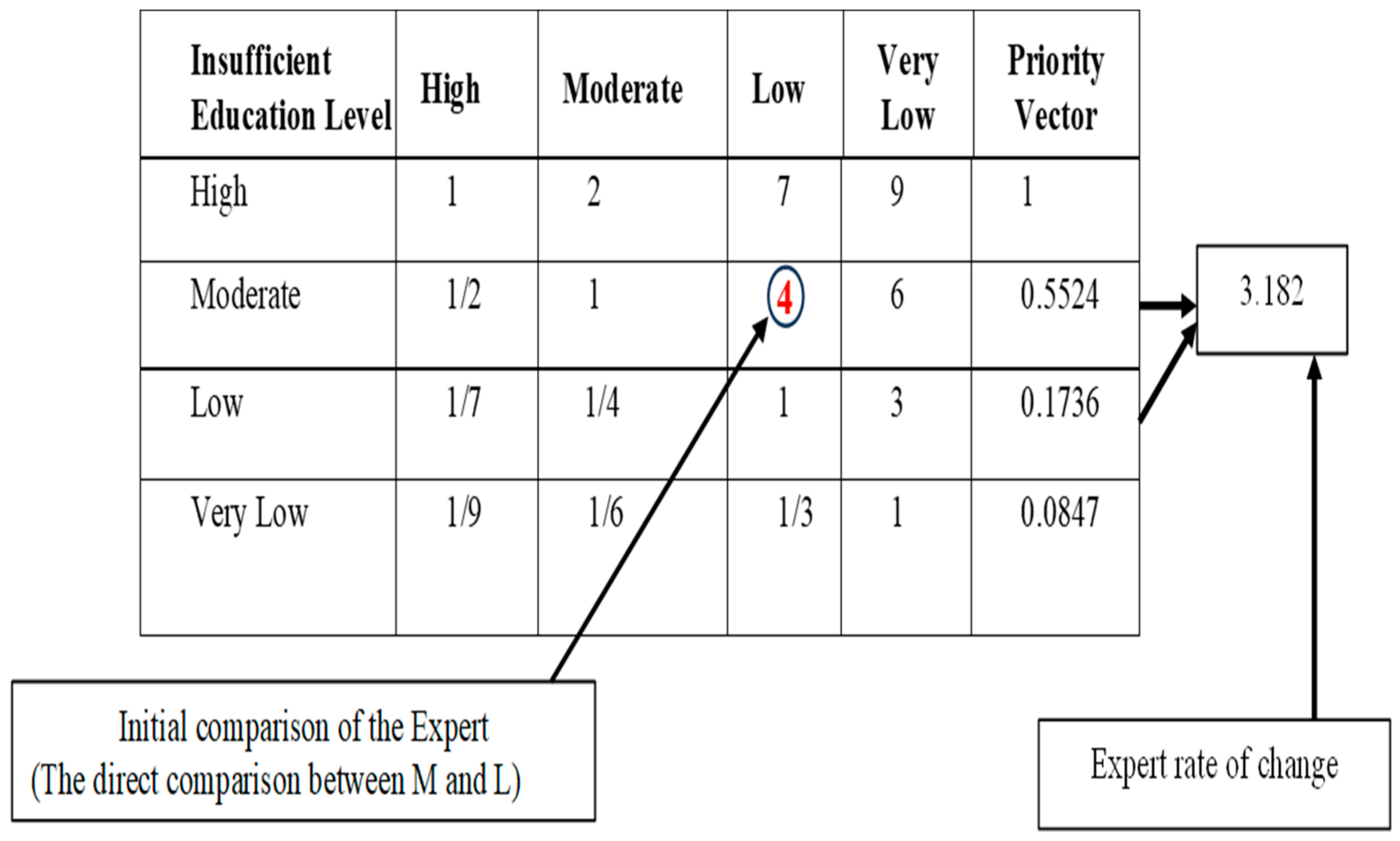
4.8. Example of LT Calculation for a Risk Model

Below is a step-by-step example of an LT calculation for a risk model. This is a simplified example, using information from the Ministry of Social Development (MDSF) to calculate the urban and social deterioration composite index (IDUS). The hierarchical model (simplified) is as follows.

Figure 11 shows a multicriteria global risk composite index. Under the criterion “Population Vulnerability”, there are two local indicators of sociodemographic susceptibility, namely, “Insufficient Level of Education” and “School Absence”. Each of these local indicators presents an absolute measurement scale. The indicator “Low Level of Education” has been used as an example to calculate LT.

First, the pairwise comparison matrix is constructed for the “Low Level of Education” indicator scale, and the upper part of the matrix is completed by the expert.

Figure 12 shows that the initial exchange value (the initial comparison) between medium and low given by the expert is 4. However, if all the possible comparisons are made between the medium and low nodes of the matrix, then the value of the expert for the rate of change at its equilibrium point is 3.182. The value obtained this way has two important advantages: it is closer to the true value that the expert has in mind, since it takes into account all the pair comparison of the matrix (all the possible paths to go from medium to low); and it is a number that belongs to an absolute ratio scale. Note that the value obtained from the expert that is applied to the PCM is a better value because the more questions that are asked about a specific issue (keeping an acceptable index of consistency), the more precise the answer will be, diminishing any possible bias that the expert might have about risk tolerance.

Following the procedure above, the direct value given by the expert is adjusted, considering all the comparisons in the matrix from 4 to 3.182. The difference is almost a 26% excess of risk. Notice that if we keep the direct value of 4, we would be in a scenario of 26% tolerance above the real acceptance tolerance level of the expert, which could lead to a higher-cost project design since the tolerance level will be set as a lower value, which will be harder to reach.

4.8.1. Interpretation of this Procedure by the Expert

In the previous PCM, the expert provided a comparison ratio (M/L) equal to 4 for the comparison in cell (3,2) between the moderate and low levels using Saaty’s fundamental scale; that is, in the “Insufficient Level of Education” indicator, the moderate level (M) is 4 times riskier than the low level (L). However, if we consider the rest of the comparisons, it is clear that at the equilibrium point, the expert is willing to go from rate of change M/L = 4 to the rate of change M/L = 3.182. This implies that the expert is susceptible to change due to greater risk and going from M/L = 4 to M/L ≈ 3, which leads to a good balance and the maximum stress value when the change ratio M/L is closer to 3. The exact value for this rate of change is precisely M/L = 0.5524/0.1736 = 3.1820.

When this rate of change value is entered into Equation (8), LT = 0.2642 (26.42%).

4.8.2. Conclusion for the Local Threshold LT

The LT value indicates that any project that presents a local risk for this indicator greater than 26.42% must be reviewed.

4.8.3. Compensatory and Non-Compensatory Method

In a compensatory approach, poor value indicators in one dimension can be compensated by good value indicators in a different dimension. Non-compensatory approaches do not allow for this tradeoff [16,35]. If a compensatory approach is applied, then the decision-maker must determine if it is acceptable to compensate a value above the threshold in this indicator with risk values below the local threshold in other indicators. If, on the other hand, the compensation approach is not acceptable due to the type of decision, then improvements or palliative measures must be taken until a value lower than the local threshold is achieved in this local indicator. The same procedure must be followed for all local indicators of the model.

4.9. Global Threshold (GT)

The global threshold (GT) is defined as the weighted superposition of the local thresholds of each measurement indicator (terminal criterion) of the risk or benefits model. In this way, once all the LT of the model have been calculated, it is possible to calculate the GT as the weighted sum of the LT. The value of the GT is given by Equation (14):

GT = Σi (LTi ∗ WGi)    I = 1, to number of indicators,

(14)

where:

• GT = global threshold;
• LTi = local threshold of indicator “i”;
• WGi = global weight of indicator “i”.

To demonstrate the procedure, we consider only four indicators (

Table 7. Example of GT calculations.

Terminal Criteria (Indicators)	LT(i)	WG(i)	LT(i) ∗ WG(i)
Exposure to greenhouse gas emission sources	0.2999	0.5288	0.1586
Exposure to pollutants (binary variable: 0–1)	0	0.1454	0
Exposure to noise emissions	0.2999	0.1604	0.0481
Exposure to micro garbage dump	0.2494	0.1654	0.0413
GT	-	1.0	0.2480

) for the previous IDUS model (Figure 9) to calculate the corresponding GT.

From Table 7, if an alternative or a project exceeds the value 0.2480 (24.80%), then the global risk is excessive and (technically) it should not be accepted as a feasible alternative. For example, in a territory subject to a risk of disaster, the planner should be prepared to increase the territory resilience against the threat in an efficient (focused) manner. To accomplish that, we need the precise amount of excessive risk to bring the risk to an acceptable level, that is, lower than the GT value. If it were a benefits model, the previous value of 0.2480 would correspond to an acceptable minimum; that is, no stock or project with a benefit less than 0.2480 should be accepted.

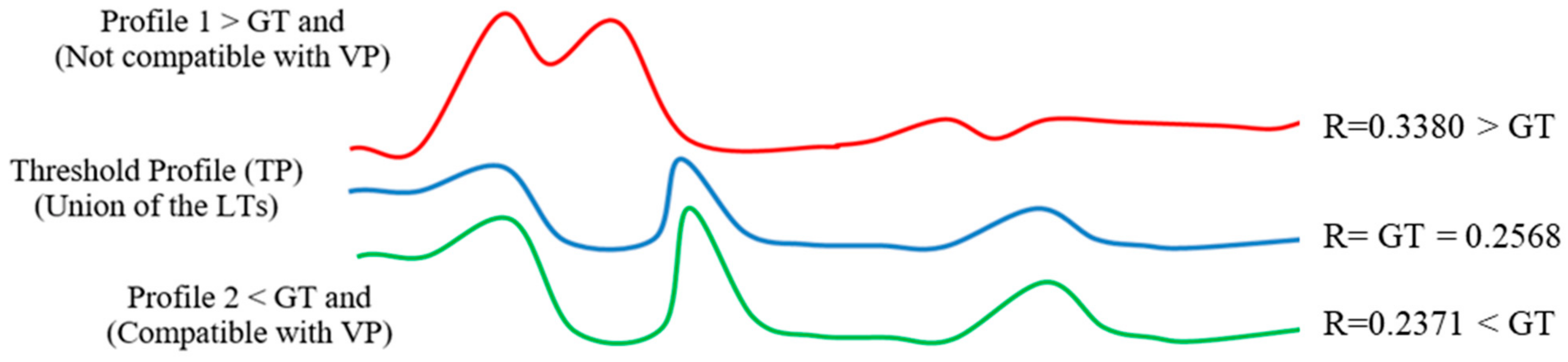
4.10. Combining Global Threshold with Compatibility Index G

A very useful application emerges when combining the G index, which measures the general behavior of the alternative, with the GT, which measures the final value of the alternative. The objective of this procedure is to increase security regarding the chosen alternative. First, it is necessary to define the G index, its conditions of use, and its mathematical foundations. The G index (Garuti index) can be defined as the mathematical generalization of the J index (Jaccard index), which was defined in 1901 and is widely used in the field of biology for species recognition [36,37]. The general expression of the index G for two vectors, A and B, is shown in Figure 13.

$$G=½ \sum \mathrm{i} (ai+bi)\frac{Min(ai, bi)}{Max(ai, bi)}$$

(15)

Conditions of vectors A and B:

A and B are stochastic vectors (they must add to 1) and represent the set of alternatives or weights. There are no negative values; that is, $ai \mathrm{and} bi$ are positive numbers.

Since this article is oriented to AHP/ANP models, there is a reduced (and more precise) expression when the vector of weights {W} is known, which is the case in AHP/ANP models; thus, we replace ½ (ai + bi) with w_i.

Therefore, the new compatibility equation for the AHP/ANP model is

$$G=\sum \mathrm{i} wi\frac{Min(ai, bi)}{Max(ai, bi)}.$$

(16)

The conditions of use, properties, and threshold of index G are now discussed.

4.10.1. Conditions of use

• Belonging and Representation

Vectors A and B belong to the same AHP/ANP structure, although they can have different values for the set of criteria weights and for the set of profiles of alternatives. For the criteria case, their weights must add to 1. For the alternatives case, they do not need to add to 1. When the alternatives are evaluated against the indicators (point to point), they represent the profiles of behavior, and some local values can be zero. In this case, it is necessary to change the coordinates for both vectors in the location where the zero appears. For example, suppose the following vectors of behavior for two alternatives A and B are A = {0.321, 0.0, 0.771} and B = {0.321, 0.003, 0.772}. They are almost the same vector (full compatibility or close is expected), but if G is calculated without changing the coordinates, then G = w₁∗ 1 + w₂ ∗ 0 + w₃ ∗ 1; if w₂ is large, then G will not reflect the big similarity between both vectors. Therefore, it is necessary to change the coordinates for the second position (the position with the zero value) so A = {0.321, (1–0), 0.771} and B = {0.321, (1–0.003), 0.771} and G = w₁ ∗ 1 + w₂ ∗ 0.997 + w₃ ∗ 1, which is the expected value of compatibility for A and B.

Suppose now that indicator 2 (i = 2) has a binary scale for the evaluation of the alternatives A and B; then, A = {0.321, 0.0, 0.771} and B = {0.321, 0.0, 0.771}, and it becomes evident that we cannot use Equation (16) directly and it is absolutely necessary to change the coordinates (otherwise division by zero will happen when calculating G). However, with the change of coordinates to A = {0.321, (1–0), 0.771} and B = {0.321, (1–0), 0.771}, then G will be exactly w1 + w2 + w3, as expected. This condition (the zero local value condition) is very important to verify before using Equation (16), especially for the risks models.

• Consistency

Vectors A and B are acceptable consistent vectors. Compatibility is intended only for consistent or near-consistent systems.

• Normalization

Vectors A and B are stochastic vectors (they must add to 1) for the criteria set. This is not necessary for the set of alternatives when working in the absolute mode of evaluation (the rating mode) since they are weighted by the {W} vector.

4.10.2. Properties

Continuity of function G: 0 ≤ G(A,B) ≤ 1

G is a continuous function and returns a positive real number in the [0–1] range. There are no singularities.

Symmetry: G(A,B) = G(B,A) The compatibility measured from A to B is equal to the compatibility measured from B to A.

• Non-Negativity

G(A,B) = 0 if A and B are perpendicular vectors. If A ⊥ B, then G(A,B) = 0 (null projection);

G(A,B) = 1 if A and B are parallel vectors. (A and B is the same vector).

• Triangular Inequality

If two of three combinations of vectors A, B, and C are compatible, then G(A,C) ≤ G(A,B) + G(B,C). The triangular inequality property allows for compatible and incompatible vectors to be combined since it requires only 2 of the 3 possible vector combinations—(A,B), (A,C), or (B,C)—to be compatible. This important degree of freedom gives the opportunity, for example, to add one value system not compatible with every component of the original system without violating the triangular inequality condition. Also, using a step-by-step pairwise comparison process, there is a possibility of gaining compatibility for the new system (the system that contained/added a new value system not compatible with all the elements of the old system).

4.10.3. Threshold of Compatibility

If G(A,B) ≥ 0.9, then A and B can be considered compatible vectors. However, for certain cases, values of G greater than or equal to 0.85 can be considered as compatible vectors. On the other hand, G = 0.65 or less can be considered a random result for compatibility.

There is an interesting parallel between metric topology (distance) and order topology (intensity of preference) through the compatibility index G.

Table 8. Similarity between metric topology with D function and order topology with G function.

Metric Topology (Distance)	Order Topology (Compatibility)
D(a,b) = D(b,a) (Symmetry)	G(A,B) = G(B,A)
D(a,b) = 0 ⇔ a = b (Non null value)	G(A,B) = 1 ⇔ A = B
D(a,c) ≤ D(a,b) + D(b,c) (triangular inequality)	G(A,C) ≤ G(A,B) + G(B,C)

Note: D = function of distance (real non negative value); G = compatibility index (real non negative value); a, b, c = scalars; A, B, C = priority vectors (stochastic vectors)

shows this parallel.

Therefore, the G index shares the same conditions of the distance function and can thus be considered a valid metric (these metric conditions are not shared in every compatibility index). This is relevant because it allows the G to be used to measure similarity (compatibility) with high precision and confidence.

4.11. Calculation of Combining GT with G

The calculation to combine GT with G begins with the construction of a virtual alternative profile made up of different values of the local thresholds (LTi). We call this profile the TP (threshold profile). A TP is necessary because sometimes it may not be enough to comply with the GT, but it is clear that the chosen alternative has a good global value and also a good profile performance; that is, sometimes, it is necessary to verify its point-to-point behavior and not just its final risk (or benefit) value. In summary, the GT threshold is a necessary condition but not always sufficient.

It is useful to determine the performance profile of the alternative for two reasons, as follows:

• To avoid unwanted compensation;
• To avoid discarding a consensual alternative (acceptable for the majority) that does not comply with the GT condition in advance.

Note that in both cases, the alternative could be efficiently adjusted in one or more of its parameters to meet both conditions, i.e., the GT value and the performance of the TP.

By constructing the TP alternative from the set of the local thresholds, it is possible to determine the global behavior of the alternative in terms of its risks (or benefits), considering both the GT and its compatibility with the TP, which makes it possible to evaluate whether an economically efficient alternative can be adjusted in a way that is also an acceptable risk or benefit alternative.

Table 9. Combination of global threshold (GT) with compatibility index G in a risks model.

lternative/Scenario	GT (Risks Model)	G	Result
A1	A1 > GT Exceeds acceptable risk	G(A1;TP) < 85% Non compatible profile (not adjustable or too complex to be adjusted)	Rejected Alternative
A2	A2 < GT Does not exceed acceptable risk	G(A2;TP) > 85% Compatible profile	Selectable alternative (no adjustment required)
A3	A3 < GT Does not exceed acceptable risk	G(A3:TP) < 85% Non-compatible profile but possible to be adjusted	Alternative possible to be adjusted
A4	A4 > GT Exceeds acceptable risk	G(A4;TP) > 85% Compatible profile	Alternative possible to be adjusted

shows how to proceed with a risks model for the four possible scenarios that are generated when combining GT with G.

From Table 9, it can be seen that if an alternative belongs to scenario 1 (case A1), it has no viability as an alternative since it exceeds the acceptable GT. Also, its general behavior or point-to-point performance is inadequate; that is, any adjustment to this alternative would require major (normally very costly) changes in order to achieve a barely acceptable result.

In scenario 2 (case A2), the opposite happens. This is a very attractive alternative since it meets the GT value and presents good general behavior (compatible with the virtual alternative behavior). Scenarios 3 and 4 are combinations of compliance where one can have good overall compliance but poor overall behavior or vice versa. In these cases, it is possible to adjust the alternative (especially if it is an alternative that is very popular with the decision makers and/or stakeholders).

There is a little but important detail to note in scenario 3 (case A3). Here, there is a possibility that A3, defined by A3 < GT and G(A3;TP) < 85%, is equally selectable despite not being compatible with TP. This situation, although uncommon, can be verified when A3 is a very-low-risk alternative; that is, A3 << GT. This situation is most likely to happen when the set of local thresholds (the priorities ones) have been established with a very lax hand. To solve this, it is enough to evaluate G(A3;Pmin) with Pmin, i.e., the profile of the union of minimum values (no null) of the scale for each indicator of the model. If G(A3;Pmin) > G(A3:TP), then A3 is directly selectable. Simply put, the A3 behavior is closer to the minimum risk profile (Pmin) than to the threshold profile (TP); therefore, even though A3 is not compatible with TP, it is still a very selectable choice. Figure 14 gives an example of a risks model in graphic form.

The TP (the blue profile in Figure 14) corresponds to the local thresholds profile of the model indicators (from which GT is obtained). Profile 1 (the red profile in Figure 14) greatly exceeds the acceptable risk (0.3880 >> 0.2568). Furthermore, it presents a risk behavior profile incompatible with TP (G = 69.1% << 85%), with almost no possibility of being corrected, so it is not an eligible alternative and should be discarded.

On the other hand, profile 2 (the green profile in Figure 14) presents a global risk value lower than GT (acceptable global risk). Furthermore, its risk behavior profile is very compatible with TP (G = 95.7% >> 85%), making it a very eligible alternative.

Note that the value 0.85 has been used as the minimum value for the G index instead of 0.90 (its normal value). This is to provide a greater degree of flexibility since in this case, G is acting as a second-party verifier order.

For alternative types A3 and A4, which are not directly eligible, the possibility of adjusting the alternative can be evaluated in a way that meets both conditions (GT and G). To make this adjustment in an efficient way, it is necessary to identify the indicator (the place in the profile) that makes the greatest contribution to G if the alternative changes its value in the scale. In order to accomplish this adjustment, the maximum positive difference between the weight of the variable (w) and the compatibility (G) between the alternative and TP must be calculated according to Equation (17):

I = Max{w(i) − G (Ai; TPi)} I = 1, to number of indicators,

(17)

where:

• I = indicator that makes the maximum contribution to G if the alternative changes its value in the scale;
• w(i) = weight of indicator “i”;
• G (Ai; TPi) = compatibility between the profiles of the alternative and the threshold profile in the “i” indicator.

Then, the possibility of modifying (redesigning) the alternative for the selected indicator must be analyzed, attempting to improve its compatibility with TP such that both conditions are met simultaneously; that is: A < GT and G(A;TP) > 85%. Note that for the benefits model, the analysis is analogous, changing the sign of the inequality for GT in Table 9.

4.12. Combining Two or More Models

Combining two or more models is useful in case more than one model is needed to assess the global risk. For example, in a risk disaster model, one normally needs two or three different models: one for threats, one for vulnerability, and sometimes one more to include capacities (resilience) to assess the global risk.

In situations like this, the global risk threshold should be calculated in the same way in which the models are combined. So, if risk is calculated only as threats (T) times vulnerability (V) or (R = T * V), then the global threshold of risk will be the threshold of threats times the threshold of vulnerability (i.e., GT = TT * TV). The combined virtual risk profile (the combined TP) is built as the multiplication of the values of both profiles, point to point. This combined TP will represent the new reference profile for the compatibility assessment with every combined risk profile of the alternatives. The rest of the process of measuring the compatibility is the same as described in Section 4.11, applying Table 9 for combined scenarios.

4.13. Some Final Thoughts about Scales and Thresholds

• Scales of measurement

In the literature, the cardinal scales are normally closely linked to the data; that is, they are built directly from the collected data using a statistical approach. This, although not incorrect, is not recommended because it makes the scale dependent on the data (in reliability and quantity), and, most importantly, it disregards the interpretation of the data. The data do not bring more information than the data themselves and this may not give any representation of the true intensity of impact; the interpretation of the data must be given by the expert from an absolute measure perspective (not relative to the data). For example, going from 40 km/h to 80 km/h, the vulnerability (in the event of an accident) does not double, as the data show; rather, it quadruples in this case, and this is not reflected by the data. Another, more personal example: if the cost of a car goes from USD 20,000 to USD 40,000, my response/impact to that change (on the Saaty scale) will not be two times more, as the data suggest, but rather much more. This interpretation of the data is very important to capture since the data themselves does not provide that information (neither implicitly nor explicitly).

• Local and global thresholds

Something similar happens when calculating local thresholds. In general, it is produced from the data, making the threshold have a functional dependence on the data (a change in the data may produce a change in the threshold value). Again, while this is not incorrect, it is not recommended (even less so than in the previously described situation); this is due to two main factors:

1.

The local thresholds, and especially the global threshold, must represent an external element with respect to the set of alternatives and not be affected by the values that they may have; otherwise, adding, changing, or eliminating alternatives will cause the threshold values to vary, and this (in general) is not reasonable. The phrase “in general” is in parentheses because there are very particular cases where this could, in fact, be reasonable.

2.

The global threshold must depend on the importance (the weight) of the terminal criteria (the indicators). In this way, the global threshold value will reflect the relative importance of the model components in the same way as the alternatives do, ensuring that it is applying the same rule of measurement in both cases. Furthermore, this form of building the global threshold makes it possible to build a virtual alternative (the threshold profile or TP) and to compare the specific behaviors of every alternative through the compatibility index G and not just their final value (the global threshold), which is not always a sufficient condition, as explained in Section 4.11.

5. Final Conclusions

The definition of acceptance thresholds is essential in the definition of evaluation scales, both at the level of individual analysis indicators and for the objective of the decision model itself. The use of traffic lights is highly widespread because it operationally proposes levels of acceptance, alertness, and urgency upon which to act. In the literature, there are few developed references on the construction of these thresholds (beyond eminently empirical approaches), and there is a certain tendency to obtain them through statistical processes, probably in line with the growth of big data and data analytics.

However, threshold setting is not exclusively statistical because when solving problems in real life—outside the academic field—professionals, companies and even universities do not necessarily have the information applicable to the decision and its context. Because of this, the data do not contain all the needed information, and generating thresholds relative to the data themselves rather than absolute reference values is deceiving.

This study reinforces the need to evaluate with absolute instead of relative measurement, to have experts who assimilate new information instead of just data, and for them to have new, complementary tools to assist them in calculating acceptance thresholds.

Applications carried out so far at government levels have delivered very good results (e.g., the results from the Ministry of Social Development, the Ministry of Housing and Urban Planning, the National Emergency Office, the ECLAC (United Nations), and the Ministry of the Environment have been encouraging). New research should consider a comparison of results as opposed to focusing on purely statistical or empirical elements in addressing a variety of different decision-making problems, including the management of remote experts, and, above all, in the application of this procedure to new, pressing social problems.

The novel contribution of this study is its proposal of an analytical procedure, based on the rate of change and center of gravity (RCCG) theoretical concepts, which provides a framework for the experts’ knowledge, making it more valuable. This procedure can be applied in different contexts, challenging other available mechanisms in the correct calculation of the scale threshold value for each indicator and of the global threshold value of the entire model. It is important to emphasize that this procedure is not intended to replace the experts’ knowledge but rather to assist them in obtaining a reliable threshold value.