Dynamical Behaviors and Abundant New Soliton Solutions of Two Nonlinear PDEs via an Efficient Expansion Method in Industrial Engineering
Abstract
:1. Introduction
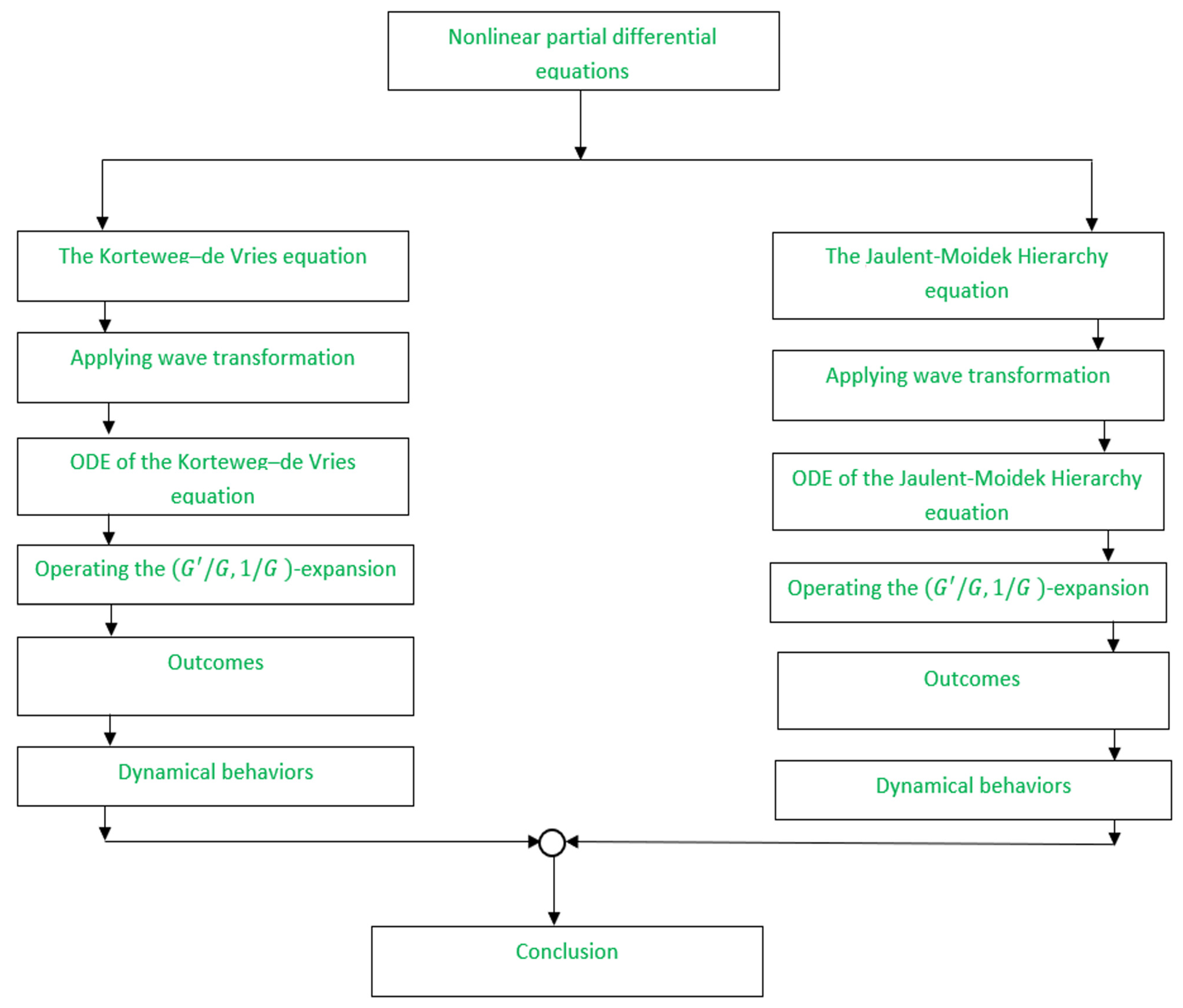
2. Basic Parts of the Proposed Method
3. Applications
3.1. The Nonlinear (1+1)-Dimensional Geophysical Korteweg–de Vries Equation
3.2. The Nonlinear (2+1)-Dimensional Jaulent–Miodek Hierarchy Equation
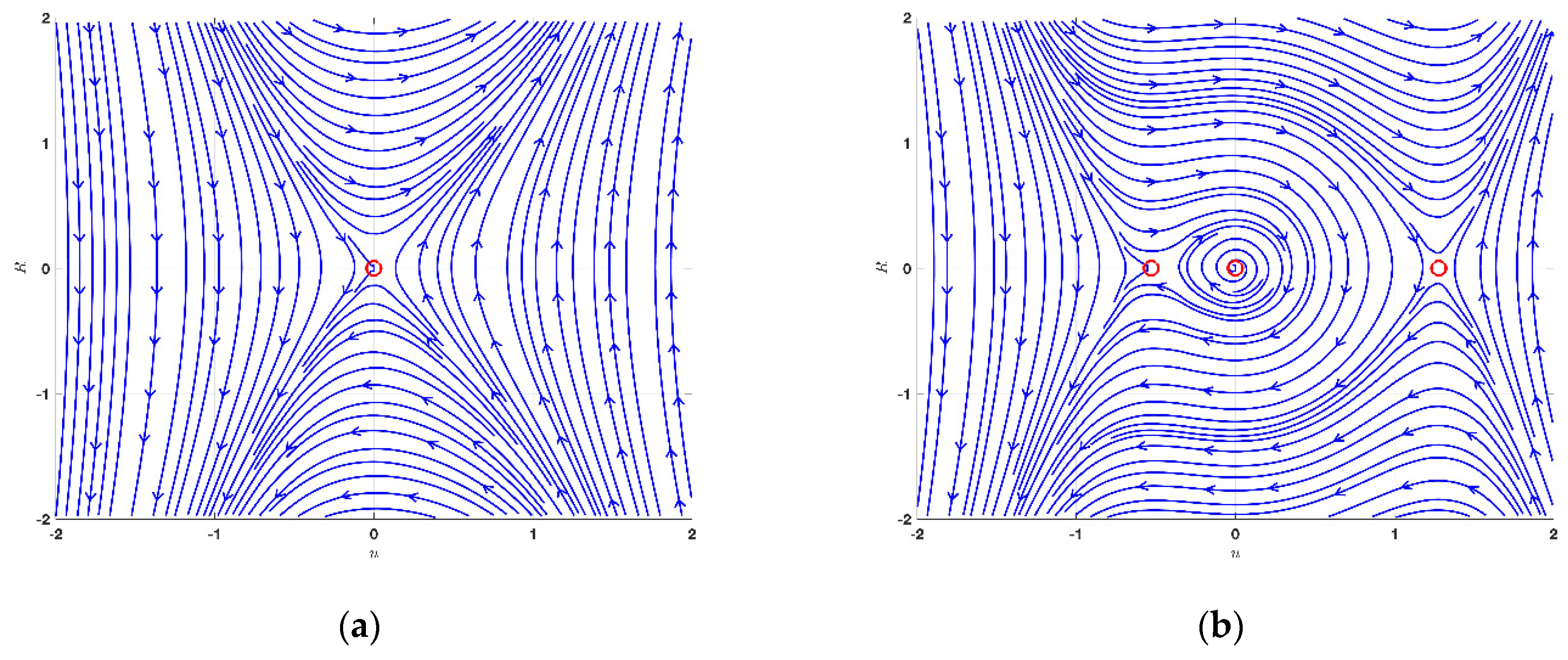
4. Bifurcation Phenomena
4.1. Bifurcation Phenomena of KdVE
- When is negative, represents a saddle point.
- When is positive, represents a center point.
- When is zero, represents a cuspid point.
4.2. Bifurcation Phenomena of JMHE
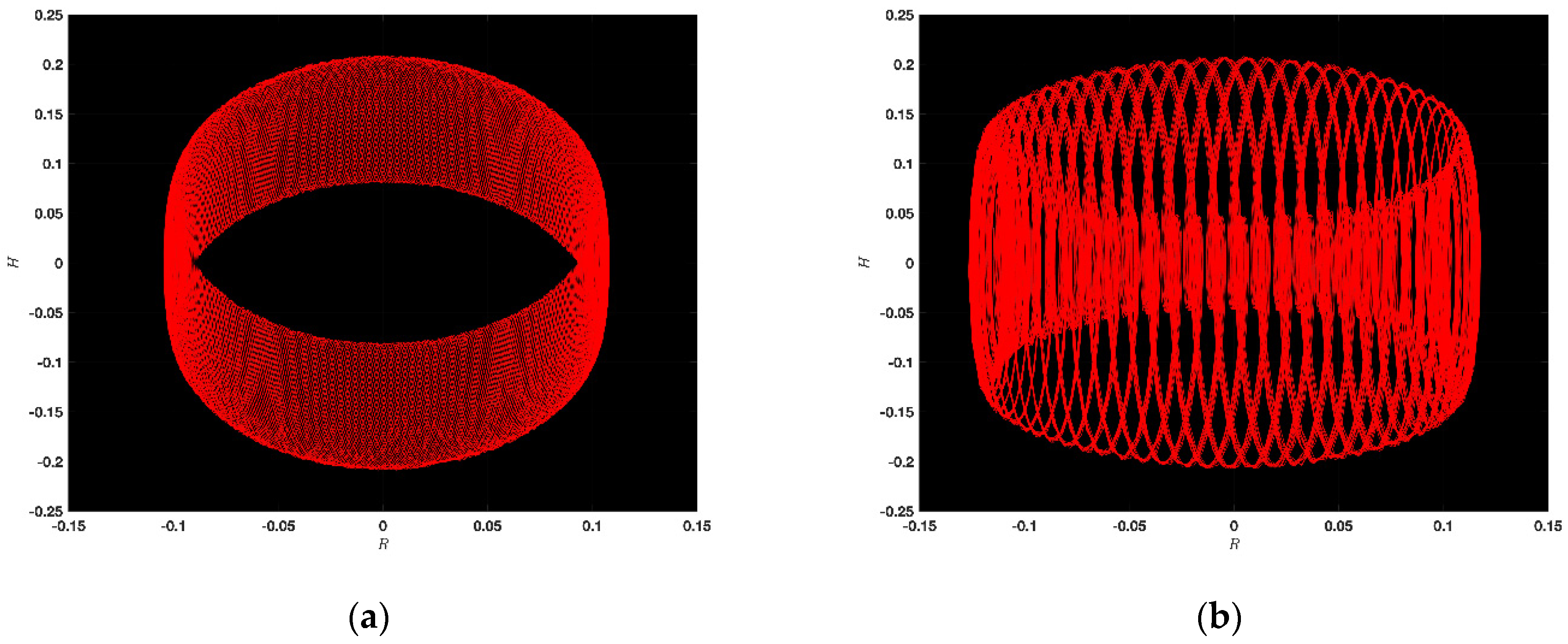
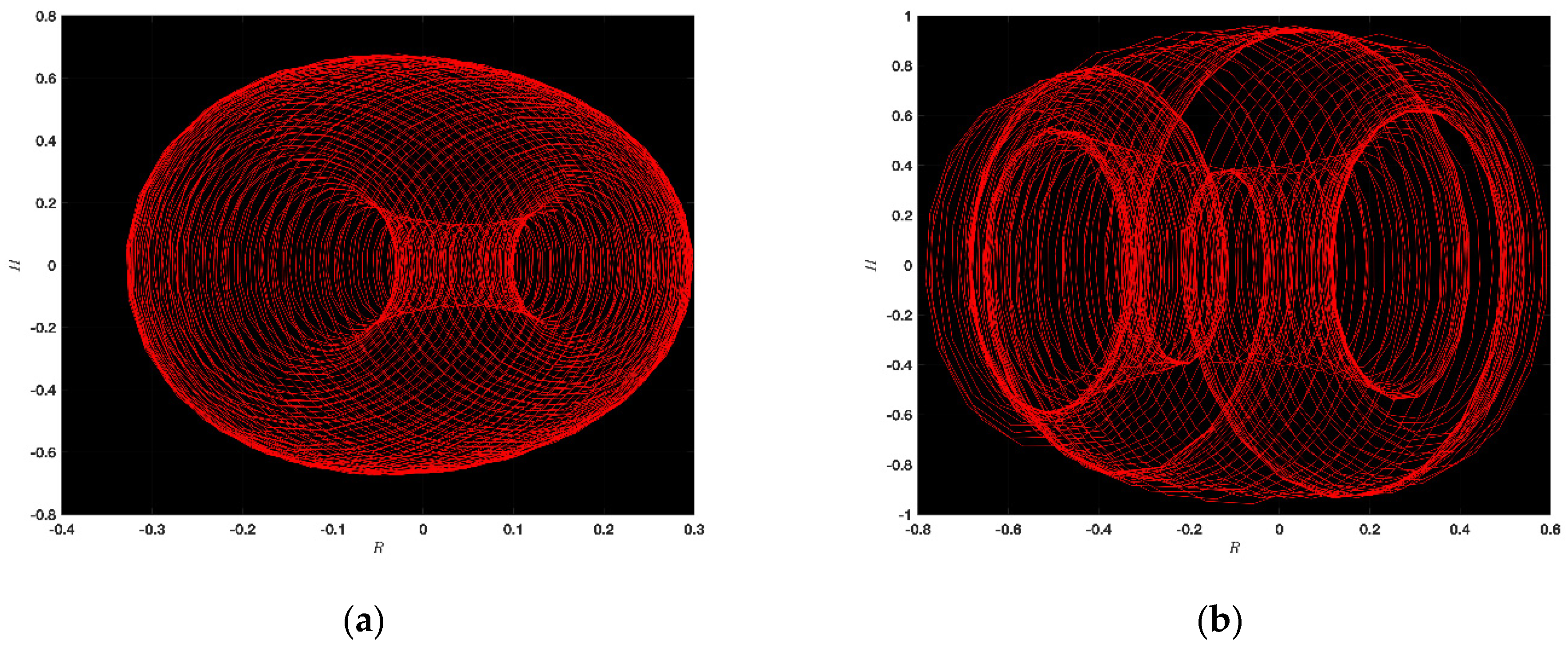
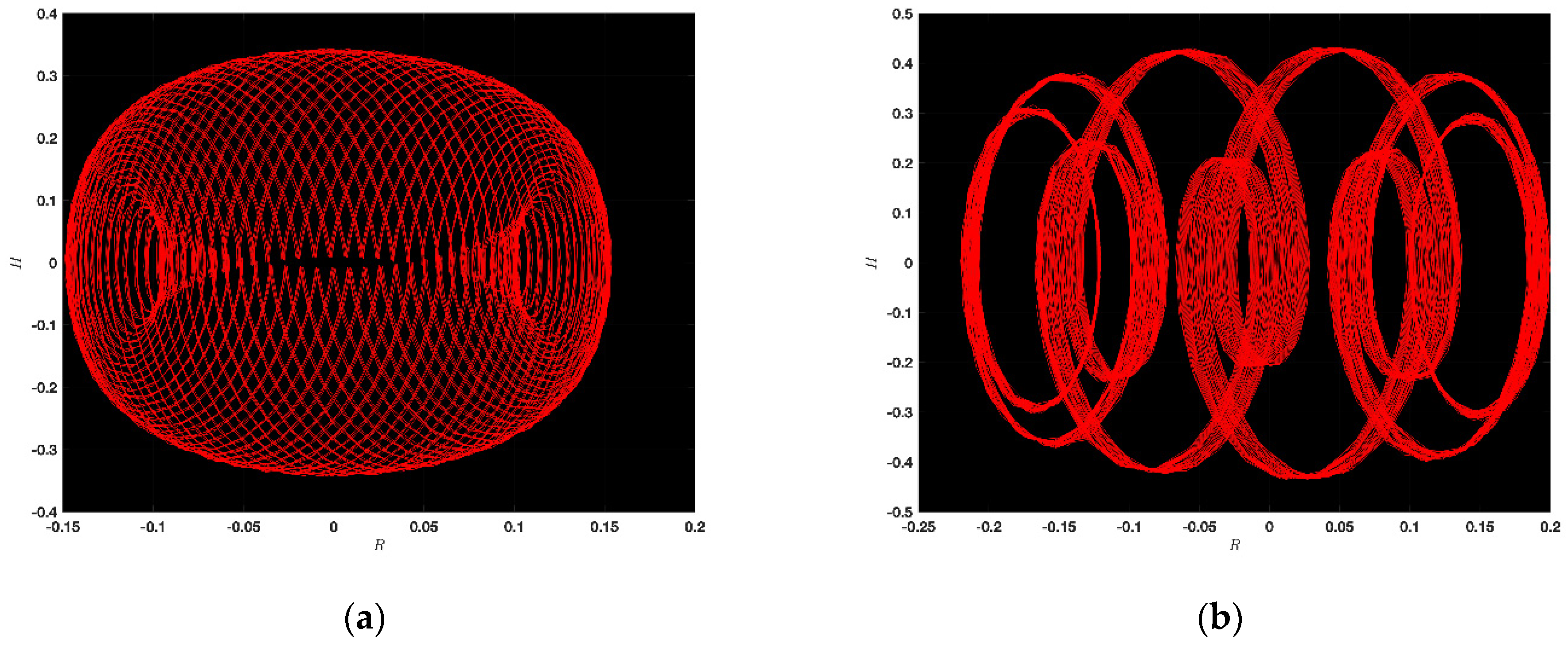
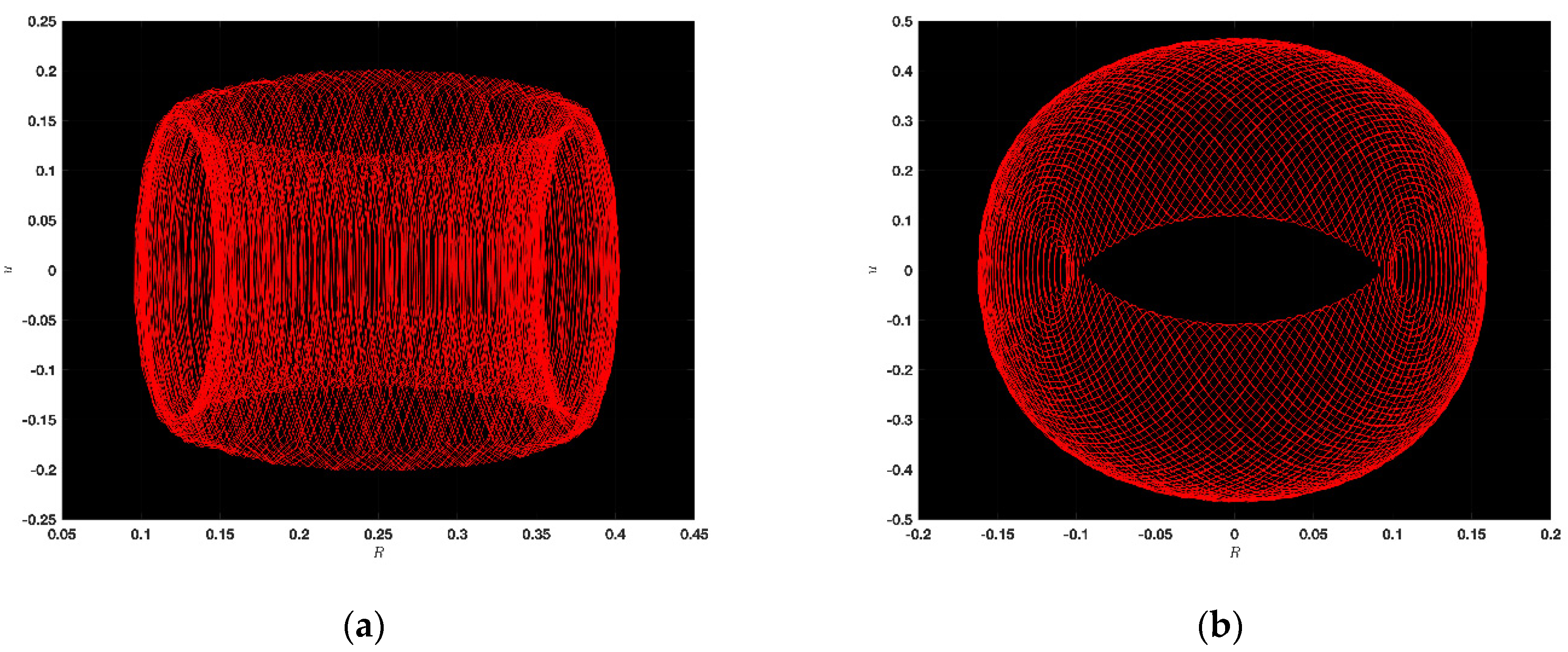
5. Chaotic Feature
5.1. Chaotic Analysis of KdVE
5.2. Chaotic Analysis of JMHE
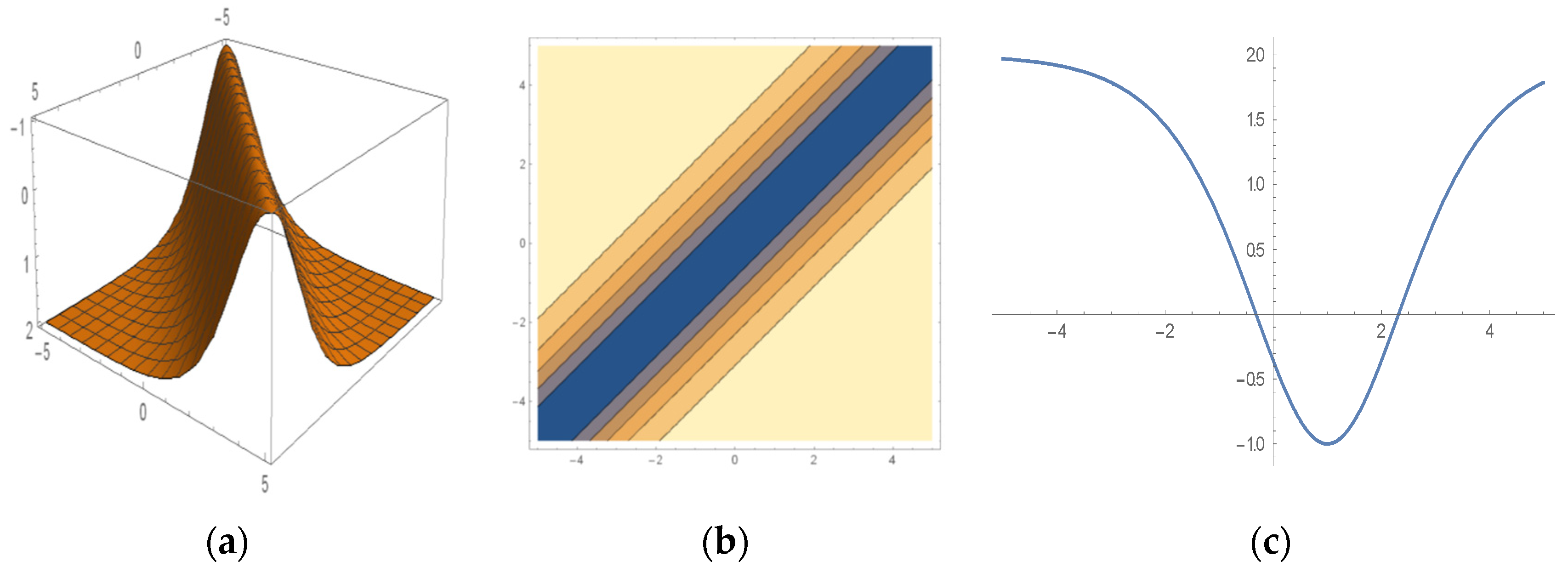
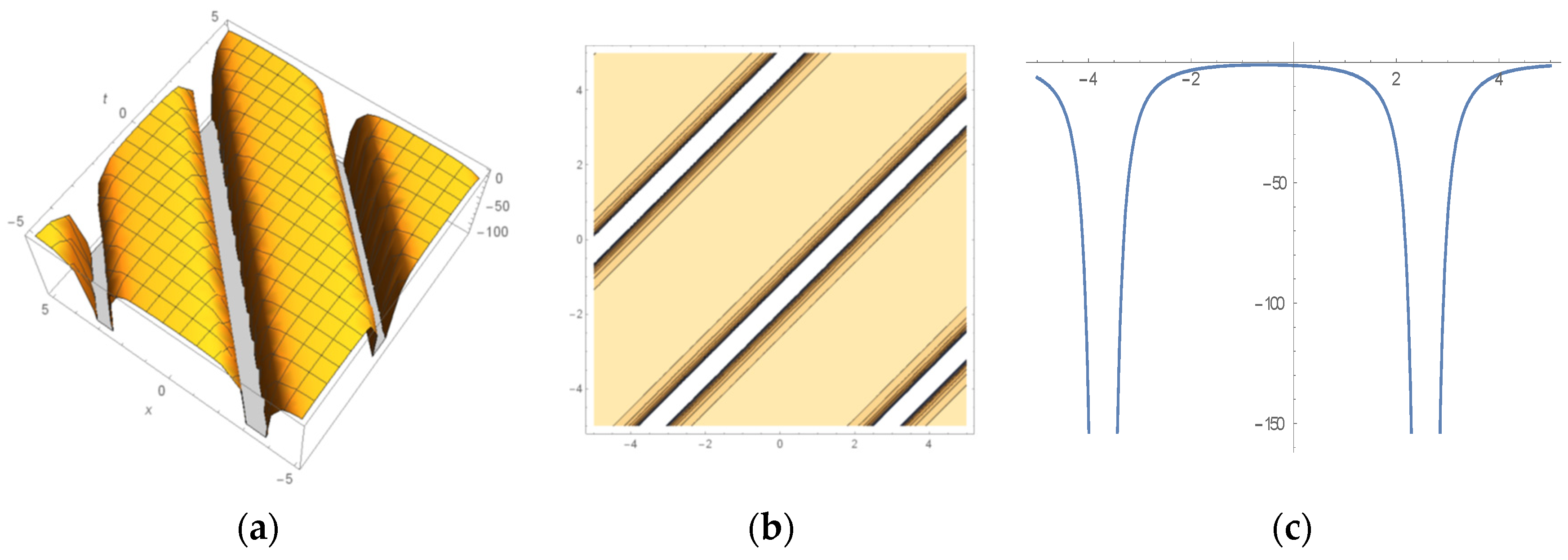
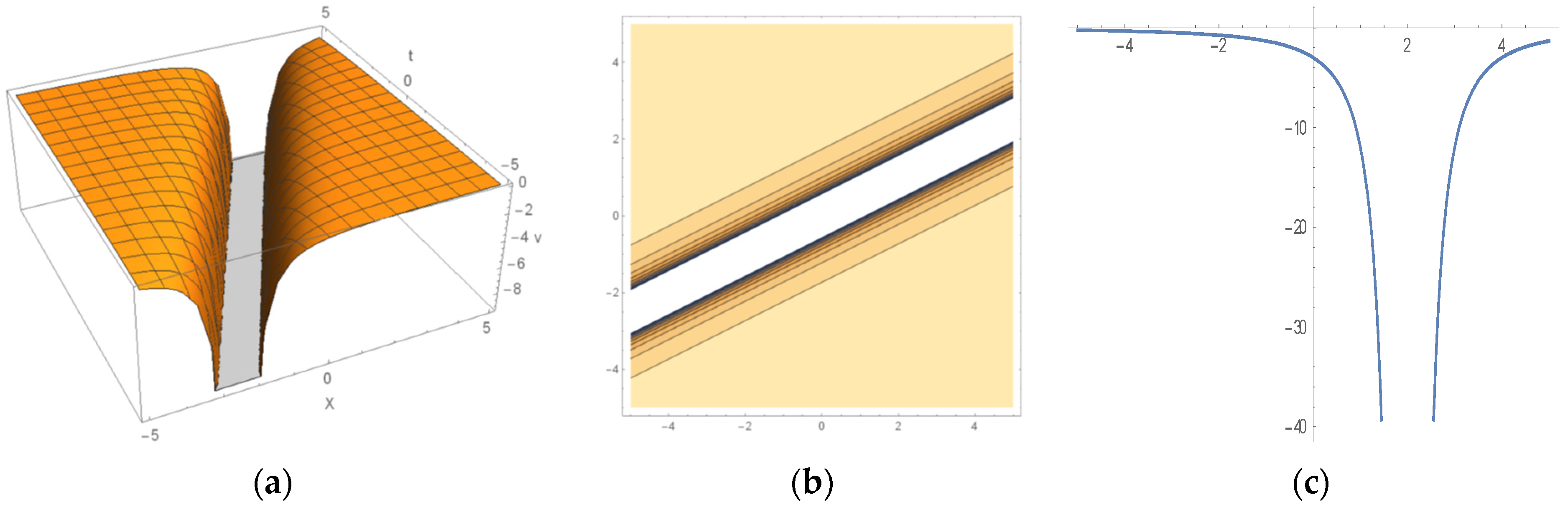
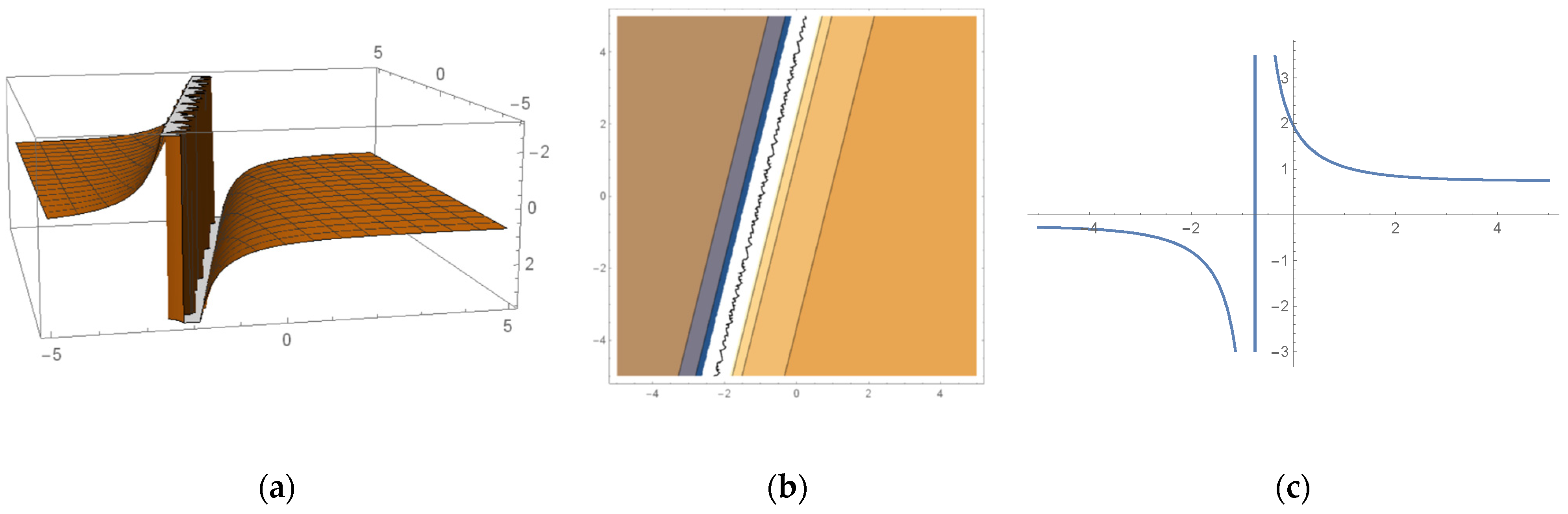
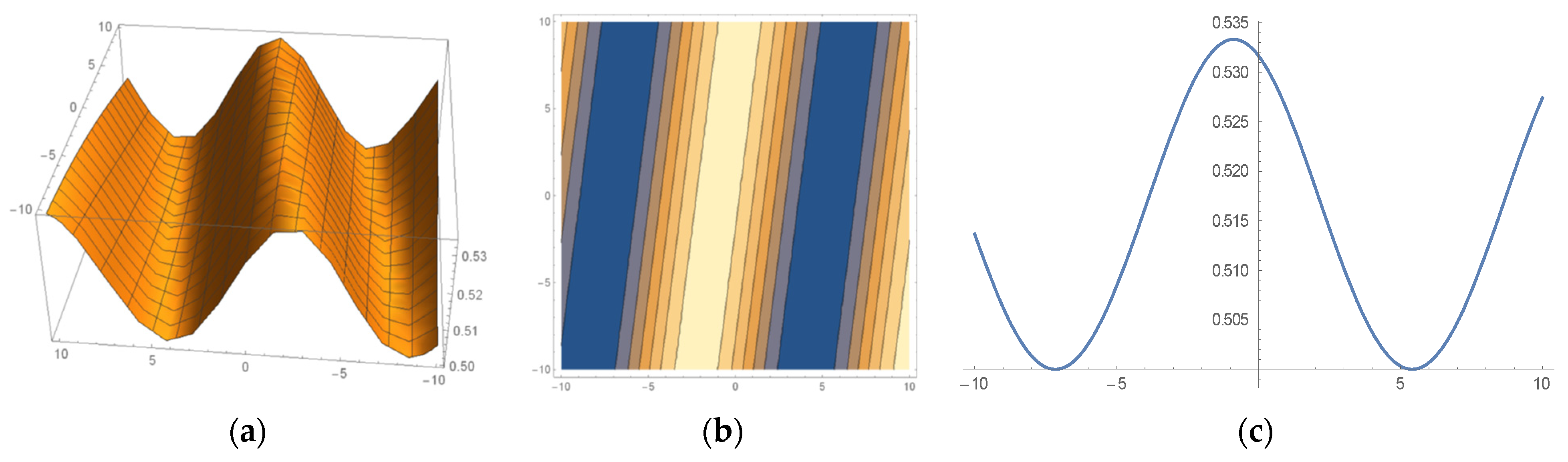
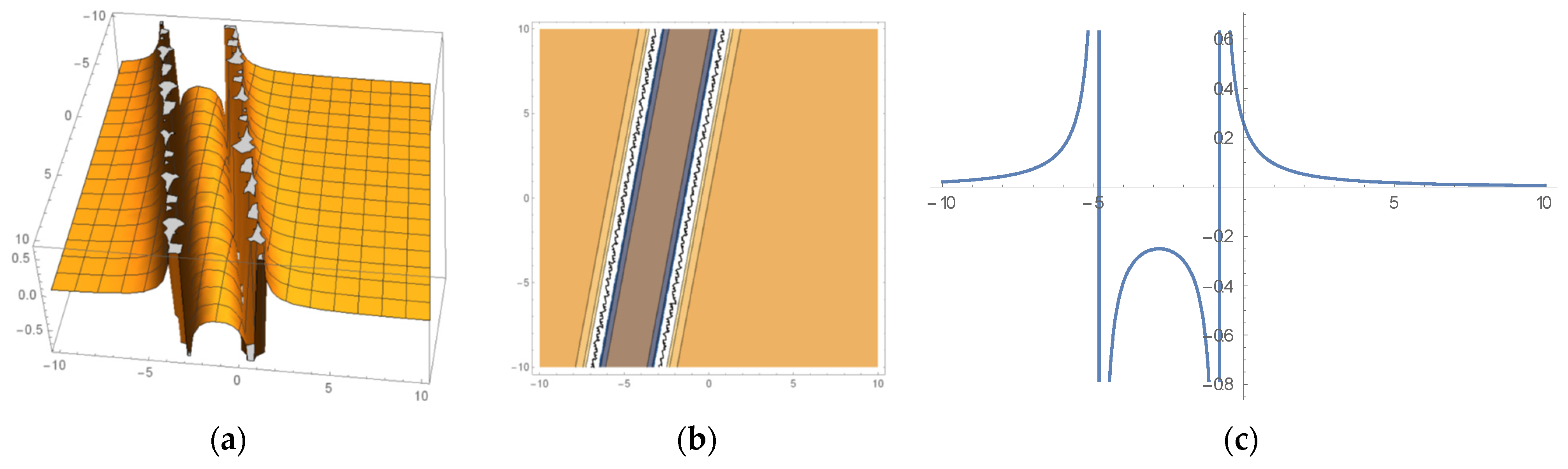
6. Some Important Graphs and Their Discussions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Misirliand, E.; Gurefe, Y. Exp-function method for solving nonlinear evolution equations. Math. Comput. Appl. 2011, 16, 258–266. [Google Scholar] [CrossRef]
- Moradi, E.; Varasteh, H.; Abdollahzadeh, A.; Mostafaei-Malekshah, M. The Exp-Function Method for Solving Two Dimensional Sine-Bratu Type Equations. Appl. Math. 2014, 5, 1212–1217. [Google Scholar] [CrossRef]
- Pandir, Y.; Akturk, T.; Gurefe, Y.; Juya, H. The Modified Exponential Function Method for Beta Time Fractional Biswas-Arshed Equation. Adv. Math. Phys. 2023, 2023, 1091355. [Google Scholar] [CrossRef]
- Zahran, E.H.M.; Khater, M.M.A. Modified extended tanh-function method and its applications to the Bogoyavlenskii equation. Appl. Math. Model. 2016, 40, 1769–1775. [Google Scholar] [CrossRef]
- El-shamy, O.; El-barkoki, R.; Ahmed, H.M.; Abbas, W.; Samir, I. Exploration of new solitons in optical medium with higher-order dispersive and nonlinear effects via improved modified extended tanh function method. Alex. Eng. J. 2023, 68, 611–618. [Google Scholar] [CrossRef]
- Almatrafi, M.B. Solitary Wave Solutions to a Fractional Model Using the Improved Modified Extended Tanh-Function Method. Fractal Fract. 2023, 7, 252. [Google Scholar] [CrossRef]
- Ali, A.T. the new generalized Jacobi elliptic function rational expansion method. J. Comput. Appl. Math. 2011, 235, 4117–4127. [Google Scholar] [CrossRef]
- Zahranand, E.H.M.; Khater, M.M.A. Extended Jacobian Elliptic Function Expansion Method and Its Applications in Biology. Appl. Math. 2015, 6, 1174–1181. [Google Scholar] [CrossRef]
- Ekici, M. Stationary optical solitons with Kudryashov’s quintuple power law nonlinearity by extended Jacobi’s elliptic function expansion. J. Nonlinear Opt. Phys. Mater. 2023, 32, 2350008. [Google Scholar] [CrossRef]
- Lu, B. The first integral method for some time fractional differential equations. J. Math. Anal. Appl. 2012, 395, 684–693. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Amer, Y.A. The First Integral Method and its Application for Deriving the Exact Solutions of a Higher-Order Dispersive Cubic-Quintic Nonlinear Schrödinger Equation. Comput. Math. Model. 2016, 27, 80–94. [Google Scholar] [CrossRef]
- Javeed, S.; Imran, T.; Ahmad, H.; Tchier, F.; Zhao, Y.H. New soliton solutions of modified (3+1)-D Wazwaz–Benjamin–Bona–Mahony and (2+1)-D cubic Klein–Gordon equations using first integral method. Open Phys. 2023, 21, 20220229. [Google Scholar] [CrossRef]
- Abdelsalam, U.M.; Ghazal, M.G.M. Analytical Wave Solutions for Foam and KdV-Burgers Equations Using Extended Homogeneous Balance Method. Mathematics 2019, 7, 729. [Google Scholar] [CrossRef]
- Rady, A.S.A.; Osman, E.S.; Khalfallah, M. The homogeneous balance method and its application to the Benjamin-Bona-Mahoney (BBM) equation. Appl. Math. Comput. 2010, 217, 1385–1390. [Google Scholar]
- Radha, B.; Duraisamy, C. The homogeneous balance method and its application for finding the exact solutions for nonlinear equations. J. Ambient Intell. Humaniz. Comput. 2021, 12, 6591–6597. [Google Scholar] [CrossRef]
- Lassas, M.; Mueller, J.L.; Siltanen, S.; Stahel, A. The Novikov–Veselov equation and the inverse scattering method: II. Computation. Nonlinearity 2012, 25, 1799–1818. [Google Scholar] [CrossRef]
- Gao, P.; Dong, H.; Ma, F. Inverse scattering via nonlinear integral equations method for a sound-soft crack with phaseless data. Appl. Math. 2018, 63, 49–165. [Google Scholar] [CrossRef]
- Grudsky, S.M.; Kravchenko, V.V.; Torba, S.M. Realization of the inverse scattering transform method for the Korteweg–de Vries equation. Math. Methods Appl. Sci. 2023, 46, 9217–9251. [Google Scholar] [CrossRef]
- Triki, H.; Taha, T.R. The sub-ODE method and soliton solutions for a higher order dispersive cubic–quintic nonlinear Schrödinger equation. Chaos Solitons Fractals 2009, 42, 1068–1072. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Seadawy, A.R.; Nimra; Ali, K.; Aziz, N. Variety of optical soliton solutions via sub-ODE approach to embedded soliton generating model in quadratic nonlinear media. Int. J. Mod. Phys. 2023, 37, 2350137. [Google Scholar] [CrossRef]
- Xu, F.; Feng, Q. A Generalized Sub-ODE Method and Applications for Nonlinear Evolution Equations. J. Sci. Res. Rep. 2013, 2, 571–581. [Google Scholar] [CrossRef]
- Cheng, C.; Jiang, Y.L. Lie group analysis method for two classes of fractional partial differential equations. Commun. Nonlinear Sci. Numer. Simul. 2015, 26, 24–35. [Google Scholar] [CrossRef]
- Du, X.X.; Tian, B.; Wu, X.Y.; Yin, H.M.; Zhang, C.R. Lie group analysis, analytic solutions and conservation laws of the (3 + 1)-dimensional Zakharov-Kuznetsov-Burgers equation in a collisionless magnetized electron-positron-ion plasma. Eur. Phys. J. Plus 2018, 133, 378. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Jun, S.; Khalique, C.M.; Shahid, A.; Fasheng, L.; Mohamed, M.S. Lie group analysis and robust computational approach to examine mass transport process using Jeffrey fluid model. Appl. Math. Comput. 2022, 421, 126936. [Google Scholar] [CrossRef]
- Paliathanasis, A.; Krishnakumar, K.; Tamizhmani, K.M.; Leach, P.G.L. Lie Symmetry Analysis of the Black-Scholes-Merton Model for European Options with Stochastic Volatility. Mathematics 2016, 4, 28. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, J. Lie symmetry analysis of fractional ordinary differential equation with neutral delay. AIMS Math. 2021, 6, 3592–3605. [Google Scholar] [CrossRef]
- Mbusi, S.O.; Adem, A.R.; Muatjetjeja, B. Lie symmetry analysis, multiple exp-function method and conservation laws for the (2+1)-dimensional Boussinesq equation. Opt. Quantum Electron. 2024, 56, 670. [Google Scholar] [CrossRef]
- Chahlaoui, Y.; Ali, A.; Ahmad, J.; Javed, S. Dynamical behavior of chaos, bifurcation analysis and soliton solutions to a Konno-Onno model. PLoS ONE 2023, 18, e0291197. [Google Scholar] [CrossRef] [PubMed]
- Tang, L. Bifurcation studies, chaotic pattern, phase diagrams and multiple optical solitons for the (2 + 1)-dimensional stochastic coupled nonlinear Schrödinger system with multiplicative white noise via Itô calculus. Results Phys. 2023, 52, 106765. [Google Scholar] [CrossRef]
- Rafiq, M.H.; Raza, N.; Jhangeer, A. Dynamic study of bifurcation, chaotic behavior and multi-soliton profiles for the system of shallow water wave equations with their stability. Chaos Solitons Fractals 2023, 171, 113436. [Google Scholar] [CrossRef]
- Rahman, M.U.; Sun, M.; Boulaaras, S.; Baleanu, D. Bifurcations, chaotic behavior, sensitivity analysis, and various soliton solutions for the extended nonlinear Schrödinger equation. Bound. Value Probl. 2024, 2024, 15. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Seadawy, A.R.; Ashraf, F.; Younis, M.; Iqbal, H.; Baleanu, D. Lump and Interaction solutions of a geophysical Korteweg–de Vries equation. Results Phys. 2020, 19, 103661. [Google Scholar] [CrossRef]
- Khalique, C.M. Closed-form solutions and conservation laws of ageneralized Hirota–Satsuma coupled KdV system of fluid mechanics. Open Phys. 2021, 19, 18–25. [Google Scholar] [CrossRef]
- Karakoc, S.B.G.; Ali, K.K.; Mehanna, M.S. Exact Traveling Wave Solutions of the Schamel-KdV Equation with Two Different Methods. Univers. J. Math. Appl. 2023, 6, 65–75. [Google Scholar] [CrossRef]
- Hou, S.; Zhang, R.; Zhang, Z.; Yang, L. On the Quartic Korteweg–de Vries hierarchy of nonlinear Rossby waves and its dynamics. Wave Motion 2024, 124, 103249. [Google Scholar] [CrossRef]
- Prins, J.; Wahls, S. Soliton Phase Shift Calculation for the Korteweg–De Vries Equation. IEEE Access 2019, 7, 122914–122930. [Google Scholar] [CrossRef]
- Naowarat, S.; Saifullah, S.; Sen, M.D.L. Periodic, Singular and Dark Solitons of a Generalized Geophysical KdV Equation by Using the Tanh-Coth Method. Symmetry 2023, 15, 135. [Google Scholar] [CrossRef]
- Saifullah, S.; Fatima, N.; Abdelmohsen, S.A.M.; Alanazi, M.M.; Ahmad, S.; Baleanu, D. Analysis of a conformable generalized geophysical KdV equation with Coriolis effect. Alex. Eng. J. 2023, 73, 651–663. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Zhang, W. Research on Traveling Wave Solutions for a Class of (3+1)-Dimensional Nonlinear Equation. J. Appl. Anal. Comput. 2017, 7, 841–856. [Google Scholar]
- Akkilic, A.N.; Sulaiman, T.A.; Shakir, A.P.; Ismael, H.F.; Bulut, H.; Shah, N.A.; Ali, M.R. Jaulent–Miodek evolution equation: Analytical methods and various solutions. Results Phys. 2023, 47, 106351. [Google Scholar] [CrossRef]
- Sadat, R.; Kassem, M. Explicit Solutions for the (2 + 1)-Dimensional Jaulent–Miodek Equation Using the Integrating Factors Method in an Unbounded Domain. Math. Comput. Appl. 2018, 23, 15. [Google Scholar] [CrossRef]
- Ige, O.E.; Oderinu, R.A.; Elzaki, T.M. Numerical Simulation of the Nonlinear Coupled Jaulent-Miodek Equation by Elzaki Transform-Adomain Polynomial Method. Adv. Math. Sci. J. 2020, 9, 10335–10355. [Google Scholar] [CrossRef]
- Cakicioglu, H.; Ozisik, M.; Secer, A.; Bayram, M. Kink Soliton Dynamic of the (2+1)-Dimensional Integro-Differential Jaulent–Miodek Equation via a Couple of Integration Techniques. Symmetry 2023, 15, 1090. [Google Scholar] [CrossRef]
- Ma, H.C.; Deng, A.P.; Yu, Y.D. Lie Symmetry Group of (2 + 1)-Dimensional Jaulent-Miodek Equation. Therm. Sci. 2014, 18, 1547–1552. [Google Scholar] [CrossRef]
- Chowdhury, M.A.; Miah, M.M.; Iqbal, M.A.; Alshehri, H.M.; Baleanu, D.; Osman, M.S. Advanced exact solutions to the nano-ionic currents equation through MTs and the soliton equation containing the RLC transmission line. Eur. Phys. J. Plus 2023, 138, 502. [Google Scholar] [CrossRef]
- Li, L.X.; Li, E.Q.; Wang, M.L. The (G′/G, 1/G)-expansion method and its application to travelling wave solutions of the Zakharov equations. Appl. Math. A J. Chin. Univ. 2010, 25, 454–462. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alurrfi, K.A.E. The (G′/G, 1/G)-Expansion Method and Its Applications to Find the Exact Solutions of Nonlinear PDEs for Nanobiosciences. Math. Probl. Eng. 2014, 2014, 521712. [Google Scholar] [CrossRef]
- Miah, M.M.; Ali, H.M.S.; Akbar, M.A.; Wazwaz, A.M. Some applications of the (G′/G, 1/G)-expansion method to find new exact solutions of NLEEs. Eur. Phys. J. Plus 2017, 132, 252. [Google Scholar] [CrossRef]
- Kaplan, M.; Bekir, A.; Akbulut, A. A generalized Kudryashov method to some nonlinear evolution equations in mathematical physics. Nonlinear Dyn. 2016, 85, 2843–2850. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alraddadi, I.; Chowdhury, M.A.; Abbas, M.S.; El-Rashidy, K.; Borhan, J.R.M.; Miah, M.M.; Kanan, M. Dynamical Behaviors and Abundant New Soliton Solutions of Two Nonlinear PDEs via an Efficient Expansion Method in Industrial Engineering. Mathematics 2024, 12, 2053. https://doi.org/10.3390/math12132053
Alraddadi I, Chowdhury MA, Abbas MS, El-Rashidy K, Borhan JRM, Miah MM, Kanan M. Dynamical Behaviors and Abundant New Soliton Solutions of Two Nonlinear PDEs via an Efficient Expansion Method in Industrial Engineering. Mathematics. 2024; 12(13):2053. https://doi.org/10.3390/math12132053
Chicago/Turabian StyleAlraddadi, Ibrahim, M. Akher Chowdhury, M. S. Abbas, K. El-Rashidy, J. R. M. Borhan, M. Mamun Miah, and Mohammad Kanan. 2024. "Dynamical Behaviors and Abundant New Soliton Solutions of Two Nonlinear PDEs via an Efficient Expansion Method in Industrial Engineering" Mathematics 12, no. 13: 2053. https://doi.org/10.3390/math12132053




