Wind Energy Production in Italy: A Forecasting Approach Based on Fractional Brownian Motion and Generative Adversarial Networks
Abstract
1. Introduction
- A stochastic approach to wind energy production forecasting in Italy, with a forward prediction horizon of one week, has been adopted. The time series is treated as an outcome of a stochastic process, a solution of an SDE.
- The solution distribution is modelled by a GAN whose generator is driven by a Brownian motion. In addition to [28], the generator is also allowed to be driven by a fractional Brownian motion (fBm) with an experimentally estimated Hurst exponent. The results obtained by the two frameworks are then compared. Similar results are found in [41], where both models show a very close complexity.
2. Methodology
2.1. Preliminaries
2.1.1. Fractional Brownian Motion
2.1.2. Definition of SDE
2.1.3. Generative Adversarial Networks
2.1.4. SDEs as GANs
2.2. Architecture
2.2.1. Generator
2.2.2. Discriminator
2.2.3. Training Loss
2.2.4. Lipschitz Regularisation
3. Experiments
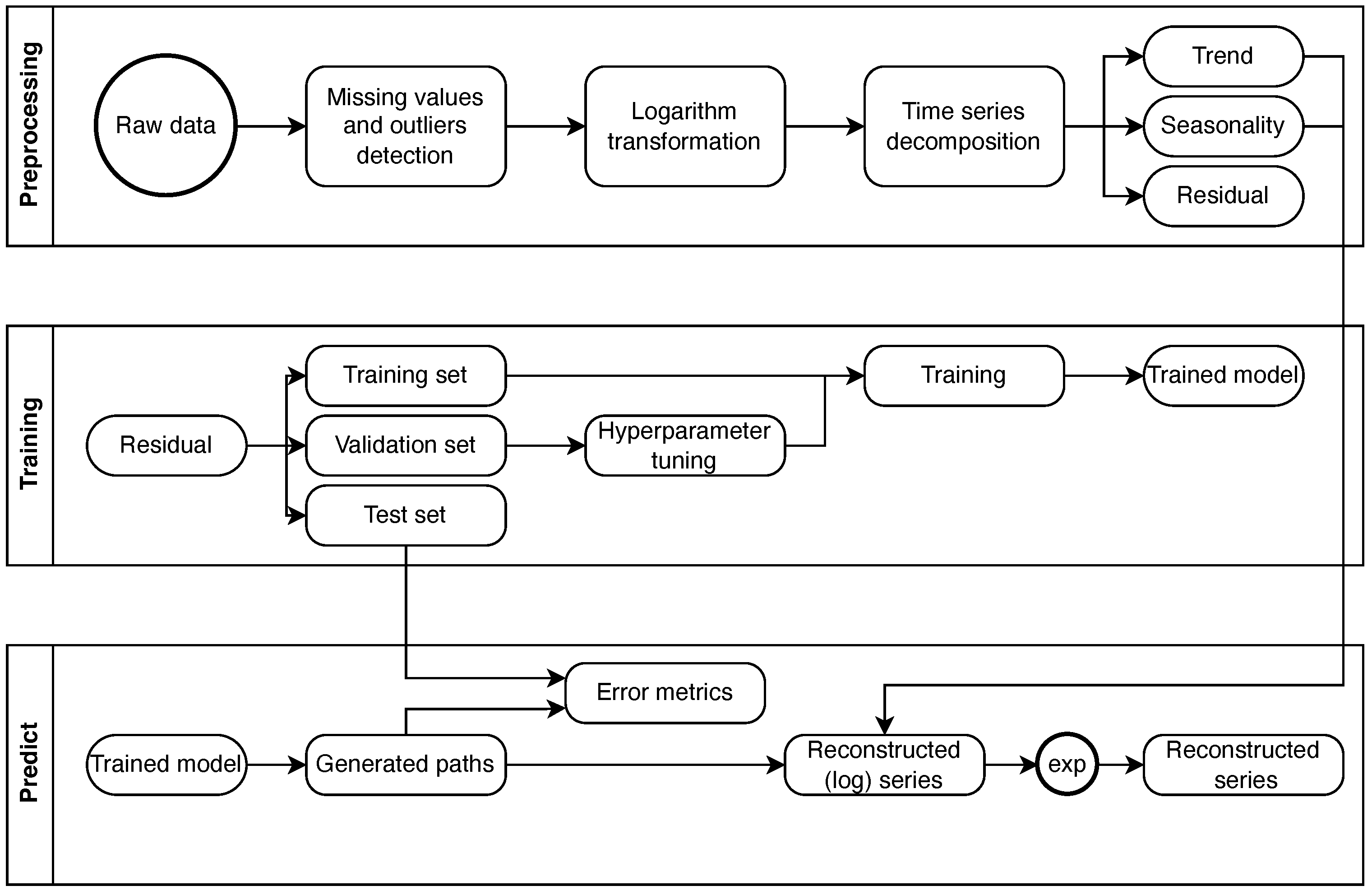
3.1. Data Preprocessing
- Missing data and potential outliers have been detected and corrected;
- The logarithmic transformations have been applied;
- The series has been decomposed into trends, seasonal and residual components. More specifically, the trend has been obtained via a rolling window smoothing of the series; the analysis of the periodogram allowed to detect the main seasonal component, i.e., annual periodicity, that was successively isolated with a Fourier decomposition; and the residual component has been tested for stationarity; both the Augmented Dickey–Fuller (ADF) test and the Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test confirmed the stationary nature of the residual component.
3.2. Model Specification
3.2.1. Software
3.2.2. Computing Infrastructure
3.2.3. Normalisation
3.2.4. Architectures
3.2.5. Optimisers
3.2.6. Hurst Index Estimation
3.3. Algorithm to Estimate H
- n represents the period of the observations, denoting the number of data points within a time series of length N under consideration;
- denotes the range of the initial n cumulative deviations from the mean;
- indicates the range of the series comprising the first n cumulative standard deviations;
- C is a positive constant.
- For each specified length , the residuals are extracted from the seasonal decomposition of the observed time series, and the mean is subsequently computed;
- The cumulative deviations are computed as ;
- The range is computed as ;
- is computed as the standard deviation of the cumulative deviations of ;
- The rescaled ranges are obtained as ;
- A linear regression of the rescaled ranges is fitted against n on a log scale;
- is estimated as the slope of the regression analysis conducted over all the different k lengths considered.
3.4. Data Size Analysis
- The rolling standard deviation is computed on a yearly basis;
- Both the minimum and maximum values of the rolling standard deviations are utilised to delineate a grid of five appropriate diffusion coefficients for the fractional Brownian motion. The range spans from the minimum value of 0.7423 to the maximum value of 0.8887, with equal spacing between each coefficient;
- A grid of nine appropriate values for H is also considered, and it spaces evenly from 0.1 to 0.9;
- For each combination of H and the diffusion coefficient, we simulate 1000 trajectories for the fBm, over 5 years of daily projections;
- The calibration algorithm for H is implemented over the trajectories generated using different data size, with RMSE computation realised for each data size selected;
- The minimum RMSE for H highlights the optimal data size.
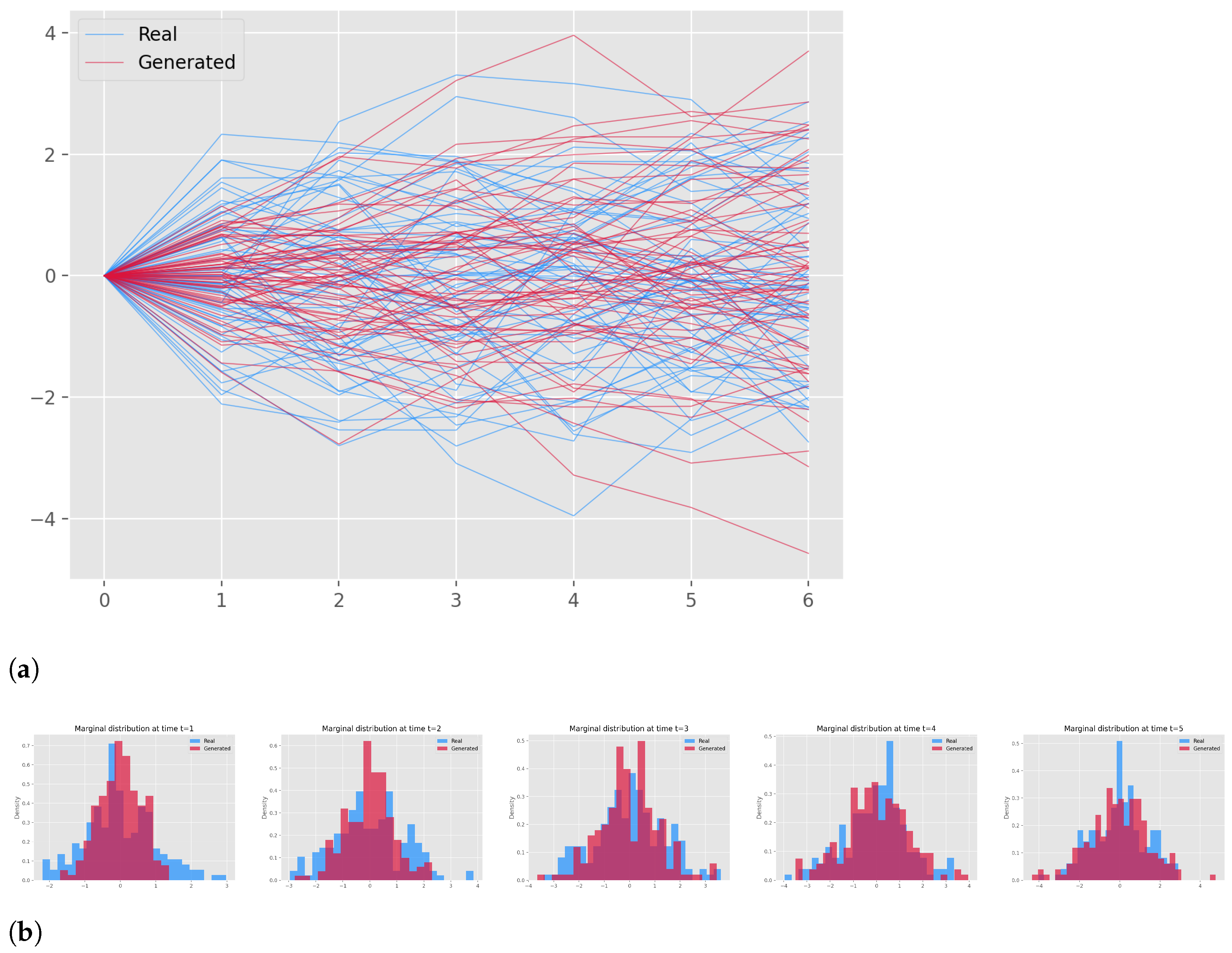
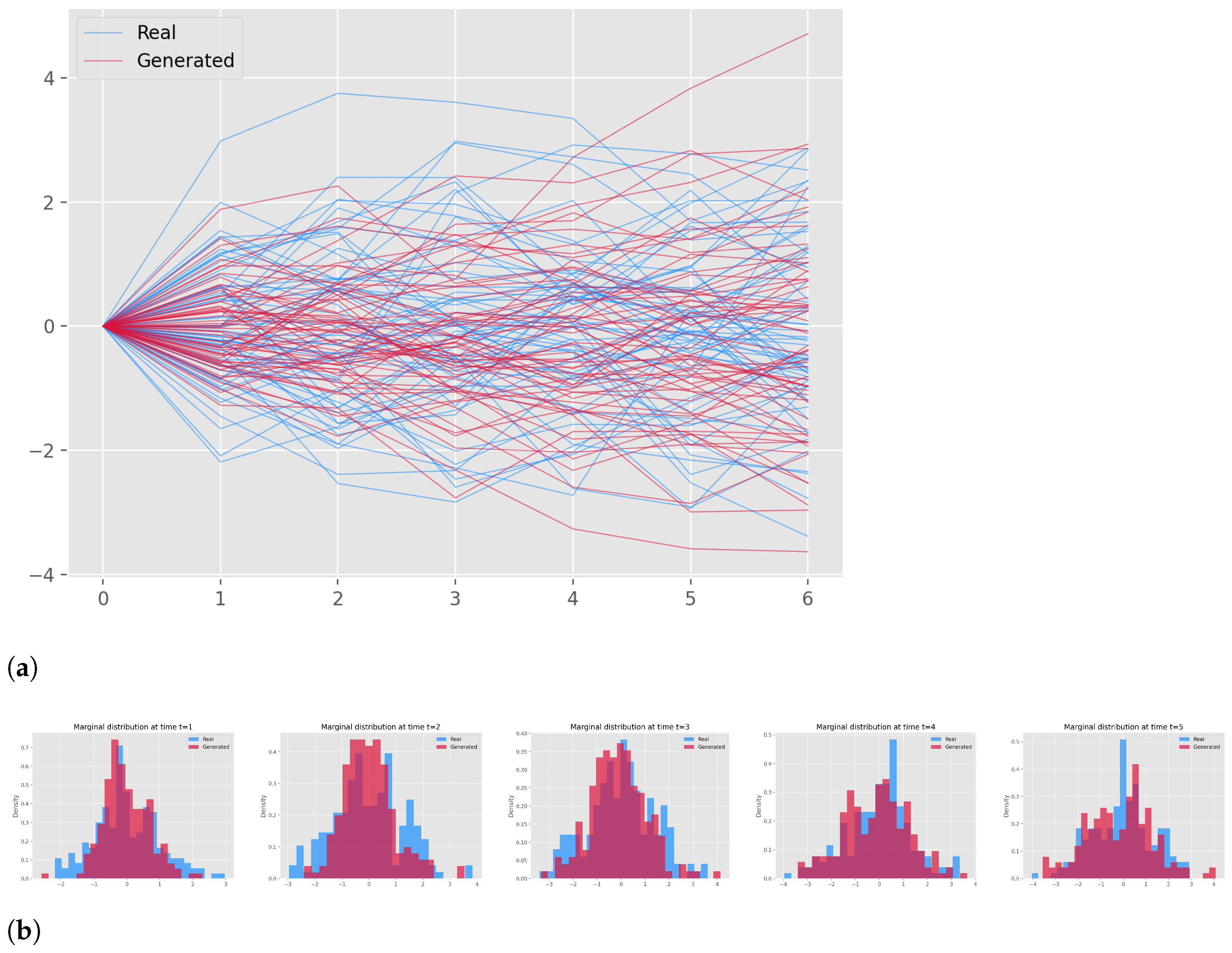
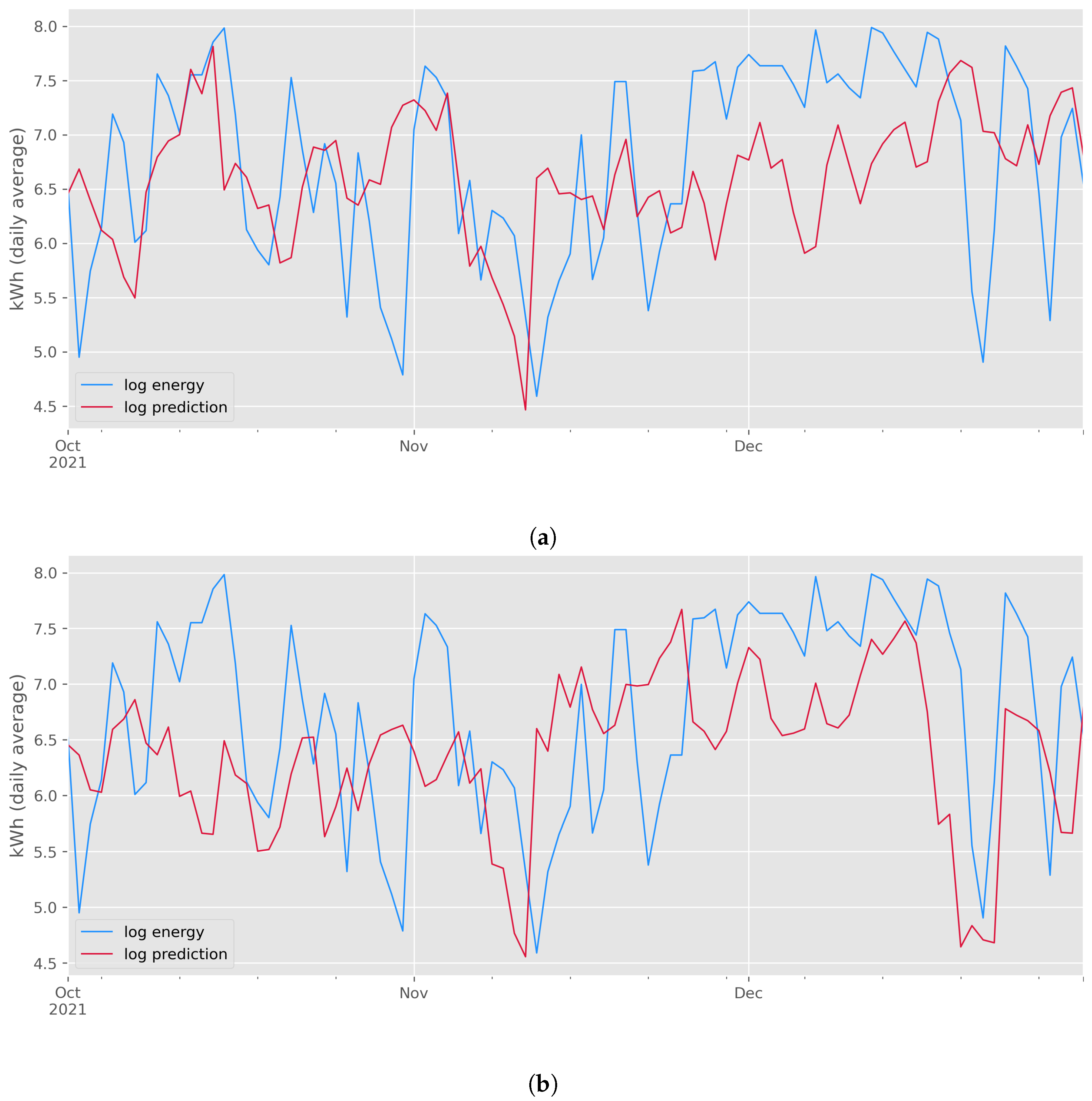
3.5. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARMA | Autoregressive moving average |
| CGAN | Conditional GAN |
| CNN | Convolutional neural network |
| CSE | Controlled differential equation |
| DTW | Dynamic Time Warping |
| fBm | Fractional Brownian motion |
| FFNN | Feedforward neural network |
| fLsm | Fractional Lévy stable motion |
| GAN | Generative adversarial network |
| GAN-GP | GAN with gradient penalty |
| MAPE | Mean absolute percentage error |
| MMD | Maximum–Minimum Discrepancy |
| NN | Neural networks |
| SDE | Stochastic differential equation |
| SeqGAN | Sequence GAN |
| VAE | Variational autoencoder |
| WGAN | Wasserstein GAN |
References
- Zhang, X.; Ma, C.; Song, X.; Zhou, Y.; Chen, W. The impacts of wind technology advancement on future global energy. Appl. Energy 2016, 184, 1033–1037. [Google Scholar] [CrossRef]
- Commission, E. Clean Energy. 2019. Available online: https://ec.europa.eu/commission/presscorner/detail/en/fs_19_6723 (accessed on 18 May 2024).
- Weron, R. Modeling and Forecasting Electricity Loads and Prices: A Statistical Approach; John Wiley & Sons: Hoboken, NJ, USA, 2006; Volume 396. [Google Scholar]
- Di Persio, L.; Fraccarolo, N. Energy consumption forecasts by gradient boosting regression trees. Mathematics 2023, 11, 1068. [Google Scholar] [CrossRef]
- Di Persio, L.; Fraccarolo, N. Investment and Bidding Strategies for Optimal Transmission Management Dynamics: The Italian Case. Energies 2023, 16, 5950. [Google Scholar] [CrossRef]
- Foley, A.M.; Leahy, P.G.; Marvuglia, A.; McKeogh, E.J. Current methods and advances in forecasting of wind power generation. Renew. Energy 2012, 37, 1–8. [Google Scholar] [CrossRef]
- Hu, J.; Heng, J.; Wen, J.; Zhao, W. Deterministic and probabilistic wind speed forecasting with de-noising-reconstruction strategy and quantile regression based algorithm. Renew. Energy 2020, 162, 1208–1226. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Zou, R.; Foley, A.M.; Al Kez, D.; Song, D.; Hu, Q.; Srinivasan, D. Sparse heteroscedastic multiple spline regression models for wind turbine power curve modeling. IEEE Trans. Sustain. Energy 2020, 12, 191–201. [Google Scholar] [CrossRef]
- Yunus, K.; Thiringer, T.; Chen, P. ARIMA-based frequency-decomposed modeling of wind speed time series. IEEE Trans. Power Syst. 2015, 31, 2546–2556. [Google Scholar] [CrossRef]
- Kavasseri, R.G.; Seetharaman, K. Day-ahead wind speed forecasting using f-ARIMA models. Renew. Energy 2009, 34, 1388–1393. [Google Scholar] [CrossRef]
- Maatallah, O.A.; Achuthan, A.; Janoyan, K.; Marzocca, P. Recursive wind speed forecasting based on Hammerstein Auto-Regressive model. Appl. Energy 2015, 145, 191–197. [Google Scholar] [CrossRef]
- Wang, J.; Wang, S.; Yang, W. A novel non-linear combination system for short-term wind speed forecast. Renew. Energy 2019, 143, 1172–1192. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Wei, X. A hybrid wind speed forecasting model based on phase space reconstruction theory and Markov model: A case study of wind farms in northwest China. Energy 2015, 91, 556–572. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.; Li, Y. Smart multi-step deep learning model for wind speed forecasting based on variational mode decomposition, singular spectrum analysis, LSTM network and ELM. Energy Convers. Manag. 2018, 159, 54–64. [Google Scholar] [CrossRef]
- Song, J.; Wang, J.; Lu, H. A novel combined model based on advanced optimization algorithm for short-term wind speed forecasting. Appl. Energy 2018, 215, 643–658. [Google Scholar] [CrossRef]
- He, X.; Nie, Y.; Guo, H.; Wang, J. Research on a Novel Combination System on the Basis of Deep Learning and Swarm Intelligence Optimization Algorithm for Wind Speed Forecasting. IEEE Access 2020, 8, 51482–51499. [Google Scholar] [CrossRef]
- Mezaache, H.; Bouzgou, H. Auto-Encoder with Neural Networks for Wind Speed Forecasting. In Proceedings of the 2018 International Conference on Communications and Electrical Engineering (ICCEE), El Oued, Algeria, 17–18 December 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Fu, W.; Wang, K.; Tan, J.; Zhang, K. A composite framework coupling multiple feature selection, compound prediction models and novel hybrid swarm optimizer-based synchronization optimization strategy for multi-step ahead short-term wind speed forecasting. Energy Convers. Manag. 2020, 205, 112461. [Google Scholar] [CrossRef]
- Niu, Z.; Yu, Z.; Tang, W.; Wu, Q.; Reformat, M. Wind power forecasting using attention-based gated recurrent unit network. Energy 2020, 196, 117081. [Google Scholar] [CrossRef]
- Yu, Y.; Han, X.; Yang, M.; Yang, J. Probabilistic Prediction of Regional Wind Power Based on Spatiotemporal Quantile Regression. In Proceedings of the 2019 IEEE Industry Applications Society Annual Meeting, Baltimore, MD, USA, 29 September–3 October 2019; pp. 1–16. [Google Scholar] [CrossRef]
- Kosovic, B.; Haupt, S.E.; Adriaansen, D.; Alessandrini, S.; Wiener, G.; Delle Monache, L.; Liu, Y.; Linden, S.; Jensen, T.; Cheng, W.; et al. A comprehensive wind power forecasting system integrating artificial intelligence and numerical weather prediction. Energies 2020, 13, 1372. [Google Scholar] [CrossRef]
- Liu, T.; Huang, Z.; Tian, L.; Zhu, Y.; Wang, H.; Feng, S. Enhancing wind turbine power forecast via convolutional neural network. Electronics 2021, 10, 261. [Google Scholar] [CrossRef]
- Shi, J.; Guo, J.; Zheng, S. Evaluation of hybrid forecasting approaches for wind speed and power generation time series. Renew. Sustain. Energy Rev. 2012, 16, 3471–3480. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H. Dynamic ensemble wind speed prediction model based on hybrid deep reinforcement learning. Adv. Eng. Informatics 2021, 48, 101290. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, S.; Zhang, W.; Peng, J.; Cai, Y. Multifactor spatio-temporal correlation model based on a combination of convolutional neural network and long short-term memory neural network for wind speed forecasting. Energy Convers. Manag. 2019, 185, 783–799. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, G.Q.; Zhou, W.; Du, W.; Lu, K.D. Wind speed forecasting using nonlinear-learning ensemble of deep learning time series prediction and extremal optimization. Energy Convers. Manag. 2018, 165, 681–695. [Google Scholar] [CrossRef]
- Wang, G.; Jia, R.; Liu, J.; Zhang, H. A hybrid wind power forecasting approach based on Bayesian model averaging and ensemble learning. Renew. Energy 2020, 145, 2426–2434. [Google Scholar] [CrossRef]
- Kidger, P.; Foster, J.; Li, X.; Lyons, T.J. Neural SDEs as Infinite-Dimensional GANs. In Proceedings of the Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; Volume 139. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2242–2251. [Google Scholar] [CrossRef]
- Yuan, R.; Wang, B.; Mao, Z.; Watada, J. Multi-objective wind power scenario forecasting based on PG-GAN. Energy 2021, 226, 120379. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Kirschen, D.; Zhang, B. Model-Free Renewable Scenario Generation Using Generative Adversarial Networks. IEEE Trans. Power Syst. 2018, 33, 3265–3275. [Google Scholar] [CrossRef]
- Chen, Y.; Li, P.; Zhang, B. Bayesian renewables scenario generation via deep generative networks. In Proceedings of the 2018 52nd Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 13–15 March 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Jiang, C.; Mao, Y.; Chai, Y.; Yu, M.; Tao, S. Scenario Generation for Wind Power Using Improved Generative Adversarial Networks. IEEE Access 2018, 6, 62193–62203. [Google Scholar] [CrossRef]
- Wei, H.; Hongxuan, Z.; Yu, D.; Yiting, W.; Ling, D.; Ming, X. Short-term optimal operation of hydro-wind-solar hybrid system with improved generative adversarial networks. Appl. Energy 2019, 250, 389–403. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, X.; Zhang, B. An Unsupervised Deep Learning Approach for Scenario Forecasts. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Z.; Liu, C.; Yu, Y.; Pang, S.; Duić, N.; Shafie-khah, M.; Catalão, J.P. Generative adversarial networks and convolutional neural networks based weather classification model for day ahead short-term photovoltaic power forecasting. Energy Convers. Manag. 2019, 181, 443–462. [Google Scholar] [CrossRef]
- Zhang, Y.; Ai, Q.; Xiao, F.; Hao, R.; Lu, T. Typical wind power scenario generation for multiple wind farms using conditional improved Wasserstein generative adversarial network. Int. J. Electr. Power Energy Syst. 2020, 114, 105388. [Google Scholar] [CrossRef]
- Liang, J.; Tang, W. Sequence Generative Adversarial Networks for Wind Power Scenario Generation. IEEE J. Sel. Areas Commun. 2020, 38, 110–118. [Google Scholar] [CrossRef]
- Sun, Z.; El-Laham, Y.; Vyetrenko, S. Neural Stochastic Differential Equations with Change Points: A Generative Adversarial Approach. In Proceedings of the ICASSP 2024–2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 6965–6969. [Google Scholar]
- Allouche, M.; Girard, S.; Gobet, E. A generative model for fBm with deep ReLU neural networks. J. Complex. 2022, 73, 101667. [Google Scholar] [CrossRef]
- Oksendal, B. Stochastic Differential Equations: An Introduction with Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Rogers, L.C.G.; Williams, D. Diffusions, Markov Processes and Martingales: Volume 2, Itô Calculus; Cambridge University Press: Cambridge, UK, 2000; Volume 2. [Google Scholar]
- Chen, R.T.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D.K. Neural ordinary differential equations. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Kidger, P.; Morrill, J.; Foster, J.; Lyons, T. Neural Controlled Differential Equations for Irregular Time Series. In Proceedings of the Advances in Neural Information Processing Systems, Online, 6–12 December 2020; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., Lin, H., Eds.; Curran Associates, Inc.: Glasgow, UK, 2020; Volume 33, pp. 6696–6707. [Google Scholar]
- Kidger, P. On neural differential equations. arXiv 2022, arXiv:2202.02435. [Google Scholar]
- Yang, L.; Gao, T.; Lu, Y.; Duan, J.; Liu, T. Neural network stochastic differential equation models with applications to financial data forecasting. Appl. Math. Model. 2022, 115, 279–299. [Google Scholar] [CrossRef]
- Kong, L.; Sun, J.; Zhang, C. Sde-net: Equipping deep neural networks with uncertainty estimates. arXiv 2020, arXiv:2008.10546. [Google Scholar]
- Gierjatowicz, P.; Sabaté-Vidales, M.; Šiška, D.; Szpruch, Ł.; Zuric, Z. Robust pricing and hedging via neural stochastic differential equations. J. Comput. Financ. 2022, 16. [Google Scholar] [CrossRef]
- Veeravalli, T.; Raginsky, M. Nonlinear controllability and function representation by neural stochastic differential equations. arXiv 2022, arXiv:2212.00896. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, D.; Karniadakis, G. Physics-Informed Generative Adversarial Networks for Stochastic Differential Equations. SIAM J. Sci. Comput. 2018, 42, A292–A317. [Google Scholar] [CrossRef]
- Kidger, P.; Morrill, J.; Foster, J.; Lyons, T. Neural controlled differential equations for irregular time series. Adv. Neural Inf. Process. Syst. 2020, 33, 6696–6707. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. Improved training of wasserstein gans. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Li, X.; Wong, T.K.L.; Chen, R.T.Q.; Duvenaud, D. Scalable gradients for stochastic differential equations. In Proceedings of the Twenty Third International Conference on Artificial Intelligence and Statistics (AISTATS), Online, 26–28 August 2020. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Qian, B.; Rasheed, K. Hurst exponent and financial market predictability. In Proceedings of the IASTED Conference on Financial Engineering and Applications, Cambridge, MA, USA, 8–10 November 2007; pp. 203–209. [Google Scholar]
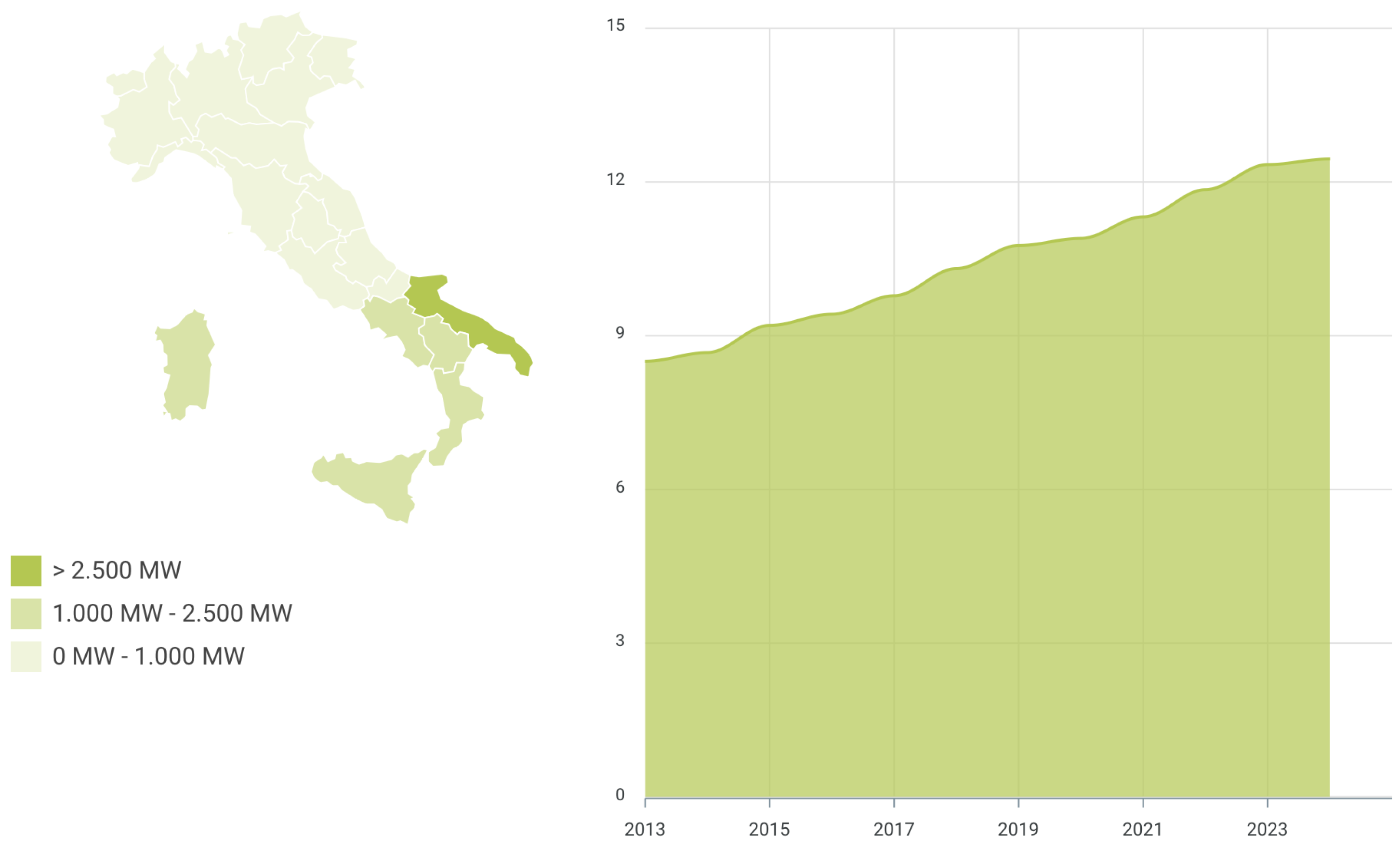

| Zone | |
|---|---|
| SUD | 0.3522 |
| Metric | Neural SDE | Neural SDE with fBm |
|---|---|---|
| DTW | 3.3078 | 3.0743 |
| MMD | 0.1042 | 0.1091 |
| Metric | Neural SDE | Neural SDE with fBm |
|---|---|---|
| MAPE | 13.40 | 14.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Persio, L.; Fraccarolo, N.; Veronese, A. Wind Energy Production in Italy: A Forecasting Approach Based on Fractional Brownian Motion and Generative Adversarial Networks. Mathematics 2024, 12, 2105. https://doi.org/10.3390/math12132105
Di Persio L, Fraccarolo N, Veronese A. Wind Energy Production in Italy: A Forecasting Approach Based on Fractional Brownian Motion and Generative Adversarial Networks. Mathematics. 2024; 12(13):2105. https://doi.org/10.3390/math12132105
Chicago/Turabian StyleDi Persio, Luca, Nicola Fraccarolo, and Andrea Veronese. 2024. "Wind Energy Production in Italy: A Forecasting Approach Based on Fractional Brownian Motion and Generative Adversarial Networks" Mathematics 12, no. 13: 2105. https://doi.org/10.3390/math12132105
APA StyleDi Persio, L., Fraccarolo, N., & Veronese, A. (2024). Wind Energy Production in Italy: A Forecasting Approach Based on Fractional Brownian Motion and Generative Adversarial Networks. Mathematics, 12(13), 2105. https://doi.org/10.3390/math12132105






