Abstract
Although Kepler’s laws can be empirically proven by applying Newton’s laws to the dynamics of two particles attracted by gravitational interaction, an explicit formula for the motion as a function of time remains undefined. This paper proposes a quasi-analytical solution to address this challenge. It approximates the real dynamics of celestial bodies with a satisfactory degree of accuracy and minimal computational cost. This problem is closely related to Kepler’s equation, as solving the equations of motion as a function of time also provides a solution to Kepler’s equation. The results are presented for each planet of the solar system, including Pluto, and the solution is compared against real orbits.
MSC:
65H10
1. Introduction
Kepler’s laws offer an empirical mathematical model for describing the motion of orbiting bodies, later proven by Newton’s analytical results [1,2]. Therefore, they are of fundamental importance in astrophysics, celestial mechanics, and Earth science [3]. Nevertheless, Kepler’s laws do not describe the motion of celestial bodies as a function of time. It is the so-called Kepler’s equation (KE) that provides the time dependence of the position of orbiting celestial bodies. Since Kepler first established this equation in 1609, several solutions of different types have been proposed, continuing up to the present day [2,4,5,6,7,8,9]. One of the significant early attempts was made by Carlini in 1819, later refined by Jacobi [9]. Because of its transcendental nature, an exact explicit solution remains elusive. There exist a vast variety of numerical methods renowned for their remarkable accuracy. These methods typically involve calculating infinite series or employing high-order iterative approaches. It is hardly possible to refer here to all these works, but we cite the most relevant ones [3,10,11,12,13,14,15,16,17,18,19]. Recently, some methods that use artificial intelligence have been proposed [20].
In this work, we present a quasi-analytical solution that gives explicit equations of motion as a function of time. This solution is quasi-analytical, because even though it gives explicit formulas, it depends on six numerical coefficients, which in turn depend on the orbital eccentricity. Our results provide an explicit solution to KE.
The Orbit Equation
The classical problem begins then, with the description of the motion of the planets according to the following equations [21]:
and
Here, are the coordinates of the planet in the polar coordinate system, with the origin at the Sun; t is the time; is the eccentricity; and , , and l are the focal parameter, the reduced mass, and the angular momentum, respectively [2]. The angle is called the true anomaly, defined as at the pericenter [19].
The inverse of the solution of Equation (1), is closely related to KE (the explicit relation will be shown in Section 4):
where E is the eccentric anomaly and M is the mean anomaly, expressed as
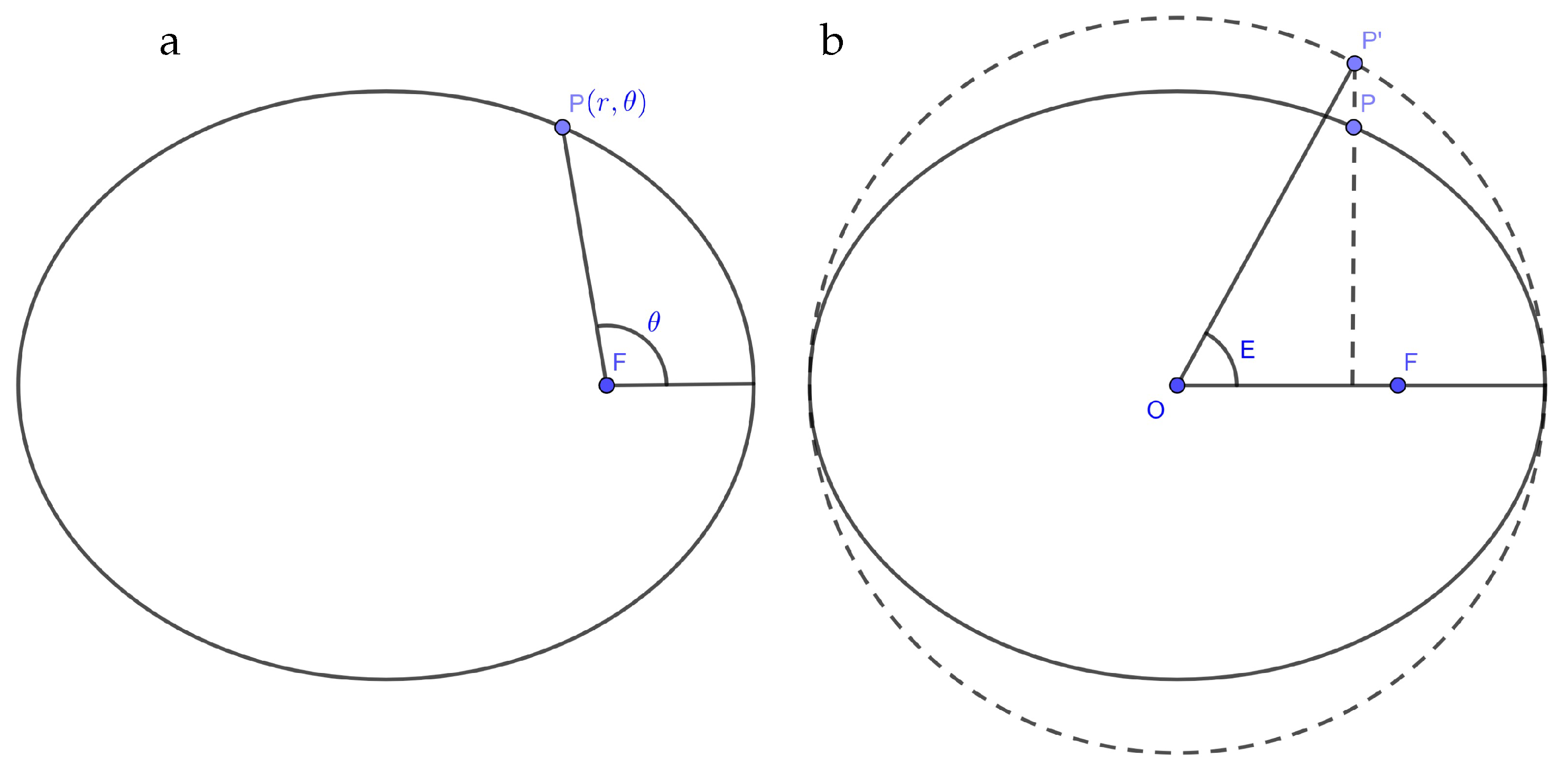
T is the orbital period. As was pointed out before, usually, E needs to be estimated by iterative methods [8] or series expansions [22]. Thus, the accuracy of the position and/or velocity of a celestial object moving in the Keplerian orbit, which may be obtained from the solution of KE, depends on the approximation method used. Figure 1 illustrates the variables involved in the problem.
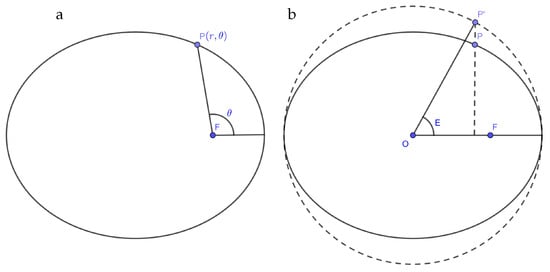
Figure 1.
Illustration of the relative position of the Sun and planet (a) and Kepler’s equation (b).
Equations (1) and (3) are both transcendental. The solution of Equation (1) gives the solution of Equation (3), and vice-versa, which has led to a vast literature concerning alternative approaches [3]. A detailed description of the different works presented in the literature on this problem can be found in [3,19].
The remainder of this paper is structured as follows. In Section 2, we present in detail, step by step, a quasi-analytical solution of Equation (1). In Section 3, the results are presented and compared with the real orbit of each planet of the solar system. In Section 4 we present the solution to KE based on the solution of Equation (1). Finally, in Section 5, we give a brief discussion and conclusions about the results obtained in this work.
2. Methodology
In the present section, a quasi-analytical method is established for solving Equation (1). For clarity, we divide the method into sections that we call steps. All calculations and graphics were performed with MATLAB 2020b (MathWorks Inc., Natick, MA USA). Now, we briefly describe each step.
Step 0: In this step, we integrate Equation (1) and introduce a normalized time , which maps the real time t from the interval to the interval , which leads us to Equation (7) for .
Step 1: In this step, we separate into two parts, and . Based on the observation that resembles the behavior of (especially for small values of ), and, taking into account its analytical form, we find the inverse of , as our zeroth approximation for .
Step 2: Assuming the exact solution has the form of Equation (14), we introduce the true argument of the arctangent function, , which gives the exact solution. Then, we introduce the function (Equation (17)) as the quotient of the true argument and the argument of the zeroth approximation, . Finally, we define the first approximation by adjusting the argument of the arctangent function, which appears in the zeroth approximation . The main idea is to make a series of adjustments in such a way that the quotient mentioned above approaches 1 as closely as possible.
Step 3: Following the logic of Step 2, we introduce the function (Equation (22)) and the argument (Equation (25)) in order to obtain the second approximation (Equation (26)). First, we propose two kinds of approximations for : linear and harmonic. This gives the approximations and (Equations (27) and (28)), respectively. These approximations give corresponding precisions of 3400 km and 470 km, respectively, for the position of the Earth and are completely analytical. They may be used in certain applications that do not require high precision.
Next, we proceed to improving the function as an analytical expression (Equation (29)), involving an arctangent function, with an argument which, in turn, is an expression that depends on six numerical coefficients (Equation (30)). In order to calculate these coefficients, we propose two methods, namely Method A and Method B.
Method A consists in calculating the coefficients for each given value of the orbital eccentricity, while Method B allows us to express these coefficients as another analytical function with corresponding numeric coefficients that are calculated for ranges of the eccentricity.
2.1. Step 0
This solution is periodic, with a period equal to , and coincides with the actual time behavior in the interval . Since the time evolution should be monotonic, we illustrate a way to extend Equation (5) to depict the time evolution by applying the following mapping:
where . In order to avoid complications related to the periodicity of the functions of involved, and the monotony of time, in what follows, we focus our work only on the half-period of the orbit, namely . The second half of the orbit may be obtained from the first part using the symmetry of the orbit.
We now propose the following change of variable:
Thus, Equation (5), in terms of and has the form:
Let us seek for the solution to Equation (7) in the form on the interval , and, as deduced from Equation (7), in .
Note the relationship between and the mean anomaly M:
2.2. Step 1
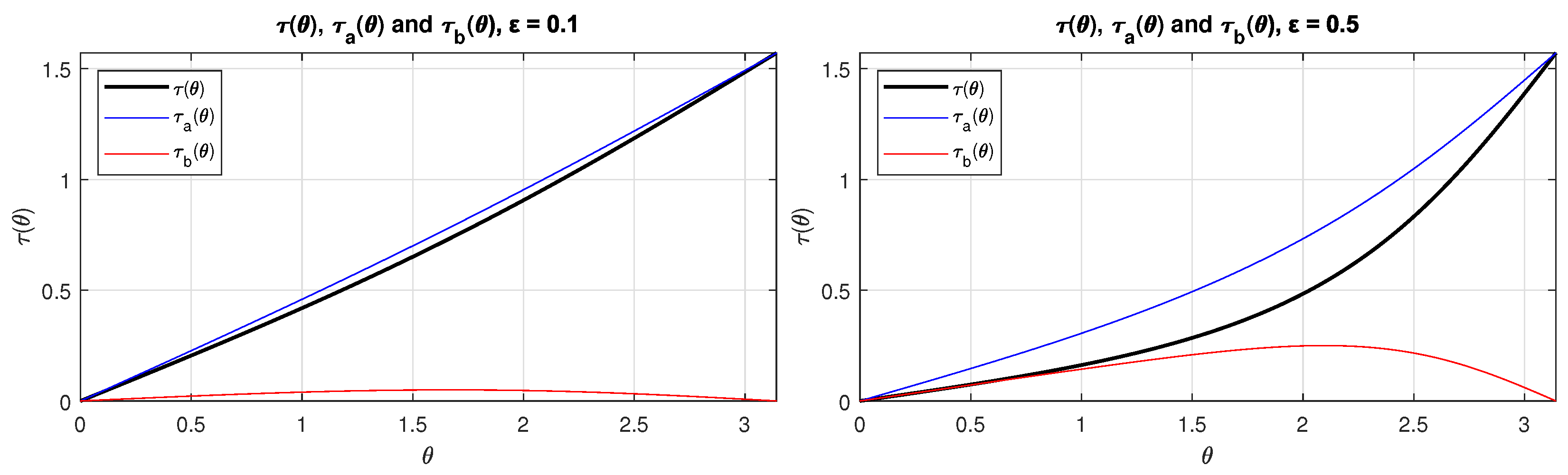
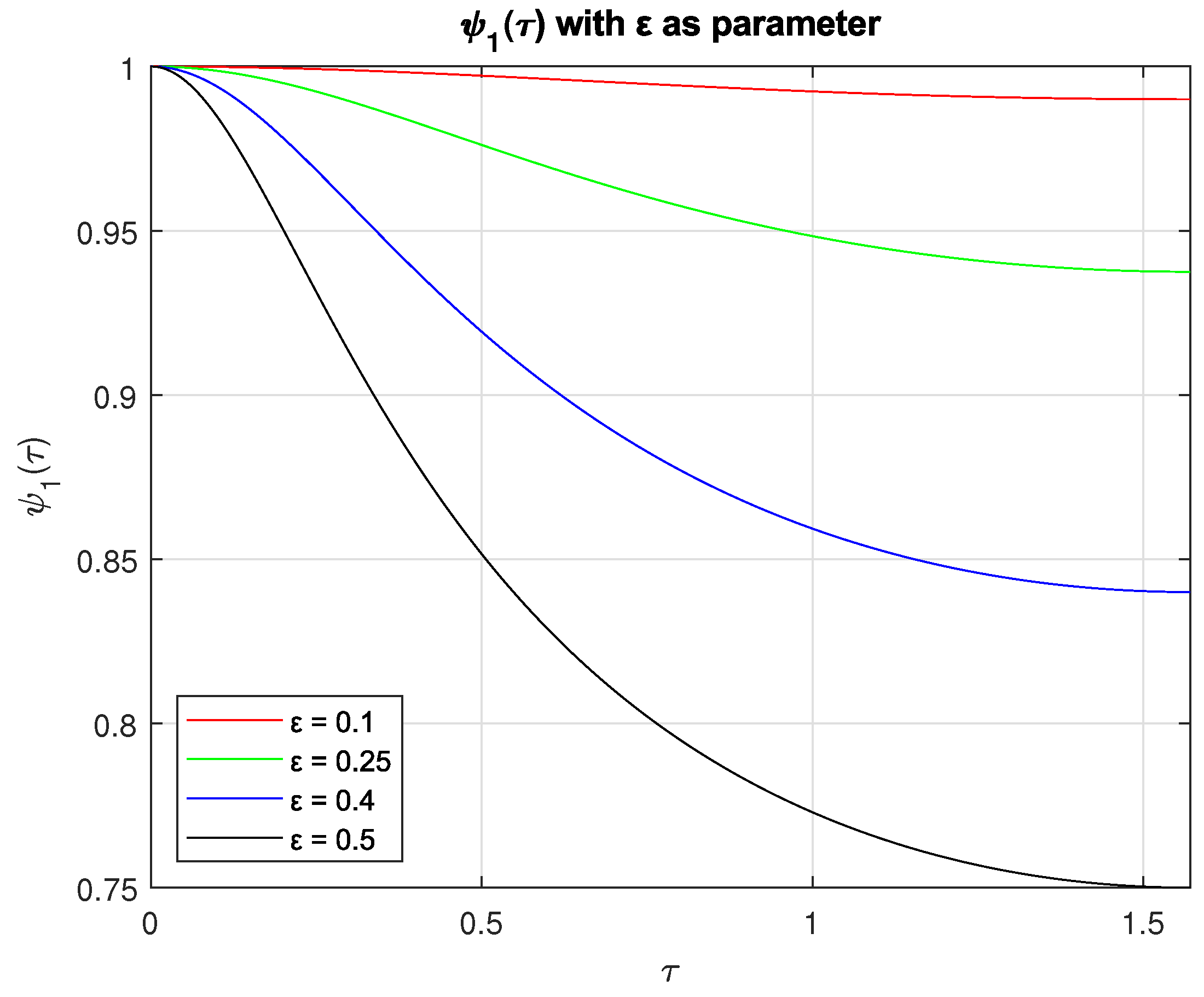
Figure 2 shows the behavior of , , and with as parameter.
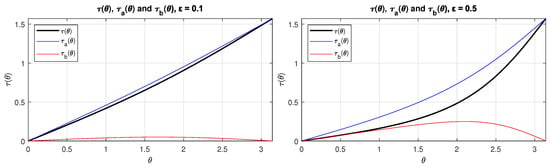
Figure 2.
Plots of , , and with = 0.1 (left) and = 0.5 (right).
Figure 2 shows how is similar to ; therefore, as our zeroth approximation , we will solve the following equation:
To solve the Equation (12), we apply the tangent function to both parts. Solving for , we obtain
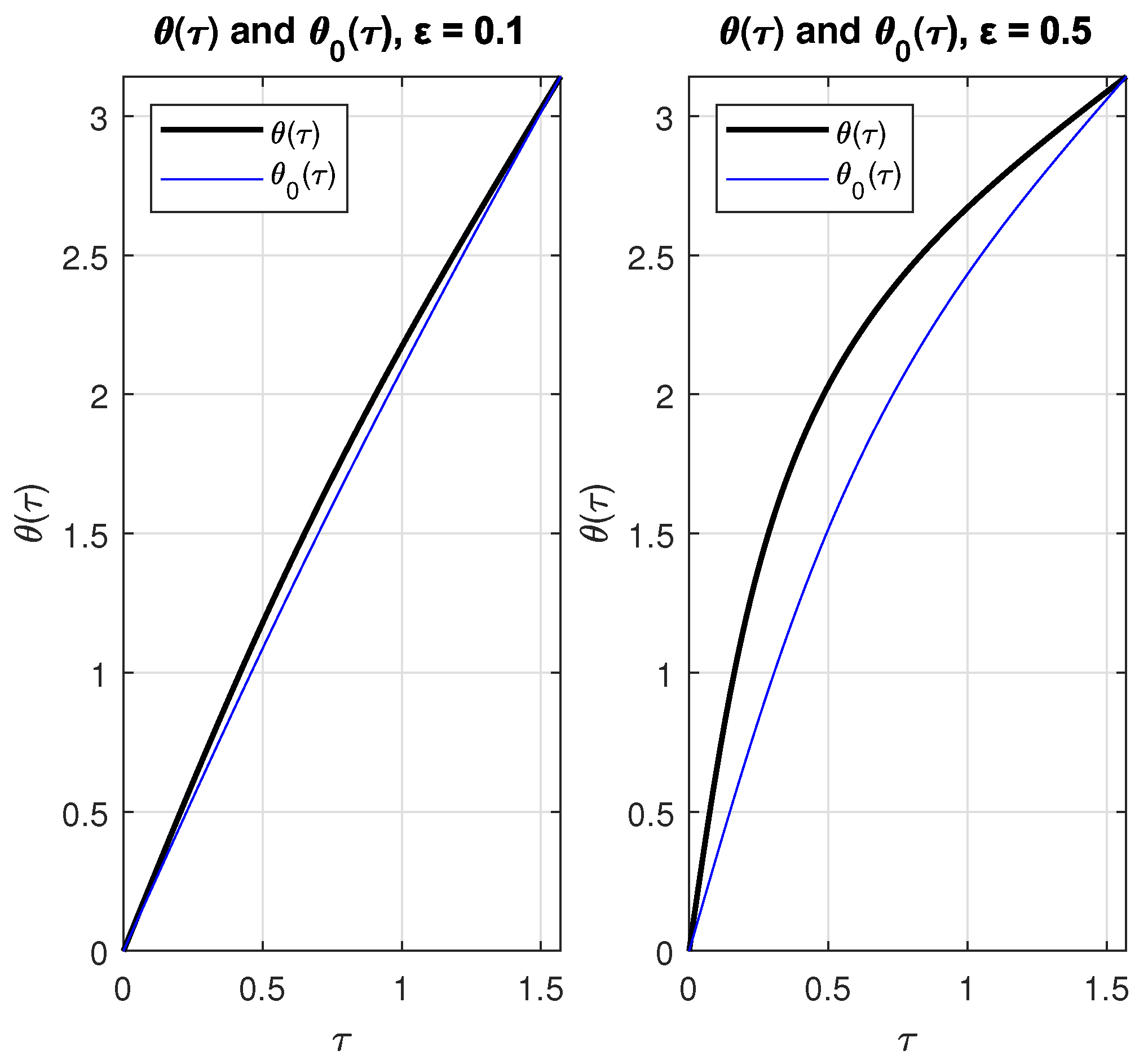
Figure 3 shows plots of and with as parameter. was obtained using Equation (7) and interchanging axes.
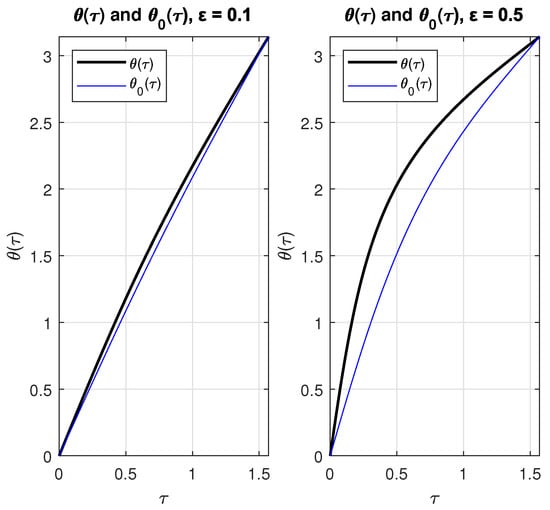
Figure 3.
Plots of and with = 0.1 (left) y = 0.5 (right).
2.3. Step 2
We introduce the functions and as follows:
so that
Now, we introduce another function , defined on the open interval :
Appendix B proves the following limits (the former is used immediately to introduce the function , and the latter is used in step 3):
and
We define approximation one, , as follows:
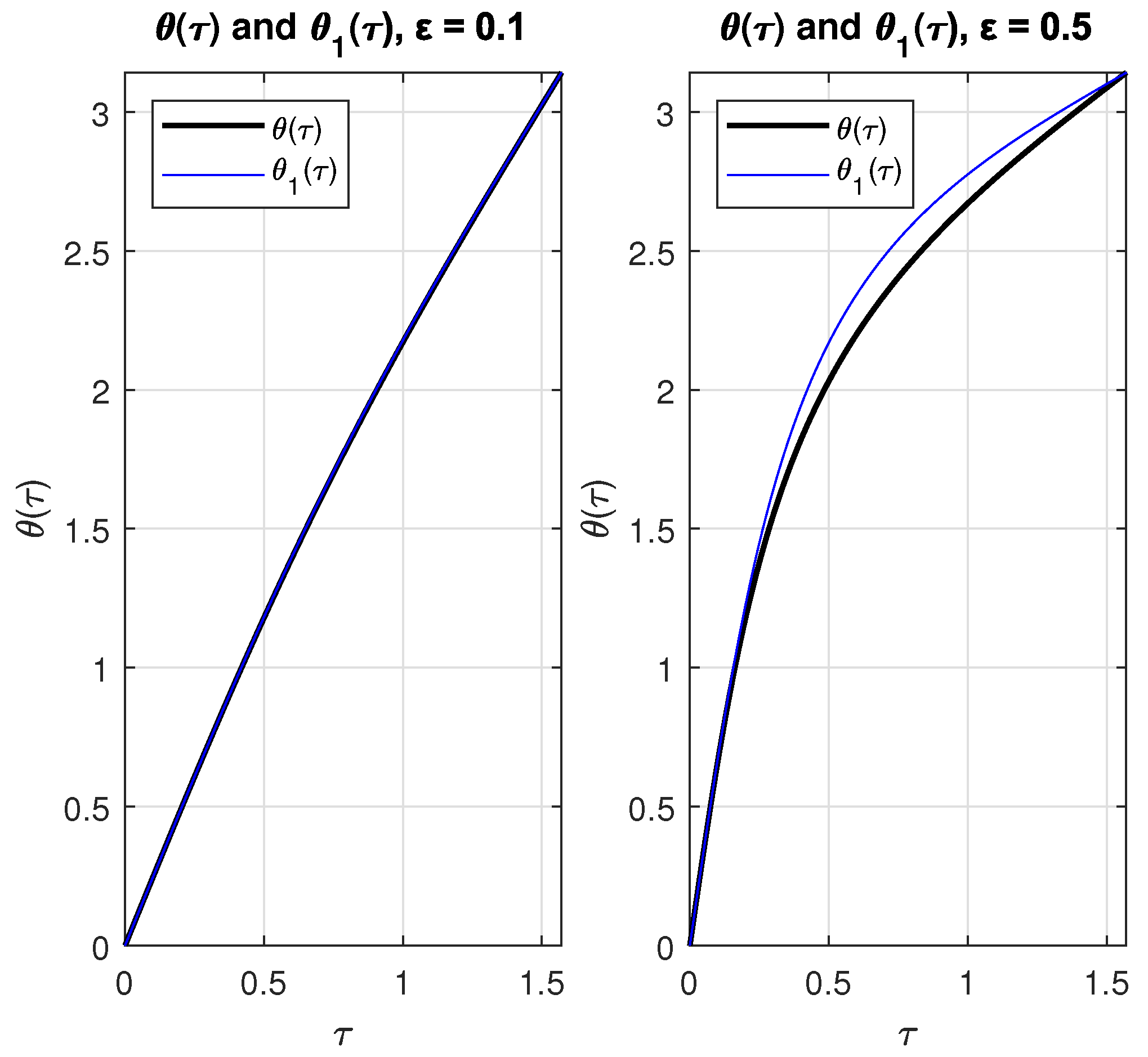
Figure 4 shows plots of and with as parameter.
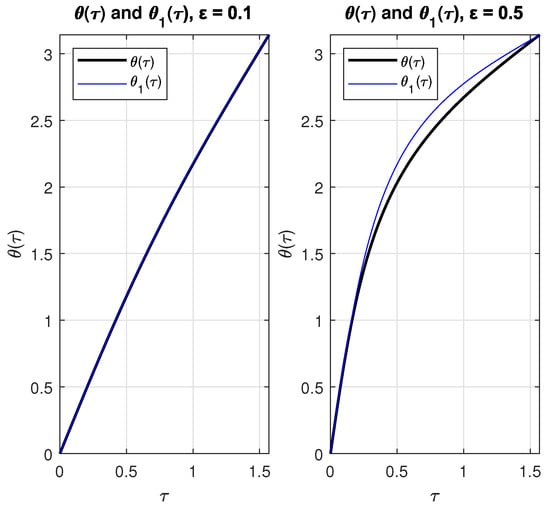
Figure 4.
Plots of and with = 0.1 (left) and = 0.5 (right).
2.4. Step 3
We introduce a new function, , defined on the open interval :
Figure 5 shows the plot of for different values of the parameter .
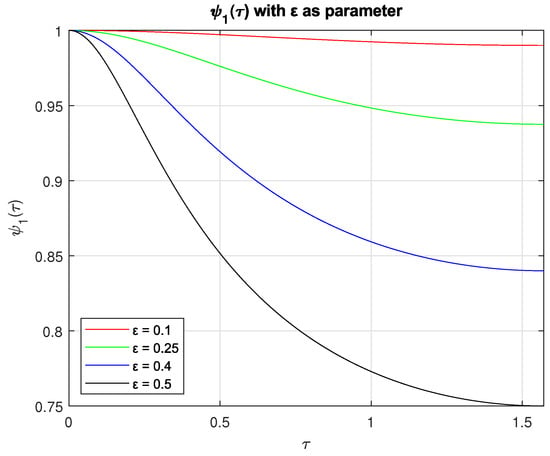
Figure 5.
Plot of with as parameter.
We introduce the function as follows:
The definition of as the product of and leads us to an apparent logical paradox, since, as follows from Equation (22), . The solution to this paradox is the fact that is an unknown function, which we are trying to approximate with the best precision possible. The existence of such a function is obvious, for it can be theoretically constructed point-wise. However, in this work, we are looking for a quasi-analytical expression for , since the exact analytical expression for it, in principle, may not even exist.
Now, we define approximation two, , as follows:
It should be noted that the approximation (Equation (21)) can be considered as the approximation with . For small values of , such as Earth’s (), has a small range (for the Earth, it will be of [0.9997, 1]) so that the approximation already gives us an acceptable result for certain applications. Thus, for the Earth, the maximum error of is of rad, which, translated to the error in the position and taking into account the average distance from the Earth to the Sun as km, is equivalent to 27,000 km, which is a little more than two diameters of the Earth. Now, approximating in a linear form, and as a cosine with period and amplitude adjusted to the range [, 1], the following corresponding approximations are obtained:
The approximation gives a maximum error of rad, which translates to 3400 km in this position (slightly more than half the Earth’s radius), and the approximation gives a maximum error of rad, which corresponds to approximately 470 km in this position.
In Figure 5, we notice that the shape of the curves resembles an arctangent function, with a mapping of the argument from (, ∞) to (, 0), with the range mapping from (, ) to (), and with the behavior of the argument being asymmetric and nonlinear. As before, we search for the approximation of the function in the following form:
where
with y () being functions of .
In order to evaluate the coefficients and (the six numerical coefficients mentioned in the introduction), two methods were developed, Method A and Method B. In Method A, the coefficients are calculated for each value of , while in Method B, they are expressed as analytical functions that, in turn, depend on other numeric coefficients, which are calculated for ranges of . As will be seen subsequently, Method A is more accurate, but less general, while Method B is slightly less accurate (especially after a certain value of ), but more general and easier to use in applications.
2.4.1. Method A
The coefficients and were calculated numerically for each eccentricity value, corresponding to every planet of the solar system, by means of RMSE (root mean square error) minimization, using MATLAB 2020b.
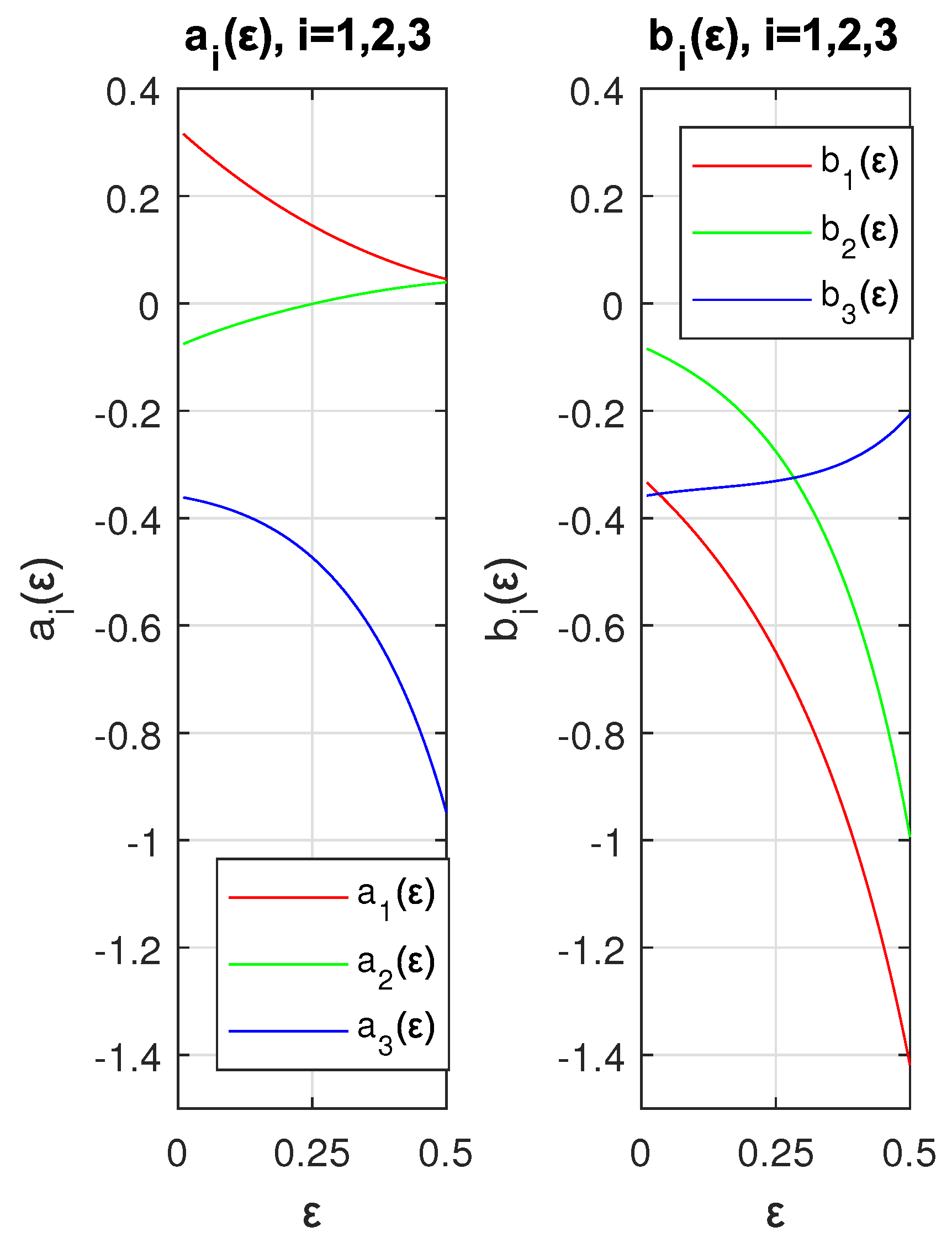
Figure 6 shows the behavior of and in the range of ∈ (0, 0.5) (this range was selected because some absolute values of and grow drastically after , which does not allow us to appreciate the behavior before ).
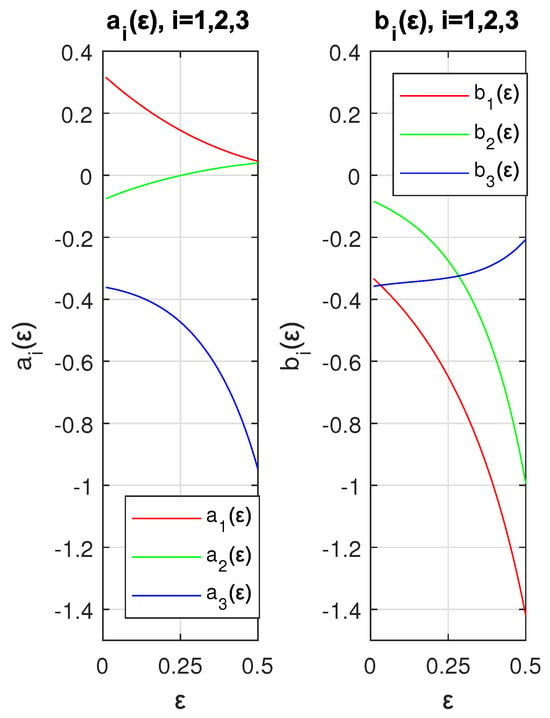
Figure 6.
Plots of (left) and (right).
Table 1 shows the values of and , as well as the error of for the Earth and Pluto, in radians, where ME is the maximum absolute error, MAE is the mean absolute error, and RMSE is the root mean square error.

Table 1.
Values of and and error in for the Earth and Pluto.
Since Table 1 serves just for illustrative purposes, the values of and were rounded to three decimal places. A detailed table including more accurate values for all planets will be shown in Section 3. For now, let us mention that the absolute maximum error in the position of the Earth is 915 meters and approximately 39,000 km (close to the value of the circumference of the Earth, or 16 Pluto diameters) for the position of Pluto (the average distance of Pluto to the Sun is approximately 5.9 billion kilometers).
2.4.2. Method B
Analyzing Figure 6, it can be seen that the shapes of the curves have the behavior of a cubic polynomial, so we search for the coefficients and in the following form:
where repeated indices imply summation.
We introduced the approximation with the same form of given by Equations (26), (29) and (30), where Equation (31) was now used to approximate the and in Equation (30).
The attempt to calculate the coefficients and in the complete range of ∈ (0,1) was not successful. Thus, it was decided to divide the range into five intervals: ∈ (0,0.1], ∈ (0.1,0.25], ∈ (0.25,0.5], ∈ (0.5,0.7], and ∈ (0.7,1). In the next section, we will present the values of and by ranges, and compare the precision of the approximation , which uses values of calculated using Method A, with that of .
3. Results
We now compare the results of our quasi-analytical solution with the real orbits of the planets of the solar system. First, we review the results obtained above in the following equations. By a change of variable,
the equations of motion in the polar coordinate system with the origin at the Sun, and in the interval of time ∈, ∈ are the following:
where is given by the following expression:
and are functions of . In what follows, we present the two methods developed for the calculation of the coefficients and .
3.1. Method A
As mentioned above, in this method, the values of and were calculated for each eccentricity by means of RMSE minimization in MATLAB 2020b. Table 2 shows the values of and , ME, MAE, and RMSE errors in , in radians, with being the average distance of the planet to the Sun in kilometers, and being the maximum error of the position in kilometers with respect to the real orbit.

Table 2.
Values of , , corresponding errors in , and absolute position for celestial bodies.
The results in Table 2 show that for small values of , the accuracy was high. However, for values of the error increased significantly (for Mercury and Pluto the error increased by 2–3 orders in comparison to the errors for the other planets).
3.2. Method B
As was pointed out before, in this method, we calculate the coefficients of a third-degree polynomial (Equation (31)) by minimizing the RMSE for the ranges of . Therefore, in this case, it is not necessary to calculate the and for each value of the eccentricity. Table 3 shows the values of the coefficients and for the different ranges of . Obviously, using this method results in errors greater than those of Method A.

Table 3.
Values of and calculated in ranges of .
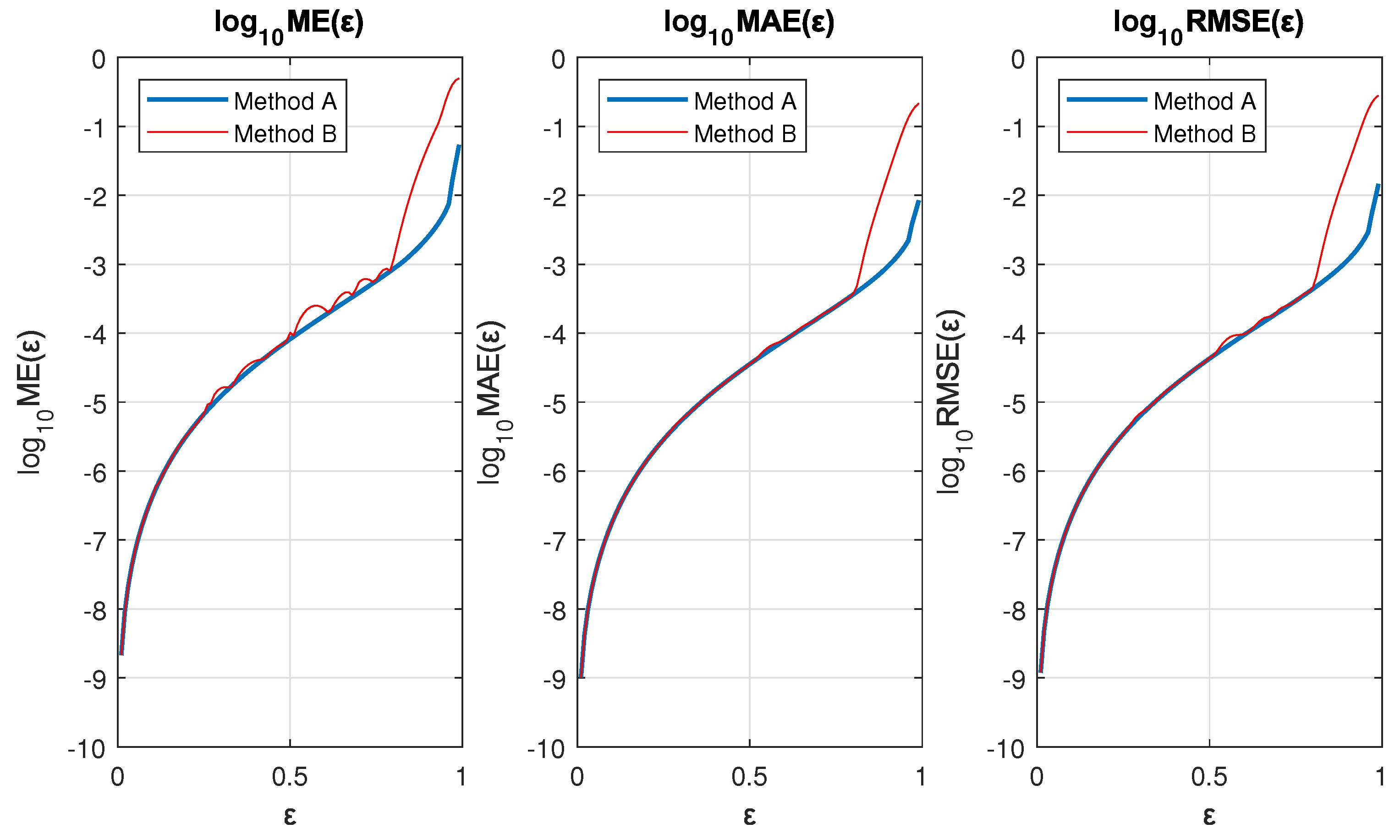
Figure 7 shows a comparison of the errors between methods A and B. As can be seen, the error in Method B was slightly higher (especially for ME) up to values of . For values of , the errors of Method B increased significantly with respect to those of Method A.
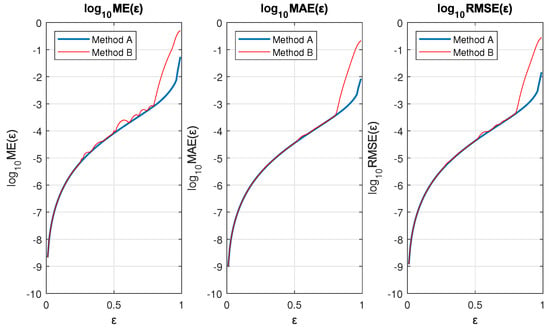
Figure 7.
Logarithmic plots of the error in as a function of for both methods.
3.3. Equations of Motion for the Planets
Finally, let us express the equations of motion of both position and velocity in the Cartesian coordinate system, with the origin at the Sun.
The equations for the position are as follows:
where and are given by Equations (33) and (34), respectively.
The equations for the velocity are as follows:
where
and
The function defined in the interval ∈ is given by Equation (35) and its derivative is the following:
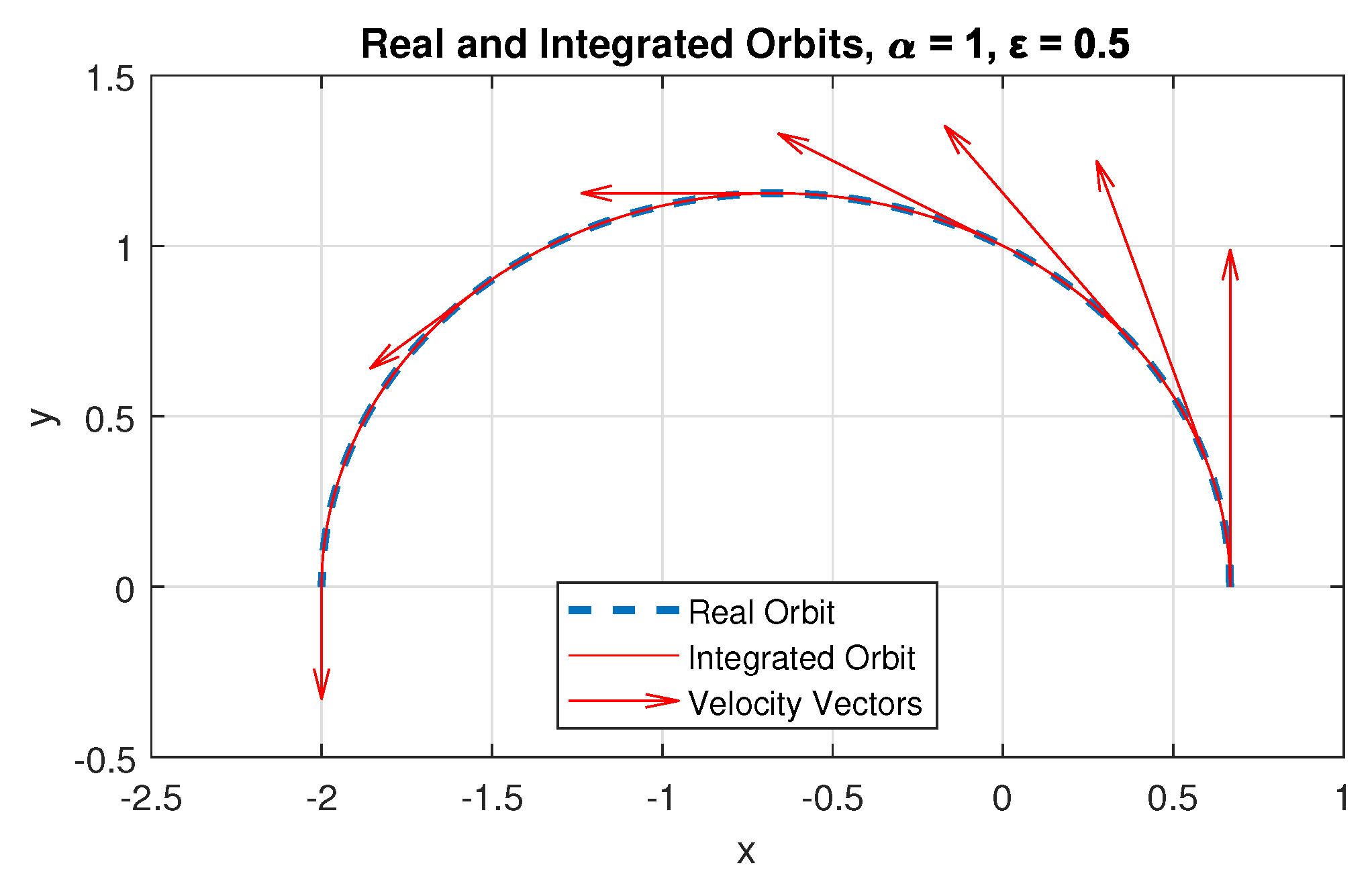
Figure 8 shows a comparison plot between the real orbit, calculated numerically using Equation (7), and the orbit obtained by numerical integration of Equation (37) (where Method A was used). Additionally, the velocity vectors are shown at an arbitrary scale at certain points of the trajectory.
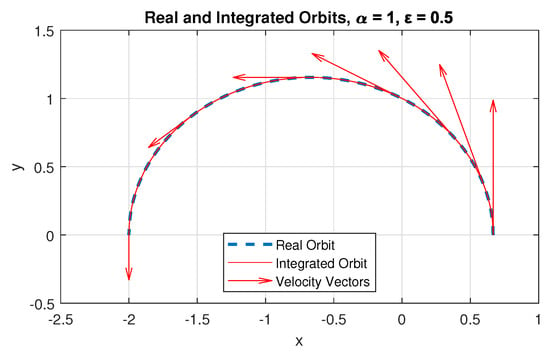
Figure 8.
Plot of the orbits, real and integrated, with and .
As can be seen in Figure 8, the integrated orbit closely resembles the behavior of the real orbit. This shows that our Method A is sufficiently accurate, even for eccentricities of the order of up to .
4. Solution to Kepler’s Equation
As can be seen from Figure 1b, it is trivial to obtain the following expression, which gives the formula for E (the eccentric anomaly), appearing in Equation (3) as a function of the polar coordinates with the center in the focus F. In what follows, we set the major semi-axis equal to one ():
where (Figure 1b). As is well known from the theory of conic sections, , since we set . Thus, Equation (42) acquires the following form:
Due to the normalization , the expression for is as follows:
Now, in order to obtain the final explicit expression for the solution of KE, , we need to express and as functions of M (the mean anomaly given by Equation (4)). So far, and r are functions of (where is given by Equation (6)). Thus, by expressing as a function of M, and r automatically become functions of M. The expression for is the following:
In order to obtain as a function of M, we use Kepler’s third law to express a as follows:
5. Remarks and Conclusions
In this work, we obtained a quasi-analytical solution for the motion of the celestial bodies as an explicit function of time in four steps. We called this solution quasi-analytical, due to the dependency on certain numerical coefficients, which in turn themselves depend on the orbital eccentricity. We proposed two methods for evaluating these coefficients: Method A and Method B. The former gives a higher degree of accuracy, but involves calculations for each value of the eccentricity, while the latter is less accurate (especially for values of ) but more practical, since it works for ranges of the eccentricity. Although there exist methods for solving Kepler’s equation up to machine precision, e.g., [11], these methods are completely numerical and require an initial guess. The aim of our work was to find a relatively simple explicit analytical solution with acceptable precision. In future work, we plan to use our results as an initial guess for the iterative procedures mentioned previously. We hypothesize that this approach will lead to highly precise results with fewer iterations.
Author Contributions
The first two authors A.N.B. and V.A.B. developed the theory and worked on the redaction together with R.C.C.-G. and C.O.M. J.L.R. collaborated on the theoretical revision of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Integration of Equation (uid1)
To solve the integral, we propose the Weierstrass change of variable:
From Equation (A1), it follows that
Substituting Equation (A2) into Equation (1), and with a little algebra, we obtain the following:
which will be left undefined for now and will eventually be evaluated in the original variables. Here, and . To facilitate the integration, the integrand is simplified using partial fractions, leaving the integral as follows:
Performing a bit of algebra and making the trigonometric substitution
where . Finally, Equation (A4) reads
The latter integral is trivial, and the former is solved using the identity , such that is left as
Appendix B. Proofs of Limits Equations (18) and (19)
We begin by solving for from Equation (14):
We introduce the variable as follows:
For the sake of simplicity, we will evaluate the limit instead of .
In order to prove limit Equation (18), we will use the Taylor expansion about zero of the following functions:
In order to demonstrate Equation (19), we use the following trigonometric identity:
References
- Krisciunas, K. Demonstrating the elliptical orbit of Mars using naked eye data. Am. J. Phys. 2019, 87, 885–893. [Google Scholar] [CrossRef]
- Goldstein, H. Classical Mechanics, 2nd ed.; Addison-Wesley: Reading, UK, 2020. [Google Scholar]
- Baisheng, W.; Zhou, Y.; Lim, C.; Zhong, H. A new solution approach via analytical approximation of the elliptic kepler equation. Acta Astronaut. 2023, 202, 303–310. [Google Scholar] [CrossRef]
- Colwell, P. Solving Kepler’s Equation over Three Centuries; Willman-Bell, Inc.: Richmond, VA, USA, 1993. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Mechanics, 3rd ed.; Elsevier Butterworth-Heinemann: Burlington, NJ, USA, 1976. [Google Scholar]
- Hagihara, Y. Celestial Mechanics: Perturbation Theory, 1st ed.; MIT Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Danby, J.M.A. Fundamentals of Celestial Mechanics: Perturbation Theory, 2nd ed.; Willmann-Bell: New York, NY, USA, 1988. [Google Scholar]
- Odell, A.W.; Gooding, R.H. Procedures for Solving Kepler’s Equation. Cel. Mech. 1986, 38, 307–334. [Google Scholar] [CrossRef]
- Sacchetti, A. Francesco Carlini: Kepler’s equation and the asymptotic solution to singular differential equations. Hist. Math. 2020, 53, 1–32. [Google Scholar] [CrossRef]
- González-Gaxiola, O.; Hernández-Linares, S. An Efficient Iterative Method for Solving the Elliptical Kepler’s Equation. Int. J. Appl. Comput. Math 2021, 7, 1–14. [Google Scholar] [CrossRef]
- Abubekerov, M.K.; Gostev, N.Y. Solution of Kepler’s equation with machine precision, Astr. Rep. 2020, 64, 1060–1066. [Google Scholar] [CrossRef]
- Dubinov, A.E.; Galidakis, I.N. Explicit solution of the Kepler equation. Phys. Part. Nuclei Lett. 2007, 4, 213–216. [Google Scholar] [CrossRef]
- Elenin, G.G.; Elenina, T.G. Parametrization of the Solution of the Kepler Problem and New Adaptive Numerical Methods Based on This Parametrization. Differ. Equ. 2018, 54, 911–918. [Google Scholar] [CrossRef]
- Markley, F.L. Kepler Equation solver. Celest. Mech. Dyn. Astron. 1995, 63, 101–111. [Google Scholar] [CrossRef]
- Simha, A. An algebra and trigonometry-based proof of Kepler’s first law. Am. J. Phys. 2021, 89, 1009–1011. [Google Scholar] [CrossRef]
- Easton, R.W.; Anderson, R.L.; Lo, M.W. Conic transfer arcs for Kepler’s problem. Am. J. Phys. 2022, 90, 666–671. [Google Scholar] [CrossRef]
- Calvo, M.; Elipe, A.; Rández, L. On the integral solution of elliptic Kepler’s equation. Celest. Mech. Dyn. Astron. 2023, 135, 26. [Google Scholar] [CrossRef]
- Borghi, R. On the Bessel solution of Kepler’s Equation. Mathematics 2024, 12, 154. [Google Scholar] [CrossRef]
- Orlando, F.; de Souza, C.F.; Zarro, C.; Terra, P. Kepler’s equation and some of its pearls. Am. J. Phys. 2018, 86, 849–858. [Google Scholar] [CrossRef]
- Zheng, M.; Luo, J.; Dang, Z. Machine Learning-Based Solution of Kepler’s Equation; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2022. [Google Scholar] [CrossRef]
- Marion, J.B. Classical Dynamics, 1st ed.; Academic Press Inc.: Cambridge, MA, USA, 1965. [Google Scholar]
- Mikkola, S.A. A cubic approximation for Kepler’s equation. Cel. Mech. 2018, 86, 849–858. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).