Research on Magnetic Levitation Control Method under Elastic Track Conditions Based on Backstepping Method
Abstract
1. Introduction
2. Modeling of the Vehicle–Guideway System
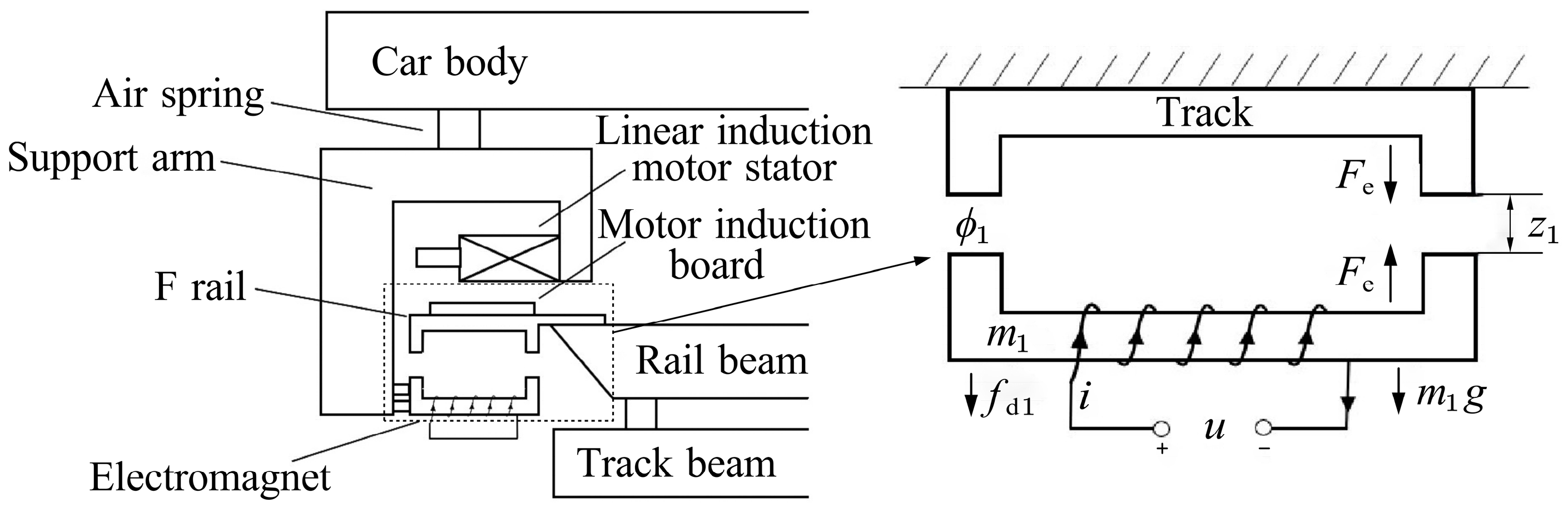
2.1. Modeling of the Single-Point Suspension System
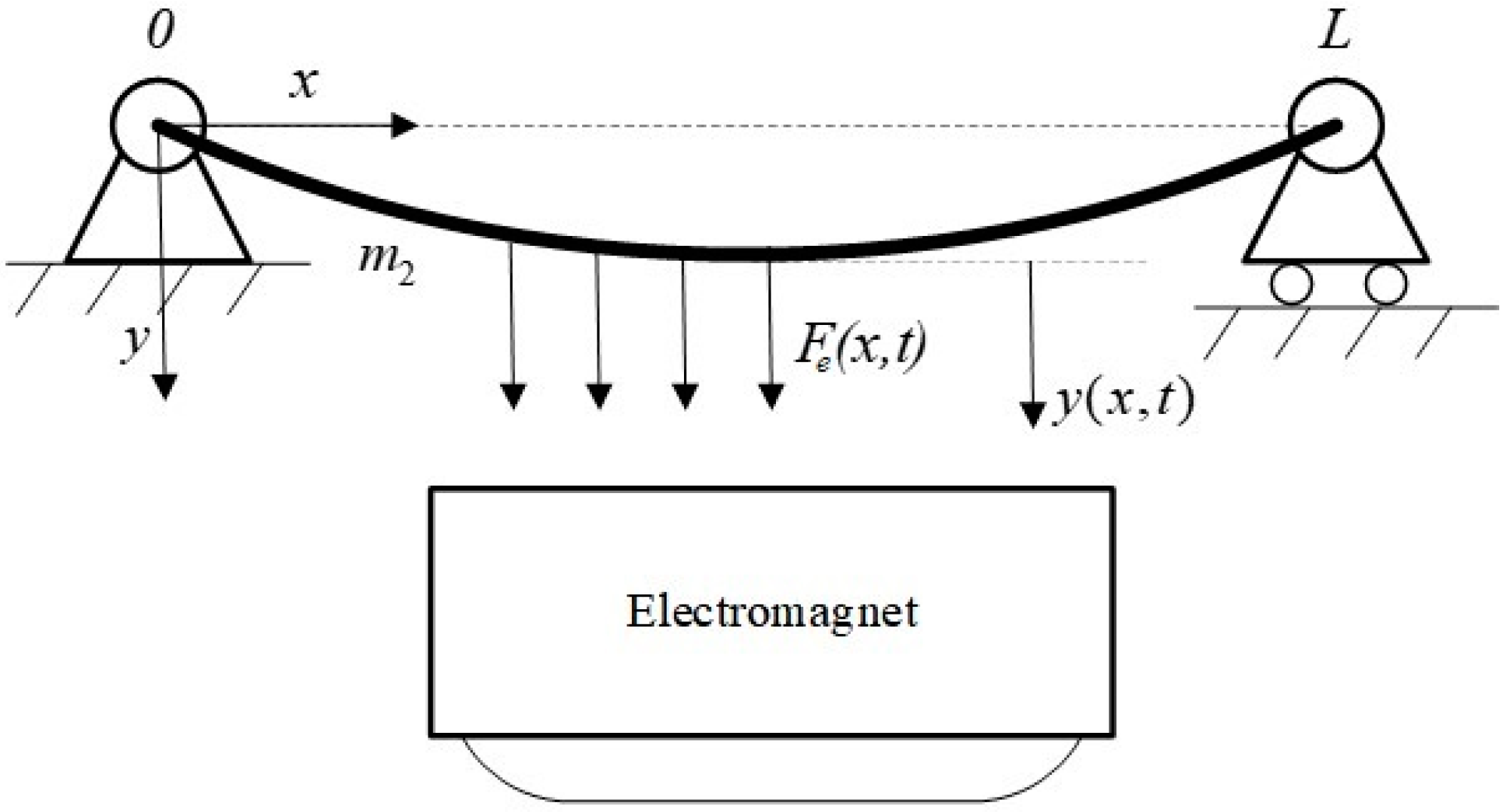
2.2. Modeling of the Vehicle–Guideway System
3. Design of the Levitation Control Scheme
3.1. Design of Control Law Based on Backstepping Method
3.2. Design of the Magnetic Flux Loop
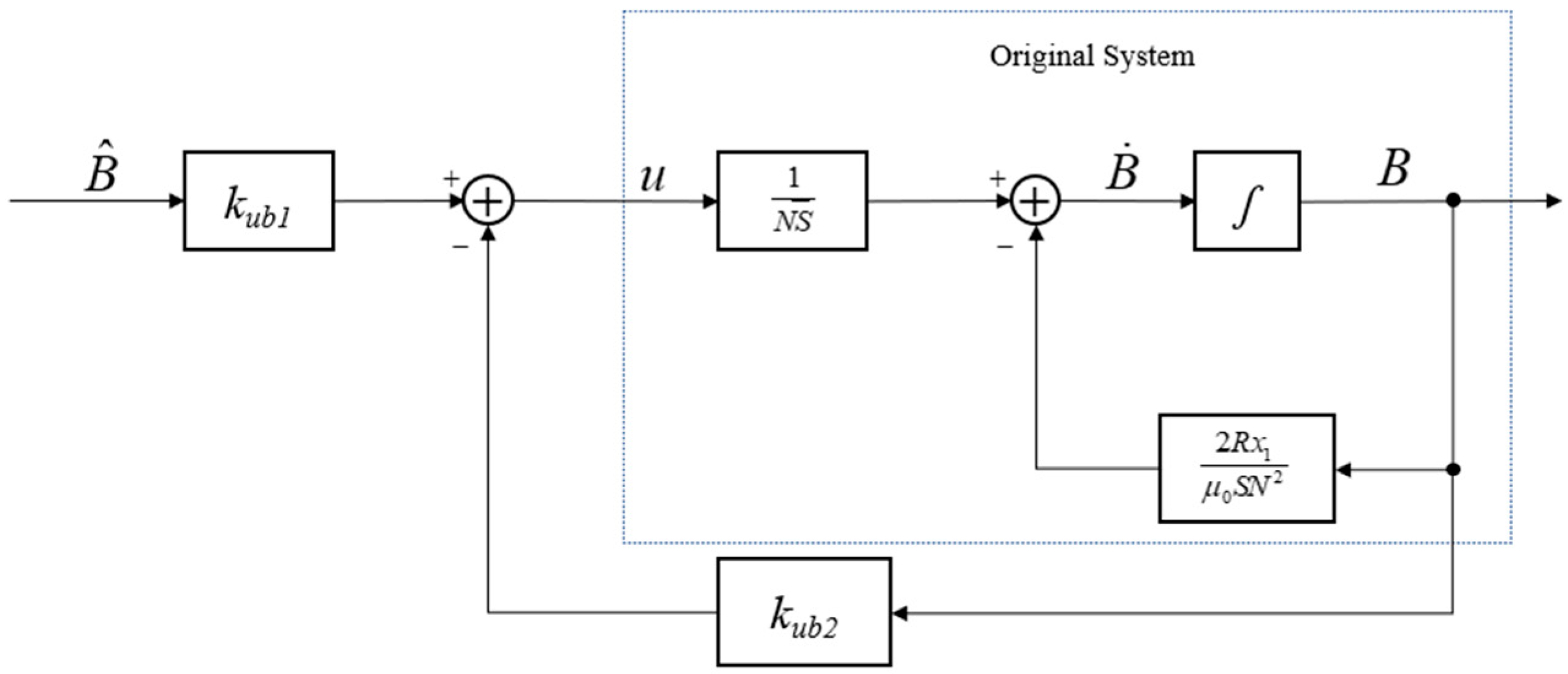
3.3. Estimation of the Track State
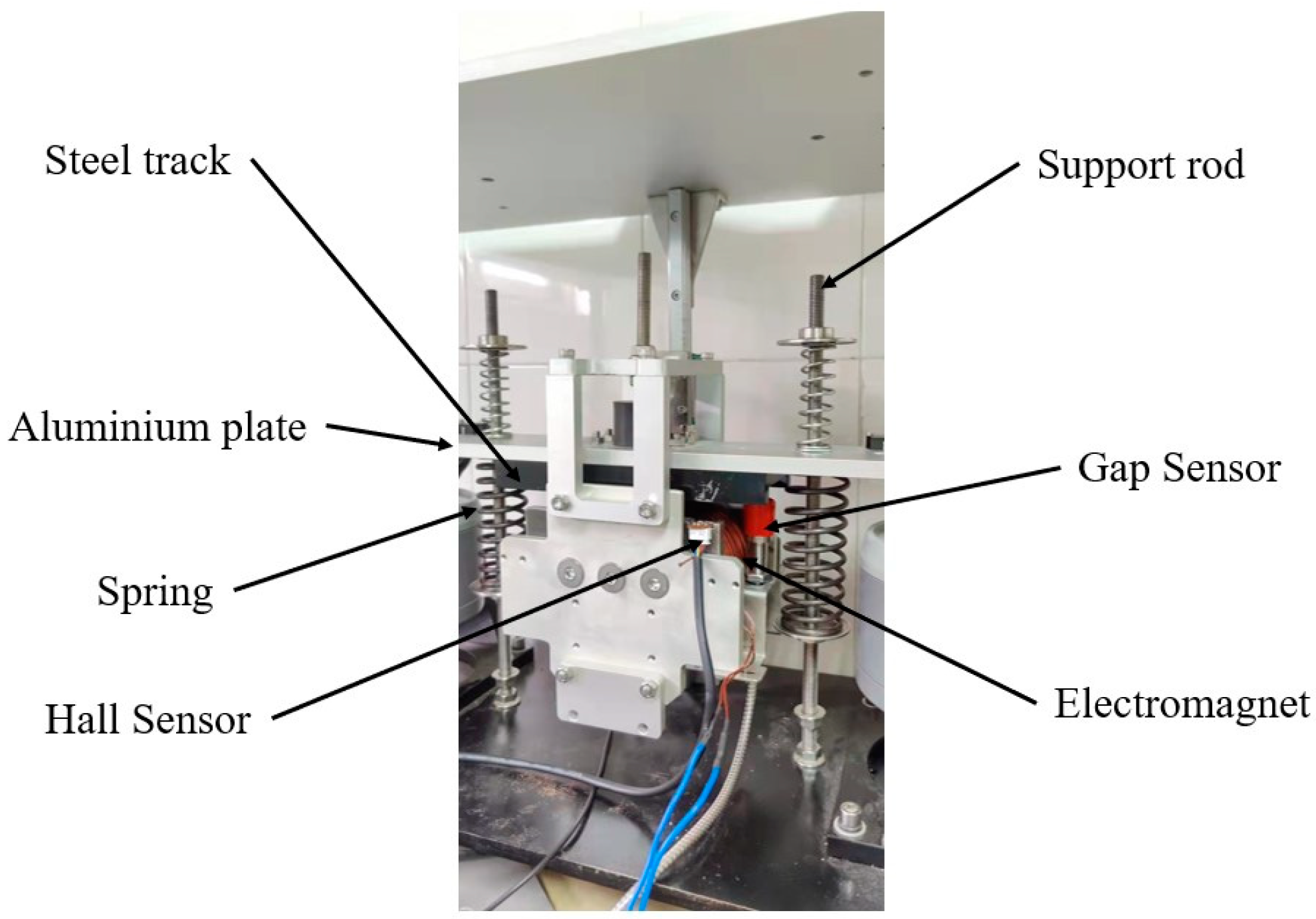
4. Experimental Verification
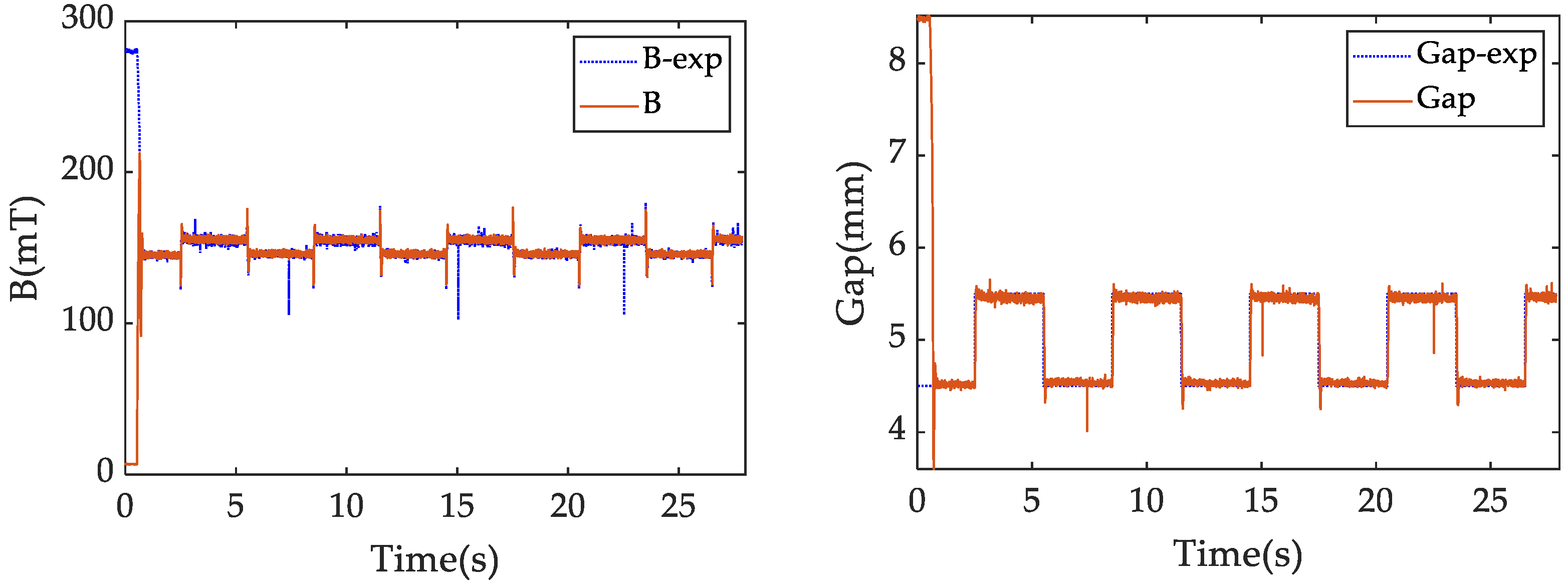
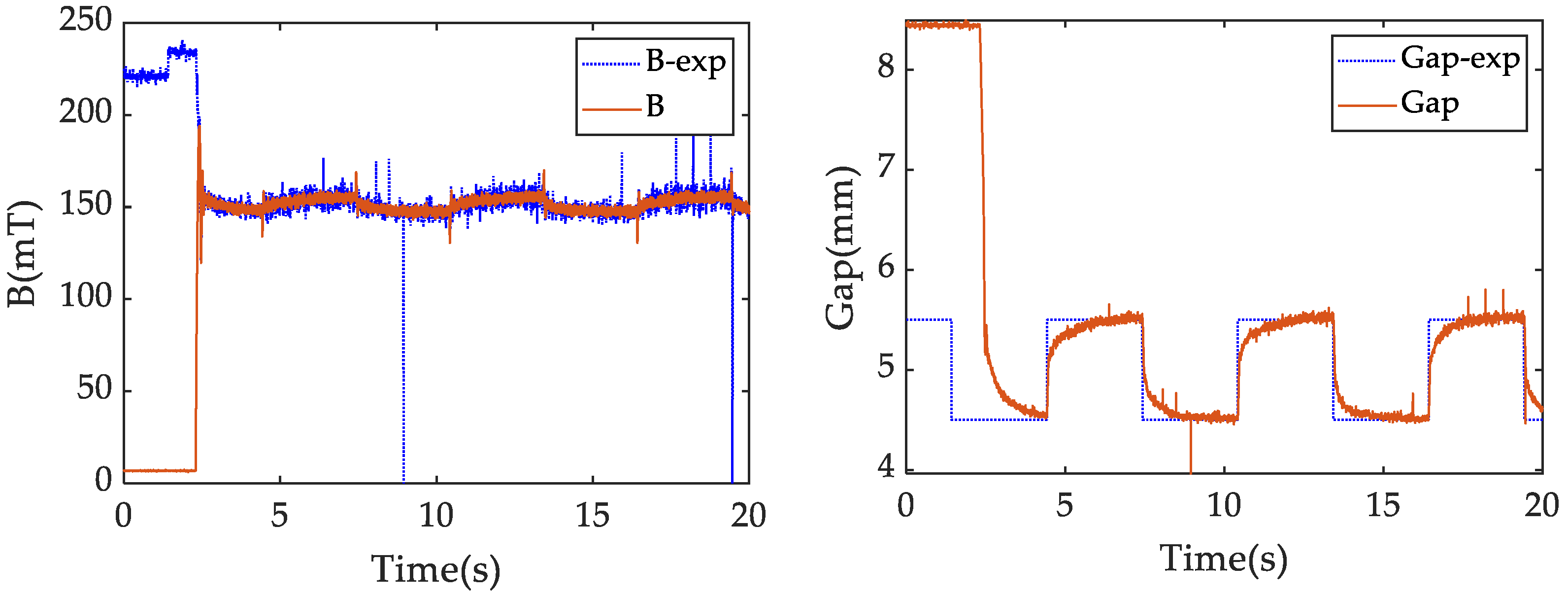
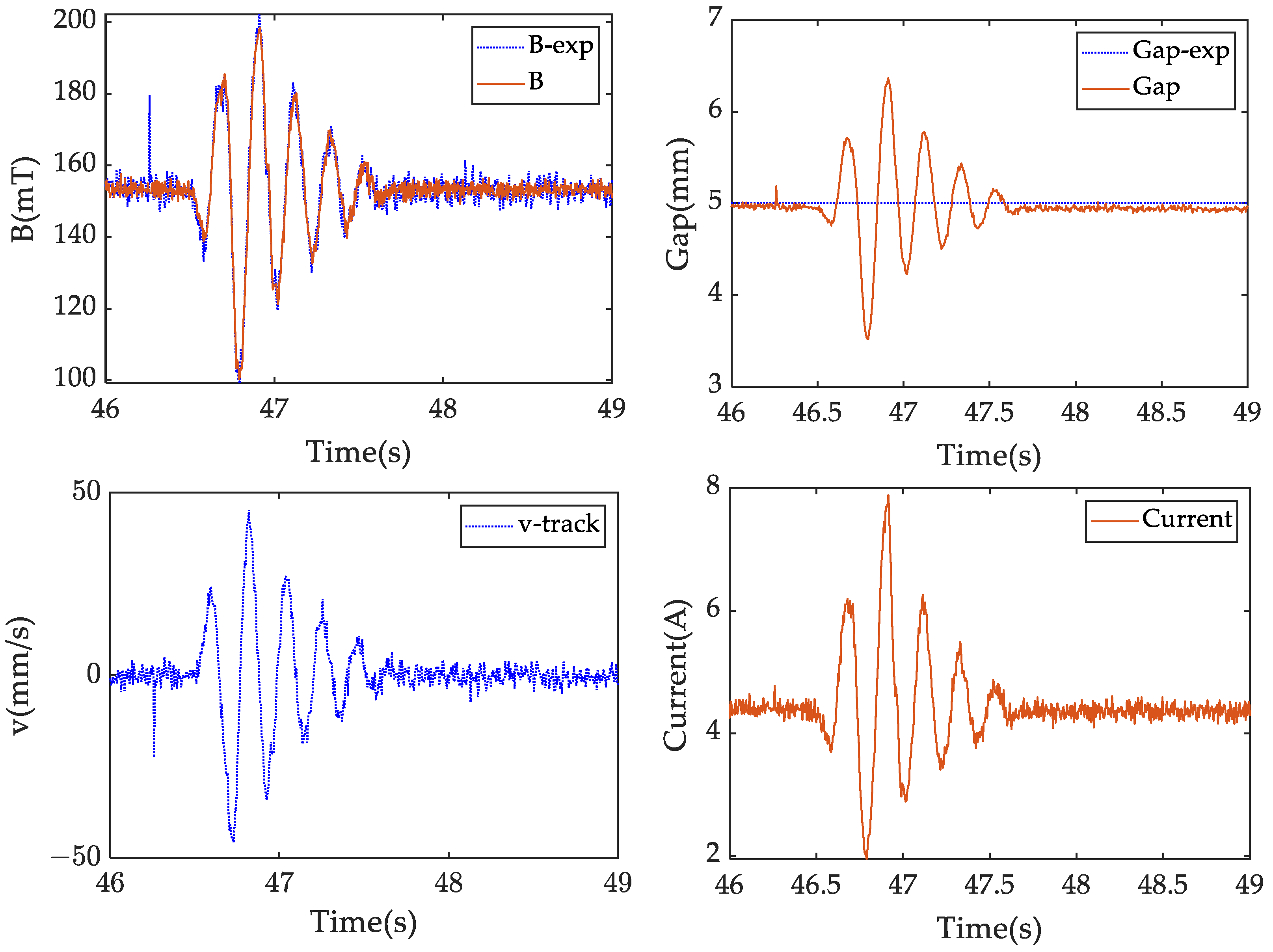
4.1. Effect of the State Feedback Controller Based on Feedback Linearization
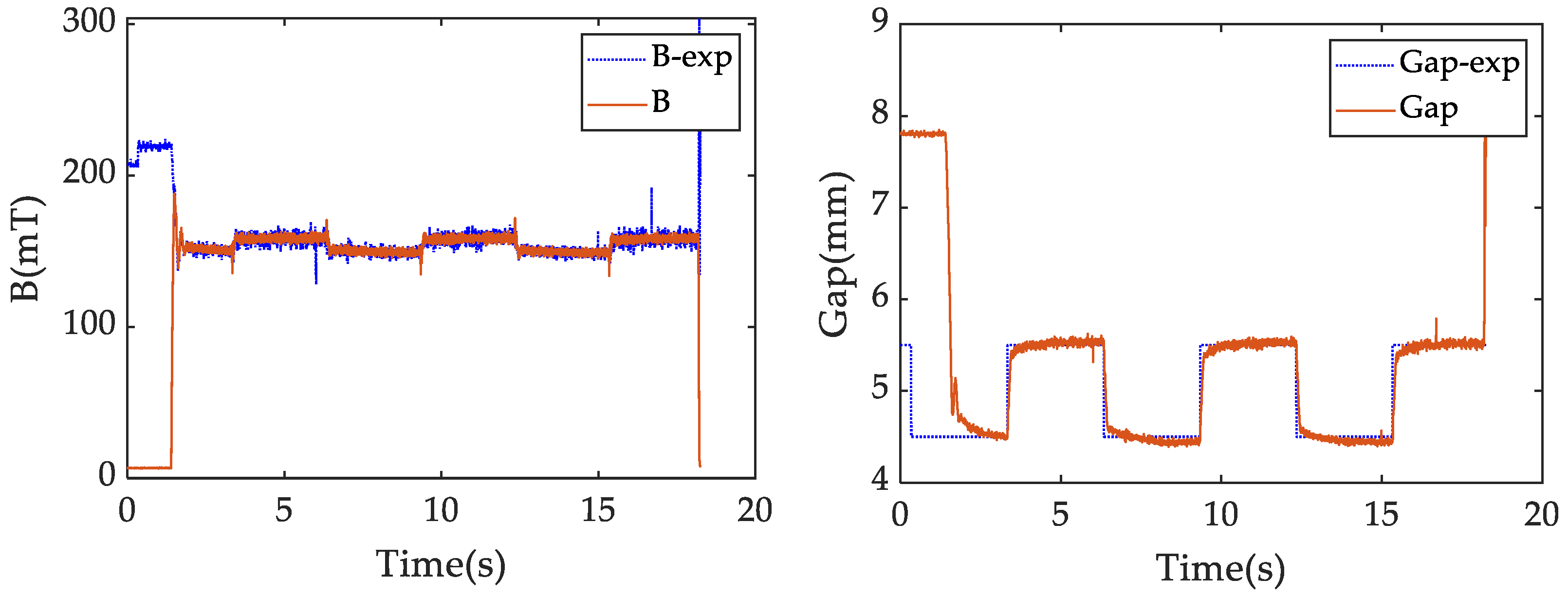
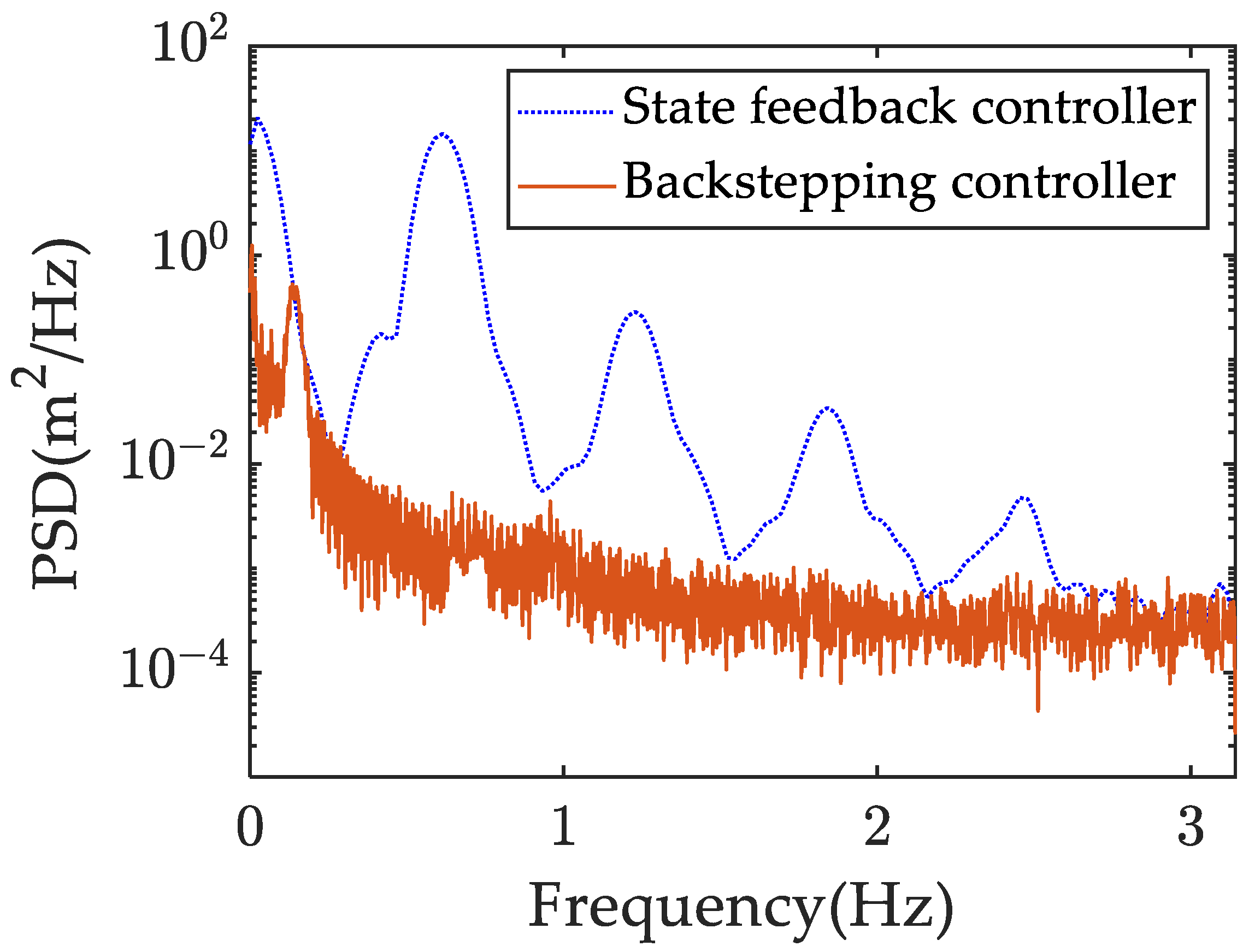
4.2. Effect of the Proposed Backstepping Controller
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, H.; Kim, K.; Lee, J. Review of maglev train technologies. IEEE Trans. Magn. 2006, 42, 1917–1925. [Google Scholar]
- Yan, L. Development and application of the maglev transportation system. IEEE Trans. Appl. Supercon. 2008, 18, 92–99. [Google Scholar]
- Wang, S.-M.; Wang, Y.-W.; Ni, Y.-Q.; Lu, Y. Real-Time Malfunction Detection of Maglev Suspension Controllers. Mathematics 2023, 11, 4045. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, J.; Chen, C.; Hu, W. Reinforcement learning-based optimal tracking control for levitation system of maglev vehicle with input time delay. IEEE Trans. Instrum. Meas. 2022, 71, 7500813. [Google Scholar] [CrossRef]
- Tian, X.; Xiang, H.; Chen, X.; Li, Y. Dynamic response analysis of high-speed maglev train-guideway system under crosswinds. J. Cent. South Univ. 2023, 30, 2757–2771. [Google Scholar] [CrossRef]
- Kim, K.; Han, J.; Han, H.; Yang, S. Coupled vibration analysis lysis of maglev vehicle–guideway while standing still or moving at low speeds. Veh. Syst. Dyn. 2015, 53, 587–601. [Google Scholar] [CrossRef]
- Li, L.; Meng, G. Analysis of the maglev vehicle and steel guideway frame coupled resonance during levitating up and landing. J. Vib. Shock 2006, 25, 46–48+75. [Google Scholar]
- Zhou, D.; Li, J.; Hansen, C.H. Suppression of the stationary maglev vehicle-bridge coupled resonance using a tuned mass damper. J. Vib. Control 2013, 19, 192–203. [Google Scholar] [CrossRef]
- Wang, D.; Li, X.; Liang, L.; Qiu, X. Influence of the track structure on the vertical dynamic interaction analysis of the low-to-medium-speed maglev train-bridge system. Adv. Struct. Eng. 2019, 22, 2937–2950. [Google Scholar] [CrossRef]
- Zeng, J.; Xia, W.; Xiang, X.; Long, Z. Research on the mechanism and control characteristics of vehicle-track beam coupled vibration for medium-speed maglev vehicle. IEEE Trans. Transp. Electr. 2022, 8, 3236–3246. [Google Scholar] [CrossRef]
- Zhang, M.; Luo, S.; Gao, C.; Ma, W. Research on the mechanism of a newly developed levitation frame with mid-set air spring. Veh. Syst. Dyn. 2018, 56, 1797–1816. [Google Scholar] [CrossRef]
- Li, J.H.; Li, J.; Zhou, D.; Wang, L. Maglev self-excited vibration suppression with a virtual sky-hooked damper. J. Cent. South Univ. 2016, 23, 1363–1371. [Google Scholar] [CrossRef]
- Song, R.; Chen, Z. Optimization and design of maglev system PID controller based on particle swarm optimization algorithm. J. Southwest Jiaotong Univ. 2015, 50, 36–43. [Google Scholar]
- Wang, B.; Zhang, Y.; Xia, C.; Li, Y.; Gong, J. Dynamic analysis of high-speed maglev train-bridge system with fuzzy proportional-integral-derivative control. J. Low Freq. Noise Vib. Act. Control. 2022, 41, 374–386. [Google Scholar] [CrossRef]
- Adil HM, M.; Ahmed, S.; Ahmad, I. Control of maglev system using supertwisting and integral backstepping sliding mode algorithm. IEEE Access 2020, 8, 51352–51362. [Google Scholar] [CrossRef]
- Alain KS, T.; Fabien, K.; Martin, S.S.; Bertrand, F.H. Robust nonsingular sliding mode control of the maglev train system: Case study. SN Appl. Sci. 2021, 3, 2523–3963. [Google Scholar] [CrossRef]
- Ni, F.; Mu, S.; Kang, J.; Xu, J. Robust controller design for maglev suspension systems based on improved suspension force model. IEEE Trans. Transp. Electr. 2021, 7, 1765–1779. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, J.; Lin, G.; Sun, N. Adaptive neural network control for maglev vehicle systems with time varying mass and external disturbance. Neural Comput. Appl. 2021, 35, 12361–12372. [Google Scholar] [CrossRef]
- Chen, C.; Xu, J.; Lin, G.; Sun, Y.; Ni, F. Model identification and nonlinear adaptive control of suspension system of high-speed maglev train. Veh. Syst. Dyn. 2022, 60, 883–905. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Q.; Liu, J. Extended State Observer-Based Saturation Integral Backstepping Control for Yaw Control of UAV Helicopters. In Proceedings of the Advances in Guidance, Navigation and Control, Shanghai, China, 5–7 November 2021; pp. 4021–4037. [Google Scholar]
- Choi, Y.; Lee, I.; An, J.; Cho, M.; Kim, C. Robust trajectory-tracking control of a rotorcraft using immersion-and-invariance-based adaptive backstepping control. Int. J. Aerosp. Eng. 2022, 2022, 8447125. [Google Scholar] [CrossRef]
- Gao, M.; Jin, X.; Ding, L. Robust adaptive backstepping INTSM control for robotic manipulators based on ELM. Neural Comput. Appl. 2022, 34, 5029–5039. [Google Scholar] [CrossRef]
- Malik, A.S.; Ahmad, I.; Rahman, A.U.; Islam, Y. Integral backstepping and synergetic control of magnetic levitation system. IEEE Access 2019, 7, 173230–173239. [Google Scholar] [CrossRef]
- Yaseen HM, S.; Siffat, S.A.; Ahmad, I.; Malik, A.S. Nonlinear adaptive control of magnetic levitation system using terminal sliding mode and integral backstepping sliding mode controllers. ISA Trans. 2021, 126, 121–133. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Sun, Y.; Gao, D.; Ma, W.; Luo, S.; Qian, Q. Dynamic modeling and adaptive sliding mode control for a maglev train system based on a magnetic flux observer. IEEE Access 2018, 6, 31571–31579. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Zhang, K.; Cui, P. Measurement and control of magnetic flux signal in a maglev system. Asian J. Control 2015, 17, 165–175. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, D.; Yu, P.; Chen, Q.; Li, J.; Li, J.H. Research on maglev train-steel beam coupling vibration suppression strategy based on flux derivative feedback. In Proceedings of the 39th Chinese Control Conference, Shenyang, China, 27–29 July 2020; pp. 5637–5642. [Google Scholar]
- Zhou, D.; Yang, Q.; Wang, L.; Li, J. Stability and control of maglev vehicle-girder coupled system considering torsional vibration of the girder. ISA Trans. 2021, 111, 309–322. [Google Scholar] [CrossRef]




| Parameter | Definition |
|---|---|
| z1 | Air gap between the track and the suspension electromagnet |
| m1 | Mass of the suspension electromagnet |
| Fe | Electromagnetic force between the electromagnet and the track |
| fd1 | External disturbance force |
| u | Voltage applied to the electromagnet winding |
| B | Magnetic flux density in the suspended air gap |
| i | Current through the winding |
| N | Number of turns of the electromagnet |
| S | Pole area of the electromagnet |
| Vacuum permeability | |
| W | Work done by the electromagnetic force on the electromagnet |
| R | Resistance on the winding |
| Fm | Magneto-motive force |
| Resistance of the electromagnet | |
| Air gap magnetic flux | |
| g | Gravitational acceleration |
| Parameter | Definition | Value |
|---|---|---|
| m1 | Mass of the levitation electromagnet | 7.40 kg |
| m2 | Mass of track | 2.66 kg |
| R | Winding resistance | 3.3 Ω |
| N | Number of turns of the winding | 830 |
| S | Pole area | 0.001 m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, P.; Zhang, T.; Zhou, D.; Li, J.; Jin, Y.; Li, Q. Research on Magnetic Levitation Control Method under Elastic Track Conditions Based on Backstepping Method. Mathematics 2024, 12, 2134. https://doi.org/10.3390/math12132134
Zhu P, Zhang T, Zhou D, Li J, Jin Y, Li Q. Research on Magnetic Levitation Control Method under Elastic Track Conditions Based on Backstepping Method. Mathematics. 2024; 12(13):2134. https://doi.org/10.3390/math12132134
Chicago/Turabian StyleZhu, Pengxiang, Te Zhang, Danfeng Zhou, Jie Li, Yuxin Jin, and Qicai Li. 2024. "Research on Magnetic Levitation Control Method under Elastic Track Conditions Based on Backstepping Method" Mathematics 12, no. 13: 2134. https://doi.org/10.3390/math12132134
APA StyleZhu, P., Zhang, T., Zhou, D., Li, J., Jin, Y., & Li, Q. (2024). Research on Magnetic Levitation Control Method under Elastic Track Conditions Based on Backstepping Method. Mathematics, 12(13), 2134. https://doi.org/10.3390/math12132134






