Mathematical Model for Optimal Agri-Food Industry Residual Streams Flow Management: A Valorization Decision Support Tool
Abstract
:1. Introduction
2. Literature Review
3. Methodology
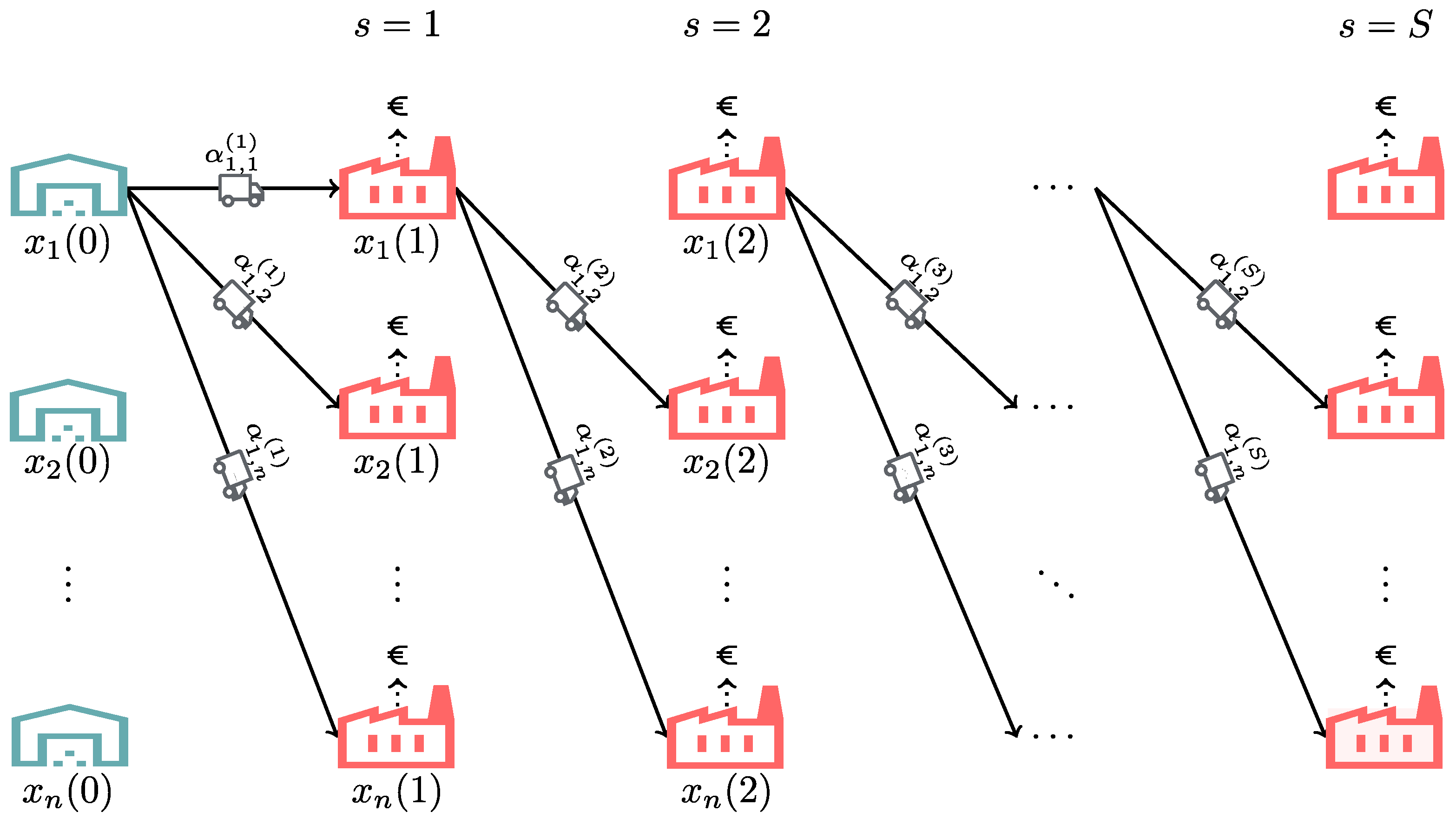
3.1. Model Description and Assumptions
- A residual stream from a given AFI (by-products) is reintroduced as raw material in a valorization route. There may be different routes available. Without loss of generality, we assume that each AFI generates only one by-product (if more than one by-product were generated, as many instances of the AFI as needed could be used).
- Available valorization routes for a given residual stream are made up of different steps. Each step corresponds to the set of BBIs that can use such a residual stream as raw material.
- The relations between the input and the outputs of a BBI are modeled as linear applications and therefore can be modeled by using a matrix. Mathematical models used for describing mass transformations in the bio-industries processes are out of the scope of this paper. However, since many of those transformations are usually modeled by using differential equations, it is not unusual to assume that some valorization processes conform to a linear transformation and therefore can be modeled by using a transformation matrix.
- BBIs use a residual stream as raw material to produce value-added products and can also generate a new residual stream. The relation between the residual stream at the input and at the output of a BBI and the relation between the residual stream at the input and the value-added products at the output of a BBI are modeled separately.
- The residual stream generated in one BBI must be sent to the next step of the valorization route.
- If a BBI does not produce a residual stream (e.g., landfills, incineration plants, waste water treatment plants, etc.) or the residual stream generated cannot be used as feedstock for another valorization process, then the valorization route ends.
- The residual stream might be modeled considering the by-products that it contains as well as considering its chemical composition.
- It is assumed that the composition of the residual stream does not change with transport or storage. This assumption may not be true in real conditions, but it could be easily overcome by including in the model a transformation matrix that represents those changes.
- A residual stream from a given BBI is never reintroduced in the same BBI.
- The profit obtained in a BBI at each step is the difference between the revenue from the sale of the value-added products obtained and the cost derived from the valorization of the residual stream used as feedstock in such step.
- The model supports the inclusion of economic, social, and environmental costs/benefits.
- BBIs are assumed to have enough capacity for processing all the residual streams that they receive.
3.2. Mathematical Formulation of the Optimization Problem
4. Results of a Case Study
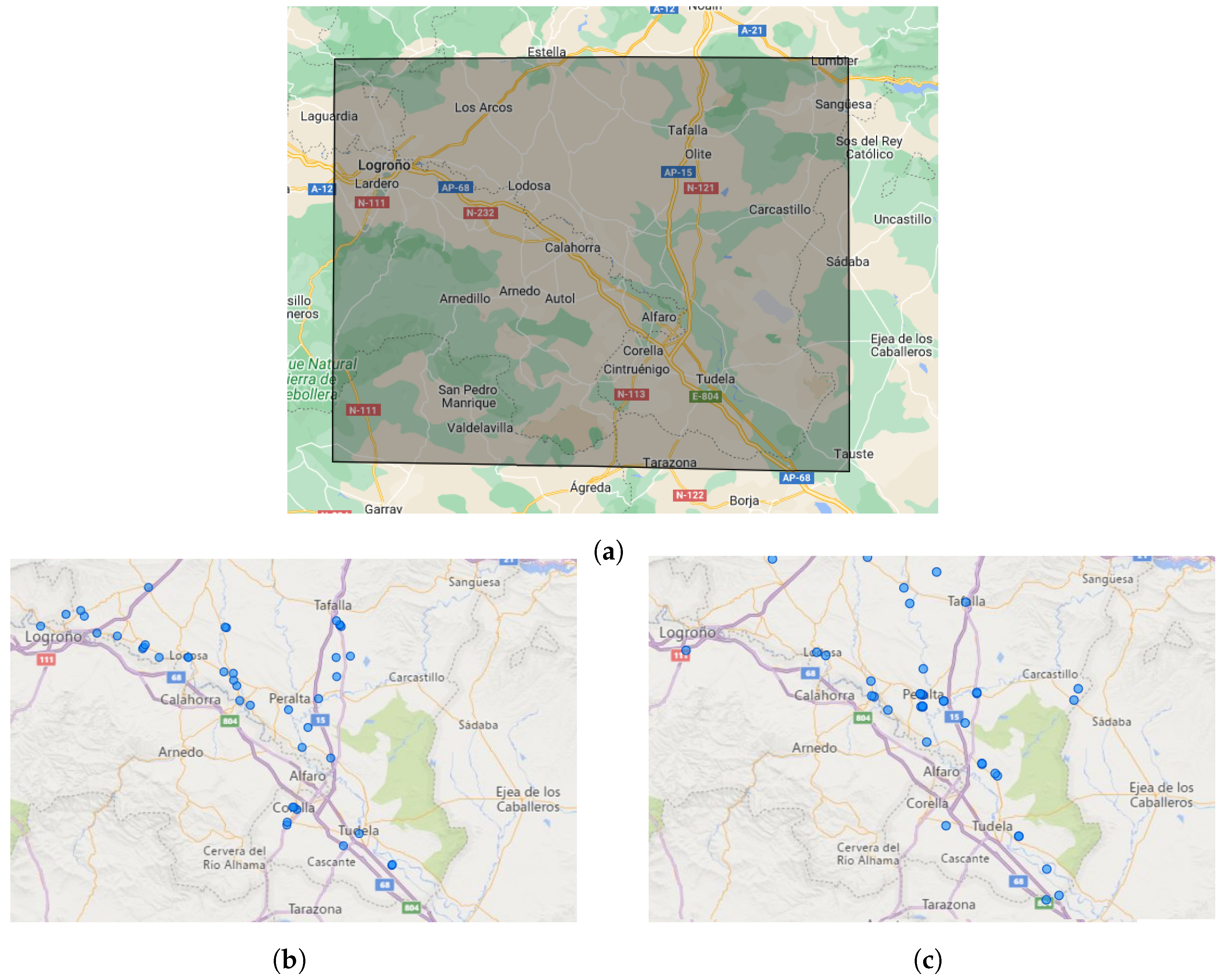
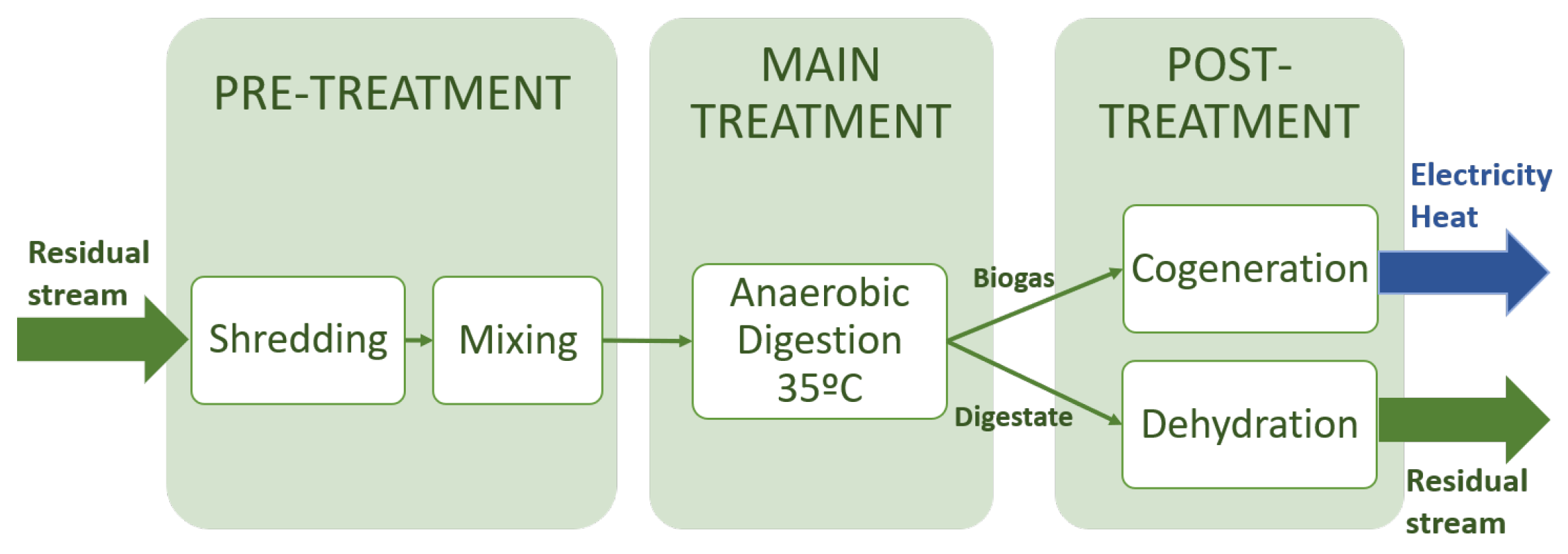
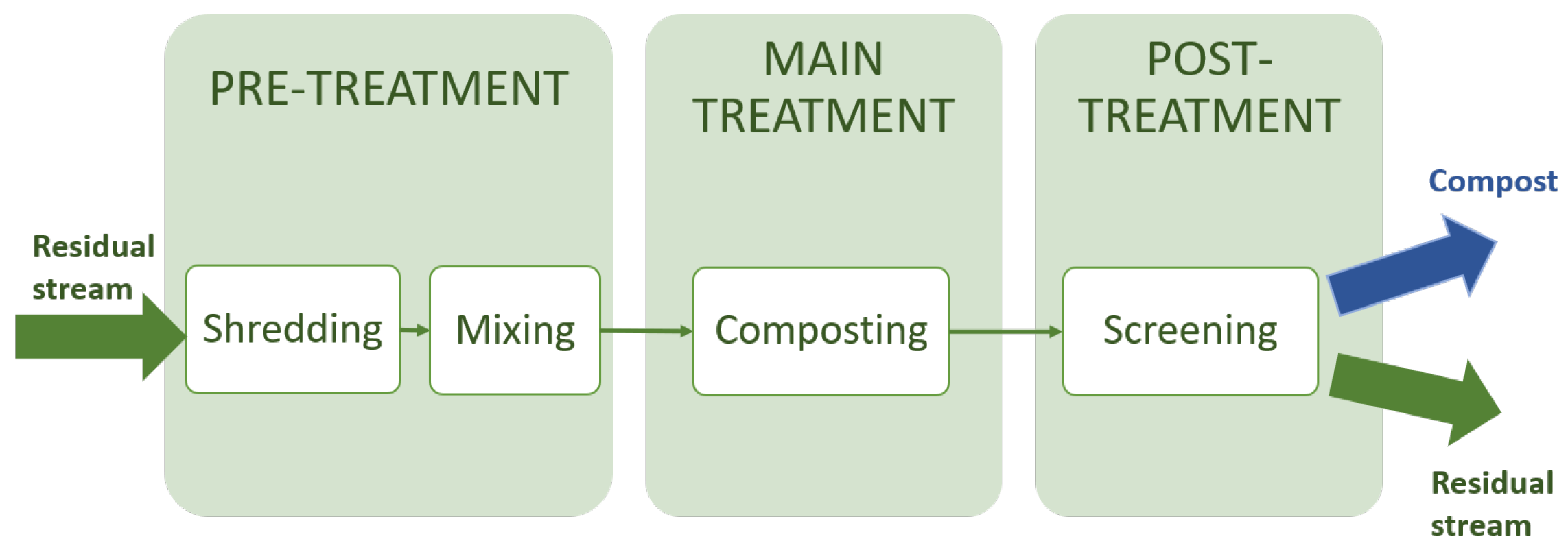
4.1. Case Study Description
4.2. Optimization Results and Sensitivity Analysis
5. Conclusions
- Given a valorization network of industries in a region, the model allows to improve the profits compared to those achieved through existing industry practices.
- Enables to test different scenarios to make informed decisions. For instance, it enables us to study the impact of variations in the selling prizes and/or the valorization costs (individually and simultaneously) in the profit and in the optimal residual stream distribution. This knowledge helps to recognize potential challenges or opportunities in advance.
- Helps to detect key factors that influence the optimal strategy and to identify optimal conditions for achieving the best strategy at a global level.
- Allows us to deal with the problem of establishing the number, size, and location of all the potential BBIs of a valorization network and to study different layouts of the network in order to determine the optimal one.
- Given a complex valorization network of industries, with many different multi-step valorization routes available, the model enables to avoid unprofitable valorization options.
- Helps to anticipate the impact of potential risks by simulating different scenarios. This will improve the resilience of the valorization network, leading to more strategic decision-making.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.; Zhang, H. Assessing Agri-Food Waste Valorization Challenges and Solutions Considering Smart Technologies: An Integrated Fermatean Fuzzy Multi-Criteria Decision-Making Approach. Sustainability 2024, 16, 6169. [Google Scholar] [CrossRef]
- Leder, N.; Kumar, M.; Rodrigues, V.S. Influential factors for value creation within the Circular Economy: Framework for Waste Valorisation. Resour. Conserv. Recycl. 2020, 158, 104804. [Google Scholar] [CrossRef]
- Berenguer, C.V.; Andrade, C.; Pereira, J.A.M.; Perestrelo, R.; Câmara, J.S. Current Challenges in the Sustainable Valorisation of Agri-Food Wastes: A Review. Processes 2023, 11, 20. [Google Scholar] [CrossRef]
- Girotto, F.; Alibardi, L.; Cossu, R. Food waste generation and industrial uses: A review. Waste Manag. 2015, 45, 32–41. [Google Scholar] [CrossRef]
- Malenica, D.; Kass, M.; Bhat, R. Sustainable Management and Valorization of Agri-Food Industrial Wastes and By-Products as Animal Feed: For Ruminants, Non-Ruminants and as Poultry Feed. Sustainability 2023, 15, 117. [Google Scholar] [CrossRef]
- Mirabella, N.; Castellani, V.; Sala, S. Current options for the valorization of food manufacturing waste: A review. J. Clean. Prod. 2014, 65, 28–41. [Google Scholar] [CrossRef]
- Stone, J.; Garcia-Garcia, G.; Rahimifard, S. Development of a pragmatic framework to help food and drink manufacturers select the most sustainable food waste valorisation strategy. J. Environ. Manag. 2019, 247, 425–438. [Google Scholar] [CrossRef]
- Lin, Z.; Ooi, J.K.; Woon, K.S. An integrated life cycle multi-objective optimization model for health-environment-economic nexus in food waste management sector. Sci. Total Environ. 2022, 816, 151541. [Google Scholar] [CrossRef]
- Maier, J.M.; Sowlati, T.; Salazar, J. Life cycle assessment of forest-based biomass for bioenergy: A case study in British Columbia, Canada. Resour. Conserv. Recycl. 2019, 146, 598–609. [Google Scholar] [CrossRef]
- Madoumier, M.; Azzaro-Pantel, C.; Tanguy, G.; Gésan-Guiziou, G. Modelling the properties of liquid foods for use of process flowsheeting simulators: Application to milk concentration. J. Food Eng. 2015, 164, 70–89. [Google Scholar] [CrossRef]
- Alexandropoulou, M.; Antonopoulou, G.; Lyberatos, G. A novel approach of modeling continuous dark hydrogen fermentation. Bioresour. Technol. 2018, 250, 784–792. [Google Scholar] [CrossRef] [PubMed]
- Montecchio, D.; Yuan, Y.; Malpei, F. Hydrogen production dynamic during cheese whey Dark Fermentation: New insights from modelization. Int. J. Hydrogen Energy 2018, 43, 17588–17601. [Google Scholar] [CrossRef]
- Van Ngo, A.; Nguyen, H.T.; Van Le, C.; Goel, R.; Terashima, M.; Yasui, H. A dynamic simulation of methane fermentation process receiving heterogeneous food wastes and modelling acidic failure. J. Mater. Cycles Waste Manag. 2016, 18, 239–247. [Google Scholar] [CrossRef]
- Xiong, Z.; Hussain, A.; Lee, J.; Lee, H.S. Food waste fermentation in a leach bed reactor: Reactor performance, and microbial ecology and dynamics. Bioresour. Technol. 2019, 274, 153–161. [Google Scholar] [CrossRef] [PubMed]
- Muhammad, A.; Younas, M.; Rezakazemi, M. Quasi-dynamic modeling of dispersion-free extraction of aroma compounds using hollow fiber membrane contactor. Chem. Eng. Res. Des. 2017, 127, 52–61. [Google Scholar] [CrossRef]
- Neviani, M.; Aliakbarian, B.; Perego, P.; Paladino, O. Extraction of polyphenols from olive pomace: Mathematical modeling and technological feasibility in a high temperature and high pressure stirred reactor. Chem. Eng. Res. Des. 2019, 141, 32–46. [Google Scholar] [CrossRef]
- Kalakul, S.; Malakul, P.; Siemanond, K.; Gani, R. Integration of life cycle assessment software with tools for economic and sustainability analyses and process simulation for sustainable process design. J. Clean. Prod. 2014, 71, 98–109. [Google Scholar] [CrossRef]
- Rathnayake, M.; Chaireongsirikul, T.; Svangariyaskul, A.; Lawtrakul, L.; Toochinda, P. Process simulation based life cycle assessment for bioethanol production from cassava, cane molasses, and rice straw. J. Clean. Prod. 2018, 190, 24–35. [Google Scholar] [CrossRef]
- Righi, S.; Baioli, F.; Dal Pozzo, A.; Tugnoli, A. Integrating Life Cycle Inventory and Process Design Techniques for the Early Estimate of Energy and Material Consumption Data. Energies 2018, 11, 970. [Google Scholar] [CrossRef]
- Cheng, L.; Anderson, C. Too conservative to hedge: How much does a corn ethanol facility lose? Int. J. Prod. Econ. 2017, 193, 654–662. [Google Scholar] [CrossRef]
- García-Velásquez, C.; Defryn, C.; van der Meer, Y. Life cycle optimization of the supply chain for biobased chemicals with local biomass resources. Sustain. Prod. Consum. 2023, 36, 540–551. [Google Scholar] [CrossRef]
- Wang, G. Multiobjective Sustainable Operation Dynamics and Optimization. IEEE Trans. Eng. Manag. 2021, 68, 1126–1138. [Google Scholar] [CrossRef]
- Cooney, R.; de Sousa, D.B.; Fernández-Ríos, A.; Mellett, S.; Rowan, N.; Morse, A.P.; Hayes, M.; Laso, J.; Regueiro, L.; Wan, A.H.; et al. A circular economy framework for seafood waste valorisation to meet challenges and opportunities for intensive production and sustainability. J. Clean. Prod. 2023, 392, 136283. [Google Scholar] [CrossRef]
- García-Velásquez, C.; Leduc, S.; van der Meer, Y. Design of biobased supply chains on a life cycle basis: A bi-objective optimization model and a case study of biobased polyethylene terephthalate (PET). Sustain. Prod. Consum. 2022, 30, 706–719. [Google Scholar] [CrossRef]
- Atashbar, N.Z.; Labadie, N.; Prins, C. Modeling and optimization of biomass supply chains: A review and a critical look. IFAC-PapersOnLine 2016, 49, 604–615. [Google Scholar] [CrossRef]
- Sun, O.; Fan, N. A Review on Optimization Methods for Biomass Supply Chain: Models and Algorithms, Sustainable Issues, and Challenges and Opportunities. Process Integr. Optim. Sustain. 2020, 4, 203–226. [Google Scholar] [CrossRef]
- Tapia, J.F.D.; Samsatli, S.; Doliente, S.S.; Martinez-Hernandez, E.; Ghani, W.A.B.W.A.K.; Lim, K.L.; Shafri, H.Z.M.; Shaharum, N.S.N.B. Design of biomass value chains that are synergistic with the food–energy–water nexus: Strategies and opportunities. Food Bioprod. Process. 2019, 116, 170–185. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, G.; Brown, R.C. Integrated supply chain design for commodity chemicals production via woody biomass fast pyrolysis and upgrading. Bioresour. Technol. 2014, 157, 28–36. [Google Scholar] [CrossRef]
- Lo, S.L.Y.; How, B.S.; Leong, W.D.; Teng, S.Y.; Rhamdhani, M.A.; Sunarso, J. Techno-economic analysis for biomass supply chain: A state-of-the-art review. Renew. Sustain. Energy Rev. 2021, 135, 110164. [Google Scholar] [CrossRef]
- Stellingwerf, H.M.; Guo, X.; Annevelink, E.; Behdani, B. Logistics and Supply Chain Modelling for the Biobased Economy: A Systematic Literature Review and Research Agenda. Front. Chem. Eng. 2022, 4, 778315. [Google Scholar] [CrossRef]
- Aboytes-Ojeda, M.; Castillo-Villar, K.K.; Eksioglu, S.D. Modeling and optimization of biomass quality variability for decision support systems in biomass supply chains. Ann. Oper. Res. 2022, 314, 319–346. [Google Scholar] [CrossRef]
- Galanopoulos, C.; Giuliano, A.; Barletta, D.; Zondervan, E. An integrated methodology for the economic and environmental assessment of a biorefinery supply chain. Chem. Eng. Res. Des. 2020, 160, 199–215. [Google Scholar] [CrossRef]
- Jayarathna, L.; Kent, G.; O’Hara, I.; Hobson, P. A Geographical Information System based framework to identify optimal location and size of biomass energy plants using single or multiple biomass types. Appl. Energy 2020, 275, 115398. [Google Scholar] [CrossRef]
- López-Díaz, D.C.; Lira-Barragán, L.F.; Rubio-Castro, E.; Ponce-Ortega, J.M.; El-Halwagi, M.M. Optimal location of biorefineries considering sustainable integration with the environment. Renew. Energy 2017, 100, 65–77. [Google Scholar] [CrossRef]
- Panteli, A.; Giarola, S.; Shah, N. Lignocellulosic supply chain MILP model: A Hungarian case study. Comput. Aided Chem. Eng. 2016, 38, 253–258. [Google Scholar] [CrossRef]
- Serrano-Hernandez, A.; Faulin, J. Locating a Biorefinery in Northern Spain: Decision Making and Economic Consequences. Socio-Econ. Plan. Sci. 2019, 66, 82–91. [Google Scholar] [CrossRef]
- Xie, Y.; Zhao, K.; Hemingway, S. Optimally Locating Biorefineries: A GIS-Based Mixed Integer Linear Programming Approach. In Proceedings of the 51st Annual Transportation Research Forum, 2010-03, Arlington, VA, USA, 11–13 March 2010; Number 1430-2016-118685. p. 15. [Google Scholar] [CrossRef]
- Barasoain-Echepare, Í. Mathematical Model for Optimal Agri-Food Industry Residual Streams Flow Management Dataset; Tecnun School of Engineering, University of Navarra: San Sebastián, Spain, 2024. [Google Scholar] [CrossRef]
- HeiGIT gGmbH. Openrouteservice. 2022. Available online: https://openrouteservice.org/ (accessed on 12 March 2024).
- Dahlquist, G.; Björck, Å. Numerical Methods; Courier Corporation: North Chelmsford, MA, USA, 2003. [Google Scholar]
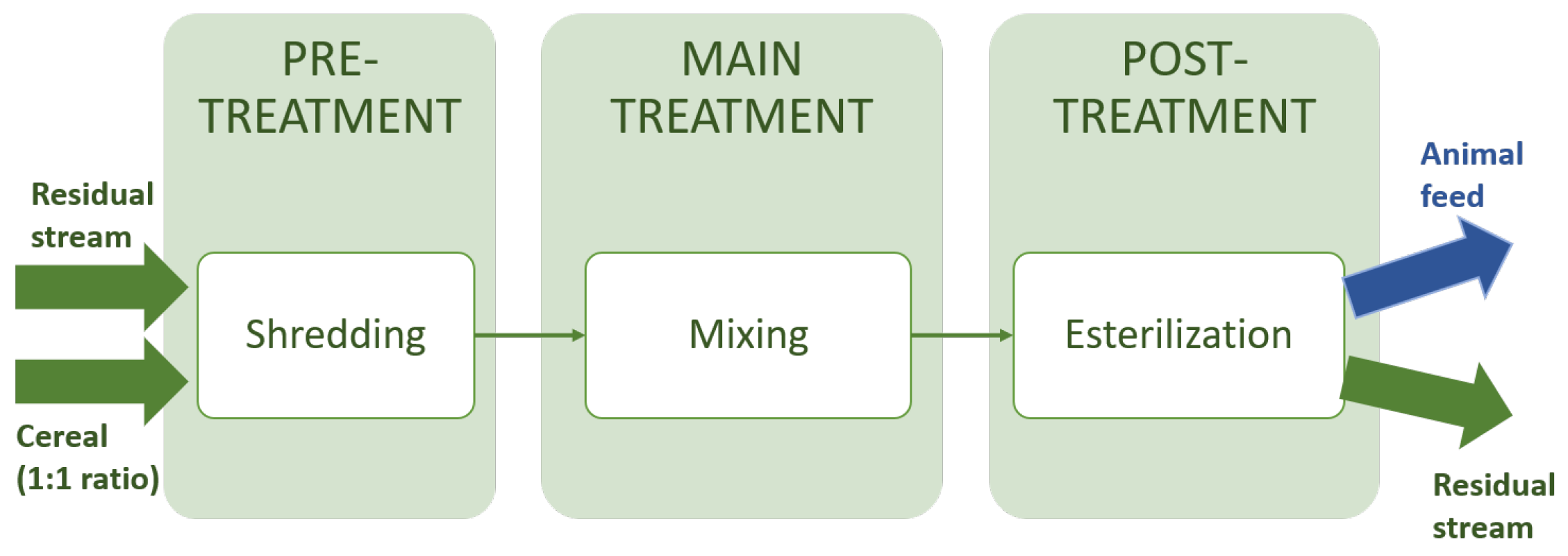

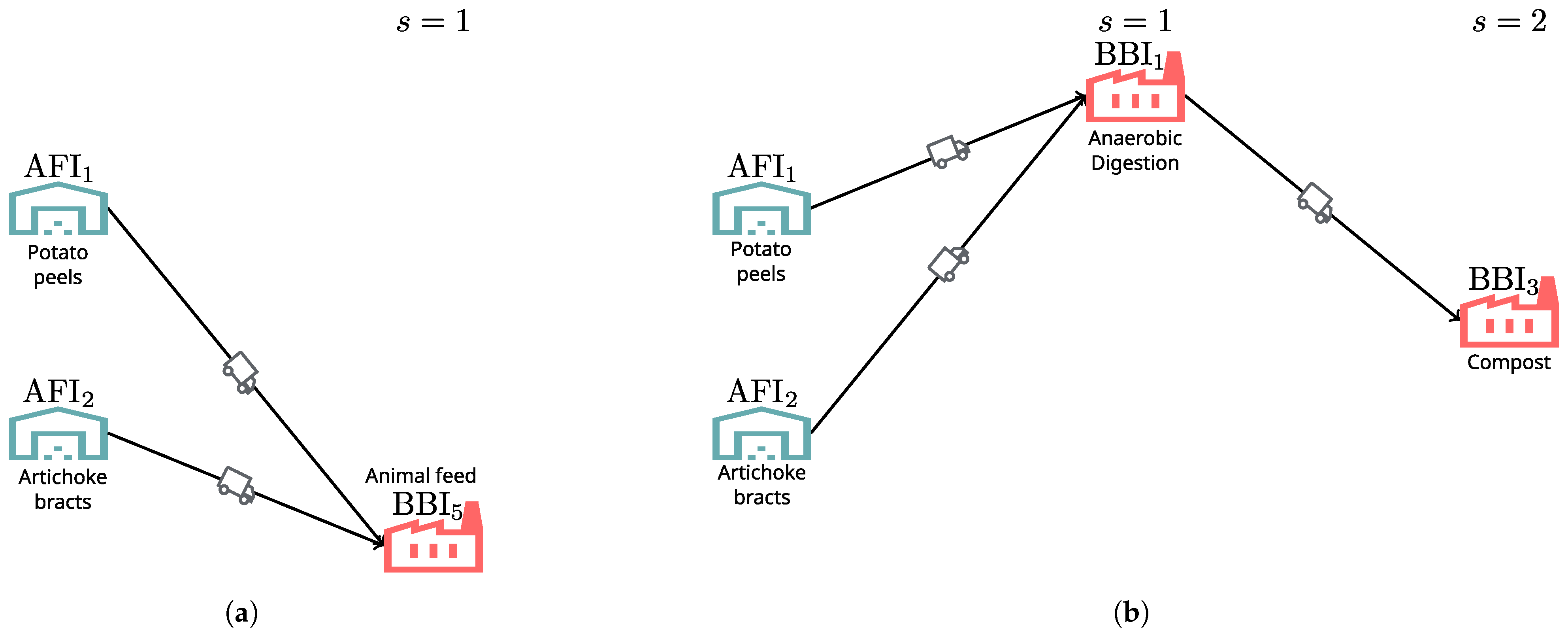
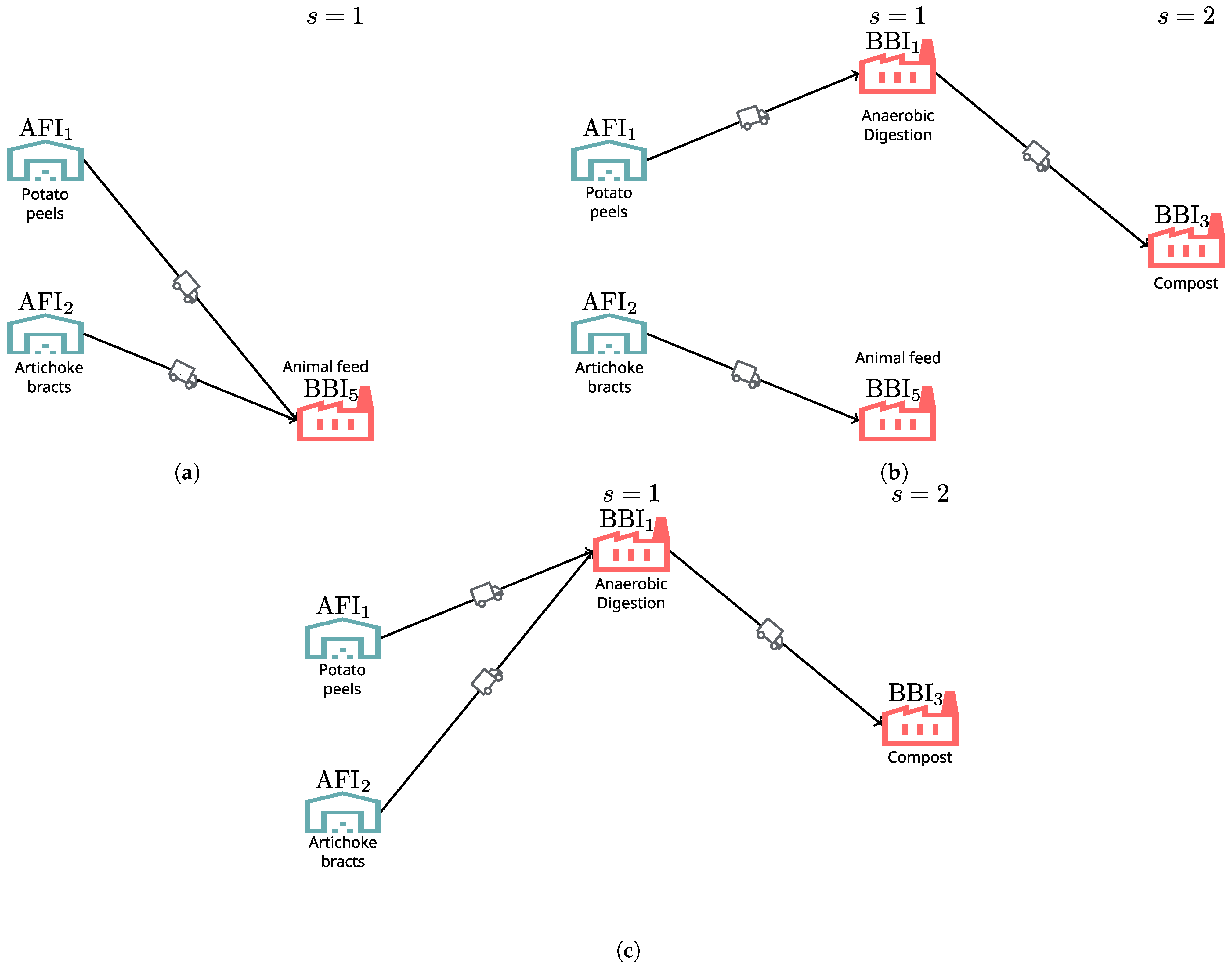
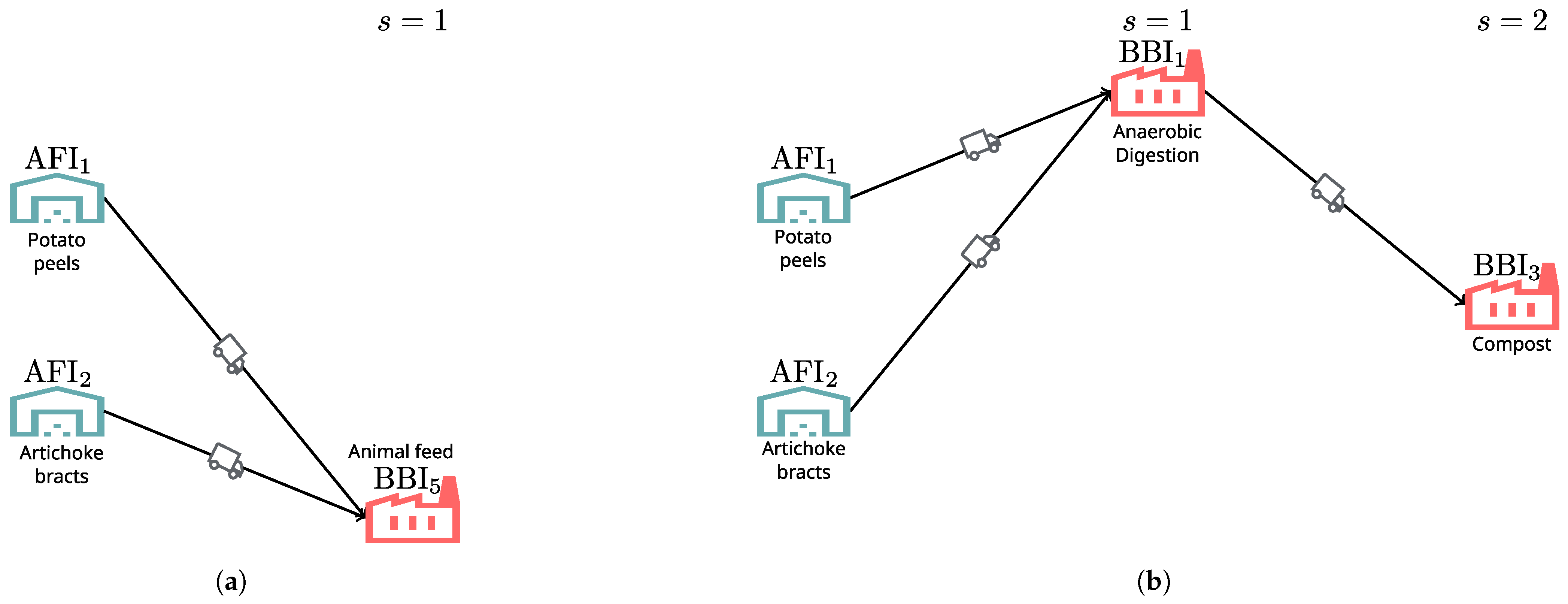
| Parameters | Description |
|---|---|
| Residual stream at the output of at step s | |
| Relation between the residual stream at the input and the output of | |
| Revenue from the sale of value-added products obtained at at step s | |
| Selling prices of the value-added products obtained at | |
| Relation between the residual stream at the input and the value-added products at the output of | |
| Cost derived from the valorization of the residual stream received at at step s | |
| Costs at derived from the valorization of the residual stream received from | |
| Profit obtained at at step s | |
| Profit obtained at at step s from the sale of value-added products obtained from the residual stream coming from | |
| Variables | Description |
| Proportion of residual stream received at from at step s |
| Parameters | Value | Unit | Notation | |
|---|---|---|---|---|
| Processing cost | BBI1 BBI2 | 9.3 | €/ton | |
| BBI3 BBI4 | 18.77 | €/ton | ||
| BBI5 | 436.51 | €/ton | ||
| Transport cost | 0.0468 | €/km ton | ||
| Selling price | biogas | 490 | €/ton | |
| compost | 34 | €/ton | ||
| animal feed | 316.83 | €/ton | ||
| 0 | 13.01 | 34.74 | 39.53 | 54.8 | 35.17 | 17.59 | |
| 0 | 16.88 | 50.92 | 41.89 | 31.37 | 16.57 | ||
| 0 | 34.61 | 38.75 | 55.93 | 38.91 | |||
| 0 | 50.62 | 78.45 | 60.1 | ||||
| 0 | 72.13 | 57.33 | |||||
| 0 | 18.41 | ||||||
| 0 |
| Value-Added Product | Selling Price | Profit | Optimal Strategy |
|---|---|---|---|
| biogas | ↑35% | ↑35% | Figure 8c |
| ↓35% | ↓35% | Figure 8c | |
| compost | ↑35% | ↑11.5% | Figure 8c |
| ↓35% | ↓11.5% | Figure 8c | |
| animal feed | ↑35% | ↑44.1% | Figure 8a |
| ↓35% | 0% | Figure 8c | |
| all | ↑35% | ↑48.6% | Figure 8b |
| ↓35% | ↓46.4% | Figure 8c |
| BBI | Processing Cost | Profit | Optimal Strategy |
|---|---|---|---|
| BBI1, BBI2 | ↑35% | ↓3.8% | Figure 9b |
| ↓35% | ↑3.8% | Figure 9b | |
| BBI3, BBI4 | ↑35% | ↓6.4% | Figure 9b |
| ↓35% | ↑6.4% | Figure 9b | |
| BBI5 | ↑35% | 0% | Figure 9b |
| ↓35% | ↑53.2% | Figure 9a | |
| all | ↑35% | ↓10.4% | Figure 9b |
| ↓35% | ↑10.4% | Figure 9b |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barasoain-Echepare, Í.; Zárraga-Rodríguez, M.; Podhorski, A.; Villar-Rosety, F.M.; Besga-Oyanarte, L.; Jaray-Valdehierro, S.; Fernández-Arévalo, T.; Sancho, L.; Ayesa, E.; Gutiérrez-Gutiérrez, J.; et al. Mathematical Model for Optimal Agri-Food Industry Residual Streams Flow Management: A Valorization Decision Support Tool. Mathematics 2024, 12, 2753. https://doi.org/10.3390/math12172753
Barasoain-Echepare Í, Zárraga-Rodríguez M, Podhorski A, Villar-Rosety FM, Besga-Oyanarte L, Jaray-Valdehierro S, Fernández-Arévalo T, Sancho L, Ayesa E, Gutiérrez-Gutiérrez J, et al. Mathematical Model for Optimal Agri-Food Industry Residual Streams Flow Management: A Valorization Decision Support Tool. Mathematics. 2024; 12(17):2753. https://doi.org/10.3390/math12172753
Chicago/Turabian StyleBarasoain-Echepare, Íñigo, Marta Zárraga-Rodríguez, Adam Podhorski, Fernando M. Villar-Rosety, Leire Besga-Oyanarte, Sofía Jaray-Valdehierro, Tamara Fernández-Arévalo, Luis Sancho, Eduardo Ayesa, Jesús Gutiérrez-Gutiérrez, and et al. 2024. "Mathematical Model for Optimal Agri-Food Industry Residual Streams Flow Management: A Valorization Decision Support Tool" Mathematics 12, no. 17: 2753. https://doi.org/10.3390/math12172753
APA StyleBarasoain-Echepare, Í., Zárraga-Rodríguez, M., Podhorski, A., Villar-Rosety, F. M., Besga-Oyanarte, L., Jaray-Valdehierro, S., Fernández-Arévalo, T., Sancho, L., Ayesa, E., Gutiérrez-Gutiérrez, J., & Insausti, X. (2024). Mathematical Model for Optimal Agri-Food Industry Residual Streams Flow Management: A Valorization Decision Support Tool. Mathematics, 12(17), 2753. https://doi.org/10.3390/math12172753









