Technological Innovation Investment Channels of Industry–University–Research Alliance Enterprises and Non-Alliance Enterprises Based on Evolutionary Game
Abstract
:1. Introduction
2. Model Construction
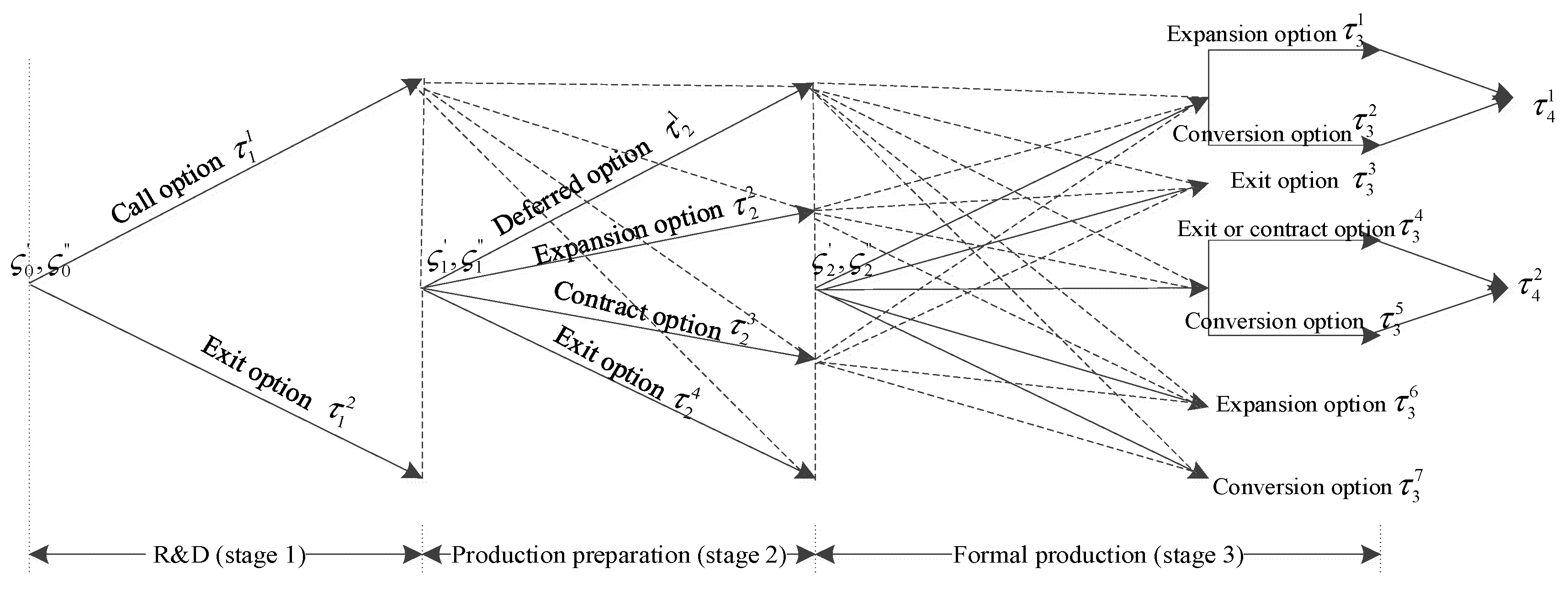
2.1. Technological Innovation Investment Channels and Different Managers’ Expectations
2.2. Model Hypothesis
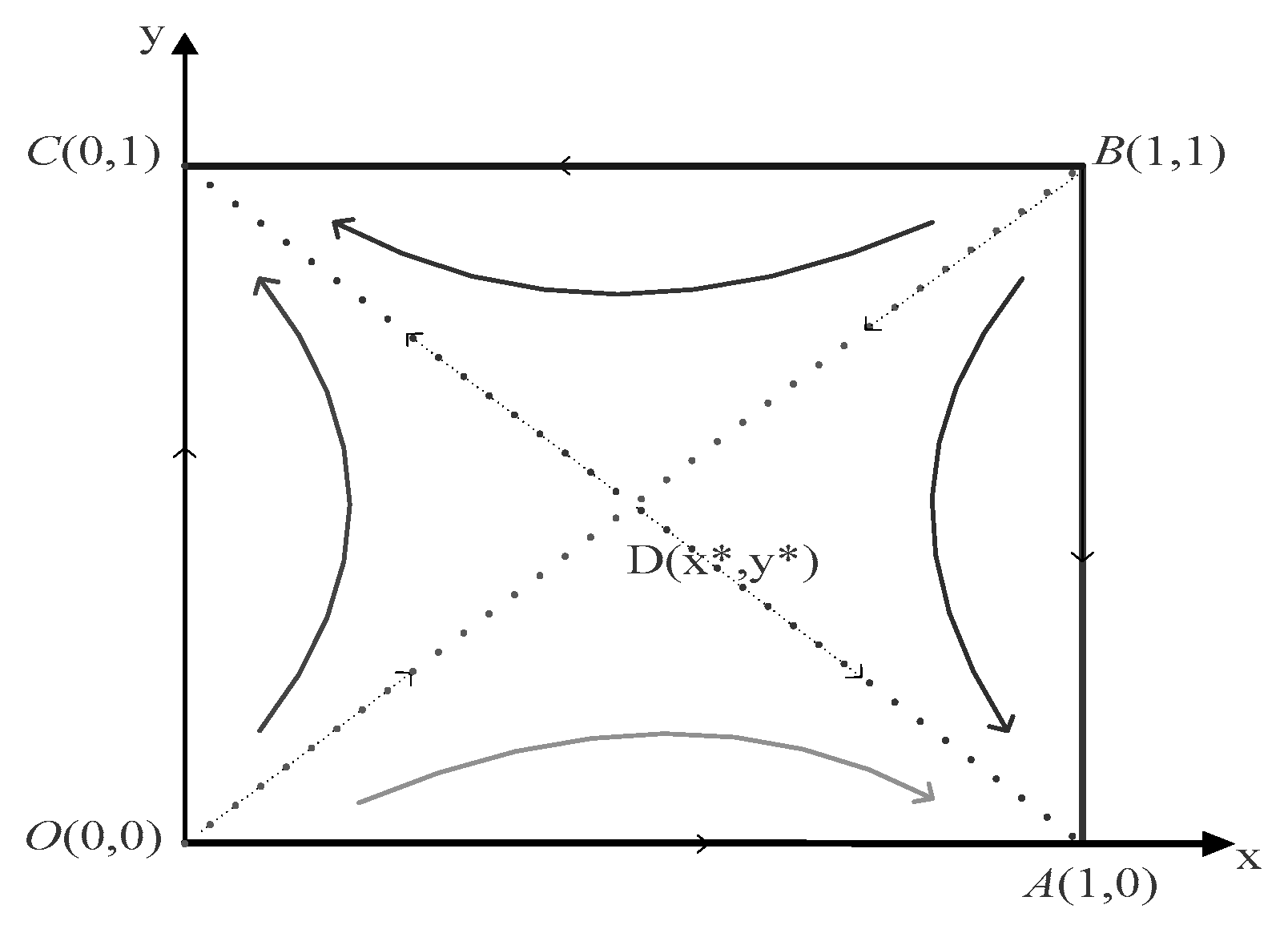
2.3. Equilibrium Analysis of Stable Strategies in Evolutionary Games
2.4. Sensitivity of Evolutionary Equilibrium of Game System to Main Parameters in Scenario 5
3. Analysis of Numerical Examples
3.1. Influence of the Number of Active Managers on the Evolution Results of the Game System
3.2. Influence of Group Capacity on the Evolution Result of Game System
3.3. Influence of the Difference in Expectation of Future Opportunity Value between the Two Types of Enterprise Managers on the Evolution Results of the Game System
3.4. Influence of the Difference of Technological Innovation Investment in R&D Stage on the Evolution Result of Game System
4. Conclusions and Management Suggestions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Rajenlall, S. Technological and non-technological innovation effects on firm performance. J. High Technol. Manag. Res. 2022, 33, 100–114. [Google Scholar] [CrossRef]
- Evan, M.F.; Stephanie, P.G.; Daniel, F.; Brittney, C.E.; Stephanie, M.M.; Cara, D. Promising technological innovations in cognitive training to treat eating-related behavior. Appetite 2018, 124, 68–77. [Google Scholar] [CrossRef]
- You, D.; Yang, X.H.; Desheng, D.; Chen, G.F. Option game with Poisson Jump Process in company radical technological innovation. Technol. Forecast. Soc. Change 2014, 81, 341–350. [Google Scholar] [CrossRef]
- Zheng, X.X.; Li, D.F. A new biform game-based investment incentive mechanism for eco-efficient innovation in supply chain. Int. J. Prod. Econ. 2023, 258, 125–136. [Google Scholar] [CrossRef]
- Li, M.Y.; Gao, X. Implementation of enterprises’ green technology innovation under market-based environmental regulation: An evolutionary game approach. J. Environ. Manag. 2022, 308, 245–260. [Google Scholar] [CrossRef]
- Wei, Y.G.; Zhu, R.Q.; Tan, L.Y. Emission trading scheme, technological innovation, and competitiveness: Evidence from China’s thermal power enterprises. J. Environ. Manag. 2022, 320, 314–356. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.F.; Yuan, C.H.; Zhang, S.M. Influences of university-industry alliance portfolio depth and breadth on growth of new technology-based firms: Evidence from China. Ind. Mark. Manag. 2022, 102, 190–204. [Google Scholar] [CrossRef]
- Kyungtaek, K.; Deokjoo, L.; Sungjoon, P. Evaluation of R&D investments in wind power in Korea using real option. Renew. Sustain. Energy Rev. 2014, 40, 335–347. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.Y.; Wu, C.Y. A real options framework for R&D planning in technology-based firms. J. Eng. Technol. Manag. 2015, 35, 93–114. [Google Scholar] [CrossRef]
- Roberto, D.H.; David, G.C.; Idalia, P.J. A real option-based model for the valuation of patent protected technological innovation projects. World Pat. Inf. 2018, 53, 24–38. [Google Scholar] [CrossRef]
- Jillian, A.; Joetta, F.; Charla, G.B.; Richard, C.W. The benefits of hiring a STEM CEO: Decision making under innovation and real options. Technol. Soc. 2022, 71, 102–114. [Google Scholar] [CrossRef]
- Cécile, A.; Jamal, A.; Selma, B.; Julien, P. Revisiting the consequences of loans secured by patents on technological firms’ intellectual property and innovation strategies. Res. Policy 2023, 52, 234–245. [Google Scholar] [CrossRef]
- Mircea, B.; Catalin, C.; Victor, V.; Corina, E.B. An Active Support Instrument for Innovation in Deep Uncertainty-The Strategic Management Ingredients in Robotics and Mechatronics. Procedia Comput. Sci. 2015, 65, 210–217. [Google Scholar] [CrossRef]
- Katja, L.; Arne, V. Business Model Gaming: A Game-Based Methodology for E-Mobility Business Model Innovation. Procedia CIRP 2017, 64, 115–120. [Google Scholar] [CrossRef]
- Chang, S.; Li, Y.; Gao, F. The impact of delaying an investment decision on R&D projects in real option game. Chaos Solitons Fractals 2016, 87, 182–189. [Google Scholar] [CrossRef]
- Lai, V.V.; Huong, T.L. Strategic growth option, uncertainty, and R&D investment. Int. Rev. Financ. Anal. 2017, 51, 16–24. [Google Scholar] [CrossRef]
- Gonzalo, M.B.; Constancio, Z.R.; José, M.; González, G. Impact of flexibility in public R&D funding: How real options could avoid the crowding-out effect. Renew. Sustain. Energy Rev. 2017, 76, 813–823. [Google Scholar] [CrossRef]
- Marta, B.; Giovanni, V. A fuzzy approach for R&D compound option valuation. Fuzzy Sets Syst. 2017, 310, 108–121. [Google Scholar] [CrossRef]
- Denis, B.; Edgard, G. Real options valuation of fusion energy R&D programme. Energy Policy 2011, 39, 116–130. [Google Scholar] [CrossRef]
- Alessandri, T.M.; Pattit, J.M. Drivers of R&D investment: The interaction of behavioral theory and managerial incentives. J. Bus. Res. 2014, 67, 151–158. [Google Scholar] [CrossRef]
- Martzoukos, S.H.; Zacharias, E. Real option games with R&D and learning spillovers. Int. J. Oi Manag. Soience 2013, 4, 236–249. [Google Scholar] [CrossRef]
- Bensoussan, A.; Diltz, D.J.; Hoe, S.R. Real options games in complete and incomplete markets with several decision makers. Soc. Ind. Appl. Math. 2010, 1, 666–728. [Google Scholar] [CrossRef]
- Anamika, D.; Anil, K.G.; Gurdeep, S. Innovation, investment and enterprise: Climate resilient entrepreneurial pathways for overcoming poverty. Agric. Syst. 2019, 172, 83–90. [Google Scholar] [CrossRef]
- Lin, B.Q.; Zhu, J.P. Determinants of renewable energy technological innovation in China under CO2 emissions constraint. J. Environ. Manag. 2019, 247, 662–671. [Google Scholar] [CrossRef] [PubMed]
- Lin, B.Q.; Luan, R.R. Do government subsidies promote efficiency in technological innovation of China’s photovoltaic enterprises? J. Clean. Prod. 2020, 254, 120–134. [Google Scholar] [CrossRef]
- Anis, O.; Tarek, B.H. Foreign investment and air pollution: Do good governance and technological innovation matter? Environ. Res. 2020, 185, 109–120. [Google Scholar] [CrossRef]
- Jiang, X.H.; Wang, L.F.; Cao, B.; Fan, X.Y. Benefit distribution and stability analysis of enterprises’ technological innovation cooperation alliance. Comput. Ind. Eng. 2021, 161, 234–246. [Google Scholar] [CrossRef]
- Ma, H.D.; Li, L.X. Could environmental regulation promote the technological innovation of China’s emerging marine enterprises? Based on the moderating effect of government grants. Environ. Res. 2021, 202, 1230–1241. [Google Scholar] [CrossRef]
- Pan, J.D.; Lin, G.B.; Xiao, W. The heterogeneity of innovation, government R&D support and enterprise innovation performance. Res. Int. Bus. Financ. 2022, 62, 101–113. [Google Scholar] [CrossRef]
- Liu, H.; Fan, L.B.; Shao, Z.X. Threshold effects of energy consumption, technological innovation, and supply chain management on enterprise performance in China′s manufacturing industry. J. Environ. Manag. 2021, 300, 1560–1573. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.Y.; Wang, C.X. Improving interaction mechanism of carbon reduction technology innovation between supply chain enterprises and government by means of differential game. J. Clean. Prod. 2021, 296, 134–146. [Google Scholar] [CrossRef]
- Chi, M.L.; Yue, K.K. Patent-investment games under asymmetric information. Eur. J. Oper. Res. 2012, 223, 441–451. [Google Scholar] [CrossRef]
- Azzurra, M.; Serena, R.; Giovanna, L.N.; Paolo, R. A real options game of alliance timing decisions in biopharmaceutical research and development. Eur. J. Oper. Res. 2017, 261, 1189–1202. [Google Scholar] [CrossRef]
- Wang, C.F.; Sun, J.C. Monetary Policy, Credit Constraints on Enterprises and Corporate R&D Investment Decision. Manag. Rev. 2017, 29, 17–27. Available online: https://journal05.magtech.org.cn/jweb_glpl/EN/Y2017/V29/I11/17 (accessed on 12 February 2019).
- Xu, Q.; Belmonte, A.; de Forest, R.; Liu, C.; Tan, Z. Strong solutions and instability for the fitness gradient system in evolutionary games between two populations. J. Differ. Equ. 2017, 262, 4021–4051. [Google Scholar] [CrossRef]
- Zhao, Z.W.; Lu, C.X. A Multi-stage Compound Real Option Model for Valvetion of Venture Capital Project. J. Syst. Manag. 2011, 20, 104–108. Available online: https://kns.cnki.net/kcms2/article/abstract?v=tc18asgQl7Qf5FQzOUivqkn4fcW-5bgoHSlnFp0uo6cwIIh3HUi4iqkc7cAINp2Fadhhkj99AOl8nc2NZVjI9ciH7Hv0w3Z3GJki-s3YFVL3XkrbcgH7VccWghyFTkt-&uniplatform=NZKPT&language=CHS (accessed on 23 March 2020).
- Rolando, P.; Fernando, O.; Francisco, G. Real option valuation of power transmission investments by stochastic simulation. Energy Econ. 2015, 47, 215–226. [Google Scholar] [CrossRef]
| Investment of Non-Alliance Enterprises | ||
|---|---|---|
| First Channel () | Second Channel () | |
| First channel () | ( ) | ( ) |
| Second channel () | (, ) | ( ) |
| Equilibrium Point | Determinant and Trace |
|---|---|
| (0,0) | |
| (1,0) | |
| (0,1) | |
| (1,1) | |
| () | |
| Equilibrium Point | Scenario 1: | Scenario 2: | Scenario 3: | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Stability | Stability | Stability | |||||||
| (0,0) | + | + | Unstable | − | Uncertainty | Unstable | + | + | Unstable |
| (1,0) | − | Uncertainty | Unstable | − | Uncertainty | Unstable | − | Uncertainty | Unstable |
| (0,1) | + | − | ESS | + | − | ESS | − | Uncertainty | Unstable |
| (1,1) | − | Uncertainty | Unstable | + | + | Unstable | + | − | ESS |
| () | Non- existence | Non- existence | Non- existence | Non- existence | Non- existence | Non- existence | Non- existence | Non- existence | Non- existence |
| Equilibrium Point | Scenario 4: | Scenario 5: | ||||
|---|---|---|---|---|---|---|
| Stability | Stability | |||||
| (0,0) | − | Uncertainty | Unstable | + | + | Unstable |
| (1,0) | + | + | Unstable | + | − | ESS |
| (0,1) | + | − | ESS | + | − | ESS |
| (1,1) | − | Uncertainty | Unstable | + | + | Unstable |
| () | Non-existence | Non-existence | Non-existence | − | Uncertainty | Saddle point |
| Scenarios | Evolutionarily Stable Strategy | ||||
|---|---|---|---|---|---|
| 1 | − | + | + | + | (Second channel input, first channel input) |
| 2 | − | − | − | + | (Second channel input, first channel input) |
| 3 | + | + | + | + | (First channel input, first channel input) |
| 4 | − | − | + | + | (Second channel input, first channel input) |
| 5 | − | + | − | + | (First channel input, second channel input) |
| (Second channel input, first channel input) |
| Alliance Enterprises (Probability of Choosing the First Channel) | Non-Alliance Enterprises (Probability of Choosing the First Channel) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | k = 30 | k = 40 | k = 50 | k = 60 | k = 70 | Time | k = 60 | k = 70 | k = 80 | k = 90 | k = 100 |
| 5 | 0.06 | 0.53 | 0.47 | 0.48 | 0.52 | 1 | 0.81 | 0.88 | 0.53 | 0.52 | 0.51 |
| 10 | 0.00 | 0.58 | 0.11 | 0.41 | 0.54 | 2 | 1.00 | 0.97 | 0.75 | 0.71 | 0.70 |
| 15 | 0.00 | 0.08 | 0.03 | 0.22 | 0.55 | 3 | 1.00 | 0.99 | 0.90 | 0.88 | 0.85 |
| 20 | 0.00 | 0.00 | 0.00 | 0.10 | 0.46 | 4 | 1.00 | 1.00 | 0.96 | 0.95 | 0.92 |
| 25 | 0.00 | 0.00 | 0.00 | 0.08 | 0.17 | 5 | 1.00 | 1.00 | 1.00 | 0.99 | 0.97 |
| 30 | 0.00 | 0.00 | 0.00 | 0.03 | 0.12 | 6 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 |
| 35 | 0.00 | 0.00 | 0.00 | 0.02 | 0.07 | 7 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 40 | 0.00 | 0.00 | 0.00 | 0.01 | 0.03 | 8 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 45 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 9 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 10 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Alliance Enterprises (Probability of Choosing the First Channel) | Non-Alliance Enterprises (Probability of Choosing the First Channel) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | K = 60 | K = 70 | K = 80 | K = 90 | K = 100 | Time | K = 60 | K = 70 | K = 80 | K = 90 | K = 100 |
| 5 | 0.35 | 0.49 | 0.06 | 0.26 | 0.56 | 1 | 0.68 | 0.65 | 0.56 | 0.54 | 0.52 |
| 10 | 0.16 | 0.00 | 0.00 | 0.07 | 0.62 | 2 | 1.00 | 0.98 | 0.79 | 0.68 | 0.63 |
| 15 | 0.09 | 0.00 | 0.00 | 0.00 | 0.58 | 3 | 1.00 | 1.00 | 0.92 | 0.86 | 0.80 |
| 20 | 0.04 | 0.00 | 0.00 | 0.00 | 0.41 | 4 | 1.00 | 1.00 | 0.99 | 0.94 | 0.87 |
| 25 | 0.01 | 0.00 | 0.00 | 0.00 | 0.14 | 5 | 1.00 | 1.00 | 1.00 | 0.99 | 0.97 |
| 30 | 0.00 | 0.00 | 0.00 | 0.00 | 0.10 | 6 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 35 | 0.00 | 0.00 | 0.00 | 0.00 | 0.06 | 7 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 40 | 0.00 | 0.00 | 0.00 | 0.00 | 0.03 | 8 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 45 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 9 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 10 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Alliance Enterprises (Probability of Choosing the First Channel) | Non-Alliance Enterprises (Probability of Choosing the First Channel) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | = 2 | = 3 | = 4 | = 5 | = 6 | Time | = 2 | = 3 | = 4 | = 5 | = 6 |
| 2 | 0.44 | 0.47 | 0.56 | 0.52 | 0.58 | 1 | 0.51 | 0.54 | 0.61 | 0.63 | 0.65 |
| 3 | 0.17 | 0.41 | 0.58 | 0.47 | 0.05 | 2 | 0.52 | 0.62 | 0.65 | 0.93 | 1.00 |
| 4 | 0.06 | 0.35 | 0.51 | 0.08 | 0.00 | 3 | 0.61 | 0.83 | 1.00 | 1.00 | 1.00 |
| 5 | 0.02 | 0.18 | 0.42 | 0.04 | 0.00 | 4 | 0.86 | 0.94 | 0.97 | 1.00 | 1.00 |
| 6 | 0.00 | 0.13 | 0.22 | 0.00 | 0.00 | 5 | 0.90 | 0.97 | 1.00 | 1.00 | 1.00 |
| 7 | 0.00 | 0.10 | 0.18 | 0.00 | 0.00 | 6 | 0.92 | 1.00 | 1.00 | 1.00 | 1.00 |
| 8 | 0.00 | 0.08 | 0.08 | 0.00 | 0.00 | 7 | 0.96 | 1.00 | 1.00 | 1.00 | 1.00 |
| 9 | 0.00 | 0.06 | 0.06 | 0.00 | 0.00 | 8 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 |
| 10 | 0.00 | 0.03 | 0.04 | 0.00 | 0.00 | 9 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 11 | 0.00 | 0.02 | 0.03 | 0.00 | 0.00 | 10 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Alliance Enterprises (Probability of Choosing the First Channel) | Non-Alliance Enterprises (Probability of Choosing the First Channel) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | = 2 | = 3 | = 4 | = 5 | = 6 | Time | = −2 | = −3 | = −4 | = −5 | = −6 |
| 2 | 0.52 | 0.48 | 0.46 | 0.44 | 0.41 | 1 | 0.55 | 0.55 | 0.55 | 0.55 | 0.55 |
| 3 | 0.51 | 0.42 | 0.07 | 0.03 | 0.00 | 2 | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 |
| 4 | 0.48 | 0.31 | 0.03 | 0.00 | 0.00 | 3 | 0.61 | 0.61 | 0.61 | 0.61 | 0.61 |
| 5 | 0.42 | 0.20 | 0.01 | 0.00 | 0.00 | 4 | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 |
| 6 | 0.28 | 0.17 | 0.00 | 0.00 | 0.00 | 5 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 7 | 0.20 | 0.14 | 0.00 | 0.00 | 0.00 | 6 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 8 | 0.14 | 0.10 | 0.00 | 0.00 | 0.00 | 7 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 9 | 0.10 | 0.06 | 0.00 | 0.00 | 0.00 | 8 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 10 | 0.07 | 0.04 | 0.00 | 0.00 | 0.00 | 9 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 11 | 0.05 | 0.03 | 0.00 | 0.00 | 0.00 | 10 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Q.; Wang, C.; Feng, T. Technological Innovation Investment Channels of Industry–University–Research Alliance Enterprises and Non-Alliance Enterprises Based on Evolutionary Game. Mathematics 2024, 12, 289. https://doi.org/10.3390/math12020289
Tang Q, Wang C, Feng T. Technological Innovation Investment Channels of Industry–University–Research Alliance Enterprises and Non-Alliance Enterprises Based on Evolutionary Game. Mathematics. 2024; 12(2):289. https://doi.org/10.3390/math12020289
Chicago/Turabian StyleTang, Qixuan, Chengjun Wang, and Tao Feng. 2024. "Technological Innovation Investment Channels of Industry–University–Research Alliance Enterprises and Non-Alliance Enterprises Based on Evolutionary Game" Mathematics 12, no. 2: 289. https://doi.org/10.3390/math12020289
APA StyleTang, Q., Wang, C., & Feng, T. (2024). Technological Innovation Investment Channels of Industry–University–Research Alliance Enterprises and Non-Alliance Enterprises Based on Evolutionary Game. Mathematics, 12(2), 289. https://doi.org/10.3390/math12020289





