Observer-Based Adaptive Fuzzy Quantized Control for Fractional-Order Nonlinear Time-Delay Systems with Unknown Control Gains

Abstract

This paper investigates the observer-based adaptive fuzzy quantized control problem for a class of fractional-order nonlinear time-delay systems with unknown control gains based on a modified fractional-order dynamic surface control (FODSC) technique and an indirect Lyapunov method. First, a fractional-order, high-gain state observer is constructed to estimate unavailable state information. Furthermore, the Nussbaum gain technique and a fractional-order filter are adopted to cope with the problem of unknown control gains and to reduce the computational complexity of the conventional recursive procedure, respectively. Moreover, through integration with the compensation mechanism and estimation model, the adaptive fuzzy quantized controllers and adaptive laws are designed to ensure that all the signals of the closed-loop system are bounded. In the end, the proposed controller is applied to a numerical example and a single-machine-infinite bus (SMIB) power system; the simulation results show the validity, superiority, and application potential of the developed control strategy.

1. Introduction

Recently, fractional-order nonlinear systems (FONSs), as the extension of integer-order nonlinear systems, have received considerable attention due to the attractive properties of fractional calculus in modeling and characterizing accurate dynamical properties of natural phenomena. To achieve the predefined control goals, numerous control methods have been presented to design controllers for FONSs, such as robust control [1,2], adaptive control [3,4], sliding mode control (SMC) [5,6], etc. In particular, the adaptive intelligent backstepping control technique has been widely used to handle the control problem of fractional-order nonlinear systems through integration with recursive control and an intelligent approximator [7,8,9]. Furthermore, motivated by the integer-order results [10,11,12,13,14,15], the modified fractional-order dynamic surface control technique was introduced to overcome the problem of computational complexity encountered in the traditional recursive procedure [16,17,18]. In [16], an auxiliary function was adopted to compensate for unknown disturbances and approximation errors. In [17], an online composite adaptive learning control method was proposed to relax the limitation generated by PE conditions. Moreover, the command-filtered backstepping control technique was extended to FONSs, which ensured that the filter error caused by the introduction of the filter could be effectively eliminated. However, the assumption that information about control gains is available prior is strictly required in the abovementioned scenario, which may result in limitations for practical applications to some extent.

The Nussbaum gain technique (originally proposed in [19]) has been widely used to address the adaptive control problem for nonlinear systems with unknown control gains, and many remarkable results have been obtained [20,21,22,23]. In [21], a composite adaptive neural control approach was developed to guarantee the convergence of the tracking error to an arbitrarily small neighborhood, even if the sign of the control gain was unavailable. In [22], an adaptive neural control algorithm the can be easily implemented in practical systems was developed for nonstrict-feedback nonlinear systems with unknown control directions and input dead zones. In contrast, only a few results have been reported for the adaptive control of FONSs without knowledge of control gains. Although the adaptive control problem for FONSs subject to unknown control gains was first investigated in [24], the observer-based adaptive control issue for fractional-order nonlinear time-delay systems (FONTDSs) with unknown control gains has not been fully investigated, which remains challenging.

Another point regarding the control of nonlinear systems is that the data to be transmitted are usually quantized in real communication systems under the influence of bandwidth limitations. Therefore, quantized control has become a very significant research topic [25,26,27,28,29]. In [27], a state-observer-based adaptive quantized control problem was studied, where a high-gain fuzzy state observer was constructed to estimate unmeasurable system states. In [28], an adaptive neural output feedback quantized control problem for FONTDSs was discussed. On the other hand, time delays usually appear in most real applications, often degrading the system’s performance and even leading to system instability. As a result, many attempts have been made to handle the adaptive control problem for nonlinear systems with time delays. In [30,31], the influence of time-varying state delays was eliminated by establishing a Lyapunov–Krasovskii functional. In [32,33], an auxiliary system was used to overcome the influence of input delays. The adaptive control issues of FONTDSs were also discussed in [34,35]. However, it is worth noting that adaptive quantized control for FONSs with time-varying delays remains an open problem.

Inspired by the observations reported above, an observer-based adaptive fuzzy quantized tracking control problem for FONTDSs with unknown control gains is investigated in this paper. The main contributions in comparison to the existing results are summarized as follows.

(1)

In most of previously reported results with respect to adaptive control for FONSs [8,9,16,17,18], the system states must be available a priori, which may not be easily satisfied in practice. In contrast to the aforementioned results, only the system output—rather than all state information—is required for the controller designed in this work by constructing a high-gain fuzzy state observer. Time-varying delays and input quantization are simultaneously considered in the investigated system. Therefore, the system model considered in this paper is more general than previous proposals.

(2)

In [8,9,16,17,18], prior knowledge of control gains of the investigated systems was assumed, which also implies that previously proposed methods in [8,9,16,17,18] may be not valid when exact information about control gains is not accessible in advance. In contrast to the methods proposed in [8,9,16,17,18], in our work, the dependence of controller design and stability analysis on control gains were fully removed by incorporating an indirect Lyapunov method and Nussbaum gain technique, making the obtained results more relaxed in comparison to the abovementioned results.

2. Preliminaries and System Description

2.1. Fractional Calculus

Definition 1

([36]). The fractional integral of order α for a function ($p\left(t\right)$) is expressed as:

$${}_{t_0}{D}_t^{-\alpha }p\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_{t_0}^t\frac{p\left(\tau \right)}{{(t-\tau )}^{1-\alpha }}d\tau$$

(1)

where $p\left(t\right)$ is an arbitrary integrable function, ${}_{t_0}{D}_t^{-\alpha }$ denotes the fractional integral of order α on $[t_0,t]$, and $\mathrm{\Gamma }(·)$ is a well-known Gamma function satisfying $\mathrm{\Gamma }\left(z\right)={\int }_0^{\infty }{e}^{-t}{t}^{z-1}dt$.

Definition 2

([36]). The Mittag–Leffler function with two parameters is expressed as follows:

$$E_{q_1,q_2}\left(z\right)=\underset{k=0}{\sum ^{\infty }}\frac{z^k}{\mathrm{\Gamma }(k{q}_1+q_2)},$$

(2)

where $q_1>0$, $q_2>0$, and z is a complex number. Using the Laplace transform for the above equation, one can obtain $\mathcal{L}\left\{t^{q_2-1}{E}_{q_1,q_2}(-\beta t^{q_1})\right\}=\frac{s^{q_1-q_2}}{s^{q_1}+\beta }$.

Definition 3

([36]). Let $p\left(t\right)$ be a real continuously differentiable function. Its Caputo fractional derivative of a function with order α is defined as:

$${}_{t_0}{D}_t^{\alpha }p\left(t\right)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}{\int }_{t_0}^t{(t-\tau )}^{n-\alpha -1}{p}^{\left(n\right)}\left(\tau \right)d\tau ,$$

(3)

where $n-1\le \alpha <n$, and $p^{\left(n\right)}$ denotes the n-th derivative.

For simplicity, we denote ${}_{t_0}{D}_t^{\alpha }$ as $D^{\alpha }$ when $t_0=0$ in the subsequent parts of this work.

Lemma 1

([37]). A FONS ($D^{\alpha }x\left(t\right)=p\left(x\left(t\right)\right)$) with order $\alpha \in (0,1)$ and pseudo-state $x\left(t\right)\in R^n$ is essentially a continuous-frequency distributed model expressed by

$$\left\{\begin{array}{cc}\hfill \frac{\partial 𝒵(\varpi ,t)}{\partial t}=& -\varpi 𝒵(\varpi ,t)+p\left(x\right(t\left)\right)\hfill \\ \hfill x\left(t\right)=& {\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right)𝒵(\varpi ,t)d\varpi \hfill \end{array}\right.$$

(4)

where ${\mu }_{\alpha }\left(\varpi \right)=\frac{sin\left(\alpha \pi \right)}{{\varpi }^{\alpha }\pi }$ denotes the weighting function of the state variable ($𝒵(\varpi ,t)$) with fractional order α, and ϖ denotes the elementary frequency.

2.2. Nussbaum-Type Function

For any continuous function ($N\left(\xi \right)$), if the properties

$$\left\{\begin{array}{c}\underset{l\to \infty }{lim}sup\frac{1}{l}{\int }_0^{l}N\left(\xi \right)d\xi =+\infty ,\hfill \\ \underset{l\to \infty }{lim}inf\frac{1}{l}{\int }_0^{l}N\left(\xi \right)d\xi =-\infty \hfill \end{array}\right.$$

(5)

hold, then $N\left(\xi \right)$ is called a Nussbaum-type function. In fact, many continuous functions can be chosen as Nussnbaum-type functions, i.e., ${\xi }^{2}sin\left(\xi \right),{\xi }^{2}cos\left(\xi \right)$ and $e^{{\xi }^2}cos(\frac{\pi }{2\xi })$. In this paper, we choose $N\left(\xi \right)={\xi }^{2}cos\left(\xi \right)$.

Lemma 2

([38]). We define two smooth functions as $\xi (·)$ on $[0,t_s)$ and $V\left(t\right)\ge 0,\forall t\in [0,t_s)$. If $N\left(\xi \right)$ is an even, smooth Nussbaum-type function satisfying

$$\begin{array}{c}\hfill V\left(t\right)\le m_1+e^{-m_2\varsigma }{\int }_0^t\phi N\left(\xi \right)\dot{\xi }{e}^{m_2\varsigma }d\varsigma +e^{-m_2\varsigma }{\int }_0^t\dot{\xi }{e}^{m_2\varsigma }d\varsigma \end{array}$$

(6)

then, $V\left(t\right),\xi \left(t\right)$ and ${\int }_0^{t}N\left(\xi \right)\dot{\xi }d\varsigma$ are bounded on $[0,t_s)$, where $m_1>0$ and $m_2>0$ are constants.

2.3. Fuzzy Logic Systems

To better achieve the abovementioned control goal, fuzzy logic systems (FLSs) are adopted in this article to handle unknown nonlinearities. We consider k fuzzy IF–THEN rules with the following form [39,40]:

${\mathbb{R}}^s$: IF $x_1$ is $F_1^s$ and … and $x_n$ is $F_n^s$

  THEN, y is $G^s,s=1,\dots ,k$

• where ${\mathbb{R}}^s$ represents the sth rule, $1\le s\le k,x_i(i=1,\dots ,n)$, and $y\in \mathbb{R}$ denotes the linguistic variables associated with the inputs and outputs of the FLSs. $F_i^s$ and $G^s$ are the fuzzy set. Then, the FLSs are described as

  $$y\left(x\right)=\frac{{\sum }_{s=1}^k{w}_s\left({\prod }_{i=1}^n{\mu }_{F_i^s}\left(x_i\right)\right)}{{\sum }_{s=1}^k\left({\prod }_{i=1}^n{\mu }_{F_i^s}\left(x_i\right)\right)}.$$

  (7)

We define the weight vector and fuzzy basis function vector as $W={[W_1,\dots ,W_k]}^T$ and $\varphi \left(x\right)={\left[{\varphi }_1,\dots ,{\varphi }_k\right]}^T$, respectively, in which ${\varphi }_s=\left[\left({\prod }_{i=1}^n{\mu }_{F_i^s}\left(x_i\right)\right)/{\sum }_{s=1}^k\left({\prod }_{i=1}^n{\mu }_{F_i^s}\left(x_i\right)\right)\right]$; then, the above expression can be represented as $y\left(x\right)=W^T\varphi \left(x\right).$

Lemma 3

([39,40]). For any continuous function ($F\left(x\right)$) defined over a compact set (Θ) and a desired level of accuracy ($o>0$), there exist an FLS such that

$$\begin{array}{c}\hfill \underset{x\in \Theta }{sup}|F\left(x\right)-W^T\varphi \left(x\right)|\le o.\end{array}$$

(8)

2.4. Nonlinear System Model

We consider FONTDSs with unknown control gains and quantized input as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill D^{\alpha }{\zeta }_i& ={\phi }_i{\zeta }_{i+1}+f_i\left({\overline{\zeta }}_i\right)+g_i\left({\overline{\zeta }}_i(t-{\tau }_i\left(t\right))\right)+d_i(\zeta ,t),i=1,\dots ,n-1\hfill \\ \hfill D^{\alpha }{\zeta }_n& ={\phi }_{n}q\left(u\right)+f_n\left({\overline{\zeta }}_n\right)+g_n\left({\overline{\zeta }}_n(t-{\tau }_n\left(t\right))\right)+d_n(\zeta ,t)\hfill \\ \hfill y& ={\zeta }_1\hfill \end{array}\right.\end{array}$$

(9)

where $\alpha$ denotes the fractional order satisfying $0<\alpha <1$; ${\overline{\zeta }}_i={\left[{\zeta }_1,\dots ,{\zeta }_i\right]}^T\in {\mathbb{R}}^i,i=1,\dots ,n$, $y\in \mathbb{R}$, and $u\in \mathbb{R}$ are the state vector, the system output, and the control input, respectively; $f_i\left({\overline{\zeta }}_i\right)$ stands for an unknown but smooth nonlinear function; ${\tau }_i\left(t\right)$ is an unknown bounded time delay satisfying specific constraints $|{\tau }_i\left(t\right)|\le \overline{\tau }$ and ${\dot{\tau }}_i\left(t\right)\le {\tau }^{\ast }\le 1$, where $\overline{\tau }$ and ${\tau }^{\ast }$ are known constants; ${\phi }_i$ is an unknown constant; $d_i(\zeta ,t)$ represents the unknown but bounded disturbance term; and $q\left(u\right)$ represents the quantized input. According to [27], the following hysteresis quantizer is considered to reduce chattering phenomena while obtaining the quantized control signal:

$$\begin{array}{c}\hfill q\left(u\right)=\left\{\begin{array}{c}{u}_i\mathrm{sgn}\left(u\right),\frac{u_i}{1+\delta }<\left|u\right|\le u_i,\dot{u}<0,\mathrm{or}\hfill \\ u_i<\left|u\right|\le \frac{u_i}{1-\delta },\dot{u}>0\hfill \\ u_i(1+\delta )\mathrm{sgn}\left(u\right),u_i<\left|u\right|\le \frac{u_i}{1-\delta },\dot{u}<0,\mathrm{or}\hfill \\ \frac{u_i}{1-\delta }<\left|u\right|\le \frac{u_i(1+\delta )}{1-\delta },\dot{u}>0\hfill \\ 0,0\le \left|u\right|<\frac{u_{min}}{1+\delta },\dot{u}<0,\mathrm{or}\hfill \\ \frac{u_{min}}{1+\delta }\le \left|u\right|\le u_{min},\dot{u}>0\hfill \\ q\left(u\left(t^{-}\right)\right),\mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

(10)

where $u_i={\varrho }^{1-i}{u}_m(i=1,2,\dots )$ with $0<\varrho <1$ and $\delta =\frac{1-\varrho }{1+\varrho }$, and $u_m$ is the range of the dead zone for a quantized input ($q\left(u\right)$) taking a value from the set $U=(0,\pm u_i,\pm u_i(1+\varrho ))$.

Remark 1.

For system (9) without time-delay terms, some adaptive control methods were presented in [8,9,16,17,18]. However, ${\phi }_i=1(i=1,\dots ,n)$ is assumed, and information about control gains was assumed to be available in advance in the aforementioned studies. Motivated by the results reported in [27,41], an adaptive fuzzy quantized control scheme is established for FONTDSs with unknown control gains by integrating an indirect Lyapunov method and Nussbaum gain technique, which can ensure that the relaxed results in comparison to those reported in [8,9,16,17,18] can be obtained.

To facilitate the stability analysis and controller design, some necessary assumptions are provided as follows.

Assumption 1

([30]). For nonlinear function $G_i(·)(i=1,2,\dots ,n)$, there exist known functions (${\chi }_i\left(z_1(t-{\tau }_i\left(t\right))\right)$), bounded functions (${\tilde{\chi }}_i\left(y_d(t-{\tau }_i\left(t\right))\right)$), and positive scalars ($m_i$) such that the following inequality holds:

$$\begin{array}{cc}\hfill |G_i\left({\overline{\zeta }}_i(t-{\tau }_i\left(t\right))\right){|}^2\le & z_1(t-{\tau }_i\left(t\right)){\chi }_i\left(z_1(t-{\tau }_i\left(t\right))\right)+{\tilde{\chi }}_i\left(y_d(t-{\tau }_i\left(t\right))\right)+m_i\hfill \end{array}$$

where $z_1=y-y_d$ and $y_d$ denote the tracking error and reference signal, respectively.

Assumption 2

([41]). The unknown control gain (${\varphi }_i$) is a non-zero and bounded constant, and there exists a positive scalar (${\overline{\varphi }}_i$) such that $|{\varphi }_i|\le {\overline{\varphi }}_i$.

Assumption 3

([42]). The reference signal ($y_d$) is a known smooth, bounded signal. Its fractional derivative ($D^{\alpha }{y}_d$) is also bounded.

2.5. Model Transformation

To overcome the negative influence caused by unknown control gains in the system (5), the transformation is expressed as

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill x_1& ={\zeta }_1\hfill \\ \hfill x_i& =\frac{{\zeta }_i}{{\phi }_{i\sim n}}\hfill \end{array}\right.\end{array}$$

(11)

where $i=2,\dots ,n,{\phi }_{i\sim n}=b_i\cdots b_n$.

Using (11), system (9) can be rewritten as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill D^{\alpha }{x}_1& =\phi x_2+F_1\left(x_1\right)+G_1\left({\overline{x}}_{1,{\tau }_1\left(t\right)}\right)+{\psi }_1\hfill \\ \hfill D^{\alpha }{x}_i& =x_{i+1}+F_i\left({\overline{x}}_i\right)+G_i\left({\overline{x}}_{i,{\tau }_i\left(t\right)}\right)+{\psi }_i,2\le i\le n-1\hfill \\ \hfill D^{\alpha }{x}_n& =q\left(u\right)+F_n\left({\overline{x}}_n\right)+G_n\left({\overline{x}}_{n,{\tau }_n\left(t\right)}\right)+{\psi }_n\hfill \\ \hfill y& =x_1\hfill \end{array}\right.\end{array}$$

(12)

where $\phi ={\prod }_{j=1}^n{\phi }_j,{\overline{x}}_n={[x_1,\dots ,x_n]}^T\in {\mathbb{R}}^n,\zeta =\overline{B}\overline{x},\overline{B}=\mathrm{diag}\left\{1,{\prod }_{j=2}^n{\phi }_j,\dots ,{\phi }_n\right\},F_i\left(x\right)=f_i\left(\zeta \right)/{\phi }_{i\sim n},G_i\left({\overline{x}}_{i,{\tau }_i\left(t\right)}\right)=$ $g_i\left({\overline{\zeta }}_{i,{\tau }_i\left(t\right)}\right)/{\phi }_{i\sim n}$ with ${\overline{\zeta }}_{i,{\tau }_i\left(t\right)}={\overline{\zeta }}_i(t-{\tau }_i\left(t\right))$, and ${\psi }_i=d_i/{\phi }_{i\sim n}$.

Based on fuzzy approximation, system (12) can be rewritten as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill D^{\alpha }{x}_1& =x_2+{\widehat{F}}_1\left({\widehat{\underline{x}}}_2\right|{\widehat{\theta }}_1)+{\theta }_1^{\ast T}{\psi }_1\left({\overline{x}}_2\right)-{\widehat{\theta }}_1^T{\psi }_1\left({\widehat{\underline{x}}}_2\right)+G_1\left({\overline{x}}_{1,{\tau }_1\left(t\right)}\right)+{\overline{\psi }}_1\hfill \\ \hfill D^{\alpha }{x}_i& =x_{i+1}+{\widehat{F}}_i\left({\widehat{\underline{x}}}_i\right|{\widehat{\theta }}_i)+{\theta }_i^{\ast T}{\psi }_i\left({\overline{x}}_i\right)-{\widehat{\theta }}_i^T{\psi }_i\left({\widehat{\underline{x}}}_i\right)+G_i\left({\overline{x}}_{i,{\tau }_i\left(t\right)}\right)+{\overline{\psi }}_i\hfill \\ \hfill D^{\alpha }{x}_n& =q\left(u\right)+{\widehat{F}}_n\left({\widehat{\underline{x}}}_n\right|{\widehat{\theta }}_n)+{\theta }_n^{\ast T}{\psi }_n\left({\overline{x}}_n\right)-{\widehat{\theta }}_n^T{\psi }_n\left({\widehat{\underline{x}}}_n\right)+G_n\left({\overline{x}}_{n,{\tau }_n\left(t\right)}\right)+{\overline{\psi }}_n\hfill \\ \hfill y& =x_1\hfill \end{array}\right.\end{array}$$

(13)

where $2\le i\le n-1,{\widehat{\underline{x}}}_i={[{\widehat{x}}_1,\dots ,{\widehat{x}}_i]}^T\in {\mathbb{R}}^i$, ${\widehat{x}}_i$ is an estimation of $x_i$, which can be directly obtained by the state observer designed herein. ${\widehat{F}}_1\left({\widehat{\underline{x}}}_2\right|{\widehat{\theta }}_1)={\widehat{\theta }}_1^T{\psi }_1\left({\widehat{\underline{x}}}_2\right),{\widehat{F}}_j\left({\widehat{\underline{x}}}_j\right|{\widehat{\theta }}_j)={\widehat{\theta }}_j^T{\psi }_j\left({\widehat{\underline{x}}}_j\right),F_1\left(x_1\right)+(\phi -1)x_2=$ ${\theta }_1^{\ast T}{\psi }_1\left({\overline{x}}_2\right)+o_1\left({\overline{x}}_2\right),F_j\left(x_j\right)={\theta }_j^{\ast T}{\psi }_j\left({\overline{x}}_j\right)+o_j\left({\overline{x}}_j\right),{\overline{\psi }}_1={\psi }_1+o_1\left({\overline{x}}_2\right),{\overline{\psi }}_j={\psi }_j+o_j\left({\overline{x}}_j\right)$ with $j=2,\dots ,n$.

The control goal of this work is to propose an observer-based adaptive fuzzy quantized control scheme for system (9) via an indirect Lyapunov method and FODSC technique such that all the signals of the closed-loop system (CLS) are bounded and the system output can track the preassigned reference signal.

3. Main Results

In this section, we propose an observer-based adaptive fuzzy quantized control scheme for FONTDS (9). First, a fractional-order, high-gain fuzzy state observer is constructed to estimate unavailable state information. Subsequently, the controller design and stability results are obtained by means of the FODSC technique, an indirect Lyapunov method, and a Lyapunov–Krasovskii functional.

3.1. High-Gain Fuzzy State Observer Design

Considering that the system states may not be not available, an FO fuzzy high-gain observer is first designed to estimate the immeasurable system states. According to system (9), the high-gain observer is constructed as:

$$\left\{\begin{array}{cc}\hfill D^{\alpha }{\widehat{x}}_1& ={\widehat{x}}_2+{\widehat{F}}_1\left({\widehat{\underline{x}}}_2\right|{\widehat{\theta }}_1)+{\mu }_1{L}_1(y-{\widehat{x}}_1)\hfill \\ \hfill D^{\alpha }{\widehat{x}}_i& ={\widehat{x}}_{i+1}+{\widehat{F}}_i\left({\widehat{\underline{x}}}_i\right|{\widehat{\theta }}_i)+{\mu }^i{L}_i(y-{\widehat{x}}_1),2\le i\le n-1\hfill \\ \hfill D^{\alpha }{\widehat{x}}_n& =q\left(u\right)+{\widehat{F}}_n\left({\widehat{\underline{x}}}_n\right|{\widehat{\theta }}_n)+{\mu }^n{L}_n(y-{\widehat{x}}_1)\hfill \end{array}\right.$$

(14)

By defining the observation error as $e=x-\widehat{x}={[e_1,\dots ,e_n]}^T$ and invoking (13) and (14), the observation error dynamics are

$$\left\{\begin{array}{cc}\hfill D^{\alpha }{e}_1& =e_2+{\theta }_1^{\ast T}{\psi }_1\left({\overline{x}}_2\right)-{\widehat{\theta }}_1^T{\psi }_1\left({\widehat{\underline{x}}}_2\right)+G_1\left({\overline{x}}_{1,{\tau }_1\left(t\right)}\right)+{\overline{\psi }}_1-{\mu }_1{L}_1(y-{\widehat{x}}_1)\hfill \\ \hfill D^{\alpha }{e}_i& =e_{i+1}+{\theta }_i^{\ast T}{\psi }_i\left({\overline{x}}_i\right)-{\widehat{\theta }}_i^T{\psi }_i\left({\widehat{\underline{x}}}_i\right)+G_i\left({\overline{x}}_{i,{\tau }_i\left(t\right)}\right)+{\overline{\psi }}_i-{\mu }^i{L}_i(y-{\widehat{x}}_1)\hfill \\ \hfill D^{\alpha }{e}_n& ={\theta }_n^{\ast T}{\psi }_n\left({\overline{x}}_n\right)-{\widehat{\theta }}_n^T{\psi }_n\left({\widehat{\underline{x}}}_n\right)+G_n\left({\overline{x}}_{n,{\tau }_n\left(t\right)}\right)+{\overline{\psi }}_n-{\mu }^n{L}_n(y-{\widehat{x}}_1)\hfill \end{array}\right.$$

(15)

where $i=2,\dots ,n-1$.

To facilitate further analysis, system (15) is rewritten as:

$$\begin{array}{cc}\hfill D^{\alpha }e=& A_{\mu L}e+\sum _{i=1}^n\left[B_i{\theta }_i^{\ast T}{\psi }_i({\overline{x}}_i,{\widehat{\underline{x}}}_i)+B_i{\tilde{\theta }}_i^T{\psi }_i\left({\widehat{\underline{x}}}_i\right)+B_i{G}_i\left({\overline{x}}_{i,{\tau }_i\left(t\right)}\right)\right]+\mathsf{\Psi }\hfill \end{array}$$

(16)

where ${\psi }_i({\overline{x}}_i,{\widehat{\underline{x}}}_i)={\psi }_i\left({\overline{x}}_i\right)-{\psi }_i\left({\widehat{\underline{x}}}_i\right),A_{\mu L}=A-LE,L={[\mu L_1,\dots ,{\mu }^n{L}_n]}^T$, $\mu >1$ is a constant, $\mathrm{\Psi }={[{\overline{\psi }}_1,\dots ,{\overline{\psi }}_n]}^T$, and $B_i={[\underset{i}{\underbrace{0,\dots ,0,1}},0\dots ,0]}^T$ with

$$\begin{array}{cc}\hfill A& =\left[\begin{array}{cccc}0& 1& & \\ 0& & \ddots & \\ ⋮& & & 1\\ 0& 0& \cdots & 0\end{array}\right],E={\left[\begin{array}{c}1\\ 0\\ ⋮\\ 0\end{array}\right]}^T.\hfill \end{array}$$

Then, through coordinate transformation of $\mathcal{E}=\chi e$ with $\chi =\mathrm{diag}\left\{1,{\mu }^{-1},\dots ,{\mu }^{1-n}\right\}$, one can obtain

$$\begin{array}{cc}\hfill D^{\alpha }\mathcal{E}=& \mu A_L\mathcal{E}+\chi \sum _{i=1}^n\left[B_i{\theta }_i^{\ast T}{\psi }_i({\overline{x}}_i,{\widehat{\underline{x}}}_i)+B_i{\tilde{\theta }}_i^T{\psi }_i\left({\widehat{\underline{x}}}_i\right)+B_i{G}_i\left({\overline{x}}_{i,{\tau }_i\left(t\right)}\right)\right]+\chi \mathrm{\Psi }\hfill \end{array}$$

(17)

where

$$\begin{array}{c}\hfill A_L=\left[\begin{array}{cccc}-L_1& 1& & \\ -L_2& & \ddots & \\ ⋮& & & 1\\ -L_n& 0& \cdots & 0\end{array}\right].\end{array}$$

It can be easily observed that $A_L$ is a strict Hurwitz matrix. Therefore, for a given matrix ($\mathcal{Q}>0$), there exists a matrix $\mathcal{P}>0$ such that the following equation holds:

$$A_L^T\mathcal{P}+\mathcal{P}{A}_L=-\mathcal{Q}.$$

(18)

To analyze the performance of the error dynamic (17), a frequency-distributed model is adopted to rewrite the system (17). According to Lemma 1, one has

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \frac{\partial {𝒵}_{\mathcal{E}}(\varpi ,t)}{\partial t}=& -\varpi {𝒵}_{\mathcal{E}}(\varpi ,t)+\mu A_L\mathcal{E}+\chi \sum _{i=1}^n\left[B_i{\theta }_i^{\ast T}{\psi }_i({\overline{x}}_i,{\widehat{\underline{x}}}_i)\right.\hfill \\ \hfill & \left.+B_i{\tilde{\theta }}_i^T{\psi }_i\left({\widehat{\underline{x}}}_i\right)+B_i{G}_i\left({\overline{x}}_{i,{\tau }_i\left(t\right)}\right)\right]+\chi \mathrm{\Psi }\hfill \\ \hfill \mathcal{E}=& {\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{\mathcal{E}}(\varpi ,t)d\varpi \hfill \end{array}\right.\end{array}$$

(19)

where ${\mu }_{\alpha }\left(\varpi \right)=sin\left(\alpha \pi \right)/\pi {\varpi }^{\alpha }$.

Then, the following Lyapunov function is selected:

$$V_0=V_{0,0}+V_{0,1}$$

(20)

where

$$\begin{array}{cc}\hfill V_{0,0}=& \frac{1}{2}{\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{\mathcal{E}}^T(\varpi ,t)\mathcal{P}{𝒵}_{\mathcal{E}}(\varpi ,t)d\varpi ,\hfill \\ \hfill V_{0,1}=& \frac{{\left|\right|\mathcal{P}\left|\right|}^2{e}^{-\sigma t}}{a(1-\overline{\tau })}\sum _{i=1}^n{\int }_{t-{\tau }_i\left(t\right)}^t{e}^{\sigma \varsigma }{z}_1\left(\varsigma \right){\chi }_i\left(z_1\left(\varsigma \right)\right)d\varsigma .\hfill \end{array}$$

The derivative of $V_0$ is calculated as:

$$\begin{array}{cc}\hfill {\dot{V}}_0=& -{\int }_0^{\infty }\varpi {\mu }_{\alpha }\left(\varpi \right){𝒵}_{\mathcal{E}}^T(\varpi ,t)\mathcal{P}{𝒵}_{\mathcal{E}}(\varpi ,t)d\varpi -\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{a}\sum _{i=1}^n{e}^{-\sigma {\tau }_i\left(t\right)}{z}_{1,{\tau }_i\left(t\right)}{\chi }_i\left(z_{1,{\tau }_i\left(t\right)}\right)\hfill \\ \hfill & -\mu {\mathcal{E}}^T\overline{\mathcal{Q}}\mathcal{E}-\sigma V_{0,1}+{\mathcal{E}}^T\mathcal{P}\chi \left[\sum _{i=1}^n{B}_i{\theta }_i^{\ast T}{\psi }_i({\overline{x}}_i,{\widehat{\underline{x}}}_i)+\sum _{i=1}^n{B}_i{\tilde{\theta }}_i^T{\psi }_i\left({\widehat{\underline{x}}}_i\right)\right.\hfill \\ \hfill & \left.+\sum _{i=1}^n{B}_i{G}_i\left({\overline{x}}_{i,{\tau }_i\left(t\right)}\right)+\mathrm{\Psi }\right]+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{a(1-\overline{\tau })}\sum _{i=1}^n{z}_1\left(t\right){\chi }_i\left(z_1\left(t\right)\right)\hfill \end{array}$$

(21)

where $z_{1,{\tau }_i\left(t\right)}=z_1(t-{\tau }_i\left(t\right)),\overline{\mathcal{Q}}=\frac{1}{2}\mathcal{Q}$.

According to Assumption 2.1 and Young’s inequality, one has

$$\left\{\begin{array}{c}{\mathcal{E}}^T\mathcal{P}\chi \sum _{i=1}^n{B}_i{\theta }_i^{\ast T}{\psi }_i({\overline{x}}_i,{\widehat{\underline{x}}}_i)\le {\mathcal{E}}^T\mathcal{E}+{\left|\right|\mathcal{P}\left|\right|}^2\sum _{i=1}^n{\theta }_i^{\ast T}{\theta }_i^{\ast }\hfill \\ {\mathcal{E}}^T\mathcal{P}\chi \sum _{i=1}^n{B}_i{\tilde{\theta }}_i^T{\psi }_i\left({\widehat{\underline{x}}}_i\right)\le {\mathcal{E}}^T\mathcal{E}+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2}\sum _{i=1}^n{\tilde{\theta }}_i^T{\tilde{\theta }}_i\hfill \\ {\mathcal{E}}^T\mathcal{P}\chi \sum _{i=1}^n{B}_i{G}_i\left({\overline{x}}_{i,{\tau }_i\left(t\right)}\right)\le \frac{b}{2}{\mathcal{E}}^T\mathcal{E}+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2b}\sum _{i=1}^n{z}_{1,{\tau }_i\left(t\right)}{\chi }_i\left(z_{1,{\tau }_i\left(t\right)}\right)+\sum _{i=1}^n{\mathit{ħ}}_i\hfill \\ {\mathcal{E}}^T\mathcal{P}\chi \mathsf{\Psi }\le \frac{1}{2}{\mathcal{E}}^T\mathcal{E}+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2}\overline{\mathrm{\Psi }}\hfill \end{array}\right.$$

(22)

where ${\mathit{ħ}}_i=\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{\varrho }\left({\tilde{\chi }}_i\left(y_d(t-{\tau }_i\left(t\right))\right)+m_i\right)$, $b=\frac{a{e}^{\sigma \tau }}{2}$ with $\tau =max\left\{{\tau }_1\left(t\right),\dots ,{\tau }_n\left(t\right)\right\}$, and $\overline{\mathrm{\Psi }}$ is an unknown constant satisfying ${\left|\right|\mathrm{\Psi }\left|\right|}^2\le \overline{\mathrm{\Psi }}$.

According to the definition of $\gamma$, we can obtain

$$\begin{array}{c}\hfill \frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2\gamma }\sum _{i=1}^n{z}_{1,{\tau }_i\left(t\right)}{\chi }_i\left(z_{1,{\tau }_i\left(t\right)}\right)-\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{a}\sum _{i=1}^n{e}^{-\sigma {\tau }_i\left(t\right)}{z}_{1,{\tau }_i\left(t\right)}{\chi }_i\left(z_{1,{\tau }_i\left(t\right)}\right)<0\end{array}$$

(23)

It follows from (22) and (23) that

$$\begin{array}{cc}\hfill {\dot{V}}_0=& -{\int }_0^{\infty }\varpi {\mu }_{\alpha }\left(\varpi \right){𝒵}_{\mathcal{E}}^T(\varpi ,t)\mathcal{P}{𝒵}_{\mathcal{E}}(\varpi ,t)d\varpi -\frac{{\sigma \left|\right|\mathcal{P}\left|\right|}^2{e}^{-\sigma t}}{a(1-\overline{\tau })}\sum _{i=1}^n{\int }_{t-{\tau }_i\left(t\right)}^t{e}^{\sigma \varsigma }{z}_1\left(\varsigma \right){\chi }_i\left(z_1\left(\varsigma \right)\right)d\varsigma \hfill \\ \hfill & -c\mu {\mathcal{E}}^T\mathcal{E}+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{a(1-\overline{\tau })}\sum _{i=1}^n{z}_1\left(t\right){\chi }_i\left(z_1\left(t\right)\right)+{\left|\right|\mathcal{P}\left|\right|}^2\sum _{i=1}^n{\theta }_i^{\ast T}{\theta }_i^{\ast }+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2}\sum _{j=1}^n{\tilde{\theta }}_j^T{\tilde{\theta }}_j\hfill \\ \hfill & +\sum _{i=1}^n{\mathit{ħ}}_i+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2}\overline{\mathrm{\Psi }}\hfill \end{array}$$

(24)

where $c={\lambda }_{min}\left(\overline{\mathcal{Q}}\right)-\frac{5+b}{2}$.

Remark 2.

In view of the complexity of the fractional derivative, it should be pointed out that the Lyapunov functions in most of the existing IO/FO results, such as those reported in [16,17,18], are rarely used to handle the control problem of FONSs subject to unknown control gains and time-varying delays. Therefore, an indirect Lyapunov method is employed to finish the predefined control goal. Moreover, the method proposed in this paper is easily extended to investigate the control problem of incommensurate FONTDSs.

3.2. FODSC-Based Adaptive Fuzzy Quantized Control Design

Step 1.

First, we define the following change of coordinates:

$$\left\{\begin{array}{cc}\hfill z_1& =y-y_d,\hfill \\ \hfill z_i& ={\widehat{x}}_i-{\lambda }_{i,f},(i=2,\dots ,n)\hfill \end{array}\right.$$

(25)

where $z_j(j=1,2,\dots ,n)$ denotes surface error, and the virtual control signal (${\eta }_{i-1}$) and ${\lambda }_{i-1,f}$ are the input and output of the modified FO filter to be designed, respectively.

The FO derivative of $z_1$ is expressed as follows:

$$\begin{array}{cc}\hfill D^{\alpha }{z}_1=& \phi \left(z_2+e_2+{\lambda }_{2,f}\right)+{\theta }_{s1}^{\ast T}{\psi }_{s1}\left(X_1\right)+G_1\left({\overline{x}}_{1,{\tau }_1\left(t\right)}\right)+{\Delta }_1\hfill \end{array}$$

(26)

where the term $F_1\left(x_1\right)-D^{\alpha }{y}_d$ is approximated by the FLS with $X_1=[x_1,y_d,D^{\alpha }{y}_d]$ and ${\Delta }_1=o_{s1}+{\psi }_1$, satisfying $\left|\right|{\Delta }_1{\left|\right|}^2\le {\Delta }_{1,M}$.

To overcome the complexity issue existing in the traditional backstepping control method, we let ${\eta }_1$ pass through the following modified FO filter to obtain a filtered signal.

$${\iota }_2{D}^{\alpha }{\lambda }_{2,f}+{\lambda }_{2,f}={\eta }_1,{\lambda }_{2,f}\left(0\right)={\eta }_1\left(0\right)$$

(27)

where ${\iota }_2>0$ is a time constant. By defining the filter error as ${ϵ}_2={\lambda }_{2,f}-{\eta }_1$, we have

$$D^{\alpha }{\lambda }_{2,f}=-\frac{{ϵ}_2}{{\iota }_2}$$

(28)

The first virtual control input (${\eta }_1$) and update laws are designed as:

$$\begin{array}{cc}\hfill & {\eta }_1=N\left(\xi \right){\underline{\eta }}_1\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & {\underline{\eta }}_1=\left({\phi }_M^2+\frac{3+2k_1}{2}\right)z_1+{\widehat{\theta }}_{s1}^T{\psi }_{s1}\left(X_1\right)+\frac{{\chi }_1\left(z_1\left(t\right)\right)}{2a(1-\overline{\tau })}+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{a(1-\overline{\tau })}\sum _{i=1}^n{\chi }_i\left(z_1\left(t\right)\right)\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & D^{\alpha }{\widehat{\theta }}_1={\psi }_1\left({\widehat{\underline{x}}}_2\right)z_1-a_1{\widehat{\theta }}_1,\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & D^{\alpha }{\widehat{\theta }}_{s1}={\psi }_{s1}\left(X_1\right)z_1-a_1{\widehat{\theta }}_{s1},\hfill \end{array}$$

(32)

where k is a positive constant, and ${\phi }_M$ is a constant satisfying $\left|\phi \right|\le {\phi }_M$.

According to (28)–(30), we have

$$D^{\alpha }{ϵ}_2=-\frac{{ϵ}_2}{{\iota }_2}+{\mathrm{\Omega }}_2(★)$$

(33)

where ${\mathrm{\Omega }}_2(·)$ is a continuous function concerning variables $z_1,\xi$. Based on previously reported results [16], there exists a constant ($M_2$) such that $|{\mathrm{\Omega }}_2(★)|\le M_2$.

According to Lemma 1, we can rewrite $D^{\alpha }{z}_1,D^{\alpha }{\tilde{\theta }}_1,D^{\alpha }{ϵ}_2$ as:

$$\left\{\begin{array}{cc}\hfill \frac{\partial {𝒵}_{z_1}(\varpi ,t)}{\partial t}=& -\varpi {𝒵}_{z_1}(\varpi ,t)+\phi \left(z_2+e_2+{\eta }_1+{ϵ}_2\right)\hfill \\ \hfill & +{\theta }_{s1}^{\ast T}{\psi }_1\left(X_1\right)+G_1\left({\overline{x}}_{1,{\tau }_1\left(t\right)}\right)+{\Delta }_1\hfill \\ \hfill z_1=& {\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{z_1}(\varpi ,t)d\varpi \hfill \end{array}\right.$$

(34)

$$\left\{\begin{array}{cc}\hfill \frac{\partial {𝒵}_{{\tilde{\theta }}_1}(\varpi ,t)}{\partial t}=& -\varpi {𝒵}_{{\tilde{\theta }}_1}(\varpi ,t)+{\psi }_1\left({\widehat{\underline{x}}}_2\right)z_1-a_1{\widehat{\theta }}_1\hfill \\ \hfill {\tilde{\theta }}_1=& {\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{{\tilde{\theta }}_1}(\varpi ,t)d\varpi \hfill \end{array}\right.$$

(35)

$$\left\{\begin{array}{cc}\hfill \frac{\partial {𝒵}_{{\tilde{\theta }}_{s1}}(\varpi ,t)}{\partial t}=& -\varpi {𝒵}_{{\tilde{\theta }}_{s1}}(\varpi ,t)+{\psi }_{s1}\left(X_1\right)z_1-a_1{\widehat{\theta }}_{s1}\hfill \\ \hfill {\tilde{\theta }}_{s1}=& {\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{{\tilde{\theta }}_{s1}}(\varpi ,t)d\varpi \hfill \end{array}\right.$$

(36)

$$\left\{\begin{array}{cc}\hfill \frac{\partial {𝒵}_{{ϵ}_2}(\varpi ,t)}{\partial t}=& -\varpi {𝒵}_{{ϵ}_2}(\varpi ,t)-\frac{{ϵ}_2}{{\iota }_2}+{\mathrm{\Omega }}_2(★)\hfill \\ \hfill {ϵ}_2=& {\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{{ϵ}_2}(\varpi ,t)d\varpi \hfill \end{array}\right.$$

(37)

Then, we select the following Lyapunov function:

$$V_1=V_0+V_{1,1}+V_{1,2}+V_{1,3}+V_{1,4}+V_{1,5}$$

(38)

where $V_{1,1}=\frac{e^{-\sigma t}}{2a(1-\overline{\tau })}{\int }_{t-{\tau }_i\left(t\right)}^t{e}^{\sigma \varsigma }{z}_1\left(\varsigma \right){\chi }_1\left(z_1\left(\varsigma \right)\right)d\varsigma ,V_{1,2}=(1/2){\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{z_1}^2(\varpi ,t)d\varpi$, $V_{1,3}=(1/2){\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{{\tilde{\theta }}_1}^T(\varpi ,t){𝒵}_{{\tilde{\theta }}_1}(\varpi ,t)d\varpi$, $V_{1,4}=(1/2){\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{{\tilde{\theta }}_{s1}}^T(\varpi ,t){𝒵}_{{\tilde{\theta }}_{s1}}(\varpi ,t)d\varpi ,V_{1,5}=(1/2){\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{{ϵ}_2}^2(\varpi ,t)d\varpi$.

The derivative of $V_1$ is

$$\begin{array}{cc}\hfill {\dot{V}}_1\le & -\left({\mathrm{\Xi }}_{0,0}+{\mathrm{\Xi }}_{0,1}+{\mathrm{\Xi }}_{1,1}+{\mathrm{\Xi }}_{1,2}+{\mathrm{\Xi }}_{1,3}\right)-\sigma (V_{0,1}+V_{1,1})+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{a(1-\overline{\tau })}\sum _{i=1}^n{z}_1\left(t\right){\chi }_i\left(z_1\left(t\right)\right)\hfill \\ \hfill & -c\mu {\mathcal{E}}^T\mathcal{E}+{\left|\right|\mathcal{P}\left|\right|}^2\sum _{i=1}^n{\theta }_i^{\ast T}{\theta }_i^{\ast }+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2}\sum _{j=1}^n{\tilde{\theta }}_j^T{\tilde{\theta }}_j+\sum _{i=1}^n{\mathit{ħ}}_i+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2}\overline{\mathrm{\Psi }}+\frac{z_1\left(t\right){\chi }_1\left(z_1\left(t\right)\right)}{2a(1-\overline{\tau })}\hfill \\ \hfill & -\frac{e^{-\sigma {\tau }_1\left(t\right)}}{2a}{z}_{1,{\tau }_1\left(t\right)}{\chi }_1\left(z_{1,{\tau }_1\left(t\right)}\right)+z_1[\phi \left(z_2+e_2+{\eta }_1+{ϵ}_2\right)+{\theta }_{s1}^{\ast T}{\psi }_1\left(X_1\right)+G_1\left({\overline{x}}_{1,{\tau }_1\left(t\right)}\right)\hfill \\ \hfill & +{\Delta }_1+{\tilde{\theta }}_1^T{\psi }_1\left({\widehat{\underline{X}}}_2\right)-{\tilde{\theta }}_1^T{\psi }_1\left({\widehat{\underline{x}}}_2\right)]-{\tilde{\theta }}_1^T\left({\psi }_1\left({\widehat{\underline{x}}}_2\right)z_1-a_1{\widehat{\theta }}_1\right)-{\tilde{\theta }}_{s1}^T\left({\psi }_1\left(X_1\right)z_1-a_1{\widehat{\theta }}_{s1}\right)\hfill \\ \hfill & +{ϵ}_2\left(-\frac{{ϵ}_2}{{\iota }_2}+{\mathrm{\Omega }}_2(★)\right)\hfill \end{array}$$

(39)

where ${\mathrm{\Xi }}_{0,0}={\int }_0^{\infty }\varpi {\mu }_{\alpha }\left(\varpi \right){𝒵}_{\mathcal{E}}^T(\varpi ,t)\mathcal{P}{𝒵}_{\mathcal{E}}(\varpi ,t)d\varpi$, ${\mathrm{\Xi }}_{0,1}={\int }_0^{\infty }\varpi {\mu }_{\alpha }\left(\varpi \right){𝒵}_{{\tilde{\theta }}_{s1}}^T(\varpi ,t){𝒵}_{{\tilde{\theta }}_{s1}}(\varpi ,t)d\varpi$, ${\mathrm{\Xi }}_{1,1}={\int }_0^{\infty }\varpi {\mu }_{\alpha }\left(\varpi \right){𝒵}_{z_1}^2(\varpi ,t)d\varpi$, ${\mathrm{\Xi }}_{1,2}={\int }_0^{\infty }\varpi {\mu }_{\alpha }\left(\varpi \right){𝒵}_{{\tilde{\theta }}_1}^T(\varpi ,t){𝒵}_{{\tilde{\theta }}_1}(\varpi ,t)d\varpi$, ${\mathrm{\Xi }}_{1,3}={\int }_0^{\infty }\varpi {\mu }_{\alpha }\left(\varpi \right)$

${𝒵}_{{ϵ}_2}^2(\varpi ,t)d\varpi$.

Substituting (29) and (30) into (37) and using Young’s inequality, one can obtain

$$\begin{array}{cc}\hfill {\dot{V}}_1\le & -\left({\mathrm{\Xi }}_{0,0}+{\mathrm{\Xi }}_{0,1}+{\mathrm{\Xi }}_{1,1}+{\mathrm{\Xi }}_{1,2}+{\mathrm{\Xi }}_{1,3}\right)-\sigma (V_{0,1}+V_{1,1})-\overline{c}\mu {\mathcal{E}}^T\mathcal{E}\hfill \\ \hfill & +{\left|\right|\mathcal{P}\left|\right|}^2\sum _{i=1}^n{\theta }_i^{\ast T}{\theta }_i^{\ast }+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2}\sum _{j=1}^n{\tilde{\theta }}_j^T{\tilde{\theta }}_j+\sum _{i=1}^n{\mathit{ħ}}_i+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2}\overline{\mathrm{\Psi }}+z_1\left(\phi z_2+\phi {\eta }_1+{\underline{\eta }}_1\right)\hfill \\ \hfill & -k_1{z}_1^2+a_1{\tilde{\theta }}_1^T{\widehat{\theta }}_1+a_1{\tilde{\theta }}_{s1}^T{\widehat{\theta }}_{s1}+\frac{{\Delta }_{1,M}}{2}+\frac{\left|\right|{\tilde{\theta }}_1{\left|\right|}^2}{2}+\overline{\mathit{ħ}}-\left(\frac{1}{{\iota }_2}-\frac{1}{2}\right){ϵ}_2^2+\frac{1}{2}{M}_2^2\hfill \end{array}$$

(40)

where $\overline{c}=c-\frac{1}{2}>0,0<{\iota }_2<2$, $\overline{\mathit{ħ}}=\frac{1}{2}\left[{\tilde{\chi }}_1\left(y_d(t-{\tau }_1\left(t\right))\right)+m_1\right]$.

We set $\dot{\xi }=z_1{\underline{\eta }}_1$. Then, invoking (40) yields

$$\begin{array}{cc}\hfill {\dot{V}}_1\le & -\left({\mathrm{\Xi }}_{0,0}+{\mathrm{\Xi }}_{0,1}+{\mathrm{\Xi }}_{1,1}+{\mathrm{\Xi }}_{1,2}+{\mathrm{\Xi }}_{1,3}\right)-\sigma V_{0,1}-\sigma V_{1,1}+\phi N\left(\xi \right)\dot{\xi }+\dot{\xi }-k_1{z}_1^2\hfill \\ \hfill & +\phi z_1{z}_2+a_1{\tilde{\theta }}_1^T{\widehat{\theta }}_1+a_1{\tilde{\theta }}_{s1}^T{\widehat{\theta }}_{s1}+\frac{M_2^2}{2}+\frac{\left|\right|{\tilde{\theta }}_1{\left|\right|}^2}{2}+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2}\sum _{j=1}^n{\tilde{\theta }}_j^T{\tilde{\theta }}_j+{\mathrm{\Lambda }}_1\hfill \end{array}$$

(41)

where ${\mathrm{\Lambda }}_1={\left|\right|\mathcal{P}\left|\right|}^2{\sum }_{i=1}^n{\theta }_i^{\ast T}{\theta }_i^{\ast }+{\sum }_{i=1}^n{\mathit{ħ}}_i+\overline{\mathit{ħ}}+\left[{\left|\right|\mathcal{P}\left|\right|}^2\overline{\mathrm{\Psi }}+{\Delta }_{1,M}\right]/2$.

Step i

($i=2,\dots ,n-1$). Similar to step 1, $D^{\alpha }{z}_i$ is calculated as:

$$\begin{array}{c}\hfill D^{\alpha }{z}_i={\widehat{x}}_{i+1}+{\widehat{\theta }}_i^T{\psi }_i\left({\widehat{\underline{x}}}_i\right)+{\mu }^i{L}_i(y-{\widehat{x}}_1)-D^{\alpha }{\lambda }_{i,f}\end{array}$$

(42)

By adopting the FO filter (${\iota }_{i+1}{D}^{\alpha }{\lambda }_{i+1,f}+{\lambda }_{i+1,f}={\eta }_i$) with ${\lambda }_{i+1,f}\left(0\right)={\eta }_i\left(0\right)$ and defining the filter error as ${ϵ}_{i+1}={\lambda }_{i+1,f}-{\eta }_i$, we can obtain

$$D^{\alpha }{\lambda }_{i+1,f}=-\frac{{ϵ}_{i+1}}{{\iota }_{i+1}},$$

(43)

The virtual control input (${\eta }_i$) and parameter update law are designed as:

$$\begin{array}{cc}\hfill & {\eta }_i=-z_{i-1}-(k_i+1)z_i-{\widehat{\theta }}_i^T{\psi }_i\left({\widehat{\underline{x}}}_i\right)-{\mu }^i{L}_i(y-{\widehat{x}}_1)+D^{\alpha }{\lambda }_{i,f}\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill & D^{\alpha }{\widehat{\theta }}_i={\psi }_i\left({\widehat{\underline{x}}}_i\right)z_i-a_i{\widehat{\theta }}_i,\hfill \end{array}$$

(45)

where $k_i$ and $a_i$ are positive constants.

Then, we can obtain

$$D^{\alpha }{ϵ}_{i+1}=-\frac{{ϵ}_{i+1}}{{\iota }_{i+1}}+{\mathrm{\Omega }}_{i+1}(★),$$

(46)

where ${\mathrm{\Omega }}_{i+1}(★)$ is a continuous function concerning variables $z_1,\dots ,z_i,{\widehat{\theta }}_1,\dots ,{\widehat{\theta }}_i,{\lambda }_{i,f},D^{\alpha }{\lambda }_{i,f}$. There exists a constant ($M_{i+1}$) such that $|{\mathrm{\Omega }}_{i+1}(★)|\le M_{i+1}$.

Similar to (34)–(37), we have

$$\left\{\begin{array}{cc}\hfill \frac{\partial {𝒵}_{z_i}(\varpi ,t)}{\partial t}=& -\varpi {𝒵}_{z_i}(\varpi ,t)+{\widehat{x}}_{i+1}+{\widehat{\theta }}_i^T{\psi }_i\left({\widehat{\underline{x}}}_i\right)\hfill \\ \hfill & +{\mu }^i{L}_i(y-{\widehat{x}}_1)-D^{\alpha }{\lambda }_{i,f}\hfill \\ \hfill z_i=& {\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{z_i}(\varpi ,t)d\varpi \hfill \end{array}\right.$$

(47)

$$\left\{\begin{array}{cc}\hfill \frac{\partial {𝒵}_{{\tilde{\theta }}_i}(\varpi ,t)}{\partial t}=& -\varpi {𝒵}_{{\tilde{\theta }}_i}(\varpi ,t)+{\psi }_i\left({\widehat{\underline{x}}}_i\right)z_i-a_i{\widehat{\theta }}_i\hfill \\ \hfill {\tilde{W}}_i=& {\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{{\tilde{\theta }}_i}(\varpi ,t)d\varpi \hfill \end{array}\right.$$

(48)

$$\left\{\begin{array}{cc}\hfill \frac{\partial {𝒵}_{{ϵ}_{i+1}}(\varpi ,t)}{\partial t}=& -\varpi {𝒵}_{{ϵ}_{i+1}}(\varpi ,t)-\frac{{ϵ}_{i+1}}{{\iota }_{i+1}}+{\mathrm{\Omega }}_{i+1}(★)\hfill \\ \hfill {ϵ}_{i+1}=& {\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{{ϵ}_{i+1}}(\varpi ,t)d\varpi \hfill \end{array}\right.$$

(49)

Then, we construct the following Lyapunov function:

$$V_i=V_{i-1}+V_{i,1}+V_{i,2}+V_{i,3}$$

(50)

where $V_{i,1}=(1/2){\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{z_i}^2(\varpi ,t)d\varpi ,V_{i,2}=(1/2){\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{{\tilde{\theta }}_i}^T(\varpi ,t){𝒵}_{{\tilde{\theta }}_i}(\varpi ,t)d\varpi$,

$V_{i,3}=(1/2){\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{{ϵ}_{i+1}}^2(\varpi ,t)d\varpi$.

Calculating the derivative of $V_i$ yields

$$\begin{array}{cc}\hfill {\dot{V}}_i\le & -\left({\mathrm{\Xi }}_{0,0}+{\mathrm{\Xi }}_{0,1}\right)-\sum _{j=1}^i\left({\mathrm{\Xi }}_{j,1}+{\mathrm{\Xi }}_{j,2}+{\mathrm{\Xi }}_{j,3}\right)-\sigma (V_{0,1}+V_{1,1})+\phi N\left(\xi \right)\dot{\xi }+\dot{\xi }+a_1{\tilde{\theta }}_{s1}^T{\widehat{\theta }}_{s1}\hfill \\ \hfill & +\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2}\sum _{j=1}^n{\tilde{\theta }}_j^T{\tilde{\theta }}_j+\sum _{j=1}^{i-1}\frac{\left|\right|{\tilde{\theta }}_j{\left|\right|}^2}{2}+\sum _{j=1}^{i-1}{a}_j{\tilde{\theta }}_j^T{\widehat{\theta }}_j-\sum _{j=1}^{i-1}{k}_j{z}_j^2+\overline{\phi }{z}_1{z}_2+z_{i-1}{z}_i+{\mathrm{\Lambda }}_{i-1}\hfill \\ \hfill & +z_i\left[z_{i+1}+{ϵ}_{i+1}+{\eta }_i+{\widehat{\theta }}_i^T{\psi }_i\left({\widehat{\underline{x}}}_i\right)+{\mu }^i{L}_i(y-{\widehat{x}}_1)-D^{\alpha }{\lambda }_{i,f}+{\tilde{\theta }}_i^T{\psi }_i\left({\widehat{\underline{x}}}_i\right)-{\tilde{\theta }}_i^T{\psi }_i\left({\widehat{\underline{x}}}_i\right)\right]\hfill \\ \hfill & -{\tilde{\theta }}_i^T\left({\psi }_i\left({\widehat{\underline{x}}}_i\right)z_i-a_i{\widehat{\theta }}_i\right)+{ϵ}_{i+1}\left(-\frac{{ϵ}_{i+1}}{{\iota }_{i+1}}+{\mathrm{\Omega }}_{i+1}(★)\right)\hfill \end{array}$$

(51)

in which $\overline{\phi }=\phi -1,{\mathrm{\Lambda }}_{i-1}={\mathrm{\Lambda }}_1+{\sum }_{j=1}^{i-1}\frac{1}{2}{M}_{j+1}^2$, $0<{\iota }_{i+1}<2$, ${\mathrm{\Xi }}_{i,1}={\int }_0^{\infty }\varpi {\mu }_{\alpha }\left(\varpi \right){𝒵}_{z_i}^2(\varpi ,t)d\varpi$,

${\mathrm{\Xi }}_{i,2}={\int }_0^{\infty }\varpi {\mu }_{\alpha }\left(\varpi \right){𝒵}_{{\tilde{\theta }}_i}^T(\varpi ,t){𝒵}_{{\tilde{\theta }}_i}(\varpi ,t)d\varpi$, ${\mathrm{\Xi }}_{i,3}={\int }_0^{\infty }\varpi {\mu }_{\alpha }\left(\varpi \right){𝒵}_{{ϵ}_{i+1}}^2(\varpi ,t)d\varpi$.

Substituting (48) into (50) and using Young’s inequality, one can obtain

$$\begin{array}{cc}\hfill {\dot{V}}_i\le & -\left({\mathrm{\Xi }}_{0,0}+{\mathrm{\Xi }}_{0,1}\right)-\sum _{j=1}^i\left({\mathrm{\Xi }}_{j,1}+{\mathrm{\Xi }}_{j,2}+{\mathrm{\Xi }}_{j,3}\right)-\sigma (V_{0,1}+V_{1,1})+\phi N\left(\xi \right)\dot{\xi }+\dot{\xi }+a_1{\tilde{\theta }}_{s1}^T{\widehat{\theta }}_{s1}\hfill \\ \hfill & +\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2}\sum _{j=1}^n{\tilde{\theta }}_j^T{\tilde{\theta }}_j+\sum _{j=1}^i\frac{\left|\right|{\tilde{\theta }}_j{\left|\right|}^2}{2}+\sum _{j=1}^i{a}_j{\tilde{\theta }}_j^T{\widehat{\theta }}_j-\sum _{j=1}^i{k}_j{z}_j^2+\overline{\phi }{z}_1{z}_2+z_i{z}_{i+1}+{\mathrm{\Lambda }}_i\hfill \end{array}$$

(52)

where ${\mathrm{\Lambda }}_i={\mathrm{\Lambda }}_1+{\sum }_{j=1}^i\frac{1}{2}{M}_{j+1}^2$.

Step n.

In this step, the control input is designed. Along with step i, we have

$$\begin{array}{c}\hfill D^{\alpha }{z}_n=q\left(u\right)+{\widehat{\theta }}_n^T{\psi }_n\left({\widehat{\underline{x}}}_n\right)+{\mu }^n{L}_n(y-{\widehat{x}}_1)-D^{\alpha }{\lambda }_{n,f}\end{array}$$

(53)

The intermediate control input ($\upsilon$) and parameter update law are designed as:

$$\begin{array}{cc}\hfill & v=z_{n-1}+(k_n+1)z_n+{\widehat{\theta }}_n^T{\psi }_n\left({\widehat{\underline{x}}}_n\right)+{\mu }^n{L}_n(y-{\widehat{x}}_1)-D^{\alpha }{\lambda }_{n,f}\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill & D^{\alpha }{\widehat{\theta }}_n={\psi }_n\left({\widehat{\underline{x}}}_n\right)z_n-a_n{\widehat{\theta }}_n\hfill \end{array}$$

(55)

Using Lemma 1 again, we can rewrite systems (53) and (55) as:

$$\left\{\begin{array}{cc}\hfill \frac{\partial {𝒵}_{z_n}(\varpi ,t)}{\partial t}=& -\varpi {𝒵}_{z_n}(\varpi ,t)q\left(u\right)+{\widehat{\theta }}_n^T{\psi }_n\left({\widehat{\underline{x}}}_n\right)\hfill \\ \hfill & +{\mu }^n{L}_n(y-{\widehat{x}}_1)-D^{\alpha }{\lambda }_{n,f}\hfill \\ \hfill z_n=& {\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{z_n}(\varpi ,t)d\varpi \hfill \end{array}\right.$$

(56)

$$\left\{\begin{array}{cc}\hfill \frac{\partial {𝒵}_{{\tilde{\theta }}_n}(\varpi ,t)}{\partial t}=& -\varpi {𝒵}_{{\tilde{\theta }}_n}(\varpi ,t)+{\psi }_n\left({\widehat{\underline{x}}}_n\right)z_n-a_n{\widehat{\theta }}_n\hfill \\ \hfill {\tilde{\theta }}_n=& {\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{{\tilde{\theta }}_n}(\varpi ,t)d\varpi \hfill \end{array}\right.$$

(57)

Then, we set the Lyapunov function as:

$$V_n=V_{n-1}+V_{n,1}+V_{n,2}$$

(58)

where $V_{n,1}=\frac{1}{2}{\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{z_n}^2(\varpi ,t)d\varpi ,V_{n,2}=\frac{1}{2}{\int }_0^{\infty }{\mu }_{\alpha }\left(\varpi \right){𝒵}_{{\tilde{\theta }}_n}^T(\varpi ,t){𝒵}_{{\tilde{\theta }}_n}(\varpi ,t)d\varpi$.

The derivative of $V_n$ is

$$\begin{array}{cc}\hfill {\dot{V}}_n\le & -\left({\mathrm{\Xi }}_{0,0}+{\mathrm{\Xi }}_{0,1}\right)-\sum _{j=1}^n\left({\mathrm{\Xi }}_{j,1}+{\mathrm{\Xi }}_{j,2}\right)-\sum _{j=1}^{n-1}{\mathrm{\Xi }}_{j,3}-\sigma (V_{0,1}+V_{1,1})+\phi N\left(\xi \right)\dot{\xi }+\dot{\xi }+a_1{\tilde{\theta }}_{s1}^T{\widehat{\theta }}_{s1}\hfill \\ \hfill & +\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2}\sum _{i=1}^n{\tilde{\theta }}_j^T{\tilde{\theta }}_j+\sum _{j=1}^i\frac{\left|\right|{\tilde{\theta }}_j{\left|\right|}^2}{2}+\sum _{j=1}^i{a}_j{\tilde{\theta }}_j^T{\widehat{\theta }}_j-\sum _{j=1}^{n-1}{k}_j{z}_j^2+\overline{\phi }{z}_1{z}_2+z_{n-1}{z}_n+{\mathrm{\Lambda }}_{n-1}\hfill \\ \hfill & +z_n\left[u+h+{\widehat{\theta }}_n^T{\psi }_n\left({\widehat{\underline{x}}}_n\right)+{\mu }^n{L}_n(y-{\widehat{x}}_1)-D^{\alpha }{\lambda }_{n,f}+{\tilde{\theta }}_n^T{\psi }_n\left({\widehat{\underline{x}}}_n\right)-{\tilde{\theta }}_n^T{\psi }_n\left({\widehat{\underline{x}}}_n\right)\right]\hfill \\ \hfill & -{\tilde{\theta }}_n^T\left({\psi }_n\left({\widehat{\underline{x}}}_n\right)z_n-a_n{\widehat{\theta }}_n\right)\hfill \end{array}$$

(59)

where ${\mathrm{\Xi }}_{n,1}={\int }_0^{\infty }\varpi {\mu }_{\alpha }\left(\varpi \right){𝒵}_{z_n}^2(\varpi ,t)d\varpi ,{\mathrm{\Xi }}_{n,2}={\int }_0^{\infty }\varpi {\mu }_{\alpha }\left(\varpi \right){𝒵}_{{\tilde{\theta }}_n}^T(\varpi ,t){𝒵}_{{\tilde{\theta }}_n}(\varpi ,t)d\varpi$.

Substituting (54) into (59) yields

$$\begin{array}{cc}\hfill {\dot{V}}_n\le & -\left({\mathrm{\Xi }}_{0,0}+{\mathrm{\Xi }}_{0,1}\right)-\sum _{j=1}^n\left({\mathrm{\Xi }}_{j,1}+{\mathrm{\Xi }}_{j,2}\right)-\sum _{j=1}^{n-1}{\mathrm{\Xi }}_{j,3}-\sigma (V_{0,1}+V_{1,1})+\phi N\left(\xi \right)\dot{\xi }+\dot{\xi }\hfill \\ \hfill & +a_1{\tilde{\theta }}_{s1}^T{\widehat{\theta }}_{s1}+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2}\sum _{j=1}^n{\tilde{\theta }}_j^T{\tilde{\theta }}_j+\sum _{j=1}^n\frac{\left|\right|{\tilde{\theta }}_j{\left|\right|}^2}{2}+\sum _{j=1}^n{a}_j{\tilde{\theta }}_j^T{\widehat{\theta }}_j-\sum _{j=1}^{n-1}{k}_j{z}_j^2+\overline{\phi }{z}_1{z}_2+{\mathrm{\Lambda }}_n\hfill \\ \hfill & -\left(k_n+\frac{1}{2}\right)z_n^2+z_{n}v+z_n\left(u+h\right)\hfill \end{array}$$

(60)

where ${\mathrm{\Lambda }}_n={\mathrm{\Lambda }}_1+{\sum }_{j=1}^{n-1}\frac{1}{2}{M}_{j+1}^2$.

Then, the actual control input is designed as:

$$u=-\frac{z_n{\upsilon }^2}{(1-\delta )\sqrt{z_n^2{\upsilon }^2+{\aleph }^2}}$$

(61)

where ℵ is a positive parameter to be determined.

Based on the abovementioned analysis, the following theorem is proposed.

Theorem 1.

For the considered FONTDS (9) under Assumptions 1–3, the presented control scheme including an FO high-gain fuzzy state observer (14); intermediate control laws (29), (30), (44) and (54); actual control law (61); and parameter update laws (31), (45) and (55) can guarantee that all the signals in the CLS are bounded and that the system output (y) can track the given reference signal ($y_d$).

Proof. 

According to Lemma 3 and given the fact that $z_{n}u<0$, we have

$$\begin{array}{cc}\hfill z_{n}h\le & \delta |z_{n}u|+|z_n|u_{min}\le -\delta z_{n}u+\frac{1}{2}{z}_n^2+\frac{1}{2}{u}_{min}^2\hfill \end{array}$$

(62)

Substituting (62) into (60), one can obtain

$$\begin{array}{cc}\hfill {\dot{V}}_n\le & -\left({\mathrm{\Xi }}_{0,0}+{\mathrm{\Xi }}_{0,1}\right)-\sum _{j=1}^n\left({\mathrm{\Xi }}_{j,1}+{\mathrm{\Xi }}_{j,2}\right)-\sum _{j=1}^{n-1}{\mathrm{\Xi }}_{j,3}-\sigma (V_{0,1}+V_{1,1})+\phi N\left(\xi \right)\dot{\xi }+\dot{\xi }\hfill \\ \hfill & +a_1{\tilde{\theta }}_{s1}^T{\widehat{\theta }}_{s1}+\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2}\sum _{j=1}^n{\tilde{\theta }}_j^T{\tilde{\theta }}_j+\sum _{j=1}^n\frac{\left|\right|{\tilde{\theta }}_j{\left|\right|}^2}{2}+\sum _{j=1}^n{a}_j{\tilde{\theta }}_j^T{\widehat{\theta }}_j-\sum _{j=1}^n{k}_j{z}_j^2+\overline{\phi }{z}_1{z}_2+{\mathrm{\Lambda }}_n\hfill \\ \hfill & +(1-\delta )z_{n}u+z_n\upsilon +\frac{1}{2}{u}_{min}^2\hfill \end{array}$$

(63)

It follows from Lemma 3 in [43] that

$$z_n\upsilon +(1-\delta )z_{n}u\le \left|z_n\upsilon \right|-\frac{z_n^2{\upsilon }^2}{\sqrt{z_n^2{\upsilon }^2+{\aleph }^2}}<\aleph .$$

(64)

Invoking (63) and (64) and utilizing Young’s inequality yields

$$\begin{array}{cc}\hfill {\dot{V}}_n\le & -\left({\mathrm{\Xi }}_{0,0}+{\mathrm{\Xi }}_{0,1}\right)-\sum _{j=1}^n\left({\mathrm{\Xi }}_{j,1}+{\mathrm{\Xi }}_{j,2}\right)-\sum _{j=1}^{n-1}{\mathrm{\Xi }}_{j,3}-\sigma (V_{0,1}+V_{1,1})\hfill \\ \hfill & +\frac{{\left|\right|\mathcal{P}\left|\right|}^2}{2}\sum _{j=1}^n{\tilde{\theta }}_j^T{\tilde{\theta }}_j-\sum _{j=1}^n\frac{a_j}{2}{\tilde{\theta }}_j^T{\tilde{\theta }}_j+(\phi N\left(\xi \right)+1)\dot{\xi }-\sum _{j=1}^n{\overline{k}}_j{z}_j^2+{\overline{\mathrm{\Lambda }}}_n\hfill \end{array}$$

(65)

where ${\overline{k}}_1=\left(k_1-\frac{{\phi }_M^2}{2}\right),{\overline{k}}_2=\left(k_2-\frac{1}{2}\right),{\overline{k}}_j=k_j(j=3,\dots ,n)$ and ${\overline{\mathrm{\Lambda }}}_n={\mathrm{\Lambda }}_n+\frac{a_1\left|\right|{\theta }_{s1}^{\ast }{\left|\right|}^2}{2}+{\sum }_{j=1}^n\frac{a_j\left|\right|{\theta }_j^{\ast }{\left|\right|}^2}{2}+\frac{1}{2}{u}_{min}^2+\aleph$.

Furthermore, by choosing the appropriate design parameters ($k_i,a_i(i=1,\dots ,n)$), the following inequality holds

$$\begin{array}{cc}\hfill {\dot{V}}_n\le & -\kappa V+{\overline{\mathrm{\Lambda }}}_n+\phi N\left(\xi \right)\dot{\xi }+\dot{\xi }\hfill \end{array}$$

(66)

where $\kappa =min\left\{\varpi ,\sigma \right\}$.

Multiplying inequality (66) by $e^{\kappa t}$ on both sides yields

$$\begin{array}{cc}\hfill e^{\kappa t}{\dot{V}}_n+\kappa V_n{e}^{\kappa t}\le & {\overline{\mathrm{\Lambda }}}_n{e}^{\kappa t}+e^{\kappa t}\phi N\left(\xi \right)\dot{\xi }+e^{\kappa t}\dot{\xi }\hfill \end{array}$$

(67)

Furthermore, we have

$$\begin{array}{c}\hfill \frac{d\left(V_n{e}^{\kappa t}\right)}{dt}\le {\overline{\mathrm{\Lambda }}}_n{e}^{\kappa t}+e^{\kappa t}\phi N\left(\xi \right)\dot{\xi }+e^{\kappa t}\dot{\xi }\end{array}$$

(68)

Then, we take the integration for (68) over $[0,t]$ to obtain

$$\begin{array}{cc}\hfill V_n\le & \frac{{\overline{\mathrm{\Lambda }}}_n}{\kappa }+\left(V_n\left(0\right)-\frac{{\overline{\mathrm{\Lambda }}}_n}{\kappa }\right)e^{-\kappa t}+e^{-\kappa t}{\int }_0^t\left(\phi N\left(\xi \right)+1\right)\dot{\xi }{e}^{\kappa \varsigma }d\varsigma \hfill \end{array}$$

(69)

By utilizing Lemma 1, it can be determined that $e^{-\kappa t}{\int }_0^t\left(\phi N\left(\xi \right)+1\right)\dot{\xi }{e}^{\kappa \varsigma }d\varsigma$ is bounded.

Subsequently, we have

$$V_n\le \frac{{\overline{\mathrm{\Lambda }}}_n}{\kappa }+\left(V_n\left(0\right)-\frac{{\overline{\mathrm{\Lambda }}}_n}{\kappa }\right)e^{-\kappa t}+\tau$$

(70)

where $\tau$ denotes the upper bound of $e^{-\kappa t}{\int }_0^t\left(\phi N\left(\xi \right)+1\right)\dot{\xi }{e}^{\kappa \varsigma }d\varsigma$. Moreover, it can be concluded from (73) that all the signals of the closed-loop system are bounded. This completes the proof. □

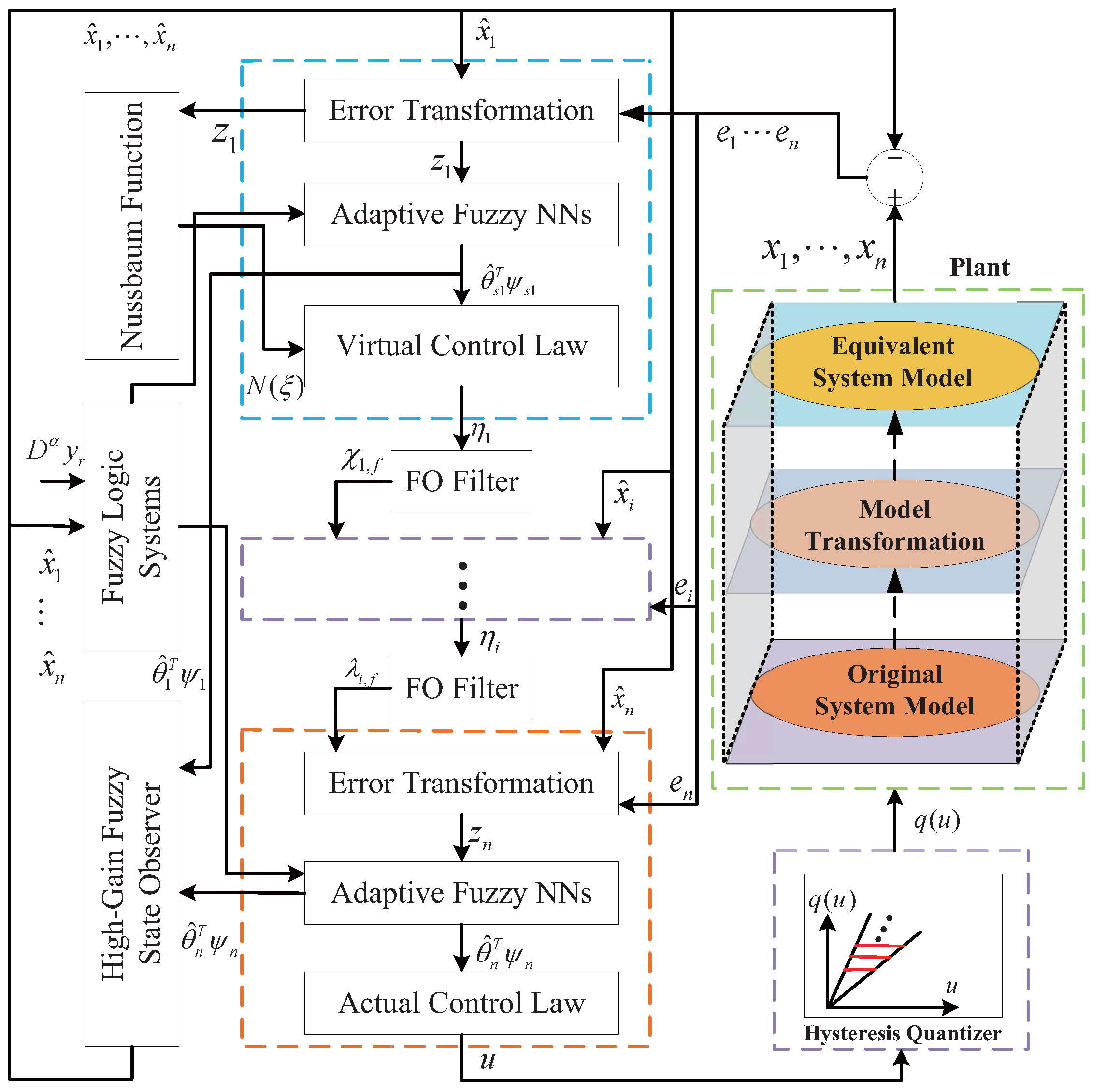
A block diagram is presented in Figure 1 to clarify the structure of the proposed control scheme.

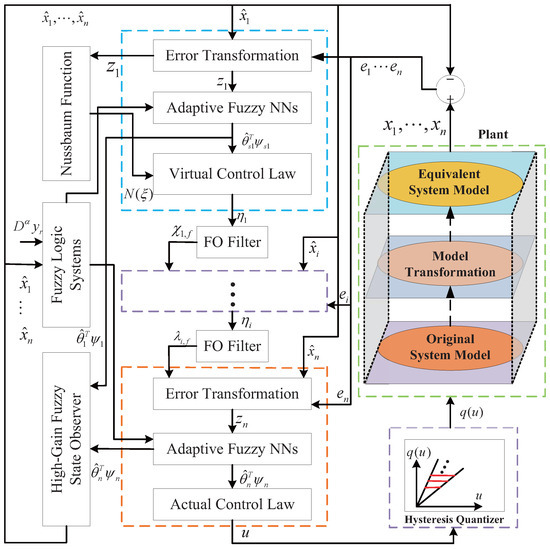
Figure 1. Block diagram of the proposed control scheme.

4. Simulation Verification

To demonstrate the effectiveness of the developed control strategy, a pair of simulation studies are conducted in this section.

4.1. Numerical Example

Example 1.

We consider the following FONTDS with unknown control gains and input quantization.

$$\left\{\begin{array}{c}{D}^{\alpha }{\zeta }_1={\phi }_1{\zeta }_2-0.5{\zeta }_1^2+\frac{{\zeta }_1^3(t-{\tau }_1\left(t\right))}{1+{\zeta }_1^2(t-{\tau }_1\left(t\right))}+d_1(\zeta ,t)\hfill \\ D^{\alpha }{\zeta }_2={\phi }_{2}q\left(u\right)+{\zeta }_1{\zeta }_2^2+\frac{{\zeta }_1^4(t-{\tau }_2\left(t\right))sin\left({\zeta }_2\right)}{1+{\zeta }_1^2(t-{\tau }_2\left(t\right))}+d_2(\zeta ,t)\hfill \\ y={\zeta }_1,\hfill \end{array}\right.$$

(71)

where $\alpha =0.9,{\phi }_1=1.5,{\phi }_2=2,d_1(\zeta ,t)=0.2sin\left(t\right)+0.1sin\left({\zeta }_1{\zeta }_2\right),d_2(\zeta ,t)=0.3cos\left(1.5t\right)+$ $0.1sin\left({\zeta }_1^2{\zeta }_2\right),{\tau }_1\left(t\right)=0.2+0.2sin\left(t\right),{\tau }_2\left(t\right)=0.1+0.1sin\left(t\right)$.

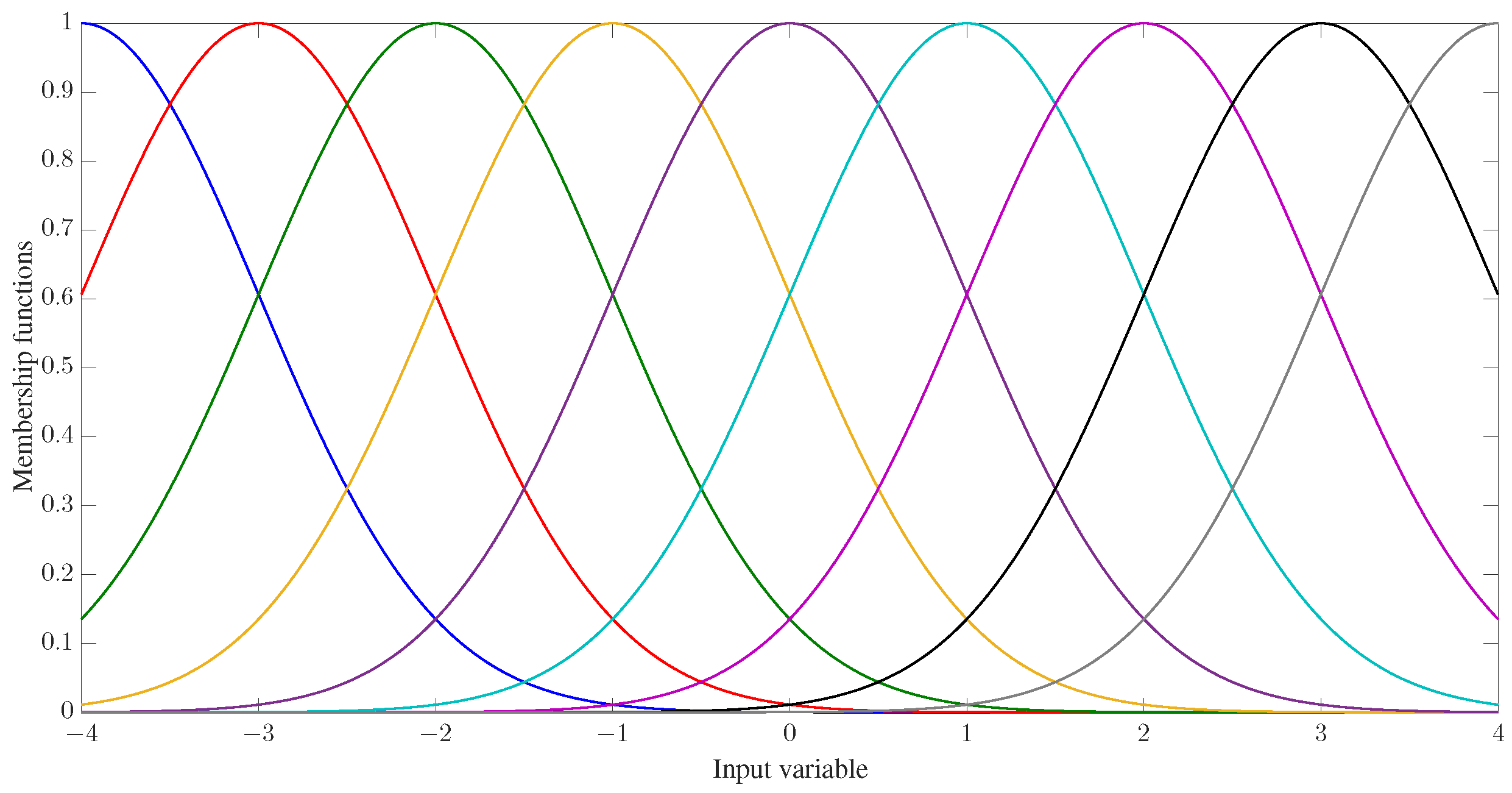
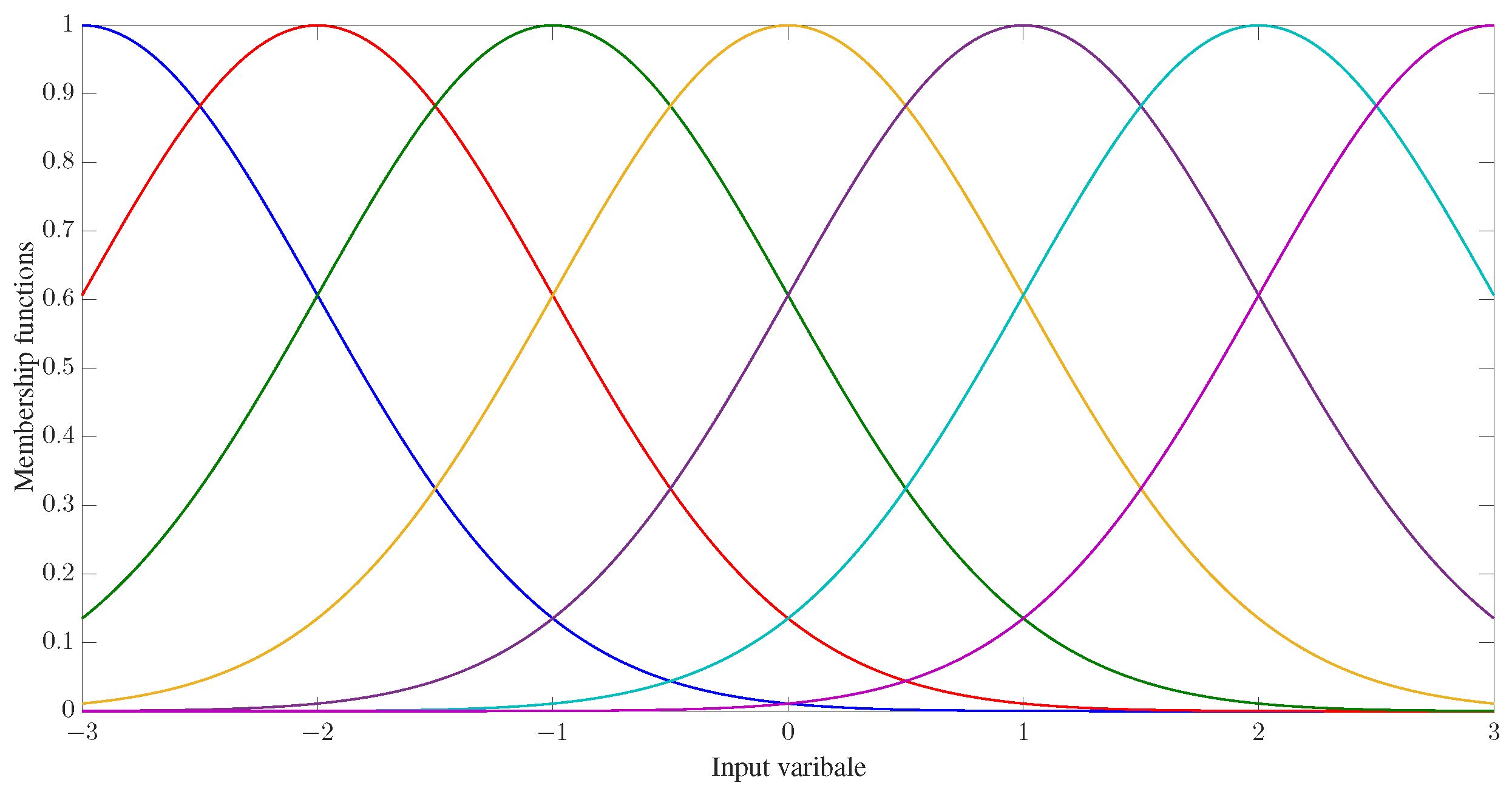
For each variable input into the FLS, we define nine Gaussian membership functions (GMFs) as: ${\mu }_{F_1^1}\left(X_1\right)=exp\left[\frac{-{(X_1-i+5)}^2}{4}\right]$ and ${\mu }_{F_1^2}\left(X_2\right)=exp\left[\frac{-{(X_2-i+5)}^2}{4}\right]$ with $i=1,2,\dots ,9$, uniformly distributed on $\left[-4,4\right]$, as demonstrated in Figure 2, where $X_1=[x_1,y_d,D^{\alpha }{y}_d]$, $X_2=[{\widehat{x}}_1,{\widehat{x}}_2]$, and ${\widehat{x}}_i$ is the estimate of the system state ($x_i=\frac{{\zeta }_i}{{\phi }_{i\sim n}}$).

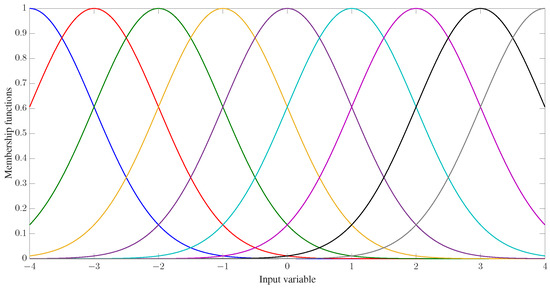
Figure 2. Membership functions of the FLSs.

The initial conditions are set as: ${\zeta }_1\left(0\right)=0.1,{\zeta }_2\left(0\right)=-0.2,{\widehat{\zeta }}_1\left(0\right)=0.2,{\widehat{\zeta }}_2\left(0\right)=-0.1,{\widehat{\theta }}_{s1}\left(0\right)={\widehat{\theta }}_1\left(0\right)={\widehat{\theta }}_2\left(0\right)=0$, and $y_d=sin\left(0.5t\right)$. To verify the effect of the selection of design parameters on system performance, we investigate the following three cases.

Case 1.

$k_1=k_2=15,a_1=a_2=5,\delta =0.6,\rho =0.25,\iota =0.01,\mu =2,L_1=15,L_2=10,{\varsigma }_1=0.02$.

Case 2.

$\delta =0.75,\rho =\frac{1}{7}$, and the other design parameters are the same as in Case 1.

Case 3.

$k_1=k_2=30,\mu =4$, and the other parameters are the same as in Case 1.

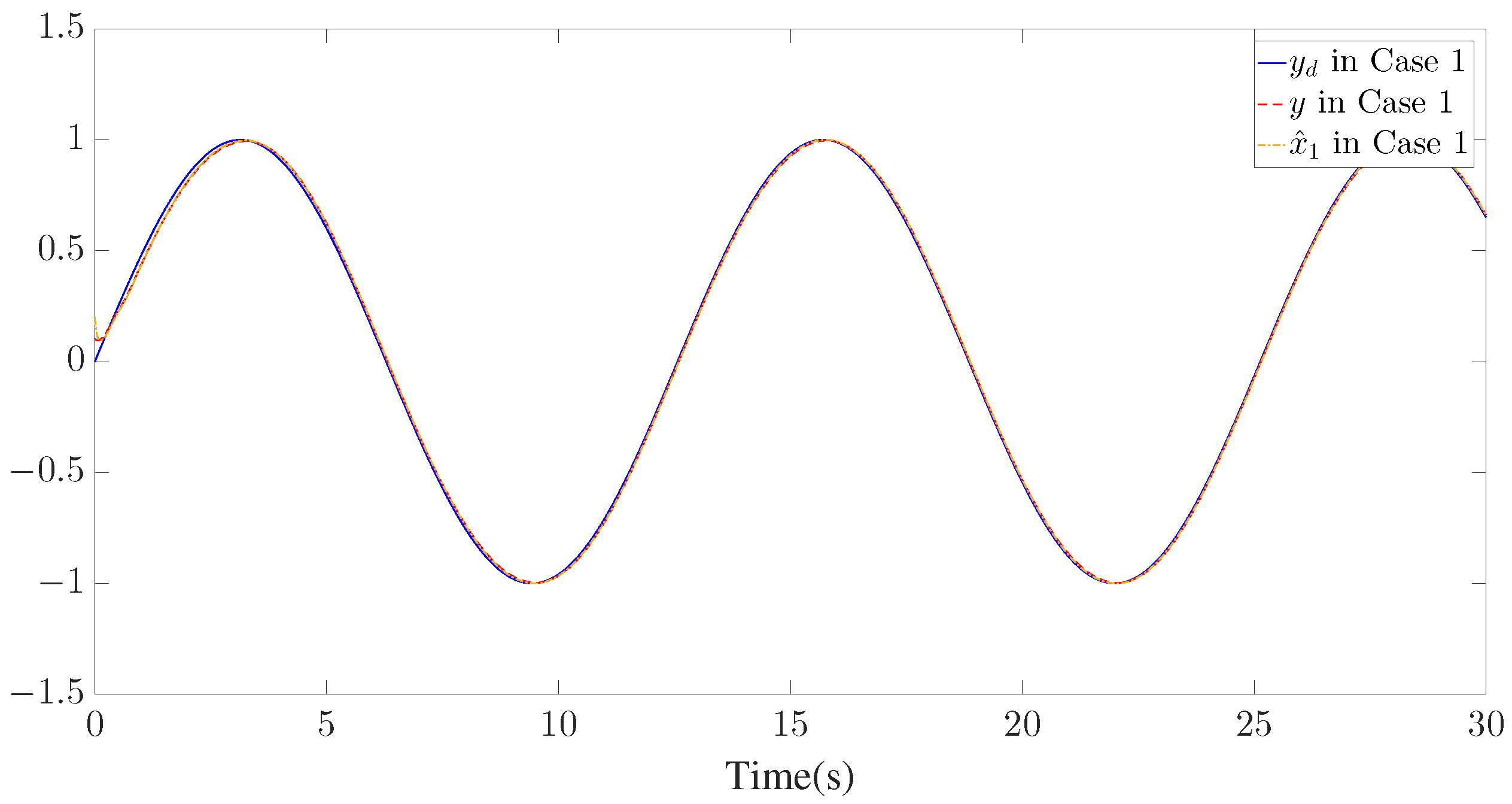
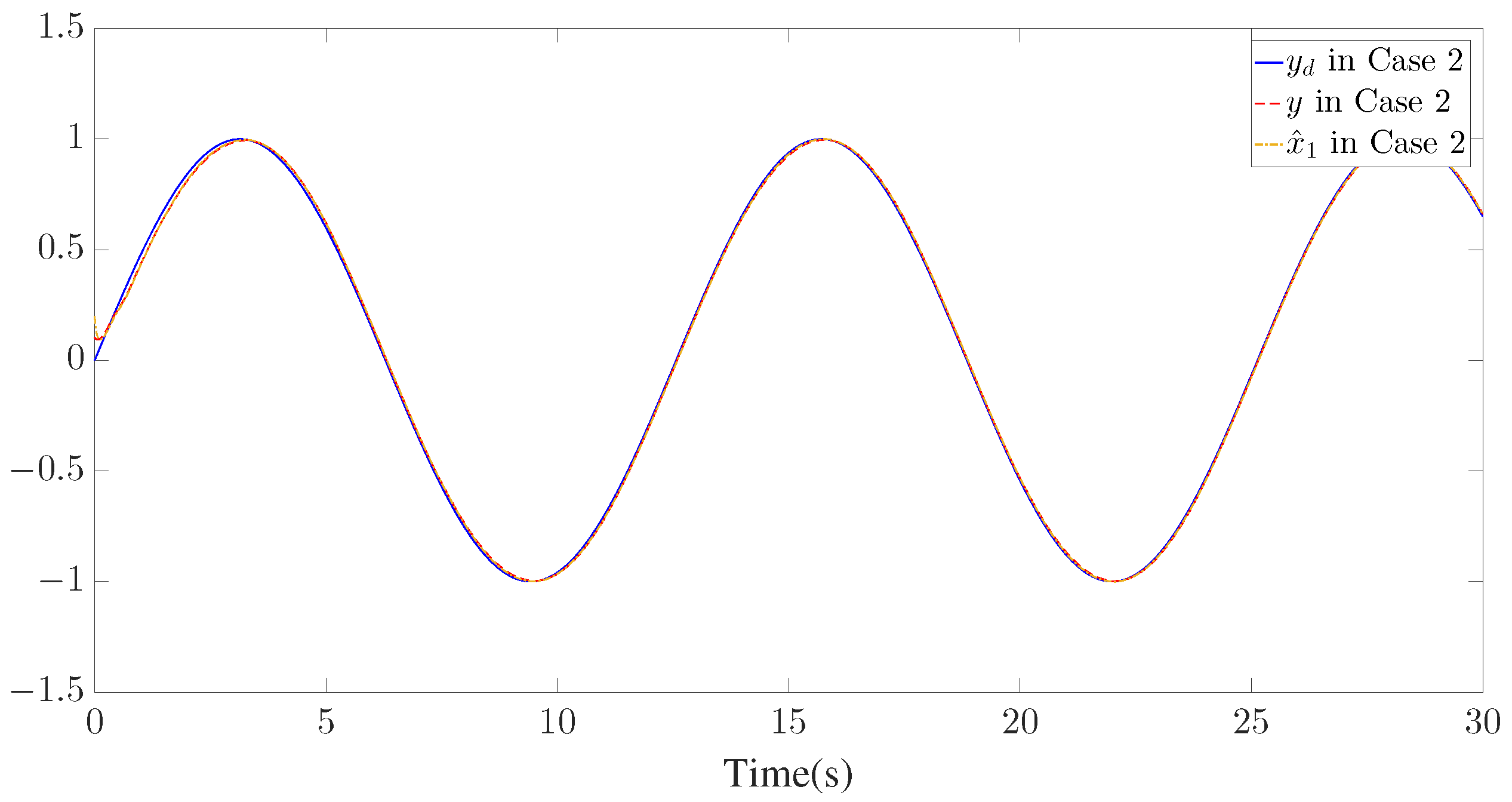
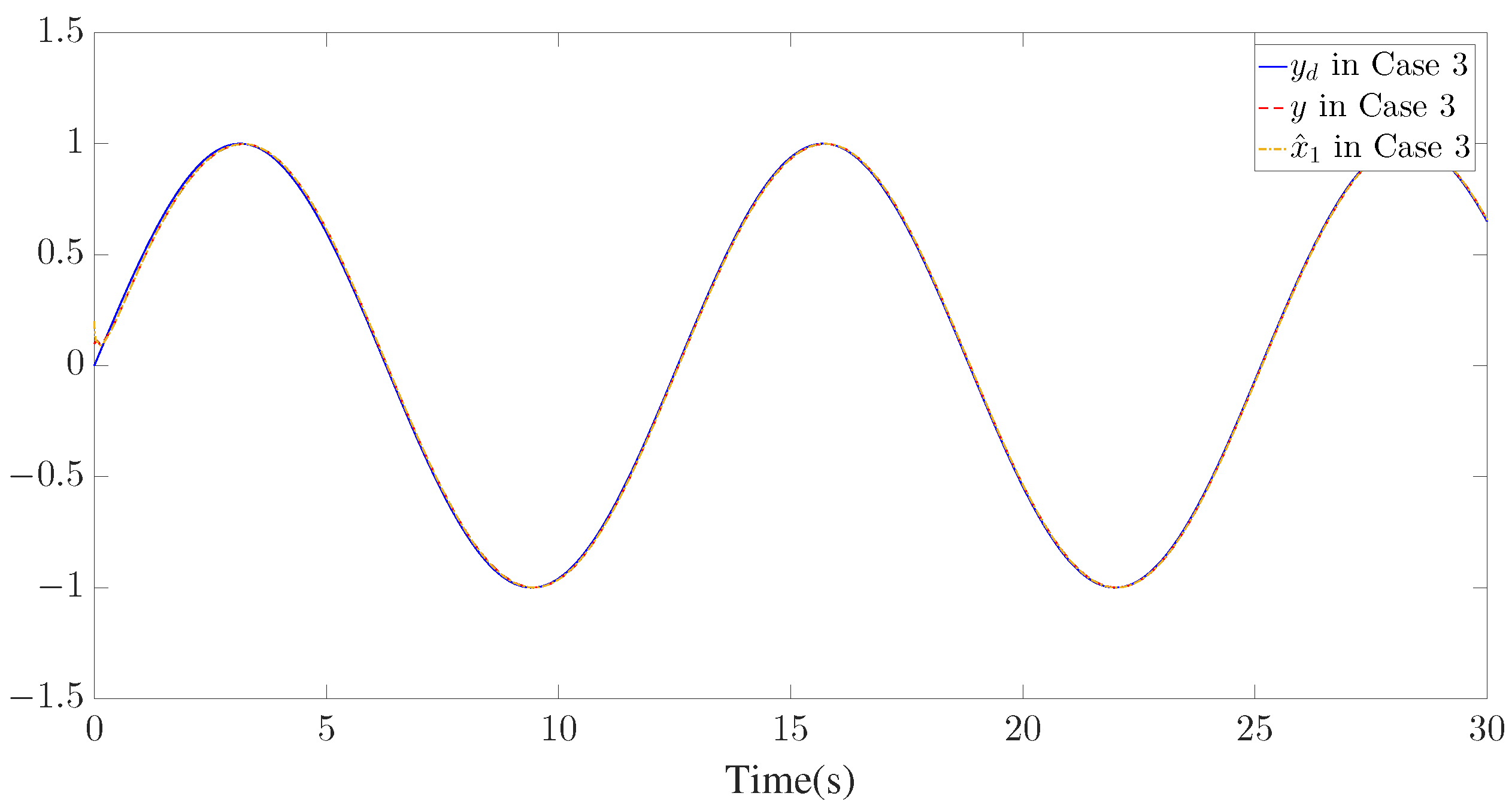
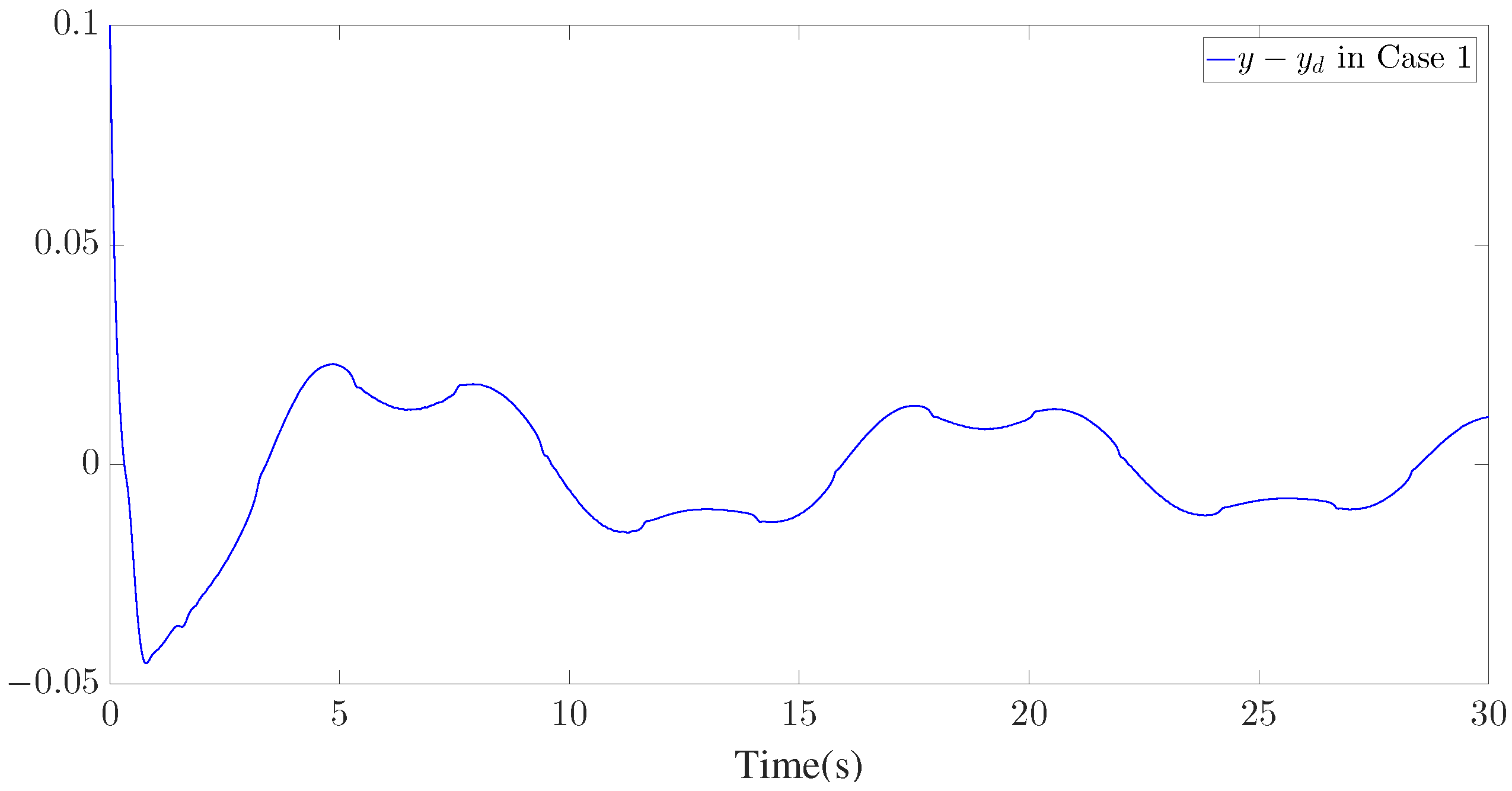
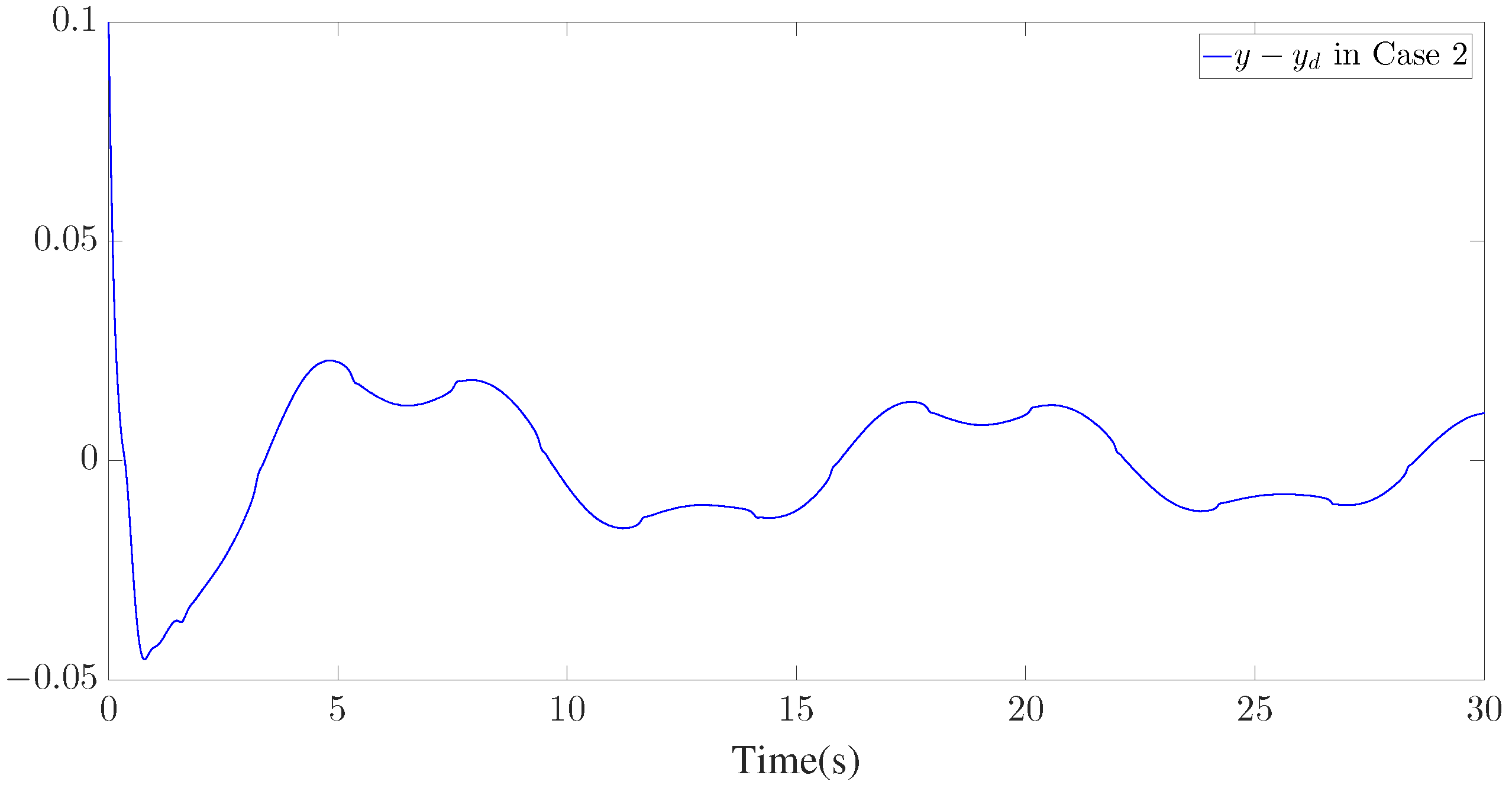
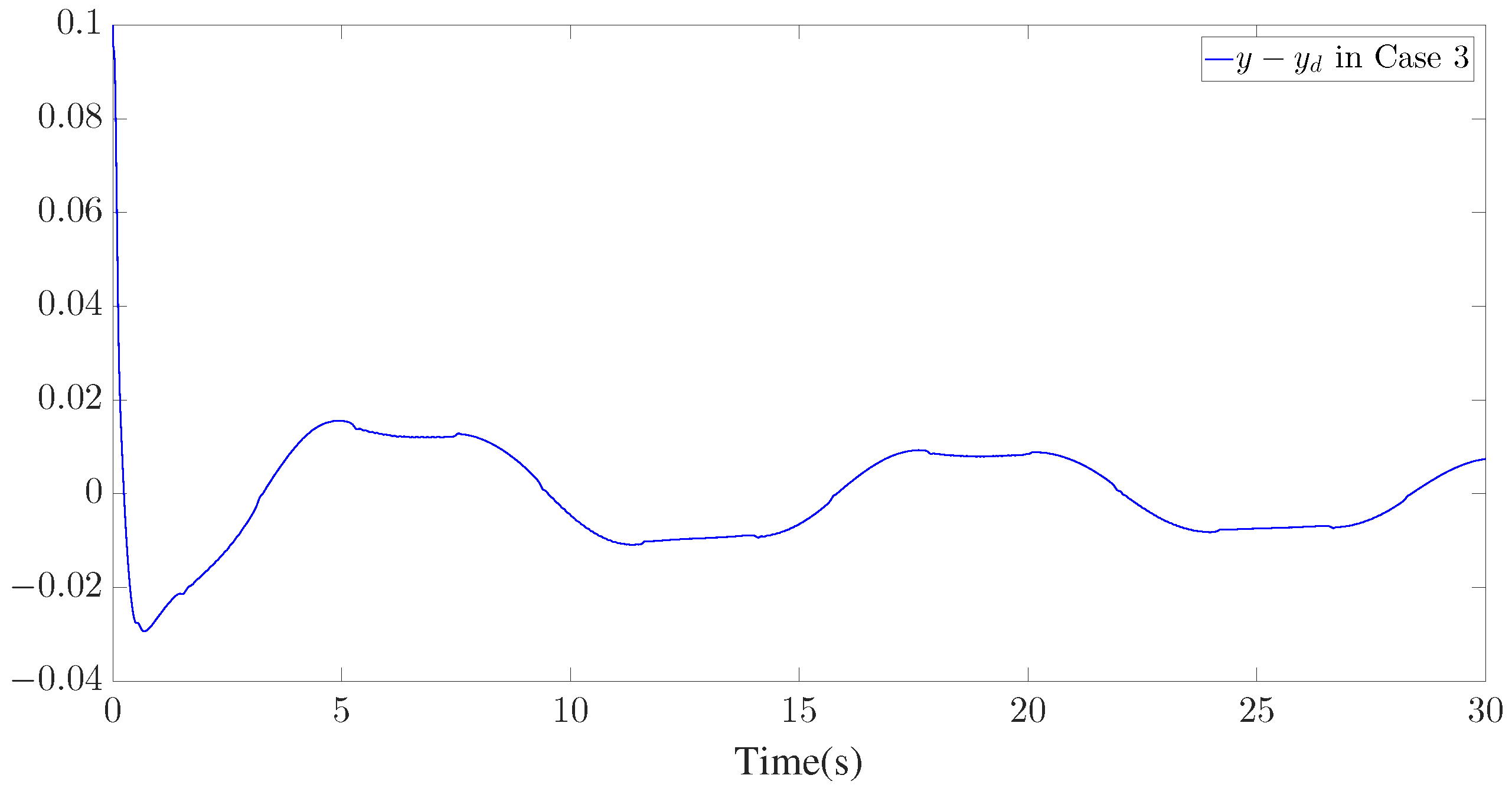
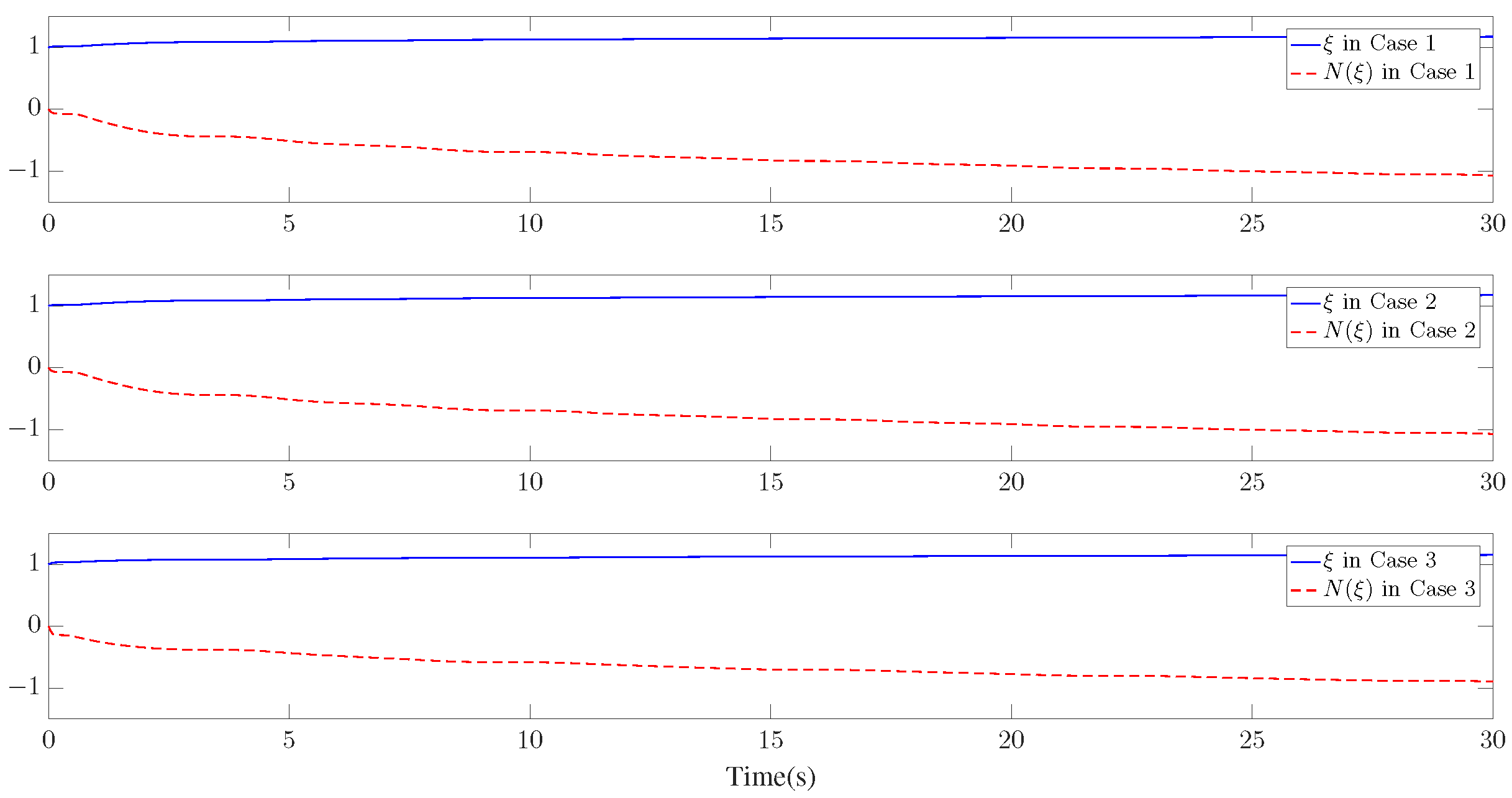
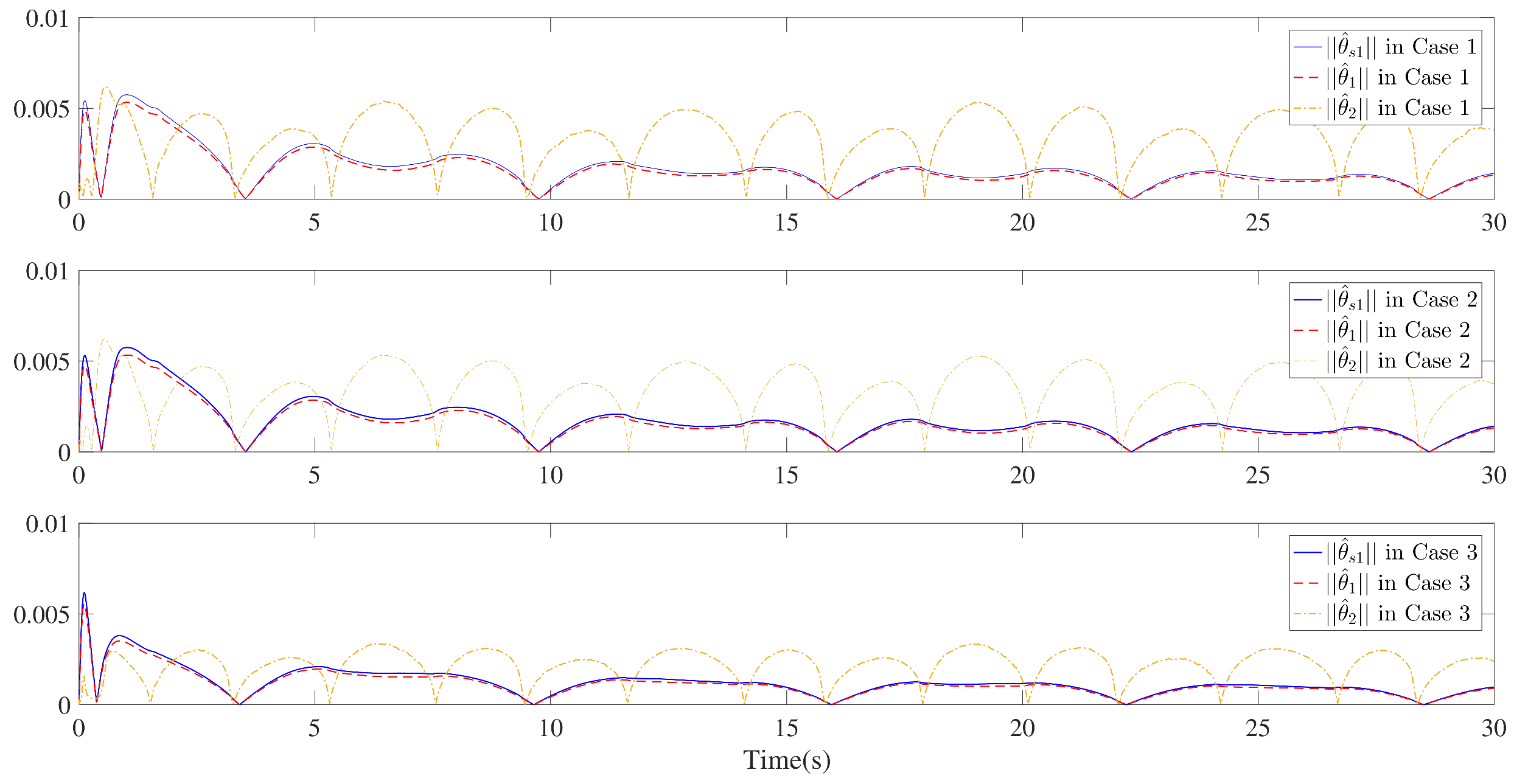
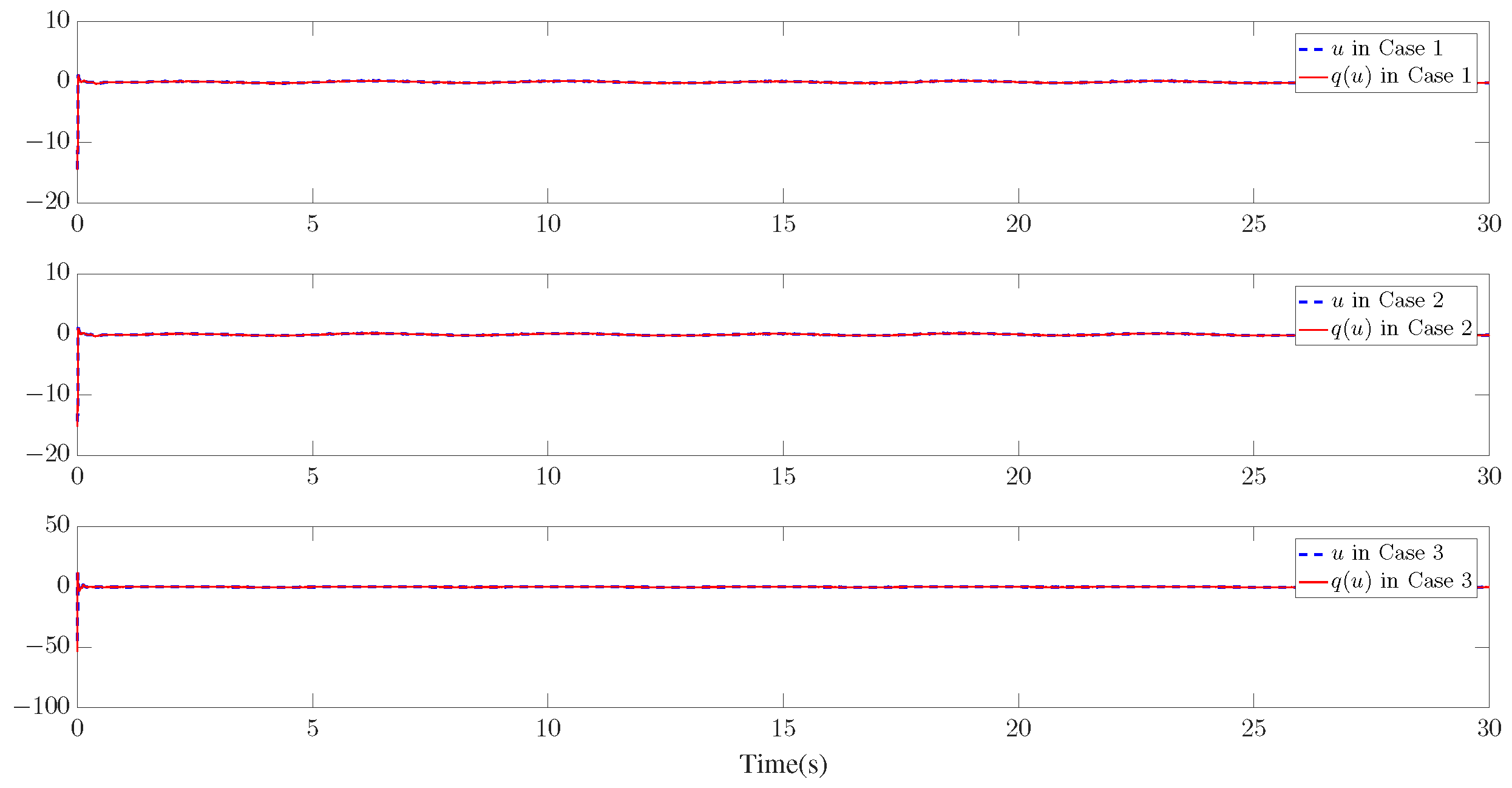
The simulation results are presented in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. Figure 3, Figure 4 and Figure 5 display the time response of the reference signal ($y_d$), system output ($x_1$), and its estimation (${\widehat{x}}_1$), respectively, for each of the three cases. The curves of the tracking error ($y-y_d$) are shown in Figure 6, Figure 7 and Figure 8.

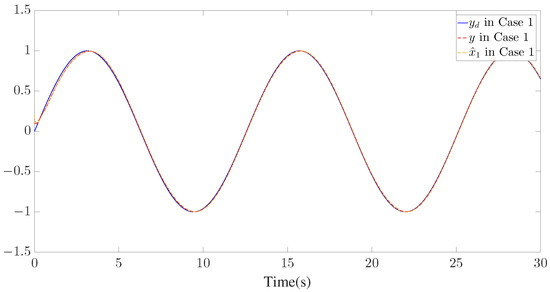
Figure 3. Trajectories of $y_d,y$, and ${\widehat{x}}_1$ for Case 1.

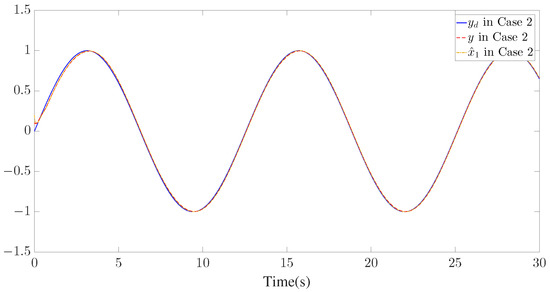
Figure 4. Trajectories of $y_d,y$, and ${\widehat{x}}_1$ for Case 2.

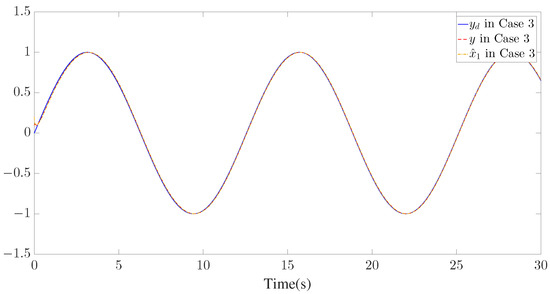
Figure 5. Trajectories of $y_d,y$, and ${\widehat{x}}_1$ for Case 3.

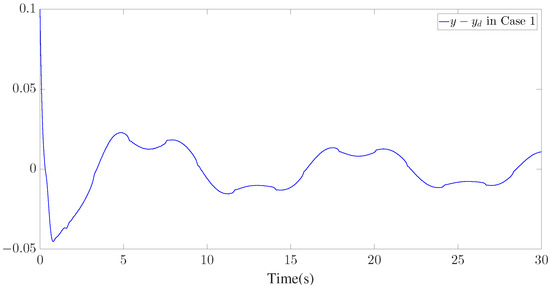
Figure 6. Tracking error of $y-y_d$ for Case 1.

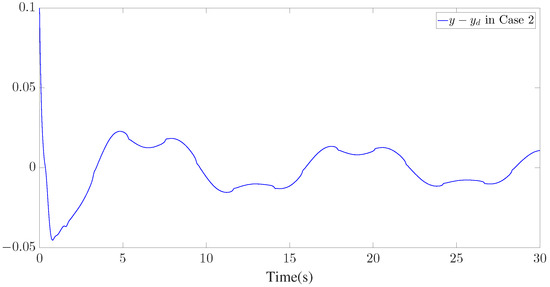
Figure 7. Tracking error of $y-y_d$ for Case 2.

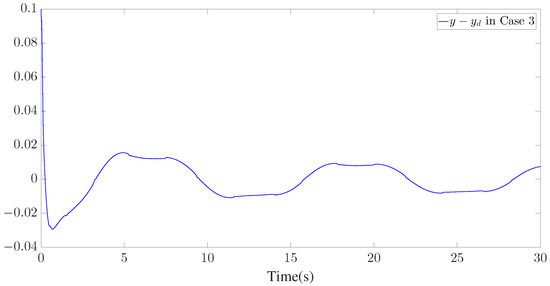
Figure 8. Tracking error of $y-y_d$ for Case 3.

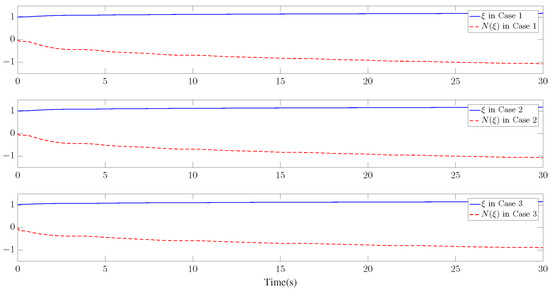
Figure 9. Trajectories of $\xi$ and $N\left(\xi \right)$ for the three cases.

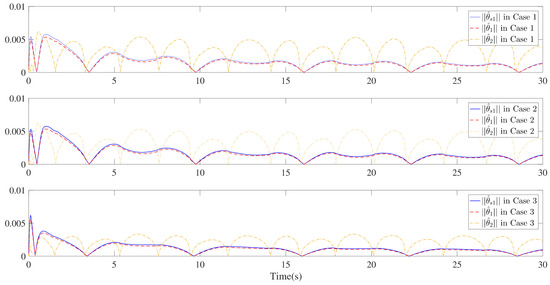
Figure 10. Trajectories of $\left|\right|{\widehat{\theta }}_{s1}\left|\right|$ and $\left|\right|{\widehat{\theta }}_i\left|\right|(i=1,2)$ for the three cases.

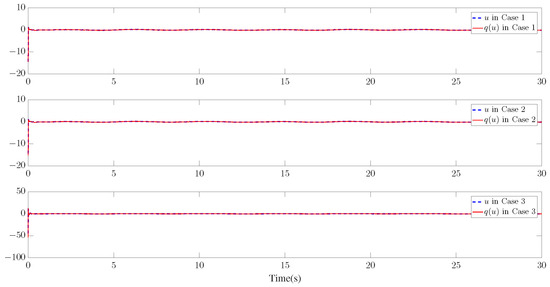
Figure 11. Trajectories of u and $q\left(u\right)$ for the three cases.

Furthermore, three kinds of performance index—integral absolute error (IAE), integral time-weighted absolute error (ITAE), and integral square error (ISE)—are introduced to quantify the tracking performance by choosing different control parameters. It can be concluded from Figure 6, Figure 7 and Figure 8 and Table 1 that better tracking performance can be achieved by increasing parameters $k_i$ and ${\mu }_i$. Meanwhile, it is easily observed that the tracking performance is degraded by increasing the quantization parameter ($\delta$), which also confirms that the larger the quantization parameter ($\delta$), the coarser the quantizer. The trajectories of the Nussbaum parameters ($\xi ,N\left(\xi \right)$) and adaptive parameters ($\left|\right|{\widehat{\theta }}_{s1}\left|\right|,\left|\right|{\widehat{\theta }}_i\left|\right|(i=1,2)$) are depicted in Figure 9 and Figure 10, respectively. The curves of the control signal (u) and the quantized control signal ($q\left(u\right)$) are presented in Figure 11. Although the tracking accuracy can be effectively enhanced by increasing $k_i$, it follows from Figure 11 that more efforts need to be dedicated to this task. Therefore, a relative tradeoff between tracking performance and control cost can be achieved by selecting appropriate design parameters. In addition, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 prove that the boundedness of the resulting signals can be guaranteed.

Table 1. Performance comparisons among different methods.

Performance Index	Item	Case 1	Case 2	Case 3
IAE	${\int }_0^T\left|z_1\left(t\right)\right|dt$	0.4701	0.4704	0.3675
ITAE	${\int }_0^{T}t\left|z_1\left(t\right)\right|dt$	4.241	4.244	3.096
ISE	${\int }_0^T{z}_1^2\left(t\right)dt$	0.017	0.017	0.0138

To further illustrate the validity and the practical potential of our method, an application example is considered in Example 2.

4.2. Application Example

Example 2.

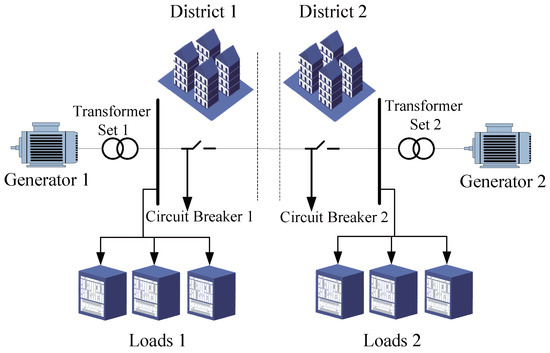
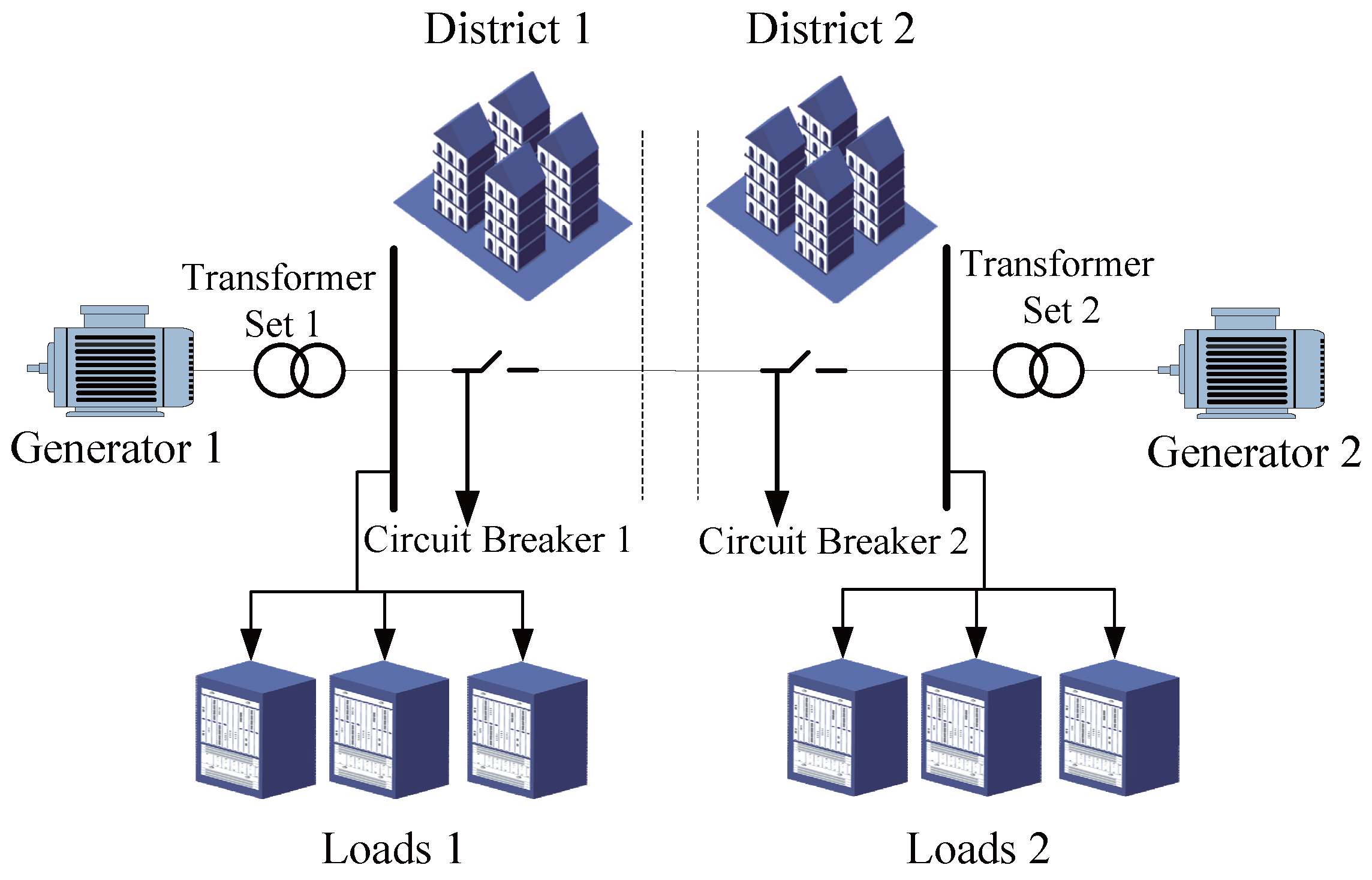
We consider the single-machine-infinite-bus (SMIB) power system shown in Figure 12. According to [44], the mathematical model of the SMIB power system can be described by the following swing equation:

$$M\ddot{\theta }+D\dot{\theta }+P_{E}sin\theta =P_M$$

(72)

where θ is the relative angle in rads, $\dot{\theta }=\omega$ denotes the relative speed in rad/s between the generator ($G_1$) and $G_2$, M denotes the moment of inertia in s, D represents the damping coefficient in p.u., $P_E$ is the maximum power of the generator in p.u., and $P_M=Asin\left(\mathrm{\Omega }t\right)$ represents the power of the machine in p.u.

Figure 12. Diagram of the SMIB power system.

Then, by defining $\theta =x_1,\omega =x_2$, the SMIB power system can be rewritten as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {\dot{x}}_1=x_2\hfill \\ & {\dot{x}}_2=-a{x}_2-bsin\left(x_1\right)+fsin\left(\mathrm{\Omega }t\right)\hfill \end{array}\right.\end{array}$$

(73)

where $a=\frac{D}{M}=0.5,b=\frac{P_E}{M}=1,\mathrm{\Omega }=1$, and $f=\frac{A}{M}=2.66$ are system parameters.

Furthermore, considering that the fractional-order model can provide a more accurate description of physical behavior and the actual system [45], the fractional-order model of the SMIB power system with input quantization and time-varying delays can be expressed as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& D^{\alpha }{x}_1=x_2+\frac{x_1^3(t-{\tau }_1\left(t\right))}{1+x_1^2(t-{\tau }_1\left(t\right))}+d_1(x,t)\hfill \\ & D^{\alpha }{x}_2=-a{x}_2-bsin\left(x_1\right)+fsin\left(\mathrm{\Omega }t\right)++\frac{x_1^4(t-{\tau }_2\left(t\right))sin\left(x_2\right)}{1+x_1^2(t-{\tau }_2\left(t\right))}+d_2(x,t)\hfill \end{array}\right.\end{array}$$

(74)

where $\alpha =0.95$ represents the fractional order, and $d_i(x,t)$ denotes the disturbance term with $i=1,2$.

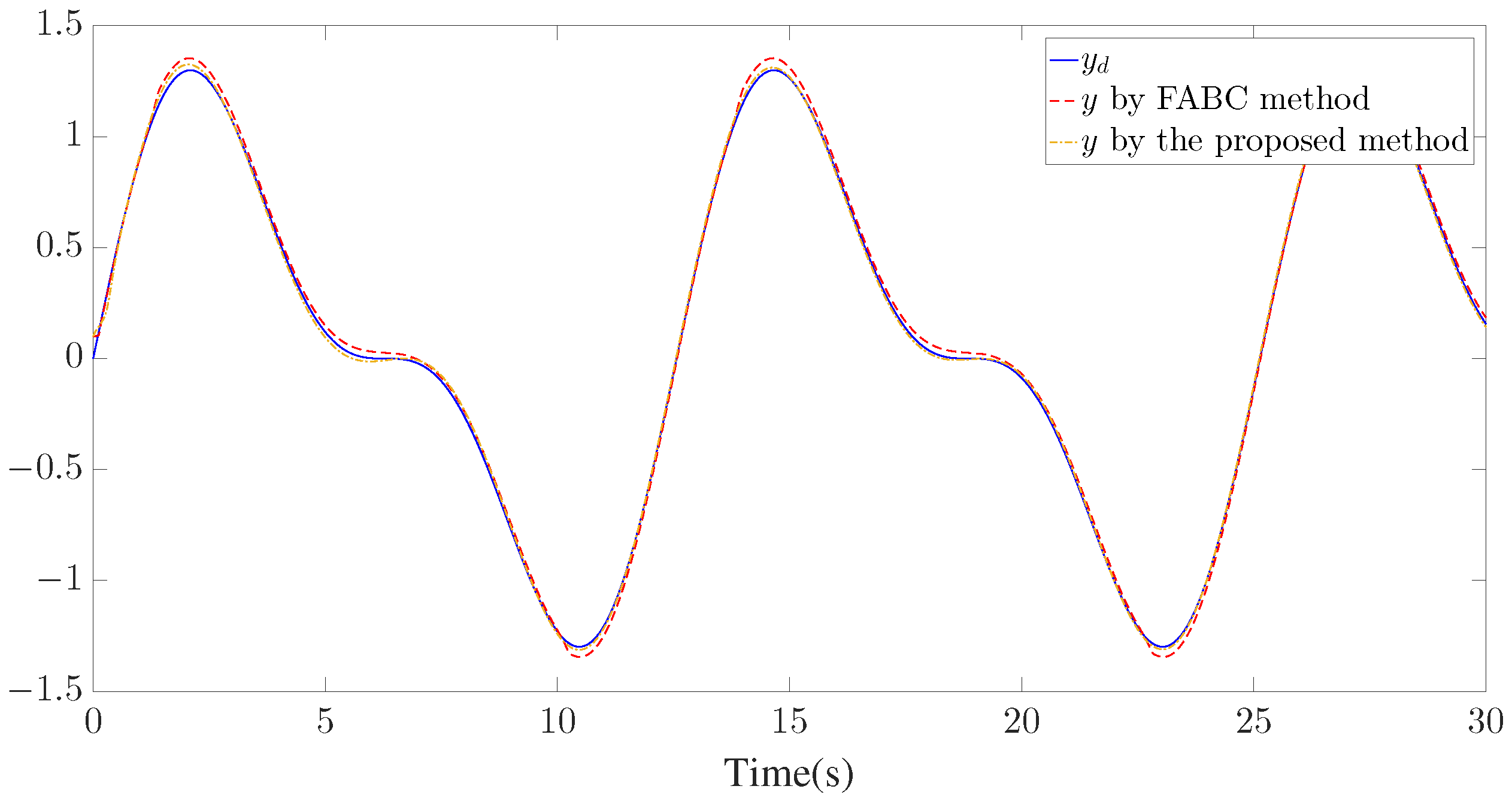
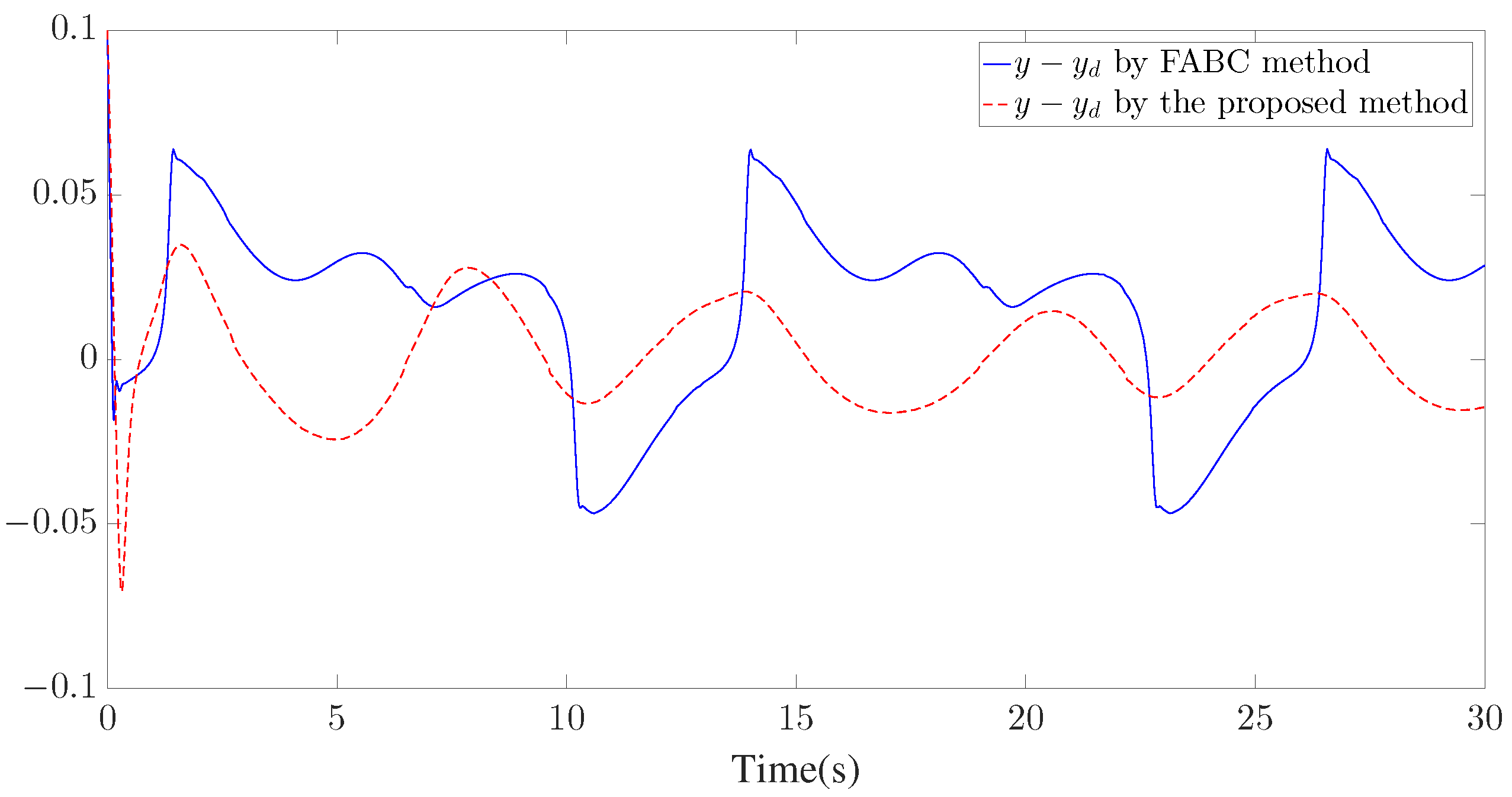
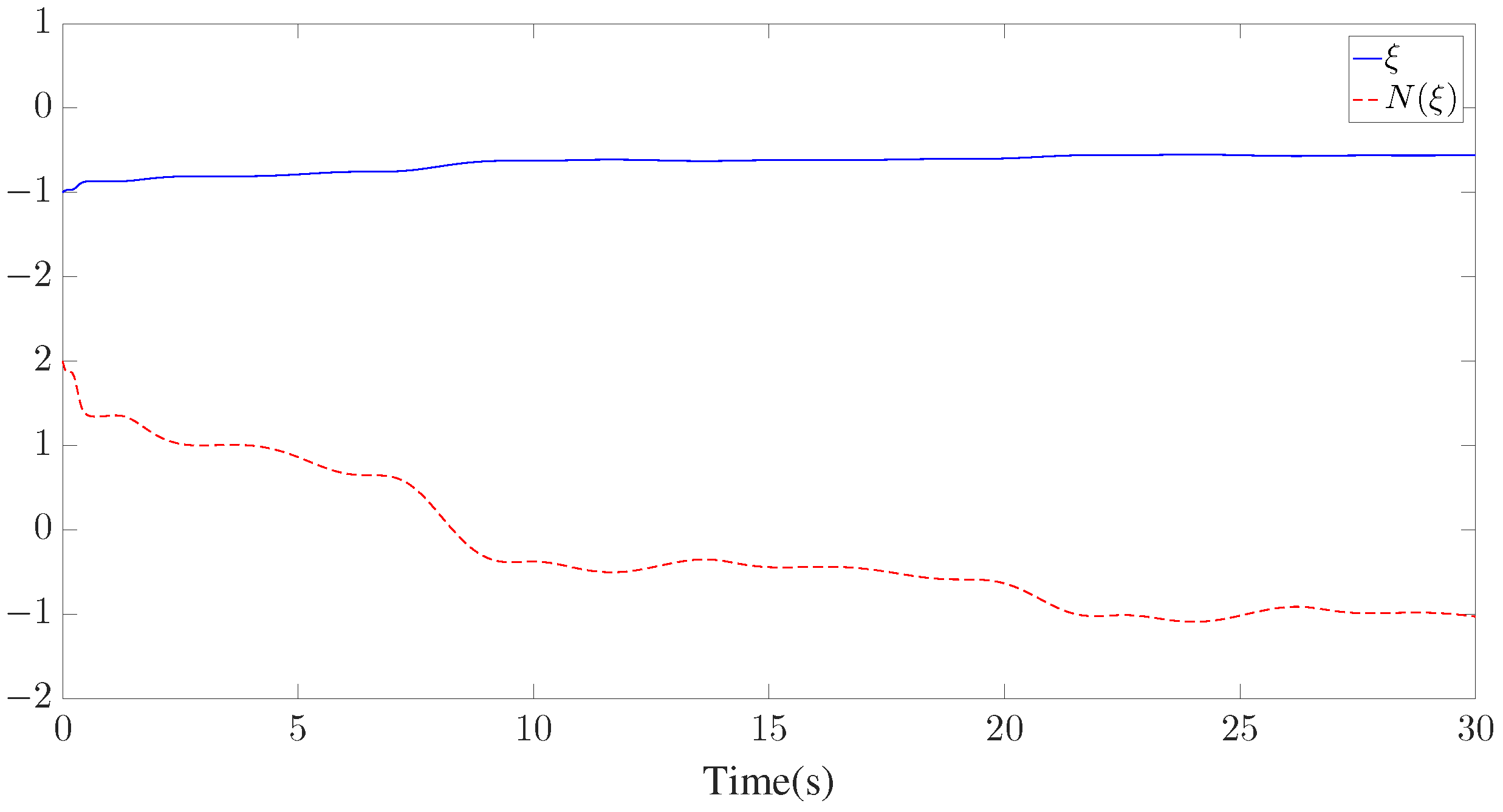
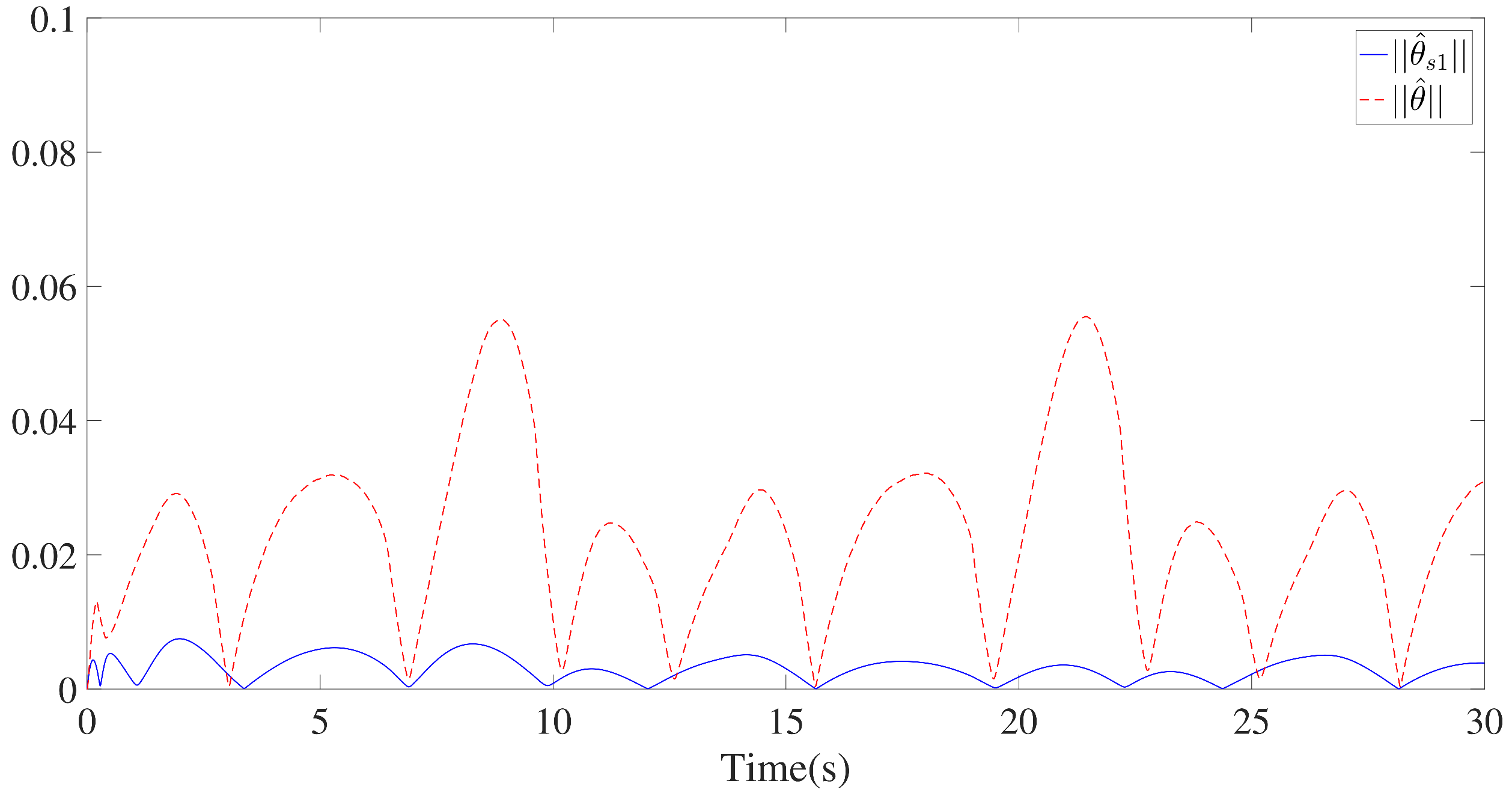
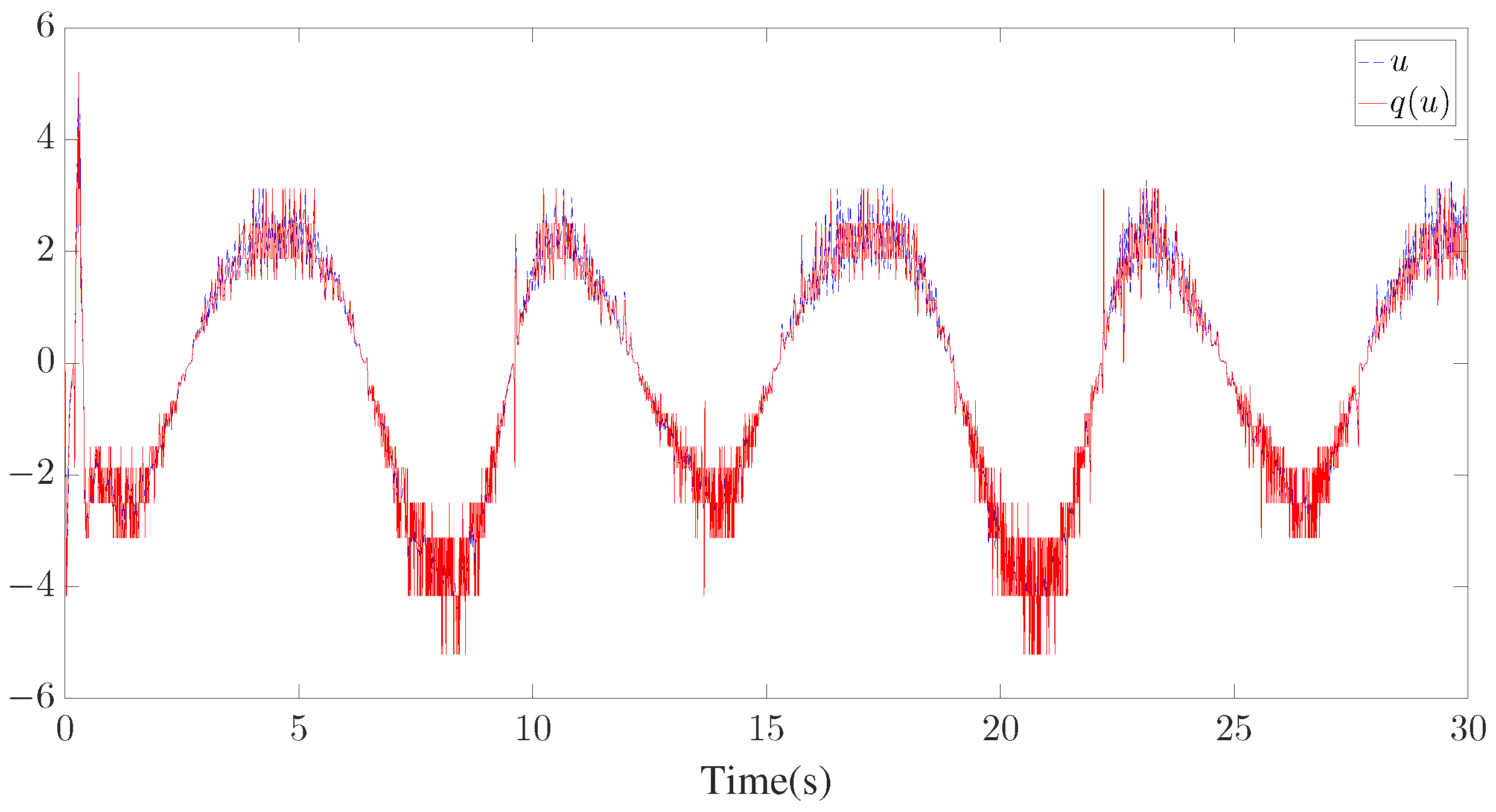
The control parameters, initial conditions, and disturbances are provided in Table 2. Similar to Example 1, seven GMFs uniformly distributed on $\left[-3,3\right]$ are defined for fuzzy approximation as shown in Figure 13. Furthermore, the fuzzy adaptive backstepping control (FABC) method proposed in [8] is used to show the superiority of the proposed method. The comparative tracking performance results are exhibited in Figure 14 and Figure 15. Figure 14 displays the trajectories of the reference trajectory ($y_d$) and the system output (y). Figure 15 depicts the time response of tracking error ($y-y_d$) under different control methods. Figure 14 and Figure 15 show that better tracking performance can be achieved by using the proposed method in comparison to the FABC method proposed in [8]. The curves of parameter $\xi$ and the Nussbaum function ($N\left(\xi \right)$) are plotted in Figure 16. The trajectories of adaptive parameters ($\left|\right|{\widehat{\theta }}_{s1}\left|\right|,\left|\right|\widehat{\theta }\left|\right|$) and control signals ($u,q\left(u\right)$) are shown in Figure 17 and Figure 18, respectively.

Table 2. Selection of simulation parameters.

Design Parameters	Disturbance Terms
$k_1=k_2=30,a_1=a_2=5,\iota =0.01$, $\delta =0.6,\rho =0.25,\mu =2,L_1=5,L_2=10$, ${\tau }_1=0.5+0.2sin\left(t\right),{\tau }_2=0.3+0.1sin\left(t\right)$.	$d_1(x,t)=0.3sin\left(1.5t\right)+0.2cos\left(x_1{x}_2\right)$, $d_2(x,t)=0.2cos\left(1.5t\right)+0.1sin\left(x_1^2{x}_2\right).$
Initial Conditions
$x_1\left(0\right)=0.1,x_2\left(0\right)=-0.1,{\widehat{x}}_1\left(0\right)={\widehat{x}}_2\left(0\right)=0,{\widehat{\theta }}_{s1}\left(0\right)=\widehat{\theta }\left(0\right)=0.$
Reference Signal
$y_r=0.5sin\left(t\right)+sin\left(0.5t\right)$

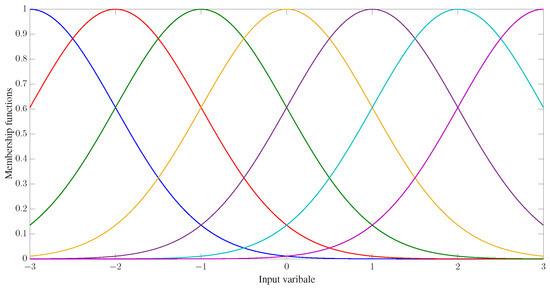
Figure 13. Membership functions of the FLSs.

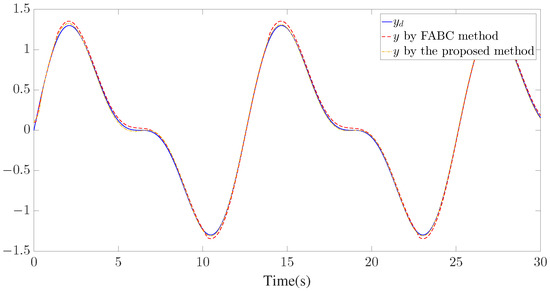
Figure 14. Trajectories of $y_d$ and y.

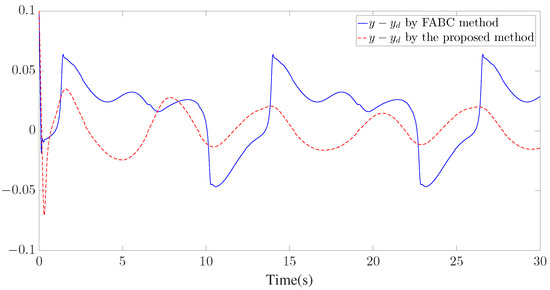
Figure 15. Trajectory of $y-y_d$.

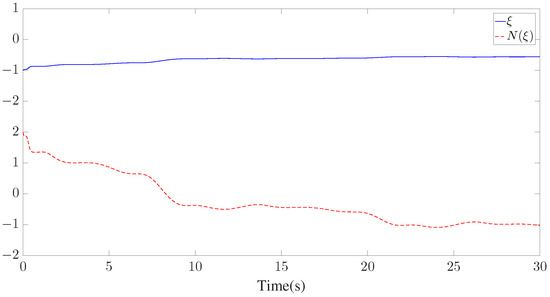
Figure 16. Trajectories of $\xi$ and $N\left(\xi \right)$.

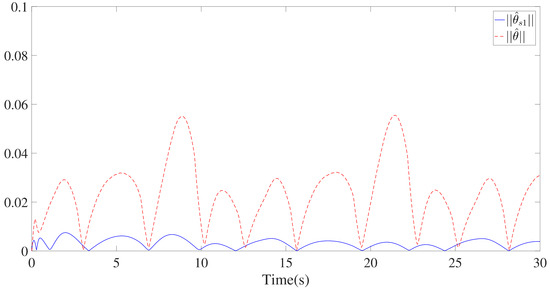
Figure 17. Trajectories of $\left|\right|{\widehat{\theta }}_{s1}\left|\right|$ and $\left|\right|\widehat{\theta }\left|\right|$.

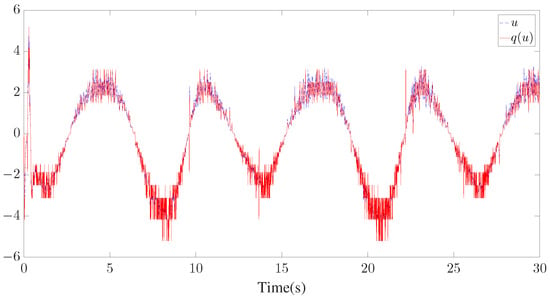
Figure 18. Trajectories of u and $q\left(u\right)$.

5. Conclusions

In this article, a high-gain observer-based adaptive fuzzy quantized tracking control strategy is proposed for FONTDSs with unknown control gains. Based on an indirect Lyapunov method, the Nussbaum gain technique, and the Lyapunov–Krasovskii functional, a recursive control framework was established, and the stability of the closed-loop system was analyzed. In contrast to most existing adaptive control results of fractional-order nonlinear systems, the proposed controller does not depend on information about all system states and control gains, which also ensures that the system output can track the given reference signal, even if time delays and input quantization cause negative effects on tracking performance. The reported simulation results prove that the presented control approach is effective.