Distributed Bipartite Consensus of Multi-Agent Systems via Disturbance Rejection Control Strategy

Abstract

This work aims to focus on analyzing the consensus control problem in cooperative–competitive networks in the occurrence of external disturbances. The primary motive of this work is to employ the equivalent input-disturbance estimation technique to compensate for the impact of external disturbances in the considered multi-agent system. In particular, a suitable low-pass filter is implemented to enhance the accuracy of disturbance estimation performance. In addition, a specific signed, connected, and structurally balanced undirected communication graph with positive and negative edge weights is considered to express the cooperation–competition communication among neighboring agents. The cooperative–competitive multi-agent system reaches its final state with same magnitude and in opposite direction under the considered structurally balanced graph. By utilizing the properties of Lyapunov stability theory and graph theory, the adequate conditions assuring the bipartite consensus of the examined multi-agent system are established as linear matrix inequalities. An illustrative example is delivered at the end to check the efficacy of the designed control scheme.

1. Introduction

The importance of cooperative control for multi-agent systems (MASs) has significantly increased due to its broad utilization in science and engineering domains [1,2,3]. Consensus is a primary concern in cooperative control for MASs. Consensus in MASs is classified as leaderless and leader–follower consensus problems. The leaderless consensus for an uncertain nonlinear MAS with unknown system parameters and unknown control directions was discussed in [4] through using the switching mechanism. The finite-time, fault-tolerant control problem for a consensus of a network of agents with uncertainties was addressed in [5] through utilizing an observer-based technique. For leader-following MASs, the event-triggered consensus protocol developed in [6] was subjected to DoS attacks and replay attacks. By designing a dynamic output-feedback control algorithm, the consensus for high-order nonlinear leader-following MASs was addressed in [7] over a finite-time domain. The authors in [8] proposed mathematical approaches to study the stability, stabilizability, and consensus of discrete-time, linear multi-agent systems.

In addition, the majority of existing results on consensus aim only toward a group of agents with cooperative interactions. However, in some practical scenarios, MASs are modeled with both competitive and cooperative interactions. To deal with such issues, a bipartite consensus is used in which the agents in MASs go to a final state in the opposite direction with the same magnitude. Initially, the author in [9] introduced an appropriate notion for consensus with cooperative and competitive interaction between agents. For a class of homogeneous agents, the bipartite consensus was addressed in [10] through using a distributed feedback controller subject in the low gain feedback approach and input saturation. Through using a connected and structurally balanced network topology, the authors in [11] discussed the bipartite consensus for a network of agents subjected to logarithmic quantization. To achieve bipartite consensus for single-integrator MASs, the authors in [12] derived the necessary and sufficient conditions in the occurrence of measurement noises. The adaptive bipartite consensus was addressed in [13] for second-order MASs under the influence of unknown external disturbances. The bipartite consensus was investigated in [14] for high-order leader following MASs subject to exogenous disturbances. The bipartite consensus was discussed in [15] for networked robotic systems with quantization, input disturbances and parametric uncertainties. Through using the pinning control technique, the finite-time bipartite consensus for a multi-agent network was studied in [16] with the aid of detail-balanced antagonistic interactions.

It should be noted that disturbances are naturally arising phenomena in many practical situations that may produce a conflicting consequence on system stability. The occurrence of disturbances may affect control systems in different ways such as production quality degradation, control device malfunctioning, etc. It was noted that various disturbance rejection techniques were developed to suppress the impacts caused by disturbances. In recent years, many researchers have focused on the estimation and rejection approach for unknown disturbances. It is important to note that equivalent-input disturbance (EID) is an efficient technique that was developed to construct an EID estimator that evaluates and rejects the impact of external disturbances. For nonlinear dynamical systems, the authors in [17] presented an EID estimator to estimate and reject the occurrence of disturbances. The authors in [18] used an EID-approach to reject both unmatched and matched disturbances for dynamical systems with time delay. The disturbance rejection problem was studied in [19] for a modified repetitive-control system through using an improved EID scheme. Disturbance rejection was addressed in [20] for a class of linear singular systems through using the modified repetitive control technique. The authors in [21] developed an EID-based sliding mode investment policy for T-S fuzzy stochastic financial systems to reject unpredictable investment fluctuations. In [22], the authors developed an improved EID estimator for a networked multi-axis motion control system to suppress the overall effects of exogenous disturbance in the occurrence of time-varying delays. As far as we know, the disturbance rejection for MASs with antagonistic interactions has not yet been completely analyzed and this serves as a inspiration for the present work.

This paper analyzes the disturbance rejection problem for a bipartite consensus of linear MASs through using an EID approach. The main features of this paper are as follows.

(i)

The bipartite consensus was studied for continuous-time linear MASs under the impact of external disturbances. A signed graph was employed to portray the cooperative and competitive communication among the agents, and the graph therein was structurally balanced.

(ii)

Using an observer-based approach and by designing a proper low-pass filter, the EID estimator was designed to estimate the disturbances.

(iii)

Through using the properties of Lyapunov stability and linear matrix inequalities (LMIs), sufficient conditions ensure that the bipartite consensus of the agents in the MASs are derived. To demonstrate the viability of the developed control protocol, an illustrative example is offered in the last section.

The subsequent sections of this work are as follows: Section 2 provides the preliminaries and system description. Section 3 gives the adequate conditions for a bipartite consensus of the examined MAS. Section 4 delivers a numerical example to verify the effectiveness of the theoretical results obtained in Section 3.

2. Problem Formulation and Preliminaries

2.1. Graph Theory

A signed undirected graph $\mathfrak{G}=\{\mathcal{H},\mathcal{E},\mathfrak{A}\}$ was chosen to describe the interaction among the agents, where $\mathcal{H}=\{v_1,v_2,\dots ,v_k\}$ denotes the collection of nodes that represent the agents, $\mathcal{E}\subset \mathcal{H}\times \mathcal{H}$ is the set of edges describing the communication between agents and $\mathfrak{A}=\left({\mathtt{a}}_{ij}\right)\in {\mathbb{R}}^{k\times k}$ is the weighted adjacency matrix of $\mathfrak{G}$. Further, ${\mathtt{a}}_{ij}<0$, ${\mathtt{a}}_{ij}>0$ denotes that the communication among the ith and jth agent is antagonistic and cooperative, respectively. Suppose, there is no information flow among agents i and j, then ${\mathtt{a}}_{ij}=0$. Denote $D=diag\left\{{\displaystyle \sum _{j=1}^k}|{\mathtt{a}}_{1j}|,{\displaystyle \sum _{j=1}^k}|{\mathtt{a}}_{2j}|,\dots ,{\displaystyle \sum _{j=1}^k}\left|{\mathtt{a}}_{kj}\right|\right\}$, then $\mathfrak{L}={\left[l_{ij}\right]}_{k\times k}$ is the Laplacian matrix of $\mathfrak{G}$ defined by $\mathfrak{L}=D-\mathfrak{A}$, that is

$$l_{ij}=\left\{\begin{array}{cc}{\displaystyle \sum _{j=1,j\ne i}}\left|{\mathtt{a}}_{ij}\right|,\hfill & \mathrm{if}i=j,\hfill \\ -{\mathtt{a}}_{ij},\hfill & \mathrm{if}i\ne j.\hfill \end{array}\right.$$

Definition 1 

([9]). Let $\mathfrak{G}\left(\mathfrak{A}\right)$ be a signed graph that has a bipartition of the nodes ${\mathcal{H}}_1,{\mathcal{H}}_2$. Suppose that $\mathcal{H}={\mathcal{H}}_1\cup {\mathcal{H}}_2,{\mathcal{H}}_1\cap {\mathcal{H}}_2=\varnothing$ with ${\mathtt{a}}_{ij}\ge 0,\forall v_i,v_j\in {\mathcal{H}}_r(r\in \{1,2\}),{\mathtt{a}}_{ij}\le 0,\forall v_i\in {\mathcal{H}}_r,v_j\in {\mathcal{H}}_s,r\ne s(r,s\in \{1,2\})$, then $\mathfrak{G}\left(\mathfrak{A}\right)$ is said to be structurally balanced; otherwise, it is called structurally unbalanced.

Definition 2 

([23]). The set describing gauge transformation is defined in the following form:

$$\begin{array}{c}\hfill \mathfrak{Q}=\left\{\mathcal{Q}\right|\mathcal{Q}=diag\left\{q\right\},q=[q_1,q_2,\dots ,q_n],q_i\in \{+1,-1\}\}.\end{array}$$

Lemma 1 

([9]). Let $\mathfrak{G}\left(\mathfrak{A}\right)$ be an undirected signed graph that is structurally balanced, then the following statements are true:

(1)

$\exists \mathcal{Q}\in \mathfrak{Q}$ is in such a way that $\mathcal{Q}\mathfrak{A}\mathcal{Q}$ has all non-negative elements,

(2)

$\mathfrak{L}$ has zero as an eigenvalue.

Remark 1. 

The graph $\mathfrak{G}$ considered in this work is structurally balanced and connected. In many practical networks, the signed graph can be bipartitioned into two subgroups, where the edges joining agents within each subgroup have cooperative interactions while the edges joining agents of different subgroups have antagonistic interactions.

2.2. System Description

Let us consider a continuous-time linear MAS containing $\mathcal{K}$ homogeneous agents with external disturbances in the following form:

$$\left\{\begin{array}{c}{\dot{x}}_i\left(t\right)=A{x}_i\left(t\right)+B{u}_i\left(t\right)+D{d}_i\left(t\right),\hfill \\ y_i\left(t\right)=C{x}_i\left(t\right),i=1,2,\dots \mathcal{K}\hfill \end{array}\right.$$

(1)

where $x_i\left(t\right)\in {\mathbb{R}}^n$, $u_i\left(t\right)\in {\mathbb{R}}^m$, $y_i\left(t\right)\in {\mathbb{R}}^s$ and $d_i\left(t\right)\in {\mathbb{R}}^p$ are the state vector, control input vector, output and external disturbance of the ith agent, respectively. Here, the known matrices A, B, C and D are of a proper dimension.

Next, to enhance the disturbance rejection performance, an EID estimator was considered in the control protocol. Let us now consider the state-dependent EID estimator $d_{ie}\left(t\right)$, which generates the same impact on the output as $d\left(t\right)$ does. Then, MAS (1) is written as

$$\left\{\begin{array}{c}{\dot{x}}_i\left(t\right)=A{x}_i\left(t\right)+B{u}_i\left(t\right)+B{d}_{ie}\left(t\right).\hfill \\ y_i\left(t\right)=C{x}_i\left(t\right).\hfill \end{array}\right.$$

(2)

Next, the state observer of MAS (1) used to estimate the EID was modeled as

$$\left\{\begin{array}{c}{\dot{\widehat{x}}}_i\left(t\right)=A{\widehat{x}}_i\left(t\right)+B{u}_{if}\left(t\right)+G[y_i\left(t\right)-{\widehat{y}}_i\left(t\right)],\hfill \\ {\widehat{y}}_i\left(t\right)=C{x}_i\left(t\right),\hfill \end{array}\right.$$

(3)

where ${\widehat{x}}_i\left(t\right)$ represents the observer state, $u_{if}\left(t\right)$ is the control response, ${\widehat{y}}_i\left(t\right)$ is the output of the $i^{th}$ agent and G is the observer gain value to be obtained. Let us now define $u_{if}\left(t\right)$ using the structure shown below:

$$u_{if}\left(t\right)=\mathfrak{K}\sum _{j\in \mathcal{K}}\left|{\mathtt{a}}_{ij}\right|(y_i\left(t\right)-sgn\left({\mathtt{a}}_{ij}\right)y_j\left(t\right)).$$

(4)

Next, the EID estimator ${\widehat{d}}_{ie}\left(t\right)$ was constructed as follows:

$${\widehat{d}}_{ie}\left(t\right)=B^{+}G\left(y_i\left(t\right)-{\widehat{y}}_i\left(t\right)\right)+u_{if}\left(t\right)-u_i\left(t\right),$$

(5)

where ${\widehat{d}}_{ie}\left(t\right)$ is the estimator of EID $d_{ie}\left(t\right)$ and $B^{+}$ is the pseudo inverse of B. A low-pass filter $F\left(s\right)$ was used to establish the accuracy in the estimation, and its state-space representation was designed as

$$\left\{\begin{array}{c}{\dot{x}}_{iF}\left(t\right)=A_F{x}_{iF}\left(t\right)+B_F{\widehat{d}}_{ie}\left(t\right),\hfill \\ {\tilde{d}}_{ie}\left(t\right)=C_F{x}_{iF}\left(t\right),\hfill \end{array}\right.$$

(6)

where $x_{iF}\left(t\right)$, ${\tilde{d}}_{ie}\left(t\right)$ are, respectively, the state of the EID estimator; the filtered disturbance estimate; and $A_F$, $B_F$ and $C_F$ are the known proper dimensional constant matrices. In order to suppress the effect of disturbances in the considered MAS, a modified controller was constructed as

$$u_i\left(t\right)=u_{if}\left(t\right)-{\tilde{d}}_{ie}\left(t\right).$$

(7)

Definition 3 

([24]). The bipartite consensus of MAS (1) was thought to be achieved if the below criterion was fulfilled:

$$\underset{t\to \infty }{lim}\parallel x_i\left(t\right)-{\displaystyle \frac{1}{\mathcal{K}}}\sum _{j=1}^{\mathcal{K}}{q}_i{q}_j{x}_j\left(t\right)\parallel =0,i=1,2,\dots \mathcal{K}.$$

Define $z_i\left(t\right)=x_i\left(t\right)-{\displaystyle \frac{1}{\mathcal{K}}}\sum _{j=1}^{\mathcal{K}}{q}_i{q}_j{x}_j\left(t\right)$. Then, System (1) reaches bipartite consensus if $\underset{t\to \infty }{lim}\parallel z_i\left(t\right)\parallel =0$.

The block diagram of an EID-based control for multi-agent systems is provided in Figure 1. Now, by letting $\Delta x_i\left(t\right)=x_i\left(t\right)-{\widehat{x}}_i\left(t\right)$, and by considering the properties of the Kronecker product to (1), (3) and (6), one can have

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)=& (I_{\mathcal{K}}\otimes A)x\left(t\right)+(\mathfrak{L}\otimes B\mathfrak{K}C)x\left(t\right)-(I_{\mathcal{K}}\otimes B{C}_F)x_F\left(t\right)+(I_{\mathcal{K}}\otimes D)d\left(t\right),\hfill \\ \hfill \dot{\widehat{x}}\left(t\right)=& (I_{\mathcal{K}}\otimes A)\widehat{x}\left(t\right)+(\mathfrak{L}\otimes B\mathfrak{K}C)x\left(t\right)+(I_{\mathcal{K}}\otimes GC)\Delta x\left(t\right),\hfill \\ \hfill {\dot{x}}_F\left(t\right)=& (I_{\mathcal{K}}\otimes A_F)x_F\left(t\right)+(I_{\mathcal{K}}\otimes B_F{C}_F)x_F\left(t\right)+(I_{\mathcal{K}}\otimes B_F{B}^{+}GC)\Delta x\left(t\right),\hfill \\ \hfill z\left(t\right)=& (\mathcal{A}\otimes I_n)x\left(t\right),\hfill \end{array}$$

where $\mathcal{A}=I_{\mathcal{K}}-{\displaystyle \frac{1}{\mathcal{K}}}\mathfrak{U}{\mathfrak{U}}^T\in {\mathbb{R}}^{\mathcal{K}\times \mathcal{K}},\mathfrak{U}=col(q_1,q_2,\dots ,q_{\mathcal{K}}),x\left(t\right)=co{l}_{\mathcal{K}}\left\{x_i\left(t\right)\right\},$ $\widehat{x}\left(t\right)=col\{{\widehat{x}}_1\left(t\right),{\widehat{x}}_2\left(t\right),\dots ,{\widehat{x}}_{\mathcal{K}}\left(t\right)\},$ $x_F\left(t\right)=co{l}_{\mathcal{K}}\{x_{1F}\left(t\right),x_{2F}\left(t\right),\dots ,x_{\mathcal{K}F}\left(t\right)\}$, $\Delta x\left(t\right)=co{l}_{\mathcal{K}}\{\Delta x_1\left(t\right),\Delta x_2\left(t\right),\dots ,\Delta x_{\mathcal{K}}\left(t\right)\},z\left(t\right)=co{l}_{\mathcal{K}}\left\{z_i\left(t\right)\right\}.$

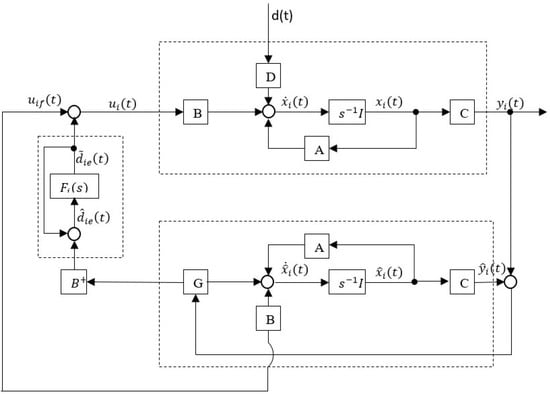
Figure 1. Configuration of EID-based multi-agent control systems.

From Lemma 1, it can be observed that there exists $\mathcal{Q}\in \mathfrak{Q}$, which ensures $\overline{\mathfrak{A}}=\mathcal{Q}\mathfrak{A}\mathcal{Q}$. In addition, $\overline{\mathfrak{A}}$ has only non-negative elements and lets $\overline{\mathfrak{L}}=\mathcal{Q}\mathfrak{L}\mathcal{Q}$ be the Laplacian matrix of the graph $\mathfrak{G}\left(\overline{\mathfrak{A}}\right)$. Next, let us use the transformations $\overline{x}=(\mathcal{Q}\otimes I)x,\check{x}=(\mathcal{Q}\otimes I)\widehat{x},$${\overline{x}}_F=(\mathcal{Q}\otimes I)x_F,\Delta \overline{x}=(\mathcal{Q}\otimes I)\Delta x$. Consequently, we obtain from the aforementioned equations that

$$\begin{array}{cc}\hfill \dot{\overline{x}}\left(t\right)=& (I_{\mathcal{K}}\otimes A)\overline{x}\left(t\right)+(\overline{\mathfrak{L}}\otimes B\mathfrak{K}C)\overline{x}\left(t\right)-(I_{\mathcal{K}}\otimes B{C}_F){\overline{x}}_F\left(t\right)+(I_{\mathcal{K}}\otimes D)\overline{d}\left(t\right),\hfill \\ \hfill \dot{\check{x}}\left(t\right)=& (I_{\mathcal{K}}\otimes A)\check{x}\left(t\right)+(\overline{\mathfrak{L}}\otimes B\mathfrak{K}C)\overline{x}\left(t\right)+(I_{\mathcal{K}}\otimes GC)\Delta \overline{x}\left(t\right),\hfill \\ \hfill {\dot{\overline{x}}}_F\left(t\right)=& (I_{\mathcal{K}}\otimes A_F){\overline{x}}_F\left(t\right)+(I_{\mathcal{K}}\otimes B_F{C}_F){\overline{x}}_F\left(t\right)+(I_{\mathcal{K}}\otimes B_F{B}^{+}GC)\Delta \overline{x}\left(t\right),\hfill \\ \hfill \overline{z}\left(t\right)=& (\overline{\mathcal{M}}\otimes I_n)\overline{x}\left(t\right),\hfill \end{array}$$

(8)

where $\overline{\mathcal{M}}=\left[\begin{array}{cccc}{\displaystyle \frac{\mathcal{K}-1}{\mathcal{K}}}& {\displaystyle \frac{-1}{\mathcal{K}}}& \cdots & {\displaystyle \frac{-1}{\mathcal{K}}}\\ *& {\displaystyle \frac{\mathcal{K}-1}{\mathcal{K}}}& \ddots & {\displaystyle \frac{-1}{\mathcal{K}}}\\ *& *& ⋮& ⋮\\ *& *& *& {\displaystyle \frac{\mathcal{K}-1}{\mathcal{K}}}\end{array}\right]$.

Choose an orthogonal matrix $\mathcal{T}\in {\mathbb{R}}^{\mathcal{K}\times \mathcal{K}}$ satisfying ${\mathcal{T}}^T\overline{\mathcal{M}}\mathcal{T}=\left[\begin{array}{cc}{I}_{\mathcal{K}-1}& 0\\ 0& 0\end{array}\right]$, where $\mathcal{T}=\left[{\mathcal{T}}_1{\mathcal{T}}_2\right]$, then ${\mathcal{T}}_2={\displaystyle \frac{I_{\mathcal{K}}}{\sqrt{\mathcal{K}}}}$ is the last column of $\mathcal{T}$, and ${\mathcal{T}}_1$ has the rest of the values in $\mathcal{T}$. Next, let us consider

$${\mathcal{T}}^T\overline{\mathcal{M}}\mathcal{T}=\check{\mathcal{M}}and{\mathcal{T}}^T\overline{\mathfrak{L}}\mathcal{T}=\left[\begin{array}{cc}{\mathfrak{L}}_1& 0\\ 0& 0\end{array}\right]=\widehat{\mathfrak{L}},$$

where ${\mathfrak{L}}_1={\mathcal{T}}_1^T\overline{\mathfrak{L}}{\mathcal{T}}_1$. Let $\check{\eta }\left(t\right)=({\mathcal{T}}^T\otimes I_{\mathcal{K}})\overline{x}\left(t\right),\check{\zeta }\left(t\right)=({\mathcal{T}}^T\otimes I_{\mathcal{K}})\check{x}\left(t\right),\check{\Gamma }\left(t\right)=({\mathcal{T}}^T\otimes I_{\mathcal{K}})\Delta \overline{x}\left(t\right),\check{\Theta }\left(t\right)=({\mathcal{T}}^T\otimes I_{\mathcal{K}}){\overline{x}}_F\left(t\right),\check{z}\left(t\right)=({\mathcal{T}}^T\otimes I_{\mathcal{K}})\overline{z}\left(t\right),\check{d}\left(t\right)=({\mathcal{T}}^T\otimes I_{\mathcal{K}})\overline{d}\left(t\right)$. Then, from (8), we have

$$\begin{array}{cc}\hfill \dot{\check{\eta }}\left(t\right)=& (\check{\mathcal{M}}\otimes A)\check{\eta }\left(t\right)+(\check{\mathcal{M}}\widehat{\mathfrak{L}}\otimes B\mathfrak{K}C)\check{\eta }\left(t\right)-(\check{\mathcal{M}}\otimes B{C}_F)\check{\Theta }\left(t\right)+(\check{\mathcal{M}}\otimes D)\check{d}\left(t\right),\hfill \\ \hfill \dot{\check{\zeta }}\left(t\right)=& (\check{\mathcal{M}}\otimes A)\check{\zeta }\left(t\right)+(\check{\mathcal{M}}\widehat{\mathfrak{L}}\otimes B\mathfrak{K}C)\check{\eta }\left(t\right)+(\check{\mathcal{M}}\otimes GC)\check{\Gamma }\left(t\right),\hfill \\ \hfill \dot{\check{\Theta }}\left(t\right)=& (\check{\mathcal{M}}\otimes A_F)\check{\Theta }\left(t\right)+(\check{\mathcal{M}}\otimes B_F{C}_F)\check{\Theta }\left(t\right)+(\check{\mathcal{M}}\otimes B_F{B}^{+}GC)\check{\Gamma }\left(t\right),\hfill \\ \hfill \check{z}\left(t\right)=& (\check{\mathcal{M}}\otimes I_n)\check{\eta }\left(t\right).\hfill \end{array}$$

It can be observed from the above set of equations that

$$\begin{array}{cc}\hfill {\dot{\check{\eta }}}_1\left(t\right)=& (I_{\mathcal{K}-1}\otimes A){\check{\eta }}_1\left(t\right)+({\mathfrak{L}}_1\otimes B\mathfrak{K}C){\check{\eta }}_1\left(t\right)-(I_{\mathcal{K}-1}\otimes B{C}_F){\check{\Theta }}_1\left(t\right)+(I_{\mathcal{K}-1}\otimes D){\check{d}}_1\left(t\right),\hfill \\ \hfill {\dot{\check{\zeta }}}_1\left(t\right)=& (I_{\mathcal{K}-1}\otimes A){\check{\zeta }}_1\left(t\right)+({\mathfrak{L}}_1\otimes B\mathfrak{K}C){\check{\eta }}_1\left(t\right)+(I_{\mathcal{K}-1}\otimes GC){\check{\Gamma }}_1\left(t\right),\hfill \\ \hfill {\dot{\check{\Theta }}}_1\left(t\right)=& (I_{\mathcal{K}-1}\otimes A_F){\check{\Theta }}_1\left(t\right)+(I_{\mathcal{K}-1}\otimes B_F{C}_F){\check{\Theta }}_1\left(t\right)+(I_{\mathcal{K}-1}\otimes B_F{B}^{+}GC){\check{\Gamma }}_1\left(t\right),\hfill \\ \hfill {\check{z}}_1\left(t\right)=& {\check{\eta }}_1\left(t\right),\hfill \end{array}$$

(9)

where $\check{\eta }\left(t\right)={[{\check{\eta }}_1^T\left(t\right),{\check{\eta }}_2^T\left(t\right)]}^T,\check{\zeta }\left(t\right)={[{\check{\zeta }}_1^T\left(t\right),{\check{\zeta }}_2^T\left(t\right)]}^T,\check{\Gamma }\left(t\right)={[{\check{\Gamma }}_1^T\left(t\right),{\check{\Gamma }}_2^T\left(t\right)]}^T,\check{\Theta }\left(t\right)={[{\check{\Theta }}_1^T\left(t\right),{\check{\Theta }}_2^T\left(t\right)]}^T,\check{z}\left(t\right)={[{\check{z}}_1^T\left(t\right),{\check{z}}_2^T\left(t\right)]}^T,\check{d}\left(t\right)={[{\check{d}}_1^T\left(t\right),{\check{d}}_2^T\left(t\right)]}^T$ and ${\dot{\check{\eta }}}_2\left(t\right)=0,{\dot{\check{\zeta }}}_2\left(t\right)=0,{\dot{\check{\Theta }}}_2\left(t\right)=0,{\check{z}}_2\left(t\right)=0$. Let us select an orthogonal matrix $\mathfrak{T}\in {\mathbb{R}}^{(\mathcal{K}-1)\times (\mathcal{K}-1)}$ satisfying ${\mathfrak{T}}^T{\mathfrak{L}}_1\mathfrak{T}=diag\{{\varrho }_2,{\varrho }_3,\dots {\varrho }_{\mathcal{K}}\}=\Delta$, where ${\varrho }_2,{\varrho }_3,\dots ,{\varrho }_{\mathcal{K}}$ are the non-zero eigenvalues of $\overline{\mathfrak{L}}$.

Let us consider $\eta \left(t\right)=({\mathfrak{T}}^T\otimes I_{\mathcal{K}}){\check{\eta }}_1\left(t\right),\zeta \left(t\right)=({\mathfrak{T}}^T\otimes I_{\mathcal{K}}){\check{\zeta }}_1\left(t\right),\Gamma \left(t\right)=({\mathfrak{T}}^T\otimes I_{\mathcal{K}}){\check{\Gamma }}_1\left(t\right),\Theta \left(t\right)=({\mathfrak{T}}^T\otimes I_{\mathcal{K}}){\check{\Theta }}_1\left(t\right),\widehat{z}\left(t\right)=({\mathfrak{T}}^T\otimes I_{\mathcal{K}}){\check{z}}_1\left(t\right),\widehat{d}\left(t\right)=({\mathfrak{T}}^T\otimes I_{\mathcal{K}}){\check{d}}_1\left(t\right)$. Then, from (9), we have

$$\begin{array}{cc}\hfill \dot{\eta }\left(t\right)=& (I_{\mathcal{K}-1}\otimes A)\eta \left(t\right)+(\Delta \otimes B\mathfrak{K}C)\eta \left(t\right)-(I_{\mathcal{K}-1}\otimes B{C}_F)\Theta \left(t\right)+(I_{\mathcal{K}-1}\otimes D)\widehat{d}\left(t\right),\hfill \\ \hfill \dot{\zeta }\left(t\right)=& (I_{\mathcal{K}-1}\otimes A)\zeta \left(t\right)+(\Delta \otimes B\mathfrak{K}C)\eta \left(t\right)+(I_{\mathcal{K}-1}\otimes GC)\Gamma \left(t\right),\hfill \\ \hfill \dot{\Theta }\left(t\right)=& (I_{\mathcal{K}-1}\otimes A_F)\Theta \left(t\right)+(I_{\mathcal{K}-1}\otimes B_F{C}_F)\Theta \left(t\right)+(I_{\mathcal{K}-1}\otimes B_F{B}^{+}GC)\Gamma \left(t\right),\hfill \\ \hfill \widehat{z}\left(t\right)=& \eta \left(t\right).\hfill \end{array}$$

From the above equations we can have the reduced-order systems as follows:

$$\begin{array}{cc}\hfill {\dot{\eta }}_i\left(t\right)=& A{\eta }_i\left(t\right)+{\varrho }_{i}B\mathfrak{K}C{\eta }_i\left(t\right)-B{C}_F{\Theta }_i\left(t\right)+D{\widehat{d}}_i\left(t\right),\hfill \\ \hfill {\dot{\zeta }}_i\left(t\right)=& A{\zeta }_i\left(t\right)+{\varrho }_{i}B\mathfrak{K}C{\eta }_i\left(t\right)+GC{\Gamma }_i\left(t\right),\hfill \\ \hfill {\dot{\Theta }}_i\left(t\right)=& A_F{\Theta }_i\left(t\right)+B_F{C}_F{\Theta }_i\left(t\right)+B_F{B}^{+}GC{\Gamma }_i\left(t\right),\hfill \\ \hfill {\widehat{z}}_i\left(t\right)=& {\eta }_i\left(t\right).\hfill \end{array}$$

Finally, from the above equations, the following augmented system is acquired:

$$\begin{array}{cc}\hfill {\dot{\varphi }}_i\left(t\right)=& \overline{A}{\varphi }_i\left(t\right)+\overline{B}{\widehat{d}}_i\left(t\right),\hfill \\ \hfill {\widehat{z}}_i\left(t\right)=& \overline{C}{\varphi }_i\left(t\right),\hfill \end{array}$$

(10)

where ${\varphi }_i\left(t\right)=\left[\begin{array}{c}{\eta }_i\left(t\right)\\ {\Gamma }_i\left(t\right)\\ {\Theta }_i\left(t\right)\end{array}\right],\overline{A}=\left[\begin{array}{ccc}A+{\varrho }_{i}B\mathfrak{K}C& 0& -B{C}_F\\ 0& A-GC& -B{C}_F\\ 0& B_F{B}^{+}GC& A_F+B_F{C}_F\end{array}\right]$ and $\overline{B}=\left[\begin{array}{c}D\\ D\\ 0\end{array}\right]$ and $\overline{C}=\left[\begin{array}{c}I\\ 0\\ 0\end{array}\right]$.

Definition 4 

([25]). Augmented System (10) is asymptotically stable with $H_{\infty }$ performance $\nu >0$ if the following condition is met:

$$\underset{0}{\overset{\infty }{\int }}{\widehat{z}}_i^T\left(t\right){\widehat{z}}_i\left(t\right)\mathrm{d}t\le {\nu }^2\underset{0}{\overset{\infty }{\int }}{d}_i^T\left(t\right)d_i\left(t\right)\mathrm{d}t,i=1,2,\dots ,\mathcal{K}$$

(11)

for any non-zero $d_i\left(t\right)$.

3. Main Results

Next, we provide two theorems to derive the adequate requirements to guarantee the bipartite consensus of the MAS under consideration. Theorem 1 provides the adequate requirements for bipartite consensus of the MAS (1) for the case of known gain parameters. Then, in Theorem 2, the results obtained in Theorem 1 are extended for unknown observer and controller gain values.

Theorem 1. 

Assume that $\mathfrak{G}$ is structurally balanced and connected. Let $(A,B)$ be controllable and $(A,C)$ be observable in (1). Then, the agents in MAS (1) asymptotically reach bipartite consensus using Control Protocol (7). If there exists a symmetric matrix $P>0$ with a proper dimension, the following inequalities are satisfied:

$$\left[{\mathfrak{C}}_{a,b}^i\right]<0,a,b=1,2,3,4,i=2,3,\dots ,\mathcal{K},$$

(12)

where

$$\begin{array}{cc}\hfill {\mathfrak{C}}_{1,1}^i& =P^{T}A+A^{T}P+{\varrho }_i{C}^T{\mathfrak{K}}^T{B}^{T}P+{\varrho }_i{P}^{T}B\mathfrak{K}C+I,{\mathfrak{C}}_{1,3}^i=-P^{T}B{C}_F,{\mathfrak{C}}_{1,4}^i=P^{T}D\hfill \\ \hfill {\mathfrak{C}}_{2,2}^i& =P^{T}A+A^{T}P-P^{T}GC-C^T{G}^{T}P,{\mathfrak{C}}_{2,3}^i=-P^{T}B{C}_F+C^T{G}^T{B}^{+T}{B}_F^{T}P,{\mathfrak{C}}_{2,4}^i=P^{T}D,\hfill \\ \hfill {\mathfrak{C}}_{3,3}^i& =P^T{A}_F+A_F^{T}P+P^T{B}_F{C}_F+C_F^T{B}_F^{T}P,{\mathfrak{C}}_{4,4}^i=-{\nu }^{2}I,\hfill \end{array}$$

and the remaining elements are zero.

Proof. 

To ensure that the MAS described in Equation (1) achieves bipartite consensus, it suffices to demonstrate that the augmented System (10) is asymptotically stable. To prove this, the following Lyapunov function was taken into account:

$$V_i\left(t\right)={\varphi }_i^T\left(t\right)\mathcal{P}{\varphi }_i\left(t\right),$$

(13)

where $\mathcal{P}=\left[\begin{array}{ccc}P& 0& 0\\ 0& P& 0\\ 0& 0& P\end{array}\right]$. Calculating the time derivative of $V_i\left(t\right)$ along the solution of (10), we obtain the following:

$$\begin{array}{cc}\hfill {\dot{V}}_i\left(t\right)& =2{\dot{\varphi }}_i^T\left(t\right)P{\varphi }_i\left(t\right)\hfill \\ \hfill & =2\left[\begin{array}{ccc}{\dot{\eta }}_i^T\left(t\right)& {\dot{\Gamma }}_i^T\left(t\right)& {\dot{\Theta }}_i^T\left(t\right)\end{array}\right]\left[\begin{array}{ccc}P& 0& 0\\ 0& P& 0\\ 0& 0& P\end{array}\right]\left[\begin{array}{c}{\eta }_i\left(t\right)\\ {\Gamma }_i\left(t\right)\\ {\Theta }_i\left(t\right)\end{array}\right]\hfill \\ \hfill & =2\{{\dot{\eta }}_i^T\left(t\right)P{\eta }_i\left(t\right)+{\dot{\Gamma }}_i^T\left(t\right)P{\Gamma }_i\left(t\right)+{\dot{\Theta }}_i^T\left(t\right)P{\Theta }_i\left(t\right)\}.\hfill \end{array}$$

(14)

Combining (13) and (14) and through using (11), it then follows that

$${\dot{V}}_i\left(t\right)\le {\Psi }_i^T\left(t\right){\mathfrak{C}}_{a,b}^i{\Psi }_i\left(t\right),$$

(15)

where $\Psi \left(t\right)={\left[\begin{array}{cccc}{\eta }_i\left(t\right)& {\Gamma }_i\left(t\right)& {\Theta }_i\left(t\right)& d_i\left(t\right)\end{array}\right]}^T,a,b=1,2,3,4,i=2,3,\dots ,\mathcal{K}$. Finally, from (12), we can have ${\dot{V}}_i\left(t\right)<0$. Hence, the augmented system (10) is asymptotically stable. Therefore, the agents in MAS (1) achieve bipartite consensus through using Control Protocol (7). This proves the theorem. □

Theorem 2. 

Suppose that $\mathfrak{G}$ is structurally balanced and connected. Assume that $(A,B)$ is controllable and $(A,C)$ is observable in (1). If there exists a symmetric matrix $X>0$ and any appropriate dimensional matrix Y, then the following inequalities are satisfied:

$$\left[{\overline{\mathfrak{C}}}_{a,b}^i\right]<0,a,b=1,2,3,4,5,i=2,3,\dots ,\mathcal{K},$$

(16)

where

$$\begin{array}{cc}\hfill {\overline{\mathfrak{C}}}_{1,1}^i& =AX+X^T{A}^T+{\varrho }_{i}BYC+{\varrho }_i{C}^T{Y}^T{B}^T,{\overline{\mathfrak{C}}}_{1,3}^i=-B{C}_{F}X,{\overline{\mathfrak{C}}}_{1,4}^i=D,{\overline{\mathfrak{C}}}_{1,5}^i=X,\hfill \\ \hfill {\overline{\mathfrak{C}}}_{2,2}^i& =AX+X^T{A}^T-WC-C^T{W}^T,{\overline{\mathfrak{C}}}_{2,3}^i=-B{C}_{F}X+C^T{W}^T{B}^{+}{B}_F^T,{\overline{\mathfrak{C}}}_{2,4}^i=D,\hfill \\ \hfill {\overline{\mathfrak{C}}}_{3,3}^i& =A_{F}X+X^T{A}_F^T+B_F{C}_{F}X+X^T{C}_F^T{B}_F^T,{\overline{\mathfrak{C}}}_{4,4}^i=-{\nu }^{2}I,{\overline{\mathfrak{C}}}_{5,5}^i=-I,\hfill \end{array}$$

and the rest of the elements are zero. Then, the agents in (1) reach bipartite consensus using Protocol (7). Further, the gain values are computed using the relation $G=WUS{X}_{11}^{-1}{S}^{-1}{U}^T$ and $\mathfrak{K}=YUS{X}_{11}^{-1}{S}^{-1}{U}^T$.

Proof. 

Select the same Lyapunov function as in the previous theorem, proceed with the similar derivation, apply Lemma 2 in [26] in (12), and then we can obtain the following:

$$\left[{\mathfrak{C}}_{a,b}^i\right]<0,a,b=1,2,3,4,5,i=2,3,\dots ,\mathcal{K},$$

(17)

where ${\mathfrak{C}}_{1,1}^i=P^{T}A+A^{T}P+{\varrho }_i{C}^T{\mathfrak{K}}^T{B}^{T}P+{\varrho }_i{P}^{T}B\mathfrak{K}C,{\mathfrak{C}}_{1,5}^i=I,{\mathfrak{C}}_{5,5}^i=-I$, and the remaining elements are the same as in (12). Next, let us define $X=P^{-1}$ and assume that $\Phi =diag[X,X,X,I,I]$. Let us pre- and post-multiply (17) using $\Phi$ and its transpose. Now, from Lemma 3 in [27], we can choose a non singular matrix $\overline{X}\in {\mathbb{R}}^{m\times m}$ satisfying $CX=\overline{X}C$, and we can let

$$U^T\left[\begin{array}{c}S\\ 0\end{array}\right]V^{T}V\left[\begin{array}{cc}{X}_{11}& 0\\ 0& X_{22}\end{array}\right]V^T={\overline{X}}_1{U}^T\left[\begin{array}{c}S\\ 0\end{array}\right]V^T,$$

and this implies that

$$\begin{array}{c}\hfill \overline{X}=U^{T}S{X}_{11}{S}^{-1}{\left(U^T\right)}^{-1},\end{array}$$

(18)

where $U\in {\mathbb{R}}^{s\times s}$, $V\in {\mathbb{R}}^{n\times n}$ are two orthogonal matrices satisfying $UCV=\left[\begin{array}{c}S\\ 0\end{array}\right]$ and $S=diag\{{\vartheta }_1,{\vartheta }_2,{\vartheta }_3,\dots ,{\vartheta }_s\}$, ${\vartheta }_i$ are the nonzero singular values of matrix C. Finally, via letting $W=G\overline{X}$ and $Y=\mathfrak{K}\overline{X}$, we can obtain the right side of inequality (16). Thus, the agents in MAS (1) reach bipartite consensus via Protocol (7). This concludes the proof of the theorem. □

Remark 2. 

If we choose $\mathcal{P}$ as $\mathcal{P}=\mathit{diag}\{P_1,P_2,P_3\}$, then its inverse would be $\mathcal{X}=\mathit{diag}\{X_1,X_2,X_3\}$. After the pre- and post-multiplication process as in Theorem 2, we have to consider the relations $C{X}_1={\overline{X}}_{1}C$ and $C{X}_2={\overline{X}}_{2}C$. Consequently, Lemma 3 in [27] should be applied for both conditions to find ${\overline{X}}_1$ and ${\overline{X}}_2$, which may lead to computational burden. Therefore, in this paper, we considered $\mathcal{P}$ as $\mathcal{P}=\mathit{diag}\{P,P,P\}$.

Remark 3. 

The authors in [28] addressed the consensus problem in the presence of unknown external disturbances for nonlinear MASs using adaptive iterative learning control. The adaptive consensus problem for linear MASs subjected to additive multi-harmonic disturbances was studied in [29]. In the future, we will apply adaptive iterative learning control to the bipartite consensus problem when it is subjected to additive multi-harmonic disturbances.

4. An Illustrative Example

Next, we provide an illustrative example to describe the validation of the obtained theoretical results. First, let us pick a continuous-time linear MAS (1) with four agents subject external disturbances. The values associated to MAS (1) are taken as follows:

$$A=\left[\begin{array}{cc}-0.001& -0.01\\ -1& -1\end{array}\right],B=\left[\begin{array}{cc}-5& 0\\ 0& -1\end{array}\right],C=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],D=\left[\begin{array}{cc}-5& 1\\ 1& -1\end{array}\right],$$

$$A_F=\left[\begin{array}{cc}-101& -10\\ -1& 0\end{array}\right],B_F=\left[\begin{array}{cc}10& 0\\ 0& -1\end{array}\right],C_F=1.$$

Let the interaction among the agents be chosen as in Figure 2. Then, the adjacency matrix corresponding to Figure 2 can be given as $\mathfrak{A}=\left[\begin{array}{cccc}0& 1& 0& 0\\ 1& 0& -2& -0.3\\ 0& -2& 0& 2\\ 0& -0.3& 2& 0\end{array}\right]$.

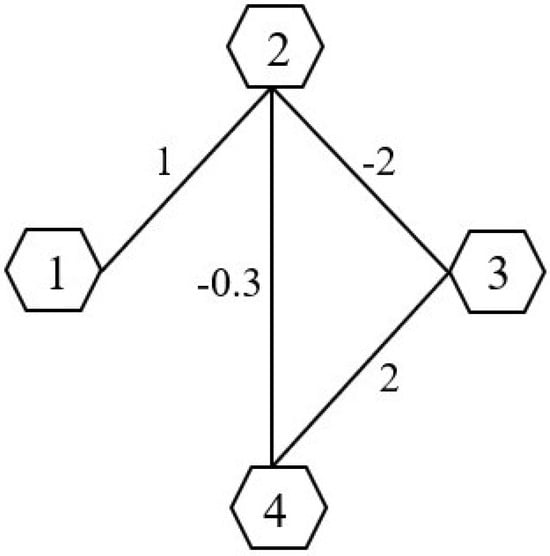
Figure 2. Communication topology between the agents.

When solving the linear matrix Inequality (16) involved in Theorem 2 through using the aforementioned parameters, the solution was found to be feasible, and we were able to calculate the gain values of the controller and observer as follows:

$$K=\left[\begin{array}{cc}2.65728& 0\\ 0& 2.6572\end{array}\right],G=\left[\begin{array}{cc}19.4822& -4.1781\\ -3.4922& 0.1858\end{array}\right]$$

Next, we exhibited the simulation through using the appropriate initial values and computed the gain matrices. Figure 3a shows the plotting of the system and observer state vectors $x_{i1},{\widehat{x}}_{i1}$$i=1,2,3,4$, and Figure 3b describes the trajectories of the state and observer $x_{i2},{\widehat{x}}_{i2}$ for $i=1,2,3,4$ in the absence of a controller, which clearly describes that the desired bipartite consensus was not reached. On the other hand, the state observer trajectories $x_{i1},{\widehat{x}}_{i1}$ for $i=1,2,3,4$ and the state observer trajectories $x_{i2},{\widehat{x}}_{i2}$ for $i=1,2,3,4$ after the execution of the proposed Controller (7) are shown in Figure 4a and Figure 4b, respectively. According to Figure 4a,b, we observed that the desired bipartite consensus performance of the considered MAS was achieved with the proposed Controller (7). Figure 5a,b represent the controller responses of the agents. Figure 6a,b portrait the trajectories of the outputs $y_i\left(t\right)$ and their estimations ${\widehat{y}}_i\left(t\right)$, $i=1,2,3,4$. Finally, Figure 7a–d show the disturbance tracking performance for the first, second, third and fourth agents, respectively, wherein we can conclude that the required disturbance estimation performances were achieved. From the above discussion, it was observed that the derived results were sufficient for MAS (1) to reach bipartite consensus.

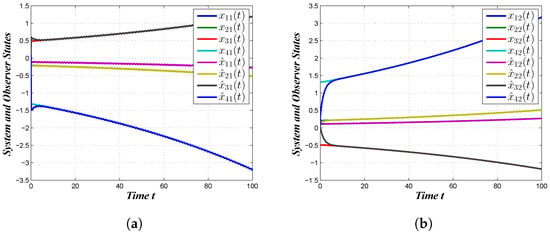
Figure 3. State and observer trajectories without control. (a) $x_{i1},{\widehat{x}}_{i1}$, $i=1,2,3,4$; (b) $x_{i2},{\widehat{x}}_{i2}$, $i=1,2,3,4$.

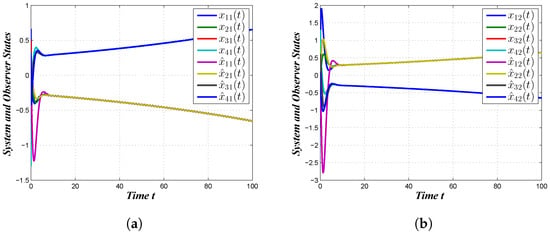
Figure 4. State and observer trajectories with control. (a) $x_{i1},{\widehat{x}}_{i1}$, $i=1,2,3,4$; (b) $x_{i2},{\widehat{x}}_{i2}$, $i=1,2,3,4$.

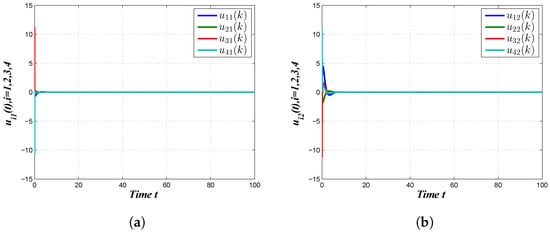
Figure 5. Control trajectories. (a) $u_{i1}$, $i=1,2,3,4$; (b) $u_{i2}$, $i=1,2,3,4$.

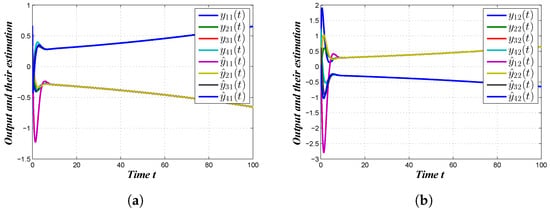
Figure 6. Output trajectories. (a) $y_{i1},{\widehat{y}}_{i1}$, $i=1,2,3,4$; (b) $y_{i2},{\widehat{y}}_{i2}$, $i=1,2,3,4$.

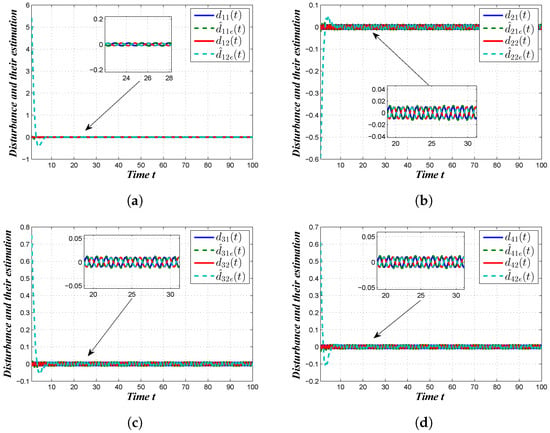
Figure 7. Disturbance tracking. (a) disturbance tracking performance for the first agent, (b) disturbance tracking performance for the second agent, (c) disturbance tracking performance for the third agent and (d) disturbance tracking performance for the fourth agent.

5. Conclusions

The bipartite consensus for continuous-time linear MASs affected by external disturbance was addressed in this work. A feedback controller was developed based on an equivalent input-disturbance rejection technique to ensure the examined MAS reached bipartite consensus. A communication graph with competitive and cooperative interaction was considered as describing the communication between agents. Using the properties of Lyapunov stability and an algebraic graph, the required conditions that assure the bipartite consensus of the examined MAS were obtained in the form of LMIs. By solving the linear matrix inequality constraints, the EID-based controller and the observer gain values were obtained. A numerical example was given at the end to demonstrate the efficacy of the designed control scheme.