A Fuzzy Variable H Strategy Based Ripple-Spreading Algorithm to Find the k Shortest Paths

Abstract

Ripple-spreading Algorithm (RSA) is a relatively new, nature-inspired, multi-agent based method for path optimization. This paper demonstrates that by modifying the micro-level behaviors of nodes and ripples, RSA achieves good scalability for solving the k shortest paths problem ($k-\mathrm{SPP}$). Initially, each node may generate k or more ripples to guarantee optimality. To improve computational efficiency for large-scale problems, we propose an approximate RSA (ARSA), where nodes generate no more than h ripples ($1\le h<k$). While this reduces optimality, it significantly improves efficiency. Further, we introduce a fuzzy variable H strategy, FVHSRSA, to strike a better balance between optimality and efficiency. The optimality/efficiency of ARSA may still suffer if it uses a constant h too small/large. This strategy allows nodes closer to the destination to generate more ripples, while nodes farther away use fewer ripples. By dynamically adjusting h, FVHSRSA achieves a better trade-off between optimality and efficiency. Comprehensive experiments on 4 common network categories validate the effectiveness and efficiency of FVHSRSA in solving the $k-\mathrm{SPP}$.

1. Introduction

As is well known, nature-inspired, multi-agent based methods have now formed an important foundation of artificial intelligence [1]. For instance, the inspiration for the genetic algorithm comes from natural selection and evolution, ant colony optimization through ant foraging behavior, particle swarm optimization is realized by learning behaviors in the group, and polar fox optimization algorithm mimics polar foxes’ hunting behavior to solve optimization problems [1,2,3,4,5,6]. As a relatively new member in the family of nature-inspired, multi-agent based methods, the ripple-spreading algorithm (RSA) appears as a combination of centralized deterministic methods and decentralized multi-agent-based evolutionary models. Usually, a centralized deterministic method has an optimality guarantee but poor flexibility for modification. In contrast, a decentralized multi-agent-based evolutionary model often has no optimality guarantee but is friendly to various problem-specific modifications. RSA inherits the merits of both categories of methods and thus exhibits great potential for applications [7]. This paper proposes a fuzzy variable H strategy based on RSA(FVHSRSA) for the k shortest paths problem ($k-\mathrm{SPP}$) to achieve a good balance between optimality and computational efficiency.

It is universally acknowledged that path optimization is important in both theoretical and practical research. The $k-\mathrm{SPP}$ is a challenging case of path optimization because it notably proposes to seek out the first k shortest paths in increasing order of length between a given OD (origin and destination) [8,9]. The $k-\mathrm{SPP}$ is very useful from the viewpoint of applications. For example, it is important to find more than one path in an uncertain environment. Still, a candidate solution is set to achieve robust, reliable, and flexible decision-making [9,10,11,12,13], and the $k-\mathrm{SPP}$ can provide strong methodological support here. In discrete multi-objective optimization problems, the complete (not only approximate) Pareto front can also be found with the $k-\mathrm{SPP}$ [14].

Generally speaking, the $k–$Shortest Path Problem ($k-\mathrm{SPP}$) can be divided into two types based on whether loops are allowed in the path [9,10]. If loops are not allowed, a node can appear in a path at most once. If loops are allowed, a node can appear in a path multiple times. In the same network, allowing loops in a path may result in the j-th shortest path becoming shorter, where $1<j\le k$. However, allowing loops in a network is usually meaningless in realistic applications. The reason is that the traveler needs to travel along a loop before continuing the journey. Therefore, it is often more cost-effective for travelers to stay at a certain node for a period of time. Consequently, we will focus on the first type here, i.e., loops are not allowed.

In contrast to optimizing paths to find the 1st shortest path, solving the $k-\mathrm{SPP}$ is significantly more complex. Since the 1950s, many methods have been reported to resolve the $k-\mathrm{SPP}$ [15,16,17,18,19,20]. In substance, the kth shortest path can only be calculated when the $(k-1)$th shortest path is determined first in most of the methods. This is because the principle of optimality of the $k-\mathrm{SPP}$ holds that the kth shortest path depends on the jth shortest paths $(j<k)$ [9]. Similarly, it is necessary to determine the jth shortest paths and reconstruct the route network when the $(j-1)$th shortest paths have already been achieved. There are many ways to rebuild the network. For example, we can remove a link in the $(j-1)$th shortest paths [16] and even transform the original network completely by redrawing nodes as links while links as nodes [18]. Besides, certain searching methods, such as the A* algorithm [21] and Dijkstra’s algorithm [22], are engaged to find the 1st shortest paths in those reconstructed networks. This form of calculating the kth shortest path by reconstructing networks based on the $(k-1)$th shortest paths is also extended to the $k-\mathrm{SPP}$ with a time window [19].

We have recently introduced a nature-inspired, multi-agent algorithm for solving the $k-\mathrm{SPP}$ [7]. This approach ensures that the $(j-1)$th shortest path does not depend on the jth shortest path’s information, and no new route networks are reconstructed. The algorithm simulates the natural ripple-spreading process by initiating a ripple relay race (RRR) from the source to the destination within the original network. The k shortest paths between the given OD pair can be determined by backtracking these k ripples when the given destination node has been activated. Thus, all of the k shortest paths between the given OD pair can be found through only a single RRR process in the original network. Therefore, the new algorithm was named the ripple-spreading algorithm (RSA), and ripples and nodes are agents in RSA [7].

In the reference [23], to ensure the optimality of the RSA in solving the $k-\mathrm{SPP}$, it is necessary for each node to generate an adequate number of ripples. However, this approach significantly increases the computational load, and this drawback becomes even more pronounced when it is applied to solve $k-\mathrm{SPP}$ in large-scale road networks. If an upper limit k is set for the number of ripples that each node can generate, the algorithm can still guarantee optimality in solving the $k-\mathrm{SPP}$. This modification improves the algorithm’s computational efficiency without sacrificing its optimality.

This paper explores the potential outcomes when each node is restricted to generating h ripples, where $1\le h<k$, rather than the full k ripples. In this way, the optimality of the algorithm is lost. For this reason of no optimality guarantee, the method reported in this paper is called approximate RSA (ARSA), which uses a small h to reduce the huge amount of computation. The optimality and computational efficiency of an algorithm are often in a trade-off relationship. In most cases, it is generally acceptable to lower the requirements for optimality to futher improve computational efficiency. In the case of ARSA for the $k-\mathrm{SPP}$, choosing a proper $1\le h<k$ plays a key role in achieving such a good balance. The value of h can be determined through fuzzy methods, considering the uncertainty and subjectivity of the decision-maker’s judgment, as well as the network topology. In recent years, methods that combine fuzzy sets and fuzzy logic have been widely applied to adjust key parameters in path optimal methods design, as well as to tune the weights of various path planning strategies, among other related optimization tasks [24,25]. To this end, a triangular membership function for each interval, as a degree of classification for fuzzy variables, is defined. Then, we establish the fuzzy rules and further introduces a properly fuzzy variable H strategy which aims to find the appropriate values of $h_{T,i}$ for each tier of nodes. Thus, this method can achieve a good balance between optimality and computational efficiency. This method is named the fuzzy variable H strategy based on RSA (FVHSRSA).

Section 2 provides a description of $k-\mathrm{SPP}$. Section 3 reports an ARSA for the $k-\mathrm{SPP}$, where each node is permitted to generate at most h ripples, $1\le h<k$. Section 4 introduces the ARSA and FVHSRSA. Section 5 discusses some further extensions of FVHSRSA. Section 6 demonstrates the ability of the reported FVHSRSA to balance effectiveness and efficiency through comprehensive experiments. Section 7 presents some significant conclusions.

2. Problem Description of $\mathit{k}$−SPP

This paper considers the k-Shortest Path Problem ($k-\mathrm{SPP}$) between a given origin-destination (OD) pair, i.e., one-to-one $k-\mathrm{SPP}$, where no loops are allowed in a path. The route network $G(V,E)$ consists of two sets: there are $N_N$ nodes in set V, and $N_L$ links in set E. We use an $N_N\times N_N$ adjacency matrix A to record this route network. The matrix entry $A(i,j)=1$ means there is a link between node i and node j for $i=1,\dots ,N_N$ and $j=1,\dots ,N_N$, while $A(i,j)=0$ indicates that nodes i and j do not have any link. This study assumes $A(i,i)=0$, which means that there are no self-links. Let $C(i,j)$ be the cost of link $A(i,j)$, which will be used to calculate the path length.

We employ an integer vector P to store an optional path, where the element $P\left(i\right)=j$ means the i-th bit of path P is node j, for $i=1,\dots ,N_P$ and $j=1,\dots ,N_N$. Here, $N_P$ is the total number of nodes in the path P. The origin and the destination are $P\left(1\right)$ and $P\left(N_P\right)$, respectively. Since loops are not allowed in the path, we propose the following conditions for any $i\ne j$, where $i=1,\dots ,N_P$ and $j=1,\dots ,N_P$:

$$P\left(i\right)\ne P\left(j\right)$$

(1)

The length of path P is its cost either, between the given OD pair, which calculated as

$$f\left(P\right)=\sum _{i=1}^{N_P-1}C(P\left(i\right),\left(P(i+1)\right)$$

(2)

$P_{SP,k}$ represents the kth shortest path. Then, the path length of the 1st shortest path is

$$f_{Min,1}=\underset{P\in \Omega }{min}f\left(P\right)$$

(3)

Satisfying Equation (1) and

$$A(P\left(i\right),P(i+1))=1,fori=1,\dots ,N_P-1$$

(4)

The $\Omega$ is the set if all candidate paths between the given OD pair.

For any $k>1$, $P_{SP,k}$ satisfies

$$f\left(P_{SP,k-1}\right)\le f\left(P_{SP,k}\right)\le P_{SP,k+1}$$

(5)

Condition (5) indicates that $f\left(P_{SP,k}\right)$ does not necessarily have the kth minimal path length between the given OD pair. In fact, $f\left(P_{SP,k}\right)$ usually has not had the same path length as $f\left(P_{SP,k-1}\right)$ or $f\left(P_{SP,k+1}\right)$, unless they are different paths.

The goal of $k-\mathrm{SPP}$ is to find out $P_{SP,1}$, $P_{SP,2}$,…, $P_{SP,k}$ from the set $\Omega$. As already mentioned before, many methods need to calculate the $P_{SP,1}$, $P_{SP,2}$,…, $P_{SP,k}$ one by one earlier in resolving the $k-\mathrm{SPP}$, and the information of $P_{SP,1}$ to $P_{SP,j-1}$ will be used to reconstruct new route networks, in order to calculate $P_{SP,j}$, for any $1<j\le k$. In other words, traditional $k-\mathrm{SPP}$ methods cannot find the jth shortest path when the information of the ($j-1$) shortest paths was not given [15,16,17,18]. Differently, the ripple-spreading algorithm (RSA) finds $P_{SP,1}$, $P_{SP,2}$,…, $P_{SP,k}$ by mimicking a RRR progress in the original route network, and the RRR progress only needs to be run once. Especially in the single run of the RRR progress, there is no need to reconstruct any route networks. The calculation of the jth shortest path is completely independent of the $(j-1)$shortest paths, $1<j\le k$, in other words, RSA can still find the jth shortest path even without the information of the $(j-1)$ shortest paths [7].

For an intuitive comparison, Figure 1 illustrates how a traditional $k-\mathrm{SPP}$ method and RSA find the 2 shortest paths between the given OD pair in the same route network. Figure 1a shows the traditional $k-\mathrm{SPP}$ method calculates the 1st shortest path $O\to 4\to 5\to D$ as the first step. Then, the traditional $k-\mathrm{SPP}$ method reconstructs 3 new route networks based on the information of the 1st shortest path $O\to 4\to 5\to D$, i.e., 3 new networks are generated by cutting off link $(O,4)$, link $(4,5)$ and link $(5,D)$ in the original network, in turn. Then, the traditional $k-\mathrm{SPP}$ method finds out the 1st shortest path in each of the 3 new route networks. In the new network, by cutting off link $(O,4)$, the 1st shortest path is $O\to 1\to 2\to 6\to 7\to 5\to D$. In the new network, by cutting off link $(4,5)$, the 1st shortest path is $O\to 4\to 3\to 8\to 9\to D$. In the new network, by cutting off link $(5,D)$, the 1st shortest path is also $O\to 4\to 3\to 8\to 9\to D$. Now, the traditional $k-\mathrm{SPP}$ method compares these 3 1st shortest paths in 3 new networks and finds out that path $O\to 4\to 3\to 8\to 9\to D$ is the shortest one. Rather differently, as shown in Figure 1b, RSA simply simulates the RRR progress in the original route network. When ripple $R_6$ reaches D at time $t=3$, the 1st shortest path in the original network, i.e., path $O\to 4\to 5\to D$, is found by backtracking $R_6$. When ripple $R_{10}$ reaches D at time $t=5$, the 2nd shortest path in the original network, i.e., path $O\to 4\to 3\to 8\to 9\to D$ is found by backtracking $R_{10}$. Clearly, in the RRR progress, no other networks but only the original network is needed, and finding the 2nd shortest path does not need any information about the 1st shortest path.

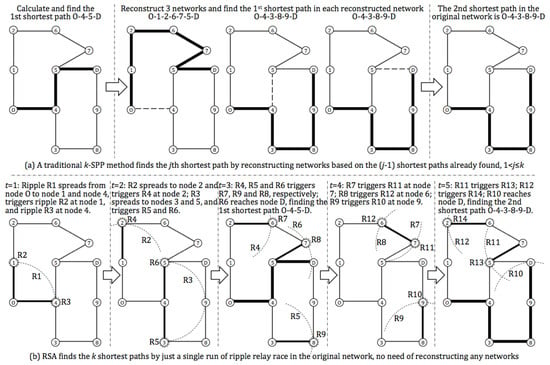
Figure 1. RSA calculates the k shortest paths differently from that of many traditional $k-\mathrm{SPP}$ methods.

3. Approximate RSA(ARSA) for the k − SPP

3.1. RSA with Optimality Guarantee for the $k-\mathrm{SPP}$

The optimization principle of RSA is to find the shortest path between a given OD pair by mimicking the phenomenon of ripple spreading in water. After the ripple spreads, it always triggers the next node that is closest to the previous ripple center. This principle provides a theoretical guarantee of RSA’s optimality [7]. Based on RSA, many path optimization problems can be addressed [7]. Essentially, RSA simulates the RRR progress in the original route network, and ripples and nodes are agents in RSA. Initially, an initial ripple is generated at the origin and then spread in all directions at a preset speed. In this way, ripples spread along the link to all nodes one by one. The node which generates ripples is activated. When a ripple reaches an unvisited node, it will activate a new one at another node and continue to spread. Therefore, as the RRR process goes on, more and more nodes will be activated, and more and more ripples will be generated at nodes. There is competition between all the ripples to travel to the destination. Then, the ripple that reaches the destination first determines the 1st shortest path between the given OD pair.

To apply the RSA to the $k-\mathrm{SPP}$, an easy method is to allow each node to generate an unlimited number of ripples. Then, during the RRR progress, the ripple that reaches the destination in the jth place determines the jth shortest path between the given OD pair [7]. However, allowing unlimited ripples at each node will cause the total number of ripples to increase exponentially as the RRR progress goes on. The step in RSA is to simulate the spread of ripples in a time unit in reference [7]. Therefore, this process increases the computational burden. Although not limiting the number of ripples generated by each node can guarantee the optimality of RSA in solving the $k-\mathrm{SPP}$, it is still not ideal.

In reference [23], we limited the number of ripples each node can generate by setting an upper bound of k in RRR progress to solve $k-\mathrm{SPP}$. With this modification, the computational complexity of RSA can be assessed as $O(k\times N_{ATU}\times N_L)$, where $N_{ATU}$ refers to the average number of analog time units consumed by ripples on each link. The relevant theoretical analysis has already been proven in reference [23], and will not be repeated here. Since the RSAs of [7,23] all have the theoretical guarantee of optimality, for distinguishing purposes, they are called optimal RSA, or ORSA for short, in this study.

Figure 2a illustrates how the ORSA of [7] solves the $k-\mathrm{SPP}$ by simulating the RRR progress in a route network. In the $k-\mathrm{SPP}$ of Figure 2, $k=2$, i.e., we need to find the 2 shortest paths between the given OD pair. The RRR progress starts from the initial ripple $R_1$ generated at node O. Ripple $R_1$ spreads out along the links of node O, reaches node 1 and node 3 at time $t=1$, and triggers a new ripple $R_2$ at node 1, and $R_3$ at node 3, in turn. At time $t=2$, ripple $R_2$ reaches node 2, triggering a new ripple $R_4$ at node 2; at the same time, ripple $R_3$ triggers $R_5$ at node 4, $R_6$ at node 6, and $R_7$ at node 4, in turn. At time $t=3$, ripple $R_6$ reaches node D, becoming the 1st ripple that has reached D, so it identifies path $O\to 3\to 6\to D$ as the 1st shortest path between O and D; some more new ripples are triggered as existing ripples keep spreading, and nodes 1 to 6 have all generated 2 ripples each by time $t=3$. At time $t=4$, ripple $R_8$ triggers $R_{14}$ at node 6 and $R_{15}$ at node 4, so by time $t=4$, nodes 4 and 6 have generated 3 ripples each; ripples $R_{10}$ and $R_{11}$ trigger $R_{16}$ and $R_{17}$ at node 7; ripple $R_{13}$ reaches node D, becoming the 2nd ripple that has reached D, so it identifies path $O\to 3\to 4\to 6\to D$ as the 2nd shortest path between O and D. Therefore, by time $t=4$, the RRR progress of Figure 2a has successfully found the $k=2$ shortest paths between O and D.

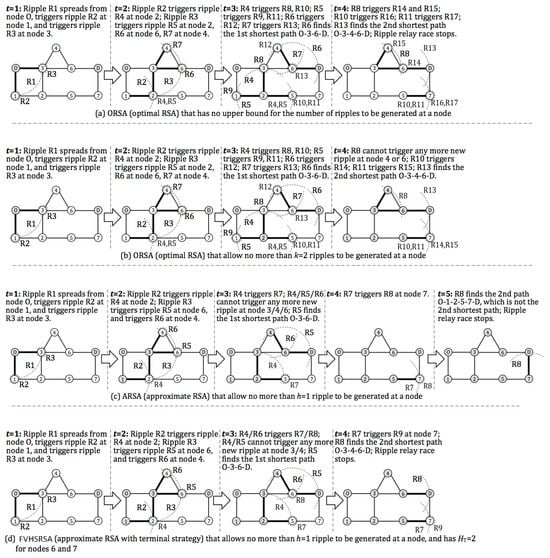
Figure 2. Examples of different RSAs to find the $k=2$ shortest paths in a route network.

Because the ORSA of Figure 2a has an unlimited number of ripples that can be generated at a node, each normal node (not O and D) can generate more than k ripples as long as there are enough incoming ripples before the RRR progress stops. For example, nodes 4 and 6 generated $3>k=2$ ripples in Figure 2a. However, the 3rd ripples generated at nodes 4 and 6, i.e., ripple $R_{15}$ and ripple $R_{14}$, actually have no use in finding the $k=2$ shortest paths between O and D, and they simply increase the overall computational burden of ORSA in Figure 2a.

Figure 2b applies the ORSA of [23] to the same $k-\mathrm{SPP}$ as in Figure 2a. The ORSA of [23] allows each node to generate no more than k ripples. For example, after time $t=2$, node 2 has already generated $k=2$ ripples, i.e., R4 and R5, so node 2 can no longer generate any more ripples after time $t=2$. In Figure 2, for the sake of illustration, a node that can no longer generate a new ripple is filled in grey color. So, node 2 becomes grey after time $t=2$. For the same reason, after time $t=3$, node 4 and node 6 also become grey. Therefore, ripple $R_8$ does not trigger any new ripple at either node 4 or node 6. Fortunately, this does not jeopardize the ability to find the k shortest paths, and the ORSA of [23] has still found the optimal results successfully, as shown in Figure 2b. Therefore, Figure 2b shows that each node can generate up to k ripples, which is enough to ensure the k shortest paths are found. In terms of computational burden, the RRR progress of Figure 2b generates 15 ripples in total. In comparison, the RRR progress of Figure 2a generates 17 ripples before finding out the 2 shortest paths between O and D. In general, as the problem scale and complexity degree of $k-\mathrm{SPP}$ increase, the ORSA of [7] will generate much more ripples than the ORSA of [23]. This implies that the latter has greater computational efficiency.

Please note that in Figure 2, node O can generate only 1 ripple, i.e., the initial ripple R1, and node D cannot generate any active ripple, i.e., a ripple triggered at D will not spread, so nodes O and D are always grey in color.

Therefore, we can summarize ORSA and ARSA as follows. ORSA is highly versatile, but in the $k-\mathrm{SPP}$, it requires generating at least k ripples for each node, which significantly increases the computational burden and wastes time. ARSA limits the number of ripples generated per node, but this compromises its optimality. Thus, we aim to achieve a good balance between optimality and computational efficiency in solving the $k-\mathrm{SPP}$ by designing strategy $H_T$.

3.2. RSA Without Optimality Guarantee for the $k-\mathrm{SPP}$

To further improve computational efficiency of RSA, we replace the original rule (no more than k ripples at each node) with a relaxed one. That is, each node (not the destination node, which can still generate no more than k ripples) can generate up to h ripples, $1\le h<k$. Thus, “no more than $h<k$ ripples at each node (except the destination)”, the optimality of RSA in solving the $k-\mathrm{SPP}$ is correspondingly reduced. Thus, the RSA with the relaxed rule is called approximate RSA (ARSA) for the $k-\mathrm{SPP}$. It also simulates the RRR progress between the given OD pair in a route network. In the RRR progress, each node can be activated to generate at most $1\le h<k$ ripples. The pseudocode of ARSA is given in Figure 3. In this study, to simplify the analysis while retaining generality, we assume that node 1 is the origin and node $N_N$ is the destination.

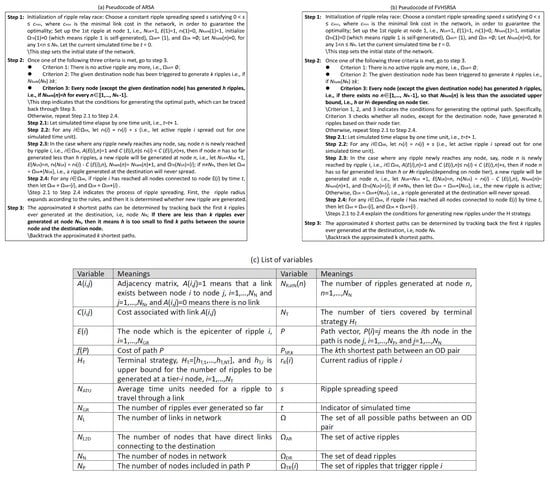
Figure 3. Pseudocodes of the proposed ARSA and FVHSRSA for the $k-\mathrm{SPP}$.

Apparently, Equation (3) in Figure 3 is introduced because of the relaxed rule of “no more than $h<k$ ripples at each node (except the destination)”. From Figure 3, we can see the following: (i) each node (except the given destination node) has been activated and generates h ripples, (ii) each node is limited to generating no more than h ripples, and (iii) if h is too small, the RRR process may output less than k paths between the given OD pair.

Figure 2c applies the ARSA to the same $k-\mathrm{SPP}$ as in Figure 2a,b. In the test of Figure 2c, the ARSA allows each node (except node D) to generate no more than $h=1$ ripple. From Figure 1c, one can see that once a node has been triggered to generate $h=1$ ripple, it then becomes grey in color, which means it can no longer be triggered to generate any more ripples. For example, at time $t=3$, ripple $R_5$ reaches node 4 and ripple $R_6$ reaches node 6. However, these nodes are not triggered because they have already generated $h=1$ ripple at time $t=2$. At time $t=2$, both ripple $R_2$ and ripple $R_3$ reach node 2 simultaneously. However, node 2 can only generate at most $h=1$ ripple according to the rule of ARSA. Randomly, $R_2$ triggers a new ripple, i.e., $R_4$ at node 2, while $R_3$ does not. Figure 2c shows that the ARSA can guarantee to find the true ith shortest path for any $1\le i\le h$. However, it does not guarantee optimality for the jth paths where $h<j\le k$. For example, in the test of Figure 2c, the ARSA finds the 1st shortest path $O\to 3\to 6\to D$ successfully at time $t=3$. However, in Figure 2c, the path associated with ripple $R_8$, i.e., the 2nd ripple that reaches node D, is path $O\to 1\to 2\to 5\to 7\to D$, and the ARSA outputs this path as the 2nd shortest path, which is not correct.

Figure 2c show that each node generates less than k ripples and cannot clearly guarantee the optimality of ARSA for the $k-\mathrm{SPP}$. Thus, for ARSA, it is crucial to explore the relationship between h and k in order to minimize the loss of optimality while maximizing computational efficiency as much as possible. Determine the value of h based on this relationship, the ARSA can achieve a good balance between optimality and computational efficiency. For example, in the test of Figure 2c, ARSA outputs 2 paths by generating only 8 ripples, about half the number generated in Figure 2a or Figure 2b. By sacrificing optimality, computational efficiency is significantly improved. In Section 6, we will mainly conduct comprehensive experiments to study the relationships between optimality, computational efficiency, and the value of $h<k$.

The ARSA in Figure 3a solves the one-to-one $k-\mathrm{SPP}$ problem, which finds k promising paths between a given OD pair. Fortunately, the extension of ARSA to one-to-all $k-\mathrm{SPP}$ is simple. In this case, we need to find k promising paths from a given origin to every other node in the network. For ARSA to solve the one-to-all $k-\mathrm{SPP}$, we can perform a single RRR run, rather than $(N_N-1)$ times for one-to-one $k-\mathrm{SPP}$. After that, the ARSA can output k promising paths from the origin to every other node. For this purpose, we modified the RRR progress at the final step. In one-to-one $k-\mathrm{SPP}$, once the destination node has been reached by k ripples, the RRR will be stopped (see Equation (2) in Figure 3a). In one-to-all $k-\mathrm{SPP}$, the RRR continues until all nodes (except the origin) generate at least k ripples. Here, the number of ripples for each node is h($h<k$).

In reference [23], we have demonstrated that the computational complexity of RSA for solving $k-\mathrm{SPP}$ is $O(k\times N_A\times N_L)$, which is consistent for both one-to-one and one-to-all $k-\mathrm{SPP}$. In this context, $N_N$, $N_L$, and $N_A$ denote the number of nodes, the number of links, and the average number of simulated time units required for a ripple to traverse a link. The primary reason for this complexity reduction is the constraint that each node can generate at most k ripples, rather than an unlimited number. Similarly, the computational complexity of ARSA for solving the $k-\mathrm{SPP}$ is also $O(h\times N_A\times N_L)$, regardless of whether it is one-to-one or one-to-all $k-\mathrm{SPP}$. Since $1\le h<k$, ARSA further reduces the computational complexity. The extent of this reduction depends on the difference between h and k. However, this reduction in computational complexity comes at the cost of some loss in optimality. Therefore, it is crucial to investigate how to set a reasonable value for h so that ARSA can achieve a good balance between optimality and computational efficiency. If ARSA can significantly improve computational efficiency while providing suboptimal solutions, it holds great potential for real-world applications.

4. Fuzzy Variable H Strategy Based on RSA

Based on subjective experience, it isn’t easy to choose a reasonable h value for the ARSA across various route networks to achieve a good balance between algorithm optimality and computational efficiency. Therefore, the ARSA presented in Section 3 is further modified and improved in this section. We can set a uniform h value for all nodes in ARSA to limit the number of ripples that nodes can generate. Furthermore, this section introduces a variable strategy $H_T$, which can adjust the h value more objectively and flexibly. In particular, the adaptive strategy $H_T$ permits nodes closer to the destination to produce more than h ripples(but not larger than k). Consequently, in the network, the majority of nodes retain smaller h values, whereas nodes near the destination can have distinct, larger h values. Additionally, we employ a fuzzy method to constrain the variable strategy $H_T$ to reasonably determine the different h values for nodes close to the destination. Consequently, the ARSA with a fuzzy variable H strategy is named fuzzy variable H strategy based on RSA (FVHSRSA), which can achieve a better balance between optimality and computational efficiency.

4.1. Basic Idea of Strategy $H_T$

Suppose we need to set different h values for nodes other than the destination in the route network, following the rules outlined above. This requires making a series of continuous decisions, particularly for the normal nodes close to the given destination, where the h value needs to be determined according to the strategy $H_T$. In fact, this decision-making method is a terminal strategy.

In various research domains, a terminal strategy is an important control and optimization method. For instance, to ensure optimal control performance, it is common to apply the theory of terminal strategies in model predictive control (MPC) and receding horizon control (RHC) [26,27]. Similarly, the widely used A* algorithm employs a heuristic function to estimate the cost from the current location to the destination, which can also be regarded as a terminal strategy for the A* algorithm [21,28].

It is noteworthy that the variable strategy $H_T$ is a general term. Its purpose, meaning, and realization are largely problem-dependent. Optimization is the primary goal of MPC, RHC, and A* algorithms, typically achieved based on constraint conditions or estimations of the final decision cost.

However, the purpose of FVHSRSA with the variable strategy $H_T$ is not to guarantee optimality but to find a good balance between optimality and computational efficiency. The variable strategy $H_T$ is introduced in this section, where we do not need to consider the last decision cost or set a cost function. Instead, we simply set an upper limit on the number of ripples that nodes close to the destination can generate. As described in Section 3, ARSA sets the same upper limit of $h<k$ for all nodes. Applying this method in large or complex networks results in a significant computational burden. In contrast, using FVHSRSA, the strategy $H_T$ only sets a larger $h<k$ for nodes close to the destination, while other normal nodes maintain a smaller h. Theoretically, FVHSRSA establishes different upper limits to the number of ripples generated by nodes near the destination, a principle that distinguishes it from ARSA.

The variable strategy $H_T$ in this section not only achieves a good balance between optimality and computational efficiency but also addresses the issue of “outputting less than k feasible paths” found in ARSA. Even if the global h value is small, this problem can be mitigated by using the variable strategy $H_T$ to assign different and appropriate h values to nodes close to the destination, something that ARSA cannot accomplish.

To maximize the balance between optimality and computational efficiency while minimizing the cost of optimality with the variable strategy $H_T$, most h values in the route network should be set as small as possible, while the h values of different nodes close to the destination should be as large as feasible. This approach allows FVHSRSA to output a sufficient number of feasible solutions, which are sub-optimal.

Ultimately, to set the h value more objectively, we introduce a fuzzy method to constrain the h values of the variable H strategy. For clarity, we denote the ARSA with the fuzzy variable H strategy as FVHSRSA.

4.2. Design of Variable Strategy $H_T$

For this part, in FVHSRSA, we first introduce the variable strategy $H_T$ and then add the fuzzy method in a later section of this paper. Overall, the variable strategy $H_T$ increases the h value for those nodes close to the destination. The h value varies according to the distance from the node to the destination. In a route network, if a node is directly connected to the destination, it is called a tier − 1 node, and the link length is ignored. If a node is not directly connected to the destination but is directly connected to a tier − 1 node, with the length of the connection also disregarded, it is referred to as a tier − 2 node. We suppose that the destination is a tier − 0 node. In general terms, if a node is directly connected to a tier − i node (where $0\le i$), and this node does not have any direct link with a $\mathrm{tier}-j$ node (for any $0\le j<i$), then this node is classified as a $\mathrm{tier}-(i+1)$ node.

Based on the method above, a variable strategy $H_T$ is introduced. It is defined by a vector $H_T=[h_{T,1},\dots ,h_{T,N_T}]$. Here, $N_T$ is the number of elements in the vector $H_T$, with $1\le N_T$. Each element $h_{T,i}$ represents the upper limit of the number of ripples that can be generated at a tier − i node. Particularly, $h_{T,i}=0$ means $h_{T,i}=h$. Figure 4 provides an illustration of tiered nodes and $H_T$. As shown in Figure 4, except for the origin and destination, there are three tiers of nodes. The impact of network topology on $h_{T,i}$ is reflected in the classification of nodes by strategy $H_T$, which is based on the number of links to the destination node. There are two elements in the vector $H_T$, thus the strategy $H_T$ applies only to two tiers, namely tier − 1 nodes and tier − 2 nodes. The h value of both tier − 1 and tier − 2 nodes is imposed differently. For all other nodes (i.e., tier − 3 nodes in Figure 4), a small h is imposed. If $h_{T,3}$ is set too high, it does not improve computational efficiency. If $h_{T,2}$ is set higher, although computational efficiency improves somewhat, its optimality is still influenced by $h_{T,1}$ (the larger $h_{T,1}$ is, the better optimality guarantee, see Section 6). Please note that Figure 4 is highly simplified for illustration purposes. In general, the number of nodes influenced by the variable strategy $H_T$ is smaller than the number of nodes with h as the upper limit.

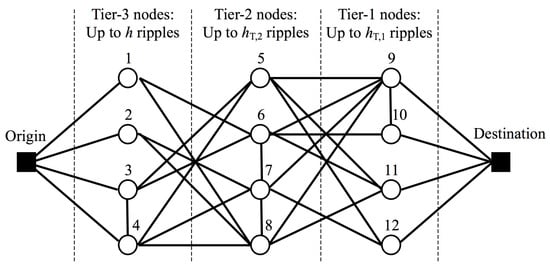
Figure 4. An illustration of tiered nodes and $H_T$.

We need to determine $N_T$ first and then design the variable strategy $H_T=[h_{T,1},\dots ,h_{T,N_T}]$. The setup of $N_T$ and $H_T$ is largely problem-dependent, and some general guidelines are as follows.

Assume that the destination is connected directly by $N_{L2D}$ nodes, then $h_{T,1}$ should be set up to satisfy.

$$N_{L2D}\times h_{T,1}\ge k$$

(6)

The above conditions enable FVHSRSA to output at least k feasible paths. For example, suppose we need to find $k=10$ shortest paths according to the network structure of Figure 4. Then we need to set $h_{T,1}\ge 3$. Otherwise, the RRR progress, which is simulated by FVHSRSA using the variable strategy $H_T$, cannot find 10 feasible paths to the destination in Figure 4.

To enhance the quality of paths under small h conditions, normally, for every $1\le i\le N_T$,

$$h_{T,i}>h$$

(7)

This means that for those nodes close to the destination, we add a little bit of computational burden (i.e., allowing more than h ripples to be generated at these nodes) to enhance the overall quality of the paths identified.

Based on the value of h, the value of $N_T$ should be set as small as possible. For example, if h is comparatively large, $N_T$ can be set to 1. Conversely, if h is very small, setting $N_T$ to 3 might be sufficient to yield a high-quality solution. In general, for any $1\le i\le j\le N_T$, the relationship between $h_{T,i}$ and $N_T$ can be expressed in terms of Equation (8).

$$h_{T,i}\ge h_{T,j}$$

(8)

The Equations (7) and (8) indicate that the number of ripples generated by a node increases as it gets closer to the destination node(this value can be obtained based on the membership function). The reason for this design is that if the given $N_T$ is small enough (i.e., most nodes are not under the variable strategy $H_T$), all or most of the k shortest paths can avoid passing through the same node far from the destination. In other words, the destination of these k shortest paths is relatively uniform, which also reduces the risk of a node. For example, all or most of the k shortest paths may pass through the same tier − 1 node, but the k shortest paths are relatively evenly distributed between tier − 2 and tier − 3 nodes.

Once the variable strategy $H_T$ is set up, we can modify the ARSA, as shown in the pseudocode in Figure 3b. A simple example of FVHSRSA is given in Figure 2d, where the proposed FVHSRSA is applied to the same $k-\mathrm{SPP}$ as in Figure 2a–c. In terms of the upper limit for the number of ripples to be generated at a node, Figure 2d is the same as Figure 2c, i.e., each node is allowed to generate no more than h = 1 ripple, except that the FVHSRSA introduces a variable strategy $H_T=\left[2\right]$, which means those nodes that have direct links connecting to node D, i.e., node 6 and node 7, are allowed to generate up to $h_{T,1}$ = 2 ripples. As a result, although ripple $R_3$ has already triggered ripple $R_5$ at node 6 at time $t=2$, ripple $R_6$ can still trigger another ripple, i.e., $R_8$ at node 6 at time $t=3$. It is ripple $R_8$ that successfully finds the true 2nd shortest path $O\to 3\to 4\to 6\to D$ at time $t=4$. So, in the test of Figure 2d, the FVHSRSA with $h=1$ and $H_T=\left[2\right]$ have found the $k=2$ shortest paths between O and D successfully, just as the ORSAs do in Figure 2a,b. The FVHSRSA achieves this by generating 9 ripples in its relay race, just 1 ripple more than the ARSA of Figure 2c and 6 to 8 ripples less than the ORSAs of Figure 2a,b. Therefore, Figure 2d intuitively demonstrates the FVHSRSA may achieve a much better trade-off between optimality and computational efficiency than the ARSA without strategy $H_T$. In Section 6, we will further investigate through experiments how to set up a proper variable strategy $H_T$ in FVHSRSA for the $k-\mathrm{SPP}$.

4.3. A Fuzzy Approach to Set Up Variable Strategy $H_T$

In theory, a variable strategy $H_T$ may help the ARSA achieve a good balance between optimality and computational efficiency. However, in practice, the benefit of variable strategy $H_T$ will heavily depend on whether the values of $H_T$ are properly set up. Although the previous sub-section gives some guidelines for setting up variable strategy $H_T$, it is largely experience based and needs a try-and-test process, which often takes time.

It is obviously desirable for an approach that, once a $k-\mathrm{SPP}$ is given, is capable of automatically choosing a proper variable strategy $H_T$ to achieve a good balance between optimality and computational efficiency. The guidelines given in the previous sub-section are largely experience-based knowledge. As is well known, fuzzy theory and methods are very powerful in dealing with experience-based knowledge [29]. Therefore, in this sub-section, we will propose a fuzzy approach for setting up a fuzzy variable strategy $H_T$ automatically according to the characteristics of a given $k-\mathrm{SPP}$. In other words, we will develop a fuzzy inference process, where the inputs are the characteristics of a given $k-\mathrm{SPP}$, and the outputs are the numerical values of $h_{T,i}$ in variable strategy $H_T$, $i=1,\cdots ,N_T$.

In this study, the characteristics of a given $k-\mathrm{SPP}$ can be described by the numerical values of some network parameters, such as the value of k, the number of nodes $N_N$, the number of links $N_L$, and the number of $\mathrm{tier}-i$ nodes, $i=1$,…,$N_T$. Besides, the parameter of ARSA for $k-\mathrm{SPP}$, i.e., h is also used as an input to the fuzzy inference process, and obviously, h is also numerical value based.

Therefore, the fuzzy inference process proposed here has numerical value based inputs and also numerical value based outputs. Then, the first step is to fuzzify inputs, and the last step is to defuzzify outputs.

The absolute value for $N_N$, $N_L$, k, h, or the number of tier − i nodes could be within a huge range. It makes little sense to directly fuzzify $N_N$, $N_L$, k, h, and the number of $\mathrm{tier}-i$ nodes. It is better to fuzzify something whose numerical value is within the range [0, 1]. So, we need to normalize the values of $N_N$, $N_L$, k, h, and the number of $\mathrm{tier}-i$ nodes. However, we usually do not pre-know the maximal values of $N_N$, $N_L$, k, h, and the number of $\mathrm{tier}-i$ nodes before all test cases of $k-\mathrm{SPP}$ are given to us, so we can hardly rely on the way of normalization by dividing the absolute value of a variable by the associated maximal value.

To make sure that we can still normalize inputs even based on a single given test case (i.e., we do not have the information of maximal values of inputs), we construct the following new variables based on $N_N$, $N_L$, k, h, and the number of $\mathrm{tier}-i$ nodes (denoted as $N_{Tier-i}$), and we will use them as inputs to our fuzzy inference process (this paper uses a triangular membership function).

$$v_{NI,1}={\displaystyle \frac{k}{N_N\times N_L}}$$

(9)

$$v_{NI,2}={\displaystyle \frac{h}{N_N\times N_L}}$$

(10)

$$v_{NI,3}={\displaystyle \frac{h}{k}}$$

(11)

$$v_{NI,4}\left(i\right)={\displaystyle \frac{h\times N_{Tier-i}}{k}},i=1,\cdots ,N_T$$

(12)

Since we usually have $k\ll N_N\times N_L$, the values of $v_{NI,1}$, $v_{NI,2}$, and $v_{NI,3}$ are within $(0,1)$. So, we only need to normalize $v_{NI,4}\left(i\right)$, $i=1,\cdots ,N_T$. To be more rigorous, we modify Equations (9) and (10) as follows:

$$v_{NI,1}=min\left(1,{\displaystyle \frac{k}{N_N\times N_L}}\right)$$

(13)

$$v_{NI,2}=min\left(1,{\displaystyle \frac{h}{N_N\times N_L}}\right)$$

(14)

The variable $v_{NI,4}\left(i\right)$ is used to determine $h_{T,i}$ in variable strategy $H_T$. Basically, if $v_{NI,4}\left(i\right)\gg 1$ (i.e., $h\times N_{Tier-i}\gg k$), then, even though a $\mathrm{tier}-i$ node can only generate no more than 1 ripple, all $\mathrm{tier}-i$ nodes can still generate much more than k ripples in total, which means the k shortest paths are unlikely to be missed out by $\mathrm{tier}-i$ nodes. In this study, we suppose $v_{NI,4}\left(i\right)=10$ is large enough for $\mathrm{tier}-i$ nodes to generate all necessary ripples associated with the k shortest paths. Therefore, we can modify Equation (12) as follows:

$$v_{NI,4}\left(i\right)={\displaystyle \frac{1}{10}}min\left(10,{\displaystyle \frac{h\times N_{Tier-i}}{k}}\right),i=1,\dots ,N_T$$

(15)

In this study, we assume $N_T$ is given and fixed as $N_T=3$, i.e., the variable strategy $H_T=[h_{T,1},h_{T,2},h_{T,3}]$ only covers tier − 1, tier − 2, and tier − 3 nodes. As will be demonstrated by the experimental results in Section 6, $N_T=3$ seems large enough to allow the first 3 tiers of nodes to generate most necessary ripples associated with the k shortest paths. Therefore, the fuzzy inference process only needs to calculate the values of $h_{T,1}$, $h_{T,2}$, and $h_{T,3}$. The numerical value range of $h_{T,1}$ to $h_{T,3}$ is $[h,k]$.

Now, we need to design a fuzzy inference process that has 4 inputs, i.e., $v_{NI,1}$ to $v_{NI,4}$, and 3 outputs, i.e., $h_{T,1}$ to $h_{T,3}$. Basically, the fuzzy inference process will calculate $h_{T,i}$, $i=1,2,3$, based on $v_{NI,1}$ to $v_{NI,4}$. Roughly speaking, the larger $v_{NI,1}$ is, the larger $h_{T,i}$ should be, while the smaller $v_{NI,2}$, $v_{NI,3}$, or $v_{NI,4}$ is, the larger $h_{T,i}$ should be.

To fuzzify $v_{NI,i}$, $i=1,\cdots ,4$, and to defuzzify $h_{T,j}$, $j=1,2,3$, we use triangle-shaped membership functions to determine how likely $v_{NI,i}$ has a fuzzy value of “large”, “medium” and “small” (LD, MD, SD), respectively. The mathematical formulas for the membership functions of these 3 fuzzy sets are as Equation (16) (i = 1, 2, 3, 4).

$$\begin{array}{cc}\hfill SD\left(v_{NI,i}\right)& ={\displaystyle \frac{0.5-v_{NI,i}}{0.5}},0\le v_{NI,i}\le 0.5\hfill \\ \hfill MD\left(v_{NI,i}\right)& =\left\{\begin{array}{cc}{\displaystyle \frac{v_{NI,i}}{0.5}}\hfill & 0\le v_{NI,i}\le 0.5,\hfill \\ {\displaystyle \frac{1-v_{NI,i}}{0.5}}\hfill & 0.5\le v_{NI,i}\le 1,\hfill \end{array}\right.\hfill \\ \hfill LD\left(v_{NI,i}\right)& ={\displaystyle \frac{v_{NI,i}-0.5}{0.5}},0.5\le v_{NI,i}\le 1\hfill \end{array}$$

(16)

Please note that to calculate different $h_{T,j}$, the membership functions of the same $v_{NI,i}$ will also be different in detail. In other words, for the same $v_{NI,i}$, there are 3 sets of membership functions: one set for calculating $h_{T,1}$, one set for $h_{T,2}$, and the last set for $h_{T,3}$.

This is because the same numerical value of $v_{NI,i}$ needs to be viewed as a different fuzzy value when calculating different $h_{T,j}$. Basically, based on the same sets of numerical values for $v_{NI,1}$ to $v_{NI,4}$, $h_{T,1}$ should stand a larger chance than $h_{T,2}$, and $h_{T,2}$ should stand a larger chance than $h_{T,3}$, to have the fuzzy value “large”, in order to be in line with the guideline of Equation (8).

Figure 5 gives the flowchart of the proposed fuzzy inference process. In addition to the input and output, there are 4 key steps. The first step mainly processes inputs according to Equations (9)–(15) and performs normalization. The second step substitutes the normalized inputs into the membership functions of the 3 sets (“large,” “medium,” and “small”). This leads to the results for the third step. Finally, the defuzzification process is applied to obtain the $h_{T,i}$ for each set.

Figure 5. Flowchart of fuzzy approach for determining variable strategy $H_T$.

The $h_{T,i}$ obtained through the membership functions can achieve a good balance between optimality and computational efficiency. However, if we aim to optimize $h_{T,i}$, this becomes a more complex situation, as it requires considering the network topology and connectivity degree. Due to limited space, here we mainly focus on explaining problem-specific issues as discussed above and skip those technical details of designing a standard fuzzy inference process, for which readers may refer to [29]. Of course, the fuzzy approach for setting up variable strategy $H_T$ proposed here could be further modified and improved, for example, in future research, using evolutionary algorithms to optimize membership functions, allowing $N_T$ to change, and then using fuzzy rules to choose a proper value for $N_T$ according to the characteristics of a given $k-\mathrm{SPP}$.

5. Further Extensions of FVHSRSA

One might worry about the demerit that ORSA has no theoretical guarantee of optimality due to the introduction of $h<k$. Actually, this demerit could somehow become a merit in many real-world applications of $k-\mathrm{SPP}$. Basically, one reason why the $k-\mathrm{SPP}$ attracts more interest in reality than the 1st shortest path problem is that a real-world routing environment is often time-varying due to various disturbances [30,31]. The $k-\mathrm{SPP}$ can provide many backup solutions in case the 1st shortest path is closed under disturbances [9,10]. However, can those backup solutions of the $k-\mathrm{SPP}$ with an optimality guarantee really give us peace of mind when the routing environment is full of disturbances?

As shown in the example of Figure 6, assume we need to find 3 paths between the given OD pair for the sake of backup solutions under disturbances. A $k-\mathrm{SPP}$ method with optimality guarantee will output paths $O\to 2\to 6\to 10\to D$, $O\to 2\to 6\to 11\to D$, and $O\to 2\to 6\to 9\to D$ as the 3 shortest paths. These 3 paths are solutions of the $k-\mathrm{SPP}$ obtained in a time-varying network, and they all include nodes 2 and 6. Unfortunately, in the case of failure of either node 2 or node 6, all of these 3 paths will become infeasible, which means we get no backup solutions at all. However, if we impose a constraint that a node (excluding the origin and the destination) can appear no more than once in all of the k backup solutions, then we get 3 paths as $O\to 2\to 6\to 10\to D$, $O\to 1\to 5\to 9\to D$, and $O\to 3\to 7\to 12\to D$. In this way, no matter which node of the network fails, the other backup paths will still work properly. This constraint reduces the failure rate of the $k-\mathrm{SPP}$ path planning. We call the $k-\mathrm{SPP}$ with such a constraint as constrained $k-\mathrm{SPP}$. Obviously, based on those solutions outputted by the constrained $k-\mathrm{SPP}$, no matter which intermediate node is closed, we will always have two good backup solutions feasible in Figure 6. Actually, in the example of Figure 6, even if any two intermediate nodes are closed simultaneously, the results of the constrained $k-\mathrm{SPP}$ will still have at least one good backup solution feasible.

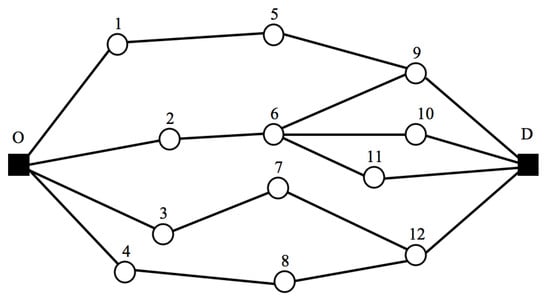
Figure 6. An example to illustrate constrained $k-\mathrm{SPP}$.

Figure 6 illustrates that the $k-\mathrm{SPP}$ with an optimality guarantee could make no sense in terms of providing backup solutions in a time-varying routing environment. In other words, the example of Figure 6 might suggest that, for the sake of better backup solutions, it could be necessary to demand that all backup solutions should not share any node (excluding the origin and the destination) for more than $1\le h<k$ times (a general form of constraint). Here, the value of h for the constraint may be determined according to how likely each node might be closed by disturbances. Therefore, the constrained $k-\mathrm{SPP}$, although lacking a traditional optimality guarantee, makes more sense in terms of providing backup solutions in reality.

The ARSA reported in Section 3 and Section 4 can be easily extended to resolve the constrained $k-\mathrm{SPP}$. We only need to make a straightforward modification as follows. Whenever a ripple reaches the destination, any node the ripple has passed through will count one more time. Once a node has counted for h times, then no more new ripple can be generated at the node, and any active ripples that have passed through the node will be updated as dead ripples immediately.

The ARSA can be extended to other path optimization problems, thanks to the flexibility in modifying RRR. As discussed in [7], many traditional methods for path optimization are centralized, global information and logic rule-based algorithms, and the demand for global information often implies difficulty in problem-specific modifications. Differently, RSA is a decentralized, multi-agent based simulation model. Each agent, i.e., node, only needs local information on its incoming ripples to decide its micro behaviors of generating and spreading new ripples. By simply modifying node micro behaviors, RSA can be easily applied to various path problems, some of which might not be friendly to traditional methods. For example, networks with time windows are much less touched by traditional $k-\mathrm{SPP}$ methods, and for a highly simplified case, a traditional $k-\mathrm{SPP}$ method may cause a computational complexity of $O(k\times r\times N_N^3)$ [19]. By simply introducing waiting and co-triggering behaviors of nodes, RSA can resolve much more general and more complicated time-window $k-\mathrm{SPP}$s, and the computational complexity is just about $O(k\times N_{ATU}\times N_L)$. For time-dependent path optimization, finding the 1st shortest path even demands a time-expanded hyper-graph of enormous size [32,33], and the $k-\mathrm{SPP}$ version has rarely been discussed. In a novel framework of co-evolutionary simulation procedure, RSA can address the $k-\mathrm{SPP}$ version of time-dependent path optimization in a network of very original size [30]. There is very little work ever reported with an optimality guarantee to target the k best solutions to project time management problems [34,35], while an RSA with some problem-specific modifications can achieve it with an optimality guarantee.

The rule of “no more than $1\le h<k$ ripples at each node” and the fuzzy variable strategy $H_T$ reported in this paper can be applied to those RSAs above in a straightforward manner. In other words, the proposed ARSA can be extended to some complicated $k-\mathrm{SPP}$ variants that are less well addressed by traditional $k-\mathrm{SPP}$ methods. Real-world applications often pursue a good trade-off between optimality and computational efficiency. Therefore, the ARSA is worth attention because it can offer more flexible solutions in terms of such a balance.

6. Experiment Results

6.1. Network Used in Experiments

This section of the experiment aims to (i) reveal the relationship between the reported ARSA optimality and computational efficiency for the $k-\mathrm{SPP}$, (ii) investigate whether the reported strategy $H_T$ can enhance the ARSA of $k-\mathrm{SPP}$, and how to appropriately design the fuzzy variable strategy $H_T$ for various network types. Thus, two experiments are performed. The first experiment compares the performance of ARSA with the variable strategy $H_T$ and without the strategy $H_T$. The second experiment compares the performance of FVHSRSA with several different h value strategies. These two experiments are conducted on four different types of networks that are very common in our daily life.

The first type of network is the grid network, where the nodes are distributed in a rectangular arrangement. Each node in this situation is only connected to its neighbors. Grid networks are commonly applied in circuit design and video game development. The second type of network is the random network. In this study, we develop a random network by modifying a grid network, i.e., introducing random disturbances to the spatial locations of the nodes in the grid network and randomly altering a small fraction of the links. Many route networks in big cities can be considered as random networks. The third type of network is generated by the method reported in reference [36]. This network, which has a small-world topology, is a common phenomenon in reality. For example, the widely recognized occurrence of “6 degrees of separation” is the result of small-world topology [37,38]. Therefore, the third type of network is referred to as a small-world network. The fourth type of network is created using the method described in reference [39]. It exhibits a scale-free topology, where the majority of nodes are sparsely connected, while a small number of central nodes possess a large number of connections to most other nodes. Scale-free topology is commonly found in both natural and man-made network systems, such as food webs, chemical reaction chains, airline route networks, the World Wide Web, and co-authorship networks [37,38,40]. Therefore, the fourth type of network is referred to as a scale-free network. Testing these four types of networks ensures that the proposed method has good application potential.

To intuitively illustrate how the $k–$shortest paths in these four network types look like, some examples of $k-\mathrm{SPP}$ with $k=12$ (i.e., the first 12 shortest paths need to be found) are given in Figure 7, Figure 8, Figure 9 and Figure 10. The networks in Figure 7, Figure 8, Figure 9 and Figure 10 have $N_N=100$ and $N_L=600$ each, and the cost of a link, i.e., $C(i,j)$, is defined as the straight line distance from node i to node j. For each network in Figure 7, Figure 8, Figure 9 and Figure 10, we apply three ARSAs to resolve the $k-\mathrm{SPP}$. The first ARSA has $h=k=12$ without the variable H strategy. The second ARSA has $h=2$ without the variable H strategy. The third ARSA is the FVHSRSA with $h=2$ and $H_T=[6,4]$, i.e., in the FVHSRSA, all nodes are allowed to generate up to $h=2$ ripples (just like in the second ARSA), except that tier − 1 nodes can generate up to 6 ripples, and tier − 2 nodes can generate up to 4 ripples.

Figure 7. Resolving $k-\mathrm{SPP}$ with k = 12 in a gird network by different ARSAs.

Figure 8. Resolving $k-\mathrm{SPP}$ with k = 12 in a random network by different ARSAs.

Figure 9. Resolving $k-\mathrm{SPP}$ with k = 12 in a small-world network by different ARSAs.

Figure 10. Resolving $k-\mathrm{SPP}$ with k = 12 in a scale-free network by different ARSAs.

It can be seen from Figure 7, Figure 8, Figure 9 and Figure 10 that the routing environments of these four networks are very different. For example, in grid networks and random networks, an optimal path from the left-bottom node to right-top node is typically close to a diagonal trajectory, while in small-world networks and scale-free networks, an optimal path usually has little resemblance to the diagonal line. This can be easily comprehended since, in grid and random networks, most nodes are only connected to their neighbors, and there will always be some nodes close to the diagonal for the next step. In small-world and scale-free networks, connections between nodes are very random, and nodes close to the diagonal may not connect to any other node near the diagonal. For example, in a grid or random network, an optimal path usually passes through many intermediate nodes, while in a small-world network or a scale-free network, an optimal path has only a few intermediate nodes (i.e., small-world characteristics), especially in scale-free networks. Due to the existence of these hub nodes, connecting a given OD pair requires traversing only one or two intermediary nodes. This non-proportional network feature is particularly advantageous in the aviation network, as it takes time to switch at an intermediate airport, so passengers tend to opt for routes with fewer flights [41].

From Figure 7, Figure 8, Figure 9 and Figure 10, one can also see that the ARSA with $h=k=12$ can always find those true 12 shortest paths, no matter what network category. The ARSA with $h=2$ has the worst performance in terms of the number of optimal paths found. Compared with the ARSA under $h=2$, the ARSAT exhibits obvious improvement in the number of optimal paths found.

However, Figure 7, Figure 8, Figure 9 and Figure 10 mainly illustrate what different categories of networks look like and how the reported ARSA with different parameter settings could work on them. Before we can make any serious conclusions about the performance of ARSA with or without variable strategy $H_T$, we need to carry out more comprehensive experiments, which are presented in the next two subsections.

6.2. Experimental Results about ARSA with and without Strategy $H_T$

Firstly, we conduct comprehensive experiments to study the relationship between the optimality and computational efficiency of the reported ARSA for the $k-\mathrm{SPP}$. In the network, each node has about 6 links on average.

Thus, the problem scale of the $k-\mathrm{SPP}$ can be determined by $N_N$ and k. In this section, the problem scale is set with $N_N=400$ and $k=100$. For each of the four network types, 100 networks are randomly generated. For each generated network, the original ARSA from Section 3 (i.e., the ARSA without variable strategy $H_T$) is applied with values of $h=5$, 10, 20, 50, and 100, respectively. Then, we implement a 3-tiered variable strategy $H_T$ for ARSA with $h=5$. In this 3-tiered strategy $H_T$, $h_{T,1}=50$, $h_{T,2}=20$, and $h_{T,3}=10$. We analyze the average path length (APL) of these paths output by ARSA. Additionally, we examine the average computational time (CT) (in seconds) that ARSA requires across 100 networks of a specific type. Furthermore, we assess the average number of paths (NPO) output by ARSA for over 100 networks in each category. Given that $k=100$, we know that the result for $h=100$ corresponds to the optimal solution of the $k-\mathrm{SPP}$ [23]. Therefore, for ARSA with $h<k$, we check how many output paths coincide with those of ARSA with $h=k$, which gives the average number of optimal paths found (NOPF) by ARSA across 100 networks of a specific category. The results for APL, CT, NPO, and NOPF are presented in Table 1, which illustrates the following.

• If the value of h is set too small, then the ARSA without $H_T$ can identify very few of the k shortest paths, i.e., a excessively small h value usually results in less than k feasible paths calculated by ARSA without $H_T$. This explains why there is a symbol of “>” in some cases of ARSA without $H_T$. Therefore, in the next few bullet points, we mainly discuss those cases without the symbol ‘>’, which means the ARSA without $H_T$ has outputted at least 100 feasible paths.
• In general, the ARSA without $H_T$ for the $k-\mathrm{SPP}$, when compared with the case of $h=k=100$, can achieve a fair trade-off between optimality and computational efficiency. As an illustration, across the 4 experimental groups, the CT value at $h=50$, ranges from approximately 39% to 59% of the CT value at $h=k=100$ (which ensures optimality), while the APL value at $h=50$ is only around 2% higher than the APL value at $h=k=100$.
• Table 1 highlights that for grid networks, specifically grid networks, ARSA without $H_T$ can substantially enhance computational efficiency while guaranteeing optimality, even when $h=50$. This is explainable because many different paths share the same 1st shortest path length in a gird network.
• For random networks, small-world networks, and scale-free networks, the optimality of ARSA without $H_T$ is lost when $h=50$. As illustrated in Figure 8, Figure 9 and Figure 10, for random networks and small-world networks, there are not many paths that share the same Average Path Length (APL). Actually, there is often only one path that has the j-th shortest APL, where $1\le j\le k$. This clarifies why the ARSA without $H_T$ is more prone to losing its optimality in such cases for random networks, small-world networks, and scale-free networks than for grid networks.
• Table 1 also implies that it is the most difficult to maintain the optimality for scale-free networks because when $h=50$, the ARSA without $H_T$ has found the fewest of the theoretical optimal $k=100$ shortest paths, i.e., the NOPF in scale-free networks has the smallest value among all the 4 network categories. It is also reasonable to see that in a scale-free network, numerous shortest paths must pass through a limited number of hub nodes. If a hub node is restricted to being utilized only $h<k$ times, several shortest paths may be excluded.
• Roughly speaking, the experimental results indicate that the CT value of ARSA without $H_T$ increases linearly as h goes up from 5 to 100 in all network categories. This is in line with the theoretical analysis in Section 3.2.

Table 1. Average results about the influence of h and variable strategy $H_T$ on approximate ripple–spreading algorithm.

${\mathit{N}}_{\mathit{N}}$ = 400, ${\mathit{N}}_{\mathit{L}}$ = 2400, k = 100		Without ${\mathit{H}}_{\mathit{T}}$ Strategy					With ${\mathit{H}}_{\mathit{T}}$ Strategy
		$\mathit{h}=\mathbf{5}$	$\mathit{h}=\mathbf{10}$	$\mathit{h}=\mathbf{20}$	$\mathit{h}=\mathbf{50}$	$\mathit{h}=\mathbf{100}$	${\mathit{H}}_{\mathit{T}}$ = [50,20,10],$\mathit{h}=\mathbf{5}$
Grid Networks	Average path length ($\times {10}^3$)	>3.1806	>3.1806	>3.1806	3.1806	3.1806	3.1806
	Computational time (in seconds)	0.27	0.50	1.22	3.85	10.26	0.29
	Number of paths outputted by ARSAT	15.00	30.00	60.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	15.00	30.00	60.00	100.00	100.00	100.00
Random Networks	Average path length ($\times {10}^3$)	>3.0220	>3.0261	>3.0163	2.9425	2.9138	2.9762
	Computational time (in seconds)	2.39	4.82	10.95	23.84	51.05	2.97
	Number of paths outputted by ARSAT	31.02	58.84	95.23	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	6.02	10.22	23.15	61.97	100.00	24.72
Small-World Networks	Average path length ($\times {10}^3$)	>5.0025	>5.4007	>4.7803	4.3921	4.3607	4.4739
	Computational time (in seconds)	5.26	13.75	20.15	44.06	72.73	13.77
	Number of paths outputted by ARSAT	44.84	80.35	98.05	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	9.22	17.98	29.26	64.72	100.00	59.28
Scale-Free Networks	Average path length ($\times {10}^3$)	>4.3582	>4.5756	>4.6430	3.3926	3.3627	3.4562
	Computational time (in seconds)	4.85	9.85	19.62	23.57	43.02	11.01
	Number of paths outputted by ARSAT	26.89	56.93	98.95	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	6.37	13.08	23.27	58.66	100.00	54.92

Table 1. Average results about the influence of h and variable strategy $H_T$ on approximate ripple–spreading algorithm.

${\mathit{N}}_{\mathit{N}}$ = 400, ${\mathit{N}}_{\mathit{L}}$ = 2400, k = 100		Without ${\mathit{H}}_{\mathit{T}}$ Strategy					With ${\mathit{H}}_{\mathit{T}}$ Strategy
		$\mathit{h}=\mathbf{5}$	$\mathit{h}=\mathbf{10}$	$\mathit{h}=\mathbf{20}$	$\mathit{h}=\mathbf{50}$	$\mathit{h}=\mathbf{100}$	${\mathit{H}}_{\mathit{T}}$ = [50,20,10],$\mathit{h}=\mathbf{5}$
Grid Networks	Average path length ($\times {10}^3$)	>3.1806	>3.1806	>3.1806	3.1806	3.1806	3.1806
	Computational time (in seconds)	0.27	0.50	1.22	3.85	10.26	0.29
	Number of paths outputted by ARSAT	15.00	30.00	60.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	15.00	30.00	60.00	100.00	100.00	100.00
Random Networks	Average path length ($\times {10}^3$)	>3.0220	>3.0261	>3.0163	2.9425	2.9138	2.9762
	Computational time (in seconds)	2.39	4.82	10.95	23.84	51.05	2.97
	Number of paths outputted by ARSAT	31.02	58.84	95.23	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	6.02	10.22	23.15	61.97	100.00	24.72
Small-World Networks	Average path length ($\times {10}^3$)	>5.0025	>5.4007	>4.7803	4.3921	4.3607	4.4739
	Computational time (in seconds)	5.26	13.75	20.15	44.06	72.73	13.77
	Number of paths outputted by ARSAT	44.84	80.35	98.05	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	9.22	17.98	29.26	64.72	100.00	59.28
Scale-Free Networks	Average path length ($\times {10}^3$)	>4.3582	>4.5756	>4.6430	3.3926	3.3627	3.4562
	Computational time (in seconds)	4.85	9.85	19.62	23.57	43.02	11.01
	Number of paths outputted by ARSAT	26.89	56.93	98.95	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	6.37	13.08	23.27	58.66	100.00	54.92

6.3. Experimental Results about the Effect of Different Strategy $H_T$

In this sub-section of experiments, we further investigate how to choose a proper variable strategy $H_T$ to improve the performance of FVHSRSA for the k − SPP. The networks used here are set up in the same way as in the previous sub-section of experiments. There are two sets of experiments, one set with $h=5$ and the other with $h=10$. For each set of experiments, we change the settings of the variable strategy $H_T=[h_{T,1},h_{T,2},h_{T,3}]$ for FVHSRSA and then apply it to every network generated. Basically, if $h_{T,i+1}\le h<h_{T,i}$, where $i=1,2,3$, then it is an i-tiered variable strategy $H_T$.

First, we provide ARSAT with five different manual settings of $H_T$, i.e., $H_T=[50,0,0],[50,20,0],[50,20,10],[50,50,50]$, and [100,100,100]. Then, we apply the fuzzy approach proposed in Section 4.3 to set up $H_T$ according to some characteristics of a given $k-\mathrm{SPP}$. Again, we focus on analyzing APL, CT, NPO, and NOPF results, which are given in Table 2 and Table 3. Based on Table 2 and Table 3 (with reference to Table 1 sometimes), one may have the following observations.

• Comparing Table 1 and Table 2, we can see that, without variable strategy $H_T$, the ARSA without $H_T$ often can’t achieve a good balance between optimality and computational efficiency, i.e., if h is too small, the ARSA without $H_T$ can hardly generate k feasible paths, while if h is too large, the CT soars up quickly, and the efficiency of this algorithm cannot be guaranteed. Thanks to the variable strategy $H_T$, the FVHSRSA with $h=5$ can achieve similar performance in terms of APL to the ARSA without $H_T$ with $h=50$, while the CT of FVHSRSA with $h=5$ is just about two to ten times than the CT of ARSA without $H_T$ with $h=50$.
• When comparing the FVHSRSA under $h=5$ with the ARSA without $H_T$ under $h=100$, which gives the theoretical optimal k shortest paths, the APL of FVHSRSA is about 3% larger than the APL of ARSA without $H_T$, but the CT of FVHSRSA may be just one-thirtieth of the CT of ARSA without $H_T$. This means the FVHSRSA with $h=5$ can significantly improve the computational efficiency with little sacrifice in optimality.
• As a result, in comparison to the ARSA without $H_T$, the proposed FVHSRSA achieves a good balance between optimality and efficiency.
• Table 2 and Table 3 present comparative results for different variable strategies applied to the FVHSRSA. In general, higher values of h and $H_T$ lead to shorter APLs, but are associated with increased CT values.
• Once the values of h and $H_T$ reached a certain threshold, although h and $H_T$ will increase, the APL will not be shorter. The CT value will continue to keep increasing. Therefore, the strategy $H_T$ needs to be set up appropriately for the FVHSRSA.
• In the experiments presented in Table 2 and Table 3, the manual setting of variable strategy $H_T=[50,20,10]$ achieves a good balanced between optimality and efficiency.
• However, finding a proper manual setting of the variable strategy $H_T$ is usually a try-and-test process, and it often takes time. The fuzzy approach of Section 4.3 for setting up the variable strategy $H_T$ is much more effective and efficient, as shown in Table 2 and Table 3. Basically, for a given $k-\mathrm{SPP}$, the fuzzy approach automatically calculates $H_T$ according to some network parameters such as $N_N$, $N_L$, the number of $\mathrm{tier}-i$ nodes, $1\le i\le N_T$, and the values of h and k are also taken into account. Table 2 and Table 3 show that the FVHSRSA with fuzzy variable strategy can often achieve a performance similar to those of the ARSAT with manual settings $H_T=[50,20,10]$ and $H_T=[50,50,50]$, which deliver well-balanced performance.
• Both manual setting of the variable strategy $H_T$ and the fuzzy method can achieve a good balance between optimality and conputational effiency. However, the fuzzy method tends to yied better results with higher probability. The determination of $h_{T,i}$ depends on various factors, such as network topology, connectivity(the average number of links per node), and even the values of $H_T$. The underlying patterns require extensive experimentation or optimization using neural networks. The $k-\mathrm{SPP}$ is a complex problem, and manual settings are often based on a limited set of factors, with a strong subjective component, which may not perform consistently across network topology. In contrast, the fuzzy method can consider multiple network characteristics(e.g., h, k, $N_N$, $N_L$, and the number of tier − i nodes) to adjust $H_T$ in a more comprehensive manner, better adapting to diverse network environments and problem scales.
• It is important to highlight that the configuration of the variable strategy $H_T$ requires further exploration when the FVHSRSA is applied to real-world scenarios. The findings presented in Table 2 and Table 3 primarily underscore the significance of this investigation in determining the optimal setup for the variable strategy $H_T$. Especially, it is worth efforts to further improve the fuzzy approach of Section 4.3, such as considering more network parameters in fuzzy inference and using a genetic algorithm to optimize membership functions. This can be done better when a particular application study is carried out.

Table 2. Average results about the influence of different variable strategies $H_T$ on approximate ripple–spreading algorithm with $h=5$.

		Manual Setup					Fuzzy Setup
${\mathit{H}}_{\mathit{T}}$		[50,0,0]	[50,20,10]	[50,50,50]	[100,100,100]	${\mathit{H}}_{\mathit{T}}$ ≤ [58,35,17]
Grid Networks	Average path length ($\times {10}^3$)	3.2351	3.2040	3.1806	3.1806	3.1806	3.1806
	Computational time (in seconds)	0.24	0.26	0.29	0.33	0.38	0.27
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	30.00	45.00	100.00	100.00	100.00	100.00
Random Networks	Average path length ($\times {10}^3$)	2.9816	2.9795	2.9762	2.9713	2.9689	2.9728
	Computational time (in seconds)	2.81	2.86	2.97	3.93	4.58	3.41
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	13.18	15.37	24.72	31.44	34.88	30.07
Small-World Networks	Average path length ($\times {10}^3$)	4.5575	4.5007	4.4739	4.4616	4.4176	4.4679
	Computational time (in seconds)	7.31	9.76	13.77	16.04	17.56	14.69
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	37.58	44.93	59.28	65.46	87.30	61.32
Scale-Free Networks	Average path length ($\times {10}^3$)	3.7516	3.5449	3.4562	3.3627	3.3627	3.3627
	Computational time (in seconds)	5.21	6.96	11.01	11.85	13.68	11.38
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	18.49	28.47	54.92	100.00	100.00	100.00

Table 2. Average results about the influence of different variable strategies $H_T$ on approximate ripple–spreading algorithm with $h=5$.

		Manual Setup					Fuzzy Setup
${\mathit{H}}_{\mathit{T}}$		[50,0,0]	[50,20,10]	[50,50,50]	[100,100,100]	${\mathit{H}}_{\mathit{T}}$ ≤ [58,35,17]
Grid Networks	Average path length ($\times {10}^3$)	3.2351	3.2040	3.1806	3.1806	3.1806	3.1806
	Computational time (in seconds)	0.24	0.26	0.29	0.33	0.38	0.27
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	30.00	45.00	100.00	100.00	100.00	100.00
Random Networks	Average path length ($\times {10}^3$)	2.9816	2.9795	2.9762	2.9713	2.9689	2.9728
	Computational time (in seconds)	2.81	2.86	2.97	3.93	4.58	3.41
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	13.18	15.37	24.72	31.44	34.88	30.07
Small-World Networks	Average path length ($\times {10}^3$)	4.5575	4.5007	4.4739	4.4616	4.4176	4.4679
	Computational time (in seconds)	7.31	9.76	13.77	16.04	17.56	14.69
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	37.58	44.93	59.28	65.46	87.30	61.32
Scale-Free Networks	Average path length ($\times {10}^3$)	3.7516	3.5449	3.4562	3.3627	3.3627	3.3627
	Computational time (in seconds)	5.21	6.96	11.01	11.85	13.68	11.38
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	18.49	28.47	54.92	100.00	100.00	100.00

Table 3. Average results about the influence of different variable strategies $H_T$ on approximate ripple–spreading algorithm with $h=10$.

		Manual Setup					Fuzzy Setup
${\mathit{H}}_{\mathit{T}}$		[50,0,0]	[50,20,10]	[50,50,50]	[100,100,100]	${\mathit{H}}_{\mathit{T}}$ ≤ [53,28,15]
Grid Networks	Average path length ($\times {10}^3$)	3.2058	3.1806	3.1806	3.1806	3.1806	3.1806
	Computational time (in seconds)	0.53	0.52	0.56	0.60	0.68	0.53
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	48.00	100.00	100.00	100.00	100.00	100.00
Random Networks	Average path length ($\times {10}^3$)	2.9733	2.9702	2.9671	2.9618	2.9606	2.9633
	Computational time (in seconds)	4.66	4.91	5.14	5.89	6.34	5.68
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	31.05	40.27	44.77	51.18	54.27	49.63
Small-World Networks	Average path length ($\times {10}^3$)	4.5053	4.4722	4.4630	4.4582	4.4126	4.4612
	Computational time (in seconds)	15.18	16.77	26.04	28.22	32.75	26.89
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	45.05	58.14	63.56	72.22	96.07	69.65
Scale-Free Networks	Average path length ($\times {10}^3$)	3.3627	3.3627	3.3627	3.3627	3.3627	3.3627
	Computational time (in seconds)	11.38	13.14	17.03	19.25	22.09	17.25
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00

Table 3. Average results about the influence of different variable strategies $H_T$ on approximate ripple–spreading algorithm with $h=10$.

		Manual Setup					Fuzzy Setup
${\mathit{H}}_{\mathit{T}}$		[50,0,0]	[50,20,10]	[50,50,50]	[100,100,100]	${\mathit{H}}_{\mathit{T}}$ ≤ [53,28,15]
Grid Networks	Average path length ($\times {10}^3$)	3.2058	3.1806	3.1806	3.1806	3.1806	3.1806
	Computational time (in seconds)	0.53	0.52	0.56	0.60	0.68	0.53
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	48.00	100.00	100.00	100.00	100.00	100.00
Random Networks	Average path length ($\times {10}^3$)	2.9733	2.9702	2.9671	2.9618	2.9606	2.9633
	Computational time (in seconds)	4.66	4.91	5.14	5.89	6.34	5.68
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	31.05	40.27	44.77	51.18	54.27	49.63
Small-World Networks	Average path length ($\times {10}^3$)	4.5053	4.4722	4.4630	4.4582	4.4126	4.4612
	Computational time (in seconds)	15.18	16.77	26.04	28.22	32.75	26.89
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	45.05	58.14	63.56	72.22	96.07	69.65
Scale-Free Networks	Average path length ($\times {10}^3$)	3.3627	3.3627	3.3627	3.3627	3.3627	3.3627
	Computational time (in seconds)	11.38	13.14	17.03	19.25	22.09	17.25
	Number of paths outputted by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00
	Number of optimal paths found by ARSAT	100.00	100.00	100.00	100.00	100.00	100.00

7. Conclusions and Future Work

In the k shortest paths problem ($k-\mathrm{SPP}$), the objective is to identify the k shortest paths between a given pair of origin and destination (OD) nodes, as opposed to merely finding the 1st shortest path. As a result, solving the $k-\mathrm{SPP}$ can be computationally expensive, as it is essential to ensure global optimality. We introduced a ripple-spreading algorithm (RSA) for the $k-\mathrm{SPP}$, which guarantees optimality and maintains reasonable computational efficiency when each node is allowed to generate at most k ripples. In this study, we modify the approach by permitting each node to generate no more than h ripples, where $1\le h<k$. We further improve the ARSA by introducing a variable strategy $H_T$ and a fuzzy variable strategy $H_T$, collectively referred to as the fuzzy variable H strategy (FVHSRSA). The overall experimental findings demonstrate that, by appropriately adjusting the value of h and designing the variable strategy $H_T$, the reported ARSA can achieve a good trade-off between optimality and computational efficiency. In real-world applications, a trade-off between optimality and computational efficiency is often more important than just optimality itself. Therefore, this study enhances the application potential of RSA for the $k-\mathrm{SPP}$.