Solving the Electronic Schrödinger Equation by Pairing Tensor-Network State with Neural Network Quantum State
Abstract
1. Introduction
2. Related Work
3. Methods
3.1. Quantum Chemistry Hamiltonians
3.2. NNQS-RNN: The NNQS Method Based on RNN Architecture
3.3. DMRG Method
3.4. Pre-Training NNQS with DMRG Method
4. Results
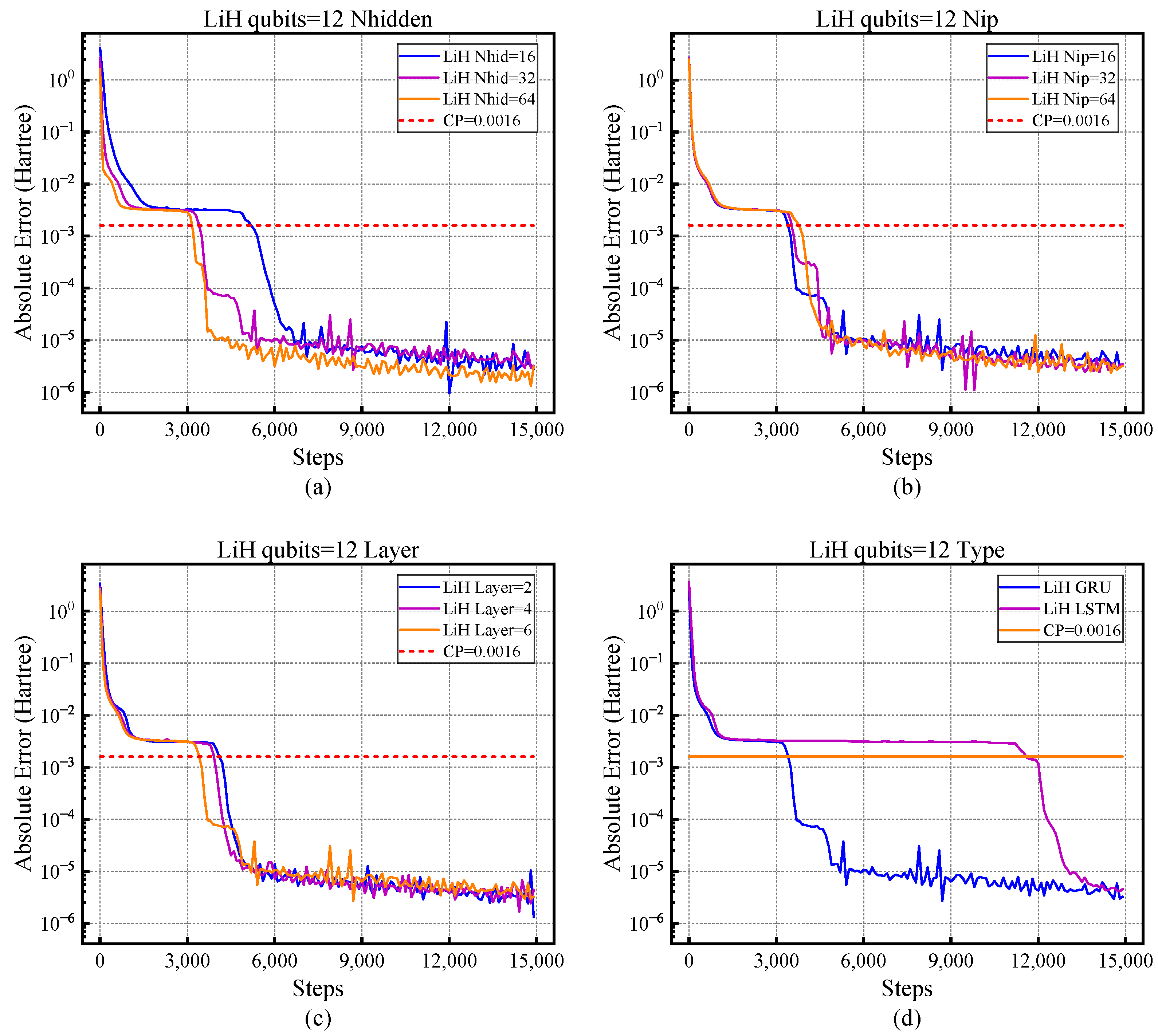
4.1. The Influence of Different Hyper-Parameters on NNQS
4.2. The Influence of DMRG Pre-Training on NNQS
4.3. The Influence of the Optimizer on NNQS
4.4. Application: Ferrocene
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shepard, R. The Multiconfiguration Self-Consistent Field Method. In Advances in Chemical Physics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1987; pp. 63–200. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Musiał, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [Google Scholar] [CrossRef]
- Coester, F.; Kümmel, H. Short-range correlations in nuclear wave functions. Nucl. Phys. 1960, 17, 477–485. [Google Scholar] [CrossRef]
- White, S.R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863–2866. [Google Scholar] [CrossRef] [PubMed]
- White, S.R.; Martin, R.L. Ab initio quantum chemistry using the density matrix renormalization group. J. Chem. Phys. 1999, 110, 4127–4130. [Google Scholar] [CrossRef]
- Boguslawski, K.; Marti, K.H.; Reiher, M. Construction of CASCI-type wave functions for very large active spaces. J. Chem. Phys. 2011, 134, 224101. [Google Scholar] [CrossRef]
- Luo, Z.; Ma, Y.; Liu, C.; Ma, H. Efficient Reconstruction of CAS-CI-Type Wave Functions for a DMRG State Using Quantum Information Theory and a Genetic Algorithm. J. Chem. Theory Comput. 2017, 13, 4699–4710. [Google Scholar] [CrossRef] [PubMed]
- Carleo, G.; Troyer, M. Solving the quantum many-body problem with artificial neural networks. Science 2017, 355, 602–606. [Google Scholar] [CrossRef] [PubMed]
- Choo, K.; Neupert, T.; Carleo, G. Two-dimensional frustrated J1–J2 model studied with neural network quantum states. Phys. Rev. B 2019, 100, 125124. [Google Scholar] [CrossRef]
- Sharir, O.; Levine, Y.; Wies, N.; Carleo, G.; Shashua, A. Deep Autoregressive Models for the Efficient Variational Simulation of Many-Body Quantum Systems. Phys. Rev. Lett. 2020, 124, 020503. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, M.; Heyl, M. Quantum Many-Body Dynamics in Two Dimensions with Artificial Neural Networks. Phys. Rev. Lett. 2020, 125, 100503. [Google Scholar] [CrossRef]
- Yuan, D.; Wang, H.R.; Wang, Z.; Deng, D.L. Solving the Liouvillian Gap with Artificial Neural Networks. Phys. Rev. Lett. 2021, 126, 160401. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Li, M.; Xiao, Q.; Chen, J.; Wang, F.; Shen, L.; Zhao, M.; Wu, W.; An, H.; He, L.; et al. AI for Quantum Mechanics: High Performance Quantum Many-Body Simulations via Deep Learning. In Proceedings of the SC22: International Conference for High Performance Computing, Networking, Storage and Analysis, Dallas, TX, USA, 13–18 November 2022; pp. 1–15. [Google Scholar] [CrossRef]
- Pfau, D.; Spencer, J.S.; Matthews, A.G.D.G.; Foulkes, W.M.C. Ab initio solution of the many-electron Schrödinger equation with deep neural networks. Phys. Rev. Res. 2020, 2, 033429. [Google Scholar] [CrossRef]
- Hermann, J.; Schätzle, Z.; Noé, F. Deep-neural-network solution of the electronic Schrödinger equation. Nat. Chem. 2020, 12, 891–897. [Google Scholar] [CrossRef] [PubMed]
- Choo, K.; Mezzacapo, A.; Carleo, G. Fermionic neural-network states for ab-initio electronic structure. Nat. Commun. 2020, 11, 2368. [Google Scholar] [CrossRef] [PubMed]
- Barrett, T.D.; Malyshev, A.; Lvovsky, A. Autoregressive neural-network wavefunctions for ab initio quantum chemistry. Nat. Mach. Intell. 2022, 4, 351–358. [Google Scholar] [CrossRef]
- Wu, Y.; Xu, X.; Poletti, D.; Fan, Y.; Guo, C.; Shang, H. A Real Neural Network State for Quantum Chemistry. Mathematics 2023, 11, 1417. [Google Scholar] [CrossRef]
- Wu, Y.; Guo, C.; Fan, Y.; Zhou, P.; Shang, H. NNQS-Transformer: An Efficient and Scalable Neural Network Quantum States Approach for Ab Initio Quantum Chemistry. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Denver, CO, USA, 12–17 November 2023; Association for Computing Machinery: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- Shang, H.; Guo, C.; Wu, Y.; Li, Z.; Yang, J. Solving Schrödinger Equation with a Language Model. arXiv 2023, arXiv:2307.09343. [Google Scholar]
- Nomura, Y.; Darmawan, A.S.; Yamaji, Y.; Imada, M. Restricted Boltzmann machine learning for solving strongly correlated quantum systems. Phys. Rev. B 2017, 96, 205152. [Google Scholar] [CrossRef]
- Huang, L.; Wang, L. Accelerated Monte Carlo simulations with restricted Boltzmann machines. Phys. Rev. B 2017, 95, 035105. [Google Scholar] [CrossRef]
- Deng, D.L.; Li, X.; Das Sarma, S. Quantum Entanglement in Neural Network States. Phys. Rev. X 2017, 7, 021021. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, J. Approximating quantum many-body wave functions using artificial neural networks. Phys. Rev. B 2018, 97, 035116. [Google Scholar] [CrossRef]
- Choo, K.; Carleo, G.; Regnault, N.; Neupert, T. Symmetries and Many-Body Excitations with Neural-Network Quantum States. Phys. Rev. Lett. 2018, 121, 167204. [Google Scholar] [CrossRef]
- Vogiatzis, K.D.; Ma, D.; Olsen, J.; Gagliardi, L.; de Jong, W.A. Pushing configuration-interaction to the limit: Towards massively parallel MCSCF calculations. J. Chem. Phys. 2017, 147, 184111. [Google Scholar] [CrossRef]
- Ma, H.; Liu, J.; Shang, H.; Fan, Y.; Li, Z.; Yang, J. Multiscale quantum algorithms for quantum chemistry. Chem. Sci. 2023, 14, 3190–3205. [Google Scholar] [CrossRef]
- McClean, J.R.; Boixo, S.; Smelyanskiy, V.N.; Babbush, R.; Neven, H. Barren plateaus in quantum neural network training landscapes. Nat. Commun. 2018, 9, 4812. [Google Scholar] [CrossRef]
- Anschuetz, E.R.; Kiani, B.T. Beyond Barren Plateaus: Quantum Variational Algorithms Are Swamped with Traps. arXiv 2022, arXiv:2205.05786. [Google Scholar]
- Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 2011, 326, 96–192. [Google Scholar] [CrossRef]
- Mitrushchenkov, A.O.; Fano, G.; Linguerri, R.; Palmieri, P. On the importance of orbital localization in QC-DMRG calculations. Int. J. Quantum Chem. 2012, 112, 1606–1619. [Google Scholar] [CrossRef]
- Li, Z.; Chan, G.K.L. Spin-Projected Matrix Product States: Versatile Tool for Strongly Correlated Systems. J. Chem. Theory Comput. 2017, 13, 2681–2695. [Google Scholar] [CrossRef] [PubMed]
- Wouters, S.; Van Neck, D. The density matrix renormalization group for ab initio quantum chemistry. Eur. Phys. J. D 2014, 68, 272. [Google Scholar] [CrossRef]
- Chan, G.K.L.; Sharma, S. The Density Matrix Renormalization Group in Quantum Chemistry. Annu. Rev. Phys. Chem. 2011, 62, 465–481. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Song, Y.; Peng, F.; Li, J.; Cheng, Y.; Zhang, L.; Ma, Y.; Tian, Y.; Luo, Z.; Ma, H. Kylin 1.0: An ab-initio density matrix renormalization group quantum chemistry program. J. Comput. Chem. 2023, 44, 1316–1328. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP 2014), Doha, Qatar, 25–29 October 2014. [Google Scholar]
- Graves, A. Long Short-Term Memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar] [CrossRef]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Martens, J.; Grosse, R.B. Optimizing Neural Networks with Kronecker-factored Approximate Curvature. arXiv 2015, arXiv:1503.05671. [Google Scholar]
- von Glehn, I.; Spencer, J.S.; Pfau, D. A Self-Attention Ansatz for Ab-initio Quantum Chemistry. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Schätzle, Z.; Szabó, P.B.; Mezera, M.; Hermann, J.; Noé, F. DeepQMC: An open-source software suite for variational optimization of deep-learning molecular wave functions. J. Chem. Phys. 2023, 159, 094108. [Google Scholar] [CrossRef]
- Harding, M.E.; Metzroth, T.; Gauss, J.; Auer, A.A. Parallel calculation of CCSD and CCSD (T) analytic first and second derivatives. J. Chem. Theory Comput. 2008, 4, 64–74. [Google Scholar] [CrossRef]
- Ishimura, K.; Hada, M.; Nakatsuji, H. Ionized and excited states of ferrocene: Symmetry adapted cluster—Configuration—Interaction study. J. Chem. Phys. 2002, 117, 6533–6537. [Google Scholar] [CrossRef]
- Sayfutyarova, E.R.; Sun, Q.; Chan, G.K.L.; Knizia, G. Automated construction of molecular active spaces from atomic valence orbitals. J. Chem. Theory Comput. 2017, 13, 4063–4078. [Google Scholar] [CrossRef]







| Molecular Systems | This Work | NAQS | RBM | FCI |
|---|---|---|---|---|
| −7.7845 | −7.7845 | −7.7777 | −7.7845 | |
| −75.0155 | −75.0155 | −74.9493 | −75.0155 | |
| −107.6599 | −107.6595 | −107.5440 | −107.6602 | |
| −39.8062 | −39.8062 | −39.7571 | −39.8063 | |
| −74.6904 | −74.6899 | −74.5147 | −74.6908 | |
| −105.1661 | −105.1662 | −105.1414 | −105.1662 | |
| −338.6979 | −338.6984 | −338.6472 | −338.6984 | |
| −87.8916 | −87.8909 | −87.3660 | −87.8927 |
| Molecular Systems | STO-6G | |
|---|---|---|
| no ckpt | 5.104793 | −69.437209 |
| 1000-th step ckpt | −2.485850 | −73.123730 |
| 2000-th step ckpt | −2.384864 | −73.343999 |
| 3000-th step ckpt | −2.202542 | −73.386116 |
| Molecular Systems | STO-6G | |
|---|---|---|
| no ckpt | 103.7935 | 1524.3876 |
| 1000-th step ckpt | 65.6547 | 1580.0200 |
| 2000-th step ckpt | 76.3441 | 944.5145 |
| 3000-th step ckpt | 113.5518 | 1032.1916 |
| Molecular Systems | STO-6G | |
|---|---|---|
| no ckpt | 2732 | 7376 |
| 1000-th step ckpt | 890 | 6925 |
| 2000-th step ckpt | 347 | 2871 |
| 3000-th step ckpt | 507 | 2358 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kan, B.; Tian, Y.; Xie, D.; Wu, Y.; Fan, Y.; Shang, H. Solving the Electronic Schrödinger Equation by Pairing Tensor-Network State with Neural Network Quantum State. Mathematics 2024, 12, 433. https://doi.org/10.3390/math12030433
Kan B, Tian Y, Xie D, Wu Y, Fan Y, Shang H. Solving the Electronic Schrödinger Equation by Pairing Tensor-Network State with Neural Network Quantum State. Mathematics. 2024; 12(3):433. https://doi.org/10.3390/math12030433
Chicago/Turabian StyleKan, Bowen, Yingqi Tian, Daiyou Xie, Yangjun Wu, Yi Fan, and Honghui Shang. 2024. "Solving the Electronic Schrödinger Equation by Pairing Tensor-Network State with Neural Network Quantum State" Mathematics 12, no. 3: 433. https://doi.org/10.3390/math12030433
APA StyleKan, B., Tian, Y., Xie, D., Wu, Y., Fan, Y., & Shang, H. (2024). Solving the Electronic Schrödinger Equation by Pairing Tensor-Network State with Neural Network Quantum State. Mathematics, 12(3), 433. https://doi.org/10.3390/math12030433








