High Dynamic Bipedal Robot with Underactuated Telescopic Straight Legs
Abstract
:1. Introduction
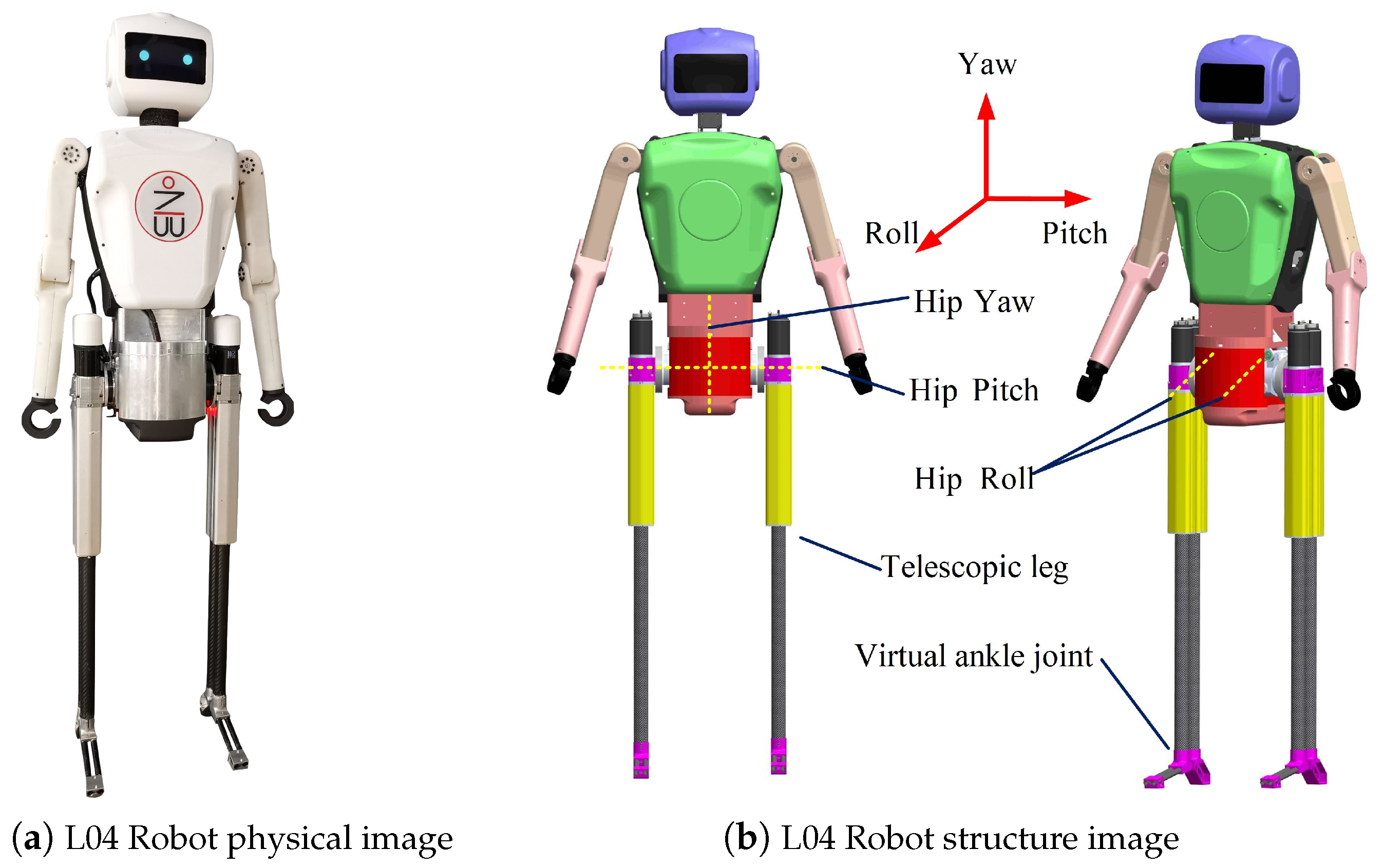
2. Design Overview
2.1. Split Coupled Hip Joint Design
2.2. Double Slider Telescopic Leg Design
3. Robotic Control
3.1. Kinematics Analysis
3.2. Lip Dynamics and Angular Momentum Derivation
3.3. Angular Momentum Trajectory Planning
3.3.1. Forward Walking
3.3.2. Lateral Walking
4. Simulation and Experiments
4.1. Simulation
4.1.1. Forward Walking
4.1.2. Lateral Walking
4.2. Physiical Test
4.2.1. Forward Walking
4.2.2. Lateral Walking
4.2.3. Robust Walking
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. ROBOTIC CONTROL
Appendix A.1. Kinematics Analysis

Appendix A.2. LIP Dynamics and Angular Momentum Derivation

References
- Zhang, C.; Zou, W.; Ma, L.; Wang, Z. Biologically inspired jumping robots: A comprehensive review. Robot. Auton. Syst. 2020, 124, 103362. [Google Scholar] [CrossRef]
- Stasse, O.; Flayols, T. An overview of humanoid robots technologies. In Biomechanics of Anthropomorphic Systems; Springer: Cham, Switzerland, 2019; pp. 281–310. [Google Scholar]
- Denny, J.; Elyas, M.; D’costa, S.A.; D’Souza, R.D. Humanoid robots–past, present and the future. Eur. J. Adv. Eng. Technol. 2016, 3, 8–15. [Google Scholar]
- Ficht, G.; Behnke, S. Bipedal humanoid hardware design: A technology review. Curr. Robot. Rep. 2021, 2, 201–210. [Google Scholar] [CrossRef]
- Takenaka, T.; Matsumoto, T.; Yoshiike, T. Real time motion generation and control for biped robot-1 st report: Walking gait pattern generation. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 1084–1091. [Google Scholar]
- Hirose, H. Development of humanoid robot ASIMO. In Proceedings of the Workshop on Explorations towards Humanoid Robot Application of IEEE/RSJ International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2001. [Google Scholar]
- Catherman, D.S.; Kaminski, J.T.; Jagetia, A. Atlas Humanoid Robot Control with Flexible Finite State Machines for Playing Soccer. In Proceedings of the 2020 SoutheastCon, Raleigh, NC, USA, 28–29 March 2020; Volume 2, pp. 1–7. [Google Scholar]
- Goswami, A.; Vadakkepat, P. Humanoid Robotics: A Reference; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Chang, L.; Piao, S.; Leng, X.; He, Z.; Zhu, Z. Inverted pendulum model for turn-planning for biped robot. Phys. Commun. 2020, 42, 101168. [Google Scholar] [CrossRef]
- Kajita, S.; Morisawa, M.; Miura, K.; Nakaoka, S.; Harada, K.; Kaneko, K.; Kanehiro, F.; Yokoi, K. Biped walking stabilization based on linear inverted pendulum tracking. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 4489–4496. [Google Scholar]
- Gong, Y.; Grizzle, J. Angular momentum about the contact point for control of bipedal locomotion: Validation in a lip-based controller. arXiv 2020, arXiv:2008.10763. [Google Scholar]
- Lapeyre, M.; Rouanet, P.; Oudeyer, P.Y. The poppy humanoid robot: Leg design for biped locomotion. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 349–356. [Google Scholar]
- Mou, H.; Xue, J.; Liu, J.; Feng, Z.; Li, Q.; Zhang, J. A Multi-Agent Reinforcement Learning Method for Omnidirectional Walking of Bipedal Robots. Biomimetics 2023, 8, 616. [Google Scholar] [CrossRef] [PubMed]
- Gan, W.; Liu, J.; Tang, J.; Xu, W.; Zhu, Y.; Li, Q. Walking Control of Telescopic Leg Bipedal Robot Based on Angular Momentum Predictive Foothold. In Proceedings of the 2023 IEEE International Conference on Robotics and Biomimetics (ROBIO), Koh Samui, Thailand, 4–9 December 2023; pp. 1–6. [Google Scholar]
- Chen, H.; Wang, B.; Hong, Z.; Shen, C.; Wensing, P.M.; Zhang, W. Underactuated motion planning and control for jumping with wheeled-bipedal robots. IEEE Robot. Autom. Lett. 2020, 6, 747–754. [Google Scholar] [CrossRef]
- Ahmad, H.; Nakata, Y.; Nakamura, Y.; Ishiguro, H. PedestriANS: A bipedal robot with adaptive morphology. Adapt. Behav. 2021, 29, 369–382. [Google Scholar] [CrossRef]
- Safartoobi, M.; Dardel, M.; Daniali, H.M. Gait cycles of passive walking biped robot model with flexible legs. Mech. Mach. Theory 2021, 159, 104292. [Google Scholar] [CrossRef]
- Raibert, M.H. Legged Robots That Balance; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Kajita, S.; Matsumoto, O.; Saigo, M. Real-time 3D walking pattern generation for a biped robot with telescopic legs. In Proceedings of the 2001 ICRA. IEEE International Conference on Robotics and Automation (Cat. No.01CH37164), Seoul, Republic of Korea, 21–26 May 2001; Volume 3, pp. 2299–2306. [Google Scholar] [CrossRef]
- Google Owned Schaft Unveils New Bipedal Robot. 2016. Available online: https://www.youtube.com/watch?v=iyZE0psQsX0 (accessed on 28 December 2023).
- Wang, K.; Shah, A.; Kormushev, P. Slider: A novel bipedal walking robot without knees. In Proceedings of the 19th International Conference Towards Autonomous Robotic Systems (TAROS 2018), Bristol, UK, 25–27 July 2018. [Google Scholar]
- Wang, K.; Marsh, D.; Saputra, R.P.; Chappell, D.; Jiang, Z.; Raut, A.; Kon, B.; Kormushev, P. Design and control of SLIDER: An ultra-lightweight, knee-less, low-cost bipedal walking robot. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 3488–3495. [Google Scholar]
- Tang, J.; Zhu, Y.; Gan, W.; Mou, H.; Leng, J.; Li, Q.; Yu, Z.; Zhang, J. Design, Control, and Validation of a Symmetrical Hip and Straight-Legged Vertically-Compliant Bipedal Robot. Biomimetics 2023, 8, 340. [Google Scholar] [CrossRef] [PubMed]
- Udai, A.D. Optimum hip trajectory generation of a biped robot during single support phase using genetic algorithm. In Proceedings of the 2008 First International Conference on Emerging Trends in Engineering and Technology, Nagpur, India, 16–18 July 2008; pp. 739–744. [Google Scholar]
- Bhardwaj, G.; Mishra, U.; Sukavanam, N.; Balasubramanian, R. Planning adaptive brachistochrone and circular arc hip trajectory for a toe-foot bipedal robot going downstairs. J. Phys. Conf. Ser. 2021, 1831, 012032. [Google Scholar] [CrossRef]
- Harata, Y.; Kato, Y.; Asano, F. Efficiency analysis of telescopic-legged bipedal robots. Artif. Life Robot. 2018, 23, 585–592. [Google Scholar] [CrossRef]
- Kajita, S.; Hirukawa, H.; Harada, K.; Yokoi, K. Introduction to Humanoid Robotics; Springer: Berlin/Heidelberg, Germany, 2014; Volume 101. [Google Scholar]
- Pratt, J.; Carff, J.; Drakunov, S.; Goswami, A. Capture point: A step toward humanoid push recovery. In Proceedings of the 2006 6th IEEE-RAS International Conference on Humanoid Robots, Genova, Italy, 4–6 December 2006; pp. 200–207. [Google Scholar]
- Hashimoto, K. Mechanics of humanoid robot. Adv. Robot. 2020, 34, 1390–1397. [Google Scholar] [CrossRef]
- Westervelt, E.R.; Grizzle, J.W.; Chevallereau, C.; Choi, J.H.; Morris, B. Feedback Control of Dynamic Bipedal Robot Locomotion; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Yokoi, K.; Hirukawa, H. The 3D linear inverted pendulum mode: A simple modeling for a biped walking pattern generation. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the the Next Millennium (Cat. No. 01CH37180), Maui, HI, USA, 29 October–3 November 2001; Volume 1, pp. 239–246. [Google Scholar]
- Raibert, M.H. Hopping in legged systems—Modeling and simulation for the two-dimensional one-legged case. IEEE Trans. Syst. Man Cybern. 1984, SMC-14, 451–463. [Google Scholar] [CrossRef]
- Townsend, M.A. Biped gait stabilization via foot placement. J. Biomech. 1985, 18, 21–38. [Google Scholar] [CrossRef] [PubMed]
- Da, X.; Harib, O.; Hartley, R.; Griffin, B.; Grizzle, J.W. From 2D design of underactuated bipedal gaits to 3D implementation: Walking with speed tracking. IEEE Access 2016, 4, 3469–3478. [Google Scholar] [CrossRef]


















| Joint | Actuator | Data | Range of Motion |
|---|---|---|---|
| Head Yaw | Robotis MX64 | 64 kgf | −90°–90° |
| Head Pitch | Robotis MX64 | 64 kgf | −45°–45° |
| Shoulder Pitch | Robotis MX64 | 64 kgf | −45°–180° |
| Shoulder Roll | Robotis MX64 | 64 kgf | 0°–90° |
| Elbow Pitch | Robotis MX64 | 64 kgf | 0°–135° |
| Hip Yaw | Maxon RE40 | 1000 N | −15° (−1.3 mm)–15° (1.6 mm) |
| Hip Roll | Maxon RE40 | 500 N | −10° (−11 mm)–10° (0.4 mm) |
| Hip Pitch | Maxon RE40 | 100 Nm | −90°–90° |
| Leg Z | Maxon RE40 | 500 N | −200 mm–0 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mou, H.; Tang, J.; Liu, J.; Xu, W.; Hou, Y.; Zhang, J. High Dynamic Bipedal Robot with Underactuated Telescopic Straight Legs. Mathematics 2024, 12, 600. https://doi.org/10.3390/math12040600
Mou H, Tang J, Liu J, Xu W, Hou Y, Zhang J. High Dynamic Bipedal Robot with Underactuated Telescopic Straight Legs. Mathematics. 2024; 12(4):600. https://doi.org/10.3390/math12040600
Chicago/Turabian StyleMou, Haiming, Jun Tang, Jian Liu, Wenqiong Xu, Yunfeng Hou, and Jianwei Zhang. 2024. "High Dynamic Bipedal Robot with Underactuated Telescopic Straight Legs" Mathematics 12, no. 4: 600. https://doi.org/10.3390/math12040600
APA StyleMou, H., Tang, J., Liu, J., Xu, W., Hou, Y., & Zhang, J. (2024). High Dynamic Bipedal Robot with Underactuated Telescopic Straight Legs. Mathematics, 12(4), 600. https://doi.org/10.3390/math12040600





