Randomized Nonuniform Sampling for Random Signals Bandlimited in the Special Affine Fourier Transform Domain
Abstract
:1. Introduction
2. Power Spectral Density in the SAFT Domain
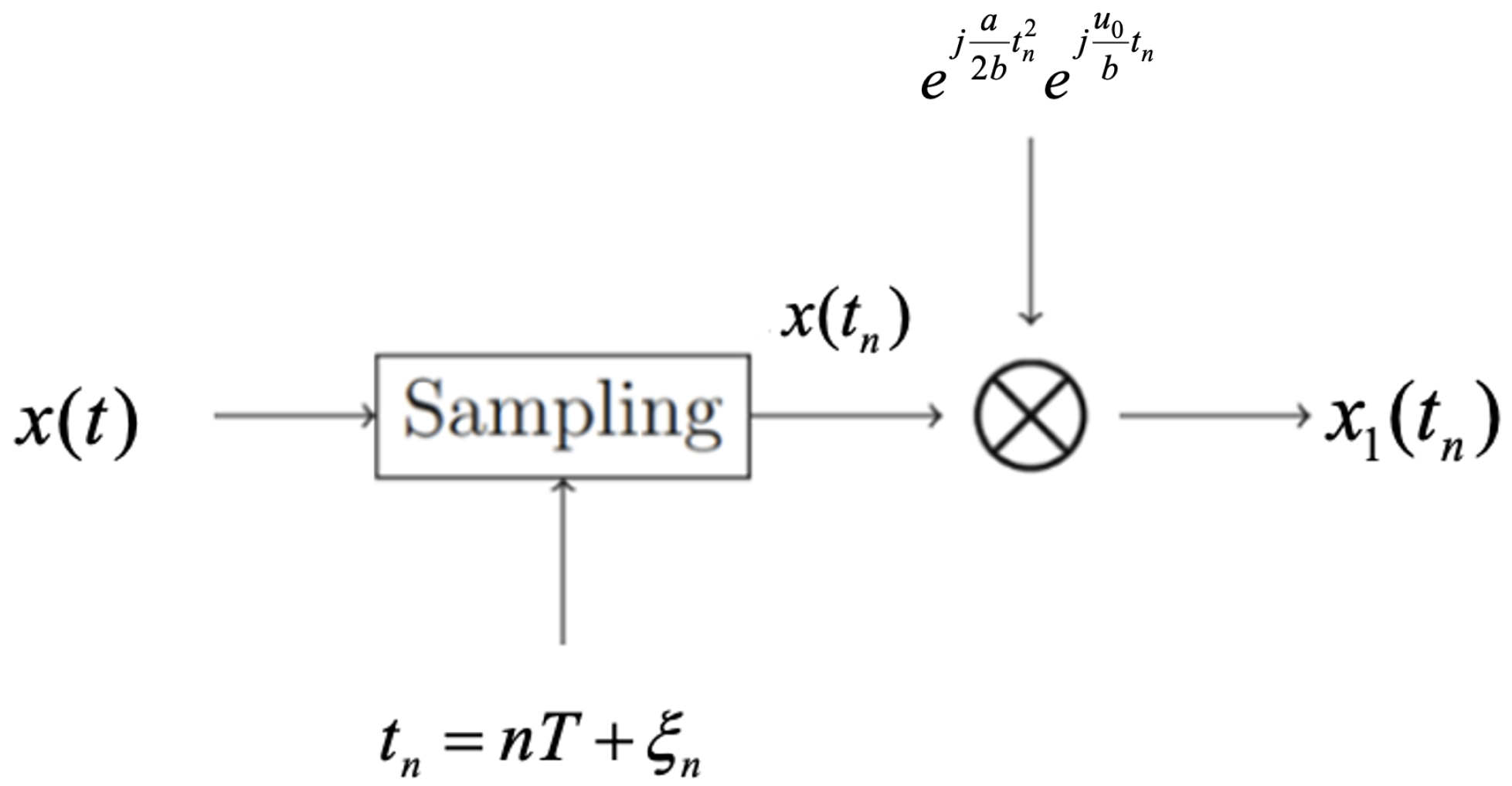
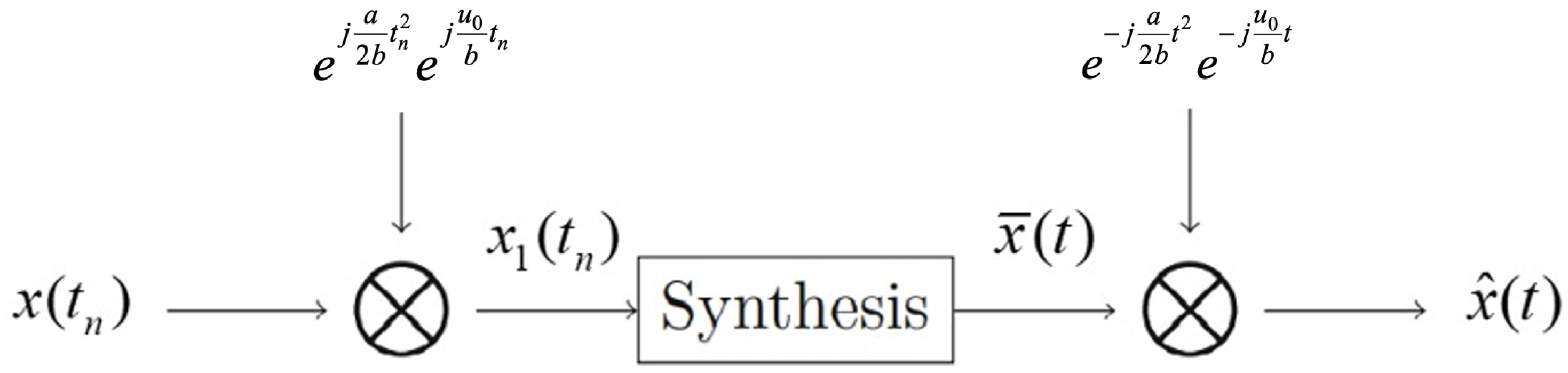
3. Nonuniform Sampling and Approximate Recovery
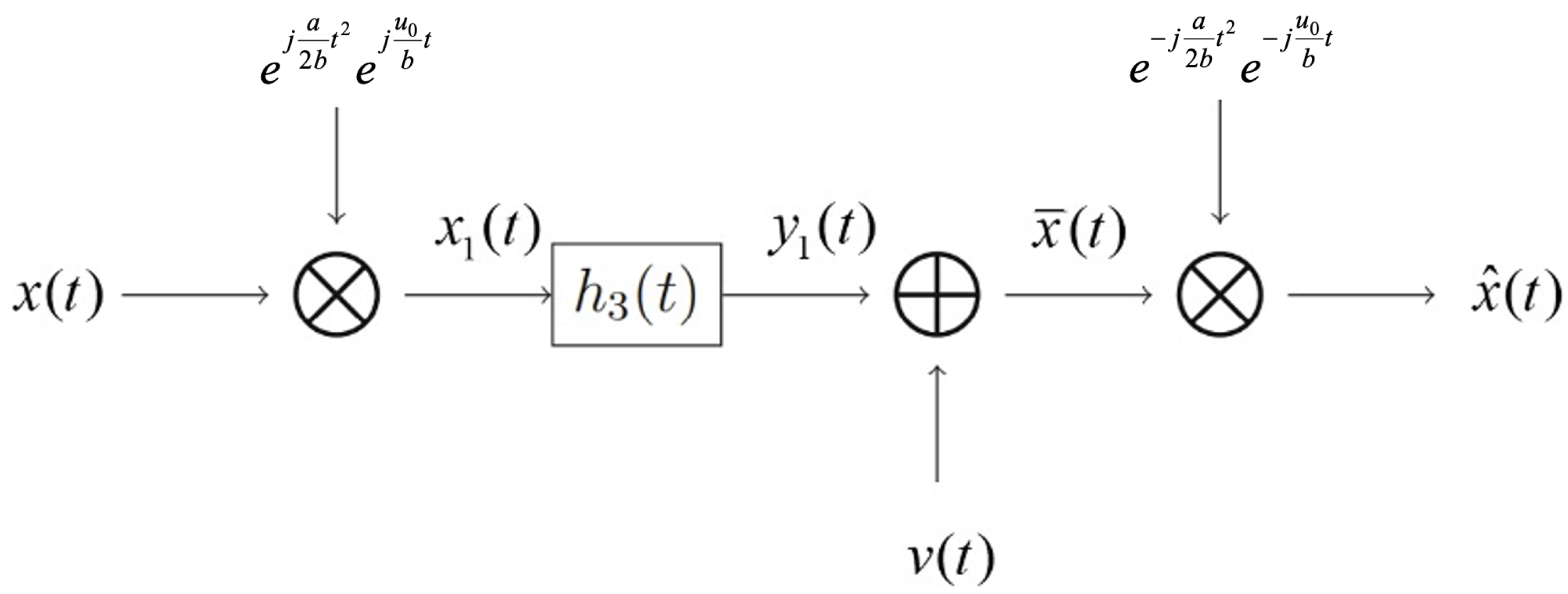
4. Error Estimate for Nonuniform Sampling
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abe, S.; Sheridan, J.T. Optical operations on wave functions as the Abelian subgroups of the special affine Fourier transformation. Opt. Lett. 1994, 19, 1801–1803. [Google Scholar] [CrossRef] [PubMed]
- Healy, J.J.; Kutay, M.A.; Ozaktas, H.M.; Sheridan, J.T. Linear Canonical Transforms: Theory and Applications; Springer Series in Optical Sciences; Springer: New York, NY, USA, 2016. [Google Scholar]
- Liu, X.; Shi, J.; Xiang, W.; Zhang, Q.; Zhang, N. Sampling expansion for irregularly sampled signals in fractional Fourier transform domain. Digit. Signal Process. 2014, 34, 74–81. [Google Scholar] [CrossRef]
- Sharma, K.; Joshi, S. Signal separation using linear canonical and fractional Fourier transforms. Opt. Commun. 2006, 265, 454–460. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, R.; Song, D.; Zhang, T.; Wu, D. Extrapolation of discrete bandlimited signals in linear canonical transform domain. Signal Process. 2014, 94, 212–218. [Google Scholar] [CrossRef]
- Xu, S.; Chai, Y.; Hu, Y. Spectral analysis of sampled band-limited signals in the offset linear canonical transform domain. Circuits Syst. Signal Process. 2015, 34, 3979–3997. [Google Scholar] [CrossRef]
- Bhandari, A.; Zayed, A.I. Shift-invariant and sampling spaces associated with the special affine Fourier transform. Appl. Comput. Harmon. Anal. 2019, 47, 30–52. [Google Scholar] [CrossRef]
- Huo, H.; Sun, W.; Xiao, L. Uncertainty principles associated with the offset linear canonical transform. Math. Methods Appl. Sci. 2019, 42, 466–474. [Google Scholar] [CrossRef]
- Xiang, Q.; Qin, K. Convolution, correlation, and sampling theorems for the offset linear canonical transform. Signal Image Video Process. 2014, 8, 433–442. [Google Scholar] [CrossRef]
- Zhi, X.; Wei, D.; Zhang, W. A generalized convolution theorem for the special affine Fourier transform and its application to filtering. Optik 2016, 127, 2613–2616. [Google Scholar] [CrossRef]
- Gao, N.; Jiang, Y. Sampling and reconstruction of multi-dimensional bandlimited signals in the special affine Fourier transform domain. Math. Meth. Appl. Sci. 2024. [Google Scholar] [CrossRef]
- Xu, S.; Huang, L.; Chai, Y.; He, Y. Nonuniform sampling theorems for bandlimited signals in the offset linear canonical transform. Circuits Syst. Signal Process. 2018, 37, 3227–3244. [Google Scholar]
- Shannon, C.E. Communication in the presence of noise. Proc. IRE 1949, 37, 10–12. [Google Scholar] [CrossRef]
- Adam, K.; Scholefield, A.; Vetterli, M. Sampling and reconstruction of bandlimited signals with multi-channel time encoding. IEEE Trans. Signal Process. 2020, 69, 1105–1119. [Google Scholar] [CrossRef]
- Aldroubi, A.; Davis, J.; Krishtal, I. Dynamic sampling: Time-space trade-off. Appl. Comput. Harmon. Anal. 2013, 34, 495–503. [Google Scholar] [CrossRef]
- Bass, R.F.; Gröchenig, K. Random sampling of bandlimited functions. Isral J. Math. 2010, 177, 1–28. [Google Scholar] [CrossRef]
- Gröchenig, K.; Romero, J.L.; Unnikrishnan, J.; Vetterli, M. On minimal trajectories for mobile sampling of bandlimited fields. Appl. Comput. Harmon. Anal. 2015, 39, 487–510. [Google Scholar] [CrossRef]
- Oktem, F.; Ozaktas, H. Exact relation between continuous and discrete linear canonical transforms. IEEE Signal Process. Lett. 2009, 16, 727–730. [Google Scholar] [CrossRef]
- Tao, R.; Li, B.; Wang, Y.; Aggrey, G. On sampling of band-limited signals associated with the linear canonical transform. IEEE Trans. Signal Process. 2008, 56, 5454–5464. [Google Scholar]
- Wei, D.; Ran, Q.; Li, Y. Multichannel sampling and reconstruction of bandlimited signals in the linear canonical transform domain. IET Signal Process. 2011, 5, 717–727. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, R.; Song, D. Recovery of bandlimited signals in linear canonical transform domain from noisy samples. Circuits Syst. Signal Process. 2014, 33, 1997–2008. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, F.; Tao, R. Randomized nonuniform sampling and reconstruction in fractional Fourier domain. Signal Process. 2016, 120, 311–322. [Google Scholar] [CrossRef]
- Stern, A. Sampling of compact signals in the offset linear canonical transform domains. Signal Image Video Process. 2007, 1, 359–367. [Google Scholar] [CrossRef]
- Xiang, Q.; Qin, K.; Huang, Q. Multichannel sampling of signals band-limited in offset linear canonical transform domains. Circuits Syst. Signal Process. 2013, 32, 2385–2406. [Google Scholar] [CrossRef]
- Xu, S.; Chai, Y.; Hu, Y.; Jiang, C.; Li, Y. Reconstruction of digital spectrum from periodic nonuniformly sampled signals in offset linear canonical transform domain. Opt. Commun. 2015, 348, 59–65. [Google Scholar] [CrossRef]
- Boche, H.; Mönich, U.J. Approximation of wide-sense stationary stochastic processes by Shannon sampling series. IEEE Trans. Inf. Theory 2010, 56, 6459–6469. [Google Scholar] [CrossRef]
- Gilles, F.; Sinuk, K. Average sampling of band-limited stochastic processes. Appl. Comput. Harmon. Anal. 2013, 35, 527–534. [Google Scholar]
- Song, Z.; Sun, W.; Zhou, X.; Hou, Z. An average sampling theorem for bandlimited stochastic processes. IEEE Trans. Inf. Theory 2007, 53, 4798–4800. [Google Scholar] [CrossRef]
- Huo, H.; Sun, W. Sampling theorems and error estimates for random signals in the linear canonical transform domain. Signal Process. 2015, 111, 31–38. [Google Scholar] [CrossRef]
- Huo, H.; Sun, W. Nonuniform sampling for random signals bandlimited in the linear canonical transform domain. Multidimens. Syst. Signal Process. 2020, 31, 927–950. [Google Scholar] [CrossRef]
- Tao, R.; Zhang, F.; Wang, Y. Sampling random signals in a fractional Fourier domain. Signal Process. 2011, 91, 1394–1400. [Google Scholar] [CrossRef]
- Xu, S.; Feng, L.; Chai, Y.; He, Y. Analysis of A-stationary random signals in the linear canonical transform domain. Signal Process. 2018, 146, 126–132. [Google Scholar] [CrossRef]
- Xu, S.; Jiang, C.; Chai, Y.; Hu, Y.; Huang, L. Nonuniform sampling theorems for random signals in the linear canonical transform domain. Int. J. Electron. 2018, 105, 1051–1062. [Google Scholar]
- Maymon, S.; Oppenheim, A.V. Sinc interpolation of nonuniform samples. IEEE Trans. Signal Process. 2011, 59, 4745–4758. [Google Scholar] [CrossRef]
- Xu, S.; Feng, L.; Chai, Y.; Hu, Y.; Huang, L. Sampling theorems for bandlimited random signals in the offset linear canonical transform domain. AEU Int. J. Electron. Commun. 2017, 81, 114–119. [Google Scholar] [CrossRef]
- Bao, Y.; Zhang, Y.; Song, Y.; Li, B.; Dang, P. Nonuniform sampling theorems for random signals in the offset linear canonical transform domain. In Proceedings of the APSIPA Annual Summit and Conference, Kuala Lumpur, Malaysia, 12–15 December 2017; pp. 94–99. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Gao, N.; Li, H. Randomized Nonuniform Sampling for Random Signals Bandlimited in the Special Affine Fourier Transform Domain. Mathematics 2024, 12, 1092. https://doi.org/10.3390/math12071092
Jiang Y, Gao N, Li H. Randomized Nonuniform Sampling for Random Signals Bandlimited in the Special Affine Fourier Transform Domain. Mathematics. 2024; 12(7):1092. https://doi.org/10.3390/math12071092
Chicago/Turabian StyleJiang, Yingchun, Ni Gao, and Haizhen Li. 2024. "Randomized Nonuniform Sampling for Random Signals Bandlimited in the Special Affine Fourier Transform Domain" Mathematics 12, no. 7: 1092. https://doi.org/10.3390/math12071092
APA StyleJiang, Y., Gao, N., & Li, H. (2024). Randomized Nonuniform Sampling for Random Signals Bandlimited in the Special Affine Fourier Transform Domain. Mathematics, 12(7), 1092. https://doi.org/10.3390/math12071092






