Analytical Study of Nonlinear Systems of Higher-Order Difference Equations: Solutions, Stability, and Numerical Simulations
Abstract
:1. Introduction
2. Main Results
2.1. Formulation of Solutions for System (1)
2.2. Formulation of Solutions for System (2)
2.3. Formulation of Solutions for System (3)
2.4. Formulation of Solutions for System (4)
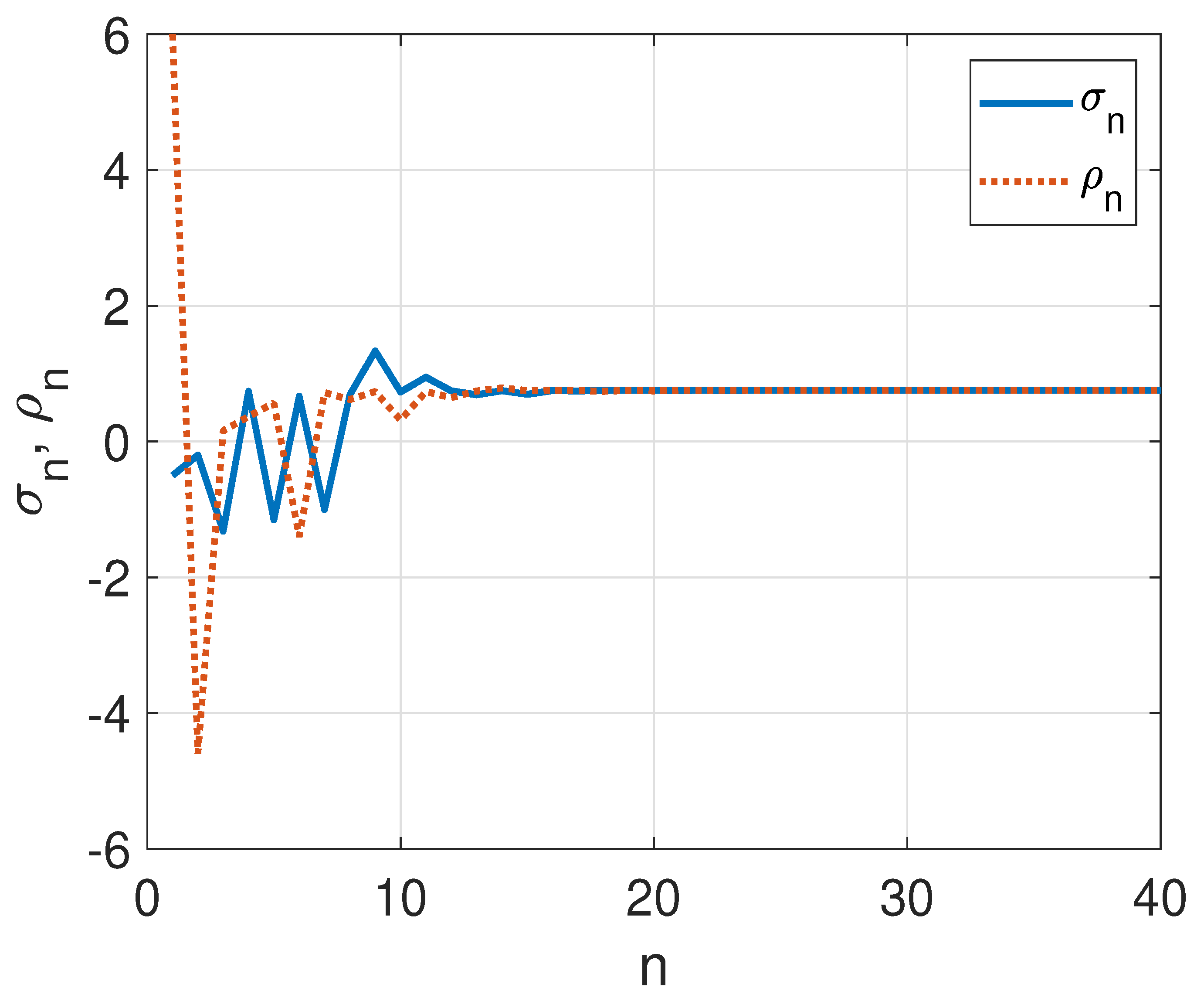
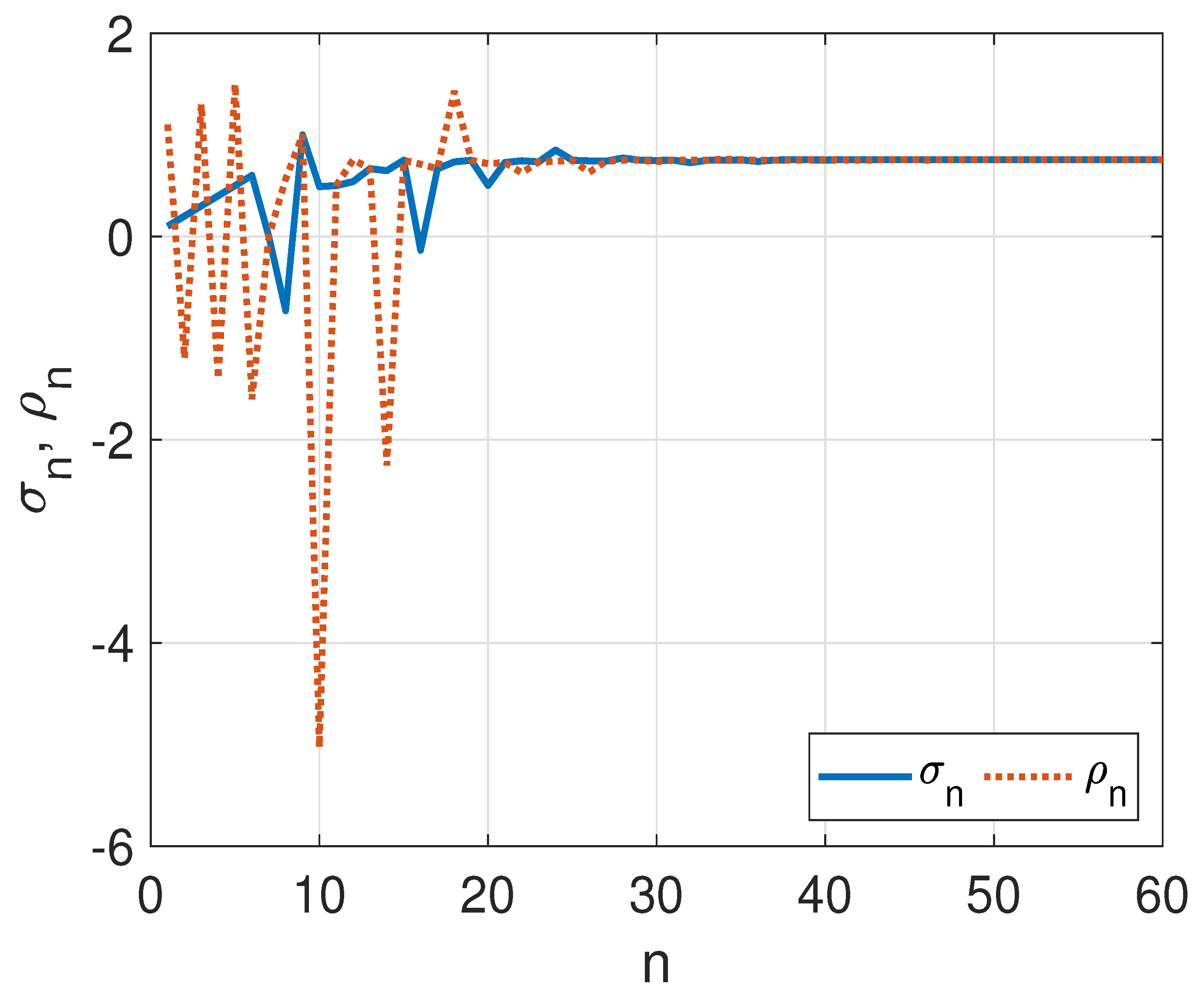
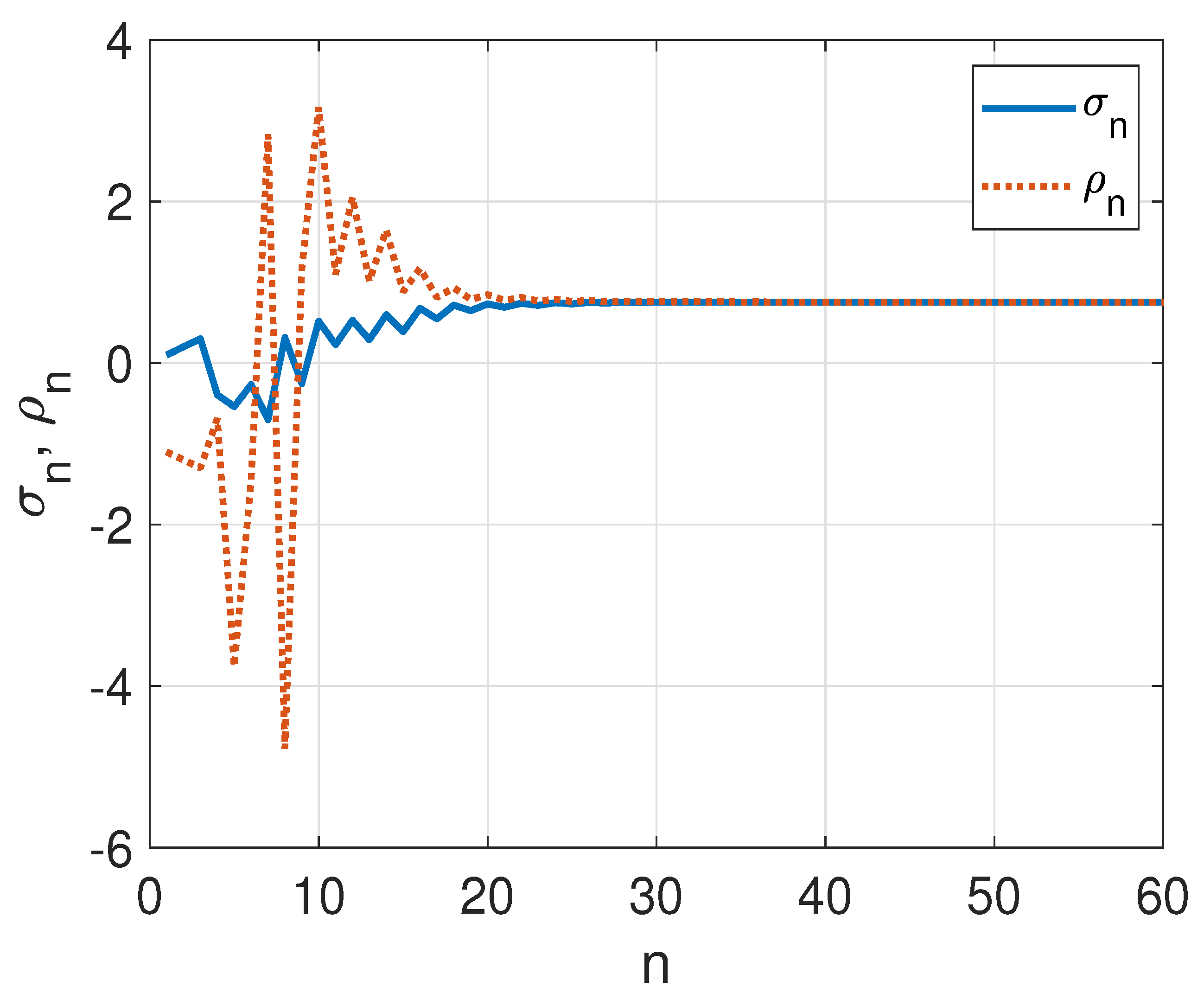
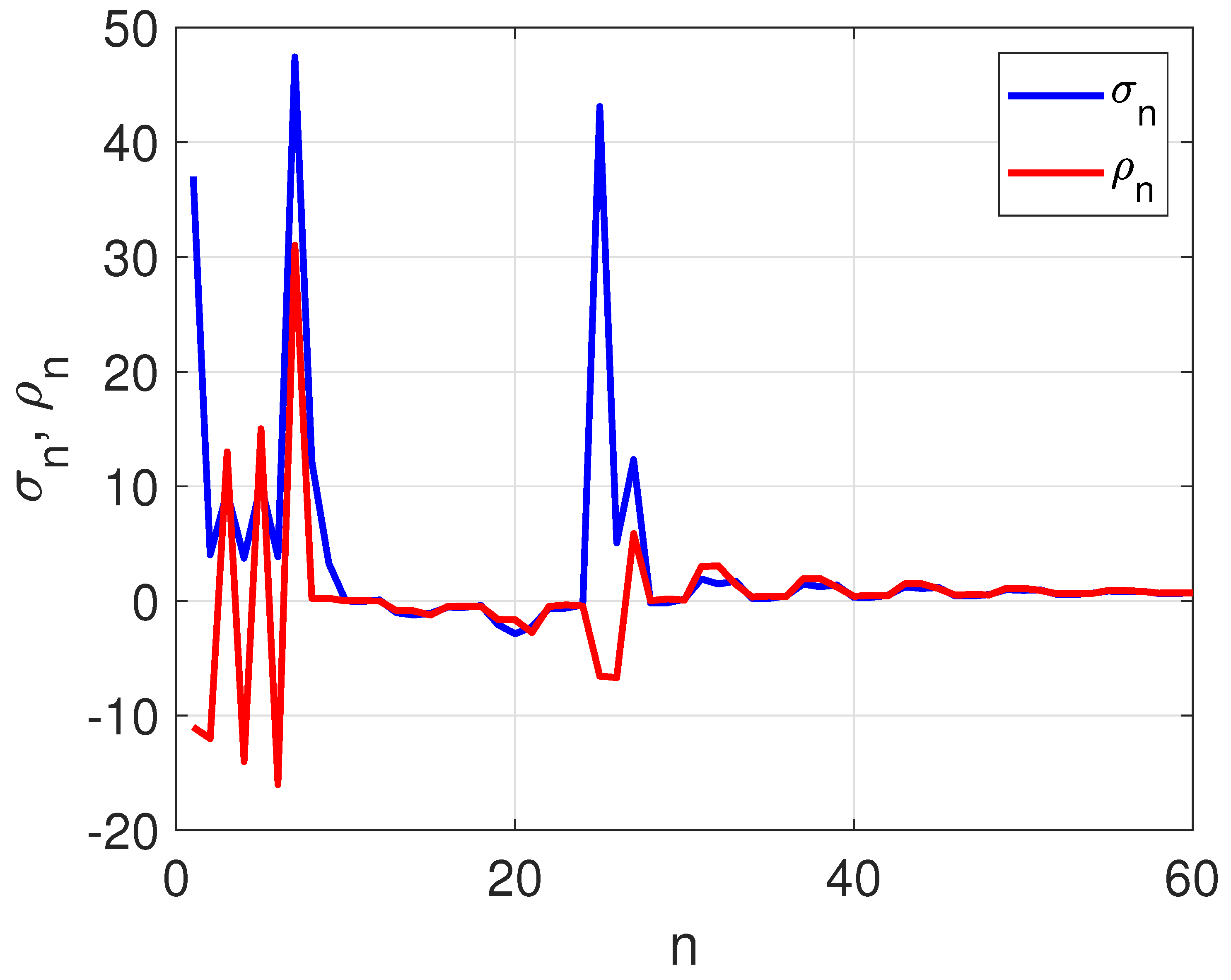
3. Illustrative Numerical Simulations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghezal, A.; Zemmouri, I. On Markov-switching asymmetric logGARCH models: Stationarity and estimation. Filomat 2023, 37, 1–19. [Google Scholar]
- Ghezal, A. Spectral representation of Markov-switching bilinear processes. São Paulo J. Math. Sci. 2023, 1–21. [Google Scholar] [CrossRef]
- Khan, A.Q.; Tasneem, M.; Younis, B.; Ibrahim, T.F. Dynamical analysis of a discrete-time COVID-19 epidemic model. Math. Meth. Appl. Sci. 2022, 46, 4789–4814. [Google Scholar] [CrossRef] [PubMed]
- Khaliq, A.; Mustafa, I.; Ibrahim, T.F.; Osman, W.M.; Al-Sinan, B.R.; Dawood, A.A.; Juma, M.Y. Stability and bifurcation analysis of fifth-order nonlinear fractional difference equation. Fractal Fract. 2023, 7, 113. [Google Scholar] [CrossRef]
- Al-Khedhairi, A.; Elsadany, A.A.; Elsonbaty, A. On the dynamics of a discrete fractional-order cournot–bertrand competition duopoly game. Math. Probl. Eng. 2022, 2022, 8249215. [Google Scholar] [CrossRef]
- Abo-Zeid, R.; Cinar, C. Global behavior of the difference equation xn+1=Axn−1B − Cxnxn−2. Bol. Sociedade Parana. Matemática 2013, 31, 43–49. [Google Scholar] [CrossRef]
- Berkal, M.; Abo-Zeid, R. On a rational (p + 1)th order difference equation with quadratic term. Univers. J. Math. Appl. 2022, 5, 136–144. [Google Scholar] [CrossRef]
- Elsayed, E.M.; Alofi, B.S. The periodic nature and expression on solutions of some rational systems of difference equations. Alex. Eng. J. 2023, 74, 269–283. [Google Scholar] [CrossRef]
- Elsayed, E.M.; Alshareef, A.; Alzahrani, F. Qualitative behavior and solution of a system of three-dimensional rational difference equations. Math. Methods Appl. Sci. 2022, 45, 5456–5470. [Google Scholar] [CrossRef]
- Elsayed, E.M.; Aloufi, B.S.; Moaaz, O. The behavior and structures of solution of fifth-order rational recursive sequence. Symmetry 2022, 14, 641. [Google Scholar] [CrossRef]
- Elsayed, E.M. Solution and attractivity for a rational recursive sequence. Discret. Dyn. Nat. Soc. 2011, 2011, 982309. [Google Scholar] [CrossRef]
- Ghezal, A. Note on a rational system of (4k + 4)-order difference equations: Periodic solution and convergence. J. Appl. Math. Comput. 2023, 69, 2207–2215. [Google Scholar] [CrossRef]
- Kara, M. Investigation of the global dynamics of two exponential-form difference equations systems. Electron. Res. Arch. 2023, 31, 6697–6724. [Google Scholar] [CrossRef]
- Elsayed, E.M.; Alshabi, K.N. The dynamical behaviour of solutions for nonlinear systems of rational difference equations. Res. Commun. Math. Math. Sci. 2023, 15, 1–20. [Google Scholar]
- Al-Basyouni, K.S.; Elsayed, E.M. On some solvable systems of some rational difference equations of third order. Mathematics 2023, 11, 1047. [Google Scholar] [CrossRef]
- Okumuş, İ.; Soykan, Y. On the solutions of systems of difference equations via Tribonacci numbers. arXiv 2019, arXiv:1906.09987. [Google Scholar] [CrossRef]
- Abo-Zeid, R. Global behavior of two third order rational difference equations with quadratic terms. Math. Slovaca 2019, 69, 147–158. [Google Scholar] [CrossRef]
- Simşek, D.; Oğul, B.; Çınar, C. Solution of the rational difference equation xn+1=xn−17/1+xn−5.xn−11. Filomat 2019, 33, 1353–1359. [Google Scholar] [CrossRef]
- Ghezal, A.; Zemmouri, I. On a solvable p-dimensional system of nonlinear difference equations. J. Math. Comput. 2022, 12, 195. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Althagafi, H.; Ghezal, A. Analytical Study of Nonlinear Systems of Higher-Order Difference Equations: Solutions, Stability, and Numerical Simulations. Mathematics 2024, 12, 1159. https://doi.org/10.3390/math12081159
Althagafi H, Ghezal A. Analytical Study of Nonlinear Systems of Higher-Order Difference Equations: Solutions, Stability, and Numerical Simulations. Mathematics. 2024; 12(8):1159. https://doi.org/10.3390/math12081159
Chicago/Turabian StyleAlthagafi, Hashem, and Ahmed Ghezal. 2024. "Analytical Study of Nonlinear Systems of Higher-Order Difference Equations: Solutions, Stability, and Numerical Simulations" Mathematics 12, no. 8: 1159. https://doi.org/10.3390/math12081159
APA StyleAlthagafi, H., & Ghezal, A. (2024). Analytical Study of Nonlinear Systems of Higher-Order Difference Equations: Solutions, Stability, and Numerical Simulations. Mathematics, 12(8), 1159. https://doi.org/10.3390/math12081159




