Two-Stage Probe-Based Search Optimization Algorithm for the Traveling Salesman Problems

Abstract

As a classical combinatorial optimization problem, the traveling salesman problem (TSP) has been extensively investigated in the fields of Artificial Intelligence and Operations Research. Due to being NP-complete, it is still rather challenging to solve both effectively and efficiently. Because of its high theoretical significance and wide practical applications, great effort has been undertaken to solve it from the point of view of intelligent search. In this paper, we propose a two-stage probe-based search optimization algorithm for solving both symmetric and asymmetric TSPs through the stages of route development and a self-escape mechanism. Specifically, in the first stage, a reasonable proportion threshold filter of potential basis probes or partial routes is set up at each step during the complete route development process. In this way, the poor basis probes with longer routes are filtered out automatically. Moreover, four local augmentation operators are further employed to improve these potential basis probes at each step. In the second stage, a self-escape mechanism or operation is further implemented on the obtained complete routes to prevent the probe-based search from being trapped in a locally optimal solution. The experimental results on a collection of benchmark TSP datasets demonstrate that our proposed algorithm is more effective than other state-of-the-art optimization algorithms. In fact, it achieves the best-known TSP benchmark solutions in many datasets, while, in certain cases, it even generates solutions that are better than the best-known TSP benchmark solutions.

1. Introduction

The traveling salesman problem (TSP) is a well-known combinatorial optimization problem, which can be specifically expressed as the problem of finding the lowest-cost route throughout a given set of cities. It has been proven to be one of the most difficult NP-hard problems, i.e., NP-complete problems [1,2], so there is no algorithm to effectively solve it in polynomial time via the conventional computer systems. Because of its wide applicability and computational complexity, many researchers have been attracted to investigating the TSP for effective and efficient solutions. Actually, a variety of feasible optimization algorithms have been designed and exploited in the last few decades. According to [2,3], these algorithms can be categorized into two main streams: exact algorithms and heuristic algorithms. Each stream offers different tradeoffs in terms of solution quality, computational efficiency, and applicability to different problem instances. The exact algorithms guarantee optimal solutions, but the execution time is increased exponentially with the problem size. They are only suitable for small-size TSPs and become rather difficult for medium- to large-scale problems, even though supercomputer systems are adopted in the computational process [4]. Therefore, the exact algorithms may become computationally prohibitive. On the other hand, heuristic algorithms are designed with some efficient search rules or systems to obtain good approximate solutions instead.

Heuristic optimization algorithms are more applicable in practice because of their ability to deal with large-scale TSPs. These algorithms, however, cannot guarantee an optimal solution but can provide a satisfactory solution with an affordable computational cost. They are generally designed with the help of certain specific knowledge and intuitive experiences to construct a reasonable route solution. During the search process, they use some greedy strategies for a better solution to guide the search operation within a limited solution space. In this way, the solutions become better and better in the sequential iterations while the search is always set in a local mode. It is clear that better heuristic algorithms require a deeper understanding of the solution domains and structures, from which high-quality solutions can be found effectively and efficiently. However, a heuristic algorithm can perform well on certain specific instances but not work well for other instances, and it is often expensive to adapt to new instances and problems. In general, heuristic algorithms can serve as building blocks for more sophisticated meta-heuristic approaches.

Meta-heuristic approaches are more generic and flexible than heuristic algorithms and are often used when heuristic approaches are insufficient or impractical. Indeed, they have been widely adopted for TSPs due to their ability to efficiently explore large solution spaces and find good approximate solutions. Most of these meta-heuristic algorithms are inspired by natural and biological behaviors and employ certain top-level strategies for the solutions of TSPs. Actually, they can offer high-quality solutions with relatively less computational cost. In such an approach, the search scheme is generally designed to guide some local improvement operators in an intelligent way so that a robust iterative generation process can be produced through a proper balance regarding the diversification and intensification strategy during each search iteration. Diversification and intensification refer to the exploration and exploitation in the solution search space, respectively. The strength of meta-heuristics is the effectiveness of the employed intensification and diversification strategy, and the efficiency depends on the decision between the global search reinforcement and convergence search in the promising region. However, they often meet with the problem of premature convergence, which traps the search process in a local optimum solution. Moreover, meta-heuristics utilize many parameters that need to be tuned. In addition, most of these approaches yield probabilistic solutions due to the randomness in the process. It may be possible to enhance the effectiveness of meta-heuristics by combining two or more algorithms into a hybrid form. The performance of the hybrid algorithm is certainly better; however, it necessitates a higher computational cost, while effective hybridization is difficult to achieve.

In 2016, a new conceptual computational model named Probe Machine (PM) was proposed by Xu [5]. It is a completely parallel computing model in which the data placement mode is nonlinear. Motivated by the probe concept and data structure of the PM, we first designed a PM-based optimization algorithm for solving symmetric TSPs [6]. It is a route construction and search procedure coupled with a certain filtering mechanism. Specifically, it starts with all the possible sub-routes consisting of three cities, and then each potential sub-route is extended and enhanced step by step from its two ends until complete routes are finally formed. At the same time, the worst routes are filtered out according to the filtering proportion value. Its advantages are the clarity of the idea and the easy implementation. However, there is no scope of modifying and developing the possible routes from the current existing potential routes, so certain potential routes may easily be left out.

To ameliorate this potential drawback, we further designed a dynamic route construction optimization algorithm for both symmetric and asymmetric TSPs through the integration of the probe concept and local search mechanism [7]. This PM-based dynamic algorithm adopts the route modification and development as the routes are built. In fact, the embedded local search operators are imposed consecutively on the retained potential routes to produce more potential routes before each subsequent expansion. In this paper, we extend and develop our previous study of the PM-based search optimization framework methodologically and theoretically. Specifically, we design a two-stage search optimization algorithm for solving both symmetric and asymmetric TSPs through the stages of probe-based route development and a self-escape mechanism. In the first stage, the key idea is to design a potential route filter in each step of the probe-based route development process such that at least a sufficient number of potential or valuable partial routes are retained in each step; hence, the probability of producing the best complete route is increased under limited computational resources. Moreover, certain local augmentation operators are further employed to extend and improve the retained potential partial routes in each step. In the second stage, a self-escape mechanism is implemented regarding the obtained complete routes from the first stage to prevent the above probe-based search from being trapped in a locally optimal solution. Therefore, a local optimal solution can be skipped and the global optimization search capability can be enhanced. In fact, it is an effective search optimization framework in which the first stage is to construct and develop a set of better complete routes step by step dynamically and the second stage is to self-escape from the stagnant routes (if possible). The main contributions of this work are summarized as follows:

• A two-stage probe-based search optimization algorithm is designed for solving both symmetric and asymmetric TSPs through the stages of probe-based route development and a self-escape mechanism. The experimental results demonstrate that our proposed algorithm performs better than the other state-of-the-art algorithms with respect to the quality of the solution over a wide range of TSP datasets.
• A proportion value threshold filter is designed and integrated into the probe-based search optimization framework to retain at least a sufficient number of potential routes in each step of the route development process. Actually, we set up an initial value for the proportion value of the potential partial route filtering in the first step and then dynamically adjust it in the following steps.
• Four local augmentation operators are designed and employed on each of the developed potential routes in an efficient manner so that all the retained potential routes are further augmented and improved consecutively at each step.
• A self-escape mechanism is further implemented on the obtained complete routes from the first stage to prevent the probe-based search from being trapped in a locally optimal solution.
• A statistical analysis is conducted to validate the computed results of our proposed algorithm against the other benchmark optimization algorithms by using the Wilcoxon signed rank test.

The rest of this paper is organized as follows. The mathematical description of the TSP is provided in Section 2. Then, the concept of the probe is introduced in Section 3. We further describe our adopted proportion threshold filter in the probe-based search in Section 4 and our employed local augmentation operators in Section 5. Section 6 presents our proposed probe-based search optimization algorithm in detail. The experimental results and discussion are summarized in Section 7. Finally, we include a brief conclusion in Section 8.

2. TSP Mathematical Description

The TSP is a path planning optimization problem of finding the lowest-cost route through a given set of cities. The route must be designed in such a way that each city is visited once and only once and eventually returns to the starting city. It is known to be NP-complete, meaning that there is no known effective algorithm that can solve it for large instances in polynomial time. As the number of cities increases, the number of possible routes grows factorially, making it computationally infeasible to find the optimal solution through brute force for large instances. Despite its computational complexity, the TSP has attracted great attention from scientists and engineers due to its great value for practical applications and its connections to other optimization problems. Until now, no general method has been able to tackle this problem effectively [8].

The TSP was first mathematically formulated by Karl Menger in 1930 [9] and, since then, it has been extensively investigated in diverse applicable fields. Typical examples of the TSP real-life applications include transport routing, circuit design, X-ray crystallography, micro-chip production, scheduling, mission planning, aviation, logistics management, DNA sequencing, data association, image processing, pattern recognition, and many more [10,11,12]. Therefore, it is very important and valuable to design and implement an effective algorithm for the TSP solution.

The TSP can be represented as a graph-theoretic problem. Let $G_n=(C,E)$ be a directed graph, where $C=\{c_1,c_2,\dots ,c_n\}$ is the set of vertices (nodes) and $E=\{e_{ij}:e_{ij}=(c_i,c_j);(c_i,c_j)\in C\times C;i\ne j;i,j=1,2,\dots ,n\}$ is the set of edges. Each vertex (node) $c_i\in C$ denotes the position of a city and each edge $e_{ij}\in E$ indicates the path from the i-th city to the j-th city. Moreover, a non-negative cost (distance) $d_{ij}\in {\mathbb{R}}^{+}$ is associated with each edge $e_{ij}\in E$ for representing the edge weight of the graph. If $d_{ij}=d_{ji};\forall e_{ij}\in E$, the graph $G_n$ is referred to as symmetric TSP, whereas the asymmetric TSP corresponds to the case with $d_{ij}\ne d_{ji}$ for at least one pair of edges $e_{ij}$ and $e_{ji}\in E$ of the graph $G_n$. The aim of this problem is to construct a complete route T with n distinct cities such that the total traveling cost (distance) function $F(T)$ of the route is minimized; i.e., the fitness function of the route $f(T)$ is maximized. Let $T=(c_1,c_2,\dots ,c_n,c_1)$ with all distinct cities $c_i\in C$ be a complete route and $F(T)$ be its route cost (distance). Then, the objective function of the TSP can be formulated as follows [13]:

$$\left.\begin{array}{c}\hfill \mathrm{Generate}\mathrm{a}\mathrm{complete}\mathrm{route}T=(c_1,c_2,\dots ,c_n,c_1)\\ \hfill {\displaystyle \mathrm{to}\mathrm{minimize}F(T)=\sum _{i=1}^{n-1}{d}_{c_i{c}_{i+1}}+d_{c_n{c}_1}}\\ \hfill \mathrm{i}.\mathrm{e}.,\mathrm{to}\mathrm{maximize}f(T)=\frac{1}{F(T)}\end{array}\right\}$$

(1)

where $d_{c_i{c}_{i+1}}$ is the cost (distance) of the local path between the cities $c_i$ and $c_{i+1}$. If $c_i(x_i,y_i)$ and $c_{i+1}(x_{i+1},y_{i+1})$ are coordinates of $c_i$ and $c_{i+1}$, then $d_{c_i{c}_{i+1}}$ is calculated by Euclidean distance as follows:

$$d_{c_i{c}_{i+1}}=\sqrt{{(x_i-x_{i+1})}^2+{(y_i-y_{i+1})}^2}.$$

(2)

3. Probe Concept

The probe is conceptually a detection device or related operator that accurately recognizes a piece of a particular structure or pattern from the whole description of an object and implements certain operations, such as connection or transmission, between the detected structures. It has been extensively used for various purposes in diverse fields like medical, engineering, biology, computer science, electronics, information security, archaeology, and so on [5,14]. In the medical field, ultrasonic probes are utilized to generate acoustic signals and detect return signals. These probes are an essential component of ultrasound systems and work by emitting high-frequency sound waves into the body or material being examined and then receiving the echoes that bounce back. On the other hand, a short single-stranded DNA or RNA fragment (approximately 20 to 500 bp) is designed as a biological probe to detect its complementary DNA sequence or locate a particular clone. In addition, the probe concept is adopted in electronics to perform various electronic tests, while archaeologists use it to interpret the soil’s nature and to decide where and how to excavate.

As a computer model, the Probe Machine (PM) [5] was developed where each probe is assumed to be an operator to make a connection between any two pieces of fiber-tailed data or to transmit information from one piece of fiber-tailed data to another if their tails are consistent. The probe in PM accomplishes three different functions. First, it accurately finds any two target data pieces with perfectly matching adjacent edges or fiber tails. Then, it takes any pair of possible target data pieces from the database of available fiber-tailed data. Finally, it performs some well-defined operations to extend fiber-tailed data step by step to a problem solution. Motivated by the probe of the PM, we design a new kind of probe for our PM-based search optimization approach to solving TSPs. In our approach, the probes are assumed to be a connection operator of city sequences or possible sub-routes that are consistent so that the complete route can be produced step by step. The sub-route consisting of $(m-1)$ edges is referred to as the m-city basis probe. The outer two edges are called the wings of the natural probe. The actual probe performs two actions such that it first finds out the required adjacent edges and then generates the next possible basis probes based on the availability of these edges. Actually, each basis probe can use its wings to accurately detect and append two other different adjacent edges on the route to extend the current route solution. In this way, each basis probe is enhanced automatically on both ends in every step of the procedure and continues until all cities are included in the basis probe, i.e., until complete (n-city) basis probes are formed. Mathematically, to arrive at a complete probe search of n-city problem, the procedure needs to execute $[\frac{n}{2}]$ steps, where

$$[\frac{n}{2}]=\left\{\begin{array}{cc}\frac{n}{2},\hfill & \mathrm{if}n\mathrm{is}\mathrm{even};\hfill \\ \frac{n-1}{2},\hfill & \mathrm{if}n\mathrm{is}\mathrm{odd}.\hfill \end{array}\right.$$

(3)

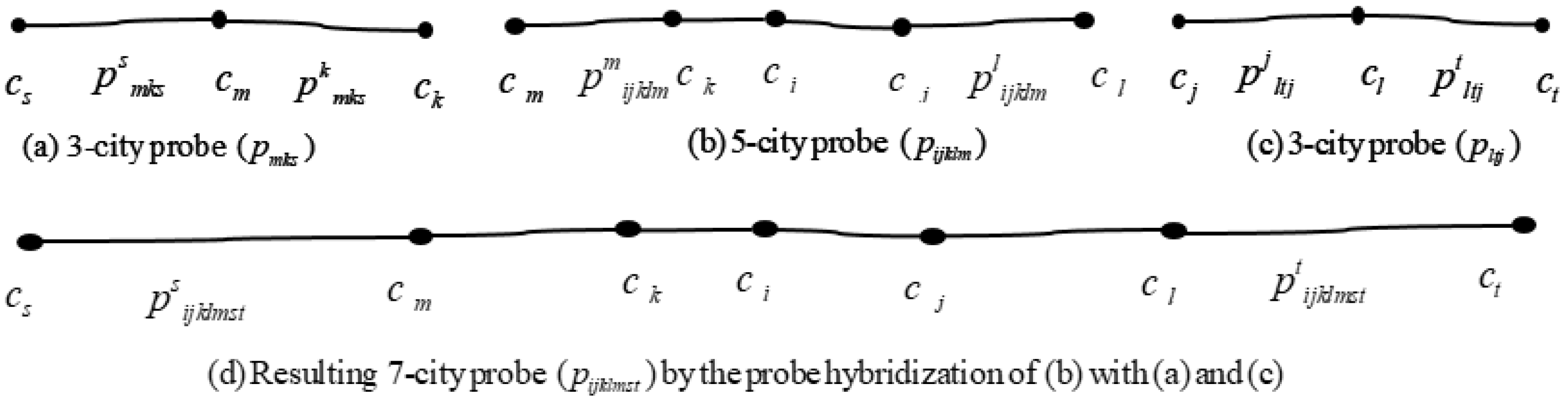
To facilitate the understanding of the network expansion mechanism of the probe, it is illustrated graphically in Figure 1. In the figure, a 5-city basis probe is hybridized with two 3-city basis probes and generates a 7-city basis probe. In our model, the first step generates 3-city basis probes, the second step generates 5-city basis probes, the third step generates 7-city basis probes, and in this way the n-th step generates n-city basis probes. The number of cities visited step-wise by the probe operation is provided in Table 1. The sample basis probes in the figure are denoted by $p_{mks}$, $p_{ijklm}$, and $p_{ltj}$, respectively. Actually, the probe $p_{mks}$ is a sub-route consisting of three cities $(c_m,c_k,c_s)$ with the wings $\omega (p_{mks})=\{p_{mks}^k,p_{mks}^s\}$. Similarly, the probe $p_{ltj}$ is a sub-route consisting of three cities $(c_l,c_t,c_j)$ having wings $\omega (p_{ltj})=\{p_{ltj}^t,p_{ltj}^j\}$, while the probe $p_{ijklm}$ is a sub-route consisting of five cities $(c_i,c_j,c_k,c_l,c_m)$ with the wings $\omega (p_{ijklm})=\{p_{ijklm}^l,p_{ijklm}^m\}$. For the expansion of the network of 5-city basis probe $p_{ijklm}$, it explores for two 3-city basis probes through the wings $p_{ijklm}^l$ and $p_{ijklm}^m$. On the other hand, the wing $p_{mks}^k$ of the basis probe $p_{mks}$ and the wing $p_{ltj}^j$ of the basis probe $p_{ltj}$ are consistent with the wings of the probe $p_{ijklm}$. The other wings of the basis probes $p_{mks}$ and $p_{ltj}$ are not consistent with the basis probe $p_{ijklm}$. After finding these types of basis probes, the 5-city basis probe $p_{ijklm}$ hybridizes with these 3-city basis probes through the wings $p_{ijklm}^l$ and $p_{ijklm}^m$. This hybridization leads to the expansion of the current network $p_{ijklm}$ and generates a 7-city basis probe comprising the cities $(c_i,c_j,c_k,c_l,c_m,c_s,c_t)$. The new 7-city basis probe is denoted by $p_{ijklmst}$, and it also has two wings, namely $p_{ijklmst}^s$ and $p_{ijklmst}^t$. In this way, the hybridized probes extend their network, and the redundant probes not being hybridized are left out.

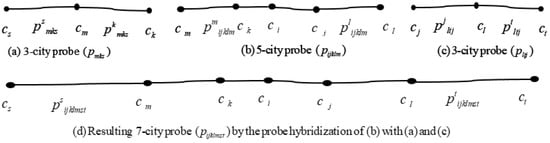
Figure 1. Illustration of probe hybridization mechanism: (a) 3-city basis probe; (b) 5-city basis probe; (c) 3-city basis probe; (d) resulting 7-city basis probe by the probe hybridization of (b) with (a,c).

Table 1. The number of cities visited step-wise by the probe operation.

Step Number	1	2	3	$\cdots$	$\cdots$	k	$k+1$	$\cdots$	$\cdots$	$[\frac{n}{2}]$
# of Cities	3	5	7	$\cdots$	$\cdots$	$2k+1$	$2k+3$	$\cdots$	$\cdots$	n

4. Adopted Filtering Mechanism

In searching for the solution of a TSP, a ”filter” typically refers to a technique or mechanism of reducing the search space or eliminating the unpromising solutions during the optimization process. This technique can play a crucial role in improving the efficiency of the algorithms that aim to determine the optimal or near-optimal solutions to the TSP. Some of the key filtering concepts used in TSPs include bounding filters, dominance rules, symmetry-breaking filters, etc. These filters can significantly improve the efficiency of the algorithms for solving the TSP, enabling the exploration of the larger spaces and finding the near-optimal solutions within a reasonable time frame.

The adopted filter of our approach is a proportion threshold filter that is set up rigorously in the probe-based search process. Actually, it assists the search operator in retaining the least but necessary number of potential partial routes in each step of the complete route development process. The potential routes of the current step are used to generate possible basis routes in the next step during the route construction process. Therefore, the performance of the probe-based search process is highly influenced by the appropriate choice of the filtering proportion value. In fact, setting an appropriate proportion value of generated routes is a rather challenging problem for the effectiveness of our approach. An inappropriate choice of proportion value leads to trapping the whole process, which not only yields a worse solution but consumes a longer computational time. Specifically, a larger proportion value may provide more chances to produce a better optimum solution. However, this also means that the number of possible basis routes generated in the next step is increased rapidly and the computational cost is increased too, and, sometimes, the model cannot even produce a feasible complete route. On account of this, it is important to set up a reasonable proportion threshold filter in the working steps so that the worst generated routes are filtered out in each filtering process. Through theoretical analysis and the experiments, we set a proportion value function ${\psi }_{2k+1}$ for the kth step as follows:

$${\psi }_{2k+1}=\frac{\gamma }{n+\sqrt[3]{k}},$$

(4)

where k denotes the step number that changes in $\{1,2,\cdots ,[\frac{n}{2}]\}$, n stands for the number of cities contained in the test dataset, and $\gamma$ is a constant. Actually, the value of $\gamma$ is dependent on the value of n and can be fitted by the trial and error method. It can be observed from the experiments that, in some cases, a smaller value of $\gamma$ is needed to provide a good solution, while, in some other cases, a larger value of $\gamma$ is required to obtain a satisfactory solution. Therefore, the value of $\gamma$ is not biased, and it offers different tradeoffs in terms of solution quality, computational efficiency, and applicability to different problem instances. The experiments and theoretical analysis demonstrate that the value of $\gamma$ lies within an interval of $[\frac{n+1}{n^3-3n^2+2n},\frac{900n+900}{n^3-3n^2+2n}]\subset {\mathbb{R}}^{+}$, i.e., $\gamma \in [\frac{n+1}{n^3-3n^2+2n},\frac{900n+900}{n^3-3n^2+2n}]\subset {\mathbb{R}}^{+}$, which is a good adjustment for computing a satisfactory solution in an acceptable time frame.

The design of the adopted filter with the threshold value in Equation (4) is based on the idea that, initially, the routes are too short to clear. As the step increases, the routes are also gradually becoming more and more clear. Thus, it is reasonable to set up a large proportion value in the first step and then to reduce with time in the following steps, i.e., ${\psi }_3>{\psi }_5>\cdots >{\psi }_{2[\frac{n}{2}]+1}$. From the experiments, it can be found that, as the number k of steps increases, the number $n_{r_l}(l=3,5,7,\dots ,n)$ of retaining potential partial routes is increased at first in a few steps and then starts to decrease. From the step where the reduction begins, it is decreased very rapidly in the remaining steps; in some cases, it even retains one single route. To mitigate this problem, we can fix the proportion value unchanged after conducting $50\%$ of the whole steps. In addition, if the number $n_{r_l}$ of retaining potential partial routes at any step is too small (e.g., $n_{r_l}=1$), it is believed that the procedure has already fallen into the trap of local optimum solution. Once trapped, it cannot jump out from there as the proportional value is still decreasing and it retains one single route in the remaining steps. To get rid of having one single possible route, the proportion value can be increased at that step. This increment is created in such a way that the number $n_{r_l}$ of retaining potential routes belongs to an interval of $[1,100]\subset \mathbb{N}$. After that, it is decreased as before in the remaining steps of the procedure. This strategy allows the proportion value to be increased in certain steps of the procedure. More precisely, it can be said that we set up an initial filtering proportion value in the first step, and then the algorithm dynamically adjusts it in the rest of the steps. Therefore, the search process is able to avoid having one single route, and hence the probability of producing a better complete route is increased.

The filtering mechanism can be explained through a concrete example. Suppose that we would like to solve a six-city symmetric TSP problem. In the first step of our approach, 60 basis sub-routes of three cities will be generated. If we set the proportion value to $\frac{1}{2}$ in the first step, then 30 potential 3-city sub-routes will be retained before leaving the first step, and the remaining 30 routes will be filtered out based on their fitness value. These retained potential basis routes are then modified and improved into good routes through the local augmentation operators, which are discussed in the next section. These good sub-routes are referred to as the root basis probes or sub-routes. In the second step, 5-city basis sub-routes will be generated using these 30 good basis routes. Let us say 180 basis sub-routes are produced in the second step, and, if we set $\frac{1}{3}$ as the proportion value in this step, then 60 basis sub-routes will be retained for route extension. These 60 basis sub-routes are used to construct 6-city complete routes, and, finally, a best 6-city complete route is found from there.

5. Employed Local Augmentation Operators

In our solution augmentation process, four types of local augmentation operators are employed consecutively on each retained potential basis probe or sub-route in each step of the route development procedure. These operators help to modify the existing sub-route iteratively and potentially improve its quality. Actually, the local augmentation operators are adopted in the first improvement manner; i.e., once an improvement is found, subsequent improvements are explored based on this improvement. In addition, a well-defined decision function for each operator is used to avoid generating a worse route and consuming a longer time. We briefly describe them in the following subsections, respectively. The pseudocode of improving potential basis probes or sub-routes through local augmentation operators is offered in Algorithm 1.

Algorithm 1: Pseudocode of the potential basis probe improvement procedure via local augmentation operators

Input: A retained potential basis probe $p_{1\times l},l=5,7,9,\cdots ,n$, Fitness value of the basis probe $f(p)$, Distance matrix $d_{n\times n}$ Output: Improved basis probe $p_{im}$, Fitness value of the improved basis probe $f(p_{im})$ For each city $c_i\in p$, $i=1$ to $n-2$ for 2-opt, $i=1$ to $n-1$ for reversion and swap, $i=1$ to n for insertion. For an n-city probe, $i-1=n$ when $i=1$ For each city $c_j\in p$, $j=i+2$ to n for 2-opt, $j=i+1$ to n for reversion and swap, $j=1$ to $n,j\ne i$ for insertion. For an n-city probe, $j+1=1$ when $j=n$ Check the inequality defined in Equations (5)–(8) of carrying operator If the inequality is satisfied, then Generate a new basis probe $p^{\prime }$ based on p by applying carrying operator Compute the fitness value of $p^{\prime }$, i.e., $f(p^{\prime })$ by using Equation (1) In case of asymmetric TSP, calculate the fitness value in reverse order also of $p^{\prime }$ and then take the best one from $\{f(p_{\mathrm{original}\mathrm{order}}^{\prime }),f(p_{\mathrm{reverse}\mathrm{order}}^{\prime })\}$ If $f(p^{\prime })>f(p)$, then Update the older potential basis probe p by assigning $p\leftarrow p^{\prime }$ Update the fitness value $f(p)$ by assigning $f(p)\leftarrow f(p^{\prime })$ End if End if End for End for Assign $p_{im}\leftarrow p$ and $f(p_{im})\leftarrow f(p)$ Return $p_{im}$ and $f(p_{im})$

5.1. The 2-Opt Operator

The 2-opt operator eliminates two edges from the existing potential basis probes and reconnects them together to create a new good basis probe or possible route. Let $(c_i,c_{i+1})$, where $i=1,2,\cdots ,n-2$, and $(c_j,c_{j+1})$, where $j=i+2,\cdots ,n$, be the two edges of a potential basis probe $p=(c_1,c_2,\cdots ,c_i,c_{i+1},\cdots ,c_j,c_{j+1},\cdots ,c_l)$, where $l=5,7,9,\cdots ,n$. Then, the 2-opt operator reverses the local path between the cities $c_{i+1}$ and $c_j$, and generates a new good basis probe, which is denoted by $p^{\prime }$ and is defined by $p^{\prime }=(c_1,c_2,\cdots ,c_i,c_j,c_{j-1},\cdots ,c_{i+2},c_{i+1},c_{j+1},\cdots ,c_l)$. To avoid generating a worse basis probe by the 2-opt operator, it can be dominated by the following decision inequality:

$$2-\mathrm{opt}(i,j):\{d(c_i,c_{i+1})+d(c_j,c_{j+1})\}>\{d(c_i,c_j)+d(c_{i+1},c_{j+1})\}.$$

(5)

5.2. Reversion Operator

The reversion operator first locates the position of two different cities of a potential basis probe and then reverses the local path between these two cities. Consider a potential basis probe $p=(c_1,c_2,\cdots ,c_{i-1},c_i,c_{i+1},\cdots ,c_{j-1},c_j,c_{j+1},\cdots ,c_l)$, where $l=5,7,9,\cdots ,n$, and the two cut points $i(i=1,2,\cdots ,n-1)$ and $j(j=i+1,\cdots ,n)$ on p. This reversion operator generates a new good basis probe, which is denoted by $p^{\prime }$ and is defined by $p^{\prime }=(c_1,c_2,\cdots ,c_{i-1},c_j,c_{j-1},\cdots ,c_{i+1},c_i,c_{j+1},\cdots ,c_l)$. To determine whether the reversion is beneficial, we can check the following inequality:

$$\mathrm{Reversion}(i,j):\{d(c_{i-1},c_i)+d(c_j,c_{j+1})\}>\{d(c_{i-1},c_j)+d(c_i,c_{j+1})\}.$$

(6)

5.3. Swap Operator

The swap operator simply exchanges the positions of two cities of a potential basis probe to create a new good basis probe. Let the two positions $i(i=1,2,\cdots ,n-1)$ and $j(j=i+1,\cdots ,n)$ be selected from a potential basis probe $p=(c_1,c_2,\cdots ,c_{i-1},c_i,c_{i+1},\cdots ,c_{j-1},c_j,c_{j+1},\cdots ,c_l)$, where $l=5,7,9,\cdots ,n$. The new good basis probe through swap operator on p is denoted by $p^{\prime }$ and is defined by $p^{\prime }=(c_1,c_2,\cdots ,c_{i-1},c_j,c_{i+1},\cdots ,c_{j-1},c_i,c_{j+1},\cdots ,c_l)$. We accept the new basis probe if the following inequality holds:

$$\mathrm{Swap}(i,j)=\left\{\begin{array}{c}\{d(c_{i-1},c_i)+d(c_i,c_{i+1})+d(c_{j-1},c_j)+d(c_j,c_{j+1})\}>\hfill \\ \{d(c_{i-1},c_j)+d(c_j,c_{i+1})+d(c_{j-1},c_i)+d(c_i,c_{j+1})\},j-i\ne 1;\hfill \\ \{d(c_{i-1},c_i)+d(c_j,c_{j+1})\}>\{d(c_{i-1},c_j)+d(c_i,c_{j+1})\},j-i=1.\hfill \end{array}\right.$$

(7)

5.4. Insertion Operator

The insertion operator first picks two positions $i(i=1,2,\cdots ,n)$ and $j(j=1,2,\cdots ,n)$ with $j\ne i$ and then the city $c_i$ is inserted into the $c_j$’s back position. Consider a potential basis probe $p=(c_1,c_2,\cdots ,c_{i-1},c_i,c_{i+1},\cdots ,c_{j-1},c_j,c_{j+1},\cdots ,c_l)$, where $l=5,7,9,\cdots ,n$. The new basis probe generated based on this operator is defined by $p^{\prime }=(c_1,c_2,\cdots ,c_{i-1},c_{i+1},\cdots ,c_{j-1},c_j,c_i,c_{j+1},\cdots ,c_l)$. In fact, the new basis probe can be accepted if the following inequality holds:

$$\mathrm{Insertion}(i,j)=\left\{\begin{array}{c}\{d(c_{i-1},c_i)+d(c_i,c_{i+1})+d(c_j,c_{j+1})\}>\hfill \\ \{d(c_{i-1},c_{i+1})+d(c_j,c_i)+d(c_i,c_{j+1})\},i<j;\hfill \\ \{d(c_{j-1},c_j)+d(c_{i-1},c_i)+d(c_i,c_{i+1})\}>\hfill \\ \{d(c_{j-1},c_i)+d(c_i,c_j)+d(c_{i-1},c_{i+1})\},i>j.\hfill \end{array}\right.$$

(8)

6. Two-Stage Search Optimization Algorithm

In order to maintain a good balance between the effectiveness and efficiency of probe-based route development, we present a two-stage search optimization algorithm for solving both symmetric and asymmetric TSPs. Functionally, the first stage is to construct and develop an appropriate set of good complete routes through the probe extension step by step dynamically, while the second stage is a self-escape loop to prevent the search from being trapped in a locally optimal solution if possible. We describe the two stages in detail in the following two subsections, respectively.

6.1. Stage 1—Good Complete Route Development

In the first stage, we consider the partial routes as basis probes and extend them step by step to construct and develop a set of good complete routes in the end. In each step, a proportion value threshold element is set as a filter to filter out the worst partial routes or basic probes. Moreover, four local augmentation operators are employed to modify and improve the existing partial routes. According to the number of cities in the given TSP, this stage consists of certain steps (defined in Equation (3) to complete the route development. Actually, except the first one, each step implements three operations: basis probes or partial route generation, basis probe filtering, and basis probe improvement. The working steps of the first stage can be described as follows:

Step-1: 3-city basis probes are generated by taking all possible local two-path routes for each city as a center. Actually, a local two-path route is generated with three cities in which one city is central or internal and the other two cities are adjacent to it. We simply refer to it as a 3-city basis probe. Considering an n-city TSP problem with city list $L=\{c_1,c_2,\cdots ,c_n\}$ where $n\ge 3$, we let $c_i\in L$ be a city located at the $i^{th}$ position and $L(c_i)$ be a set of cities adjacent to $c_i$; i.e., $L(c_i)=L-\{c_i\}$. Then, the set of possible local two-path routes with internal city $c_i(i=1,2,\cdots ,n)$, with adjacent cities $c_j$ and $c_k$, can be defined by $L^2(c_i)$ as follows:

$$L^2(c_i)=\{c_j{c}_i{c}_k\triangleq p_{ijk}:c_j,c_k\in L(c_i);i\ne j,k;j\ne k;j=1,2,\cdots ,n,\mathrm{and}k=1,2,\cdots ,n\},$$

(9)

where $p_{ijk}$ represents a 3-city basis probe whose outer two wings are $p_{ijk}^j=e_{ij}$ and $p_{ijk}^k=e_{ik}$, respectively. Actually, it can utilize these two wings to extend and develop the route in the next step. In total, the set of possible 3-city basis probes is a union of all $L^2(c_i)$ provided as follows:

$${\mathsf{\Omega }}_3={\cup }_{i=1}^n{L}^2(c_i)={\cup }_{i=1}^n\{p_{ijk}:c_j,c_k\in L(c_i);i\ne j,k;j\ne k;j=1,2,\cdots ,n,\mathrm{and}k=1,2,\cdots ,n\}$$

(10)

After generating all the possible basis probes, the quality or fitness function $f(p_{ijk})$ of basis probe $p_{ijk}$ can be defined and computed from its cost (distance). That is, the quality of the basis probe is inversely proportional to its cost (distance); i.e., the basis probe with a higher value of $f(p_{ijk})$ is fitter and vice versa. Then, these basis probes can be ordered through the fitness function; e.g., the order of the fittest basis probe is 1, the order of the next fittest one is 2, etc. Finally, we retain certain potential basis probes from all the generated ones with the help of a threshold value filter (defined in Equation (4)). These retained basis probes are considered as the good and root probes of this step. Actually, root probes are 3-city potential basis probes that are kept for further route extension. Assuming that ${\psi }_3$ is just the threshold value of the filter or proportion value threshold element at this step, the set of the retained good and root basis probes can be constructed as follows:

$${\mathsf{\Pi }}_3=\{p_{ijk}:p_{ijk}\in {\mathsf{\Omega }}_3;\mathrm{the}\mathrm{order}\mathrm{of}(p_{ijk})\le {\psi }_3{n}_{p_3};n_{p_3}=|{\mathsf{\Omega }}_3|\},$$

(11)

where $n_{p_3}$ denotes the number of generated 3-city basis probes in ${\mathsf{\Omega }}_3$. For clarity, we let $n_{g_3}=|{\mathsf{\Pi }}_3|$ be the number of the retained good and root basis probes of ${\mathsf{\Pi }}_3$.

Step-2: In this step, we generate 5-city basis probes with the retained good basis 3-city probes obtained from Step-1. Indeed, each retained good basis probe of Step-1 can be hybridized with other consistent 3-city basis probes and generate the next possible 5-city basis probes. Actually, the set of possible 5-city basis probes can be constructed through the connection operations as follows:

$${\mathsf{\Omega }}_5=\{p_{ijklm}:\forall p_{ijk}\in {\mathsf{\Pi }}_3;\forall p_{jli},p_{kim}\in {\mathsf{\Omega }}_3;l\ne m;l,m\ne i,j,k\},$$

(12)

where $p_{ijklm}\triangleq c_l{c}_j{c}_i{c}_k{c}_m$ indicates a 5-city basis probe as it is a route of 5 different cities. The outer two wings of this basis probe are $p_{ijklm}^l=e_{lj}$ and $p_{ijklm}^m=e_{km}$, respectively. Like in Step-1, the quality or fitness function $f(p_{ijklm})$ of basis probe $p_{ijklm}$ can be defined and computed in the same way to order the basis probes. Once the basis probes are constructed and their orders are obtained, the lower fitness basis probes are filtered out while the good potential basis probes are retained according to the threshold value of the filter. Actually, assuming that the filtering threshold or proportion value at this step is ${\psi }_5$ (defined in Equation (4)), the set of possible potential basis probes can be constructed as follows:

$$T_5=\{p_{ijklm}:p_{ijklm}\in {\mathsf{\Omega }}_5;\mathrm{order}\mathrm{of}(p_{ijklm})\le {\psi }_5{n}_{p_5};n_{p_5}=|{\mathsf{\Omega }}_5|\},$$

(13)

where $n_{p_5}$ is the number of generated 5-city basis probes of ${\mathsf{\Omega }}_5$. The number $n_{r_5}$ of retaining potential basis probes can be denoted as $n_{r_5}=|T_5|$. For the possible improvement of each potential basis probe $p_{ijklm}\in T_5$, four local search operators (explained in Section 5) are implemented consecutively on it. If any better or fitter basis probe is developed, the earlier basis probe is directly replaced by the better basis probe. As a result, these retained potential probes are developed and improved. For clarity, we refer to the improved basis probes as the good basis probes. Therefore, the set of good basis 5-city probes can be constructed as follows:

$${\mathsf{\Pi }}_5=\{p_{ijklm}^{\prime }:p_{ijklm}^{\prime }=LS(p_{ijklm});\forall p_{ijklm}\in T_5;f(p_{ijklm}^{\prime })\ge f(p_{ijklm})\},$$

(14)

where $p_{ijklm}^{\prime }$ denotes the improved basis probe of $p_{ijklm}$, $LS$ denotes the total operation of implementing the four local augmentation operators consecutively, $f(p_{ijklm}^{\prime })$ and $f(p_{ijklm})$ are the fitness functions of the developed and original basis probes, respectively. Therefore, it can be easily found that $n_{g_5}=|{\mathsf{\Pi }}_5|\le n_{r_5}=|T_5|$ since ${\mathsf{\Pi }}_5\subseteq T_5$.

Like Step-2, the basis probe generation, filtering, and improvement operations can be carried out in the remaining steps of the complete route development process. In general, after completing the filtering task of the $(k+1)$th step, we obtain the set of $(2k+3)$-city potential basis probes, which can be denoted by $T_{2k+3}$ and constructed by

$$\begin{array}{cc}\hfill T_{2k+3}& =\{p_{ijklm\cdots tsvuhg}:p_{ijklm\cdots tsvuhg}\in {\mathsf{\Omega }}_{2k+3};\mathrm{order}\mathrm{of}(p_{ijklm\cdots tsvuhg})\le {\mathsf{\Psi }}_{2k+3}{n}_{p_{2k+3}};\hfill \\ \hfill & n_{p_{2k+3}}=|{\mathsf{\Omega }}_{2k+3}|\}.\hfill \end{array}$$

(15)

In Equation (15), $p_{ijklm\cdots tsvuhg}$ is a retained $(2k+3)$-city potential basis probe, ${\mathsf{\Omega }}_{2k+3}$ denotes the set of possible generated basis probes at the $(k+1)$th step, being expressed by Equation (17), $n_{p_{2k+3}}$ denotes the number of basis probes in ${\mathsf{\Omega }}_{2k+3}$, and ${\mathsf{\Psi }}_{2k+3}$ is the filtering proportion value at the $(k+1)$th step. Each retained potential basis probe $p_{ijklm\cdots tsvuhg}$ is further improved by the four local augmentation operators. Thus, the set of $(2k+3)$-city good basis probes is obtained at the end of the $(k+1)$th step, which is provided by

$$\begin{array}{cc}\hfill {\mathsf{\Pi }}_{2k+3}& =\{p_{ijklm\cdots tsvuhg}^{\prime }:p_{ijklm\cdots tsvuhg}^{\prime }=LS(p_{ijklm\cdots tsvuhg});\forall p_{ijklm\cdots tsvuhg}\in T_{2k+3};\hfill \\ \hfill & f(p_{ijklm\cdots tsvuhg}^{\prime })\ge f(p_{ijklm\cdots tsvuhg})\},\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\mathsf{\Omega }}_{2k+3}& =\{p_{ijklm\cdots tsvuhg}:\forall p_{ijklm\cdots tsvu}\in {\mathsf{\Pi }}_{2k+1};\forall p_{vht},p_{usg}\in {\mathsf{\Omega }}_3;h\ne g;\hfill \\ \hfill & h,g\ne v,t,\cdots ,l,j,i,k,m,\dots ,s,u\},\hfill \end{array}$$

(17)

In Equation (16), $p_{ijklm\cdots tsvuhg}^{\prime }$ is the improved basis probe obtained by implementing the four local search operators on the basis probe $p_{ijklm\cdots tsvuhg}$, $f(p_{ijklm\cdots tsvuhg}^{\prime })$ and $f(p_{ijklm\cdots tsvuhg})$ represent the fitness values of the improved and original basis probes, respectively.

In Equation (17), $p_{ijklm\cdots tsvuhg}\triangleq \{\underset{(2k+3)-\mathrm{city}\mathrm{generated}\mathrm{probe}}{\underbrace{c_h\stackrel{(2k+1)-\mathrm{city}\mathrm{good}\mathrm{probe}}{\overbrace{c_v{c}_t\dots c_l{c}_j{c}_i{c}_k{c}_m\dots c_s{c}_u}}{c}_g}}$ is a $(2k+3)$-city generated basis probe having the outer wings $p_{ijklm\cdots tsvuhg}^h=e_{vh}$ and $p_{ijklm\cdots tsvuhg}^g=e_{ug}$, ${\mathsf{\Pi }}_{2k+1}$ is the set of $(2k+1)$-city good basis probes obtained from the $k^{th}$ step, and $p_{vht}$ and $p_{usg}$ represent the 3-city basis probes in ${\mathsf{\Omega }}_3$.

In this way, after executing the last step, the route development process has produced a set of good basis probes, ${\mathsf{\Pi }}_n$, where each good basis probe consists of n cities, being a complete one or a complete route for the TSP. It should be noted that, in the last step of the even-number TSP, one city remains to be connected and thus the basis probe uses any one of its wings to include the remaining city properly.

6.2. Stage 2—Self-Escape Mechanism

After the first stage, we arrive at a set of good complete basis probes or routes as the search result of the TSP. However, there may be some stagnant complete basis probes that can be considered as being trapped in a locally optimal solution during our route development and search process. In order to alleviate this locally trapped search problem, we can couple our general route development and search process (the first stage) with a self-escape mechanism, which is referred to as the second stage, i.e., Stage 2. Through this self-escape mechanism, we can enhance the diversity of the complete basis probes and further improve the search results. In fact, the self-escape mechanism was first introduced in the PSO algorithm by Wang et al. [15] in 2007. Recently, Wang et al. [16] applied it to promote the performance of the DSOS algorithm. Here, we utilize it to solve our locally trapped search problem such that, as a complete basis probe is trapped in a local optimum solution, we enforce it to effectively jump out of itself and search for the better complete basis probe. Specifically, this self-escape mechanism accomplishes two different tasks: first, identifying whether a complete basis probe is trapped in a local optimum, and, second, if it is, helping it to jump out of itself to develop a new solution.

Let $p_l,p_{best}\in {\mathsf{\Pi }}_n$, where $p_l(l=1,2,\dots ,g_n)$ and $p_{best}$ represent a complete basis probe and the current best basis probe in ${\mathsf{\Pi }}_n$, respectively. We can judge whether a complete basis probe $p_l$ is a local optimum solution if and only if the following inequality holds [15,16]:

$$|{\mathsf{\Gamma }}_l|<\frac{1}{g_n}\sum _{l=1}^{g_n}|{\mathsf{\Gamma }}_l|,$$

(18)

where

$${\mathsf{\Gamma }}_l=E(p_l)\cup E(p_{best}),$$

(19)

where $E(p_l)$ and $E(p_{best})$ denote the sets of edges in $p_l$ and $p_{best}$, respectively, ${\mathsf{\Gamma }}_l$ denotes the set of common edges between $E(p_l)$ and $E(p_{best})$, $|{\mathsf{\Gamma }}_l|$ denotes the number of common edges in ${\mathsf{\Gamma }}_l$, and $g_n$ is the number of complete basis probes in ${\mathsf{\Pi }}_n$. That is, if the inequality Equation (18) holds, it is believed that $p_l$ is trapped in a local optimum solution. In such a situation, we implement the self-escape mechanism on $p_l$ as the following 3-opt operator such that we can transform it into promising basis probes.

We first remove 3 edges from the stagnant complete basis probe and divide it into three partial routes as it is considered a ring route. We then connect these partial routes in different ways to generate new complete routes that may be better than the original route. For example, let $p_l$ be a stagnant complete basis probe and its three edges, namely $(c_i,c_{i+1(modn)})$ with $i=0,1,2,\cdots ,n-1$, $(c_j,c_{j+1(modn)})$, where $j=i+m(modn)$ and $m=1,2,\dots ,n-3$, and $(c_k,c_{k+1(modn)})$, where $k=i+t(modn)$ and $t=m+1,\dots ,n-1$ are selected. Removing these 3 edges from $p_l$ makes 3 partial routes, namely $p_{lq}$, where q = 1, 2, 3. The reverse of these partial routes is denoted by $p_{lq}^{\prime }$, where q = 1, 2, 3. Then, the new complete probe can be generated by combining $p_{lq}$ and $p_{lq}^{\prime }$ in the following seven different ways:

• $\{p_{l1}^{\prime },p_{l2},p_{l3}\}$, Judge by the inequality $\{d(c_i,c_{i+1(modn)})+d(c_k,c_{k+1(modn)})\}>\{d(c_i,c_k)+d(c_{i+1(modn)},c_{k+1(modn)})\}$
• $\{p_{l1},p_{l2},p_{l3}^{\prime }\}$, Judge by the inequality $\{d(c_j,c_{j+1(modn)})+d(c_k,c_{k+1(modn)})\}>\{d(c_j,c_k)+d(c_{j+1(modn)},c_{k+1(modn)})\}$
• $\{p_{l1},p_{l2}^{\prime },p_{l3}\}$, Judge by the inequality $\{d(c_i,c_{i+1(modn)})+d(c_j,c_{j+1(modn)})\}>\{d(c_i,c_j)+d(c_{i+1(modn)},c_{j+1(modn)})\}$
• $\{p_{l1},p_{l2}^{\prime },p_{l3}^{\prime }\}$, Judge by the inequality $\{d(c_i,c_{i+1(modn)})+d(c_j,c_{j+1(modn)})+d(c_k,c_{k+1(modn)})\}>\{d(c_i,c_j)+d(c_{i+1(modn)},c_k)+d(c_{j+1(modn)},c_{k+1(modn)})\}$
• $\{p_{l1}^{\prime },p_{l2}^{\prime },p_{l3}\}$, Judge by the inequality $\{d(c_i,c_{i+1(modn)})+d(c_j,c_{j+1(modn)})+d(c_k,c_{k+1(modn)})\}>\{d(c_i,c_k)+d(c_{j+1(modn)},c_{i+1(modn)})+d(c_j,c_{k+1(modn)})\}$
• $\{p_{l1}^{\prime },p_{l2},p_{l3}^{\prime }\}$, Judge by the inequality $\{d(c_i,c_{i+1(modn)})+d(c_j,c_{j+1(modn)})+d(c_k,c_{k+1(modn)})\}>\{d(c_i,c_{j+1(modn)})+d(c_k,c_j)+d(c_{i+1(modn)},c_{k+1(modn)})\}$
• $\{p_{l1}^{\prime },p_{l2}^{\prime },p_{l3}^{\prime }\}$, Judge by the inequality $\{d(c_i,c_{i+1(modn)})+d(c_j,c_{j+1(modn)})+d(c_k,c_{k+1(modn)})\}>\{d(c_i,c_{j+1(modn)})+d(c_k,c_{i+1(modn)})+d(c_j,c_{k+1(modn)})\}$

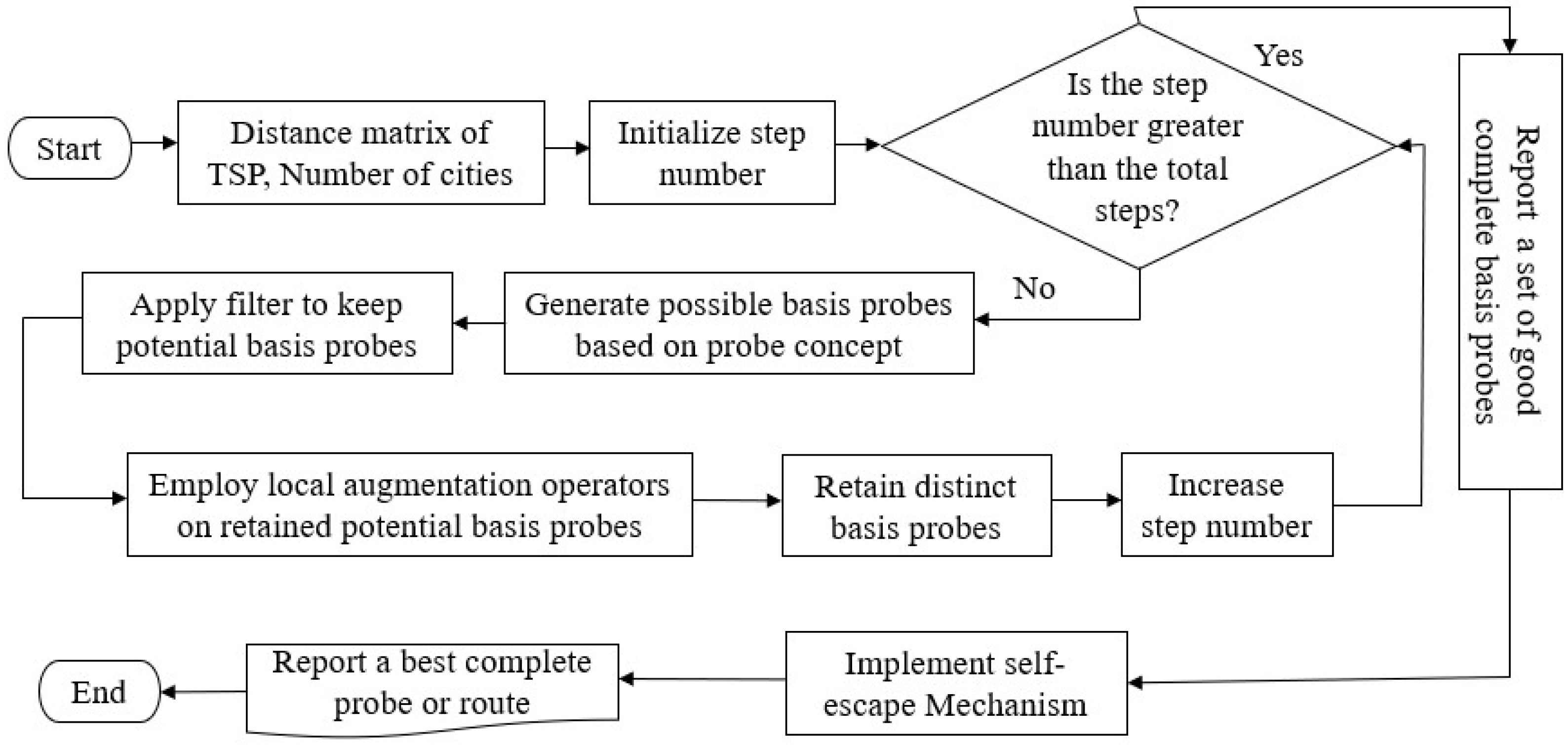
We use the cases of 3, 6, and 7 for the symmetric TSP and all cases for the asymmetric TSP to generate new complete basis probes. The flowchart and pseudocode of our proposed two-stage search optimization algorithm are sketched in Figure 2 and Algorithm 2, respectively.

Algorithm 2: Pseudocode of the proposed two-stage probe-based search optimization algorithm

Input: Distance matrix $d_{n\times n}$, Problem size n, Filter ${\mathsf{\Psi }}_{2k+1}$ Output: Best complete probe $p_{best}$, Fitness of best complete probe $f(p_{best})$ For each city $c_i$, $i=1$ to n Construct 3-city basis probes $p_{ijk}$ with center $c_i$ and insert them in a set ${\mathsf{\Omega }}_3$ Calculate fitness value $f(p_{ijk})$ of each basis probe $p_{ijk}\in {\mathsf{\Omega }}_3$ End for Determine order of each basis probe $p_{ijk}\in {\mathsf{\Omega }}_3$ on the basis of $f(p_{ijk})$ Retain potential basis probes based on filter ${\mathsf{\Psi }}_3$ and insert them in a set ${\mathsf{\Pi }}_3$ For each step k, $k=2$ to maximum step, $[\frac{n}{2}]$ Construct new basis probes $p_{ijk\dots 2k+1}$ based on retained potential basis probes $p_{ijk\dots 2k-1}\in {\mathsf{\Pi }}_{2k-1}$ and insert them in a set ${\mathsf{\Omega }}_{2k+1}$ Calculate fitness value $f(p_{ijk\dots 2k+1})$ of each new basis probe $p_{p_{ijk\dots 2k+1}}\in {\mathsf{\Omega }}_{2k+1}$ Determine order of each basis probe $p_{ijk\dots 2k+1}\in {\mathsf{\Omega }}_{2k+1}$ on the basis of $f(p_{ijk\dots 2k+1})$ Retain potential basis probes based on filter ${\mathsf{\Psi }}_{2k+1}$ and insert them in a set $T_{2k+1}$ For each basis probe $p_{ijk\dots 2k+1}^l\in T_{2k+1}$, $l=1$ to $n_{r_{2k+1}}=|T_{2k+1}|$ Improve the retained potential basis probe $p_{ijk\dots 2k+1}^l$ by applying (i) 2-opt operator (ii) Insertion operator (iii) Reversion operator (iv) Swap operator Let $p_{ijk\dots 2k+1(im)}^l$ be the improved probe and $f(p_{ijk\dots 2k+1(im)}^l)$ be its fitness value If $f(p_{ijk\dots 2k+1(im)}^l)>f(p_{ijk\dots 2k+1}^l)$, then Update the retained potential basis probe $p_{ijk\dots 2k+1}^l$ by assigning $p_{ijk\dots 2k+1}^l\leftarrow p_{ijk\dots 2k+1(im)}^l$ Update fitness value $f(p_{ijk\dots 2k+1}^l)$ by assigning $f(p_{ijk\dots 2k+1}^l)\leftarrow f(p_{ijk\dots 2k+1(im)}^l)$ End if End for The set $T_{2k+1}$ of retained potential basis probes is updated and identified as a set of good basis probes ${\mathsf{\Pi }}_{2k+1}$ End for Apply self-escape mechanism on each stagnant complete basis probe (if any) of ${\mathsf{\Pi }}_{2[\frac{n}{2}]+1}$ Determine best complete probe $p_{best}$ from ${\mathsf{\Pi }}_{2[\frac{n}{2}]+1}$, $p_{best}=p_{ijk\dots 2[\frac{n}{2}]+1(best)}$ and its fitness value $f(p_{best})$ Return best complete probe $p_{best}$ and its fitness value $f(p_{best})$

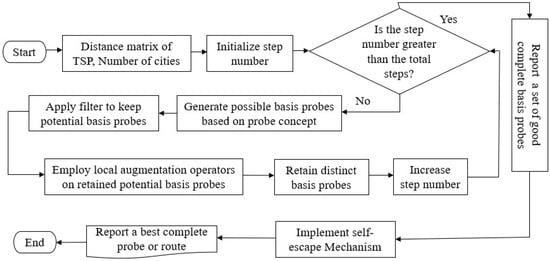
Figure 2. Flowchart of the proposed two-stage probe-based search optimization algorithm.

7. Experimental Results and Analysis

In this section, various experiments are carried out to evaluate the performance of our proposed algorithm on the typical benchmark datasets of the TSP with a different number of cities [17,18,19,20]. The obtained experimental results are further compared with the best-known TSP benchmark results reported by the data library, as well as with the results obtained by the state-of-the-art algorithms. Finally, a rigorous statistical analysis is conducted to substantiate the advantages of our proposed algorithm against the other state-of-the-art optimization algorithms.

7.1. Experimental Configurations and Evaluation Protocol

To conduct the experiments on the datasets whose city size is up to 561, we use a desktop computer with the specifications of Intel Core i5-4590 $3.30$ GHz processors, 8 GB RAM, and 64-bit Windows 10 operating system. For the other datasets, we run with a 2 core GPU Linux operating system due to requiring high computational resources. The proposed algorithm is implemented in MATLAB R2019a programming language for all the simulations. Two performance evaluation indicators, error (measured in %) and computational time (measured in seconds), are calculated to evaluate the performance of the proposed algorithm. The percentage deviation of the simulated result from the best-known results (i.e., error) is enumerated based on the following formulae:

$$\mathrm{Error}(\%)=\frac{Z(p)-Z^{\ast }(p)}{Z^{\ast }(p)}\times 100,$$

(20)

where $Z(p)$ and $Z^{\ast }(p)$ denote the obtained solution and best-known solution on a particular TSP dataset, respectively. For the execution time, we run the algorithm 10 times independently on each TSP dataset and compute the average and standard deviation (SD) of the times.

7.2. Performance Evaluation and Analysis

In this subsection, we conduct the experiments of our proposed algorithm on 83 symmetric and 18 asymmetric benchmark TSP test problems to evaluate its performance. Actually, the experimental results are summarized in Table 2, where the “BKS” column element indicates the best-known solution reported by the data library, while the “Our Result” column element indicates the solution obtained by our proposed algorithm. The “Difference” and “Error$(\%)$” column elements denote the deviation and the percentage deviation of the obtained result from the best-known result, respectively. The computational time(s) column element denotes the average execution time (in seconds) of the algorithm with the SD value in 10 runs. We boldface the names of the datasets whose best-known solutions or new solutions are obtained by our proposed algorithm.

Table 2. Computational results of our proposed algorithm for 83 symmetric and 18 asymmetric benchmark TSP datasets.

S/N	Datasets	No. of Cities	BKS	Our Result	Difference	Error $(\%)$	Computational Time (s)
Symmetric Travelling Salesman Problem (STSP)
1	burma14	14	3323.000	3323.000	0.00000	0.00000	0.00840000$\pm 0.005700$
2	p01	15	291.0000	291.0000	0.00000	0.00000	0.00710000$\pm 0.002700$
3	F15	15	1105.000	1105.000	0.00000	0.00000	0.12410000$\pm 0.010400$
4	ulysses16	16	6859.000	6859.000	0.00000	0.00000	0.04010000$\pm 0.002800$
5	gr17	17	2085.000	2085.000	0.00000	0.00000	0.00820000$\pm 0.002300$
6	C20	20	62,575.00	62,575.00	0.00000	0.00000	0.15070000$\pm 0.005400$
7	S21	21	60,000.00	60,000.00	0.00000	0.00000	0.87340000$\pm 0.082000$
8	gr21	21	2707.000	2707.000	0.00000	0.00000	0.06220000$\pm 0.003800$
9	ulysses22	22	7013.000	7013.000	0.00000	0.00000	2.26550000$\pm 0.091800$
10	gr24	24	1272.000	1272.000	0.00000	0.00000	0.66050000$\pm 0.016800$
11	fri26	26	937.0000	937.0000	0.00000	0.00000	0.02900000$\pm 0.005500$
12	bays29	29	2020.000	2020.000	0.00000	0.00000	0.03010000$\pm 0.004600$
13	bayg29	29	1610.000	1610.000	0.00000	0.00000	0.03540000$\pm 0.004600$
14	wi29	29	27,603.00	27,601.00	−2.0000	−0.0072	0.19490000$\pm 0.005300$
15	C30	30	62,716.00	62,716.00	0.00000	0.00000	0.30170000$\pm 0.011600$
16	ncit30	30	48,873.00	48,872.00	−1.0000	−0.0020	0.56890000$\pm 0.020600$
17	F32	32	84,180.00	84,180.00	0.00000	0.00000	0.34970000$\pm 0.009600$
18	C40	40	62,768.00	62,768.00	0.00000	0.00000	0.55040000$\pm 0.026900$
19	F41	41	68,168.00	68,168.00	0.00000	0.00000	1.75490000$\pm 0.102800$
20	dantzig42	42	699.0000	699.0000	0.00000	0.00000	0.27560000$\pm 0.003400$
21	swiss42	42	1273.000	1273.000	0.00000	0.00000	0.16430000 $\pm 0.006000$
22	gr48	48	5046.000	5046.000	0.00000	0.00000	0.78070000$\pm 0.021500$
23	att48	48	10,628.00	10,628.00	0.00000	0.00000	0.47480000 $\pm 0.014700$
24	hk48	48	11,461.00	11,461.00	0.00000	0.00000	0.71980000$\pm 0.011700$
25	brazil58	58	25,395.00	25,395.00	0.00000	0.00000	0.13380000 $\pm 0.006700$
26	ncit64	64	6400.000	6400.000	0.00000	0.00000	1.09990000$\pm 0.009400$
27	pr76	76	108,159.0	108,159.0	0.00000	0.00000	1.88750000$\pm 0.015000$
28	pg88	88	6548.000	6544.000	−4.0000	−0.0611	5.79330000$\pm 0.091300$
29	gr96	96	55,209.00	55,209.00	0.00000	0.00000	59.1940000$\pm 0.835700$
30	rd100	100	7910.000	7910.000	0.00000	0.00000	1.20260000 $\pm 0.025700$
31	kroA100	100	21,282.00	21,282.00	0.00000	0.00000	62.6235000$\pm 2.465600$
32	kroB100	100	22,141.00	22,139.08	−1.9200	−0.00870	35.3965000$\pm 0.767400$
33	kroC100	100	20,749.00	20,749.00	0.00000	0.00000	161.282400$\pm 3.299000$
34	kroD100	100	21,294.00	21,294.00	0.00000	0.00000	5.74360000$\pm 0.040300$
35	kroE100	100	22,068.00	22,068.00	0.00000	0.00000	94.3792000$\pm 1.119300$
36	lin105	105	14,379.00	14,379.00	0.00000	0.00000	189.325800$\pm 1.374200$
37	pr107	107	44,303.00	44,301.68	−1.3200	−0.0030	85.5968000$\pm 0.555200$
38	gr120	120	6942.000	6942.000	0.00000	0.00000	88.2677000$\pm 2.551300$
39	pr124	124	59,030.00	59,030.00	0.00000	0.00000	7.40980000$\pm 0.450500$
40	ch130	130	6110.000	6110.000	0.00000	0.00000	333.304540$\pm 1.121356$
41	pr136	136	96,772.00	96,770.92	−1.0800	−0.00112	549.330100$\pm 9.581700$
42	gr137	137	69,853.00	69,853.00	0.00000	0.00000	119.285700$\pm 0.847900$
43	pr144	144	58,537.00	58,535.22	−1.7800	−0.00304	0.88570000$\pm 0.020300$
44	ch150	150	6528.000	6530.900	2.90000	0.04442	589.790700$\pm 8.477500$
45	kroA150	150	26,524.00	26,524.00	0.00000	0.00000	346.632200$\pm 3.379500$
46	kroB150	150	26,130.00	26,127.36	−2.6400	−0.0101	730.277200$\pm 2.632800$
47	pr152	152	73,682.00	73,682.00	0.00000	0.00000	198.222800$\pm 3.427600$
48	u159	159	42,080.00	42,075.67	−4.3300	−0.01028	4.60580000$\pm 0.235000$
49	si175	175	21,407.00	21,407.00	0.00000	0.00000	526.824300$\pm 3.132500$
50	brg180	180	1950.000	1950.000	0.00000	0.00000	10.8813000$\pm 0.573100$
51	qa194	194	9352.000	9353.660	1.66000	0.01775	899.238500$\pm 12.65310$
52	kroA200	200	29,368.00	29,385.72	17.7200	0.06033	277.726900$\pm 0.901200$
53	kroB200	200	29,437.00	29,441.38	4.38000	0.01488	217.566400$\pm 4.342400$
54	gr202	202	40,160.00	40,187.00	27.0000	0.06723	163.689300$\pm 3.651700$
55	tsp225	225	3916.000	3865.004	−50.996	−1.30225	145.628300$\pm 0.862400$
56	ts225	225	126,643.0	126,643.0	0.00000	0.00000	1363.19560$\pm 15.66020$
57	pr226	226	80,369.00	80,374.33	5.33000	0.00663	1643.20400$\pm 17.55140$
58	gr229	229	134,602.0	134,658.0	56.0000	0.04160	658.919400$\pm 6.308800$
59	gil262	262	2378.000	2389.050	11.0500	0.46467	4659.63020$\pm 55.62780$
60	pr264	264	49,135.00	49,135.00	0.00000	0.00000	1981.23760$\pm 22.60660$
61	a280	280	2579.000	2587.800	8.80000	0.34121	7792.27620$\pm 67.94830$
62	pr299	299	48,191.00	48,200.16	9.16000	0.01900	1261.25450$\pm 17.86110$
63	lin318	318	42,029.00	42,082.42	53.4200	0.12710	1307.43090$\pm 4.553100$
64	rd400	400	15,281.00	15,307.15	26.1500	0.17112	2434.54950$\pm 343.0932$
65	fl417	417	11,861.00	11,914.45	53.4500	0.45063	17,069.3660$\pm 1581.106$
66	att532	532	27,686.00	27,786.00	100.000	0.36119	26,496.9020$\pm 1888.922$
67	ali535	535	202,339.0	203,016.0	677.000	0.33459	60,731.8600$\pm 2354.098$
68	si535	535	48,450.00	48,450.00	0.00000	0.00000	390,160.000$\pm 912.5270$
69	pa561	561	2763.000	2775.000	12.0000	0.43431	69,279.8030$\pm 1121.304$
70	u574	574	36,905.00	37,049.29	144.290	0.39098	74,990.6660$\pm 4201.612$
71	rat575	575	6773.000	6851.730	78.7300	1.16241	74,209.5970$\pm 2722.342$
72	p654	654	34,643.00	34,646.83	3.83000	0.01106	105,823.570$\pm 1893.281$
73	d657	657	48,912.00	49,127.83	215.830	0.44126	102,080.410$\pm 3084.854$
74	gr666	666	294,358.0	295,988.0	1630.00	0.55375	104927.200$\pm 3639.270$
75	u724	724	41,910.00	42,124.40	214.400	0.51157	128,591.020$\pm 3094.913$
76	rat783	783	8806.000	8934.090	128.090	1.45458	154466.440$\pm 5676.663$
77	pr1002	1002	259,045.0	259,250.0	205.000	0.07914	180,250.380$\pm 6114.756$
78	si1032	1032	92,650.00	92,650.00	0.00000	0.00000	235990.000$\pm 1234.210$
79	pcb1173	1173	56,892.00	57,528.29	636.290	1.11842	259,876.200$\pm 13,507.02$
80	d1291	1291	50,801.00	51,618.54	817.540	1.60929	329533.800$\pm 12680.29$
81	rl1323	1323	270199.0	272,083.96	1884.96	0.69762	646416.070$\pm 9695.350$
82	fl1400	1400	20,127.00	20,315.84	188.840	0.93824	737,727.33$\pm 8046.5143$
83	d1655	1655	62,128.00	63,268.61	1140.61	1.83590	12,166.5.30$\pm 28,064.93$
Aymmetric Travelling Salesman Problem (ATSP)
1	br17	17	39.00000	39.00000	0.00000	0.00000	0.00890000$\pm 0.002700$
2	ftv33	34	1286.000	1286.000	0.00000	0.00000	0.19100000$\pm 0.006800$
3	ftv35	36	1473.000	1473.000	0.00000	0.00000	0.38450000 $\pm 0.009900$
4	ftv38	39	1530.000	1530.000	0.00000	0.00000	31.7042000$\pm 0.396400$
5	p43	43	5620.000	5620.000	0.00000	0.00000	0.18200000 $\pm 0.006900$
6	ftv44	45	1613.000	1613.000	0.00000	0.00000	28.6533000$\pm 0.290400$
7	ftv47	48	1776.000	1776.000	0.00000	0.00000	51.4585000$\pm 1.589600$
8	ry48p	48	14,422.00	14,422.00	0.00000	0.00000	33.9627000$\pm 0.754800$
9	ft53	53	6905.000	6905.000	0.00000	0.00000	134.984900$\pm 1.949300$
10	ftv55	56	1608.000	1608.000	0.00000	0.00000	35.1772000$\pm 0.669600$
11	ftv64	65	1839.000	1850.000	11.0000	0.59815	18.8923000$\pm 0.177000$
12	ftv70	71	1950.000	1950.000	0.00000	0.00000	94.5148000$\pm 3.095900$
13	ft70	70	38,673.00	38,869.00	196.000	0.50681	178.463400$\pm 1.380800$
14	kro124p	100	36,230.00	36,230.00	0.00000	0.00000	4.31640000$\pm 0.094300$
15	rbg323	323	1326.000	1331.000	5.00000	0.37707	3268.51000$\pm 178.4000$
16	rbg358	358	1163.000	1164.000	1.00000	0.08598	4293.80000$\pm 451.2900$
17	rbg403	403	2465.000	2465.000	0.00000	0.00000	7500.67580$\pm 278.5200$
18	rbg443	443	2720.000	2720.000	0.00000	0.00000	8742.91860$\pm 366.8200$
Average Percentage Error (SD):						0.137823 (0.381285)

Note: Best-known solution or a new solution obtained by our proposed algorithm is set in bold.

It can be observed from Table 2 that our proposed algorithm yields the closest best-known solutions on the considered symmetric and asymmetric TSP test problems. In fact, the errors are very small. Our proposed algorithm has found exactly the best-known solution for each symmetric TSP dataset whose city size is up to 180 (except ch150) and some other symmetric TSP datasets such as tsp225, ts225, pr264, si535, and si1032, and almost all the asymmetric TSP datasets (except ftv64, ft70, rbg323, and rbg358). Specifically, in some cases (shown separately in Table 3), it exhibits a strong global exploration capability and produces better solutions than the best-known solutions with negative percentage error entries in the table. Statistically, our proposed algorithm obtains exactly the best-known solution in $65.06\%$ of the symmetric datasets (54 out of 83), and in $77.78\%$ of the asymmetric datasets (14 out of 18). For the rest of the TSP test problems, the loss of efficiency is no more than $1.84\%$ and $0.60\%$ for symmetric and asymmetric cases, respectively. In addition, the error belongs to an interval of $[0.007\%,0.70\%]$ in $26.73\%$ (27 out of 101) cases, while only in $4.95\%$ (5 out of 101) cases is it more than $1\%$. Furthermore, the average error over the entire 101 datasets is $0.14\%$, with a standard deviation value of $0.38$, which strongly demonstrates the outstanding performance of our proposed algorithm.

Table 3. Best solutions found thus far by our proposed algorithm compared with the best-known solutions from data library.

S/N	Datasets	No. of Cities	BKS	Our Result	Difference	Error $(\%)$	Computational Time (s)
1	wi29	29	27,603.00	27,601.00	−2.0000	−0.0072	0.19490000$\pm 0.005300$
2	ncit30	30	48,873.00	48,872.00	−1.0000	−0.0020	0.56890000$\pm 0.020600$
3	pg88	88	6548.000	6544.000	−4.0000	−0.0611	5.79330000$\pm 0.091300$
4	kroB100	100	22,141.00	22,139.08	−1.9200	−0.00870	35.3965000$\pm 0.767400$
5	pr107	107	44,303.00	44,301.68	−1.3200	−0.0030	85.5968000$\pm 0.555200$
6	pr136	136	96,772.00	96,770.92	−1.0800	−0.00112	549.330100$\pm 9.581700$
7	pr144	144	58,537.00	58,535.22	−1.7800	−0.00304	0.88570000$\pm 0.020300$
8	kroB150	150	26,130.00	26,127.36	−2.6400	−0.0101	730.277200$\pm 2.632800$
9	u159	159	42,080.00	42,075.67	−4.3300	−0.01028	4.60580000$\pm 0.235000$
10	tsp225	225	3916.000	3865.004	−50.996	−1.30225	145.628300$\pm 0.862400$

Note: The new solution obtained by our proposed algorithm is set in bold.

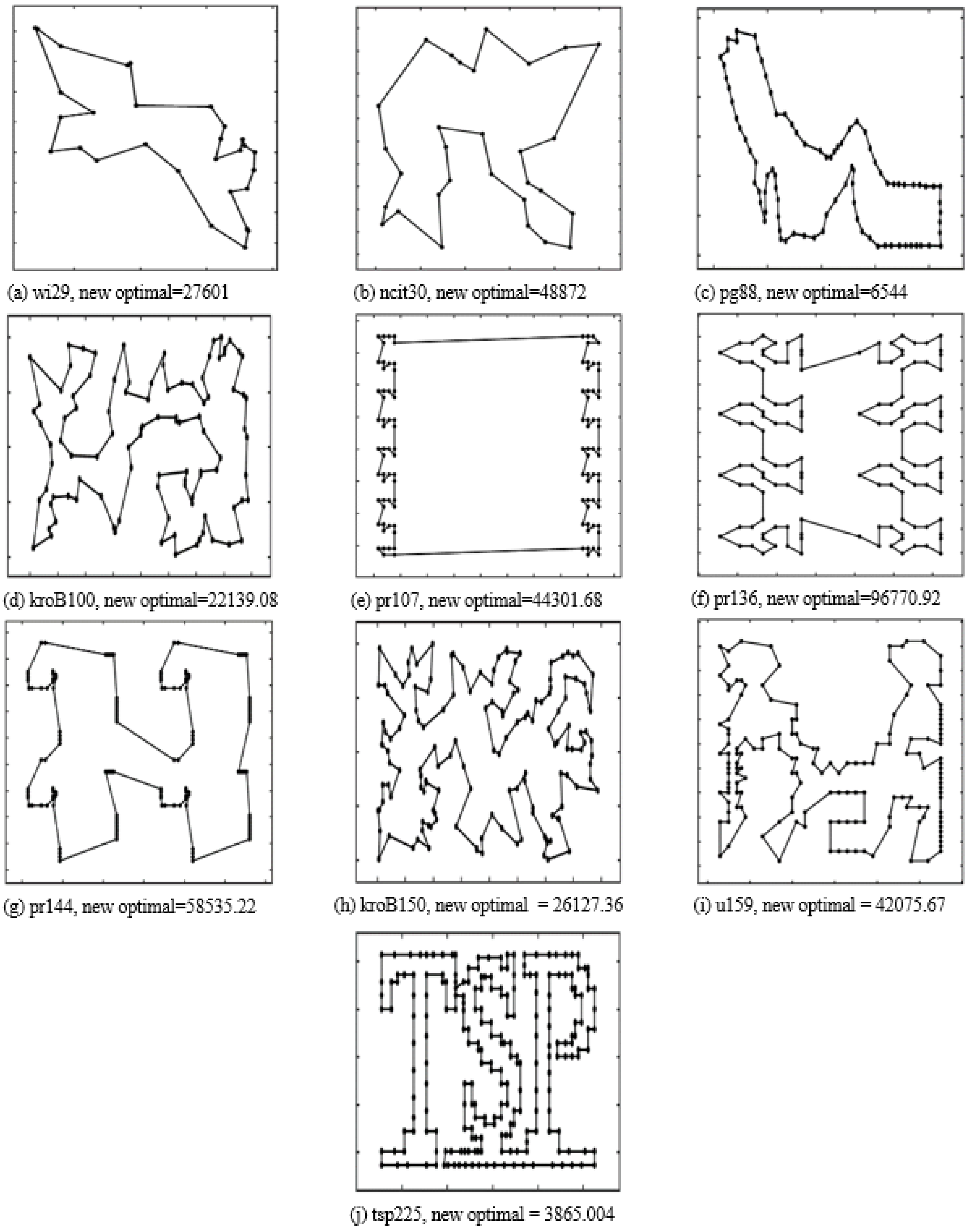
On the other hand, in terms of execution time, our proposed algorithm consumes a small amount of time to solve a small-scale TSP problem. As the scale of the TSP problem expands $(n<417)$, its computational time may be relatively increased or decreased. For example, it takes $59.19$ s to solve the gr96 problem, while it requires only $10.88$ s for the brg180 problem. In the case of large-scale datasets $(n\ge 417)$, it is rapidly increased with the scale of the TSP problem. Although our proposed algorithm takes a longer time in the large-scale case, the quality of the solution is satisfactory (the maximum error is equal to $1.84\%$). On average, its computational time is acceptable. Therefore, we can consider that our proposed algorithm is a reliable search optimization method that can provide a good-quality solution for a general TSP within an acceptable time frame. Most importantly, it is deterministic; i.e., we run it to obtain the same result on a TSP dataset or problem at any time. The new best routes with the route length found by our proposed algorithm are further displayed in Figure 3.

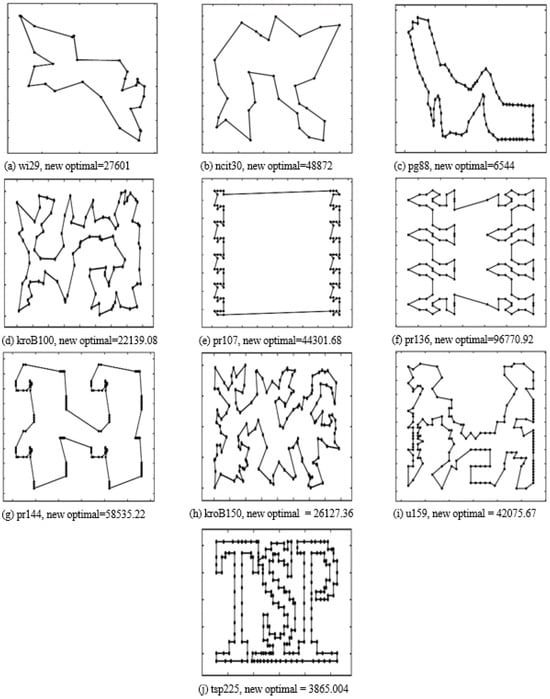
Figure 3. The new best route with route length found by our proposed algorithm for the datasets (a) wi29, (b) ncit30, (c) pg88, (d) kroB100, (e) pr107, (f) pr136, (g) pr144, (h) kroB150, (i) u159, and (j) tsp225.

7.3. Performance Comparison

In this subsection, we further compare our proposed algorithm with the state-of-the-art optimization algorithms. Table 4 describes the details of our selected state-of-the-art optimization algorithms for solving the TSPs. Specifically, our proposed algorithm is first compared with the state-of-the-art optimization algorithms with a self-escape mechanism and then compared with the other state-of-the-art algorithms (without a self-escape mechanism). Actually, the experimental results of our proposed approach are compared with those of the comparative algorithms reported in the literature, displayed in Table 5, Table 6, Table 7 and Table 8. The average (of solution route length) on all the TSP problems or datasets and the number of BKSs found corresponding to each comparison are presented at the bottom of each compared algorithm. Indeed, the number of BKSs found indicates how many datasets in which the algorithm can exactly find the best-known solution.

Table 4. List of state-of-the-art optimization algorithms of TSPs considered for comparison.

S/N	Abbreviation	Authors	Year	Name of the Optimization Algorithms
1	SEHDPSO [15]	Wang et al.	2007	Self-escape hybrid discrete particle swarm optimization algorithm
2	ASA-GS [21]	Geng et al.	2011	Adaptive simulated annealing algorithm with greedy search
3	GSA-ACO-PSO [22]	Chen and Chien	2011	Genetic simulated annealing ant colony system with particle swarm optimization algorithm
4	GA-PSO-ACO [23]	Deng et al.	2012	Hybrid swarm intelligence optimization algorithm based on the genetic algorithm, particle swarm optimization and ant colony optimization
5	HGA+2local [24]	Wang	2014	Hybrid genetic algorithm with two local optimization strategies
6	DIWO [25]	Zhou et al.	2015	Discrete invasive weed optimization algorithm
7	IBA [26]	Osaba et al.	2016	Improved discrete bat algorithm
8	DSOS [27]	Ezugwu and Adewumi	2017	Discrete symbiotic organisms search algorithm
9	DWCA [28]	Osaba et al.	2018	Discrete water cycle algorithm
10	IVNS [29]	Hore et al.	2018	Improving variable neighborhood search algorithm
11	ABCSS [30]	Khan and Maiti	2019	A swap sequence based artificial bee colony algorithm
12	ECSDSOS [16]	Wang et al.	2019	Discrete symbiotic organism search with excellence coefficients and self-escape mechanism
13	HSIHM+2local [31]	Boryczka and Szwarc	2019	Harmony search algorithm with additional improvement of harmony memory
14	MCF-ABC [32]	Choong et al.	2019	Artificial bee colony algorithm with modified choice function
15	PRGA($(2019)$) [33]	Kaabi and Harrath	2019	Permutation rules and genetic algorithm
16	DSCA+LS [34]	Tawhid and Savsani	2019	Discrete sine-cosine algorithm with local search
17	MMA [2]	Naser et al.	2019	A multi-matching approximation algorithm
18	DSMO [35]	Akhand et al.	2020	Discrete spider monkey optimization algorithm
19	VDWOA [36]	Zhang et al.	2021	An improved whale optimization algorithm
20	SCGA [37]	Deng et al.	2021	A hybrid cellular genetic algorithm
21	MPSO [3]	Yousefikhoshbakht	2021	A modified metaheuristic algorithm
22	DSSA [8]	Zhang and Han	2022	Discrete sparrow search algorithm
23	DA-GVNS [38]	Karakostas and Sifaleras	2022	A double-adaptive general variable neighborhood search algorithm

Table 5. Performance comparison of our proposed algorithm with the state-of-the-art optimization algorithms containing self-escape mechanism.

Comparison with SEHDPSO							Comparison with ECSDSOS
S/N	Datasets	Scale	BKS	SEHDPSO(2007) [15]		Our Error $(\%)$	S/N	Datasets	Scale	BKS	ECSDSOS(2019) [16]		Our Error $(\%)$
				PDavg. $(\%)$	PDbest $(\%)$						PDavg. $(\%)$	PDbest $(\%)$
1	pr76	76	108,159	0.05000	0.02000	0.00000	1	kroA100	100	21,282.0	0.04793	0.00000	0.00000
2	kroB100	100	22,141.0	0.09000	0.0000	−0.00870	2	kroB100	100	22,141.0	0.04968	0.00452	−0.00870
3	kroC100	100	20,749.0	0.01000	0.0000	0.00000	3	kroC100	100	20,749.0	0.01928	0.00000	0.00000
4	kroD100	100	21,294.0	0.05000	0.1200	0.00000	4	kroD100	100	21,294.0	0.18785	0.00000	0.00000
5	rd100	100	7910.00	0.25000	0.3000	0.00000	5	kroE100	100	22,068.0	0.24410	0.02266	0.00000
6	lin105	105	14,379.0	0.03000	0.0000	0.00000	6	pr107	107	44,303.0	0.22120	0.00000	−0.0029
7	pr107	107	44,303.0	0.18000	0.0000	−0.0029	7	pr124	124	59,030.0	0.20159	0.00000	0.00000
8	pr124	124	59,030.0	0.23000	0.3000	0.00000	8	pr136	136	96,772.0	0.52834	0.00930	−0.00001
9	bier127	127	118,282	0.10000	0.0000	0.00974	9	pr144	144	58,537.0	0.24087	0.00000	−0.0030
10	ch130	130	6110.00	0.29000	0.1100	0.00000	10	ch150	150	6528.00	0.45415	0.39828	0.04442
11	kroA150	150	26,524.0	0.05000	0.0000	0.00000	11	pr152	152	73,682.0	0.25450	0.00000	0.00000
12	kroB150	150	26,130.0	0.18000	0.1000	−0.0101	12	pr226	226	80,369.0	0.30236	0.00000	0.00663
13	u159	159	42,080.0	0.00000	0.0000	−0.01028	13	pr264	264	49,135.0	0.10909	0.00000	0.00000
14	kroB200	200	29,437.0	0.25000	0.0500	0.01488	14	pr299	299	48,191.0	1.32075	0.61630	0.01900
15	ts225	225	126,643	0.08000	0.0200	0.00000	15	lin318	318	42,029.0	0.89938	0.48062	0.12710
16	tsp225	225	3916.00	0.23000	0.0000	−1.30225	16	rd400	400	15,281.0	1.17793	0.69367	0.17112
17	a280	280	2579.00	0.15000	0.0300	0.34121	17	fl417	417	11,861.0	1.94672	0.76722	0.45063
18	rd400	400	15,281.0	0.25000	0.1600	0.17112	18	pr439	439	107,217.0	2.28788	1.28338	0.20000
19	p654	654	34,643.0	0.93000	0.4100	0.01000	19	u574	574	36,905.0	1.73229	0.97277	0.39000
20	u724	724	41,910.0	0.64000	0.2200	0.51000	20	d657	657	48,912.0	1.69120	1.16127	0.44000
Average				0.20200	0.09200	−0.013864	21	u724	724	41,910.0	1.05249	0.51778	0.51000
BKS found/No. of datasets				1/20	8/20	14/20	22	pr1002	1002	259,045.0	2.13205	1.20982	0.07000
							23	rl1323	1323	270,199.0	1.84053	0.79756	0.69000
							24	d1655	1655	62,128.0	2.58177	1.89126	1.84000
							Average				0.89683	0.45110	0.20601
						BKS found/No. of datasets					0/24	9/24	11/24

Table 6. Performance comparison of our proposed algorithm with the other state-of-the-art optimization algorithms (ASA-GS, GSA-ACO-PSO, HGA+2local, IVNS, HSIHM+2local, ABCSS, DSMO, MMA, and DSCA+LS).

Comparison with ASA-GS(2011) [21]					Comparison with IVNS(2018) [29]					Comparison with DSMO(2020) [35]
S/N	Datasets	ASA-GS		Our Result	S/N	Datasets	IVNS		Our Result	S/N	Datasets	DSMO		Our Result
		Average	Best				Average	Best				Average	Best
1	eil51	428.87	428.87	428.87	1	gr17	2085	2085	2085	1	burma14	30.87	30.87	30.87
2	berlin52	7544.37	7544.37	7544.36	2	gr21	2707	2707	2707	2	ulysses16	73.99	73.99	73.99
3	st70	677.11	677.11	677.11	3	gr24	1272	1272	1272	3	ulysses22	75.4	75.31	75.31
4	eil76	544.37	544.37	544.37	4	fri26	937	937	937	4	bayg29	9074.15	9074.15	9074.15
5	pr76	108,159	108,159	108,159	5	bays29	2020	2020	2020	5	eil51	436.96	428.86	428.86
6	rat99	1219.49	1219.24	1219.24	6	dantzig42	699	699	699	6	berlin52	7633.6	7544.37	7544.36
7	rd100	7910.4	7910.4	7910	7	swiss42	1273	1273	1273	7	st70	702.64	677.11	677.11
8	kroA100	21,285.4	21,285.4	21,282	8	gr48	5046	5046	5046	8	eil76	572.7	558.68	544.37
9	kroB100	22,139.1	22,139.1	22,139.08	9	eil51	428.98	428.98	428.87	9	pr76	111299.3	108,159.4	108,159
10	kroC100	20,750.8	20,750.8	20,749	10	berlin52	7544.36	7544.36	7544.36	10	gr96	530.45	518.38	510.89
11	kroD100	21,301.0	21,294.3	21,294	11	brazil58	25,592.72	25,425	25,395	11	rat99	1291.93	1225.56	1219.24
12	kroE100	22,112.3	22,106.3	22,068	12	st70	677.11	677.11	677.11	12	kroA100	22,024.27	21,298.21	21,282
13	eil101	640.51	640.21	641.32	13	eil76	552.57	545.39	544.37	13	kroB100	23,022.37	22,308	22,139.08
14	lin105	14,383	14,383	14,379	14	pr76	108,159	108,159	108,159	14	rd100	8377.76	8041.3	7910
15	pr107	44,301.7	44,301.7	44,301.68	15	rat99	1241.26	1240.38	1219.24	15	eil101	674.4	648.66	641.32
16	pr124	59,030.7	59,030.7	59,030	16	rd100	7918.36	7910.4	7910	16	lin105	15114	14383	14,379
17	bier127	118,349	118,294	118,293.52	17	kroA100	21,695.79	21,618.2	21,282	17	pr107	45,666.99	44,385.86	44,301.68
18	ch130	6121.15	6110.72	6110	18	kroB100	22,140.20	22,139.07	22,139.08	18	pr124	62,443.49	60,285.21	59,030
19	pr136	97,078.9	96,966.3	96,770.92	19	kroB100	20,809.29	20,750.76	20,749	19	pr136	102872	97,538.68	96,770.92
20	pr144	58,545.6	58,535.2	58,535.22	20	kroD100	21,490.62	21,294.29	21,294	20	gr137	736.67	709.48	706.29
21	ch150	6539.8	6530.9	6530.90	21	kroE100	22,193.8	22,174.6	22,068	21	kroA150	28354.09	27591.44	26,524
22	kroA150	26,538.6	26,524.9	26,524	22	eil101	648.27	642.31	641.32	22	kroB150	27,576.16	26,601.94	26,127.36
23	kroB150	26,178.1	26,140.7	26,127.36	23	lin105	14,395.64	14,383	14,379	23	pr152	76,526.77	74,243.91	73,682
24	pr152	73,694.7	73,683.6	73,682	24	pr107	44,314.92	44,301.68	44,301.68	24	u159	42,598.3	42,598.3	42,075.67
25	u159	42,398.9	42,392.9	42,075.67	25	pr124	59,051.82	59,030.74	59,030	25	rat195	2488.55	2372.89	2342.25
26	rat195	2348.05	2345.22	2342.25	26	bier127	119,006.39	118,974.6	118,293.52	26	d198	16,270.47	15,978.13	15,868.04
27	kroA200	29,438.4	29,411.5	29,385.72	27	ch130	6153.72	6140.66	6110	27	kroA200	31,828.64	30,481.35	29,385.72
28	kroB200	29,513.1	29,504.2	29,441.38	28	pr136	97,985.84	97,979.11	96,770.92	28	kroB200	31,781.62	30,716.5	29,441.38
29	ts225	126,646	126,646	126,643	29	pr144	58,563.97	58,535.22	58,535.22	29	gr202	508.81	501.83	486.96
30	pr226	80,687.4	80,542.1	80,374.33	30	ch150	6644.95	6639.52	6530.90	30	tsp225	4162.79	4013.68	3865.004
31	gil262	2398.61	2393.64	2389.05	31	kroA150	26,947.17	26,943.31	26,524	31	pr226	85,935.69	83,587.98	80,374.33
32	pr264	49,138.9	49,135	49,135	32	kroB150	26,537.04	26,527.57	26,127.36	32	gr229	1730.46	1683.45	1660.12
33	pr299	48,326.4	48,269.2	48,200.16	33	pr152	73,855.11	73,847.6	73,682	33	gil262	2627.87	2543.15	2389.05
34	lin318	42,383.7	42,306.7	42,082.42	34	u159	42,467.61	42,436.23	42,075.67	34	pr299	51,747.99	50,579.82	48,200.16
35	rd400	15,429.8	15,350.7	15,307.15	35	rat195	2453.81	2450.14	2342.25	35	lin318	45,460.25	44,118.66	42,082.42
36	fl417	12,043.8	11,940.4	11,914.45	36	d198	16,079.28	16,075.84	15,868.04	36	linhp318	45,730.57	43,831.44	42,529
37	rat575	6904.82	6872.11	6851.73	37	kroA200	30,339.67	30,300.56	29,385.72	37	fl417	12,950.77	12,218.98	11,914.45
38	u724	42,470.4	42,274.7	42,124.40	38	kroB200	30,453.22	30,447.30	29,441.38	38	gr431	2042.77	1993.15	1974.70
39	rat783	8982.19	8954.36	8934.09	39	pr226	80,514.64	80,469.31	80,374.33	39	pr439	116,379.2	112,105.2	107,431.43
40	pr1002	264,274	263,512	259,250	40	gil262	2501.86	2492.85	2389.05	40	d493	37,861.14	36,844.63	35,772
41	pcb1173	57,820.5	57,760.6	57,528.29	41	pr264	51,197.14	51,155.38	49,135	Average		26,930.42	26,064.29	25,490.64
42	d1291	52,252.3	51,751.2	51,618.54	42	pr299	50,373.12	50,271.69	48,200.16	BKS found/No. of datasets		3/40	5/40	21/40
43	rl1323	273,444	271,964	272,083.96	43	lin318	43,964.93	43,924.08	42,082.42	Comparison with MMA(2019) [2]
44	fl1400	20,782.2	20,647.4	20,315.84	44	rd400	16,250.21	16,155.91	15,307.15	S/N	Datasets	BKS	MMA	Our Result
45	d1655	64,155.9	63,635.9	63,268.61	45	fl417	12,183.14	12,180.78	11,914.45	1	wi29	27,603	28,387.0	27,601.0
Average		45,273.63	45,173.58	45,026.82	46	pr439	111,771.2	111,750.3	107,431.43	2	dj38	6656	6656.00	6659.40
BKS found/No. of datasets		3/45	5/45	19/45	47	pcb442	50,800.24	50,783.55	51,362	3	eil51	426	430.000	428.870
Comparison with GSA-ACO-PSO(2011) [22]					48	u574	39,629.11	39,573.88	37,049.29	4	berlin52	7542	7574.00	7544.40
S/N	Datasets	GSA-ACO-PSO		Our Result	49	rat575	7362.51	7349.81	6851.730	5	st70	675	691.000	677.109
		Average	Best		50	u724	45,729.71	45,725.39	42,124.40	6	eil76	538	540.000	544.370
1	eil51	427.27	427	428.87	51	rat783	9707.364	9707.166	8934.090	7	rat99	1211	1239.00	1219.240
2	berlin52	7542	7542	7544.36	52	pr1002	280,563.9	280,368.2	259,250.0	8	kroA100	21,282	21,367.0	21,282.00
3	ncit64	6400	6400	6400	53	pcb1173	63,435.95	63,354.82	57,528.29	9	kroB100	22,141	23,251.0	22,139.08
4	eil76	540.20	538	544.37	54	d1291	56,095.33	56,088.31	51,618.54	10	kroC100	20,749	21,461.0	20,749.00
5	rd100	7987.57	7910	7910	55	rl1323	295,611.2	295,607.3	272,083.96	11	kroD100	21,294	22,066.0	21,294.00
6	kroA100	21,370.47	21,282	21,282	56	fl1400	21,085.98	21,040.65	20,315.84	12	kroE100	22,068	22,590.0	22,068.00
7	kroB100	22,282.87	22,141	22,139.08	57	d1655	70,337.23	69,992.49	63,268.61	13	eil101	629	641.000	641.0000
8	kroC100	20,878.97	20,749	20,749	Average		39324.49	39291.12	37766.82	14	lin105	14,379	15,127.0	14,379.00
9	kroD100	21,620.47	21,309	21,294	BKS found/No. of datasets		10/57	12/57	27/57	15	pr124	59,030	59,824.0	59,030.00
10	kroE100	22,183.47	22,068	22,068	Comparison with HSIHM+2local$(2019)$ [31]					16	bier127	118,282	121,942.0	118,293.52
11	eil101	635.23	630	641.32	S/N	Datasets	HSIHM+2local		Our Result	17	ch130	6110	6281.000	6110.000
12	lin105	14,406.37	14,379	14,379			Average	Best		18	xqf131	564	592.0000	566.4200
13	bier127	119,421.83	118,282	118,293.52	1	br17	39	39	39	19	ch150	6528	6661.000	6530.900
14	ch130	6205.63	6141	6110	2	ftv33	1320.57	1286	1286	20	kroA150	26,524	27,244.00	26,524.00
15	ch150	6563.70	6528	6530.90	3	ftv35	1490.6	1473	1473	21	kroB150	26,130	27,155.00	26,127.36
16	kroA150	26,899.20	26,524	26,524	4	ftv38	1547.13	1530	1530	22	u159	42,080	44,027.00	42,075.67
17	kroB150	26,448.33	26,130	26,127.36	5	p43	5620.27	5620	5620	23	qa194	9352	9437.000	9353.660
18	kroA200	29,738.73	29,383	29,385.72	6	ftv44	1645.4	1613	1613	24	kroA200	29,368	30,450.00	29,385.72
19	kroB200	30,035.23	29,541	29,441.38	7	ftv47	1800.43	1776	1776	Average			21,068.04	20,467.65
20	lin318	43,002.90	42,487	42,082.42	8	ry48p	14,513.9	14,495	14,422	BKS found/No. of datasets			1/24	12/24
21	rat575	6933.87	6891	6851.73	9	ft53	7148.3	6983	6905	Comparison with DSCA+LS(2019) [34]
22	rat783	9079.23	8988	8934.09	10	ftv55	1625.17	1608	1608	S/N	Datasets	DSCA+LS		Our Result
23	rl1323	280,181.47	277,642	272,083.96	11	ftv64	1876.2	1846	1850			Average	Best
24	fl1400	21,349.63	20,593	20,315.84	12	ftv70	2027.83	1977	1950	1	pr76	108,159	108,159	108,159
25	d1655	65,621.13	64,151	63,268.61	13	ft70	39,722.03	39,212	38,869	2	kroA100	21,282	21,282	21,282
Average		32,710.23	32,346.24	32,053.18	14	kro124p	38,348.2	37,213	36,230	3	kroB100	22,141	22,141	22,139.08
BKS found/No. of datasets		2/25	13/25	11/25	15	ftv170	3393.07	2999	2928	4	kroC100	20,749	20,749	20,749.00
Comparison with HGA+2local(2014) [24]					16	rbg323	1555.4	1502	1331	5	kroD100	21,300	21,294	21,294
S/N	Datasets	HGA+2local		Our Result	17	rbg358	1424.63	1342	1164	6	kroE100	22,068	22,068	22,068.00
		Average	Best		18	rbg403	2637.8	2597	2465	7	lin105	14,379	14,379	14,379
1	pr76	108,255.94	108,159.42	108,159	19	rbg443	2914.33	2853	2720	8	pr107	44,303	44,303	44,301.68
2	kroA100	21,312.45	21,285.44	21,282	Average		6876.33	6734.95	6619.95	9	pr124	59,030	59,030	59,030
3	kroC100	20,812.22	20,750.76	20,749.00	BKS found/No. of datasets		1/19	8/19	14/19	10	ch130	6124	6111	6110
4	kroD100	21,344.67	21,294.29	21,294	Comparison with ABCSS$(2019)$ [30]					11	pr136	97,164.6	96,928	96,770.92
5	lin105	14,422.89	14,382.99	14,379	S/N	Datasets	ABCSS		Our Result	12	pr144	58,537	58,537	58,535.22
6	pr107	44,341.67	44,301.68	44,301.68			Average	Best		13	kroA150	26,525.4	26,524	26,524
7	pr124	59,094.13	59,030.73	59,030	1	gr17	2085	2085	2085	14	kroB150	26,134.8	26,130	26,127.36
8	ch130	6130.277	6110.72	6110	2	bays29	2020	2020	2020	15	pr152	73,682	73,682	73,682
9	pr136	97,019.291	96,785.852	96,770.92	3	swiss42	1273	1273	1273	16	kroB200	29,467.4	29,447	29,441.38
10	pr144	58,535.22	58,535.22	58,535.22	4	eil51	427.01	427	428.87	17	ts225	126,709.8	126,643	126,643
11	kroA150	26,597.78	26,524.86	26,524	5	berlin52	7542	7542	7544.36	18	tsp225	3917	3916	3865.004
12	kroB150	26,335.85	26,127.35	26,127.36	6	kroA100	21,287.19	21,282	21,282	19	pr226	80,380.4	80,369	80,374.33
13	pr152	73,765.70	73,683.63	73,682	7	lin105	14,379.10	14,379	14,379	20	pr264	49,135	49135	49,135
14	kroB200	29,583.38	29,450.50	29,441.38	8	pr124	59,054.64	59,030	59,030	21	pr299	48,306.8	48,250	48,200.16
15	ts225	128,295.65	128,141.92	126,643	9	pr152	73,691.64	73,682	73,682	22	lin318	42,221.4	42167	42,082.42
16	tsp225	3892.88	3878.66	3865.004	10	kroA200	29,469.00	29,450	29,385.72	23	rd400	15,422.6	15,408	15,307.15
17	pr226	80,534.39	80,436.04	80,374.33	11	br17	39	39	39	24	fl417	11,933.4	11,920	11,914.45
18	pr264	49,163.26	49,151.22	49,135	12	ftv33	1286	1286	1286	25	rat575	6898.6	6881	6851.730
19	pr299	49,757.66	49,462.43	48,200.16	13	ry48p	14,452.79	14,422	14,422	26	rat783	9402.4	9343	8934.090
20	lin318	42,877.24	42,624.34	42,082.42	14	ftv55	1642.19	1629	1608	27	pr1002	272,739.6	272,323	259,250
21	rd400	16,143.96	16,049.59	15,307.15
Average		46581.74	46484.17	46285.36	Average		16332.04	16324.71	16318.93	Average		48819.01	48782.19	48264.81
BKS found/No. of datasets		2/21	4/21	16/21	BKS found/No. of datasets		6/14	11/14	11/14	BKS found/No. of datasets		11/27	17/27	18/27

Table 7. Performance comparison of our proposed algorithm with the other state-of-the-art optimization algorithms (IBA, DWCA, DSOS, MCF-ABC, GA-PSO-ACO, DIWO, PRGA, MPSO, SCGA, and VDWOA).

Comparison with IBA(2016) [26]					Comparison with DSOS(2017) [27]					Comparison with GA-PSO-ACO(2012) [23]
S/N	Datasets	IBA		Our Result	S/N	Datasets	DSOS		Our Result	S/N	Datasets	GA-PSO-ACO		Our Result
		Average	Best				Average	Best				Average	Best
1	eil51	428.1	426	428.87	1	eil51	427.90	426	428.87	1	eil51	431.84	426	428.87
2	berlin52	7542.0	7542	7544.36	2	berlin52	7542	7542	7544.36	2	berlin52	7544.37	7544.37	7544.36
3	kroA100	21,445.3	21,282	21,282	3	st70	679.20	675	677.11	3	st70	694.60	679.60	677.11
4	kroB100	22,506.4	22,140	22,139.08	4	eil76	547.40	542	544.37	4	eil76	550.16	545.39	544.37
5	kroC100	21,050.0	20,749	20,749	5	pr76	108,548.37	108,159	108,159	5	pr76	110,023	109,206	108,159
6	kroD100	21,593.4	21,294	21,294	6	rat99	1228.37	1224	1219.24	6	rat99	1275	1218	1219.24
7	kroE100	22,349.6	22,068	22,068	7	kroA100	21,409.50	21,282	21,282	7	rd100	8039	7936	7910
8	pr107	44,793.8	44,303	44,301.68	8	kroB100	22,339.20	22,140	22,139.08	8	kroD100	21,484	21,394	21,294
9	pr124	59,412.1	59,030	59,030	9	kroC100	20,881.60	20,749	20,749	9	eil101	637.93	633.07	641.32
10	pr136	99,351.2	97,547	96,770.92	10	kroD100	21,493.10	21,294	21,294	10	lin105	14,521	14,397	14,379
11	pr144	58,876.2	58,537	58,535.22	11	kroE100	22,231.10	22,068	22,068	11	pr107	44,589	44,316	44,301.68
12	pr152	74,676.9	73,921	73,682	12	eil101	650.60	640	641.32	12	pr124	60,157	59,051	59,030
13	pr264	50,908.3	49,756	49,135	13	lin105	14,431.73	14,381	14,379	13	bier127	120,301	118,476	118,293.52
14	pr299	49,674.1	48,310	48,200.16	14	pr107	44,445.10	44,314	44,301.68	14	ch130	6203.47	6121.15	6110
15	br17	39	39	39	15	pr124	59,429.10	59,030	59,030	15	pr144	58,662	58,595	58,535.22
16	ftv33	1318.1	1286	1286	16	pr136	97,673.20	97,437	96,770.92	16	kroA150	26,803	26,676	26,524
17	ftv35	1493.7	1473	1473	17	pr144	58,817.10	58,565	58,535.22	17	pr152	73,989	73,861	73,682
18	ftv38	1562.0	1530	1530	18	ch150	6552.58	6542	6530.90	18	u159	42,506	42,395	42,075.67
19	p43	5620	5620	5620	19	pr152	74,785.70	74,013	73,682	19	rat195	2362	2341	2342.25
20	ftv44	1683.7	1613	1613	20	kroA200	29,651.23	29,477	29,385.72	20	kroA200	31,015	29,731	29,385.72
21	ftv47	1863.6	1796	1776	21	tsp225	-	3877	3865.004	21	gil262	2439	2399	2389.05
22	ry48p	14,544.8	14,422	14,422	22	pr226	-	80,407	80,374.33	22	pr299	48,763	48,662	48,200.16
23	ft53	7294.1	7001	6905	23	pr264	52,798.90	50,454	49,135	23	lin318	42,771	42,633	42,082.42
24	ftv55	1737.5	1608	1608	24	pr299	50,335.20	49,162	48,200.16	24	rd400	15,503	15,464	15,307.15
25	ftv64	1999.2	1879	1850	25	lin318	42,972.42	42,201	42,082.42	25	rat575	6952	6912	6851.73
26	ftv70	2233.2	2111	1950	26	rat575	7117.32	7073	6851.73	26	u724	42,713	42,657	42,124.40
27	ft70	40,309.7	39,901	38,869	27	rat783	9102.67	9045	8934.09	27	rat783	9126	9030	8934.09
28	kro124p	39,213.7	37,538	36,230	28	pr1002	278,381.51	272,381	259,250	28	pr1002	266,774	265,987	259,250
29	rbg323	1640.9	1615	1331	Average		40,556.62	40,182.14	39,573.38	29	d1291	52,443	52,378	51,618.54
Average		23,350.37	22,977.14	22,815.94	BKS found/No. of datasets		1/28	11/28	14/28	30	d1655	65,241	64,401	63,268.61
BKS found/No. of datasets		3/29	18/29	23/29	Comparison with MCF-ABC$(2019)$ [32]					Average		39,483.78	39,202.19	38,770.12
Comparison with DWCA(2018) [28]					S/N	Datasets	BKS	MCF-ABC	Our Result	BKS found/No. of datasets		0/30	1/30	11/30
S/N	Datasets	DWCA		Our Result	1	swiss42	1273	1273	1273	Comparison with DIWO(2015) [25]
		Average	Best		2	att48	10,628	10,628	10,628	S/N	Datasets	DIWO		Our Error$(\%)$
1	eil51	428.4	426	428.87	3	pr76	108,159	108,159	108,159			PDavg.$(\%)$	PDbest$(\%)$
2	berlin52	7542.0	7542	7544.36	4	rd100	7910	7910	7910	1	att48	0.0021	0.0021	0.0000
3	kroA100	21,348.1	21,282	21,282	5	kroA100	21,282	21,282	21,282	2	eil51	0.6999	0.6741	0.6737
4	kroB100	22,450.7	22,178	22,139.08	6	kroB100	22,141	22,141	22,139.08	3	berlin52	0.0313	0.0313	0.0318
5	kroC100	20,934.7	20,769	20,749	7	kroC100	20,749	20,749	20,749	4	st70	0.3125	0.3125	0.3124
6	kroD100	21,529.6	21,361	21,294	8	kroD100	21,294	21,294	21,294	5	kroA100	0.0375	0.0161	0.0000
7	kroE100	22,246.2	22,130	22,068	9	kroE100	22,068	22,068	22,068	6	kroB100	0.8816	0.6471	−0.0087
8	pr107	44,647.1	44,442	44,301.68	10	lin105	14,379	14,379	14,379	7	pr107	0.4837	0.3096	−0.0029
9	pr124	59,338.9	59,030	59,030	11	pr107	44,303	44,303	44,301.68	8	pr136	0.9400	0.2356	−0.00001
10	pr136	98,761.4	97,488	96,770.92	12	gr120	6942	6942	6942	9	chn144	0.8935	0.1016	0.40853
11	pr144	58,734.6	58,537	58,535.22	13	pr124	59,030	59,030	59,030	10	kroA150	0.7780	0.7401	0.00000
12	pr152	74,202.6	73,682	73,682	14	ch130	6110	6110	6110	11	kroB150	0.3229	0.2789	−0.0101
13	pr264	49,528.6	49,310	49,135	15	pr136	96,772	96,772	96,770.92	12	d198	0.6691	0.4304	0.55792
14	br17	39	39	39	16	gr137	69,853	69,853	69,853	13	tsp225	2.3949	0.4470	−1.30225
15	ftv33	1308.7	1286	1286	17	pr144	58,537	58,537	58,535.22	14	pr226	0.2238	0.0117	0.00663
16	ftv35	1485.8	1473	1473	18	kroA150	26,524	26,524	26,524	15	a280	0.7679	0.4297	0.34121
17	ftv38	1549.0	1530	1530	19	kroB150	26,130	26,130	26,127.36	16	rd400	2.4229	1.7153	0.17112
18	p43	5620	5620	5620	20	pr152	73,682	73,682	73,682	17	pcb442	2.1731	1.6137	1.15010
19	ftv44	1665.0	1613	1613	21	u159	42,080	42,080	42,075.67	18	att532	1.8737	1.2981	0.36119
20	ftv47	1827.8	1776	1776	22	si175	21,407	21,407	21,407	19	pr1002	3.1873	2.6970	0.07914
21	ry48p	14,517.8	14,429	14,422	23	brg180	1950	1950	1950	Average		1.0050	0.6312	0.14578
22	ft53	7199.4	6971	6905	24	tsp225	3916	3916	3865.004	BKS found/No. of datasets		0/19	0/19	8/19
23	ftv55	1691.4	1608	1608	25	ts225	126,643	126,643	126,643	Comparison with PRGA($(2019)$) [33]
24	ftv64	1961	1900	1850	26	pr264	49,135	49,135	49,135	S/N	Datasets	BKS	PRGA	Our Result
25	ftv70	2126.2	2014	1950	27	si535	48,450	48,498.3	48,450	1	rat99	1211	1218	1219.24
26	ft70	40,111.1	39,669	38,869	28	si1032	92,650	92,650	92,650	2	kroB100	22,141	22,407	22,139.08
27	kro124p	39,252.8	37,412	36,230	Average			39430.19	39426.18	3	kroA100	21,282	21,292	21,282
Average		23,038.81	22,796.93	22,671.52	BKS found/No. of datasets			27/28	28/28	4	rd100	7910	8020	7910
BKS found/No. of datasets		3/27	14/27	23/27						5	lin105	14,379	14,434	14,379
Comparison with MPSO$(2021)$ [3]										6	ch130	6110	6283	6110
S/N	Datasets	MPSO		Our Result	S/N	Datasets	MPSO		Our Result	7	ch150	6528	6580	6530.90
		Average	Best				Average	Best		8	d198	15,780	15,884	15,868.04
1	burma14	3323	3323	3323	19	pr144	58,612	58,537	58,535.22	9	kroA200	29,368	29,368	29,385.72
2	gr17	2085	2085	2085	20	ch150	6579	6528	6530.90	Average			13942.89	13869.33
3	gr21	2707	2707	2707	21	kroA150	26,711	26,524	26,524	BKS found/No. of datasets			1/9	5/9
4	gr24	1272	1272	1272	22	pr152	73,915	73,682	73,682	Comparison with SCGA$(2021)$ [37]
5	fri26	937	937	937	23	d198	16,024	15,780	15,868.04	S/N	Datasets	SCGA		Our Result
6	bayg29	1610	1610	1610	24	kroA200	29,818	29,533	29,385.72			Average	Best
7	bays29	2020	2020	2020	25	ts225	128,385	126,643	126,643	1	att48	33,526.87	33,523.71	33,522
8	att48	10,628	10,628	10,628	26	pr226	80,990	80,545	80,374.33	2	berlin52	7544.37	7544.37	7544.36
9	pr76	108,159	108,159	108,159	27	pr264	50,178	49,325	49,135	3	bier127	118,469.71	118,293.52	118,293.52
10	kroA100	21,292	21,282	21,282	28	a280	2632	2598	2587.80	4	ch130	6199.59	6183.03	6110
11	kroB100	22,141	22,141	22,139.08	29	pr299	48,589	48,332	48,200.16	5	eil51	431.77	428.87	428.87
12	rd100	8054	7910	7910	30	lin318	45,391	43,710	42,082.42	6	eil76	549.47	547.17	544.37
13	lin105	14,379	14,379	14,379	31	rd400	16,503	15,892	15,307.15	7	kroA100	21,379.27	21,285.44	21,282
14	pr107	44,303	44,303	44,301.68	32	pr439	115,994	111,875	107,431.43	8	kroA200	29,671.55	29,533.06	29,385.72
15	pr124	59,113	59,030	59,030	33	si535	52,326	50,388	48,450	9	oliver30	423.74	423.74	423.74
16	bier127	118,282	118,282	118,293.52	34	u574	39,757	36,905	37,049.29	10	pr107	44,301.68	44,301.68	44,301.68
17	ch130	6176	6110	6110	35	rat575	7355	7014	6851.730	11	pr136	97,042.31	96,795.40	96,770.92
18	pr136	97,543	96,772	96,770.92						12	pr152	73,683.64	73,683.64	73,682
Average							37,822.37	37,336.03	37,074.15	Average		36,101.99	36,045.30	36,024.09
BKS found/No. of datasets							13/35	25/35	23/35	BKS found/No. of datasets		1/12	1/12	6/12
Comparison with VDWOA$(2021)$ [36]
S/N	Datasets	BKS	VDWOA	Our Result	S/N	Datasets	BKS	VDWOA	Our Result	S/N	Datasets	BKS	VDWOA	Our Result
1	oliver30	420	420	423.74	5	eil76	538	554	544.37	9	ch150	6528	6863	6530.90
2	eil51	426	429	428.87	6	pr76	108,159	108,353	108,159	10	d198	15,780	16,313	15,868.04
3	berlin52	7542	7542	7544.36	7	kroA100	21,282	21,721	21,282	11	tsp225	3916	4136	3865.004
4	st70	675	676	677.11	8	pr107	44,303	45,030	44,301.68	12	fl417	11,861	12,462	11,914.45
Average													18,708.25	18,461.63
BKS found/No. of datasets													2/12	4/12

Table 8. Performance comparison of our proposed algorithm with the other state-of-the-art optimization algorithms (DSSA and DA-GVNS).

Comparison with DSSA(2022) [8]					Comparison with DA-GVNS(2022) [38]
S/N	Datasets	DSSA		Our Results	S/N	Datasets	BKS	DA-GVNS	Our Results	S/N	Datasets	BKS	DA-GVNS	Our Results
		Average	Best
1	att48	33,522	33,522	33,522	1	br17	39	39	39	35	kroA100	21,282	21,282	21,282
2	eil51	426.6	426	428	2	ft53	6905	7011	6905	36	kroB100	22,141	22,165	22,139.08
3	berlin52	7542	7542	7544.36	3	ft70	38,673	39,585	38,869	37	kroC100	20,749	20,749	20,749
4	st70	675.15	675	677.11	4	ftv33	1286	1286	1286	38	kroD100	21,294	21,294	21,294
5	pr76	108,159	108,159	108,159	5	ftv35	1473	1473	1473	39	kroE100	22,068	22,121	22,068
6	kroA100	21,290.2	21,282	21,282	6	ftv38	1530	1535	1530	40	kroA150	26,524	26,817	26,524
7	kroB100	22,173.1	22,141	22,139.08	7	ftv44	1613	1631	1613	41	kroB150	26,130	26,256	26,127.36
8	kroC100	20,770.5	20,749	20,749	8	ftv47	1778	1788	1776	42	kroA200	29,368	29,807	29,385.72
9	kroD100	21,319.05	21,294	21,294	9	ftv55	1608	1636	1608	43	kroB200	29,437	30,015	29,441.38
10	kroE100	22,091.9	22,068	22,068	10	ftv64	1839	1895	1850	44	lin105	14,379	14,390	14,379
11	lin105	14,379	14,379	14,379	11	ftv70	1950	2078	1950	45	lin318	42,029	43,201	42,082.42
12	pr107	44,322	44,303	44,301.68	12	kro124p	36,230	36,403	36,230	46	pcb442	50,778	53,009	51,362
13	pr124	59,030	59,030	59,030	13	p43	5620	5620	5620	47	pcb1173	56,892	61,725	57,528.29
14	ch130	6153.65	6110	6110	14	rbg323	1326	1451	1331	48	pr76	108,159	108,159	108,159
15	pr136	97,302.35	96,920	96,770.92	15	rbg358	1163	1276	1164	49	pr107	44,303	44,303	44,301.68
16	pr144	58,537	58,537	58,535.22	16	rbg403	2465	2481	2465	50	pr124	59,030	59,050	59,030
17	ch150	6590.15	6528	6530.9	17	rbg443	2720	2761	2720	51	pr136	96,772	97,062	96,770.92
18	kroA150	26,699.85	26,525	26,524	18	ry48p	14,422	14,465	14,422	52	pr144	58,537	58,537	58,535.22
19	kroB150	26,220.4	26,130	26,127.36	19	bays29	2020	2020	2020	53	pr152	73,682	73,839	73,682
20	pr152	73,731.35	73,682	73,682	20	bier127	118,282	119,122	118,293.52	54	pr226	80,369	80,880	80,374.33
21	u159	42,262.75	42,080	42,075.67	21	brazil58	25,395	25,395	25,395	55	pr264	49,135	49,880	49,135
22	kroA200	29,682.15	29,459	29,385.72	22	ch130	6110	6154	6110	56	pr299	48,191	49,719	48,200.16
23	kroB200	29,850.55	29,564	29,441.38	23	ch150	6528	6595	6530.9	57	pr439	107,217	112,600	107,431.43
24	tsp225	3926.05	3916	3865.004	24	d1291	50,801	54,778	51,618.54	58	pr1002	259,045	277,867	259,250
25	pr226	80,369.2	80,369	80,374.33	25	d1655	62,128	67,292	63,268.61	59	rat195	2323	2364	2342.25
26	pr264	49,271.85	49,135	49,135	26	dantzig42	699	699	699	60	rat575	6773	7179	6851.73
27	lin318	42,742.7	42,495	42,082.42	27	fl417	11,861	12,019	11,914.45	61	rat783	8806	9445	8934.09
28	pr439	107,844.9	107,494	107,431.4	28	fl1400	20,127	21,858	20,315.84	62	rd100	7910	7910	7910
29	pr1002	266,352.4	264,212	259,250	29	fri26	937	937	937	63	rd400	15,281	15,915	15,307.15
30	pr299	48,605.05	48,409	48,200.16	30	gil262	2378	2451	2389.05	64	rl1323	270,199	292,819	272,083.96
31	rat575	6961.7	6938	6851.73	31	gr17	2085	2085	2085	65	swiss42	1273	1273	1273
32	rat783	9163	9097	8934.09	32	gr21	2707	2707	2707	66	u159	42,080	42,168	42,075.67
					33	gr24	1272	1272	1272	67	u574	36,905	39,583	37,049.29
					34	gr48	5046	5046	5046	68	u724	41,910	44,814	42,124.4
Average		43,373.98	43,224.06	43,027.52									34,162.38	33,068.18
BKS found/No. of datasets		6/32	22/32	19/32									20/68	41/68

7.3.1. Comparison with Self-Escape Mechanism-Based Algorithms

We begin by comparing our proposed algorithm with the state-of-the-art optimization algorithms with the self-escape mechanism. In fact, the self-escape strategy or mechanism was adopted to solve symmetric TSPs [15,16]. In the self-escape hybrid DPSO (SEHDPSO) algorithm [15], the five nearest neighbors for each node were considered to skip out the local optimum of the current best route. On the other hand, a swap-based randomized local search operator was coupled with the self-escape hybrid DSOS (ECSDSOS) algorithm [16] to find a satisfactory solution. However, these algorithms tend to produce a longer route or relatively worse solution. To find a better-quality solution, we actually employ an efficient 3-opt operator in our proposed algorithm at the self-escape mechanism stage.

Specifically, Table 5 displays the comparison results of our proposed algorithm with self-escape mechanism-based algorithms such as the SEHDPSO and ECSDSOS algorithms. In comparison with the SEHDPSO algorithm, it can be seen from Table 5 that our proposed algorithm finds better solutions than the average as well as the best solutions of the SEHDPSO algorithm in almost all the TSP test problems or datasets. In fact, the average error of our proposed algorithm over 20 datasets is $-0.013864\%$, which is significantly better than the average error $0.20200\%$ and the best solution error $0.09200\%$ of the SEHDPSO algorithm. At the same time, our proposed algorithm captures the best-known solutions in more datasets (fourteen cases) than the SEHDPSO algorithm (one case and eight cases in the two versions). In comparison with the ECSDSOS algorithm, it can also be seen from Table 5 that the average error and BKS finding number of our proposed algorithm over 24 datasets are $0.20601\%$ and 11, respectively, while those of the ECSDSOS algorithm are, respectively, $0.89683\%$ and 0 (on the average solution version), and $0.45110\%$ and 9 (on the best solution version). In addition, our proposed algorithm yields new solutions on certain datasets (negative entries in the table), but neither of these two algorithms can find such a solution. It can be further observed from Table 5 that, for certain small-scale datasets, all three algorithms are capable of finding the best-known solution. However, as the scale becomes larger and larger, our proposed algorithm shows better performance than both the SEHDPSO and ECSDSOS algorithms.

7.3.2. Comparison with the Other State-of-the-Art Optimization Algorithms

We further compare our proposed algorithm with the other typical state-of-the-art optimization algorithms without a self-escape mechanism. Actually, those optimization algorithms were tested on different sets of datasets. Thus, we use different sets of datasets in each group to compare the proposed algorithm with them. Specifically, Table 6, Table 7 and Table 8 offer side-by-side comparisons between our proposed algorithm and 21 state-of-the-art TSP-solving optimization algorithms.

The performance comparison of our proposed algorithm with ASA-GS [21], GSA-ACO-PSO [22], HGA+2local [24], IVNS [29], HSIHM+2local [31], ABCSS [30], DSMO [35], MMA [2], and DSCA+LS [34] is illustrated in Table 6. According to Table 6, in comparison with ASA-GS, GSA-ACO-PSO, HGA+2local, IVNS, DSMO, and DSCA+LS for the symmetric TSP datasets, our proposed algorithm achieves better results than the average results of all six algorithms in almost all the datasets except in one case of ASA-GS, in four cases of GSA-ACO-PSO, and in one case of IVNS. On the other hand, in comparison with the best results of these algorithms, the performance of our proposed algorithm is only inferior in two cases out of forty-five with ASA-GS, in six cases out of twenty-five regarding GSA-ACO-PSO, no worse out of twenty-one with HGA+2local, in one case out of fifty-seven related to IVNS, no worse out of forty concerning DSMO, and in one case out of twenty-seven connected to DSCA+LS. On the remaining test datasets, our proposed algorithm achieves better or equal scores with the above six algorithms. In addition to these, our proposed algorithm traces the best-known solution in nineteen cases as compared with five out of forty-five for ASA-GS, in eleven cases as compared with thirteen out of twenty-five for GSA-ACO-PSO, in sixteen cases as compared with four out of twenty-one for HGA+2local, in twenty-seven cases as compared with twelve out of fifty-seven for IVNS, in twenty-one cases as compared with five out of forty for DSMO, and in eighteen cases as compared with seventeen out of twenty-seven for DSCA+LS. It is also notable that, for some small-scale datasets, our proposed algorithm yields similar scores to these comparative algorithms. However, as the scale becomes larger and larger, it finds better results than these six comparative optimization algorithms.

As demonstrated in Table 6, it is clear that, in most of the considered datasets, except three small-scale datasets, namely ftv64, eil51, and berlin 52, our proposed algorithm is better than HSIHM+2local and ABCSS for symmetric and asymmetric TSPs. On the test dataset ftv64, its solution is not better than the best solution of HSIHM+2local, but it is better than the average one. It is noticed that our proposed algorithm determines the best-known solution in 14 and 11 datasets, whereas HSIHM+2local and ABCSS provide such a solution in eight and eleven datasets, respectively. It is also observed that, for some small-scale datasets, all three algorithms determine the best-known solutions. As the scale becomes increasingly large, our proposed algorithm achieves greater global exploration capability than both the HSIHM+2local and ABCSS algorithms. As shown in Table 6, it is observed that our proposed algorithm outperforms the deterministic algorithm MMA for symmetric TSP datasets on nearly all the considered datasets. Indeed, MMA performs better regarding dj38 and eil76 and achieves the best-known solution in one case, while our proposed algorithm is better in 22 datasets and captures the best-known solutions in 12 cases. In addition, MMA is suitable only for small-size TSP datasets, whereas our proposed algorithm can be applied to solve small- and relatively large-scale datasets. Therefore, it can be concluded that the performance of our proposed algorithm is better in $87.5\%$ (21 out of 24) cases compared to MMA.

Table 7 and Table 8 demonstrate the comparison of our proposed algorithm with IBA [26], DWCA [28], DSOS [27], MCF-ABC [32], GA-PSO-ACO [23], DIWO [25], PRGA [33], MPSO [3], SCGA [37], VDWOA [36], DSSA [8], and DA-GVNS [38]. According to Table 7 and Table 8, in comparison with DSOS, GA-PSO-ACO, DIWO, MPSO, SCGA, and DSSA for the symmetric TSP datasets, our proposed algorithm provides better results than the average results of all six algorithms regarding almost all the datasets except in two cases of DSOS, in one case of GA-PSO-ACO, in one case of DIWO, and in four cases of DSSA. On the other hand, compared with the best results of these algorithms, the performance of our algorithm is inferior in five cases out of twenty-eight with DSOS, in four cases out of thirty regarding GA-PSO-ACO, in three cases out of nineteen related to DIWO, in three cases out of thirty-five with MPSO, no worse out of twelve concerning SCGA, and in five cases out of thirty-two connected to DSSA. On the remaining test datasets, our proposed algorithm achieves better or equal results with these six algorithms. In addition, our proposed algorithm obtains the best-known solution in fourteen cases as compared with eleven out of twenty-eight by DSOS, in eleven cases as compared with one out of thirty by GA-PSO-ACO, in eight cases as compared with zero out of nineteen by DIWO, in twenty-three cases as compared with twenty-five out of thirty-five by MPSO, in six cases as compared with one out of twelve by SCGA, and in nineteen cases as compared with twenty-two out of thirty-two by DSSA. In a word, the solutions obtained by our algorithm have better accuracy than those obtained by the above six comparative algorithms.

According to the results in Table 7 and Table 8, in comparison with IBA, DWCA, and DA-GVNS for symmetric and asymmetric test problems, our proposed algorithm produces better or equal solutions compared to the average as well as the best solutions of these three algorithms in each considered dataset by excluding two smaller datasets, namely eil51 and berlin52. Moreover, our proposed algorithm obtains the best-known solution in 23 cases as compared with 18 out of 29 by IBA, in 23 cases as compared with 14 out of 27 by DWCA, and in 41 cases as compared with 20 out of 68 by DA-GVNS. It is also observed that our proposed algorithm significantly outperforms these three algorithms regarding almost all the datasets. Specifically, regarding the large-scale datasets, it obtains more accurate results than these three comparative algorithms. As demonstrated in Table 7, in comparison with the best results of MCF-ABC, VDWOA, and PRGA for symmetric test problems, it is apparent that our proposed algorithm achieves worse solutions than those computed by VDWOA and PRGA on the datasets of oliver30, berlin52, st70, rat99, and kroA200. On the rest of the test datasets, it obtains similar or better results than the best of these algorithms. Actually, our proposed algorithm obtains the best-known solution in twenty-eight cases as compared with twenty-seven out of twenty-eight by MCF-ABC, in four cases as compared with two out of twelve by VDWOA, and in five cases as compared with one out of nine by PRGA. It is also evident that MCF-ABC has a strong capability regarding escaping the local optimum; nevertheless, this algorithm is not capable of producing a better solution, which is obtained by our algorithm in seven cases.

From the above discussion and analysis, it can be determined that our proposed algorithm achieves better results on both the average and best solutions compared to all 21 algorithms regarding almost all the TSP test datasets. Overall, regarding the test datasets, the average route length of our proposed algorithm is actually smaller than that of each comparative algorithm. Furthermore, our proposed algorithm traces the best-known solutions in many more datasets than each of the comparative algorithms. Therefore, our proposed algorithm is superior to these benchmark optimization algorithms in terms of solution quality. In the literature, it is generally believed that meta-heuristics and hybridization optimization algorithms can provide good-quality solutions for the TSPs. However, our proposed algorithm has better performance than such optimization algorithms, including recently improved ones. Apart from this, most benchmark algorithms (except IBA, DWCA, ABCSS, and DA-GVNS) are designed with many fine-tuned parameters to solve either the symmetric TSP or asymmetric TSP, while our proposed algorithm is capable of handling both of these cases by tuning only one parameter. Furthermore, our proposed algorithm is designed without any randomness, so running it multiple times on a dataset always produces the same result. Thus, it is deterministic, while most of the existing standard optimization algorithms are probabilistic and their solutions may change in every single run. In this way, it is quite convenient for practical applications.

7.4. Statistical Analysis

To determine the difference between the performance of our proposed and comparative optimization algorithms, we finally undertake a rigorous statistical analysis in this subsection. Actually, the popular Wilcoxon signed rank test [32,39] at the $95\%$ confidence level is implemented to statistically examine the superior performance of the proposed algorithm against the other standard optimization algorithms. In this non-parametric test, we evaluate our proposed algorithm with one of the comparative optimization algorithms. The test statistic is calculated by the following formula:

$$W_{cal,N}=min(W^{-1},W^{+}),$$

(21)

where N is the number of datasets tested by the two algorithms. If the two algorithms perform equally on a dataset, we ignore this dataset and adjust the value of N accordingly. $W^{-1}$ denotes the sum of ranks of the datasets on which our proposed algorithm performs better than the comparative algorithm, while $W^{+}$ denotes the sum of ranks of the datasets on which the comparative algorithm dominates our proposed algorithm. Moreover, the rank of the dataset is defined by the ascending order of the absolute error difference of the two algorithms (i.e., the rank 1 to the dataset with the smallest absolute difference, rank 2 to the next, etc.). $min(W^{-1},W^{+})$ returns to the minimum value of $\{W^{-},W^{+}\}$.

The critical values corresponding to N effective datasets ($W_{cri,N}$) at different confidence levels can be found in [39]. If $W_{cal,N}>W_{cri,N}$, it failed to reject the null hypothesis ($H_0$: there is no significant difference regarding the performance of the two algorithms). On the other hand, the null hypothesis is rejected under the condition $W_{cal,N}\le W_{cri,N}$, and the statistical test concludes that there is a significant difference regarding the performance of the two algorithms. Since most of the comparative algorithms (except MMA) are probabilistic, we perform the statistical test separately with the percentage deviation of average results (PDavg.(%)) and percentage deviation of best results ((PDbest.(%))). The test results are summarized in Table 9, where ‘*’ indicates that the test result is undetermined (for a critical value at $95\%$ confidence level, value of N must be ≥6) and ‘-’ means the original reference did not provide any results.

Table 9. Statistical test results based on the performance of our proposed algorithm against each state-of-the-art optimization algorithm.

Comparisons	Test with PDavg. (%)						Test with PDbest (%)
	$\mathit{N}$	${\mathit{W}}^{-}$	${\mathit{W}}^{+}$	${\mathit{W}}_{\mathit{cal},\mathit{N}}$	${\mathit{W}}_{\mathit{cri},\mathit{N}}$	Sign.	$\mathit{N}$	${\mathit{W}}^{-}$	${\mathit{W}}^{+}$	${\mathit{W}}_{\mathit{cal},\mathit{N}}$	${\mathit{W}}_{\mathit{cri},\mathit{N}}$	Sign.
Proposed Algorithm Vs.						Diff.						Diff.
SEHDPSO(2007) [15]	20	196	14	14	52	yes	17	118	35	35	34	no
ASA-GS(2011) [21]	41	844	17	17	279	yes	38	702	39	39	235	yes
GSA-ACO-PSO(2011) [22]	24	276	24	24	81	yes	18	115	56	56	40	no
GA-PSO-ACO(2012) [23]	30	461	4	4	137	yes	30	441	54	54	137	yes
HGA+2local(2014) [24]	20	210	0	0	52	yes	19	189	1	1	46	yes
DIWO(2015) [25]	19	188	2	2	46	yes	19	168	22	22	46	yes
IBA$(2016)$ [26]	27	375	3	3	107	yes	16	125	11	11	29	yes
DSOS(2017) [27]	26	348	3	3	98	yes	22	199	54	54	65	yes
DWCA$(2018)$ [28]	25	322	3	3	89	yes	16	124	12	12	29	yes
IVNS(2018) [29]	46	1063	18	18	361	yes	44	972	18	18	327	yes
ABCSS$(2019)$ [30]	9	33	12	12	5	no	4	6	4	4	*	*
ECSDSOS(2019) [16]	24	300	0	0	81	yes	18	168	3	3	40	yes
HSIHM+2local$(2019)$ [31]	18	171	0	0	40	yes	11	65	1	1	10	yes
MCF-ABC$(2019)$ [32]	8	36	0	0	3	yes	-	-	-	-	-	-
PRGA($(2019)$) [33]	-	-	-	-	-	-	9	41	4	4	5	yes
DSCA+LS(2019) [34]	19	190	0	0	46	yes	16	133	3	3	29	yes
MMA(2019) [2]	23	270	6	6	73	yes	23	270	6	6	73	yes
DSMO$(2020)$ [35]	37	703	0	0	221	yes	34	595	0	0	182	yes
VDWOA$(2021)$ [36]	-	-	-	-	-	-	12	68	10	10	13	yes
SCGA$(2021)$ [37]	10	55	0	0	8	yes	8	36	0	0	3	yes
MPSO$(2021)$ [3]	25	300	3	3	89	yes	18	137	34	34	40	yes
DSSA$(2022)$ [8]	28	376	30	30	116	yes	21	181	50	50	58	yes
DA-GVNS$(2022)$ [38]	50	1275	0	0	434	yes	-	-	-	-	-	-

According to the test results of Table 9, on the test with PDavg.(%), in all the cases (except ABCSS), the statistical test yields $W_{cal,N}\le W_{cri,N}$ with $W^{-}>W^{+}$. That is, the test suggests that our proposed algorithm is significantly better in comparison with all the comparative algorithms except ABCSS. Moreover, our proposed algorithm is still comparable with ABCSS due to having $W^{-}>W^{+}$. Therefore, our proposed algorithm outperforms all the state-of-the-art comparative algorithms. Specifically, it significantly dominates eight recent optimization algorithms because $W^{+}=0$. On the other hand, on the test with PDbest(%), the test results indicate that the performance of our proposed algorithm is significantly better than all the comparative algorithms (except SEHDPSO and GSA-ACO-PSO) owing to $W_{cal,N}\le W_{cri,N}$ and $W^{-}>W^{+}$. Its performance against SEHDPSO and GSA-ACO-PSO is not statistically sound; however, our proposed algorithm is still comparable with them due to having $W^{-}>W^{+}$.

8. Conclusions

We have established a reliable two-stage optimization algorithm to deterministically solve both symmetric and asymmetric TSPs, which utilizes the probe concept to design the local augmentation operators for dynamically generating and developing TSP routes step by step. It also utilizes a proportion value to filter out the worst routes automatically during each step. Furthermore, a self-escape mechanism is imposed on each stagnant complete route for its further possible variation and improvement. It is demonstrated by the experiments on various real-world TSP datasets that our proposed algorithm outperforms the state-of-the-art optimization algorithms with respect to solution accuracy. In addition, it can ascertain the best-known solution regarding a significant number of datasets and even determine a new solution in certain cases (as shown in Table 3). In fact, our proposed algorithm is designed without randomness so that it is a deterministic algorithm, which can be a benefit over the existing algorithms in certain ways. Moreover, our proposed algorithm can deal with both symmetric and asymmetric TSPs by fitting only one parameter, while most of the existing standard optimization algorithms are designed with many fine-tuned parameters for either symmetric or asymmetric problems.

The main drawback of our proposed optimization algorithm is the computational time required to solve large-scale datasets. In fact, as the number of cities becomes larger, a general computer system will eventually run out of memory and cease functioning. It would be beneficial to extend the current work by investigating ways to improve the computational time required to solve large-scale datasets. In the future, we plan to improve the computational complexity by integrating our algorithm with the Delaunay Triangulation (DT) geometric concept because DT can provide potential edges rather than all the edges that are more likely to appear in an optimal solution of the TSP even though it does not contain a route of the TSP [40,41]. We also plan to apply this framework to solve other NP-complete problems, such as the vehicle routing problem, the job-shop scheduling problem, the flow-shop scheduling problem, etc.