Abstract Convergence Analysis for a New Nonlinear Ninth-Order Iterative Scheme

Abstract

This study presents a comprehensive analysis of the semilocal convergence properties of a high-order iterative scheme designed to solve nonlinear equations in Banach spaces. The investigation is carried out under the assumption that the first derivative of the associated nonlinear operator adheres to a generalized Lipschitz-type condition, which broadens the applicability of the convergence analysis. Furthermore, the research demonstrates that, under an additional mild assumption, the proposed scheme achieves a remarkable ninth-order rate of convergence. This high-order convergence result significantly contributes to the theoretical understanding of iterative schemes in infinite-dimensional settings. Beyond the theoretical implications, the results also have practical relevance, particularly in the context of solving complex systems of equations and integral equations that frequently arise in applied mathematics, physics, and engineering disciplines. Overall, the findings provide valuable insights into the behavior and efficiency of advanced iterative schemes in Banach space frameworks. The comparative analysis with existing schemes also demonstrates that the ninth-order iterative scheme achieves faster convergence in most cases, particularly for smaller radii.

1. Introduction

Many systems and processes in applied mathematics, biological sciences, and engineering exhibit nonlinear behaviors, necessitating efficient numerical schemes that offer high accuracy and manageable computational cost as described in [1,2,3]. While existing numerical schemes address this need, there is still ample opportunity for advancements in numerical analysis. The importance of solving nonlinear equations extends beyond theoretical mathematics because discretizing many ordinary, partial, integral, and integro-differential equations results in nonlinear systems requiring numerical solutions [4,5,6,7,8]. Indeed, nonlinear models are prevalent not only in academic research and physical industries, but also in medical sciences and various real-world applications, including GPS triangulation, combustion, heat transfer, and fluid flow [9,10].

A nonlinear equation, or system of them, mathematically describes the relationship between variables in a problem, based on a specific model and its assumptions. This relationship is commonly represented as:

$$\xi \left(x\right)=0,$$

(1)

where $\xi :\mathrm{\Omega }\subseteq B\to B_1$ represent a nonlinear mapping, where B and $B_1$ are Banach spaces and $\mathrm{\Omega }\ne x$ is a non-empty, open, convex subset of B. Obtaining exact, closed-form, or analytical solutions for these nonlinear systems is typically a challenge. However, iterative schemes based on fixed point theory offer approximate numerical solutions that achieve a specified accuracy level, as documented in [11,12]. As a result, a diverse range of iterative techniques have been established, and their convergence properties have been rigorously investigated within the Banach spaces. A common approach for estimating the convergence order of these schemes relies on Taylor series expansions, which require assumptions about the existence and boundedness of higher-order derivatives $({\xi }^{\left(n\right)},n=1,2,\dots )$. One such three-step scheme has recently been proposed in [13], having ninth-order convergence:

$$\begin{array}{cc}\hfill y_n& =x_n-{\displaystyle \frac{2\xi \left(x_n\right){\xi }^{\prime }\left(x_n\right)}{2{\xi }^{\prime }{\left(x_n\right)}^2-\xi \left(x_n\right){\xi }^{″}\left(x_n\right)}},\hfill \\ \hfill z_n& =y_n-{\displaystyle \frac{\xi \left(y_n\right)}{{\xi }^{\prime }\left(y_n\right)}},\hfill \\ \hfill x_{n+1}& =y_n-\left({\displaystyle \frac{\xi \left(y_n\right)+\xi \left(z_n\right)}{{\xi }^{\prime }\left(y_n\right)}}\right).\hfill \end{array}$$

(2)

where $n=0,1,2,\dots$. Since many iterative schemes utilize only first-order derivatives, these higher-order assumptions can be restrictive and inapplicable in some cases.

The convergence of an iterative scheme hinges on the initial approximation, particularly how close it is to the true solution, regardless of the scheme’s theoretical order of convergence. Iterative schemes that exhibit local convergence require that the initial approximation be sufficiently near the solution; conversely, globally convergent schemes are largely independent of the initial guess. Much recent work has focused on local convergence, with analysts often using only first-order derivative assumptions to avoid Taylor expansions. Convergence analyzes based on the local and semi-local Banach space are valuable tools for investigating these schemes [14,15,16].

It is worth noting that the study of iterative methods is conducted mainly in two cases: First in the local convergence analysis where conditions about a neighborhood of the solution are found ensuring the convergence of the sequence generated by the method. Secondly, in the semilocal analysis of convergence, the conditions depend on the initial point.

In both cases a radius of convergence is found based on the initial information; uniqueness of the solution domains as well as error distances of the form $\parallel x^{*}-x_n\parallel$ and $\parallel x_{n+1}-x_n\parallel$. This research paper is structured as follows: Section 2 discusses the main findings including local and semilocal analysis for the convergence of the chosen iterative scheme while Section 3 uses such analyses to solve some numerical problems. At the end, Section 4 briefly shows conclusion of the major contributions in the paper and suggests future research directions.

2. Convergence Without Taylor’s Approach

Local analysis leverages information in the vicinity of a solution to determine the bounds of the convergence region, estimate iteration errors, and establish conditions for the uniqueness of the solution within a specified area. In contrast, semi-local analysis centers on the convergence of an iterative scheme from a given starting point, using majorizing sequences to guarantee convergence of the iterates. The following points highlight:

(i)

Local analysis necessitates knowledge of the solution, while semilocal analysis requires knowledge of the starting point.

(ii)

To understand convergence behavior, establishing local convergence results is crucial, as they reveal the sensitivity in selecting initial guesses. Semilocal results demand a sufficiently accurate initial guess to ensure the iterative sequence converges to the correct solution.

Using the Taylor’s expansion in [13], the authors proved, via the following Theorem, the ninth-order convergence of their proposed iterative scheme given in (2).

Theorem 1.

Let $\gamma \in \mathrm{\Omega }$ be a simple root of the differentiable function $\xi :\mathrm{\Omega }\subset \mathbb{R}\to \mathbb{R}$, where D is an open interval. Then, the three-step iterative scheme defined in Equation (2) exhibits ninth-order convergence, with its asymptotic error term given by:

$${\epsilon }_{n+1}={\displaystyle \frac{1}{128}}{\left({\displaystyle \frac{{\xi }^{″}\left(\gamma \right)}{{\xi }^{\prime }\left(\gamma \right)}}\right)}^8{\epsilon }_n^9+\mathcal{O}\left({\epsilon }_n^{10}\right),$$

(3)

where ${\epsilon }_n=x_n-\gamma$ shows the error at the nth iteration.

There are certain limitations (as given below) if the Taylor series is used to prove the convergence of the iterative scheme (2) or (4):

$\left(Q_1\right)$

The function $\xi$ must be at least four times differentiable $B_1=B_2=\mathbb{R}$ (see Theorem 1).

For example, suppose $B_1=B=\mathbb{R}$, and $\mathrm{\Omega }=\left[-2,{\displaystyle \frac{3}{2}}\right]$. Define $\xi \left(x\right)$ on $\mathrm{\Omega }$ by

$$\xi \left(x\right)=\left\{\begin{array}{cc}a{x}^{4}logx+a_1{x}^6+a_2{x}^5,\hfill & x\ne 0\hfill \\ 0,\hfill & x=0,\hfill \end{array}\right.$$

where $a\ne 0$ and $a_1+a_2=0.$

Notice that $x^{*}\in \mathrm{\Omega }$, since $\xi \left(1\right)=0$, but ${\xi }^{\left(4\right)}$ is not continuous at $x=0\in \mathrm{\Omega }$.

Thus, Theorem 1 cannot assure the convergence of the scheme (4) to $x^{*}=\mathrm{\Omega }$. But scheme (2) converges if say $a=a_1=1,a=-1$ and $x_0=0.95.$ Consequently, the sufficient conditions of Theorem 1 can be weakened.

$\left(Q_2\right)$

There are no a priori upper estimates on the norms $\left|\right|x_k-x^{*}\left|\right|.$ Consequently, we do not know in advance about the number of iterations to be carried out to reach a predetermined error tolerance.

$\left(Q_3\right)$

There is no information about a neighborhood in $x^{*}$ that contains only one solution.

$\left(Q_4\right)$

The more challenging semilocal analysis of convergence for scheme (4) has not been studied before.

$\left(Q_5\right)$

Can this scheme be applied to more general domains than $\mathbb{R}$?

We respond positively to the limitations $\left(Q_1\right)$–$\left(Q_5\right)$. In particular,

$\left(Q_1\right)\prime$

The local analysis uses only conditions in the function ${\xi }^{\prime }$ that appear only in the scheme (2). Thus, the example in $\left(L_1\right)$ can be handled under this approach.

$\left(Q_2\right)\prime$

The number of iterations to be performed to achieve a predecided error tolerance is known in advance, since upper error bounds on $\left|\right|x_k-x^{*}\left|\right|$ are developed under the present approach.

$\left(Q_3\right)\prime$

Isolation results for the solution $x^{*}$ become available.

$\left(Q_4\right)\prime$

The scheme is applicable on E, where $E=\mathbb{R}$ or $E=\mathbb{C}$ (the complex plane).

$\left(Q_5\right)\prime$

A semilocal analysis of convergence for the scheme (4) is presented depending on majorizing sequences.

Note that both types of analysis are based on the concept of generalized continuity for ${\xi }^{\prime }$. Based on the aforementioned comments, and to emphasize that we work in a more general setting, we consider the differentiable function $\xi :D\subset E\to E,$ and the equation.

Keeping these points in mind, we will investigate the local and semilocal convergence of the ninth-order iterative scheme proposed in [13].

The three-step scheme (2) is can be also written for $x_0\in \mathrm{\Omega }$ and each $n=0,1,2\dots$ by

$$\begin{array}{cc}\hfill H_n& ={\xi }^{\prime }\left(x_n\right)-{\displaystyle \frac{1}{2}}{\xi }^{\prime }{\left(x_n\right)}^{-1}{\xi }^{″}\left(x_n\right){\xi }^{\prime }\left(x_n\right)\xi \left(x_n\right),\hfill \\ \hfill y_n& =x_n-H_n^{-1}\xi \left(x_n\right),\hfill \\ \hfill z_n& =y_n-\xi {\left(y_n\right)}^{-1}\xi \left(y_n\right),\hfill \\ \hfill x_{n+1}& =y_n-{\xi }^{\prime }{\left(y_n\right)}^{-1}(\xi \left(y_n\right)+\xi \left(z_n\right)).\hfill \end{array}$$

(4)

2.1. (LAC) Local Analysis of Convergence

It is convenient to use some abbreviations such as:

• FNDC: A function which is nondecreasing and continuous.
• MPZF: The minimal positive zero of a function.

Let $A=[0,+\infty )$,

Suppose:

($E_1$)

There exists FNDC ${\kappa }_0:A\to A$ such that $1-{\kappa }_0\left(t\right)$ has MPZF which is denoted by $s_0$. Define the interval $A_0=[0,s_0)$.

($E_2$)

There exist FNDC functions $\kappa :A_0\to A$ and ${\kappa }_1:A_0\to A$.

Define the functions $p:A_0\to A,$ $q:A_0\to A$ for some $h>0$ by

$p\left(t\right)={\displaystyle \frac{h}{2}}{\displaystyle \frac{{\kappa }_1\left(t\right)}{1-{\kappa }_0\left(t\right)}},$ and $q\left(t\right)={\kappa }_0\left(t\right)+{\displaystyle \frac{h}{2}}{\displaystyle \frac{{\kappa }_1\left(t\right)}{1-{\kappa }_0\left(t\right)}}.$

($E_3$)

The function $1-q\left(t\right)$ has MPZF in $A_0$, which is denoted by $s_1$. Define the interval $A_1=[0,s)$, where $s=min\{s_0,s_1\}$.

($E_4$)

The function $1-g_1\left(t\right)$ has MPZF in the interval $A_1$, which is denoted by $R_1$, where $g_1:A_1\to A$,

$$g_1\left(t\right)={\displaystyle \frac{{\mathit{\int }}_0^1\kappa \left((1-\phi )t\right)d\phi }{1-{\kappa }_0\left(t\right)}}+{\displaystyle \frac{p\left(t\right)(1+{\mathit{\int }}_0^1{\kappa }_0\left(\phi t\right)d\phi )}{(1-{\kappa }_0\left(t\right))(1-q\left(t\right))}}.$$

(5)

($E_5$)

The function $1-{\kappa }_0\left(g_1\left(t\right)t\right)$ has MPZF in the interval $A_1$, which is denoted by $s_2$. Define the interval $A_2=[0,s_2)$. Define the functions $g_2:A_2\to A$ and $g_3:A_2\to A$ by

$$g_2\left(t\right)={\displaystyle \frac{{\mathit{\int }}_0^1\kappa \left((1-\phi )g_1\left(t\right)t\right)d\phi }{1-{\kappa }_0\left(g_1\left(t\right)t\right)}}$$

(6)

and

$$g_3\left(t\right)={\displaystyle \frac{{\mathit{\int }}_0^1\kappa \left((1-\phi )g_1\left(t\right)t\right)d\phi +(1+{\mathit{\int }}_0^1{\kappa }_0\left(\phi g_2\left(t\right)t\right)d\phi )g_2\left(t\right)}{1-{\kappa }_0\left(g_1\left(t\right)t\right)}},$$

(7)

respectively.

($E_6$)

The functions $1-g_2\left(t\right)$ and $1-g_3\left(t\right)$ have MPZF in the interval $A_2$, which are denoted by $R_2$ and $R_3$, respectively. Define

$$R^{*}=min\left\{R_i\right\}i=1,2,3.$$

(8)

The real number $R^{*}$ is a convergence radius for the scheme (8) (see Theorem 2). We will use the notation $S(x,a)=\{y\in B:\parallel x-y\parallel <a\}$ for some $a>0$ to denote an open ball. Moreover, $S[x,a]$ is the notation for a closed ball.

Next, we connect $h,{\kappa }_0,\kappa ,$ and ${\kappa }_1$ to the operators on the scheme (4).

($E_7$)

There exist $h>0,$ a solution $x^{*}\in \mathrm{\Omega }$ of the equation $\xi \left(x\right)=0$ and an invertible linear operator L such that for each $u\in \mathrm{\Omega }$

$$\parallel L^{-1}({\xi }^{\prime }\left(u\right)-L)\parallel \le {\kappa }_0(\parallel u-x^{*}\parallel )$$

(9)

and

$$\parallel L^{-1}\parallel \le h.$$

(10)

Define the region $M=\mathrm{\Omega }\cap S(x^{*},s_0).$

($E_8$)

$\parallel L^{-1}({\xi }^{\prime }\left(u_2\right)-{\xi }^{\prime }\left(u_1\right))\parallel \le \kappa (\parallel u_2-u_1\parallel ),$ for each $u_2,u_1\in M$

and

$\parallel L^{-1}{\xi }^{″}\left(x\right)\xi \left(x\right)\parallel \le {\kappa }_1(\parallel x-x^{*}\parallel )$ for each $x\in M$.

and

($E_9$)

$S[x^{*},R]\subset \mathrm{\Omega }.$

Let $A^{*}=[0,R^{*})$. Then, it follows by the conditions $\left(E_1\right)$–$\left(E_9\right)$ that for each $t\in A^{*}$

$$0\le {\kappa }_0\left(t\right)<1,$$

(11)

$$0\le p\left(t\right),$$

(12)

$$0\le q\left(t\right)<1$$

(13)

and

$$0\le g_i\left(t\right)<1.$$

(14)

Remark 1.

(i) 

It is worth noting that the items $\left(E_1\right)$–$\left(E_9\right)$ are standard sufficient convergence conditions for the study of iterative methods [15,17].

In particular, the conditions $\left(E_1\right)$–$\left(E_9\right)$ define the majorant functions $g_i$, whose smallest positive zeros are always needed to define the radius of convergence of the method (see (4)). The radius of convergence defines a ball about the solution $x^{*}$. Then, it is shown in Theorem 2 that as long as we select an initial point $x_0$ from that ball, the convergence of the method to $x^{*}$ is assured. Moreover, generalized continuity the conditions $\left(E_7\right)$ and $\left(E_8\right)$ needed to control the derivatives ${\xi }^{\prime }$, ${\xi }^{″}$ connect and the majorizing functions ${\kappa }_0$,κ and ${\kappa }_1$ to these derivatives. Furthermore, a condition of the type $\left(E_9\right)$ is always present and defines a ball inside which the iterates lie. It is worth noting that the functions ${\kappa }_0$, κ and ${\kappa }_1$ provide sharper error distances $\parallel x_{n+1}-x_n\parallel$ and $\parallel x^{*}-x_n\parallel$ and weaker sufficient convergence conditions than results from Lipschitz-Hölder conditions [16,18]. Finally, one can look at the first two numerical examples, where the major functions ${\kappa }_0$, κ and ${\kappa }_1$ are calculated.

(ii) 

Some choices for the operator L can be $L=I$ (the identity operator),or $L={\xi }^{\prime }\left(\overline{x}\right)$ for some auxiliary point $\overline{x}\in \mathrm{\Omega }$ with $\overline{x}\ne x^{*}$ or $L={\xi }^{\prime }\left(x^{*}\right)$. The last choice for L implies that $x^{*}$ is a simple solution of the equation $\xi \left(x\right)=0$. But notice that no such hypothesis is made or implied by $\left(E_1\right)-\left(E_9\right)$. Consequently, the new result can be applied to find solutions of multiplicity larger than one.

Define the region $M_0=S(x^{*},R^{*})-\left\{x^{*}\right\}.$

Next, the main LAC is presented for scheme (4).

Theorem 2.

Suppose that the conditions $\left(E_1\right)$–$\left(E_9\right)$ hold. Then, if the starting point $x_0\in M_0$, all the iterates $\left\{x_n\right\}$ generated by the scheme (4) are well defined in $S(x^{*},R^{*})$, are contained in $S(x^{*},R^{*})$, and converge to $x^{*}$. Moreover, the following items hold

$$\parallel y_n-x^{*}\parallel \le g_1(\parallel x_n-x^{*}\parallel )\parallel x_n-x^{*}\parallel \le \parallel x_n-x^{*}\parallel <R,$$

(15)

$$\parallel z_n-x^{*}\parallel \le g_2(\parallel x_n-x^{*}\parallel )\parallel x_n-x^{*}\parallel \le \parallel x_n-x^{*}\parallel$$

(16)

and

$$\parallel x_{n+1}-x^{*}\parallel \le g_3(\parallel x_n-x^{*}\parallel )\parallel x_n-x^{*}\parallel \le \parallel x_n-x^{*}\parallel .$$

(17)

Proof. 

Items (15)–(17) are shown using induction. Pick $\overline{u}\in M_0$. Then, by the condition $\left(E_7\right)$, (8) and (11) one can have

$$\parallel L^{-1}({\xi }^{\prime }\left(\overline{u}\right)-L)\parallel \le {\kappa }_0(\parallel \overline{u}-x^{*}\parallel )\le {\kappa }_0\left(R\right)<1.$$

(18)

In view of (18) and the Banach lemma on invertible operators [10], ${\xi }^{\prime }{\left(\overline{u}\right)}^{-1}\in \mathcal{L}({\mathcal{B}}_1,\mathcal{B})$ and

$$\parallel {\xi }^{\prime }{\left(\overline{u}\right)}^{-1}L\parallel \le {\displaystyle \frac{1}{1-{\kappa }_0(\parallel \overline{u}-x^{*}\parallel )}}.$$

(19)

We need some estimates

$$\begin{array}{cc}\hfill \parallel L^{-1}(H_m-L)\parallel & =\parallel L^{-1}(({\xi }^{\prime }\left(x_m\right)-L)-{\displaystyle \frac{1}{2}}{\xi }^{\prime }{\left(x_m\right)}^{-1}{\xi }^{″}\left(x_m\right)\xi \left(x_m\right))\parallel \hfill \\ \hfill & \le \parallel L^{-1}({\xi }^{\prime }\left(x_m\right)-L)\parallel +{\displaystyle \frac{\parallel L^{-1}\parallel }{2}}\parallel {\xi }^{\prime }{\left(x_m\right)}^{-1}L\parallel \parallel L^{-1}{\xi }^{″}\left(x_m\right)\xi \left(x_m\right)\parallel .\hfill \\ \hfill & \le {\kappa }_0(\parallel x_m-x^{*}\parallel )+{\displaystyle \frac{h}{2}}{\displaystyle \frac{{\kappa }_1(\parallel x_m-x^{*}\parallel )}{1-{\kappa }_0(\parallel x_m-x^{*}\parallel )}}=q_m<1,\hfill \end{array}$$

(20)

where we used $\left(E_7\right)$, $\left(E_8\right)$, (13) and (19), so

$$\parallel H_m^{-1}L\parallel \le {\displaystyle \frac{1}{1-q_m}}.$$

(21)

Moreover, we have

$$\begin{array}{cc}\hfill \parallel L^{-1}({\xi }^{\prime }\left(x_m\right)-H_m)\parallel & ={\displaystyle \frac{1}{2}}\parallel L^{-1}\left({\xi }^{\prime }{\left(x_m\right)}^{-1}L\right)\left(L^{-1}{\xi }^{″}\left(x_m\right)\xi \left(x_m\right)\right)\parallel \hfill \\ \hfill & \le {\displaystyle \frac{h}{2}}{\displaystyle \frac{{\kappa }_1(\parallel x_m-x^{*}\parallel )}{1-{\kappa }_0(\parallel x_m-x^{*}\parallel )}}=p_m.\hfill \end{array}$$

Consequently, the iterate $\left(y_m\right)$ is well-defined due to the first substep of scheme (4) and can be expressed as:

$$\begin{array}{cc}\hfill y_m-x^{*}& =x_m-x^{*}-{\xi }^{\prime }{\left(x_m\right)}^{-1}\xi \left(x_m\right)+({\xi }^{\prime }{\left(x_m\right)}^{-1}-H_m^{-1})\xi \left(x_m\right)\hfill \\ \hfill & =x_m-x^{*}-{\xi }^{\prime }{\left(x_m\right)}^{-1}\xi \left(x_m\right)-H_m^{-1}(\xi \left(x_m\right)-H_m){\xi }^{\prime }{\left(x_m\right)}^{-1}\xi \left(x_m\right).\hfill \end{array}$$

(22)

Notice that

$$x_m-x^{*}-{\xi }^{\prime }{\left(x_m\right)}^{-1}\xi \left(x_m\right)=\left[{\xi }^{\prime }{\left(x_m\right)}^{-1}L\right]$$

(23)

$$\left[L^{-1}{\mathit{\int }}_0^1\left({\xi }^{\prime }(x^{*}+\phi (x_m-x^{*}))-{\xi }^{\prime }\left(x_m\right)\right)d\phi (x_m-x^{*})\right],$$

(24)

so by ($E_8$), ($E_7$),

$$\parallel x_m-x^{*}\parallel \le {\displaystyle \frac{{\mathit{\int }}_0^1\kappa ((1-\phi )\parallel x_m-x^{*}\parallel )d\phi \parallel x_m-x^{*}\parallel }{1-{\kappa }_0(\parallel x_m-x^{*}\parallel )}},$$

(25)

$$\parallel L^{-1}({\xi }^{\prime }\left(x_m\right)-H_m)\parallel \le p_m,$$

(26)

$$\begin{array}{cc}\hfill \parallel L^{-1}\xi \left(x_m\right)\parallel & =\parallel L^{-1}(\xi \left(x_m\right)-\xi \left(x^{*}\right))\parallel \hfill \\ \hfill & =∥L^{-1}{\mathit{\int }}_0^1\left({\xi }^{\prime }(x^{*}+\phi (x_m-x^{*}))-L+L\right)d\phi (x_m-x^{*})∥\hfill \\ \hfill & \le \left(1+{\mathit{\int }}_0^1{\kappa }_0(\phi \parallel x_m-x^{*}\parallel )d\phi \right)\parallel x_m-x^{*}\parallel .\hfill \end{array}$$

(27)

By (18), (19), (14) (for $i=1$), and (25)–(27) estimate (22) gives

$$\begin{array}{cc}\hfill \parallel y_m-x^{*}\parallel & \le [{\displaystyle \frac{{\mathit{\int }}_0^1\kappa ((1-\phi )\parallel x_m-x^{*}\parallel )d\phi }{1-{\kappa }_0(\parallel x_m-x^{*}\parallel )}}\hfill \\ \hfill & +{\displaystyle \frac{p_m(1+{\mathit{\int }}_0^1{\kappa }_0(\phi \parallel x_m-x^{*}\parallel \left)d\phi \right)}{(1-q_m)(1-{\kappa }_0(\parallel x_m-x^{*}\parallel \left)\right)}}]\parallel x_m-x^{*}\parallel \hfill \\ \hfill & \le g_1(\parallel x_m-x^{*}\parallel )\parallel x_m-x^{*}\parallel \le \parallel x_m-x^{*}\parallel <R.\hfill \end{array}$$

(28)

Thus, the iterate $y_m\in S(x^{*},R)$,

$$\parallel {\xi }^{\prime }{\left(y_m\right)}^{-1}L\parallel \le {\displaystyle \frac{1}{1-{\kappa }_0(\parallel y_m-x^{*}\parallel )}},$$

(29)

the item (15) holds for $n=m$ and the iterates $z_m$ and $x_{m+1}$ exist by the last two substeps of the scheme (4).

Furthermore, we can write

$$z_m-x^{*}=y_m-x^{*}-{\xi }^{\prime }{\left(y_m\right)}^{-1}\xi \left(y_m\right),$$

(30)

$$\begin{array}{cc}\hfill \parallel z_m-x^{*}\parallel & \le {\displaystyle \frac{{\mathit{\int }}_0^1{\kappa }_0((1-\phi )\parallel y_m-x^{*}\parallel )d\phi \parallel y_m-x^{*}\parallel }{1-{\kappa }_0(\parallel y_m-x^{*}\parallel )}}\hfill \\ \hfill & \le g_2(\parallel x_m-x^{*}\parallel )\parallel x_m-x^{*}\parallel \le \parallel x_m-x^{*}\parallel ,\hfill \end{array}$$

(31)

$$x_{m+1}-x^{*}=y_m-x^{*}-{\xi }^{\prime }{\left(y_m\right)}^{-1}\xi \left(y_m\right)-{\xi }^{\prime }{\left(y_m\right)}^{-1}\xi \left(z_m\right),$$

(32)

so

$$\begin{array}{cc}\hfill \parallel x_{m+1}-x^{*}\parallel & \le {\displaystyle \frac{{\mathit{\int }}_0^1{\kappa }_0((1-\phi )\parallel y_m-x^{*}\parallel )d\phi \parallel y_m-x^{*}\parallel }{1-{\kappa }_0(\parallel y_m-x^{*}\parallel )}}\hfill \\ \hfill & +{\displaystyle \frac{(1+{\mathit{\int }}_0^1{\kappa }_0(\phi \parallel z_m-x^{*}\parallel \left)d\phi \right)\parallel z_m-x^{*}\parallel }{1-{\kappa }_0(\parallel y_m-x^{*}\parallel )}}\hfill \\ \hfill & \le g_3(\parallel x_m-x^{*}\parallel )\parallel x_m-x^{*}\parallel \le \parallel x_m-x^{*}\parallel .\hfill \end{array}$$

(33)

Hence, the items (16) and (17) hold if $n=m$, and the iterates $y_m$ and $x_{m+1}\in$$S(x^{*},R^{*})$.

Finally, for $c=g_3(\parallel x_0-x^{*}\parallel )\in [0,1)$, we get from (33)

$$\parallel x_{m+1}-x^{*}\parallel \le c\parallel x_m-x^{*}\parallel \le c^{m+1}\parallel x_0-x^{*}\parallel <R^{*}.$$

(34)

Therefore, we conclude that ${lim}_{m\to +\infty }{x}_m=x^{*}.$  □

Next, a region is determined with $x^{*}$ the solution of equation $\xi \left(x\right)=0.$

Proposition 1.

Suppose that the condition $\left(E_7\right)$ holds in $S(x^{*},s_3)$ for some $s_3>0$ and there exists $s_4\ge s_3$ such that

$${\mathit{\int }}_0^1{\kappa }_0\left(\phi s_4\right)d\phi <1.$$

(35)

Define the region $M_1=\mathrm{\Omega }\cap S[x^{*},s_4]$. Then, the only solution of the equation $\xi \left(x\right)=0$ in the region $M_1$ is $x^{*}$.

Proof. 

Suppose that there exist $\overline{y}\in M_1$ such that $\xi \left(\overline{y}\right)=0$ and $\overline{y}\ne x^{*}$. Let us consider the linear operator $L_1={\mathit{\int }}_0^1{\xi }^{\prime }(x^{*}+\phi (\overline{y}-x^{*}))d\phi .$ In view of the condition $\left(E_7\right)$ and (35), we get

$$\parallel L^{-1}(L_1-L)\parallel \le {\mathit{\int }}_0^1{\kappa }_0(\phi \parallel \overline{y}-x^{*}\parallel )d\phi \le {\mathit{\int }}_0^1{\kappa }_0\left(\phi s_4\right)d\phi <1.$$

(36)

Therefore, $L^{-1}\in \mathcal{L}(B_1,B)$. Finally, from the identity

$$\overline{y}-x^{*}=L_1^{-1}(\xi \left(\overline{y}\right)-\xi \left(x^{*}\right))=L_1^{-1}\left(0\right)=0,$$

(37)

we conclude that $\overline{y}=x^{*}$.  □

Remark 2.

Under all the conditions $\left(E_1\right)$–$\left(E_9\right)$, we can take $s_3=R^{*}$ in the Proposition 1.

2.2. (SLAC) Semilocal Analysis of Convergence

The analysis is similar to LAC. But $x^{*},{\kappa }_0,\kappa$ and ${\kappa }_1$ are exchanged by $x_0,v_0,v$ and $v_1$, respectively, as follows:

Suppose that:

($T_1$)

There exists FNDC $v_0:A\to A$ such that the function $1-v_0\left(t\right)$ has MPZF, which is denoted by $r_0$. Define the interval $A_3=[0,r_0)$.

($T_2$)

There exist FNDC $v:A_3\to A$$v_1:A_3\to A$ and $h>0$.

Define for ${\tau }_0=0$, some ${\mu }_0\ge 0$, the scale sequence $\left\{{\tau }_n\right\}$ by:

$$\begin{array}{cc}\hfill {\lambda }_n& ={\mathit{\int }}_0^{1}v\left((1-\phi )({\mu }_n-{\tau }_n)\right)d\phi ({\mu }_n-{\tau }_n)+{\displaystyle \frac{h}{2}}{\displaystyle \frac{v_1\left({\tau }_n\right)({\mu }_n-{\tau }_n)}{1-v_0\left({\tau }_n\right)}},\hfill \\ \hfill {\eta }_n& ={\mu }_n+{\displaystyle \frac{{\lambda }_n}{1-v_0\left({\mu }_n\right)}},\hfill \\ \hfill {\beta }_n& =\left(1+{\mathit{\int }}_0^1{v}_0({\mu }_n+\phi ({\eta }_n-{\mu }_n))d\phi \right)({\eta }_n-{\mu }_n)+{\lambda }_n,\hfill \\ \hfill {\tau }_{n+1}& ={\mu }_n+{\displaystyle \frac{{\lambda }_n+{\beta }_n}{1-v_0\left({\mu }_n\right)}},\hfill \\ \hfill {\overline{q}}_n& =v_0\left({\tau }_n\right)+{\displaystyle \frac{h}{2}}{\displaystyle \frac{v_1\left({\tau }_n\right)}{1-v_0\left({\tau }_n\right)}},\hfill \end{array}$$

(38)

$${\chi }_{n+1}={\mathit{\int }}_0^{1}v\left((1-\phi )({\tau }_{n+1}-{\tau }_n)\right)d\phi ({\tau }_{n+1}-{\tau }_n)+(1+v_0\left({\tau }_n\right))({\tau }_{n+1}-{\mu }_n)+{\displaystyle \frac{1}{2}}{\displaystyle \frac{v_1\left({\tau }_n\right)({\mu }_n-{\tau }_n)}{1-v_0\left({\tau }_n\right)}}$$

(39)

and

$${\mu }_{n+1}={\tau }_{n+1}+{\displaystyle \frac{{\chi }_{n+1}}{(1-{\overline{q}}_{n+1})}}.$$

(40)

The sequence denoted by $\left\{{\tau }_n\right\}$ will be demonstrated in Theorem (3) to be a majorizing sequence for the sequence $\left\{x_n\right\}$ that is generated by (4). But let us first develop a general condition for its convergence.

($T_3$)

There exists $r\in [0,r_0)$ such that for each $n=0,1,2,\dots$,

$$v_0\left({\tau }_n\right)<1,v_0\left({\mu }_n\right)<1,{\overline{q}}_n<1\mathrm{and}{\tau }_n\le r_0.$$

(41)

It follows by this condition and (38) that there exists $r^{*}\in [0,r]$ such that

$$0\le {\tau }_n\le {\mu }_n\le {\eta }_n\le {\tau }_{n+1}$$

(42)

and

$$\underset{n\to +\infty }{lim}{\tau }_n=r^{*}.$$

(43)

The limit point $r^{*}$ is the least upper bound of the sequence $\left\{{\tau }_n\right\}$ which is unique. As in the local analysis, the functions $v_0$v and $v_1$ relate to the operators on the scheme (4).

($T_4$)

There exists $x_0\in \mathrm{\Omega },h>0$ and an invertible operator L such that for each $\tilde{u}\in \mathrm{\Omega }$,

$$\left|\right|L^{-1}({\xi }^{\prime }\left(\tilde{u}\right)-L)\left|\right|\le v_0\left(\right||\tilde{u}-x_0\left|\right|)$$

(44)

and $\parallel L^{-1}\parallel \le h.$

Notice that the conditions ($T_1$), ($T_4$) (for $\tilde{u}=x_0$) and the second condition in ($T_5$) (for $\tilde{x}=x_0$) give as in the local case

$$\left|\right|L^{-1}(T_0-L)\left|\right|\le {\overline{q}}_0<1.$$

(45)

So, the linear operator $T_0$ is invertible and we can choose ${\mu }_0\ge \left|\right|T_0^{-1}\xi \left(x_0\right)\left|\right|$.

($T_5$)

$\left|\right|L^{-1}({\xi }^{\prime }\left({\tilde{u}}_2\right)-{\xi }^{\prime }\left({\tilde{u}}_1\right))\left|\right|\le v\left(\right||{\tilde{u}}_2-{\tilde{u}}_1\left|\right|),\mathrm{for}\mathrm{each}{\tilde{u}}_2,{\tilde{u}}_1\in M_4.$

and

$$\left|\right|L^{-1}{\xi }^{″}\left(\tilde{x}\right)\xi \left(\tilde{x}\right)\left|\right|\le v_1\left(\right||\tilde{x}-x_0\left|\right|),$$

(46)

Define the region $M_4=\mathrm{\Omega }\cap S(x_0,r_0)$ and for each $\tilde{x}\in M_4$.

($T_6$)

$S[x_0,{\tau }^{*}]\subset \mathrm{\Omega }.$

Remark 3.

As in the local case, one can choose $L=I$ or $L={\xi }^{\prime }\left(d\right)$ for some auxiliary point $d\in \mathrm{\Omega }$ with $d\ne x_0$ or $L={\xi }^{\prime }\left(x_0\right)$ or some other choice as long as the conditions $\left(T_1\right)$–$\left(T_6\right)$ hold.

Next, we provide the SAC for the scheme (4).

Theorem 3.

Assuming conditions $\left(T_1\right)$ through $\left(T_6\right)$ are satisfied, the iterative sequence $\left\{x_n\right\}$ generated by the scheme is well-defined within the ball $S(x_0,{\tau }^{*})$, remains within $S(x_0,{\tau }^{*})$ for all $n=0,1,2,\dots$, and converges to a solution $x^{*}\in S[x_0,{\tau }^{*}]$ of the nonlinear equation $\xi \left(x\right)=0$. Furthermore, the following error estimates are valid for all $n=0,1,2,\dots$.

$$\parallel x^{*}-x_n\parallel \le {\tau }^{*}-{\tau }_n.$$

(47)

Proof. 

Induction is employed to show the assertions

$$\parallel y_n-x_n\parallel \le {\mu }_n-{\tau }_n,$$

(48)

$$\parallel z_n-y_n\parallel \le {\eta }_n-{\mu }_n,$$

(49)

and

$$\parallel x_{n+1}-y_n\parallel \le {\tau }_{n+1}-{\mu }_n.$$

(50)

Assertion (48) holds if $n=0$ by (38) and the choice of ${\mu }_0$, since

$$\parallel y_0-x_0\parallel =\parallel T_0^{-1}\xi \left(x_0\right)\parallel \le {\mu }_0={\mu }_0-{\tau }_0<{\tau }^{*}$$

(51)

and the iterate $y_0\in S(x_0,{\tau }^{*})$.

By induction on the integer m and the first substep on the scheme (4), we can write in turn

$$\begin{array}{cc}\hfill \xi \left(y_m\right)& =\xi \left(y_m\right)-\xi \left(x_m\right)-T_m(y_m-x_m)\hfill \\ \hfill & =\xi \left(y_m\right)-\xi \left(x_m\right)-\left({\xi }^{\prime }\left(x_m\right)-{\displaystyle \frac{1}{2}}{\xi }^{\prime }{\left(x_m\right)}^{-1}{\xi }^{″}\left(x_m\right)\xi \left(x_m\right)\right)(y_m-x_m)\hfill \\ \hfill & =\xi \left(y_m\right)-\xi \left(x_m\right)-{\xi }^{\prime }\left(x_m\right)(y_m-x_m)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\xi }^{\prime }{\left(x_m\right)}^{-1}{\xi }^{″}\left(x_m\right)\xi \left(x_m\right)(y_m-x_m).\hfill \end{array}$$

(52)

We need the estimates

$$\begin{array}{cc}\hfill & \parallel L^{-1}(\xi \left(y_m\right)-\xi \left(x_m\right)-{\xi }^{\prime }\left(x_m\right)(y_m-x_m))\parallel \hfill \\ \hfill & =\parallel {\mathit{\int }}_0^1{L}^{-1}({\xi }^{\prime }(x_m+\phi (y_m-x_m))-{\xi }^{\prime }\left(x_m\right))(y_m-x_m)\parallel \hfill \\ \hfill & \le {\mathit{\int }}_0^{1}v(\phi \parallel y_m-x_m\parallel )d\phi \parallel y_m-x_m\parallel \hfill \\ \hfill & \le {\mathit{\int }}_0^{1}v\left(\phi ({\mu }_m-{\tau }_m)\right)d\phi ({\mu }_m-{\tau }_m),\left(\mathrm{by}\left(T_5\right)\right),\hfill \end{array}$$

(53)

$$\parallel {\xi }^{\prime }{\left(x_m\right)}^{-1}L\parallel \le {\displaystyle \frac{1}{1-v_0(\parallel x_m-x_0\parallel )}}\le {\displaystyle \frac{1}{1-v_0\left({\tau }_m\right)}},\left(\mathrm{by}\left(T_4\right)\right)$$

(54)

$$\parallel L^{-1}{\xi }^{″}\left(x_m\right)\xi \left(x_m\right)\parallel \le v_1(\parallel x_m-x_0\parallel )\le v_1\left({\tau }_m\right)$$

(55)

(by ($T_5$)) and using the triangle inequality.

Then, by summing up (53)–(55), estimate (52) gives

$$\begin{array}{cc}\hfill \parallel L^{-1}\xi \left(y_m\right)\parallel & \le {\mathit{\int }}_0^{1}v\left(\phi ({\mu }_m-{\tau }_m)\right)d\phi ({\mu }_m-{\tau }_m)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\displaystyle \frac{v_1\left({\tau }_m\right)({\mu }_m-{\tau }_m)}{1-v_0\left({\tau }_m\right)}}={\lambda }_m.\hfill \end{array}$$

(56)

Then, by the second substep of scheme (4), (54) (for $x_m=y_m$) and (56), we have

$$\begin{array}{cc}\hfill \parallel z_m-y_m\parallel & =\parallel {\xi }^{\prime }{\left(y_m\right)}^{-1}L\left[L^{-1}\xi \left(y_m\right)\right]\parallel \hfill \\ \hfill & \le \parallel {\xi }^{\prime }{\left(y_m\right)}^{-1}L\parallel \parallel L^{-1}\xi \left(y_m\right)\parallel \le {\displaystyle \frac{{\lambda }_m}{1-v_0\left({\mu }_m\right)}}={\eta }_m-{\beta }_m\hfill \end{array}$$

(57)

and

$$\begin{array}{cc}\hfill \parallel z_m-x_0\parallel & \le \parallel z_m-y_m\parallel +\parallel y_m-x_0\parallel \hfill \\ \hfill & \le {\eta }_m-{\mu }_m+{\mu }_m-{\tau }_0={\eta }_m<{\tau }^{*}.\hfill \end{array}$$

(58)

So, (49) holds for $m=n$ and the iterate $z_m\in S(x_0,{\tau }^{*})$.

We can write

$$\xi \left(z_m\right)=\xi \left(z_m\right)-\xi \left(y_m\right)+\xi \left(y_m\right).$$

(59)

But

$$\xi \left(z_m\right)-\xi \left(y_m\right)={\mathit{\int }}_0^1{\xi }^{\prime }(y_m+\phi (z_m-y_m))d\phi (z_m-y_m),$$

(60)

so we get

$$\begin{array}{cc}\hfill & \parallel L^{-1}(\xi \left(z_m\right)-\xi \left(y_m\right))\parallel \hfill \\ \hfill & =\parallel L^{-1}\left[{\mathit{\int }}_0^1\left({\xi }^{\prime }(y_m+\phi (z_m-y_m))-L+L\right)d\phi \right](z_m-y_m)\parallel .\hfill \\ \hfill & \le (1+{\mathit{\int }}_0^1{v}_0(\parallel y_m-x_0\parallel +\phi \parallel z_m-y_m\parallel \left)d\phi \right)\parallel z_m-y_m\parallel \hfill \\ \hfill & \le (1+{\mathit{\int }}_0^1{v}_0({\mu }_m+\phi ({\eta }_m-{\mu }_m))d\phi )({\eta }_m-{\mu }_m).\hfill \end{array}$$

(61)

Then, by (38), (56) and (61), identity (59) gives

$$\parallel L^{-1}\xi \left(z_m\right)\parallel \le \parallel L^{-1}(\xi \left(z_m\right)-\xi \left(y_m\right))\parallel +\parallel L^{-1}\xi \left(y_m\right)\parallel \le {\lambda }_m+{\mu }_m.$$

(62)

By the third substep of the scheme (4), (54) (for $y_m=x_m$) and (62), we obtain

$$\begin{array}{cc}\hfill \parallel x_{m+1}-y_m\parallel & \le \parallel {\xi }^{\prime }{\left(y_m\right)}^{-1}L\parallel (\parallel L^{-1}\xi \left(y_m\right)\parallel +\parallel L^{-1}\xi \left(z_m\right)\parallel )\hfill \\ \hfill & \le {\displaystyle \frac{{\lambda }_m+{\beta }_m}{1-v_0\left({\mu }_m\right)}}={\tau }_{m+1}-{\mu }_m\hfill \end{array}$$

(63)

and

$$\begin{array}{cc}\hfill \parallel x_{m+1}-x_0\parallel & \le \parallel x_{m+1}-y_m\parallel +\parallel y_m-x_0\parallel \hfill \\ \hfill & \le {\tau }_m-{\mu }_m+{\mu }_m+{\tau }_0={\tau }_{m+1}<{\tau }^{*}.\hfill \end{array}$$

(64)

So, the assertion (50) holds for $m=n$ and the iterate $x_{m+1}\in S(x_0,{\tau }^{*})$.

As in (52), the first substep of the scheme (4) gives in turn

$$\begin{array}{cc}\hfill \xi \left(x_{m+1}\right)& =\xi \left(x_{m+1}\right)-\xi \left(x_m\right)-T_m(y_m-x_m)\hfill \\ \hfill & -{\xi }^{\prime }\left(x_m\right)(x_{m+1}-x_m)+{\xi }^{\prime }\left(x_m\right)(x_{m+1}-x_m)\hfill \\ \hfill & =\xi \left(x_{m+1}\right)-\xi \left(x_m\right)-{\xi }^{\prime }\left(x_m\right)(x_{m+1}-x_m)\hfill \\ \hfill & -\left[{\xi }^{\prime }\left(x_m\right)-{\displaystyle \frac{1}{2}}{\xi }^{\prime }{\left(x_m\right)}^{-1}{\xi }^{″}\left(x_m\right)\xi \left(x_m\right)\right](y_m-x_m)\hfill \\ \hfill & +{\xi }^{\prime }\left(x_m\right)(x_{m+1}-x_m)\hfill \\ \hfill & =\xi \left(x_{m+1}\right)-\xi \left(x_m\right)-{\xi }^{\prime }\left(x_m\right)(x_{m+1}-x_m)\hfill \\ \hfill & +{\xi }^{\prime }\left(x_m\right)(x_{m+1}-y_m)+{\displaystyle \frac{1}{2}}{\xi }^{\prime }{\left(x_m\right)}^{-1}{\xi }^{\prime }\left(x_m\right)\xi \left(x_m\right)(y_m-x_m)\hfill \end{array}$$

(65)

leading to

$$\begin{array}{cc}\hfill \parallel L^{-1}\xi \left(x_{m+1}\right)\parallel & \le {\mathit{\int }}_0^{1}v\left((1-\phi )({\tau }_{m+1}-{\tau }_m)\right)d\phi ({\tau }_{m+1}-{\tau }_m)\hfill \\ \hfill & +(1+v_0\left({\tau }_m\right))({\tau }_{m+1}-{\mu }_m)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\nu }_1\left({\tau }_m\right)({\mu }_m-{\tau }_m)}{1-v_0\left({\tau }_m\right)}}={\chi }_{m+1}.\hfill \end{array}$$

(66)

The iterate $y_{m+1}$ is well defined by (64) and we can write

$$\begin{array}{cc}\hfill \parallel y_{m+1}-x_{m+1}\parallel & \le \parallel T_{m+1}^{-1}L\parallel \parallel L^{-1}\xi \left(x_{m+1}\right)\parallel \hfill \\ \hfill & \le {\displaystyle \frac{{\chi }_{m+1}}{1-{\overline{q}}_{m+1}}}={\mu }_{m+1}-{\tau }_{m+1}\hfill \end{array}$$

(67)

and

$$\begin{array}{cc}\hfill \parallel y_{m+1}-x_0\parallel & \le \parallel y_{m+1}-x_{m+1}\parallel +\parallel x_{m+1}-x_0\parallel \hfill \\ \hfill & \le {\mu }_{m+1}-{\tau }_{m+1}+{\tau }_{m+1}-{\tau }_0={\mu }_{m+1}<{\tau }^{*}.\hfill \end{array}$$

(68)

By (57), (58), (63), (64), (67) and (68), the induction for assertions (48)–(50) is completed, and all iterates $z_m,y_m,x_m\in S(x_0,x^{*}).$ Notice that the sequence $\left\{{\tau }_m\right\}$ is Cauchy and convergent by the condition ($T_3$). Thus, by(48)–(50) and

$$\parallel x_{m+1}-x_m\parallel \le {\tau }_{m+1}-{\tau }_m,$$

(69)

the sequence $\left\{x_m\right\}$ is also Cauchy in the Banach space B. Hence, there exists $x^{*}\in S[x_0,x^{*}]$ such that

$$\underset{m\to +\infty }{lim}{x}_m=x^{*}.$$

(70)

Moreover, by letting $m\to \infty$ in (66) and using the continuity of the operator $\xi$, we deduce that $\xi \left(x^{*}\right)=0$.

If $j=0,1,2,\dots$, estimate (69) and the triangle inequality give

$$\parallel x_{m+j}-x_m\parallel \le {\tau }_{m+j}-{\tau }_m.$$

(71)

Finally, by letting $j\to \infty$ in (71), we show (47).  □

Next, a region is specified containing only one solution of the equation $\xi \left(x\right)=0$.

Proposition 2.

Suppose that there exists a solution $\overline{z}\in S(x_0,{\delta }_0)$ of the equation $\xi \left(x\right)=0$ for some $\delta >0$; the condition $\left(T_4\right)$ holds in the ball $S(x_0,\delta )$ and there exists ${\delta }_1\ge {\delta }_0$ such that

$${\mathit{\int }}_0^1{v}_0\left((1-\phi ){\delta }_0+\phi {\delta }_1\right)d\phi <1.$$

(72)

Set $M_3=\mathrm{\Omega }\cap S[x_0,{\delta }_1]$.

Then, the only solution of the equation $\xi \left(x\right)=0$ in the region $M_3$ is ${\overline{z}}_0$.

Proof. 

Suppose there exists $\tilde{z}\in M_3$ such that $\xi \left(\tilde{z}\right)=0$ and $\tilde{z}\ne \overline{z}$. Define the linear operator

$$L_2={\mathit{\int }}_0^1{\xi }^{\prime }\left(\overline{z}+\phi (\tilde{z}-\overline{z})\right)d\phi .$$

(73)

Then, it follows by the condition $\left(T_4\right)$ and (72) that

$$\parallel L_1^{-1}(L_2-L)\parallel \le {\mathit{\int }}_0^1{v}_0\left((1-\phi )\parallel \overline{z}-x_0\parallel +\phi \parallel \tilde{z}-x_0\parallel \right)d\phi$$

(74)

$$\le {\mathit{\int }}_0^1{v}_0\left((1-\phi ){\delta }_0+\phi {\delta }_1\right)d\phi <1.$$

(75)

So, the linear operator $L_2$ is invertible. Finally, from the identity

$$\tilde{z}-\overline{z}=L_2^{-1}(\xi \left(\tilde{z}\right)-\xi \left(\overline{z}\right))=L_2^{-1}\left(0\right)=0,$$

(76)

we conclude that $\tilde{z}=\overline{z}$.  □

Remark 4.

(i) 

The efficiency of an iterative method depends on the closeness of the starting point to the solution, i.e., on how small $\parallel T_0^{-1}\xi \left(x_0\right)\parallel$ should be. In the condition $\left(T4\right)$ we used this quantity to define the first nonzero number which helps generate the majorizing sequence for the sequence (see (38)). Then, in condition $\left(T1\right)$ we determine the upper bound $r_0$ of this sequence by simply solving a scalar equation. Then, in the condition $\left(T3\right)$ we provide sufficient convergence ensuring the majorizing sequence is nondecreasing. This fact together with the upper bound $r_0$ guarantee the convergence of the majorizing sequence and consequently that of $\left\{x_n\right\}$.

(ii) 

The limit point $r^{*}$ can be replaced in the condition $\left(T_6\right)$ by $r_0$.

(iii) 

Under all the conditions $\left(T_1\right)$–$\left(T_6\right)$, one can choose $\tilde{z}=x^{*}$ and $r_1=r^{*}$ in the Proposition 2.

3. Numerical Experiments

We present several numerical problems and their solutions using the iterative scheme discussed earlier. Each problem illustrates a different approach to solving nonlinear equations through the application of the proposed method. The calculations are based on different mathematical models, each demonstrating the practical application of the theory presented in the earlier sections. To compare the iterative scheme with other existing methods, we used three well-known numerical methods to solve nonlinear equations. The performance of each method was evaluated on the basis of comparison of the radii of the convergence balls. The three existing methods used for comparison are denoted by HM, PCNM, and DJNM and can be found in [10,19,20]; respectively. For the numerical experiments presented in this section, the effectiveness of the proposed ninth-order iterative scheme (4) has been evaluated by comparing its radii of convergence with existing methods for different non-linear problems.

Problem 1.

Let $B_i=B={\mathbb{R}}^3$ and $\mathrm{\Omega }=S_{(0,1)}$. Define the mapping $\xi :\mathrm{\Omega }\to {\mathbb{R}}^3$ for $a={(a_1,a_2,a_3)}^{tr}$ as

$$\xi \left(a\right)={\left(a_3,{\displaystyle \frac{e-1}{2}}{a}_2^2+a_2,e^{a_1}-1\right)}^{tr}.$$

(77)

It follows by this definition that the Jacobian ${\xi }^{\prime }$ is given by

$${\xi }^{\prime }\left(a\right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& (e-1)a_2+1& 0\\ 0& 0& e^{a_1}\end{array}\right].$$

(78)

Notice that by (77) and (78), $a^{*}=(0,0,0)$ solves the equation $\xi \left(a\right)=0$ and ${\xi }^{\prime }\left(a^{*}\right)=I$. Moreover, the conditions $\left(E_1\right)-\left(E_8\right)$ hold if

$$s_0={\displaystyle \frac{1}{e-1}},{\kappa }_0\left(t\right)=(e-1)t,\kappa \left(t\right)=e^{-t}t$$

(79)

and

$${\kappa }_1\left(t\right)=e^{-t}\left(1+{\displaystyle \frac{e-1}{2}}t\right)t.$$

(80)

Then, calculate the $R^{*}$ using equation (8) as

$$R^{*}=0.229452.$$

(81)

The radii of the proposed scheme (4) and the other three methods taken for comparison are given in Table 1.

Table 1. Estimates of radii for Problem 1 using (4) and other three methods taken for comparison.

Radii	${\mathit{R}}_1$	${\mathit{R}}_2$	${\mathit{R}}_3$	$\mathit{R}=min\left\{{\mathit{R}}_{\mathit{i}}\right\}$
Scheme (4)	0.229452	0.264277	0.246246	0.21314
HM [10]	0.508853	0.591459	0.278050	0.278050
PCNM [19]	0.479901	0.479901	0.479869	0.479869
DJNM [20]	0.766228	0.766228	0.585308	0.585308

Table 1. Estimates of radii for Problem 1 using (4) and other three methods taken for comparison.

Radii	${\mathit{R}}_1$	${\mathit{R}}_2$	${\mathit{R}}_3$	$\mathit{R}=min\left\{{\mathit{R}}_{\mathit{i}}\right\}$
Scheme (4)	0.229452	0.264277	0.246246	0.21314
HM [10]	0.508853	0.591459	0.278050	0.278050
PCNM [19]	0.479901	0.479901	0.479869	0.479869
DJNM [20]	0.766228	0.766228	0.585308	0.585308

For Problem 1 (Table 1), the proposed iterative scheme (4) yielded radii values of $R_1=0.229452,R_2=0.264277$, and $R_3=0.246246$, with a minimum radius of $R=0.21314$. Compared to the HM method ($R=0.278050$), and the PCNM and DJNM methods (around $0.479869$ and $0.585308$, respectively), the scheme (4) demonstrated competitive performance, with smaller radii indicating potentially faster convergence.

Problem 2.

Let $\mathrm{\Omega }=U[0,1]$ and ${\mathbb{B}}_{\infty }=\mathbb{B}=C[0,1]$. Let $\mathcal{H}$ be a Hammerstein operator. We study the nonlinear integral equation of the first kind associated with $\mathcal{H}$, where $\mathcal{H}$ is defined by

$$\mathcal{H}\left(u\right)\left(x\right)=u\left(x\right)-7{\mathit{\int }}_0^{1}x\lambda u{\left(\lambda \right)}^{3}d\lambda .$$

(82)

The calculation for the derivative gives

$${\mathcal{H}}^{\prime }\left(u\left(q\right)\right)\left(x\right)=q\left(x\right)-21{\mathit{\int }}_0^{1}x\lambda u{\left(\lambda \right)}^{2}q\left(\lambda \right)d\lambda ,$$

(83)

for $q\in C[0,1]$. By this value of the operator ${\mathcal{H}}^{\prime }$, the conditions $\left(E_1\right)$–$\left(E_8\right)$ are verified so that we choose

$$\begin{array}{cc}\hfill {\kappa }_0\left(t\right)& =10.5t,{\kappa }_1\left(t\right)=1+10.5t,{\kappa }_2=21t.\hfill \end{array}$$

In Table 2, we present the radii of the iterative scheme (4) and the other three methods taken for comparison for Problem 2.

Table 2. Estimates of radii for Problem 2 using (4) and the other three methods taken for comparison.

Radii	${\mathit{R}}_1$	${\mathit{R}}_2$	${\mathit{R}}_3$	$\mathit{R}=min\left\{{\mathit{R}}_{\mathit{i}}\right\}$
Scheme (4)	0.999994	0.563769	0.578072	0.563769
HM [10]	0.333405	0.436717	0.939975	0.333405
PCNM [19]	0.999997	0.139438	0.381371	0.139438
DJNM [20]	0.001004	0.001004	0.180887	0.001004

Table 2. Estimates of radii for Problem 2 using (4) and the other three methods taken for comparison.

Radii	${\mathit{R}}_1$	${\mathit{R}}_2$	${\mathit{R}}_3$	$\mathit{R}=min\left\{{\mathit{R}}_{\mathit{i}}\right\}$
Scheme (4)	0.999994	0.563769	0.578072	0.563769
HM [10]	0.333405	0.436717	0.939975	0.333405
PCNM [19]	0.999997	0.139438	0.381371	0.139438
DJNM [20]	0.001004	0.001004	0.180887	0.001004

In Problem 2 (Table 2), the radii for the proposed scheme were $R_1=0.999994,R_2=0.563769$, and $R_3=0.578072,$ with a minimum radius of $R=0.563769$. In contrast, the HM method had a radius of $R=0.333405$, PCNM showed a smaller radius of $R=0.139438$, and DJNM provided a radius of $R=0.001004$, suggesting that the DJNM method might offer faster convergence for this specific problem.

Problem 3.

Let $B_i=B={\mathbb{R}}^2$ and $\mathrm{\Omega }=S_{(0,1)}$. Define the mapping $\xi :\mathrm{\Omega }\to {\mathbb{R}}^2$ for $a={(a_1,a_2)}^{tr}$ as

$$\xi \left(a\right)={\left(sin{a}_1,{\displaystyle \frac{1}{3}}(e^{a_2}+2a_2-1)\right)}^{tr}.$$

(84)

It follows by this definition that the Jacobian ${\xi }^{\prime }$ is given by

$${\xi }^{\prime }\left(a\right)=\left[\begin{array}{cc}cos{a}_1& 0\\ 0& {\displaystyle \frac{1}{3}}(e^{a_2}+2)\end{array}\right].$$

(85)

Notice that by (84) and (85), $a^{*}=(0,0)$ solves the equation $\xi \left(a\right)=0$ and ${\xi }^{\prime }\left(a^{*}\right)=I$. Moreover, the conditions $\left(E_1\right)-\left(E_8\right)$ hold.

$${\kappa }_0\left(t\right)=t,\kappa \left(t\right)=1$$

(86)

and

$${\kappa }_1\left(t\right)=\left(1+{\displaystyle \frac{1}{2}}t\right)t.$$

(87)

Calculating the $R^{*}$ using equation (8), we obtain

$$R^{*}=0.001006.$$

(88)

The radii for the iterative scheme (4) and the other three methods taken for comparison are given in Table 3 as follows.

Table 3. Estimates of radii for Problem 3 using (4) and the other three methods taken for comparison.

Radii	${\mathit{R}}_1$	${\mathit{R}}_2$	${\mathit{R}}_3$	$\mathit{R}=min\left\{{\mathit{R}}_{\mathit{i}}\right\}$
Scheme (4)	0.001006	0.682127	0.683738	0.001006
HM [10]	0.001006	0.776006	0.824589	0.001006
PCNM [19]	0.666666	0.666668	0.605945	0.605945
DJNM [20]	0.001004	0.001005	0.780583	0.001004

Table 3. Estimates of radii for Problem 3 using (4) and the other three methods taken for comparison.

Radii	${\mathit{R}}_1$	${\mathit{R}}_2$	${\mathit{R}}_3$	$\mathit{R}=min\left\{{\mathit{R}}_{\mathit{i}}\right\}$
Scheme (4)	0.001006	0.682127	0.683738	0.001006
HM [10]	0.001006	0.776006	0.824589	0.001006
PCNM [19]	0.666666	0.666668	0.605945	0.605945
DJNM [20]	0.001004	0.001005	0.780583	0.001004

For Problem 3 (Table 3), the radii for the iterative scheme (4) were $R_1=0.001006,R_2=0.682127$, and $R_3=0.683738$, with a minimum radius of $R=0.001006$, indicating excellent performance and high efficiency in solving the nonlinear system in Problem 3. The HM method yielded $R=0.001006$, PCNM had $R=0.605945$, and DJNM was similar to HM with $R=0.001004$. Overall, the proposed iterative scheme (4) achieved smaller radii of convergence in Problems 1 and 3, suggesting its potential to outperform other methods when smaller radii are crucial. However, for certain cases such as Problem 2, the DJNM method appeared to provide faster convergence, highlighting that the optimal method may be context-dependent based on the specific characteristics of the problem.

Problem 4.

Consider the problem where $B_1=B_2=\mathrm{\Omega }=\mathbb{R}$, and let $x={({\eta }_1,{\eta }_2,\dots ,{\eta }_j)}^{tr}$. We define a logarithmic operator as follows:

$$\xi \left(x\right)=ln(1+{\eta }_k)-{\displaystyle \frac{k}{20}},k=1,2,\dots ,j,$$

(89)

and consider the nonlinear system $\xi \left(x\right)=0$. Setting $j=100$ and using an initial guess of $x_0={(0.5,0.5,\dots ,0.5)}^{tr}$, the application of scheme (4) converges to the solution $x^{*}={(1,1,\dots ,1)}^{tr}$ in three iterations.

Problem 5.

Let $X=Y={\mathbb{R}}^n$, where $n=2$ is a natural integer. Both X and Y are equipped with the norm $|·|$, and for a matrix A, we define $\left|A\right|={max}_{1\le i\le n}{\sum }_{j=1}^n\left|a_{ij}\right|$.

Consider the two-point boundary value problem:

$$u^{″}+u^2=0,$$

(90)

on the interval $[0,1]$, subject to the boundary conditions:

$$u\left(0\right)=u\left(1\right)=0.$$

To discretize this equation, we divide the interval $[0,1]$ into m equal parts, each of length $h={\displaystyle \frac{1}{m}}$, and define the coordinates of the points as $x_i=ih$ for $i=0,1,2,\dots ,m$. A second-order finite difference discretization of Equation (90) leads to the following system of nonlinear equations:

$$\xi \left(u\right)=\left\{\begin{array}{cc}{u}_{i-1}-2u_i+u_{i+1}+h^2{u}_i^2=0\hfill & \mathrm{for}i=1,2,\dots ,m-1u_0=u_m=0,\hfill \end{array}\right.$$

where $u={[u_1,u_2,\dots ,u_{m-1}]}^{tr}$. The Frechet derivative of this system is given by:

$${\xi }^{\prime }\left(u\right)=\left(\begin{array}{ccccccc}{\displaystyle \frac{2u_1}{m^2}}-2& 1& 0& 0& \dots & 0& 0\\ 1& {\displaystyle \frac{2u_2}{m^2}}-2& 1& 0& \dots & 0& 0\\ 0& 1& {\displaystyle \frac{2u_3}{m^2}}-2& 1& \dots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& \dots & ⋮& ⋮\\ 0& 0& 0& 0& \dots & 1& {\displaystyle \frac{2u(m-1)}{m^2}}-2\end{array}\right).$$

(91)

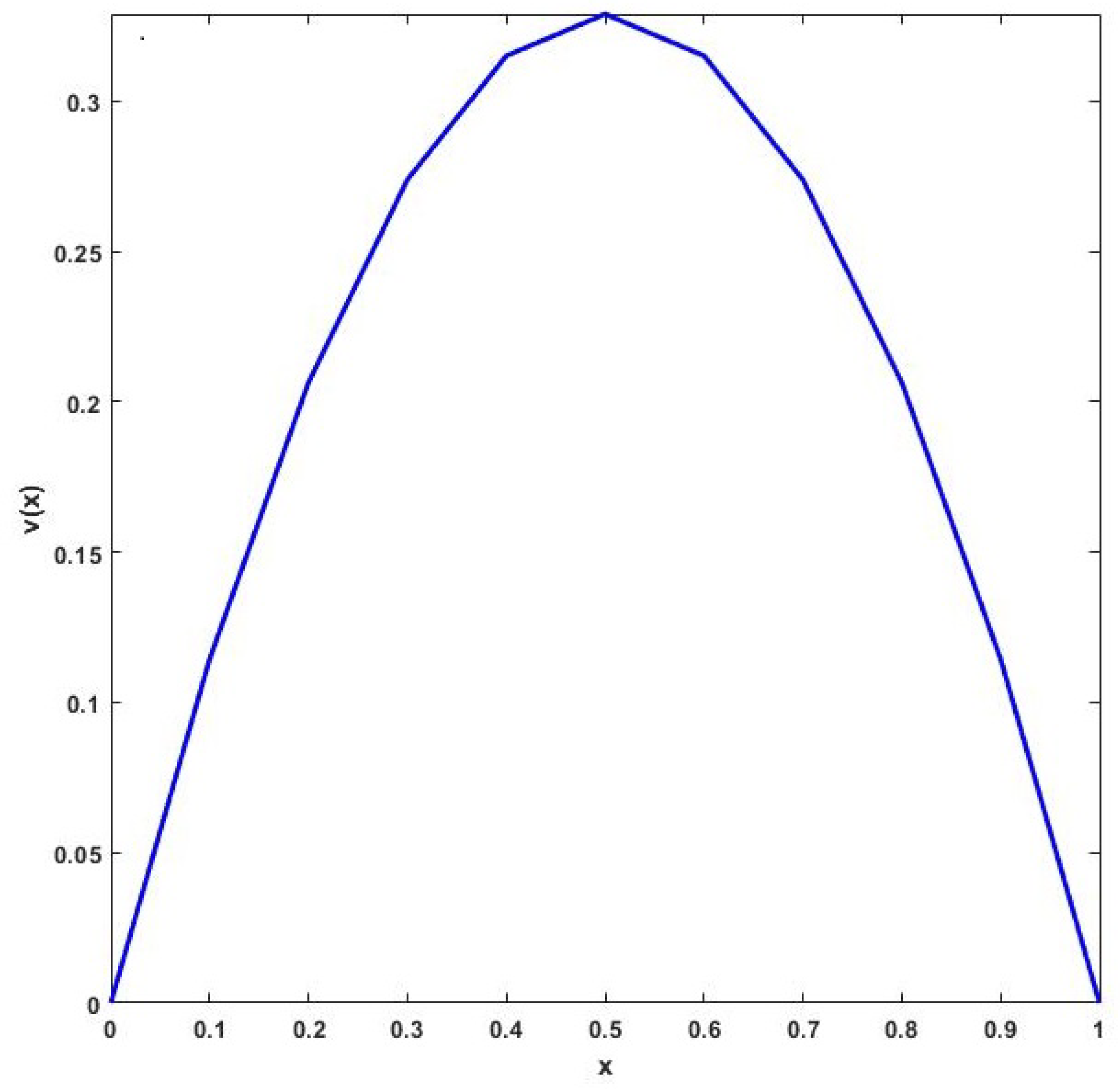
Let $m=101$, $x={[5,5,\dots ,5]}^{tr}$, and $\theta =1$. To solve the system (Steps 1, 2, and 3 in the iterative scheme), the MATLAB R2024b routine linsolve, which uses LU factorization with partial pivoting, is employed. Figure 1 plots the numerical solution.

Figure 1. Solution for the Bratu’s Problem 5.

4. Conclusions and Future Remarks

A comprehensive investigation of the abstract convergence analysis of a ninth-order iterative scheme is presented within the framework of Banach spaces. Unlike traditional approaches relying on Taylor series expansions, this study establishes generalized convergence criteria using only first-order derivatives. This operator-based analysis provides a novel perspective on the convergence behavior of iterative processes. By avoiding the use of higher-order derivatives, which may not exist or be readily available, this methodology overcomes limitations of previous research, thereby expanding the applicability of the scheme beyond conditions stipulated by earlier findings. The theoretical analysis is substantiated through numerical examples. Importantly, the analytical techniques employed can be adapted and applied to other iterative schemes, enhancing their versatility. Future research may extend the proposed ninth-order scheme to systems of nonlinear equations and explore its performance under weaker smoothness assumptions. Further research into its behavior in infinite-dimensional Banach spaces, as well as its resilience to noisy or inexact data, is needed to improve its practical application. Our technique shall be employed to extend other iterative schemes in future works [9,11,12,14,15,16,21,22].