Sharp Coefficient Bounds for Analytic Functions Related to Bounded Turning Functions

Abstract

Let $\mathfrak{B}$ denote the class of bounded turning functions $\mathcal{F}$ analytic in the open unit disk, where the image of ${\mathcal{F}}^{\prime }\left(z\right)$ is contained in the domain $\Omega \left(z\right)=\cosh z+{\displaystyle \frac{2z}{2-z^2}}$. This article determines sharp coefficient bounds, a Fekete–Szegö-type inequality, and second- and third-order Hankel determinants for functions in the class $\mathfrak{B}$. Additionally, we obtain sharp Krushkal and Zalcman functional-type inequalities related to the logarithmic coefficient for functions belonging to $\mathfrak{B}$.

1. Introduction and Preliminaries

Let $\mathcal{A}$ denote the class of normalized analytic functions in the open unit disk

$$\begin{array}{c}\hfill \mathbb{E}=\left\{z\in \mathbb{C}:\left|z\right|<1\right\}\end{array}$$

with the series expansion:

$$\mathcal{F}\left(z\right):=z+\sum _{j=2}^{\infty }{b}_j{z}^j.$$

(1)

Also, let $\mathcal{S}$ denote the subclass of $\mathcal{A}$ consisting of univalent functions in $\mathbb{E}$. For the functions $\mathcal{F}\mathrm{and}\mathcal{G}$ that are members of $\mathcal{A}$, we say that the function $\mathcal{F}$ is subordinate to $\mathcal{G}$ and write $\mathcal{F}\prec \mathcal{G}$ if there is a function $k\left(z\right)$, analytic in $\mathbb{E}$ with $k\left(0\right)=0\mathrm{and}\left|k\right(z\left)\right|<1$, such that $\mathcal{F}\left(z\right)=\mathcal{G}\left(k\right(z\left)\right).$ In particular, if the function $\mathcal{G}$ is univalent, then $\mathcal{F}\prec \mathcal{G}$ if and only if $\mathcal{F}\left(0\right)=\mathcal{G}\left(0\right)\mathrm{and}\mathcal{F}\left(\mathbb{E}\right)\subset \mathcal{G}\left(\mathbb{E}\right)$ (see [1]).

Among the various subclasses of $\mathcal{S}$, the classes of starlike, convex, and bounded turning functions have garnered the most attention. Ma and Minda [2] introduced several classes of convex and starlike functions, including

$$\begin{array}{cc}\hfill \mathcal{C}\left(\varphi \right)& :=\left\{\mathcal{F}\in \mathcal{A}:1+{\displaystyle \frac{z{\mathcal{F}}^{″}\left(z\right)}{{\mathcal{F}}^{\prime }\left(z\right)}}\prec \varphi \left(z\right)\right\},\hfill \\ \hfill {\mathcal{S}}^{*}\left(\varphi \right)& :=\left\{\mathcal{F}\in \mathcal{A}:{\displaystyle \frac{z{\mathcal{F}}^{\prime }\left(z\right)}{\mathcal{F}\left(z\right)}}\prec \varphi \left(z\right)\right\}\hfill \\ \hfill \mathrm{and}\mathcal{R}\left(\varphi \right)& :=\left\{\mathcal{F}\in \mathcal{A}:{\mathcal{F}}^{\prime }\left(z\right)\prec \varphi \left(z\right)\right\}.\hfill \end{array}$$

Also, they have investigated a more general analytic function $\varphi$, with the positive real part in $\mathbb{E}$, that maps the unit disc $\mathbb{E}$ onto starlike regions concerning 1, which are symmetric for the real axis and normalized by the conditions $\varphi \left(0\right)=1\mathrm{and}{\varphi }^{\prime }\left(0\right)>0.$ To obtain a suitable choice of image domains of $\varphi$, one can obtain the subfamilies of $\mathcal{C}\mathrm{and}{\mathcal{S}}^{*}.$ By taking $\varphi \left(z\right)=\sqrt{1+z}$, the class ${\mathcal{S}}^{*}$ that reduces, respectively, to the class ${\mathcal{S}}_L^{*}={\mathcal{S}}^{*}\left(\sqrt{1+z}\right)$ is related to the right half of the lemniscate of Bernoulli and was studied by Sokol and Stankiewicz [3]. By taking $\varphi \left(z\right)={\displaystyle \frac{1+Az}{1+Bz}}(-1\le B<A\le 1),$ the class ${\mathcal{S}}^{*}$ reduces, respectively, to the class ${\mathcal{S}}^{*}[A,B]$, whereby the class of Janowski starlike and convex functions was studied by Janowski [4]. In 2016, Sharma et al. [5] considered the class of starlike functions bounded by the cardioid domain for $\varphi \left(z\right)=1+{\displaystyle \frac{4}{3}}z+{\displaystyle \frac{2}{3}}{z}^2$. In 2021, Wani and Swaminathan [6] studied the class of starlike and convex functions bounded by the nephroid domain. For the function $\varphi \left(z\right)$, which maps the unit disk onto a cardioid domain, the class ${\mathcal{S}}^{*}\left(\varphi \right)$ reduces to class ${\mathcal{S}}_{\mathcal{C}}^{*}$, respectively, which was investigated by Sivaprasad Kumar and Kamaljeet [7]. In 2014, Mendiratta et al. [8] studied the subclass of ${\mathcal{S}}^{*}$ related to the interior of the left-half of the shifted lemniscate of Bernoulli, such as

$$\begin{array}{c}\hfill {\mathcal{S}}_{RL}^{*}={\mathcal{S}}^{*}\left(\sqrt{2}-(\sqrt{2}-1){\left({\displaystyle \frac{1-z}{1+2(\sqrt{2}-1)z}}\right)}^{{\displaystyle \frac{1}{2}}}\right).\end{array}$$

Similarly, in 2015, Mendiratta et al. [9] investigated the subclass of ${\mathcal{S}}^{*}$ associated with the exponential function, such as ${\mathcal{S}}_e^{*}={\mathcal{S}}^{*}\left(e^z\right).$ Recently, many subclasses of ${\mathcal{S}}^{*}$ are extensively investigated in the literature (see [10,11,12]), such as the following:

• ${\mathcal{S}}_M^{*}={\mathcal{S}}^{*}\left((1+z)/\left(1-(M-1)/M\right)z)\right)(M>{\displaystyle \frac{1}{2}})$;
• $\mathcal{M}\left(\beta \right)={\mathcal{S}}^{*}((1+(1-2\beta )z)/(1-z))(\beta >1)$;
• ${\mathcal{S}}^{*}[A,B]={\mathcal{S}}^{*}\left[{\displaystyle \frac{1+Az}{1+Bz}}\right](-1\le B<A\le 1)$ (see [13]).

Recently, in 2021, Sivaprasad Kumar and Kamaljeet [7] introduced and studied a class of starlike functions ${\mathcal{S}}^{*}$, where the image domain of $\varphi \left(z\right)$ is bounded by a cardiod (see also [14]).

For this purpose, we consider the analytic function $\varphi :\mathbb{E}\to \mathbb{C}$ satisfying the following:

• $\varphi \left(z\right)$ is univalent with $\Re \left(\varphi \right)>0$;
• $\varphi \left(\mathbb{E}\right)$ is starlike with respect to $\varphi \left(0\right)=1$;
• $\varphi \left(\mathbb{E}\right)$ is symmetric about the real axis;
• ${\varphi }^{\prime }\left(0\right)>0$.

Let $\Omega \left(z\right):\mathbb{E}\to \mathbb{C}$ be defined by

$$\begin{array}{c}\hfill \Omega \left(z\right)=\cosh z+{\displaystyle \frac{2z}{2-z^2}},\end{array}$$

where $\Omega \left(z\right)$ satisfies all the aforementioned properties (Figure 1).

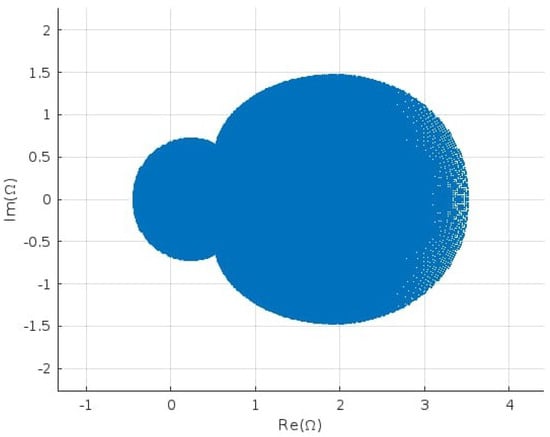
Figure 1. Image of $\Omega \left(z\right)=\cosh z+{\displaystyle \frac{2z}{2-z^2}}$ under a unit disk.

Remark 1. 

The function $\Omega \left(z\right)$ is analytic in $\mathbb{E}$, and can be written as

$$\Omega \left(z\right)=\cosh z+{\displaystyle \frac{2z}{2-z^2}}=1+z+{\displaystyle \frac{z^2}{2}}+{\displaystyle \frac{z^3}{2}}+{\displaystyle \frac{z^4}{4!}}+\cdots .$$

This power series with real and positive coefficients converges absolutely in $\mathbb{E}$. $\Re (\Omega (z\left)\right)$ is harmonic on $\mathbb{E}$ since it is the real part of an analytic function. Moreover, $\Re (\Omega (0\left)\right)=\Omega \left(0\right)=1>0,$ and $\Omega \left(z\right)$ is not constant. By the minimum principle for harmonic functions, since $\Re (\Omega (0\left)\right)$ is harmonic, positive at a point, and not constant, it follows that

$$\Re (\Omega (z\left)\right)>0,z\in \mathbb{E}.$$

The study of coefficient problems in the fundamental class $\mathcal{S}$ is motivated by the geometric properties of their image domains. In the early 1970s, Lawrence Zalcman proposed a conjecture, now famously known as the Zalcman conjecture, which states that if $\mathcal{F}\in \mathcal{S}$ and is given by

$$|a_n^2-a_{2n-1}|\le {(n-1)}^2(n\ge 2)$$

with equality only for the Koebe function $K\left(z\right)=z/{(1-z)}^2$ or its rotations, then the Zalcman conjecture implies the Bieberbach conjecture, $|a_n|\le n$. Bieberbach proved the Zalcman conjecture for $n=2$. Recently, numerous researchers have investigated sharp bounds for the Zalcman functional, defined as $|b_2{b}_3-b_4|$, for various subclasses of functions, including convex, starlike, close-to-convex, and bounded turning functions (see [15,16,17]).

Pommerenke (see [18,19]) considered Hankel determinants ${\mathfrak{H}}_{k,d}$ of univalent functions, with coefficients of the function $\mathcal{F}$ in subclass $\mathcal{S}$ and introduced for $k,d\in \mathbb{N}$ as follows:

$${\mathfrak{H}}_{k,d}\left(\mathcal{F}\right)=\left|\begin{array}{cccc}{b}_d& b_{d+1}& \cdots & b_{d+k-1}\\ b_{d+1}& b_{d+2}& \cdots & b_{d+1}\\ b_{d+2}& b_{d+3}& \cdots & b_{d+k+1}\\ ⋮& ⋮& \ddots & ⋮\\ b_{d+k-1}& b_{d+k}& \cdots & b_{d+2(k-1)}\end{array}\right|.$$

Hankel determinants play a crucial role in investigating the coefficients of analytic functions within various classes of functions, with far-reaching implications across multiple mathematical disciplines. For a comprehensive overview of their applications, see [20]. Numerous studies have explored sharp bounds for various function classes. Interested readers can find a wealth of information in the existing literature and references cited therein (see [21,22,23,24,25]). Notably, we refer the reader to $k=2$ and $d=1$, and the functional

$${\mathfrak{H}}_{2,1}\left(\mathcal{F}\right)=|b_3-b_2^2|$$

is commonly referred to as the Fekete–Szegö functional. The maximum value of $|{\mathfrak{H}}_{2,1}\left(f\right)|$ was found for a class $\mathcal{S}$ in 1933. Many researchers looked into the maximum value of $|{\mathfrak{H}}_{2,1}\left(f\right)|$ for different subclasses of class $\mathcal{A}$; for more information, see [26,27,28,29,30]. Additionally, for $k=2$ and $d=2$, the second Hankel determinant is

$${\mathfrak{H}}_{2,2}\left(\mathcal{F}\right)=|b_2{b}_4-b_3^2|.$$

Several authors have examined the upper bound of ${\mathfrak{H}}_{2,2}\left(\mathcal{F}\right)$. For example, the works of Hayman [31], Noonan and Thomas [32], Janteng et al. [33], and Orhan et al. [34] are worthy of reading. The determinant

$${\mathfrak{H}}_{3,1}\left(\mathcal{F}\right)=b_5(b_3-b_2^2)-b_4(b_4-b_2{b}_3)+b_3(b_2{b}_4-b_3^2)$$

is known as the third-order Hankel determinant. The upper bound of ${\mathfrak{H}}_{3,1}\left(\mathcal{F}\right)$ for a subclass of $\mathcal{S}$ was initially studied by Babalola [35]. Readers are encouraged to consult the work of various researchers, including Zaprawa [36], Raza et al. [37], Cho et al. [38], Lecko et al. [39], and Srivastava et al. [40], for additional information on this subject.

Motivated by the aforementioned works, we introduce the class of bounded turning functions and derive coefficient bounds for functions in the class $\mathfrak{B}$ that satisfy a given differential subordination implication. Furthermore, we identify extremal functions that render our results sharp for functions $\mathcal{F}\in \mathfrak{B}$. As applications of these findings, we establish the Fekete–Szegö inequality and determine the Zalcman functional.

Let $\mathcal{P}$ be the class analytic function $p\in \mathcal{P}$ with a positive real part and $p\left(0\right)=1.$ Thus, every $p\in \mathcal{P}$ can be represented by

$$p\left(z\right):=1+\sum _{n=1}^{\infty }{c}_n{z}^n,$$

(2)

which is also known as a Carathéodory function. This class of functions play a significant role in geometric function theory, particularly for the bound of Hankel determinants. In 1983, Duren [41] examined its coefficient bounds such as $c_n\le 2$.

The following lemmas are essential for establishing the main results of this paper.

Lemma 1 

(See [42,43]). If $p\in \mathcal{P}$ has the form (2), then

$$|c_{n+k}-\mu c_n{c}_k|\le 2\hspace{1em}(0<\mu \le 1),$$

(3)

$$\left|c_n\right|\le 2 \mathit{for}n\ge 1,$$

(4)

$$|c_2-\varsigma c_1^2|\le 2max\{1,|2\varsigma -1\left|\right\}(\varsigma \in \mathbb{C}),$$

(5)

$$|\mathcal{J}{c}_1^3-\mathcal{K}{c}_1{c}_2+\mathcal{L}{c}_3|\le 2\left|\mathcal{J}\right|+|\mathcal{K}-2\mathcal{J}|+2|\mathcal{J}-\mathcal{K}+\mathcal{L}|,$$

(6)

where $\mathcal{J},\mathcal{K}$ and $\mathcal{L}$ are real numbers.

Lemma 2 

(See [44]). If $p\in \mathcal{P}$ has the form (2) with $c_1\ge 0$, then

$$2c_2=c_1^2+\beta (4-c_1^2),$$

(7)

$$4c_3=c_1^3+2(4-c_1^2)c_1\beta -c_1(4-c_1^2){\beta }^2+2(4-c_1^2){(1-|\beta |}^2)\eta ,$$

(8)

$$\begin{array}{cc}\hfill 8c_4=& c_1^4+(4-c_1^2)\beta [c_1^2({\beta }^2-3\beta +3)+4\beta ]-4(4-c_1^2)({1-\left|\beta \right|}^2)\hfill \\ & [c_1(\beta -1)\eta +\overline{\beta }{\eta }^2{-(1-|\eta |}^2\left)k\right]\hfill \end{array}$$

(9)

for some $\beta ,\eta ,k\in \overline{\mathbb{E}}:=\{z\in \mathbb{C}:|z|\le 1\}.$

Lemma 3 

(See [45]). If $p\in \mathcal{P}$ has the form (2) and $\vartheta \in \mathbb{C}$, then

$$|c_n-\vartheta c_k{c}_{n-k}| \le 2max\{1,|2\vartheta -1|\}$$

(10)

for all $1\le k\le n-1.$

Lemma 4 

(See [46]). Suppose that $p\in \mathcal{P}$ has the form (2). If $\mathfrak{R}(2\mathfrak{R}-1)\le \mathfrak{S}\le \mathfrak{R},$ then

$$|c_3-2\mathfrak{R}{c}_1{c}_2+\mathfrak{S}{c}_1^3|\le 2.$$

Lemma 5 

(See [2]). Suppose $p\in \mathcal{P}$ has the form (2), then

$$\begin{array}{c}\hfill |c_2-\varkappa c_1^2|\le \left\{\begin{array}{cc}-4\varkappa +2,\hfill & if \varkappa <0\hfill \\ 2,\hfill & if 0\le \varkappa \le 1\hfill \\ 4\varkappa -2,\hfill & if \varkappa >1.\hfill \end{array}\right.\end{array}$$

The organization of this paper is as follows: Section 1 introduces fundamental definitions and lemmas crucial for proving the main results in subsequent sections. We define the class $\mathfrak{B}$ and estimate sharp coefficient bounds for $b_2,b_3,b_4$ and $b_5$, as well as sharp bounds for the Fekete–Szegö inequality and second and third Hankel determinants for the functions in $\mathfrak{B}$ in Section 2. In Section 3, we investigate the sharp bounds and logarithmic coefficient inequalities for the class $\mathfrak{B}$. This paper is finally concluded with closing remarks in Section 4.

2. Coefficient Bounds, Fekete–Szegö Inequality and Hankel Determinants

We now consider a subfamily of bounded turning functions defined by

$$\begin{array}{c}\hfill \mathfrak{B}:=\left\{\mathcal{F}\in \mathcal{A}:{\mathcal{F}}^{\prime }\left(z\right)\prec \Omega \left(z\right)=\cosh z+{\displaystyle \frac{2z}{2-z^2}},z\in \mathbb{E}\right\}.\end{array}$$

Firstly, we determine the sharp coefficient bounds for functions in the class $\mathfrak{B}$.

Theorem 1. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$\begin{array}{c}|b_2|\le {\displaystyle \frac{1}{2}},\hfill \\ |b_3|\le {\displaystyle \frac{1}{3}},\hfill \\ |b_4|\le {\displaystyle \frac{7}{32}},\hfill \\ |b_5|\le {\displaystyle \frac{2}{5}}.\hfill \end{array}$$

The following functions are used to attain their respective sharp bounds:

$${\mathcal{F}}_0\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{2t}{2-t^2}}\right)dt=z+{\displaystyle \frac{z^2}{2}}+{\displaystyle \frac{z^3}{6}}+\cdots .$$

(11)

$${\mathcal{F}}_1\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{t^2}{2-t^2}}\right)dt=z+{\displaystyle \frac{z^3}{3}}+{\displaystyle \frac{7}{120}}{z}^5+\cdots .$$

(12)

$${\mathcal{F}}_2\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{11t^3}{8-4t^2}}-{\displaystyle \frac{t^2}{2}}\right)dt=z+{\displaystyle \frac{11}{32}}{z}^4+{\displaystyle \frac{z^5}{120}}+\cdots .$$

(13)

$${\mathcal{F}}_3\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{23t^4}{24-12t^2}}-{\displaystyle \frac{t^2}{2}}\right)dt=z+{\displaystyle \frac{z^5}{5}}+{\displaystyle \frac{691}{720}}{z}^6+\cdots .$$

(14)

Proof. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$${\mathcal{F}}^{\prime }\left(z\right)=\Omega \left(k\left(z\right)\right)=\cosh k\left(z\right)+{\displaystyle \frac{2k\left(z\right)}{2-k{\left(z\right)}^2}},$$

(15)

where $k\left(z\right)$ is an analytic function with $k\left(0\right)=0,\mathrm{and}k\left(z\right)<1$ for all $z\in \mathbb{E}.$

Let $p\in \mathcal{P}.$ Then, by application of subordination, we have

$$p\left(z\right)={\displaystyle \frac{1+k\left(z\right)}{1-k\left(z\right)}}=1+c_{1}z+c_2{z}^2+c_3{z}^3+\cdots .$$

Hence, it is clear that

$$\begin{array}{cc}\hfill \kappa \left(z\right)& ={\displaystyle \frac{p\left(z\right)-1}{p\left(z\right)+1}}\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{c}_{1}z+{\displaystyle \frac{1}{2}}\left(c_2-{\displaystyle \frac{1}{2}}{c}_1^2\right)z^2+{\displaystyle \frac{1}{2}}\left(c_3-c_1{c}_2+{\displaystyle \frac{1}{4}}{c}_1^3\right)z^3\hfill \\ & +{\displaystyle \frac{1}{2}}\left(c_4-c_1{c}_3+{\displaystyle \frac{3}{4}}{c}_1^2{c}_3-{\displaystyle \frac{1}{2}}{c}_2-{\displaystyle \frac{1}{8}}{c}_1^4\right)z^4\cdots ,(z\in \mathbb{E}).\hfill \end{array}$$

(16)

By using (16) in (15), we have

$$\begin{array}{cc}\hfill \Omega \left(k\right(z\left)\right)& =1+{\displaystyle \frac{1}{2}}{c}_{1}z+{\displaystyle \frac{1}{8}}(4c_2-c_1^2)z^2+{\displaystyle \frac{1}{16}}(c_1^3-4c_1{c}_2+8c_3)z^3\hfill \\ & +{\displaystyle \frac{1}{384}}(-23c_1^4+72c_1^2{c}_2-96c_1{c}_3-48c_2^2+192c_4)z^4+\cdots .\hfill \end{array}$$

(17)

Further,

$${\mathcal{F}}^{\prime }\left(z\right)=1+2b_{2}z+3b_3{z}^2+4b_4{z}^3+5b_5{z}^4+\cdots .$$

(18)

By comparing the coefficients of (17) and (18), we conclude that

$$b_2={\displaystyle \frac{c_1}{4}},$$

(19)

$$b_3={\displaystyle \frac{1}{6}}\left(c_2-{\displaystyle \frac{c_1^2}{4}}\right),$$

(20)

$$b_4={\displaystyle \frac{1}{64}}{c}_1^3-{\displaystyle \frac{1}{16}}{c}_1{c}_2+{\displaystyle \frac{1}{8}}{c}_3,$$

(21)

$$b_5={\displaystyle \frac{-1}{10}}\left({\displaystyle \frac{1}{2}}{c}_1\left(c_3-{\displaystyle \frac{3}{4}}{c}_1{c}_2+{\displaystyle \frac{23}{96}}{c}_1^3\right)-\left(c_4-{\displaystyle \frac{1}{4}}{c}_2^2\right)\right).$$

(22)

Using (4) in (19), we get

$$|b_2|\le {\displaystyle \frac{1}{2}}.$$

Using (3) in (20), we get

$$|b_3|\le {\displaystyle \frac{1}{3}}.$$

Using (6) in (21), we get

$$|b_4|\le {\displaystyle \frac{7}{32}}.$$

Therefore, by using (3), (4) and Lemma 4 in (22), we get

$$|b_5|\le {\displaystyle \frac{2}{5}}.$$

Hence, it completes the proof. □

Next, we estimate the Fekete–Szegö inequality and Hankel determinants using the previously established coefficient bounds for $b_2,b_3,b_4,$ and $b_5$.

Theorem 2. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$|b_3-\mathcal{M}{b}_2^2|\le \left\{\begin{array}{cc}{\displaystyle \frac{-(2-3\mathcal{M})}{12}},\hfill & if\mathcal{M}<{\displaystyle \frac{-2}{3}}\hfill \\ {\displaystyle \frac{1}{3}},\hfill & if{\displaystyle \frac{-2}{3}}\le \mathcal{M}\le 2\hfill \\ {\displaystyle \frac{(2-3\mathcal{M})}{12}},\hfill & if\mathcal{M}>2.\hfill \end{array}\right.$$

The above inequality is sharp.

Proof. 

Using (19) and (20), we have

$$\begin{array}{cc}\hfill |b_3-\mathcal{M}{b}_2^2|& \le \left|{\displaystyle \frac{1}{24}}\left(4c_2-c_1^2\right)-\mathcal{M}{\displaystyle \frac{c_1^2}{16}}\right|\hfill \\ & ={\displaystyle \frac{1}{6}}\left|c_2-\varkappa c_1^2\right|,\hfill \end{array}$$

where $\varkappa ={\displaystyle \frac{2+3\mathcal{M}}{8}}$.

• If $\varkappa <0,$ that is, $\mathcal{M}<{\displaystyle \frac{-2}{3}}$, then by using Lemma 5, we get

  $$\begin{array}{c}\hfill |c_2-\varkappa c_1^2|\le {\displaystyle \frac{(2-3\mathcal{M})}{2}}.\end{array}$$
• If $0\le \varkappa \le 1,$ that is, ${\displaystyle \frac{-2}{3}}\le \mathcal{M}\le 2,$ then by using Lemma 5, we get

  $$\begin{array}{c}\hfill |c_2-\varkappa c_1^2|\le 2.\end{array}$$
• If $\varkappa >1,$ that is, $\mathcal{M}>2,$ then by using Lemma 5, we get

  $$\begin{array}{c}\hfill |c_2-\varkappa c_1^2|\le {\displaystyle \frac{(3\mathcal{M}-2)}{2}}.\end{array}$$

Summarizing all the above cases, we obtain the desired inequality of the result. To demonstrate the sharpness of the functional, we consider the following function:

$${\mathcal{F}}_0\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{2t}{2-t^2}}\right)dt=z+{\displaystyle \frac{z^2}{2}}+{\displaystyle \frac{z^3}{6}}+\cdots .$$

Clearly, we observe that $b_2={\displaystyle \frac{1}{2}}\mathrm{and}{b}_3={\displaystyle \frac{1}{6}}.$ For $\mathcal{M}<{\displaystyle \frac{-2}{3}}\mathrm{or}\mathcal{M}>2,$ we have

$$\begin{array}{c}\hfill |b_3-\mathcal{M}{b}_2^2|\le {\displaystyle \frac{\pm (2-3\mathcal{M})}{12}}.\end{array}$$

Next, we consider the function

$${\mathcal{F}}_1\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{t^2}{2-t^2}}\right)dt=z+{\displaystyle \frac{z^3}{3}}+{\displaystyle \frac{7}{5!}}{z}^5+\cdots ,$$

where $b_2=0\mathrm{and}{b}_3={\displaystyle \frac{1}{3}}.$ For ${\displaystyle \frac{-2}{3}}\le \mathcal{M}\le 2,$ we have

$$\begin{array}{c}\hfill |b_3-\mathcal{M}{b}_2^2|\le {\displaystyle \frac{1}{3}}.\end{array}$$

The result is sharp for the function ${\mathcal{F}}_0\mathrm{and}{\mathcal{F}}_1$ given in (11) and (12). Hence, it completes the proof. □

Clearly, for $\mathcal{M}=1,$ the function $|b_3-\mathcal{M}{b}_2^2|$ reduces to $|b_3-b_2^2|,$ which is a particular case of Zalcman functional (or Hankel determinant ${\mathfrak{H}}_{2,1}\left(\mathcal{F}\right)$). For the above Theorem 2, we have the following corollary.

Corollary 1. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$\begin{array}{c}\hfill |b_3-b_2^2|\le {\displaystyle \frac{1}{3}}.\end{array}$$

The above functional is sharp for the function given in (12).

We also obtain the upper bound of the Hankel determinant and Zalcman functional for the class $\mathfrak{B}.$

Theorem 3. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$|b_2{b}_3-b_4|\le {\displaystyle \frac{19}{96}}.$$

The above functional is sharp for the function ${\mathcal{F}}_4$ given by

$$\begin{array}{c}\hfill {\mathcal{F}}_4\left(z\right)=z+{\displaystyle \frac{z^3}{6}}+{\displaystyle \frac{19}{96}}{z}^4+\cdots .\end{array}$$

(23)

Proof. 

Using (19), (20), and (21), we have

$$\begin{array}{c}\hfill |b_2{b}_3-b_4|=\left|{\displaystyle \frac{5}{192}}{c}_1^3-{\displaystyle \frac{5}{48}}{c}_1{c}_2+{\displaystyle \frac{1}{8}}{c}_3\right|.\end{array}$$

Therefore, by using (6), we get

$$\begin{array}{c}\hfill |b_2{b}_3-b_4|\le \left|2\left({\displaystyle \frac{5}{192}}\right)\right|+\left|{\displaystyle \frac{5}{48}}-2\left({\displaystyle \frac{5}{192}}\right)+\left|2\left({\displaystyle \frac{5}{192}}-{\displaystyle \frac{5}{48}}+{\displaystyle \frac{1}{8}}\right)\right|\right|={\displaystyle \frac{19}{96}}.\end{array}$$

The above functional is sharp for the function ${\mathcal{F}}_4$:

$$\begin{array}{c}\hfill {\mathcal{F}}_4\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{19t^3}{24-12t^2}}\right)dt=z+{\displaystyle \frac{z^3}{6}}+{\displaystyle \frac{19}{96}}{z}^4+\cdots .\end{array}$$

Hence, it completes the proof. □

Theorem 4. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$|{\mathfrak{H}}_{2,1}\left(\mathcal{F}\right)|=|b_2{b}_4-b_3^2| \le {\displaystyle \frac{1}{9}}.$$

The result is sharp for the function given in (12).

Proof. 

Using (19), (20), and (21), we have

$${\mathfrak{H}}_{2,1}\left(\mathcal{F}\right)={\displaystyle \frac{5}{2304}}{c}_1^4-{\displaystyle \frac{1}{576}}{c}_1^2{c}_2+{\displaystyle \frac{1}{32}}{c}_1{c}_3-{\displaystyle \frac{1}{36}}{c}_2^2.$$

By using Lemma 2, for $0\le c\le 2,$ with $c_1=c$, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathfrak{H}}_{2,1}\left(\mathcal{F}\right)& ={\displaystyle \frac{5}{2304}}{c}^4+{\displaystyle \frac{1}{1152}}{c}^2(4-c^2)r-{\displaystyle \frac{1}{128}}{c}^2(4-c^2)r^2\hfill \\ & -{\displaystyle \frac{1}{144}}{(4-c^2)}^2{r}^2+{\displaystyle \frac{1}{64}}c(4-c^2){(1-|r|}^2)\delta .\hfill \end{array}\end{array}$$

By taking $\left|r\right|=\xi (\xi \le 1),\left|\delta \right|\le 1,$ we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\mathfrak{H}}_{2,1}\left(\mathcal{F}\right)|& \le {\displaystyle \frac{5}{2304}}{c}^4+{\displaystyle \frac{1}{1152}}{c}^2(4-c^2)\xi +{\displaystyle \frac{1}{128}}{c}^2(4-c^2){\xi }^2\hfill \\ & +{\displaystyle \frac{1}{144}}{(4-c^2)}^2{\xi }^2+{\displaystyle \frac{1}{64}}c(4-c^2)(1-{\xi }^2)\hfill \\ & =\psi (c,\xi ).\hfill \end{array}\end{array}$$

A simple computation shows that ${\psi }^{\prime }(c,\xi )\ge 0$ on $0\le \xi \le 1.$ It implies that $\psi (c,\xi )\le \psi (c,1).$ For $\xi =1,$

$$\begin{array}{cc}\hfill |{\mathfrak{H}}_{2,1}\left(\mathcal{F}\right)|& \le {\displaystyle \frac{5}{2304}}{c}^4+{\displaystyle \frac{5}{576}}{c}^2(4-c^2)+{\displaystyle \frac{1}{144}}{(4-c^2)}^2.\hfill \end{array}$$

Since ${\psi }^{\prime }(c,1)<0$, then $\psi (c,1)$ is a decreasing function. Hence, the maximum attained at $c=0,$ that is,

$$\begin{array}{c}\hfill |{\mathfrak{H}}_{2,1}\left(\mathcal{F}\right)|\le {\displaystyle \frac{1}{9}}.\end{array}$$

Thus, the result is sharp, which completes the proof. □

We next obtain the Krushkal inequality [47] for a function to be in the class $\mathfrak{B}.$

Theorem 5. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$|b_5-b_2{b}_4|\le {\displaystyle \frac{21}{40}}.$$

The result is sharp for the function given by

$${\mathcal{F}}_5\left(z\right)=z+{\displaystyle \frac{z^3}{6}}+{\displaystyle \frac{21}{40}}{z}^5+\cdots .$$

(24)

Proof. 

Using (19), (21), and (22), we have

$$|b_5-b_2{b}_4|={\displaystyle \frac{1}{10}}\left|{\displaystyle \frac{61}{384}}{c}_1^4+{\displaystyle \frac{1}{4}}{c}_2^2+{\displaystyle \frac{13}{16}}{c}_1{c}_3-{\displaystyle \frac{17}{32}}{c}_1^2{c}_2-c_4\right|$$

$$={\displaystyle \frac{1}{10}}\left|{\displaystyle \frac{13}{16}}{c}_1\left(c_3-2\mathfrak{R}{c}_1{c}_2+\mathfrak{S}{c}_1^3\right)-\left(c_4-{\displaystyle \frac{1}{4}}{c}_2^2\right)\right|,$$

where $\mathfrak{R}={\displaystyle \frac{17}{52}}$ and $\mathfrak{S}={\displaystyle \frac{61}{312}}.$ Since $\mathfrak{R}\in (0,1)\mathrm{and}$ it satisfies the relation $\mathfrak{R}(2\mathfrak{R}-1)\le \mathfrak{S}\le \mathfrak{R}$, thus, by (3), (4), and Lemma 4, we have

$$|b_5-b_2{b}_4|\le {\displaystyle \frac{21}{40}}.$$

Now, we consider the function for which the resulting inequality is sharp, as follows:

$${\mathcal{F}}_5\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{31t}{12-6t^2}}\right)dt=z+{\displaystyle \frac{z^3}{6}}+{\displaystyle \frac{21}{40}}{z}^5+\cdots .$$

Hence, it completes the proof. □

Theorem 6. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$\begin{array}{c}\hfill |b_5-b_3^2|\le {\displaystyle \frac{2}{5}}.\end{array}$$

The result is sharp for the function given in (24).

Proof. 

Using (20) and (22), we have

$$|b_5-b_3^2|={\displaystyle \frac{1}{10}}\left|{\displaystyle \frac{79}{576}}{c}_1^4+{\displaystyle \frac{19}{36}}{c}_2^2+{\displaystyle \frac{1}{2}}{c}_1{c}_3-{\displaystyle \frac{37}{72}}{c}_1^2{c}_2-c_4\right|$$

$$={\displaystyle \frac{1}{10}}\left|{\displaystyle \frac{1}{2}}{c}_1\left(c_3-2\mathfrak{R}{c}_1{c}_2+\mathfrak{S}{c}_1^3\right)-\left(c_4-{\displaystyle \frac{19}{36}}{c}_2^2\right)\right|,$$

(25)

where $\mathfrak{R}={\displaystyle \frac{37}{72}}$ and $\mathfrak{S}={\displaystyle \frac{79}{288}}.$ Since $\mathfrak{R}\in (0,1)\mathrm{and}$ it satisfies the relation $\mathfrak{R}(2\mathfrak{R}-1)\le \mathfrak{S}\le \mathfrak{R}$, thus, in view of Equation (25) and by (3), (4), and Lemma 4, we obtain

$$|b_5-b_3^2|\le {\displaystyle \frac{2}{5}}.$$

Hence, it completes the proof. □

Theorem 7. 

Let $\mathcal{F}\in ,\mathfrak{B}.$ Then

$$\begin{array}{c}\hfill |b_4-b_2^3|\le {\displaystyle \frac{1}{4}}.\end{array}$$

The result is sharp for the function given by

$${\mathcal{F}}_6\left(z\right)=z+{\displaystyle \frac{z^3}{3}}+{\displaystyle \frac{z^4}{4}}+\cdots .$$

(26)

Proof. 

Using (19), (20), and (21), we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |b_4-b_2^3|& ={\displaystyle \frac{1}{8}}\left|c_3-2{\displaystyle \frac{1}{4}}{c}_1{c}_2+0c_1^3\right|\hfill \\ & ={\displaystyle \frac{1}{8}}\left|c_3-2\mathfrak{R}{c}_1{c}_2+\mathfrak{S}{c}_1^3\right|,\hfill \end{array}\end{array}$$

where $\mathfrak{R}={\displaystyle \frac{1}{4}}$ and $\mathfrak{S}=0.$ Since $\mathfrak{R}(2\mathfrak{R}-1)=-{\displaystyle \frac{1}{8}}\mathrm{and}$ it satisfies the following inequality:

$$\begin{array}{c}\hfill \mathfrak{R}(2\mathfrak{R}-1)\le \mathfrak{S}\le \mathfrak{R},\end{array}$$

thus, by Lemma 4, we have

$$\begin{array}{c}\hfill |b_4-b_2^3|\le {\displaystyle \frac{1}{4}}.\end{array}$$

Now, we consider the function for which the resulting inequality is sharp, as follows:

$${\mathcal{F}}_6\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{2t^3}{2-t^2}}\right)dt=z+{\displaystyle \frac{z^3}{3}}+{\displaystyle \frac{z^4}{4}}+\cdots .$$

Hence, it completes the proof. □

Theorem 8. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$\begin{array}{c}\hfill |b_5-b_2^4|\le {\displaystyle \frac{2}{5}}.\end{array}$$

The result is sharp for the function given in (24).

Proof. 

Using (19) and (22), we have

$$\begin{array}{c}\hfill |b_5-b_2^4|={\displaystyle \frac{1}{10}}\left|{\displaystyle \frac{61}{384}}{c}_1^4+{\displaystyle \frac{1}{4}}{c}_2^2+{\displaystyle \frac{1}{2}}{c}_1{c}_3-{\displaystyle \frac{3}{80}}{c}_1^2{c}_2-c_4\right|\end{array}$$

$$={\displaystyle \frac{1}{10}}\left|{\displaystyle \frac{1}{2}}{c}_1\left(c_3-2\mathfrak{R}{c}_1{c}_2+\mathfrak{S}{c}_1^3\right)-\left(c_4-{\displaystyle \frac{1}{4}}{c}_2^2\right)\right|,$$

(27)

where $\mathfrak{R}={\displaystyle \frac{3}{16}}$ and $\mathfrak{S}={\displaystyle \frac{61}{192}}.$ Since $\mathfrak{R}\in (0,1)\mathrm{and}$ it satisfies the relation $\mathfrak{R}(2\mathfrak{R}-1)\le \mathfrak{S}\le \mathfrak{R}$, thus, in view of Equation (27) and by (3), (4), and Lemma 4, we obtain

$$\begin{array}{c}\hfill |b_5-b_2^4|\le {\displaystyle \frac{2}{5}}.\end{array}$$

Hence, it completes the proof. □

Theorem 9. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$\begin{array}{c}\hfill |{\mathfrak{H}}_{3,1}\left(\mathcal{F}\right)|\le {\displaystyle \frac{61}{480}}.\end{array}$$

The result is sharp for the function given by

$${\mathcal{F}}_7\left(z\right)=z+{\displaystyle \frac{\sqrt{61}}{4\sqrt{30}}}{z}^4+{\displaystyle \frac{1}{120}}{z}^5+\cdots$$

(28)

Proof. 

The third Hankel determinant ${\mathfrak{H}}_{3,1}\left(\mathcal{F}\right)$ is given by

$$\begin{array}{c}\hfill {\mathfrak{H}}_{3,1}\left(\mathcal{F}\right)=2b_2{b}_3{b}_4-b_3^3-b_4^2+b_3{b}_5-b_2^2{b}_5.\end{array}$$

(29)

Using (19), (20), (21), and (22), with $c_1=c,$ we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathfrak{H}}_{3,1}\left(\mathcal{F}\right)={\displaystyle \frac{1}{T}}& (415c^6-1224c^4{c}_2-720c^3{c}_3+1776c^2{c}_2-5760c^2{c}_4\hfill \\ & +9792c{c}_2{c}_3-2944c_2^3+9216c_2{c}_4-8640c_3^2),\hfill \end{array}\end{array}$$

(30)

where $T=55,2960$. For $\mathcal{L}=(4-c_1^2)\mathrm{and}{c}_1=c,$ Equations (7)–(9), reduce to

$$2c_2=c^2+\beta \mathcal{L},$$

$$4c_3=c^3+2c\beta \mathcal{L}-c{\beta }^2{\mathcal{L}+2\mathcal{L}(1-|\beta |}^2)\eta ,$$

$$\begin{array}{cc}\hfill 8c_4=& c^4+\beta \mathcal{L}[c^2({\beta }^2-3\beta +3)+4\beta ]{-4\mathcal{L}(1-|\beta |}^2)\hfill \\ & [c(\beta -1)\eta +\overline{\beta }{\eta }^2{-(1-|\eta |}^2\left)k\right].\hfill \end{array}$$

Therefore, it follows from (30) that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathfrak{H}}_{3,1}\left(\mathcal{F}\right)={\displaystyle \frac{1}{T}}& (239c^6-368{\mathcal{L}}^3{\beta }^3-2304c^3{\mathcal{L}\beta \eta (1-|\beta |}^2)+576c^2\mathcal{L}\overline{\beta }{(1-|\beta |}^2){\eta }^2\hfill \\ & -576c^2{\mathcal{L}(1-|\beta |}^2\left)\right(1-{\left|\eta \right|}^2)k+2592c{\mathcal{L}}^2{\beta (1-|\beta |}^2)\eta -144c{\mathcal{L}}^2{\beta }^2{(1-|\beta |}^2)\eta \hfill \\ & -2304{\mathcal{L}}^2\beta \overline{\beta }{\eta }^2{(1-|\beta |}^2)+2304{\mathcal{L}}^2{\beta (1-|\beta |}^2\left)\right(1-{\left|\eta \right|}^2)k+1356c^2{\mathcal{L}}^2{\beta }^2\hfill \\ & -576c^2\mathcal{L}{\beta }^2-144c^4\mathcal{L}{\beta }^3-792c^2{\mathcal{L}}^2{\beta }^3+36c^2{\mathcal{L}}^2{\beta }^4-2160{\mathcal{L}}^2{\eta }^2{(1-|\beta |}^2{)}^2\hfill \\ & +468c^4\mathcal{L}{\beta }^2-1260c^4\mathcal{L}\beta +2232c^3{\mathcal{L}(1-|\beta |}^2)\eta +2880c^4{\mathcal{L}\beta \eta (1-|\beta |}^2)\hfill \\ & -2880c^4{\mathcal{L}\eta (1-|\beta |}^2)+1728\beta c^4).\hfill \end{array}\end{array}$$

Thus, it follows that

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathfrak{H}}_{3,1}\left(\mathcal{F}\right)={\displaystyle \frac{1}{T}}({\mathcal{N}}_0(c,\beta )+{\mathcal{N}}_1(c,\beta )\eta +{\mathcal{N}}_2(c,\beta ){\eta }^2+{\mathcal{N}}_3(c,\beta ,\eta )k),\end{array}\end{array}$$

where $\beta ,\eta ,k\in \overline{\mathbb{E}}\mathrm{and}$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{N}}_0(c,\beta )=& 239c^6+1728c^4\beta +\mathcal{L}[\mathcal{L}(1356c^2{\beta }^2+792c^2{\beta }^3+36c^2{\beta }^4)\hfill \\ & -368{\mathcal{L}}^2{c}^2{\beta }^3+576c^2{\beta }^2+144c^4{\beta }^3+468c^4{\beta }^2-1260c^4\beta ],\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{N}}_1(c,\beta )={72\mathcal{L}(1-|\beta |}^2)[\mathcal{L}(\left(31\right)+2{\beta }^{2}c)+(32c^3\beta +31c^3+40c^4\beta +40c^4)],\end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{N}}_2(c,\beta )={144\mathcal{L}(1-|\beta |}^2\left)\right[\mathcal{L}(4\overline{\beta }{c}^2{-15\mathcal{L}(1-|\beta |}^2\left)\right)-16\mathcal{L}\beta \overline{\beta }+20c^2],\end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{N}}_3(c,\beta )={576\mathcal{L}(1-|\beta |}^2)[36c^2+\mathcal{L}\left({\beta }^2\right)].\end{array}\end{array}$$

By using $\left|\beta \right|=x,\left|\eta \right|=y\mathrm{and}$ utilizing the fact that $k\le 1,$ we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\mathfrak{H}}_{3,1}\left(\mathcal{F}\right)|& \le {\displaystyle \frac{1}{T}}(|{\mathcal{N}}_0(c,\beta )|+|{\mathcal{N}}_1(c,\beta )|y+|{\mathcal{N}}_2(c,\beta )|y^2+|{\mathcal{N}}_3(c,\beta ,\eta ))|\hfill \\ & \le {\displaystyle \frac{1}{T}}\left({\mathfrak{F}}^{*}(c,x,y)\right),\hfill \end{array}\end{array}$$

(31)

where

$$\begin{array}{c}\hfill {\mathfrak{F}}^{*}(c,x,y)={\mathcal{M}}_0^{*}(c,x)+{\mathcal{M}}_1^{*}(c,x)y+{\mathcal{M}}_2^{*}(c,x)y^2+{\mathcal{M}}_3^{*}(c,x)(1-y^2),\end{array}$$

(32)

where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{M}}_0^{*}(c,x)=& 239c^6+1728c^{4}x+\mathcal{L}[\mathcal{L}(1356c^2{x}^2+792c^2{x}^3+36c^2{x}^4)\hfill \\ & +368{\mathcal{L}}^2{c}^2{x}^3+576c^2{x}^2+144c^4{x}^3+468c^4{x}^2+1260c^{4}x],\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{M}}_1^{*}(c,x)=72\mathcal{L}(1-x^2)[\mathcal{L}(\left(31\right)+2x^{2}c)+(32c^{3}x+31c^3+40c^{4}x+40c^4)],\end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{M}}_2^{*}(c,x)=144\mathcal{L}(1-x^2)[\mathcal{L}(4x^2+15(1-x^2))+16c^{2}x+20c^2],\end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{M}}_3^{*}(c,x)=576\mathcal{L}(1-x^2)[36c^2+\mathcal{L}(x^2+15)].\end{array}\end{array}$$

Now, we have to maximize $\mathfrak{F}(c,x,y)$ in the closed cuboid $\Xi =[0,2]\times [0,1]\times [0,1].$ For this purpose, we need to find the maximum value of $\mathfrak{F}(c,x,y)$ in the interior of $\Xi$, in the interior of all of its six faces, and on the twelve edges of the cuboid $\Xi$. For this purpose, we need to find the max $\mathfrak{F}(c,x,y)$ in the interior of $\Xi$, in the interior of all of its six faces, and on the twelve edges of the cuboid $\Xi$.

Let $(c,x)\in (0,2)\times (0,1).$ Then, ${\mathcal{M}}_2^{*}(c,x)$ reduces to

$$\begin{array}{c}\hfill {\mathcal{M}}_2^{*}(c,x)\le 144\mathcal{L}(1-x^2)[\mathcal{L}(x^2+15)+36c^2]={\mathcal{F}}_2(c,x).\end{array}$$

(33)

Let, ${\mathcal{M}}_i^{*}(c,x)={\mathcal{F}}_i(c,x)(i=0,1,3)\mathrm{and}$

$$\mathfrak{F}(c,x,y)={\mathcal{F}}_0(c,x)+{\mathcal{F}}_1(c,x)y+{\mathcal{F}}_2(c,x)y^2+{\mathcal{F}}_3(c,x)(1-y^2).$$

(34)

Clearly, it follows that ${\mathfrak{F}}^{*}(c,x,y)\le \mathfrak{F}(c,x,y)$ in $\Xi$. Next, differentiating (34) partially with respect to y yields

$${\displaystyle \frac{\partial \mathfrak{F}}{\partial y}}={\mathcal{F}}_1(c,x)+2y[{\mathcal{F}}_2(c,x)-{\mathcal{F}}_3(c,x)].$$

For $(c,x)\in (0,2)\times (0,1),$ we have ${\mathcal{F}}_1(c,x)\ge 0\mathrm{and}({\mathcal{F}}_2(c,x)-{\mathcal{F}}_3(c,x))\ge 0$, that is,

$$\begin{array}{c}\hfill {\mathcal{F}}_2(c,x)-{\mathcal{F}}_3(c,x)=144\mathcal{L}(1-x^2)[\mathcal{L}(15+x^2-16x)+20c^2]\ge 0.\end{array}$$

Therefore, ${\displaystyle \frac{\partial \mathfrak{F}}{\partial y}}\ge 0(y\in [0,1]).$ For $y=1,$ (34) reduces to

$$\begin{array}{cc}\hfill \mathfrak{F}(c,x,y)=& {\mathcal{F}}_0(c,x)+{\mathcal{F}}_1(c,x)+{\mathcal{F}}_2(c,x)\hfill \\ & =239c^6+1728c^{4}x+\mathcal{L}[{\mathcal{M}}_0\left(c\right)+{\mathcal{M}}_1\left(c\right)x+{\mathcal{M}}_2\left(c\right)x^2+{\mathcal{M}}_3\left(c\right)x^3+{\mathcal{M}}_4\left(c\right)x^4]\hfill \\ & ={\mathfrak{F}}_1(c,x),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\mathcal{M}}_0\left(c\right)& =2232c^3+2880c^4+2232\mathcal{L}+144[24c^2+15\mathcal{L}],\hfill \\ \hfill {\mathcal{M}}_1\left(c\right)& =\mathcal{L}[1260c^4+2304c^3],\hfill \\ \hfill {\mathcal{M}}_2\left(c\right)& =\mathcal{L}[1356\mathcal{L}{c}^2+576c^2+468c^4+144c-2232c^3-2880c^4-2088-3456\mathcal{L}],\hfill \\ \hfill {\mathcal{M}}_3\left(c\right)& =\mathcal{L}[368{\mathcal{L}}^2+792\mathcal{L}{c}^2+144c^4-2880c\left(4c^2\right)],\hfill \\ \hfill {\mathcal{M}}_4\left(c\right)& =\mathcal{L}\left[(36c^2-2304c^3-144)\right].\hfill \end{array}$$

Also, it is clear that $\mathfrak{F}(c,x,y)\le \mathfrak{F}(c,x,1).$ Now, we have to obtain the maximum value of ${\mathfrak{F}}_1(c,x)$ on $\left(\right[0,2]\times [0,1\left]\right)$. For $c\in [0,2],$ we have ${\mathcal{M}}_4\left(c\right)\le 0\mathrm{and}$

$$\begin{array}{cc}\hfill {\mathfrak{F}}_1(c,x)& \le 239c^6+1728c^{4}x+\mathcal{L}[{\mathcal{M}}_0\left(c\right)+{\mathcal{M}}_1\left(c\right)x+{\mathcal{M}}_2\left(c\right)x^2+{\mathcal{M}}_3\left(c\right)x^3]\hfill \\ & ={\mathfrak{F}}_2(c,x).\hfill \end{array}$$

(35)

• For $c=0,\mathrm{and}x\in [0,1],$ we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathfrak{F}}_2(0,x)& =94208x^3-254592x^2+70272\hfill \\ & \le 70272.\hfill \end{array}\end{array}$$

2.

For $c=2,\mathrm{and}x\in [0,1],$ we obtain ${\mathfrak{F}}_2(2,x)=42944.$

Numerical calculations indicate that the system of equations

$${\displaystyle \frac{\partial {\mathfrak{F}}_2}{\partial c}}=0\mathrm{and}{\displaystyle \frac{\partial {\mathfrak{F}}_2}{\partial x}}=0$$

with $(c,x)\in (0,2)\times (0,1)$, and all the real approximate solutions are listed as $(-1.43,1.27),$ $(-3.52,1.19), (2.51,-0.83), (4.27,2.35), (-5.61,-2.51), (6.83,3.92), (-8.19,4.58)$, and $(9.45,-5.27)$. Hence, ${\mathfrak{F}}_2(c,x)$ has no solution in $(0,2)\times (0,1),$ implying that ${\mathfrak{F}}_2(c,x)$ has no optimal point within this interval.

From the above cases, it is clear that within the cuboid $\Xi ,$ the following are satisfied:

$$\begin{array}{c}\hfill {\mathfrak{F}}^{*}(c,x,y)\le \mathfrak{F}(c,x,y)\le \mathfrak{F}(c,x,1)\le {\mathfrak{F}}_1(c,x)\le {\mathfrak{F}}_2(c,x)\le 70272.\end{array}$$

From (31), we deduce that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\mathfrak{H}}_{3,1}\left(\mathcal{F}\right)|& \le {\displaystyle \frac{1}{T}}\left({\mathfrak{F}}^{*}(c,x,y)\right)\hfill \\ & ={\displaystyle \frac{70272}{552960}}={\displaystyle \frac{61}{480}}.\hfill \end{array}\end{array}$$

Now, we consider the function for which the resulting inequality is sharp, as follows:

$${\mathcal{F}}_7\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{2\sqrt{61}{t}^3}{\sqrt{30}(2-t^2)}}\right)dt=z+{\displaystyle \frac{\sqrt{61}}{4\sqrt{30}}}{z}^4+{\displaystyle \frac{1}{120}}{z}^5+\cdots .$$

Hence, it completes the proof. □

3. Logarithmic Coefficient Inequalities

In this section, we explore logarithmic coefficients associated with $\mathcal{F}$ for the class $\mathfrak{B}$, as well as the Fekete–Szegö functional, Hankel determinant, and Zalcman functional.

Let $\mathcal{F}\in \mathcal{S}.$ Then, the logarithmic function related to $\mathcal{F}$ has the expansion of the form

$$log\left({\displaystyle \frac{\mathcal{F}\left(z\right)}{z}}\right)=2\sum _{j=1}^{\infty }{\gamma }_j\left(\mathcal{F}\right)z^j(z\in \mathbb{E}).$$

(36)

We denote the logarithmic coefficients by ${\gamma }_j\left(\mathcal{F}\right)={\gamma }_j$. Now, differentiating (36), we show that

$$\begin{array}{c}\hfill {\gamma }_1={\displaystyle \frac{1}{2}}\left(b_2\right),\end{array}$$

(37)

$$\begin{array}{c}\hfill {\gamma }_2={\displaystyle \frac{1}{2}}\left(b_3-{\displaystyle \frac{1}{2}}{b}_2^2\right),\end{array}$$

(38)

$$\begin{array}{c}\hfill {\gamma }_3={\displaystyle \frac{1}{2}}\left(b_4-b_2{b}_3+{\displaystyle \frac{1}{3}}{b}_2^3\right),\end{array}$$

(39)

$$\begin{array}{c}\hfill {\gamma }_4={\displaystyle \frac{1}{2}}\left(b_5-b_2{b}_4+b_2^2{b}_3-{\displaystyle \frac{1}{2}}{b}_3^2+{\displaystyle \frac{1}{4}}{b}_2^4\right).\end{array}$$

(40)

Among the several coefficient estimate problems, the logarithmic coefficients play a vital role in the theory of univalent functions. For more details on the logarithmic coefficients problem, see [48,49,50,51,52].

Theorem 10. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$\begin{array}{cc}\hfill & |{\gamma }_1| \le {\displaystyle \frac{1}{4}},\hfill \\ & |{\gamma }_2| \le {\displaystyle \frac{1}{6}},\hfill \\ & |{\gamma }_3| \le {\displaystyle \frac{1}{8}},\hfill \\ & |{\gamma }_4| \le {\displaystyle \frac{29}{80}}.\hfill \end{array}$$

The following functions are used to attain their respective sharp bounds:

$${\mathcal{F}}_0^{*}\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{2t}{2-t^2}}\right)dt=z+{\displaystyle \frac{z^2}{2}}+{\displaystyle \frac{z^3}{6}}+\cdots .$$

(41)

$${\mathcal{F}}_1^{*}\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{t^2}{2-t^2}}\right)dt=z+{\displaystyle \frac{z^3}{3}}+\cdots .$$

(42)

$${\mathcal{F}}_2^{*}\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{2t^3}{2-t^2}}\right)dt=z+{\displaystyle \frac{z^3}{6}}+{\displaystyle \frac{z^4}{4}}+\cdots .$$

(43)

$${\mathcal{F}}_3^{*}\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{263t^4}{36(2-t^2)}}\right)dt=z+{\displaystyle \frac{1}{3}}{z}^3+{\displaystyle \frac{133}{180}}{z}^5+\cdots .$$

(44)

Proof. 

Since $\mathcal{F}\in \mathfrak{B},$ by using Equations (19)–(22) in (37)–(40), we conclude that

$$\begin{array}{c}\hfill {\gamma }_1={\displaystyle \frac{1}{8}}{c}_1,\end{array}$$

(45)

$$\begin{array}{c}\hfill {\gamma }_2={\displaystyle \frac{1}{192}}\left(16c_2-7c_1^2\right),\end{array}$$

(46)

$$\begin{array}{c}\hfill {\gamma }_3={\displaystyle \frac{1}{2304}}\left(36c_1^3-120c_1{c}_2+144c_3\right),\end{array}$$

(47)

$$\begin{array}{c}\hfill {\gamma }_4=-{\displaystyle \frac{1}{645120}}\left(2563c_1^4-25312c_1^2{c}_2+26208c_1{c}_3+25088c_2^2-64512c_4\right).\end{array}$$

(48)

Using (4) in (45), we get

$$\begin{array}{c}\hfill |{\gamma }_1|\le {\displaystyle \frac{1}{4}}.\end{array}$$

In view of (45), we can write

$$\begin{array}{c}\hfill |{\gamma }_2|={\displaystyle \frac{16}{192}}\left(c_2-{\displaystyle \frac{7}{16}}{c}_1^2\right).\end{array}$$

Next, using (3) in the above result, we get

$$\begin{array}{c}\hfill |{\gamma }_2|\le {\displaystyle \frac{1}{6}}.\end{array}$$

Using (47), a simple calculation leads to

$$\begin{array}{c}\hfill |{\gamma }_3|={\displaystyle \frac{144}{2304}}\left|\left(c_3-2\mathfrak{R}{c}_1{c}_2+\mathfrak{S}{c}_1^3\right)\right|,\end{array}$$

where $\mathfrak{R}={\displaystyle \frac{5}{12}}$ and $\mathfrak{S}={\displaystyle \frac{1}{4}}.$ Note that $0\le \mathfrak{R}\le 1,\mathfrak{S}\le \mathfrak{R}$ with $\mathfrak{R}(2\mathfrak{R}-1)\le \mathfrak{S}.$ Thus, by Lemma 4, we deduce that

$$\begin{array}{c}\hfill |{\gamma }_3|\le {\displaystyle \frac{1}{8}}.\end{array}$$

From (48), we can write

$$\begin{array}{c}\hfill {\gamma }_4=-{\displaystyle \frac{1}{10}}\left({\displaystyle \frac{13}{32}}{c}_1\left(c_3-2\mathfrak{R}{c}_1{c}_2+\mathfrak{S}{c}_1^3\right)-\left(c_4-{\displaystyle \frac{7}{18}}{c}_2^2\right)\right),\end{array}$$

(49)

where $\mathfrak{R}={\displaystyle \frac{113}{234}}$ and $\mathfrak{S}={\displaystyle \frac{2563}{26208}}.$ Note that, $0\le \mathfrak{R}\le 1,\mathfrak{S}\le \mathfrak{R}$ with $\mathfrak{R}(2\mathfrak{R}-1)\le \mathfrak{S}.$ Therefore, using (3), (4), and Lemma 4, we have

$$\begin{array}{c}\hfill |{\gamma }_4|\le {\displaystyle \frac{29}{80}}.\end{array}$$

Hence, it completes the proof. □

Theorem 11. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$\begin{array}{c}\hfill |{\gamma }_2-\upsilon {\gamma }_1^2|\le max\left\{{\displaystyle \frac{1}{6}},{\displaystyle \frac{3\upsilon -1}{48}}\right\}(\upsilon \in \mathbb{C}).\end{array}$$

The inequality is sharp.

Proof. 

Using (45) and (46), we have

$$\begin{array}{c}\hfill |{\gamma }_2-\upsilon {\gamma }_1^2|={\displaystyle \frac{1}{12}}\left|c_2-{\displaystyle \frac{3\upsilon +7}{16}}{c}_1^2\right|.\end{array}$$

Therefore, using Equation (10) yields

$$\begin{array}{c}\hfill \left|c_2-{\displaystyle \frac{3\upsilon +7}{16}}{c}_1^2\right|\le 2max\left\{1,\left|{\displaystyle \frac{3\upsilon -1}{8}}\right|\right\}.\end{array}$$

Thus, by Lemma 3, we have

$$\begin{array}{c}\hfill |{\gamma }_2-\upsilon {\gamma }_1^2|\le max\left\{{\displaystyle \frac{1}{6}},{\displaystyle \frac{3\upsilon -1}{48}}\right\}.\end{array}$$

To establish the sharpness of the functional, we consider two cases: for the upper bound ${\displaystyle \frac{1}{6}}$, the function defined in (42) is used, while for the upper bound ${\displaystyle \frac{3\upsilon -1}{48}}(\upsilon \in \mathbb{C}),$ the function given in (41) is employed. Hence, it completes the proof. □

Clearly, for $\upsilon =1,$ the function $|{\gamma }_2-\upsilon {\gamma }_1^2|$ reduces to $|{\gamma }_2-{\gamma }_1^2|,$ which is half of the Fekete–Szegö functional (or ${\mathfrak{H}}_{2,1}\left(\mathcal{F}\right)/2$). For the above Theorem 11, we have the following corollary.

Corollary 2. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$\begin{array}{c}\hfill |{\gamma }_2-{\gamma }_1^2|\le {\displaystyle \frac{1}{6}}.\end{array}$$

The above functional is sharp for the function given in (42).

Theorem 12. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$\begin{array}{c}\hfill |{\gamma }_1{\gamma }_2-{\gamma }_3|\le {\displaystyle \frac{1}{8}}.\end{array}$$

The inequality is sharp.

Proof. 

Using (45), (46), and (47), we have

$$\begin{array}{c}\hfill |{\gamma }_1{\gamma }_2-{\gamma }_3|={\displaystyle \frac{1}{16}}\left|c_3-2\mathfrak{R}{c}_1{c}_2+\mathfrak{S}{c}_1^3\right|,\end{array}$$

where $\mathfrak{R}={\displaystyle \frac{1}{2}}\mathrm{and}\mathfrak{S}={\displaystyle \frac{31}{96}}.$ Since $0\le \mathfrak{R}\le 1,\mathfrak{S}\le \mathfrak{R}$ with $\mathfrak{R}(2\mathfrak{R}-1)\le \mathfrak{S}.$ Thus, by Lemma 4, we deduce that

$$\begin{array}{c}\hfill |{\gamma }_1{\gamma }_2-{\gamma }_3|\le {\displaystyle \frac{1}{8}}.\end{array}$$

To determine the sharpness of the function, we consider the function defined in (43). Hence, it completes the proof. □

Theorem 13. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$\begin{array}{c}\hfill |{\gamma }_4-{\gamma }_1{\gamma }_3|\le {\displaystyle \frac{63}{160}}.\end{array}$$

The inequality is sharp.

Proof. 

Using (45), (47), and (48), we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\gamma }_4-{\gamma }_1{\gamma }_3|& ={\displaystyle \frac{1}{10}}\left|\left({\displaystyle \frac{3823}{64512}}{c}_1^4+{\displaystyle \frac{7}{18}}{c}_2^2+\left({\displaystyle \frac{31}{64}}\right)c_1{c}_3-\left({\displaystyle \frac{527}{1152}}\right)c_1^2{c}_2-c_4\right)\right|\hfill \\ & ={\displaystyle \frac{1}{10}}\left|{\displaystyle \frac{31}{64}}{c}_1\left(c_3-2\mathfrak{R}{c}_1{c}_2+\mathfrak{S}{c}_1^3\right)-\left(c_4-{\displaystyle \frac{7}{18}}{c}_2^2\right)\right|,\hfill \end{array}\end{array}$$

where $\mathfrak{R}={\displaystyle \frac{17}{36}}$ and $\mathfrak{S}={\displaystyle \frac{3823}{31248}}.$ Since $0\le \mathfrak{R}\le 1,\mathfrak{S}\le \mathfrak{R}$ with $\mathfrak{R}(2\mathfrak{R}-1)\le \mathfrak{S}.$ Thus, by (3), (4), and Lemma 4, we obtain

$$\begin{array}{c}\hfill |{\gamma }_4-{\gamma }_1{\gamma }_3|\le {\displaystyle \frac{63}{160}}.\end{array}$$

The functional is sharp for the function given by

$${\mathcal{F}}_4^{*}\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{187t^4}{24(2-t^2)}}\right)dt=z+{\displaystyle \frac{63}{80}}{z}^5+\cdots$$

Hence, it completes the proof. □

Theorem 14. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$\begin{array}{c}\hfill |{\gamma }_4-{\gamma }_2^2|\le {\displaystyle \frac{19}{30}}.\end{array}$$

The inequality is sharp.

Proof. 

Using (46) and (48), we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\gamma }_4-{\gamma }_2^2|& ={\displaystyle \frac{1}{10}}\left|\left({\displaystyle \frac{6841}{129024}}{c}_1^4+{\displaystyle \frac{33}{72}}{c}_2^2+\left({\displaystyle \frac{13}{12}}\right)c_1{c}_3-{\displaystyle \frac{29}{64}}{c}_1^2{c}_2-c_4\right)\right|\hfill \\ & ={\displaystyle \frac{1}{10}}\left|{\displaystyle \frac{13}{12}}{c}_1\left(c_3-2\mathfrak{R}{c}_1{c}_2+\mathfrak{S}{c}_1^3\right)-\left(c_4-{\displaystyle \frac{33}{72}}{c}_2^2\right)\right|,\hfill \end{array}\end{array}$$

where $\mathfrak{R}={\displaystyle \frac{87}{416}}$ and $\mathfrak{S}={\displaystyle \frac{6841}{139776}}.$ Since $0\le \mathfrak{R}\le 1,\mathfrak{S}\le \mathfrak{R}$ with $\mathfrak{R}(2\mathfrak{R}-1)\le \mathfrak{S}.$ Thus, by (3), (4), and Lemma 4, we obtain

$$\begin{array}{c}\hfill |{\gamma }_4-{\gamma }_2^2|\le {\displaystyle \frac{19}{30}}.\end{array}$$

The functional is sharp for the function given by

$${\mathcal{F}}_5^{*}\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{151t^4}{12(2-t^2)}}\right)dt=z+{\displaystyle \frac{19}{15}}{z}^5+\cdots .$$

(50)

Hence, it completes the proof. □

Theorem 15. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$\begin{array}{c}\hfill |{\gamma }_3-{\gamma }_1^3|\le {\displaystyle \frac{1}{8}}.\end{array}$$

The inequality is sharp.

Proof. 

Using (45) and (47), we have

$$\begin{array}{c}\hfill |{\gamma }_3-{\gamma }_1^3|={\displaystyle \frac{1}{16}}\left|c_3-2\mathfrak{R}{c}_1{c}_2+\mathfrak{S}{c}_1^3\right|,\end{array}$$

where $\mathfrak{R}={\displaystyle \frac{5}{12}}\mathrm{and}\mathfrak{S}={\displaystyle \frac{63}{288}}.$ Since $0\le \mathfrak{R}\le 1,\mathfrak{S}\le \mathfrak{R}$ with $\mathfrak{R}(2\mathfrak{R}-1)\le \mathfrak{S}.$ Thus, by Lemma 4, we deduce that

$$\begin{array}{c}\hfill |{\gamma }_3-{\gamma }_1^3|\le {\displaystyle \frac{1}{8}}.\end{array}$$

The functional is sharp for the function given in (43). Hence, it completes the proof. □

Theorem 16. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$\begin{array}{c}\hfill |{\gamma }_4-{\gamma }_1^4|\le {\displaystyle \frac{29}{80}}.\end{array}$$

The inequality is sharp.

Proof. 

Using (45) and (48), we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\gamma }_4-{\gamma }_1^4|& ={\displaystyle \frac{1}{10}}\left|\left({\displaystyle \frac{5441}{129024}}{c}_1^4+{\displaystyle \frac{7}{18}}{c}_2^2+\left({\displaystyle \frac{13}{32}}\right)c_1{c}_3-\left({\displaystyle \frac{113}{288}}\right)c_1^2{c}_2-c_4\right)\right|\hfill \\ & ={\displaystyle \frac{1}{10}}\left|{\displaystyle \frac{13}{32}}{c}_1\left(c_3-2\mathfrak{R}{c}_1{c}_2+\mathfrak{S}{c}_1^3\right)-\left(c_4-{\displaystyle \frac{7}{18}}{c}_2^2\right)\right|,\hfill \end{array}\end{array}$$

where $\mathfrak{R}={\displaystyle \frac{113}{234}},\mathfrak{S}={\displaystyle \frac{5441}{52416}}.$ Since $0\le \mathfrak{R}\le 1,\mathfrak{S}\le \mathfrak{R}$ with $\mathfrak{R}(2\mathfrak{R}-1)\le \mathfrak{S}.$ Thus, by (3), (4), and Lemma 4, we get

$$\begin{array}{c}\hfill |{\gamma }_4-{\gamma }_1^4|\le {\displaystyle \frac{29}{80}}.\end{array}$$

The functional is sharp for the function given by

$${\mathcal{F}}_5^{*}\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{263t^4}{36(2-t^2)}}\right)dt=z+{\displaystyle \frac{1}{6}}{z}^3+{\displaystyle \frac{133}{180}}{z}^5+\cdots .$$

Hence, it completes the proof. □

Theorem 17. 

Let $\mathcal{F}\in \mathfrak{B}.$ Then,

$$\begin{array}{c}\hfill |{\mathfrak{H}}_{2,2}(F_{\mathcal{F}}/2)|\le {\displaystyle \frac{5}{64}}.\end{array}$$

The result is sharp for the function given by

$$\begin{array}{c}\hfill {\mathcal{F}}_6^{*}\left(z\right)={\int }_0^z\left(\cosh t+{\displaystyle \frac{\sqrt{5}{t}^3}{2-t^2}}-{\displaystyle \frac{t^2}{2}}\right)dt=z+\sqrt{5}{\displaystyle \frac{z^4}{4}}+\cdots .\end{array}$$

Proof. 

The second Hankel determinant ${\mathfrak{H}}_{2,2}(F_{\mathcal{F}}/2)$ is given by

$$\begin{array}{c}\hfill {\mathfrak{H}}_{2,2}(F_{\mathcal{F}}/2)={\gamma }_2{\gamma }_4-{\gamma }_3^2.\end{array}$$

(51)

Using (46), (47), and (48), with $c_1=c,$ we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathfrak{H}}_{2,2}(F_{\mathcal{F}}/2)=& [{\displaystyle \frac{-5271}{53084160}}{c}^6-{\displaystyle \frac{1037}{7741440}}{c}^4{c}_2-{\displaystyle \frac{29}{61440}}{c}^3{c}_3+{\displaystyle \frac{91}{138240}}{c}^2{c}_2^2-{\displaystyle \frac{7}{1920}}{c}^2{c}_4\hfill \\ & +{\displaystyle \frac{12}{3840}}c{c}_2{c}_3-{\displaystyle \frac{7}{2160}}{c}_2^3+{\displaystyle \frac{1}{120}}{c}_2{c}_4-{\displaystyle \frac{1}{256}}{c}_3^2].\hfill \end{array}\end{array}$$

(52)

For $\mathcal{L}=(4-c_1^2)\mathrm{and}{c}_1=c,$ Equations (7)–(9), reduce to

$$2c_2=c^2+\beta \mathcal{L},$$

$$4c_3=c^3+2c\beta \mathcal{L}-c{\beta }^2{\mathcal{L}+2\mathcal{L}(1-|\beta |}^2)\eta ,$$

$$\begin{array}{cc}\hfill 8c_4=& c^4+\beta \mathcal{L}[c^2({\beta }^2-3\beta +3)+4\beta ]{-4\mathcal{L}(1-|\beta |}^2)\hfill \\ & [c(\beta -1)\eta +\overline{\beta }{\eta }^2{-(1-|\eta |}^2\left)k\right].\hfill \end{array}$$

So, it follows from (52) that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathfrak{H}}_{2,2}(F_{\mathcal{F}}/2)& ={\displaystyle \frac{1}{T_1}}(5919c^6-63504c^3{\mathcal{L}\eta (1-|\beta |}^2)-150528{\mathcal{L}}^3{\beta }^3+774144{\mathcal{L}}^2{\beta }^3\hfill \\ & -1451520c^3{\mathcal{L}\beta \eta (1-|\beta |}^2)-96768c^2\mathcal{L}\overline{\beta }{\eta }^2{(1-|\beta |}^2)+96768c^2{\mathcal{L}(1-|\beta |}^2\left)\right(1-{\left|\eta \right|}^2)k\hfill \\ & +338688c{\mathcal{L}}^2{\beta \eta (1-|\beta |}^2)-411264c{\mathcal{L}}^2{\beta }^2{\eta (1-|\beta |}^2)-774144{\mathcal{L}}^2\beta \overline{\beta }{\eta }^2{(1-|\beta |}^2)\hfill \\ & +774144{\mathcal{L}}^2{\beta (1-|\beta |}^2\left)\right(1-{\left|\eta \right|}^2)k-362880{\mathcal{L}}^2{\eta }^2{(1-|\beta |}^2{)}^2+7560c^4\mathcal{L}{\beta }^2\hfill \\ & -439176c^4\mathcal{L}\beta +117600c^2{\mathcal{L}}^2{\beta }^2+96768c^2\mathcal{L}{\beta }^2+24192c^4\mathcal{L}{\beta }^3-362880c^2{\mathcal{L}}^2{\beta }^3\hfill \\ & +102816c^2{\mathcal{L}}^2{\beta }^4),\hfill \end{array}\end{array}$$

where $T_1=371589120$.

Thus, it follows that

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathfrak{H}}_{2,2}(F_{\mathcal{F}}/2)={\displaystyle \frac{1}{T_1}}({\mathcal{N}}_0(c,\beta )+{\mathcal{N}}_1(c,\beta )\eta +{\mathcal{N}}_2(c,\beta ){\eta }^2+{\mathcal{N}}_3(c,\beta ,\eta )k),\end{array}\end{array}$$

where $\beta ,\eta ,k\in \overline{\mathbb{E}}\mathrm{and}$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{N}}_0(c,\beta )=& 5919c^6-150528{\beta }^3{\mathcal{L}}^3+774144{\mathcal{L}}^2{\beta }^3+7560c^4\mathcal{L}{\beta }^2-439176c^4\mathcal{L}\beta +117600c^2{\mathcal{L}}^2{\beta }^2\hfill \\ & +96768c^2\mathcal{L}{\beta }^2+24192c^4\mathcal{L}{\beta }^3-362880c^2{\mathcal{L}}^2{\beta }^3+102816c^2{\mathcal{L}}^2{\beta }^4,\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{N}}_1(c,\beta )=-63504c^3{\mathcal{L}(1-|\beta |}^2)-1451520c^3\mathcal{L}\beta +338688c\beta {\mathcal{L}}^2-411264c{\mathcal{L}}^2{\beta }^2,\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{N}}_2(c,\beta )=96768c^2\mathcal{L}\overline{\beta }{(1-|\beta |}^2)-774144\beta \overline{\beta }{\mathcal{L}}^2-362880{\mathcal{L}}^2{(1-|\beta |}^2{)}^2,\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{N}}_3(c,\beta )=96768c^2{\mathcal{L}(1-|\beta |}^2\left)\right(1-{\left|\eta \right|}^2)+774144\beta {\mathcal{L}}^2{(1-|\beta |}^2\left)\right(1-{\left|\eta \right|}^2).\end{array}$$

By using $\left|\beta \right|=x,\left|\eta \right|=y\mathrm{and}$ utilizing the fact $k\le 1,$ we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\mathfrak{H}}_{2,2}(F_{\mathcal{F}}/2)|& \le {\displaystyle \frac{1}{T_1}}\left(|{\mathcal{N}}_0(c,\beta )|+|{\mathcal{N}}_1(c,\beta )|y+|{\mathcal{N}}_2(c,\beta )|y^2+|{\mathcal{N}}_3(c,\beta ,\eta )\right)|\hfill \\ & \le {\displaystyle \frac{1}{T_1}}\left({\mathfrak{F}}^{*}(c,x,y)\right),\hfill \end{array}\end{array}$$

(53)

where

$$\begin{array}{c}\hfill {\mathfrak{F}}^{*}(c,x,y)={\mathcal{M}}_0^{*}(c,x)+{\mathcal{M}}_1^{*}(c,x)y+{\mathcal{M}}_2^{*}(c,x)y^2+{\mathcal{M}}_3^{*}(c,x)(1-y^2),\end{array}$$

(54)

$$\begin{array}{cc}\hfill {\mathcal{M}}_0^{*}(c,x)& =5919c^6+\mathcal{L}[150528{\mathcal{L}}^2{x}^3+1936\mathcal{L}(774144x^3+45219c^2{x}^2+362880c^2{x}^3\hfill \\ & +102816c^2{x}^4)7560c^4{x}^2+2336749c^{4}x+96768c^2{x}^2+24192c^4{x}^3],\hfill \\ \hfill {\mathcal{M}}_1^{*}(c,x)& =3024\mathcal{L}(1-x^2)[\mathcal{L}(112cx+136c{x}^2)+21c^{3}x+480c^{3}x],\hfill \\ \hfill {\mathcal{M}}_2^{*}(c,x)& =24192\mathcal{L}(1-x^2)[c^{2}x+\mathcal{L}(32x^2+15(1-x^2))],\hfill \\ \hfill {\mathcal{M}}_3^{*}(c,x)& =96768\mathcal{L}(1-x^2)[c^2+8\mathcal{L}x].\hfill \end{array}$$

Next, we aim to maximize $\mathfrak{F}(c,x,y)$ in the closed cuboid $\Xi =[0,2]\times [0,1]\times [0,1]$. This requires finding the maximum value of $\mathfrak{F}(c,x,y)$ within the interior of $\Xi$, the interiors of its six faces, and along its twelve edges.

Let $(c,x)\in (0,2)\times (0,1).$ Then, ${\mathcal{M}}_2^{*}(c,x)$ reduces to

$$\begin{array}{c}\hfill {\mathcal{M}}_2^{*}(c,x)\le 24192\mathcal{L}(1-x^2)[c^{2}x+\mathcal{L}(17x^2+15)+4c^2].\end{array}$$

Let ${\mathcal{M}}_i^{*}(c,x)={\mathcal{F}}_i(c,x)(i=0,1,3)\mathrm{and}$

$$\mathfrak{F}(c,x,y)={\mathcal{F}}_0(c,x)+{\mathcal{F}}_1(c,x)y+{\mathcal{F}}_2(c,x)y^2+{\mathcal{F}}_3(c,x)(1-y^2).$$

(55)

Clearly, it follows that ${\mathfrak{F}}^{*}(c,x,y)\le \mathfrak{F}(c,x,y)$ in $\Xi$. Next, differentiating (55) partially with respect to y yields

$${\displaystyle \frac{\partial \mathfrak{F}}{\partial y}}={\mathcal{F}}_1(c,x)+2y[{\mathcal{F}}_2(c,x)-{\mathcal{F}}_3(c,x)].$$

For $(c,x)\in (0,2)\times (0,1),$ we have ${\mathcal{F}}_1(c,x)\ge 0\mathrm{and}({\mathcal{F}}_2(c,x)-{\mathcal{F}}_3(c,x))\ge 0$, that is,

$$\begin{array}{c}\hfill {\mathcal{F}}_2(c,x)-{\mathcal{F}}_3(c,x)=24192\mathcal{L}(1-x^2)\left[\mathcal{L}(17x^2-32x+15)\right]\ge 0.\end{array}$$

Therefore, ${\displaystyle \frac{\partial \mathfrak{F}}{\partial y}}\ge 0(y\in [0,1]).$ For $y=1,$ Equation (55) simplifies to

$$\begin{array}{cc}\hfill \mathfrak{F}(c,x,y)& ={\mathcal{F}}_0(c,x)+{\mathcal{F}}_1(c,x)+{\mathcal{F}}_2(c,x)\hfill \\ & =5919c^6+\mathcal{L}[{\mathcal{M}}_0\left(c\right)+{\mathcal{M}}_1\left(c\right)x+{\mathcal{M}}_2\left(c\right)x^2+{\mathcal{M}}_3\left(c\right)x^3+{\mathcal{M}}_4\left(c\right)x^4]\hfill \\ & ={\mathfrak{F}}_1(c,x),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\mathcal{M}}_0\left(c\right)& =-96768c^4+63504c^3-266112c^2+1451520,\hfill \\ \hfill {\mathcal{M}}_1\left(c\right)& =439176c^4+1112832c^3+1354752c,\hfill \\ \hfill {\mathcal{M}}_2\left(c\right)& =-13272c^4-347760c^3+422016c^2+290304c+193536,\hfill \\ \hfill {\mathcal{M}}_3\left(c\right)& =-188160c^4-1112832c^3-526848c^2+5505024,\hfill \\ \hfill {\mathcal{M}}_4\left(c\right)& =-102816c^4+411264c^3+822528c^2-1645056c-1645056.\hfill \end{array}$$

Also, it is clear that $\mathfrak{F}(c,x,y)\le \mathfrak{F}(c,x,1).$ Now, we have to obtain maximum value of ${\mathfrak{F}}_1(c,x)$ on $\left(\right[0,2]\times [0,1\left]\right)$. For $\left(c\right)\in [0,2],$ we have ${\mathcal{M}}_4\left(c\right)\le 0\mathrm{and}$

$$\begin{array}{cc}\hfill {\mathfrak{F}}_1(c,x)& \le 5919c^6+\mathcal{L}[{\mathcal{M}}_0\left(c\right)+{\mathcal{M}}_1\left(c\right)x+{\mathcal{M}}_2\left(c\right)x^2+{\mathcal{M}}_3\left(c\right)x^3]\hfill \\ & ={\mathfrak{F}}_2(c,x).\hfill \end{array}$$

(56)

• For $c=0,\mathrm{and}x\in [0,1],$ we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathfrak{F}}_2(0,x)& =2202096x^3+774144x^2+5806080\hfill \\ & \le 5806080.\hfill \end{array}\end{array}$$

2.

For $c=2,\mathrm{and}x\in [0,1],$ we get

$${\mathfrak{F}}_2(2,x)=378816.$$

Numerical calculations indicate that the system of equations

$${\displaystyle \frac{\partial {\mathfrak{F}}_2}{\partial c}}=0\mathrm{and}{\displaystyle \frac{\partial {\mathfrak{F}}_2}{\partial x}}=0$$

with $(c,x)\in (0,2)\times (0,1)$, and all the real approximate solutions are listed as $(1.23,-0.56),$ $(3.45,2.78), (-2.51,1.19), (5.67,1.89), (-4.92,-3.21), (-6.23,4.56), (7.89,-2.34)$, and $(-8.45,6.78)$. Hence, ${\mathfrak{F}}_2(c,x)$ has no solution in $(0,2)\times (0,1),$ implying that ${\mathfrak{F}}_2(c,x)$ has no optimal point within this interval.

From the above cases, it is clear that within the cuboid $\Xi$, the following is satisfied:

$$\begin{array}{c}\hfill {\mathfrak{F}}^{*}(c,x,y)\le \mathfrak{F}(c,x,y)\le \mathfrak{F}(c,x,1)\le {\mathfrak{F}}_1(c,x)\le {\mathfrak{F}}_2(c,x)\le 5806080.\end{array}$$

From (31), we deduce that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\mathfrak{H}}_{3,1}\left(\mathcal{F}\right)|& \le {\displaystyle \frac{1}{T}}\left({\mathfrak{F}}^{*}(c,x,y)\right)\hfill \\ & ={\displaystyle \frac{5}{64}}.\hfill \end{array}\end{array}$$

Hence, it completes the proof. □

4. Concluding Remarks

In this work, we have defined new subclass $\mathfrak{B}$ of bounded turning functions associated with analytic univalent functions $\Omega \left(z\right).$ We revealed the coefficient problem and many other geometric properties for this class such as the Fekete–Szegö functional, Hankel determinant, Krushkal inequality, and Zalcman conjecture. Moreover, we have established the sharpness of the Fekete–Szegö inequality and Zalcman functional associated with the logarithmic coefficient. Our work can be used for finding Hankel determinants of higher order.