A Novel Iterative Algorithm Applied to Totally Asymptotically Nonexpansive Mappings in CAT(0) Spaces

Abstract

In this paper we introduce a new iterative algorithm for approximating fixed points of totally asymptotically quasi-nonexpansive mappings on CAT(0) spaces. We prove a strong convergence theorem under suitable conditions. The result we obtain improves and extends several recent results stated by many others; they also complement many known recent results in the literature. We then provide some numerical examples to illustrate our main result and to display the efficiency of the proposed algorithm.

1. Introduction

Let $(X,d)$ be a given metric space and let $x,y$ be two poins in X with $d(x,y)=l$. By a geodesic path from x to y we mean an isometry $c:[0,l]\to c([0,1])\subset X$ with the property that $c(0)=x,$ $c(l)=y.$ The image of each geodesic path between two given points is said to be a geodesic segment. We call $(X,d)$ a geodesic space if every two points of X can be joined by a geodesic segment. By definition, a geodesic triangle $▵(x,y,z)$ consists of three points $x,y,z$ together with the three segments that join each pair of these points. A comparison triangle of a geodesic triangle $▵(x,y,z)$, which will be denoted by $\overline{▵}(x,y,z)$ or $▵(\overline{x},\overline{y},\overline{z}),$ is a triangle in the plane ${\mathbb{R}}^2$ such that $d(x,y)=d_{{\mathbb{R}}^2}(\overline{x},\overline{y}),$ $d(x,z)=d_{{\mathbb{R}}^2}(\overline{x},\overline{z}),$ and $d(y,z)=d_{{\mathbb{R}}^2}(\overline{y},\overline{z}).$ This is a consequence of the triangle inequality; and it is well-known that it is unique up to isometry. In [1] Bridson and Haefliger have proved that such a triangle always exists. A geodesic segment joining two points $x,y$ in a geodesic space X is denoted by $[x,y].$ Every point z in the segment is represented by $\alpha x\oplus (1-\alpha )y,$ where $\alpha \in [0,1],$ that is, $[x,y]:=\{\alpha x\oplus (1-\alpha )y:\alpha \in [0,1]\}.$ A subset $\mathcal{C}$ of a metric space X is called convex if for all $x,y\in \mathcal{C},$ $[x,y]\subset \mathcal{C}.$ A geodesic space is called a CAT(0) space if for every geodesic triangle ▵ and its comparison $\overline{▵},$ the following inequality holds true: $d(x,y)\le d_{{\mathbb{R}}^2}(\overline{x},\overline{y})$ for all $x,y\in ▵$ and $\overline{x},\overline{y}\in \overline{▵}.$ A complete CAT(0) space is often called a Hadamard space (see [2,3]). We mention in passsing that an $\mathbb{R}$-tree, a Hadamard manifold, and the Hilbert ball endowed with the hyperbolic metric are typical examples of CAT(0) spaces. For more information on CAT(0) spaces, the interested reader is referred to [4,5,6]. A geodesic space $(X,d)$ is called hyperbolic (see for instance [7,8]) if, for any $x,y,z\in X:$

$$d(\frac{1}{2}z\oplus \frac{1}{2}x,\frac{1}{2}z\oplus \frac{1}{2}y)\le \frac{1}{2}d(x,y)$$

Note that every normed space, and every CAT(0) space is a hyperbolic space. Bashir Ali in [9] constructed an example of a hyperbolic space that is not a normed space. Therefore the class of hyperbolic spaces properly includes the class of normed spaces.

Definition 1.

Let $\{x_n\}$ be a bounded sequence in a CAT(0) space $(X,d).$

(1) 

The asymptotic radius $r(\{x_n\})$ of $\{x_n\}$ is given by:

$$r(\{x_n\}):=\underset{x\in X}{inf}\{r(x,\{x_n\})\}$$

where $r(x,\{x_n\}):={lim\; sup}_{n\to \infty }d(x_n,x).$

(2) 

The asymptotic center $A(\{x_n\})$ of $\{x_n\}$ is the set:

$$A(\{x_n\}):=\{x\in X:r(x,\{x_n\})=r(\{x_n\})\}$$

In 2006, Dhompongsa et al. [10] observed that for a bounded sequence $\{x_n\}$ in a CAT(0) space, $A(\{x_n\})$ is a singleton.

Definition 2.

Let $\mathcal{C}$ be a nonempty, closed convex subset of a CAT(0) space $(X,d)$. A mapping $T:\mathcal{C}\to \mathcal{C}$ is said to be uniformly L-Lipschitzian if there exists a constant $L\ge 0$ such that:

$$d(T^{n}x,T^{n}y)\le Ld(x,y),\forall x,y\in \mathcal{C},andn\in \mathbb{N}$$

It is now time to recall the concept of ▵-convergence in a given CAT(0) space.

Definition 3.

Let $(X,d)$ be a CAT(0) space. A sequence $\{x_n\}$ in X is said to ▵-converge to $x\in X$ if and only if x is the unique asymptotic center of all subsequences of $\{x_n\}$. In this case, we write $▵-{lim}_{n\to \infty }{x}_n=x$ and call x the $▵-limitof\{x_n\}$.

In the following, we recall some basic facts regarding the nonlinear mappings on CAT(0) spaces.

Let $\mathcal{C}$ be a nonempty subset of a CAT(0) spaces $(X,d)$. A self-mapping $T:\mathcal{C}\to \mathcal{C}$ is called nonexpansive if $d(Tx,Ty)\le d(x,y)$ for all $x,y\in \mathcal{C}$ and is called quasi-nonexpansive if $Fix(T)=\{x\in \mathcal{C}:Tx=x\}\ne \varnothing$ and $d(Tx,p)\le d(x,p)$ for all $x\in \mathcal{C}$ and $p\in Fix(T).$ The class of quasi-nonexpansive mappings properly contains the class of nonexpansive mappings with fixed points; see, for example, [11]. A mapping T is called asymptotically nonexpansive [12] if there exists a sequence $\{k_n\}\subset [1,\infty )$ such that $k_n\to 1$ as $n\to \infty$ and, for every $n\in \mathbb{N}:$

$$d(T^{n}x,T^{n}y)\le k_{n}d(x,y),\forall x,y\in \mathcal{C}$$

If $Fix(T)\ne \varnothing$ and there exists a sequence $\{k_n\}\subset [1,\infty )$ such that $k_n\to 1$ as $n\to \infty$ and, for every $n\in \mathbb{N}:$

$$d(T^{n}x,p)\le k_{n}d(x,p),\forall x\in \mathcal{C},andp\in Fix(T)$$

then T is called an asymptotically quasi-nonexpansive mapping. A mapping T is called totally asymptotically nonexpansive if there exist null sequences ${\{u_n\}}_{n=1}^{\infty }$ and ${\{v_n\}}_{n=1}^{\infty }$ of nonnegative numbers (i.e., $u_n,v_n\to 0$ as $n\to \infty$) and a strictly increasing function $\psi :[0,\infty )\to [0,\infty )$ with $\psi (0)=0$ such that:

$$d(T^{n}x,T^{n}y)\le d(x,y)+u_n\psi (d(x,y))+v_n,\forall x,y\in \mathcal{C}$$

A mapping T is called totally asymptotically quasi-nonexpansive if $Fix(T)\ne \varnothing$ and there exist null sequences ${\{u_n\}}_{n=1}^{\infty }$ and ${\{v_n\}}_{n=1}^{\infty }$ of nonnegative numbers (i.e., $u_n,v_n\to 0$ as $n\to \infty$) and a strictly increasing function $\psi :[0,\infty )\to [0,\infty )$ with $\psi (0)=0$ such that:

$$d(T^{n}x,p)\le d(x,p)+u_n\psi (d(x,p))+v_n,\forall x\in \mathcal{C},andp\in Fix(T)$$

We recall that the concept of asymptotically nonexpansive mappings was first introduced by Goebel and Kirk [12]. Then Alber et al. [13] introduced the class of totally asymptotically nonexpansive mappings that generalizes several classes of maps that are extensions of asymptotically nonexpansive mappings. These classes of maps were extensively studied by several authors (see, e.g., [14,15,16,17,18,19], to list just a few). We remark that according to the Example 1 of [20], the class of totally asymptotically nonexpansive mappings properly contains the class of asymptotically nonexpansive mappings.

We now turn to recall some well-known iteration processes. The Mann iteration process is defined by the sequence $\{x_n\}:$

$$\left\{\begin{array}{c}{x}_1\in \mathcal{C}\hfill \\ x_{n+1}=(1-{\alpha }_n)x_n+{\alpha }_{n}T(x_n),n\ge 1\hfill \end{array}\right.$$

where ${\{{\alpha }_n\}}_{n=1}^{\infty }$ is a sequence in $(0,1).$

Further, the Ishikawa iteration process is defined as the sequence $\{x_n\}:$

$$\left\{\begin{array}{c}{x}_1\in \mathcal{C}\hfill \\ x_{n+1}=(1-{\alpha }_n)x_n+{\alpha }_{n}T(y_n)\hfill \\ y_n=(1-{\beta }_n)x_n+{\beta }_{n}T(x_n),n\ge 1\hfill \end{array}\right.$$

where ${\{{\alpha }_n\}}_{n=1}^{\infty }$ and ${\{{\beta }_n\}}_{n=1}^{\infty }$ are some numerical sequences in $(0,1).$

In 2016, Huang in [21], introduced the following algorithm for a family of nonexpansive mappings in a CAT(0) space:

$$\left\{\begin{array}{c}{x}_1\in \mathcal{C}\hfill \\ x_{n+1}={\alpha }_{n}f(x_n)⨁(1-{\alpha }_n)T_n(x_n),n\ge 1\hfill \end{array}\right.$$

(1)

where ${\{{\alpha }_n\}}_{n=1}^{\infty }$ is a sequence in $(0,1)$ and f is a ϕ-weak contraction on $\mathcal{C}.$

Further, in 2016, Balwant Singh Thakur, Dipti Thakur and Mihai Postolache in [22], introduced the following algorithm for nonexpansive mappings in uniformly convex Banach spaces:

$$\left\{\begin{array}{c}{x}_1\in \mathcal{C}\hfill \\ z_n=(1-{\beta }_n)x_n+{\beta }_{n}T(x_n)\hfill \\ y_n=T((1-{\alpha }_n)x_n+{\alpha }_n{z}_n)\hfill \\ x_{n+1}=T(y_n)\hfill \end{array}\right.$$

(2)

where ${\{{\alpha }_n\}}_{n=1}^{\infty }$ and ${\{{\beta }_n\}}_{n=1}^{\infty }$ are real sequences in $(0,1).$

In this paper, inspired by the Algorithms $(1)$ and $(2)$, we introduce a new iterative algorithm for approximating fixed points of totally asymptotically quasi-nonexpansive mappings in CAT(0) spaces. We prove some strong convergence theorems under suitable conditions. The results we obtain improve and extend several recent results stated by many others; they also complement many known results in the literature. We then provide two numerical examples to illustrate our main result and to display the efficiency of the proposed algorithm.

2. Preliminaries

Throughout this paper, we denote by $\mathbb{N}$ the set of positive integers and by $\mathbb{R}$ the set of real numbers. We write $x_n\rightharpoonup x$ to indicate that the sequence ${\{x_n\}}_{n=1}^{\infty }$ converges weakly to x, and $x_n\to x$ to indicate that the sequence ${\{x_n\}}_{n=1}^{\infty }$ converges strongly to x. We begin by recalling some known facts on the space CAT(0).

Lemma 1.

([23], Lemma 2) Let $\{a_n\},$ $\{{\varpi }_n\}$ and $\{{\xi }_n\}$ be sequences of nonnegative real numbers such that $a_{n+1}\le (1+{\varpi }_n)a_n+{\xi }_n,$ for all $n\ge 1.$ If ${\sum }_{n=1}^{\infty }{\varpi }_n<\infty$ and ${\sum }_{n=1}^{\infty }{\xi }_n<\infty ,$ then ${lim}_{n\to \infty }{a}_n$ exists. Moreover, if there exists a subsequence $\{a_{n_j}\}$ of $\{a_n\}$ such that $a_{n_j}\to 0$ as $j\to \infty ,$ then $a_n\to 0$ as $n\to \infty .$

Lemma 2.

([24], Lemma 4.5) Let x be a given point in a CAT(0) space $(X,d)$ and $\{t_n\}$ be a sequence in a closed interval $[a,b]$ with $0<a\le b<1$ and ${\displaystyle 0<a(1-b)\le \frac{1}{2}.}$ Suppose that $\{x_n\}$ and $\{y_n\}$ are two sequences in X such that:

(1) 

${lim\; sup}_{n\to \infty }d(x_n,x)\le r,$

(2) 

${lim\; sup}_{n\to \infty }d(y_n,x)\le r,$

(3) 

${lim\; sup}_{n\to \infty }d((1-t_n)x_n\oplus t_n{y}_n,x)=r$

for some $r\ge 0.$ Then ${lim}_{n\to \infty }d(x_n,y_n)=0.$

Lemma 3.

The following assertions in a CAT(0) space hold:

$({\mathcal{A}}_1)$

Every bounded sequence in a complete $CAT(0)$ space has a ▵-convergent subsequence [25].

$({\mathcal{A}}_2)$

If $\{x_n\}$ is a bounded sequence in a closed convex subset $\mathcal{C}$ of a complete CAT(0) space $(X,d)$, then the asymptotic center of $\{x_n\}$ is in $\mathcal{C}$ [26].

$({\mathcal{A}}_3)$

If $\{x_n\}$ is a bounded sequence in a complete CAT(0) space $(X,d)$ with $A(\{x_n\})=\{p\},$ $\{{\nu }_n\}$ is a subsequence of $\{x_n\}$ with $A(\{{\nu }_n\})=\{\nu \},$ and the sequence $\{d(x_n,\nu )\}$ converges, then $p=\nu$ [27].

Lemma 4.

([14], Theorem 2.8) Let $\mathcal{C}$ be a nonempty bounded closed convex subset of complete CAT(0) space $(X,d)$ and $T:\mathcal{C}\to \mathcal{C}$ be a totally asymptotically nonexpansive and uniformly L-Lipschitzian mapping. If $\{x_n\}$ is a bounded sequence in $\mathcal{C}$ such that ${lim}_{n\to \infty }d(x_n,T(x_n))=0$ and $▵-{lim}_{n\to \infty }{x}_n=p,$ then $T(p)=p.$

Theorem 5.

([28], Corollary 3.2) Let $\mathcal{C}$ be a nonempty bounded closed convex subset of complete CAT(0) space $(X,d)$ and $T:\mathcal{C}\to \mathcal{C}$ be a continuous totally asymptotically nonexpansive mapping. Then T has a fixed point.

3. Approximation Result

We begin this section by proving a strong convergence theorem for a totally asymptotically quasi-nonexpansive mapping.

Theorem 6.

Let $(X,d)$ be a complete CAT(0) space, $\mathcal{C}$ be a nonempty, closed convex subset of $(X,d)$ and $T:\mathcal{C}\to \mathcal{C}$ be a uniformly L-Lipschitzian and totally asymptotically quasi-nonexpansive mapping with sequences ${\{u_n\}}_{n=1}^{\infty },$ ${\{v_n\}}_{n=1}^{\infty }$ satisfying ${\sum }_{n=1}^{\infty }{u}_n<\infty$ and ${\sum }_{n=1}^{\infty }{v}_n<\infty ,$ and strictly increasing mapping $\psi :[0,\infty )\to [0,\infty )$ with $\psi (0)=0.$ Let ${\{{\alpha }_n\}}_{n=1}^{\infty },$ ${\{{\beta }_n\}}_{n=1}^{\infty }$ and ${\{{\gamma }_n\}}_{n=1}^{\infty }$ be sequences in $(0,1)$ and suppose that the following conditions are satisfied:

(C1) 

there exist constants $a,b$ such that $0<a\le {\alpha }_n\le b<1$ for all $n\in \mathbb{N},$

(C2) 

there exists a constant M such that $\psi (r)\le Mr$ for all $r\ge 0.$

Then ${\{x_n\}}_{n=1}^{\infty }$ defined by:

$$\left\{\begin{array}{c}{x}_1\in \mathcal{C}\hfill \\ z_n=(1-{\alpha }_n)x_n\oplus {\alpha }_n{T}^n(x_n)\hfill \\ y_n=(1-{\beta }_n)z_n\oplus {\beta }_n{T}^n(z_n)\hfill \\ x_{n+1}=(1-{\gamma }_n)T^n(z_n)\oplus {\gamma }_n{T}^n(y_n)\hfill \end{array}\right.$$

(3)

is ▵-convergent to some $p\in Fix(T).$

Proof. 

Since T is uniformly L-Lipschitzian, we have T is continuous. By using Theorem 5, we get $Fix(T)\ne \varnothing .$ Next, we will divide the proof into three steps.

Step 1. First, we will prove that ${lim}_{n\to \infty }d(x_n,x^{*})$ exists for each $x^{*}\in Fix(T),$ where $\{x_n\}$ is defined by $(3)$. For this purpose, let $x^{*}\in Fix(T),$ using the fact that ${\{{\alpha }_n\}}_{n=1}^{\infty }\subset (0,1)$ and by the condition $(\mathbf{C}\mathbf{2})$ we obtain:

$$\begin{array}{cc}d(z_n,x^{*})\hfill & =d((1-{\alpha }_n)x_n\oplus {\alpha }_n{T}^n(x_n),x^{*})\hfill \\ & \le (1-{\alpha }_n)d(x_n,x^{*})+{\alpha }_{n}d(T^n(x_n),x^{*})\hfill \\ & \le (1-{\alpha }_n)d(x_n,x^{*})+{\alpha }_n\left[d(x_n,x^{*})+u_n\psi (d(x_n,x^{*}))+v_n\right]\hfill \\ & =d(x_n,x^{*})+{\alpha }_n\left[u_n\psi (d(x_n,x^{*}))+v_n\right]\hfill \\ & \le d(x_n,x^{*})+u_n\psi (d(x_n,x^{*}))+v_n\hfill \\ & \le (1+M{u}_n)d(x_n,x^{*})+v_n\hfill \end{array}$$

(4)

for all $n\in \mathbb{N}.$ Also, we have:

$$\begin{array}{cc}\hfill d(y_n,x^{*})& =d((1-{\beta }_n)z_n\oplus {\beta }_n{T}^n(z_n),x^{*})\hfill \\ & \le (1-{\beta }_n)d(z_n,x^{*})+{\beta }_{n}d(T^n(z_n),x^{*})\hfill \\ & \le (1-{\beta }_n)d(z_n,x^{*})+{\beta }_n\left[d(z_n,x^{*})+u_n\psi (d(z_n,x^{*}))+v_n\right]\hfill \\ & =d(z_n,x^{*})+{\beta }_n\left[u_n\psi (d(z_n,x^{*}))+v_n\right]\hfill \\ & \le d(z_n,x^{*})+u_n\psi (d(z_n,x^{*}))+v_n\hfill \\ & \le (1+M{u}_n)d(z_n,x^{*})+v_n\hfill \\ & \le {(1+M{u}_n)}^{2}d(x_n,x^{*})+(1+M{u}_n)v_n+v_n\hfill \end{array}$$

(5)

for all $n\in \mathbb{N}.$ From $(3)$–$(5)$ and using the fact that ${\{{\gamma }_n\}}_{n=1}^{\infty }\subset (0,1),$ we conclude that:

$$\begin{array}{cc}d(x_{n+1},x^{*})\hfill & =d((1-{\gamma }_n)T^n(z_n)\oplus {\gamma }_n{T}^n(y_n),x^{*})\hfill \\ & \le (1-{\gamma }_n)d(T^n(z_n),x^{*})+{\gamma }_{n}d(T^n(y_n),x^{*})\hfill \\ & \le (1-{\gamma }_n)\left[d(z_n,x^{*})+u_n\psi (d(z_n,x^{*}))+v_n\right]\hfill \\ & +{\gamma }_n\left[d(y_n,x^{*})+u_n\psi (d(y_n,x^{*}))+v_n\right]\hfill \\ & \le (1-{\gamma }_n)\left[(1+M{u}_n)\left((1+M{u}_n)d(x_n,x^{*})+v_n\right)+v_n\right]\hfill \\ & +{\gamma }_n\left[(1+M{u}_n)\left({(1+M{u}_n)}^{2}d(x_n,x^{*})+(1+M{u}_n)v_n+v_n\right)+v_n\right]\hfill \\ & \le (1-{\gamma }_n){(1+M{u}_n)}^{2}d(x_n,x^{*})+(1-{\gamma }_n)(1+M{u}_n)v_n+(1-{\gamma }_n)v_n\hfill \\ & +{\gamma }_n{(1+M{u}_n)}^{3}d(x_n,x^{*})+{(1+M{u}_n)}^2{v}_n+{\gamma }_n(1+M{u}_n)v_n+{\gamma }_n{v}_n\hfill \\ & =(1+{\varpi }_n)d(x_n,x^{*})+{\xi }_n\hfill \end{array}$$

(6)

where ${\varpi }_n:=5M{u}_n+4{(M{u}_n)}^2+{(M{u}_n)}^3$ and ${\xi }_n:=\left[{(1+M{u}_n)}^2+(1+M{u}_n)+1\right]v_n.$ Forasmuch as ${\sum }_{n=1}^{\infty }{u}_n<\infty$ and ${\sum }_{n=1}^{\infty }{v}_n<\infty ,$ it follows that ${\sum }_{n=1}^{\infty }{\varpi }_n<\infty$ and ${\sum }_{n=1}^{\infty }{\xi }_n<\infty .$ Hence by Lemma 1, ${lim}_{n\to \infty }d(x_n,x^{*})$ exists.

Step 2. In this step, we will prove that ${lim}_{n\to \infty }d(x_n,T(x_n))=0.$ Without loss of generality, we may assume that:

$$\mathbf{r}:=\underset{n\to \infty }{lim}d(x_n,x^{*})$$

(7)

From $(4)$, we conclude that:

$$\underset{n\to \infty }{lim\; sup}d(z_n,x^{*})\le \mathbf{r}$$

(8)

Now, Using the fact that T being a totally asymptotically nonexpansive mapping and $(8)$, we have:

$$\begin{array}{cc}\hfill {\displaystyle \underset{n\to \infty }{lim\; sup}}d(T^n(z_n),x^{*})& \le {\displaystyle \underset{n\to \infty }{lim\; sup}}\left[d(z_n,x^{*})+u_n\psi (d(z_n,x^{*}))+v_n\right]\hfill \\ & \le {\displaystyle \underset{n\to \infty }{lim\; sup}}\left[(1+M{u}_n)d(z_n,x^{*})+v_n\right]\hfill \\ & \le \mathbf{r}\hfill \end{array}$$

(9)

By the same above argument, we get:

$$\underset{n\to \infty }{lim\; sup}d(T^n(x_n),x^{*})\le \mathbf{r}$$

(10)

Now, we can write:

$$\begin{array}{cc}\hfill \mathbf{r}={\displaystyle \underset{n\to \infty }{lim\; sup}}d(x_{n+1},x^{*})& ={\displaystyle \underset{n\to \infty }{lim\; sup}}d((1-{\gamma }_n)T^n(z_n)\oplus {\gamma }_n{T}^n(y_n),x^{*})\hfill \\ & \le {\displaystyle \underset{n\to \infty }{lim\; sup}}\left[(1-{\gamma }_n)d(T^n(z_n),x^{*})+{\gamma }_{n}d(T^n(y_n),x^{*})\right]\hfill \\ & \le (1-{\gamma }_n)\mathbf{r}+{\gamma }_n{\displaystyle \underset{n\to \infty }{lim\; sup}}d(T^n(y_n),x^{*})\hfill \\ & \le (1-{\gamma }_n)\mathbf{r}+{\gamma }_n{\displaystyle \underset{n\to \infty }{lim\; sup}}\left[d(y_n,x^{*})+u_n\psi (d(y_n,x^{*}))+v_n\right]\hfill \\ & \le (1-{\gamma }_n)\mathbf{r}+{\gamma }_n{\displaystyle \underset{n\to \infty }{lim\; sup}}d(y_n,x^{*})\hfill \end{array}$$

by arranging the above inequality, we conclude that:

$$\mathbf{r}\le \underset{n\to \infty }{lim\; sup}d(y_n,x^{*})$$

(11)

which implies that:

$$\mathbf{r}\le \underset{n\to \infty }{lim\; sup}d(z_n,x^{*})$$

(12)

From $(8)$ and $(12)$, we have:

$$\mathbf{r}=\underset{n\to \infty }{lim\; sup}d(z_n,x^{*})=\underset{n\to \infty }{lim\; sup}d((1-{\alpha }_n)x_n\oplus {\alpha }_n{T}^n(x_n),x^{*})$$

(13)

By using Lemma 2 with $(7)$, $(10)$ and $(13)$, we have:

$$\underset{n\to \infty }{lim}d(x_n,T^n(x_n))=0.$$

(14)

From $(5)$ and $(7)$, we have:

$$\underset{n\to \infty }{lim\; sup}d(y_n,x^{*})\le \mathbf{r}$$

(15)

Now, by Combining $(11)$ and $(15)$, we have:

$$\mathbf{r}=\underset{n\to \infty }{lim\; sup}d(y_n,x^{*})=\underset{n\to \infty }{lim\; sup}d((1-{\beta }_n)z_n\oplus {\beta }_n{T}^n(z_n),x^{*})$$

(16)

Again, by using Lemma 2 with $(8)$, $(9)$ and $(16)$, we have:

$$\underset{n\to \infty }{lim}d(z_n,T^n(z_n))=0$$

(17)

Using the definition of totally asymptotically nonexpansive mapping and $(14)$, we conclude that:

$$\begin{array}{cc}d(T^n(z_n),T^n(x_n))\hfill & \le d(z_n,x_n)+u_n\psi (d(z_n,x_n))+v_n\hfill \\ & \le (1+M{u}_n)d(z_n,x_n)+v_n\hfill \\ & =(1+M{u}_n)d((1-{\alpha }_n)x_n\oplus {\alpha }_n{T}^n(x_n),x_n)+v_n\hfill \\ & \le (1+M{u}_n)\left[(1-{\alpha }_n)d(x_n,x_n)+{\alpha }_{n}d(T^n(x_n),x_n)\right]+v_n\to 0,n\to \infty \hfill \end{array}$$

(18)

Also, by the same argument and $(17)$, we have:

$$\begin{array}{cc}d(T^n(y_n),T^n(z_n))\hfill & \le d(y_n,z_n)+u_n\psi (d(y_n,z_n))+v_n\hfill \\ & \le (1+M{u}_n)d(y_n,z_n)+v_n\hfill \\ & =(1+M{u}_n)d((1-{\beta }_n)z_n\oplus {\beta }_n{T}^n(z_n),z_n)+v_n\hfill \\ & \le (1+M{u}_n)\left[(1-{\beta }_n)d(z_n,z_n)+{\beta }_{n}d(T^n(z_n),z_n)\right]+v_n\to 0,n\to \infty \hfill \end{array}$$

(19)

By using the triangle inequality and $(18)$ and $(19)$, we have:

$$\underset{n\to \infty }{lim}d(T^n(x_n),T^n(y_n))=0,\forall n\in \mathbb{N}$$

(20)

Again, by using the triangle inequality and $(18)$ and $(20)$, we have:

$$\begin{array}{cc}d(x_n,x_{n+1})\hfill & =d(x_n,(1-{\gamma }_n)T^n(z_n)\oplus {\gamma }_n{T}^n(y_n))\hfill \\ & \le (1-{\gamma }_n)d(x_n,T^n(z_n))+{\gamma }_{n}d(x_n,T^n(y_n))\hfill \\ & \le \left[d(x_n,T^n(x_n))+d(T^n(x_n),T^n(z_n))\right]\hfill \\ & +\left[d(x_n,T^n(x_n))+d(T^n(x_n),T^n(y_n))\right]\to 0,n\to \infty \hfill \end{array}$$

(21)

Finally, with $(14)$ and $(21)$, we conclude that:

$$\begin{array}{cc}\hfill d(x_n,T(x_n))& \le d(x_n,x_{n+1})+d(x_{n+1},T^{n+1}(x_{n+1}))+d(T^{n+1}(x_{n+1}),T^{n+1}(x_n))+d(T^{n+1}(x_n),T(x_n))\hfill \\ & \le d(x_n,x_{n+1})+d(x_{n+1},T^{n+1}(x_{n+1}))+Ld(x_{n+1},x_n)+Ld(T^n(x_n),x_n)\to 0,n\to \infty \hfill \end{array}$$

Therefore, Step 2 is proved.

Step 3. Define:

$${\mathrm{\Omega }}_{▵}(x_n):=\bigcup _{\{{\nu }_n\}\subseteq \{x_n\}}A(\{{\nu }_n\})\subseteq Fix(T)$$

We claim that the sequence $\{x_n\}$ ▵-converges to a fixed point of T and ${\mathrm{\Omega }}_{▵}(x_n)$ consists of exactly one point. Assume that $\nu \in {\mathrm{\Omega }}_{▵}(x_n).$ From the definition of ${\mathrm{\Omega }}_{▵}(x_n),$ there is a subsequence $\{{\nu }_n\}$ of $\{x_n\}$ such that $A(\{{\nu }_n\})=\{\nu \}.$ From assertion $({\mathcal{A}}_1)$ in Lemma 3, there exists a subsequence $\{{\rho }_n\}$ of $\{{\nu }_n\}$ such that $▵-{lim}_{n\to \infty }{\rho }_n=\rho \in \mathcal{C}.$ Using Lemma 4, we conclude that $\rho \in Fix(T).$ Since $\{d({\nu }_n,\rho )\}$ converges, by assertion $({\mathcal{A}}_2)$ in Lemma 3, we obtain $\nu =\rho .$ Therefore ${\mathrm{\Omega }}_{▵}(x_n)\subseteq Fix(T).$ Finally, we show that ${\mathrm{\Omega }}_{▵}(x_n)$ consists of exactly one point. Let $\{{\nu }_n\}$ be a subsequence of $\{x_n\}$ such that $A(\{{\nu }_n\})=\{\nu \}$ and let $A(\{x_n\})=\{x\}.$ We have already seen that $\nu =\rho \in Fix(T).$ Since $\{d(x_n,\rho )\}$ converges, by assertion $({\mathcal{A}}_3)$ in Lemma 3, we have $x=\rho \in Fix(T)$, that is, ${\mathrm{\Omega }}_{▵}(x_n)=x.$ This completes the proof. ☐

Remark. 

We note that each nonexpansive mapping is an asymptotically nonexpansive mapping with a sequence $\{k_n:=1\}$ for all $n\in \mathbb{N}$ and each asymptotically nonexpansive mapping is a $(\{u_n\},\{v_n\},\psi )$-totally asymptotically nonexpansive mapping with two sequences $\{v_n:=k_n-1\}$ and $\{u_n=:0\}$ for all $n\in \mathbb{N}$ and ψ being the identity mapping. Also, we see that each asymptotically nonexpansive mapping is a uniformly L-Lipschitzian mapping with $L:={sup}_{n\in \mathbb{N}}\{k_n\}.$

3.1. Numerical Results

In the following, we supply a numerical example of totally asymptotically quasi-nonexpansive mappings satisfying the conditions of Theorem 6, and some numerical experiment results to explain the conclusion of our Algorithm $(3)$.

Example 1.

Consider $X=\mathbb{R}$ with its usual metric, so X is also a complete CAT(0) space. Let $\mathcal{C}=[-1,1]$ which clearly is a bounded closed convex subset of X. Define the mapping $T:\mathcal{C}⟶\mathcal{C}$ by ${\displaystyle T(x)=\frac{x}{2}.}$ Let $\psi :[0,\infty )\to [0,\infty )$ be a strictly increasing mapping with $\psi (0)=0.$ Let ${\displaystyle u_n=\frac{1}{n^2}}$ and ${\displaystyle v_n=\frac{1}{n^3}}$ for all $n\ge 1.$ Since the sequences ${\{u_n\}}_{n=1}^{\infty },$ ${\{v_n\}}_{n=1}^{\infty }$ satisfying $u_n,v_n\to 0$ as $n\to \infty ,$ for all $x,y\in \mathcal{C},$ we have:

$$\begin{array}{cc}\hfill |T^n(x)-T^n(y)|-|x-y|-u_n\psi (|x-y|)-v_n& {\displaystyle \le \frac{1}{2^n}|x-y|-|x-y|-u_n\psi (|x-y|)-v_n}\hfill \\ & \le |x-y|-|x-y|-u_n\psi (|x-y|)-v_n\le 0\hfill \end{array}$$

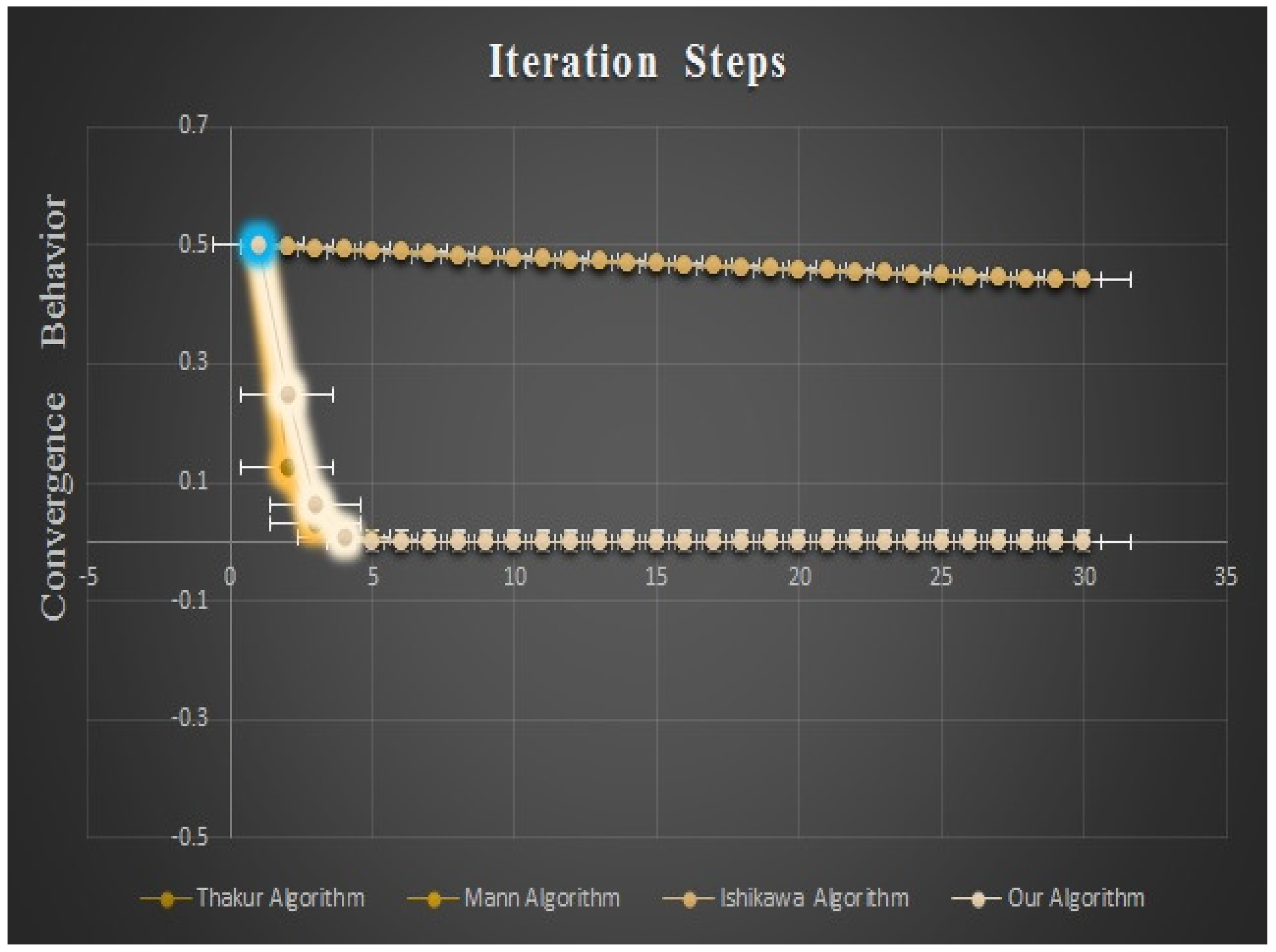
So T is a totally asymptotically quasi-nonexpansive mapping. Clearly, zero is the only fixed point of the mappings T. Put ${\displaystyle {\alpha }_n={\beta }_n={\gamma }_n=\frac{1}{n+100}.}$ By using MATHEMATICA, we computed the iterates of Equation $(3)$ for initial point ${\displaystyle x_1=\frac{1}{2}\in [-1,1].}$ Finally, by the numerical experiments we compared Mann iteration process, Ishikawa iteration process and Thakur iteration process with our Equation $(3)$ (see Table 1). Moreover, the convergence behaviors of these algorithms are shown in Figure 1. We conclude that $x_n$ converges to zero.

Table 1. Numerical results corresponding to ${\displaystyle x_1=\frac{1}{2}}$ for 30 steps.

Numerical Results
Step	Our Algorithm	Mann Algorithm	Ishikawa Algorithm	Thakur Algorithm
1	$0.5$	$0.5$	$0.5$	$0.5$
2	$0.24875$	$0.497525$	$0.497512$	$0.124994$
3	$0.0617258$	$0.495086$	$0.495062$	$0.031247$
4	$0.00764955$	$0.492683$	$0.492647$	$0.00781137$
5	$0.000473746$	$0.490314$	$0.490267$	$0.00195275$
6	$0.0000146667$	$0.487979$	$0.487921$	$0.000488166$
7	$2.27019\times {10}^{-7}$	$0.485677$	$0.485609$	$0.000122036$
8	$1.75699\times {10}^{-9}$	$0.483408$	$0.483329$	$0.0000305077$
9	$6.79935\times {10}^{-12}$	$0.481169$	$0.481081$	$7.62659\times {10}^{-6}$
10	$1.31573\times {10}^{-14}$	$0.478963$	$0.478864$	$1.90657\times {10}^{-6}$
11	$1.27312\times {10}^{-17}$	$0.476785$	$0.476678$	$4.76623\times {10}^{-7}$
12	$6.15991\times {10}^{-21}$	$0.474638$	$0.474521$	$1.19151\times {10}^{-7}$
13	$1.49034\times {10}^{-24}$	$0.472519$	$0.472393$	$2.97865\times {10}^{-8}$
14	$1.80303\times {10}^{-28}$	$0.470428$	$0.470293$	$7.44634\times {10}^{-9}$
15	$1.09074\times {10}^{-32}$	$0.468365$	$0.468222$	$1.86151\times {10}^{-9}$
16	$3.29949\times {10}^{-37}$	$0.466328$	$0.466177$	$4.65361\times {10}^{-10}$
17	$4.99085\times {10}^{-42}$	$0.464318$	$0.464159$	$1.16336\times {10}^{-10}$
18	$3.77489\times {10}^{-47}$	$0.462334$	$0.462167$	$2.90829\times {10}^{-11}$
19	$1.42770\times {10}^{-52}$	$0.460375$	$0.460200$	$7.27046\times {10}^{-12}$
20	$2.70005\times {10}^{-58}$	$0.458441$	$0.458259$	$1.81755\times {10}^{-12}$
21	$2.55333\times {10}^{-64}$	$0.456531$	$0.456341$	$4.54372\times {10}^{-13}$
22	$1.20738\times {10}^{-70}$	$0.454644$	$0.454448$	$1.13589\times {10}^{-13}$
23	$2.85483\times {10}^{-77}$	$0.452781$	$0.452578$	$2.83963\times {10}^{-14}$
24	$3.37533\times {10}^{-84}$	$0.450940$	$0.450730$	$7.09885\times {10}^{-15}$
25	$1.99550\times {10}^{-91}$	$0.449122$	$0.448906$	$1.77465\times {10}^{-15}$
26	$5.89910\times {10}^{-99}$	$0.447325$	$0.447103$	$4.43649\times {10}^{-16}$
27	$8.72003\times {10}^{-107}$	$0.445550$	$0.445322$	$1.10909\times {10}^{-16}$
28	$6.44537\times {10}^{-115}$	$0.443796$	$0.443561$	$2.77263\times {10}^{-17}$
29	$2.38219\times {10}^{-123}$	$0.442063$	$0.441822$	$6.93138\times {10}^{-18}$
30	$4.40250\times {10}^{-132}$	$0.440349$	$0.440103$	$1.73279\times {10}^{-18}$

Figure 1. Convergence behaviors corresponding to ${\displaystyle x_1=\frac{1}{2}}$ for 30 steps.

Example 2.

Consider $X={\mathbb{R}}^2$ equipped with the Euclidean norm. Let $x=(x_1,x_2)\in {\mathbb{R}}^2,$ then the squared distance of x from the origin is:

$${\parallel x\parallel }^2=x_1^2+x_2^2$$

Consider $\mathcal{C}$ as the closed unit disk:

$$\mathcal{C}=\{(x_1,x_2)\in {\mathbb{R}}^2:x_1^2+x_2^2\le 1\}$$

which is bounded, closed, and convex in X. We define the mapping ${\mathrm{Rot}}_{\theta }:\mathcal{C}⟶\mathcal{C}$ by:

$${\mathrm{Rot}}_{\theta }(x_1,x_2):=\left[\begin{array}{cc}cos(\theta )& -sin(\theta )\\ sin(\theta )& cos(\theta )\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$$

Let ${\displaystyle \theta =\frac{\pi }{4}}$. It is easy to see that ${\mathrm{Rot}}_{\theta }$ is nonexpansive, since for all $(x_1,x_2),(y_1,y_2)\in \mathcal{C},$ we have:

$$\begin{array}{cc}\hfill \parallel {\mathrm{Rot}}_{\theta }(x_1,x_2)-{\mathrm{Rot}}_{\theta }(y_1,y_2)\parallel & {\displaystyle =\frac{1}{2}\parallel \left[\begin{array}{c}{x}_1-x_2\\ x_1+x_2\end{array}\right]-\left[\begin{array}{c}{y}_1-y_2\\ y_1+y_2\end{array}\right]\parallel }\hfill \\ & {\displaystyle =\frac{1}{2}\parallel \left[\begin{array}{c}(x_1-y_1)-(x_2-y_2)\\ (x_1-y_1)+(x_2-y_2)\end{array}\right]\parallel }\hfill \\ & {\displaystyle =\frac{1}{2}\sqrt{{[(x_1-y_1)-(x_2-y_2)]}^2+{[(x_1-y_1)+(x_2-y_2)]}^2}}\hfill \\ & {\displaystyle =\frac{\sqrt{2}}{2}\sqrt{{(x_1-y_1)}^2+(x_2-y_2)2}}\hfill \\ & {\displaystyle =\frac{\sqrt{2}}{2}\parallel x-y\parallel }\hfill \end{array}$$

Let $\psi :[0,\infty )\to [0,\infty )$ be a strictly increasing mapping with $\psi (0)=0,$ and let ${\displaystyle u_n=\frac{1}{n^2}}$ and ${\displaystyle v_n=\frac{1}{n^3}}$ for all $n\ge 1.$ Since the sequences ${\{u_n\}}_{n=1}^{\infty }$ and ${\{v_n\}}_{n=1}^{\infty }$ satisfy $u_n,v_n\to 0$ as $n\to \infty$, it follows that for all $x,y\in \mathcal{C}$ and $n\ge 1,$ we have:

$$\begin{array}{cc}\hfill \parallel {\mathrm{Rot}}_{\theta }^n(x)-{\mathrm{Rot}}_{\theta }^n(y)\parallel -\parallel x-y\parallel -u_n\psi (\parallel x-y\parallel )-v_n& {\displaystyle \le {(\frac{\sqrt{2}}{2})}^n\parallel x-y\parallel -\parallel x-y\parallel -u_n\psi (\parallel x-y\parallel )-v_n}\hfill \\ & \le \parallel x-y\parallel -\parallel x-y\parallel -u_n\psi (\parallel x-y\parallel )-v_n\hfill \\ & \le 0\hfill \end{array}$$

This means that ${\mathrm{Rot}}_{\theta }$ is a totally asymptotically quasi-nonexpansive mapping. Clearly, zero is the only fixed point of the mapping ${\mathrm{Rot}}_{\theta }$ for ${\displaystyle \theta =\frac{\pi }{4}.}$ In this case, our algorithm is the following:

$$\left\{\begin{array}{c}{x}_{(1)}=(x_{{(1)}_1},x_{{(1)}_2})\in \mathcal{C}\hfill \\ (z_{{(n)}_1},z_{{(n)}_2})=(1-{\alpha }_n)(x_{{(n)}_1},x_{{(n)}_2})+{\alpha }_n{\mathrm{Rot}}_{\theta }^n(x_{{(n)}_1},x_{{(n)}_2})\hfill \\ (y_{{(n)}_1},y_{{(n)}_2})=(1-{\beta }_n)(z_{{(n)}_1},z_{{(n)}_2})+{\beta }_n{\mathrm{Rot}}_{\theta }^n(z_{{(n)}_1},z_{{(n)}_2})\hfill \\ (x_{{(n+1)}_1},x_{{(n+1)}_2})=(1-{\gamma }_n){\mathrm{Rot}}_{\theta }^n(z_{{(n)}_1},z_{{(n)}_2})+{\gamma }_n{\mathrm{Rot}}_{\theta }^n(y_{{(n)}_1},y_{{(n)}_2})\hfill \end{array}\right.$$

(22)

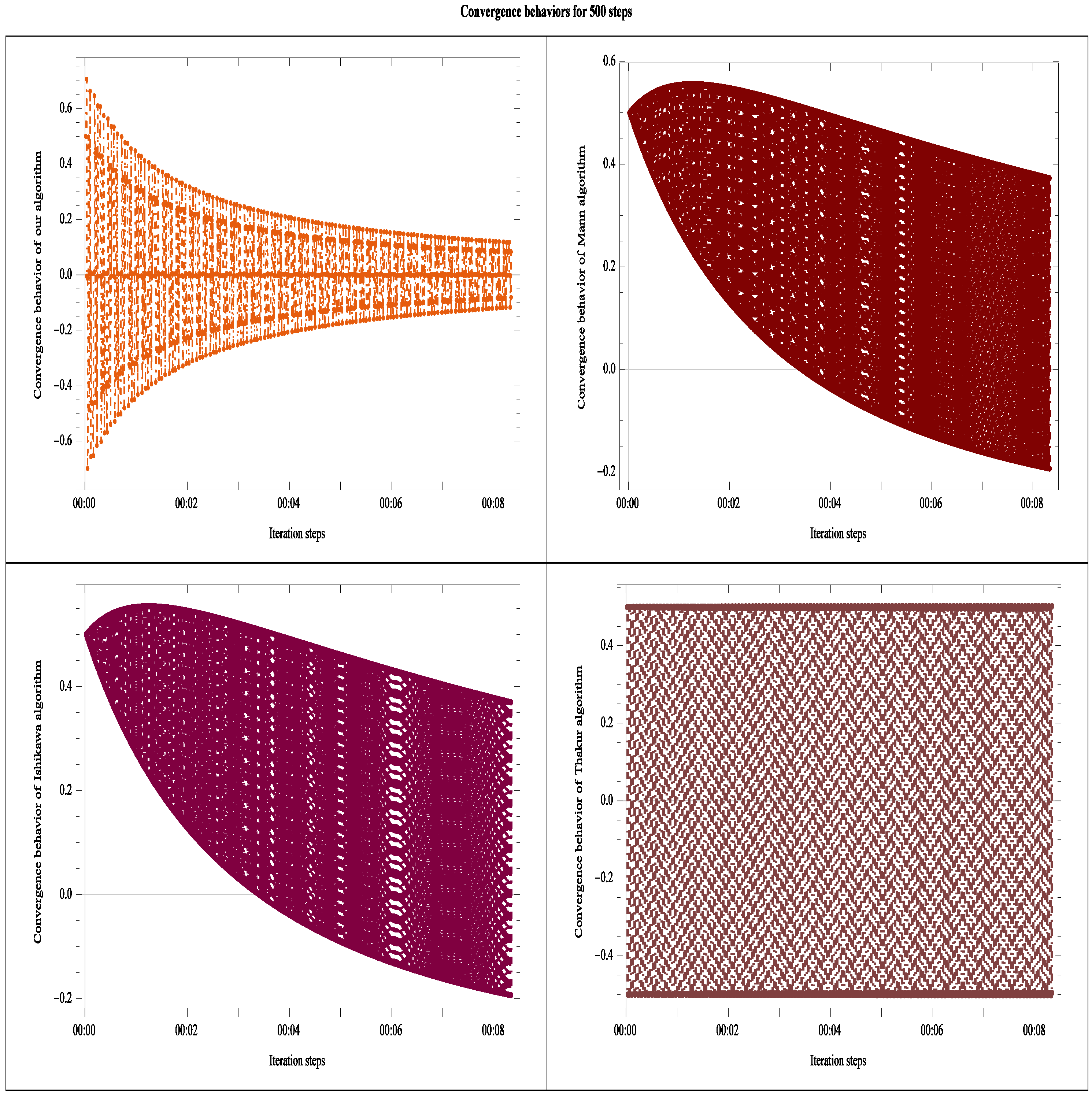
Put ${\displaystyle {\alpha }_n={\beta }_n={\gamma }_n=\frac{1}{n+100}.}$ By using MATHEMATICA, we computed the iterates of Algorithm $(22)$ for initial point ${\displaystyle x_{(1)}=(\frac{1}{2},\frac{1}{2})\in \mathcal{C}}$ for 500 steps. Finally, by the numerical experiments we compared Mann iteration process, Ishikawa iteration process and Thakur iteration process with our Algorithm $(22)$ (see Table 2). The convergence behaviors of these algorithms are shown in Figure 2. The conclusion is that $x_n$ converges to zero.

Table 2. Numerical results corresponding to ${\displaystyle x_{(1)}=(\frac{1}{2},\frac{1}{2})}$ for 30 steps.

Numerical Results
Step	Our Algorithm	Mann Algorithm	Ishikawa Algorithm	Thakur Algorithm
1	$(0.5,0.5)$	$(0.5,0.5)$	$(0.5,0.5)$	$(0.5,0.5)$
2	$(0.705,-0.005)$	$(0.502,0.495)$	$(0.502,0.495)$	$(0.499,-0.500)$
3	$(-0.012,-0.698)$	$(0.504,0.490)$	$(0.504,0.490)$	$(-0.500,-0.499)$
4	$(-0.474,0.497)$	$(0.506,0.485)$	$(0.506,0.485)$	$(-0.499,0.500)$
5	$(0.464,-0.487)$	$(0.508,0.480)$	$(0.508,0.480)$	$(0.500,0.499)$
6	$(0.011,0.662)$	$(0.510,0.476)$	$(0.510,0.475)$	$(0.499,-0.500)$
7	$(-0.656,0.005)$	$(0.511,0.471)$	$(0.511,0.471)$	$(-0.500,-0.499)$
8	$(-0.463,-0.462)$	$(0.513,0.466)$	$(0.513,0.466)$	$(-0.499,0.500)$
9	$(-0.463,-0.462)$	$(0.515,0.462)$	$(0.515,0.461)$	$(0.500,0.499)$
10	$(-0.652,0.005)$	$(0.516,0.457)$	$(0.516,0.457)$	$(0.499,-0.500)$
11	$(0.011,0.646)$	$(0.518,0.453)$	$(0.518,0.452)$	$(-0.500,-0.499)$
12	$(0.439,-0.460)$	$(0.519,0.448)$	$(0.519,0.448)$	$(-0.499,0.500)$
13	$(-0.431,0.452)$	$(0.521,0.444)$	$(0.521,0.443)$	$(0.500,0.499)$
14	$(-0.010,-0.615)$	$(0.522,0.439)$	$(0.522,0.439)$	$(0.499,-0.500)$
15	$(0.610,-0.0048)$	$(0.524,0.435)$	$(0.523,0.434)$	$(-0.500,-0.499)$
16	$(0.431,0.429)$	$(0.525,0.431)$	$(0.525,0.430)$	$(-0.499,0.500)$
17	$(0.431,0.429)$	$(0.526,0.426)$	$(0.526,0.426)$	$(0.500,0.499)$
18	$(0.607,-0.005)$	$(0.528,0.422)$	$(0.527,0.421)$	$(0.499,-0.500)$
19	$(-0.010,-0.602)$	$(0.529,0.418)$	$(0.526,0.417)$	$(-0.500,-0.499)$
20	$(-0.410,0.429)$	$(0.530,0.414)$	$(0.530,0.413)$	$(-0.499,0.500)$
21	$(0.402,-0.421)$	$(0.531,0.409)$	$(0.531,0.409)$	$(0.500,0.499)$
22	$(0.009,0.575)$	$(0.532,0.405)$	$(0.532,0.405)$	$(0.499,-0.500)$
23	$(-0.570,0.004)$	$(0.533,0.401)$	$(0.533,0.401)$	$(-0.500,-0.499)$
24	$(-0.403,-0.401)$	$(0.534,0.397)$	$(0.534,0.397)$	$(-0.499,0.500)$
25	$(-0.403,-0.401)$	$(0.535,0.393)$	$(0.535,0.392)$	$(0.500,0.499)$
26	$(-0.567,0.004)$	$(0.536,0.389)$	$(0.536,0.389)$	$(0.499,-0.500)$
27	$(0.009,0.563)$	$(0.537,0.385)$	$(0.537,0.385)$	$(-0.500,-0.498)$
28	$(0.384,-0.401)$	$(0.538,0.382)$	$(0.538,0.381)$	$(-0.498,0.500)$
29	$(-0.378,0.395)$	$(0.539,0.378)$	$(0.536,0.377)$	$(0.500,0.498)$
30	$(-0.008,-0.539)$	$(0.540,0.373)$	$(0.539,0.373)$	$(0.498,-0.500)$

Figure 2. Convergence behaviors corresponding to ${\displaystyle x_{(1)}=(\frac{1}{2},\frac{1}{2})}$ for 500 steps.