Fuzzy Filters of Hoops Based on Fuzzy Points

Abstract

In this paper, we define the concepts of $(\in ,\in )$ and $(\in ,\in \vee q)$-fuzzy filters of hoops, discuss some properties, and find some equivalent definitions of them. We define a congruence relation on hoops by an $(\in ,\in )$-fuzzy filter and show that the quotient structure of this relation is a hoop.

1. Introduction

The hoop, which was introduced by Bosbach in [1,2], is naturally-ordered commutative residuated integral monoids. Several properties of hoops are displayed in [3,4,5,6,7,8,9,10,11,12,13,14]. The idea of the quasi-coincidence of a fuzzy point with a fuzzy set, which was introduced in [15], has played a very important role in generating fuzzy subalgebras of $BCK/BCI$-algebras, called $(\alpha ,\beta )$-fuzzy subalgebras of $BCK/BCI$-algebras, introduced by Jun [16]. Moreover, $(\in ,\in \vee q)$-fuzzy subalgebra is a useful generalization of a fuzzy subalgebra in $BCK/BCI$-algebras. Many researcher applied the fuzzy structures on logical algebras [17,18,19,20,21,22]. Now, in this paper, we want to introduce these notions and investigate the existing fuzzy subsystems on hoops. Borzooei and Aaly Kologani in [8] defined the concepts of filters, (positive) implicative and fantastic filters of the hoop, and discussed their properties. Then, they defined a congruence relation on the hoop by a filter and proved that the quotient structure of this relation is a hoop. Finally, they investigated under what conditions that quotient structure will be the Brouwerian semilattice, Heyting algebra, and the Wajsberg hoop.

The aim of the paper is to define the concepts of $(\in ,\in )$-fuzzy filters and $(\in ,\in \vee q)$-fuzzy filters of hoops, discuss some properties and find equivalent definitions of them. By using an $(\in ,\in )$-fuzzy filter of hoops, we define a congruence relation on hoops, and we show that the quotient structure of this relation forms a hoop.

2. Preliminaries

By a hoop, we mean an algebraic structure $(H,\odot ,\to ,1)$ in which $(H,\odot ,1)$ is a commutative, monoid and for any $x,y,z\in H$, the following assertions are valid.

(H1)

$x\to x=1$.

(H2)

$x\odot (x\to y)=y\odot (y\to x)$.

(H3)

$x\to (y\to z)=(x\odot y)\to z$(See [1,2]).

For any $x,y\in H$, we can define a relation ≤ on hoop H by $x\le y$ if and only if $x\to y=1$. It is easy to see that $(H,\le )$ is a poset. Therefore, in any hoop H, if for any $x\in H$, there exists an element $0\in H$ such that $0\le x$, then H is called a bounded hoop. Let $x^0=1,x^n=x^{n-1}\odot x$, for any $n\in \mathbb{N}$. If H is a bounded hoop, then we define a negation “ ′ ” on H by $x^{\prime }=x\to 0$, for all $x\in H$. By a sub-hoop of a hoop H, we mean a subset S of H that satisfies the condition:

$$\begin{array}{c}\hfill (\forall x,y\in H)(x,y\in S\Rightarrow x\odot y\in S,x\to y\in S).\end{array}$$

(1)

Note that every non-empty sub-hoop contains the element 1.

Proposition 1.

[23] Let $(H,\odot ,\to ,1)$ be a hoop. Then, the following conditions hold, for all $x,y,z\in H$:

• $(i)$$(H,\le )$ is a meet-semilattice such that $x\wedge y=x\odot (x\to y)$.
• $(ii)$$x\odot y\le z$ if and only if $x\le y\to z$.
• $(iii)$$x\odot y\le x,y$ and $x^n\le x$, for any $n\in \mathbb{N}$.
• $(iv)$$x\le y\to x$.
• $(v)$$1\to x=x$ and $x\to 1=1$.
• $(vi)$$x\le (x\to y)\to y$.
• $(vii)$$(x\to y)\odot (y\to z)\le (x\to z)$.
• $(viii)$$x\le y$ implies $x\odot z\le y\odot z$, $z\to x\le z\to y$ and $y\to z\le x\to z$.

Let F be a non-empty subset of a hoop H. Then, F is called a filter of H if, for any $x,y\in F$, $x\odot y\in F$ and, for any $y\in H$ and $x\in F$, if $x\le y$, then $y\in F$ (see [23]).

Let X be a nonempty set, $x\in X$ and $t\in (0,1]$. The fuzzy point with support x and value t is defined as:

$$\mu (y):=\left\{\begin{array}{cc}t\in (0,1]\hfill & \mathrm{if}y=x,\hfill \\ 0\hfill & \mathrm{if}y\ne x,\hfill \end{array}\right.$$

and is denoted by $x_t.$

For a fuzzy point $x_t$ and a fuzzy set $\lambda$ in a set X, Pu and Liu [15] defined the symbol $x_t\alpha \lambda ,$ where $\alpha \in \{\in ,q,\in \vee q,\in \wedge q\}.$ This means that, $x_t\in \lambda$ (resp. $x_{t}q\lambda$) if $\lambda (x)\ge t$ (resp. $\lambda (x)+t>1$). Then, $x_t$ is said to belong to (resp. be quasi-coincident with) a fuzzy set $\lambda .$ Moreover, $x_t\in \vee q\lambda$ (resp. $x_t\in \wedge q\lambda$) means that $x_t\in \lambda$ or $x_{t}q\lambda$ (resp. $x_t\in \lambda$ and $x_{t}q\lambda$).

From now one, we let H denote a hoop, unless otherwise specified.

3. $\mathbf{(}\mathit{\alpha }\mathbf{,}\mathit{\beta }\mathbf{)}$-Fuzzy Filters for $\mathbf{(}\mathit{\alpha }\mathbf{,}\mathit{\beta }\mathbf{)}\mathbf{\in }\mathbf{\left\{}\mathbf{\right(}\mathbf{\in }\mathbf{,}\mathbf{\in }\mathbf{)}\mathbf{,}\mathbf{(}\mathbf{\in }\mathbf{,}\mathbf{\in }\mathbf{\vee }\mathit{q}\mathbf{\left)}\mathbf{\right\}}$

In this section, we define $(\alpha ,\beta )$-fuzzy filters of hoops for $(\alpha ,\beta )\in \{(\in ,\in ),(\in ,\in \vee q)\}$, and we investigate some of their properties. Furthermore, we define a congruence relation on hoops by these filters and prove that the corresponding quotients are a bounded hoop.

Definition 1.

Let $(\alpha ,\beta )\in \{(\in ,\in ),(\in ,\in \vee q)\}$. Let λ be a fuzzy set of H. Then, λ is called an $(\alpha ,\beta )$-fuzzy filter of H if the following assertions are valid.

$$(\forall x\in H)(\forall t\in (0,1])(x_t\alpha \lambda \Rightarrow 1_t\beta \lambda ),$$

(2)

$$(\forall x,y\in H)(\forall t,k\in (0,1])(x_t\alpha \lambda ,{(x\to y)}_k\alpha \lambda \Rightarrow y_{min\{t,k\}}\beta \lambda ).$$

(3)

Example 1.

On the set $H=\{0,a,b,1\}$, we define two operations ⊙ and → on H by:

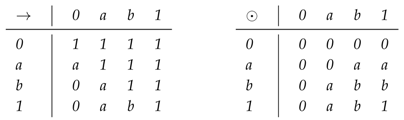Then, (H, ⊙, →, 1) is a hoop. Define the fuzzy set λ in H by $\lambda (0)=\lambda (a)=0.4$, $\lambda (b)=0.6$, and $\lambda (1)=0.8$. Then, λ is an $(\in ,\in )$-fuzzy filter of H, and it is clear that λ is an $(\in ,\in \vee q)$-fuzzy filter of H.

Theorem 1.

A fuzzy set λ in H is an $(\in ,\in )$-fuzzy filter of H if and only if the following conditions hold:

$$(\forall x\in H)(\lambda (1)\ge \lambda (x)),$$

(4)

$$(\forall x,y\in H)(\lambda (y)\ge min\{\lambda (x),\lambda (x\to y)\}).$$

(5)

Proof. 

Let $\lambda$ be an $(\in ,\in )$-fuzzy filter of H and $x\in H$ such that $\lambda (x)=t$. Since $\lambda$ is an $(\in ,\in )$-fuzzy filter of H, by Definition 1, $\lambda (1)\ge t=\lambda (x)$. Therefore, $\lambda (1)\ge \lambda (x)$. Now, let $x,y\in H$. If $\lambda (x)=t$ and $\lambda (x\to y)=k$, then $x_t\in \lambda$ and ${(x\to y)}_k\in \lambda$. Since $\lambda$ is an $(\in ,\in )$-fuzzy filter of H, we have $y_{min\{t,k\}}\in \lambda$, so:

$$\lambda (y)\ge min\{t,k\}=min\{\lambda (x),\lambda (x\to y)\}$$

Conversely, suppose $x\in H$ and $t\in (0,1]$. If $x_t\in \lambda$, then $\lambda (x)\ge t$. Since $\lambda (1)\ge \lambda (x)$, we have $\lambda (1)\ge t$, and so, $1_t\in \lambda$. Furthermore, if $x_t\in \lambda$ and ${(x\to y)}_k\in \lambda$, then by assumption,

$$\lambda (y)\ge min\{\lambda (x),\lambda (x\to y)\}\ge min\{t,k\}$$

Hence, $y_{min\{t,k\}}\in \lambda$. Therefore, $\lambda$ is an $(\in ,\in )$-fuzzy filter of H. □

Proposition 2.

If λ is an $(\in ,\in )$-fuzzy filter of H, then the following statement holds.

$$\begin{array}{c}\hfill (\forall x,y\in H)(x\le y\Rightarrow \lambda (x)\le \lambda (y)).\end{array}$$

(6)

Proof. 

Let $x,y\in H$ such that $x\le y$. Therefore, it is clear that $x\to y=1$. Since $\lambda$ is an $(\in ,\in )$-fuzzy filter of H, by Theorem 1, $\lambda (1)\ge \lambda (x)$ and $\lambda (y)\ge min\{\lambda (x),\lambda (x\to y)\}$, for any $x,y\in H$. Then:

$$\lambda (y)\ge min\{\lambda (x),\lambda (x\to y)\}=min\{\lambda (x),\lambda (1)\}=\lambda (x)$$

Hence, $\lambda (y)\ge \lambda (x)$. □

Theorem 2.

A fuzzy set λ in H is an $(\in ,\in )$-fuzzy sub-hoop of H such that, for any $x\in H$, $\lambda (x)\le \lambda (1)$. Then, for any $x,y,z\in H$, the following statements are equivalent:

• $(i)$ λ is an $(\in ,\in )$-fuzzy filter of H,
• $(ii)$ if ${(x\to y)}_t\in \lambda$ and ${(y\to z)}_k\in \lambda$, then ${(x\to z)}_{min\{t,k\}}\in \lambda$,
• $(iii)$ if ${(x\to y)}_t\in \lambda$ and ${(x\odot z)}_k\in \lambda$, then ${(y\odot z)}_{min\{t,k\}}\in \lambda$.

Proof. 

$(i)\Rightarrow (ii)$ Let $\lambda$ be an $(\in ,\in )$-fuzzy filter of H such that ${(x\to y)}_t\in \lambda$ and ${(y\to z)}_k\in \lambda$. Then, $\lambda (x\to y)\ge t$ and $\lambda (y\to z)\ge k$. By Proposition 1(vii), $x\to y\le (y\to z)\to (x\to z)$. Then, by Proposition 2,

$$\lambda (x\to y)\le \lambda ((y\to z)\to (x\to z))$$

Since ${(x\to y)}_t\in \lambda$, we have ${((y\to z)\to (x\to z))}_t\in \lambda$. Thus, by (i),

$$\begin{array}{ccc}\hfill min\{t,k\}& \le & min\{\lambda (x\to y),\lambda (y\to z)\}\hfill \\ & \le & min\{\lambda ((y\to z)\to (x\to z)),\lambda (y\to z)\}\hfill \\ & \le & \lambda (x\to z)\hfill \end{array}$$

Hence, ${(x\to z)}_{min\{t,k\}}\in \lambda$.

• $(ii)\Rightarrow (i)$ It is enough to let $x=1$.
• $(i)\Rightarrow (iii)$ Let $\lambda$ be an $(\in ,\in )$-fuzzy filter of H such that ${(x\to y)}_t\in \lambda$ and ${(x\odot z)}_k\in \lambda$. Then, by Proposition 1(vi), $z\odot x\odot (x\to y)\le z\odot y$. Thus, $x\to y\le (z\odot x)\to (z\odot y)$. By Proposition 2, $\lambda (x\to y)\le \lambda ((z\odot x)\to (z\odot y))$, so:

  $$\begin{array}{ccc}\hfill min\{t,k\}& \le & min\{\lambda (x\to y),\lambda (z\odot x)\}\hfill \\ & \le & min\{\lambda (z\odot x),\lambda ((z\odot x)\to (z\odot y))\}\hfill \\ & \le & \lambda (z\odot y)\hfill \end{array}$$

  Hence, ${(y\odot z)}_{min\{t,k\}}\in \lambda$.
• $(iii)\Rightarrow (i)$ It is enough to let $z=1$. □

Theorem 3.

Let λ be an $(\in ,\in )$-fuzzy filter of H, $x,y\in H$, and $t\in (0,1]$. Define:

$$x{\equiv }_{\lambda }yifandonlyif{(x\to y)}_t\in \lambda and{(y\to x)}_t\in \lambda$$

Then, ${\equiv }_{\lambda }$ is a congruence relation on H.

Proof. 

It is clear that ${\equiv }_{\lambda }$ is reflexive and symmetric. Now, we prove that ${\equiv }_{\lambda }$ is transitive. For this, suppose $x{\equiv }_{\lambda }y$ and $y{\equiv }_{\lambda }z$. Then, there exists $t,m\in (0,1]$ such that ${(x\to y)}_t\in \lambda \mathrm{and}{(y\to x)}_t\in \lambda$, and also, ${(y\to z)}_m\in \lambda \mathrm{and}{(z\to y)}_m\in \lambda$. By Proposition 1(vii), $x\to y\le (y\to z)\to (x\to z)$, and by Proposition 2, we have:

$$\begin{array}{ccc}\hfill min\{t,m\}& \le & min\{\lambda (x\to y),\lambda (y\to z)\}\hfill \\ & \le & min\{\lambda (y\to z),\lambda ((y\to z)\to (x\to z))\}\hfill \\ & \le & \lambda (x\to z)\hfill \end{array}$$

Hence, ${(x\to z)}_{min\{t,m\}}\in \lambda$. In a similar way, we get that:

$$\begin{array}{ccc}\hfill min\{t,m\}& \le & min\{\lambda (z\to y),\lambda (y\to x)\}\hfill \\ & \le & min\{\lambda (y\to x),\lambda ((y\to x)\to (z\to x))\}\hfill \\ & \le & \lambda (z\to x)\hfill \end{array}$$

Hence, ${(z\to x)}_{min\{t,m\}}\in \lambda$. Therefore, $x{\equiv }_{\lambda }z$. Suppose that $x{\equiv }_{\lambda }y$. We show that $x\odot z{\equiv }_{\lambda }y\odot z$, for any $x,y,z\in H$. Since $x{\equiv }_{\lambda }y$, for any $t\in (0,1]$, we have ${(x\to y)}_t\in \lambda \mathrm{and}{(y\to x)}_t\in \lambda$. Since $y\odot z\le y\odot z$, $y\le z\to (y\odot z)$. By Proposition 1(viii), $x\to y\le x\to (z\to (y\odot z))$, and so, $x\to y\le (x\odot z)\to (y\odot z)$. Since $\lambda$ is an $(\in ,\in )$-fuzzy filter of H, by Proposition 2, we have:

$$t\le \lambda (x\to y)\le \lambda ((x\odot z)\to (y\odot z))$$

Hence, ${((x\odot z)\to (y\odot z))}_t\in \lambda$. In a similar way, since $x\odot z\le x\odot z$, we get $x\le z\to (x\odot z)$. By Proposition 1(viii), $y\to x\le y\to (z\to (x\odot z))$, and so, $y\to x\le (y\odot z)\to (y\odot z)$. Since $\lambda$ is an $(\in ,\in )$-fuzzy filter of H, by Proposition 2, we have:

$$t\le \lambda (y\to x)\le \lambda ((y\odot z)\to (x\odot z))$$

Hence, ${((y\odot z)\to (x\odot z))}_t\in \lambda$. Therefore, $x\odot z{\equiv }_{\lambda }y\odot z$. Finally, suppose that $x{\equiv }_{\lambda }y$; we show that $x\to z{\equiv }_{\lambda }y\to z$, for any $x,y,z\in H$. Since $x{\equiv }_{\lambda }y$, for any $t\in (0,1]$, we have ${(x\to y)}_t\in \lambda \mathrm{and}{(y\to x)}_t\in \lambda$. By Proposition 1(vii) and Proposition 2,

$$t\le \lambda (x\to y)\le \lambda ((y\to z)\to (x\to z))$$

and:

$$t\le \lambda (y\to x)\le \lambda ((x\to z)\to (y\to z))$$

Hence, $x\to z{\equiv }_{\lambda }y\to z$. It is easy to see that $z\to x{\equiv }_{\lambda }z\to y$. Therefore, ${\equiv }_{\lambda }$ is a congruence relation on H. □

Theorem 4.

Let $\frac{H}{{\equiv }_{\lambda }}=\{{[a]}_{\lambda }\mid a\in H\}$, and operations ⊗ and ⇝ on $\frac{H}{{\equiv }_{\lambda }}$ are defined as follows:

$${[a]}_{\lambda }\otimes {[b]}_{\lambda }={[a\odot b]}_{\lambda }\mathrm{and}{[a]}_{\lambda }⇝{[b]}_{\lambda }={[a\to b]}_{\lambda }$$

Then, $(\frac{H}{{\equiv }_{\lambda }},\otimes ,⇝,{[1]}_{\lambda })$ is a hoop.

Proof. 

We have ${[a]}_{\lambda }={[b]}_{\lambda }$ and ${[c]}_{\lambda }={[d]}_{\lambda }$ if and only if $a{\equiv }_{\lambda }b$ and $c{\equiv }_{\lambda }d$. Since ${\equiv }_{\lambda }$ is the congruence relation on H, then all above operations are well-defined. Thus, by routine calculation, we can see that $\frac{H}{{\equiv }_{\lambda }}$ is a hoop. □

Now, we define a relation on $\frac{H}{{\equiv }_{\lambda }}$ by:

$${[a]}_{\lambda }\le {[b]}_{\lambda }\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{(a\to b)}_t\in \lambda ,\mathrm{for}\mathrm{any}a,b\in H\mathrm{and}t\in (0,1]$$

It is easy to see that $(\frac{H}{{\equiv }_{\lambda }},\le )$ is a poset.

Note: According to the definition of the congruence relation, it is clear that:

$${[1]}_{\lambda }=\{a\in H\mid {(a\to 1)}_t\in \lambda \mathrm{and}{(1\to a)}_t\in \lambda \}=\{a\in H\mid a_t\in \lambda \}.$$

Therefore, as we define a relation on quotient, ${[a]}_{\lambda }\le {[b]}_{\lambda }$ if and only if ${(a\to b)}_t\in \lambda$, it is similar to writing ${[a]}_{\lambda }\le {[b]}_{\lambda }$ if and only if ${[a]}_{\lambda }\to {[b]}_{\lambda }\in {[1]}_{\lambda }$.

Theorem 5.

If λ is a non-zero $(\in ,\in )$-fuzzy filter of H, then the set:

$$\begin{array}{c}\hfill H_0:=\{x\in H\mid \lambda (x)\ne 0\}\end{array}$$

(7)

is a filter of H.

Proof. 

Let $x\in H_0$. Since $\lambda (x)\ne 0$, we conclude that there exists $t\in (0,1]$ such that $\lambda (x)\ge t$. Moreover, from $\lambda$ being an $(\in ,\in )$-fuzzy filter of H, by Definition 1, $x_t\in \lambda$, then $1_t\in \lambda$. Hence, $\lambda (1)\ge \lambda (x)=t\ne 0$, and so, $1\in H_0$. Now, suppose that $x,x\to y\in H_0$. Then, there exist $t,k\in (0,1]$, such that $\lambda (x)\ge t$ and $\lambda (x\to y)\ge k$, and so, $x_t\in \lambda$ and ${(x\to y)}_k\in \lambda$. Thus, by Definition 1, $y_{min\{t,k\}}\in \lambda$, and so, $\lambda (y)\ge min\{t,k\}\ne 0$. Hence, $y\in H_0$. Therefore, $H_0$ is a filter of H. □

Proposition 3.

If λ is a non-zero $(\in ,\in \vee q)$-fuzzy filter of H, then $\lambda (1)>0$.

Proof. 

Let $\lambda (1)=0$. Since $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, by Theorem 1, for any $x\in H$, $\lambda (x)\le \lambda (1)=0$. Hence, for any $x\in H$, $\lambda (x)=0$, and so, $\lambda$ is a zero $(\in ,\in \vee q)$-fuzzy filter of H, which is a contradiction. Therefore, $\lambda (1)>0$. □

Theorem 6.

For any filter F of H and $t\in (0,0.5]$, there exists an $(\in ,\in \vee q)$-fuzzy filter λ of H such that its ∈-level set is equal to F.

Proof. 

Let $t\in (0,0.5]$ and $\lambda :H\to [0,1]$ be defined by $\lambda (x)=t$, for any $x\in F$, and $\lambda (x)=0$, otherwise. By this definition, it is clear that $U(\lambda ;t)=F$. Therefore, it is enough to prove that $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H. Let $x\in H$. Then, $\lambda (x)=0$ or $\lambda (x)=t$. Since F is a filter of H and $1\in F$, we have $t=\lambda (1)\ge \lambda (x)$, for any $x\in H$. Now, suppose that $x_t\in \lambda$ and ${(x\to y)}_k\in \lambda$. We consider the following cases:

• Case 1: If $\lambda (x)=t$ and $\lambda (x\to y)=t$, then $x,x\to y\in F$. Since F is a filter of H, we have $y\in F$, and so, $\lambda (y)\ge min\{\lambda (x),\lambda (x\to y)\}=t$. Hence, $y_t\in \lambda$. Therefore, $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H.
• Case 2: If $\lambda (x)=t$ and $\lambda (x\to y)=0$, then it is clear that:

  $$\lambda (y)\ge min\{\lambda (x),\lambda (x\to y)\}=0$$

  Hence, $y_0\in \lambda$. Therefore, $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H.
• Case 3: If $\lambda (x)=0$ and $\lambda (x\to y)=0$, then it is clear that:

  $$\lambda (y)\ge min\{\lambda (x),\lambda (x\to y)\}=0$$

  Hence, $y_0\in \lambda$. Therefore, $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H.

Therefore, in all cases, $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H and $U(\lambda ;t)=F$. □

For any fuzzy set $\lambda$ in H and $t\in (0,1]$, we define three sets that are called the ∈-level set, q-set, and $\in \vee q$-set, respectively, as follows.

$$\begin{array}{c}\hfill \begin{array}{c}U(\lambda ;t):=\{x\in H\mid \lambda (x)\ge t\}.\hfill \\ {\lambda }_q^t:=\{x\in H\mid x_{t}q\lambda \}.\hfill \\ {\lambda }_{\in \vee q}^t:=\{x\in H\mid x_t\in \vee q\lambda \}.\hfill \end{array}\end{array}$$

Theorem 7.

Given a fuzzy set λ in H, the following statements are equivalent.

(i)

The nonempty ∈-level set $U(\lambda ;t)$ of λ is a filter of H, for all $t\in (0.5,1]$.

(ii)

λ satisfies the following assertions.

$$(\forall x\in H)(\lambda (x)\le max\{\lambda (1),0.5\}).$$

(8)

$$(\forall x,y\in H)(max\{\lambda (y),0.5\}\ge min\{\lambda (x\to y),\lambda (x)\}).$$

(9)

Proof. 

Let $x\in H$ and $t\in (0.5,1]$ such that $\lambda (x)=t$. Then, $x\in U(\lambda ;t)$. Since $U(\lambda ;t)$ is a filter of H, $1\in U(\lambda ;t)$. Thus, $\lambda (1)\ge t$. Moreover, since $t\in (0.5,1]$, we have $max\{\lambda (1),0.5\}\ge \lambda (1)\ge t=\lambda (x)$. Hence, $max\{\lambda (1),0.5\}\ge \lambda (x)$. Now, suppose $x,y\in H$ and $t,k\in (0.5,1]$ such that $\lambda (x)=t$ and $\lambda (x\to y)=k$. Then, $x,x\to y\in U(\lambda ;min\{t,k\})$. Since $U(\lambda ;min\{t,k\})$ is a filter of H, we have $y\in U(\lambda ;min\{t,k\})$. Thus, $\lambda (y)\ge min\{t,k\}$. From $t,k\in (0.5,1]$, we conclude that,

$$max\{\lambda (y),0.5\}\ge min\{t,k\}=min\{\lambda (x),\lambda (x\to y)\}$$

Hence,

$$max\{\lambda (y),0.5\}\ge min\{\lambda (x),\lambda (x\to y)\}$$

Conversely, let $x\in U(\lambda ;t)$. Then, $\lambda (x)\ge t$. Since $t\in (0.5,1]$, by assumption:

$$t\le \lambda (x)\le max\{\lambda (1),0.5\}=\lambda (1)$$

Thus, $\lambda (1)\ge t$, so $1\in U(\lambda ;t)$. Now, suppose that $x,x\to y\in U(\lambda ;t)$, for any $x,y\in H$ and $t\in (0.5,1]$. Then, $\lambda (x)\ge t$ and $\lambda (x\to y)\ge t$. By assumption,

$$max\{\lambda (y),0.5\}\ge min\{\lambda (x\to y),\lambda (x)\}\ge t$$

Since $t\in (0.5,1]$, we have $\lambda (y)\ge t$, so $y\in U(\lambda ;t)$. Hence, $U(\lambda ;t)$ is a filter of H. □

It is clear that every $(\in ,\in )$-fuzzy filter of H is an $(\in ,\in \vee q)$-fuzzy filter of H. However, the converse may not be true, in general.

Example 2.

On the set $H=\{0,a,b,c,d,1\}$, we define two operations ⊙ and → as follows:

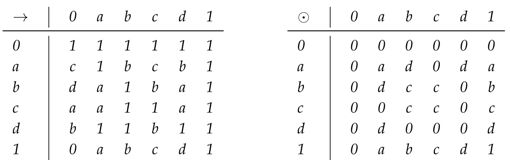By routine calculations, it is clear that $(H,\odot ,\to ,0,1)$ is a bounded hoop. Define a fuzzy set λ in H as follows:

$$\begin{array}{c}\hfill \lambda :H\to [0,1],x\mapsto \left\{\begin{array}{c}0.1\mathrm{if}x=0,\hfill \\ 0.1\mathrm{if}x=a,\hfill \\ 0.2\mathrm{if}x=b,\hfill \\ 0.3\mathrm{if}x=c,\hfill \\ 0.1\mathrm{if}x=d,\hfill \\ 0.5\mathrm{if}x=1\hfill \end{array}\right.\end{array}$$

It is easy to see that λ is an $(\in ,\in \vee q)$-fuzzy filter of hoop H, but it is not an $(\in ,\in \vee q)$-fuzzy filter of H; because:

$$0.2=\lambda (b)\ngeqq min\{\lambda (c),\lambda (c\to b)\}=min\{\lambda (c),\lambda (1)\}=min\{0.3,0.5\}=0.3$$

However, it is not an $(\in ,\in )$-fuzzy filter of H.

Now, we investigate under which conditions any $(\in ,\in \vee q)$-fuzzy filter is an $(\in ,\in )$-fuzzy filter.

Theorem 8.

If an $(\in ,\in \vee q)$-fuzzy filter λ of H satisfies the condition:

$$\begin{array}{c}\hfill (\forall x\in H)(\lambda (x)<0.5),\end{array}$$

(10)

then λ is an $(\in ,\in )$-fuzzy filter of H.

Proof. 

Let $x_t\in \lambda$, for any $x\in H$ and $t\in (0,0.5)$. Since $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, by Definition 1, $1_t\in \lambda$ or $1_{t}q\lambda$. If $1_t\in \lambda$, then the proof is clear. If $1_{t}q\lambda$, then $\lambda (1)+t>1$. Since $t\in (0,0.5)$, $1-t\in [0.5,1]$, then $\lambda (1)>t$. Hence, $1_t\in \lambda$. Now, suppose that $x_t\in \lambda$ and ${(x\to y)}_k\in \lambda$. From $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, by Definition 1, $y_{min\{t,k\}}\in \lambda$ or $y_{min\{t,k\}}q\lambda$. If $y_{min\{t,k\}}\in \lambda$, then the proof is complete. However, if $y_{min\{t,k\}}q\lambda$, then $\lambda (y)+min\{t,k\}>1$, and so, $\lambda (y)>1-min\{t,k\}$. Since $t\in (0,0.5)$, we have $1-min\{t,k\}\in [0.5,1]$, and so, $\lambda (y)>min\{t,k\}$. Then, $y_{min\{t,k\}}\in \lambda$. Therefore, $\lambda$ is an $(\in ,\in )$-fuzzy filter of H. □

Theorem 9.

If λ is an $(\in ,\in \vee q)$-fuzzy filter of H, then the q-set ${\lambda }_q^t$ is a filter of H, for all $t\in (0.5,1]$.

Proof. 

Let $x\in {{\lambda }_q}^t$, for any $x\in H$ and $t\in (0.5,1]$. Then, $\lambda (x)+t>1$, and so, $\lambda (x)>1-t$. Since $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, by Definition 1, we have $1_{1-t}\in \lambda$ or $1_{1-t}q\lambda$. If $1_{1-t}q\lambda$, then it is clear that $\lambda (1)>t$. Since $t\in (0.5,1]$, we have $\lambda (1)+t>2t>1$, and so, $1\in {{\lambda }_q}^t$. If $1_{1-t}\in \lambda$, then $\lambda (1)\ge 1-t$, and so, $\lambda (1)+t>1$. Thus, in both cases, $1\in {{\lambda }_q}^t$. Now, suppose that $x,x\to y\in {{\lambda }_q}^t$, for any $x,y\in H$ and $t\in (0.5,1]$. Then, $\lambda (x)+t>1$ and $\lambda (x\to y)+t>1$, and so, $\lambda (x)>1-t$ and $\lambda (x\to y)>1-t$. Since $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, by Definition 1, we have $y_{min\{1-t,1-t\}}\in \lambda$ or $y_{min\{1-t,1-t\}}q\lambda$. If $y_{1-t}\in \lambda$, then $\lambda (y)>1-t$, and so, $\lambda (y)+t>1$. If $y_{1-t}q\lambda$, then $\lambda (y)+1-t>1$, and so, $\lambda (y)>t$. Since $t\in (0.5,1]$, we have $\lambda (y)+t>2t>1$. Hence, in both cases, $y\in {{\lambda }_q}^t$. Therefore, ${{\lambda }_q}^t$ is a filter of H, for any $t\in (0.5,1]$. □

Theorem 10.

A fuzzy set λ in H is an $(\in ,\in \vee q)$-fuzzy filter of H if and only if the following assertion is valid.

$$\begin{array}{c}\hfill (\forall x,y\in H)\left(\begin{array}{c}\lambda (1)\ge min\{\lambda (x),0.5\}\hfill \\ \lambda (y)\ge min\{\lambda (x),\lambda (x\to y),0.5\}\hfill \end{array}\right).\end{array}$$

(11)

Proof. 

Let $x_t\in \lambda$, for any $x\in H$ and $t\in (0,1]$. Since $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, we have $1_t\in \lambda$ or $1_{t}q\lambda$. It means that $\lambda (1)\ge t$ or $\lambda (1)>1-t$. Therefore, $\lambda (1)\ge min\{\lambda (x),0.5\}$. In a similar way, if $x_t\in \lambda$ and ${(x\to y)}_k\in \lambda$, for any $x,y\in H$ and $t,k\in (0,1]$, since $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, then we have $y_{min\{t,k\}}\in \lambda$ or $y_{min\{t,k\}}q\lambda$. This means that $\lambda (y)\ge min\{t,k\}$ or $\lambda (1)>min\{1-t,1-k\}$. Therefore, $\lambda (y)\ge min\{\lambda (x),\lambda (x\to y),0.5\}$. Conversely, let $x_t\in \lambda$, for any $t\in (0,1]$ and $x\in H$. Then, by assumption, we have $\lambda (1)\ge min\{\lambda (x),0.5\}$. If $t\in (0,0.5]$, then $\lambda (1)\ge \lambda (x)=t$, and so, $1_t\in \lambda$. If $t\in (0.5,1]$, then $\lambda (1)\ge 0.5$, and so, $\lambda (1)+t>t+0.5>1$; thus, $1_{t}q\lambda$. Hence, $1_t\in \vee q\lambda$. Now, suppose that $x_t\in \lambda$ and ${(x\to y)}_k\in \lambda$, for any $x,y\in H$ and $t,k\in (0,1]$. Then, by assumption, we have $\lambda (y)\ge min\{\lambda (x),\lambda (x\to y),0.5\}$. If $t,k\in (0,0.5]$, then:

$$\lambda (y)\ge min\{\lambda (x),\lambda (x\to y),0.5\}=min\{t,k\}$$

Hence, $y_{min\{t,k\}}\in \lambda$. If $t,k\in (0.5,1]$, then:

$$\lambda (y)\ge min\{\lambda (x),\lambda (x\to y),0.5\}=0.5$$

Therefore, $\lambda (y)+min\{t,k\}>min\{t,k\}+0.5>1$. Thus, $y_{min\{t,k\}}q\lambda$. Hence, $y_{min\{t,k\}}\in \vee q\lambda$. Therefore, $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H. □

Theorem 11.

A fuzzy set λ in H is an $(\in ,\in \vee q)$-fuzzy filter of H if and only if the non-empty ∈-level set $U(\lambda ;t)$ of λ is a filter of H, for all $t\in (0,0.5]$.

Proof. 

Let $\lambda$ be an $(\in ,\in \vee q)$-fuzzy filter of H and $x\in U(\lambda ;t)$, for any $t\in (0,0.5]$. Then, $\lambda (x)\ge t$, and so, $x_t\in \lambda$. Since $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, $1_t\in \lambda$ or $1_{t}q\lambda$. If $1_t\in \lambda$, then it is clear that $1\in U(\lambda ;t)$, and if $1_{t}q\lambda$, then $\lambda (1)>1-t$. Since $t\in (0,0.5]$, $1-t\in (0.5,1]$, so $\lambda (1)>1-t>t$. Thus, $1\in U(\lambda ;t)$. Now, suppose that $x,x\to y\in U(\lambda ;t)$, then $\lambda (x)\ge t$ and $\lambda (x\to y)\ge t$, and so, $x_t\in \lambda$ and ${(x\to y)}_t\in \lambda$. Since $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, $y_t\in \lambda$ or $y_{t}q\lambda$. If $y_t\in \lambda$, then it is clear that $y\in U(\lambda ;t)$, and if $y_{t}q\lambda$, then $\lambda (y)>1-t$. Since $t\in (0,0.5]$, $1-t\in (0.5,1]$, so $\lambda (y)>1-t>t$. Thus, $y\in U(\lambda ;t)$. Therefore, $U(\lambda ;t)$ is a filter of H, for any $t\in (0,0.5]$.

Conversely, suppose $U(\lambda ;t)$ is a filter of H and $x_t\in \lambda$, for any $x\in H$ and $t\in (0,0.5]$. Then, $\lambda (x)\ge t$, so $x\in U(\lambda ;t)$. Since $U(\lambda ;t)$ is a filter of H, $1\in U(\lambda ;t)$, so $\lambda (1)\ge t$. Hence, $1_t\in \lambda$, and so, $1_t\in \vee q\lambda$. Now, let $x_t\in \lambda$ and ${(x\to y)}_k\in \lambda$, for any $x,y\in H$ and $t,k\in (0,0.5]$. Then, $\lambda (x)\ge t$ and $\lambda (x\to y)\ge k$, and so, $x,x\to y\in U(\lambda ;min\{t,k\})$. Since $U(\lambda ;t)$ is a filter of H, $y\in U(\lambda ;min\{t,k\})$, and so, $\lambda (y)\ge min\{t,k\}$. Hence, $y_{min\{t,k\}}\in \lambda$. Therefore, $y_{min\{t,k\}}\in \vee q\lambda$. Therefore, $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, for any $t\in (0,0.5]$. □

Theorem 12.

A fuzzy set λ in H is an $(\in ,\in \vee q)$-fuzzy filter of H if and only if the following assertion is valid.

$$\begin{array}{c}\hfill (\forall x,y\in H)\left(\begin{array}{c}\lambda (x\odot y)\ge min\{\lambda (x),\lambda (y),0.5\}\hfill \\ x\le y\Rightarrow \lambda (y)\ge min\{\lambda (x),0.5\}\hfill \end{array}\right).\end{array}$$

(12)

Proof. 

Assume that $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H and $x,y\in H$. Then, by Theorem 11, $U(\lambda ;t)$ is a filter of H, for any $t\in (0,0.5]$. If $x,y\in U(\lambda ;t)$ and $t\in (0,0.5]$, then $x\odot y\in U(\lambda ;t)$. Thus, $\lambda (x\odot y)\ge t=min\{\lambda (x),\lambda (y)\}$. If $t\in (0.5,1]$, it is clear that $\lambda (x\odot y)\ge min\{\lambda (x),\lambda (y),0.5\}$. Now, suppose $x\le y$. If $\lambda (x)\ge t$ and $t\in (0,0.5]$, then $x\in U(\lambda ;t)$. Since $U(\lambda ;t)$ is a filter of H, $y\in U(\lambda ;t)$. Thus, $\lambda (y)\ge \lambda (x)$, for $t\in (0,0.5]$. If $t\in (0.5,1]$, then $\lambda (y)\ge min\{\lambda (x),0.5\}$.

Conversely, let $\lambda$ be a fuzzy set in H that satisfies the condition (12). Since $x\le 1$ for all $x\in H$, we have $\lambda (1)\ge min\{\lambda (x),0.5\}$ for all $x\in H$. Since $x\odot (x\to y)\le y$ for all $x,y\in H$, we get:

$$\begin{array}{cc}\hfill \lambda (y)& \ge min\{\lambda (x\odot (x\to y)),0.5\}\hfill \\ & \ge min\{min\{\lambda (x),\lambda (x\to y),0.5\},0.5\}\hfill \\ & =min\{\lambda (x),\lambda (x\to y),0.5\}\hfill \end{array}$$

for all $x,y\in H$. It follows from Theorem 10 that $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H. □

Theorem 13.

A fuzzy set λ in H is an $(\in ,\in \vee q)$-fuzzy filter of H if and only if ${\lambda }_{\in \vee q}^t$ is a filter of H, for all $t\in (0,1]$ (we call ${\lambda }_{\in \vee q}^t$ an $\in \vee q$-level filter of λ).

Proof. 

Let $\lambda$ be an $(\in ,\in \vee q)$-fuzzy filter of H and $x\in {\lambda }_{\in \vee q}^t$, for any $x\in H$ and $t\in (0,1]$. Then, $x\in U(\lambda ;t)$ or $x\in {\lambda }_q^t$. This means that $x_t\in \lambda$ or $x_{1-t}\in \lambda$. Since $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, we have, if $x_t\in \lambda$, then $1_t\in \lambda$ or $1_{t}q\lambda$. Furthermore, if $x_{1-t}\in \lambda$, then $1_{1-t}\in \lambda$ or $x_{1-t}q\lambda$; this means that $x_{t}q\lambda$ or $x_t\in \lambda$. Hence, in both cases, $1_t\in \vee q\lambda$, and so, $1\in {\lambda }_{\in \vee q}^t$. In a similar way, let $x,x\to y\in {\lambda }_{\in \vee q}^t$, for $x,y\in H$ and $t\in (0,1]$. Then, $x,x\to y\in U(\lambda ;t)$ or $x,x\to y\in {\lambda }_q^t$ or $x\in U(\lambda ;t)$ and $x\to y\in {\lambda }_q^t$. Therefore, we have the following cases:

• Case 1: if $x,x\to y\in U(\lambda ;t)$, then $x_t\in \lambda$ and ${(x\to y)}_t\in \lambda$. Since $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, $y_t\in \lambda$ or $y_{t}q\lambda$. Therefore, $y\in {\lambda }_{\in \vee q}^t$.
• Case 2: if $x,x\to y\in {\lambda }_q^t$, then $x_{1-t}\in \lambda$ and ${(x\to y)}_{1-t}\in \lambda$. Since $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, $y_{1-t}\in \lambda$ or $y_{1-t}q\lambda$. It is equivalent to $y_{t}q\lambda$ or $y_t\in \lambda$, respectively. Therefore, $y\in {\lambda }_{\in \vee q}^t$.
• Case 3: if $x\in U(\lambda ;t)$ and $x\to y\in {\lambda }_q^t$, then $x_t\in \lambda$ and ${(x\to y)}_{1-t}\in \lambda$. Since $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, $\lambda (y)\ge min\{1-t,t\}$, and so, it is equal to $y_t\in \lambda$ or $y_{t}q\lambda$. Thus, in both cases, $y\in {\lambda }_{\in \vee q}^t$.

Therefore, ${\lambda }_{\in \vee q}^t$ is a filter of H.

Conversely, let $x_t\in \lambda$, for any $x\in H$ and $t\in (0,1]$. Since ${\lambda }_{\in \vee q}^t$ is a filter of H, $1\in {\lambda }_{\in \vee q}^t$. Then, $1_t\in \vee q\lambda$. Now, suppose that $x_t\in \lambda$ and ${(x\to y)}_k\in \lambda$, for any $x,y\in H$ and $t,k\in (0,1]$. Then, it is clear that $x,x\to y\in {\lambda }_{\in \vee q}^{min\{t,k\}}$. Since ${\lambda }_{\in \vee q}^t$ is a filter of H, $y\in {\lambda }_{\in \vee q}^{min\{t,k\}}$. Therefore, $y_{min\{t,k\}}\in \lambda$ or $y_{min\{t,k\}}q\lambda$. Hence, $y_{min\{t,k\}}\in \vee q\lambda$. Therefore, $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H. □

Theorem 14.

Let $f:H\to K$ be a homomorphism of hoops. If λ and μ are $(\in ,\in \vee q)$-fuzzy filters of H and K, respectively, then:

(i)

$f^{-1}(\mu )$ is an $(\in ,\in \vee q)$-fuzzy filter of H.

(ii)

If f is onto and λ satisfies the condition:

$$\begin{array}{c}\hfill (\forall T\subseteq H)(\exists x_0\in T)\left(\lambda (x_0)=\underset{x\in T}{sup}\lambda (x)\right),\end{array}$$

(13)

then $f(\lambda )$ is an $(\in ,\in \vee q)$-fuzzy filter of K.

Proof. 

$(i)$ Let $x_t\in f^{-1}(\mu )$, for any $x\in H$ and $t\in (0,1]$. Then, $f{(x)}_t\in \mu$. Since $\mu$ is an $(\in ,\in \vee q)$-fuzzy filter of H, we have $f{(1)}_t\in \vee q\mu$. Thus, $1_t\in \vee q{f}^{-1}(\mu )$. Now, suppose $x_t\in f^{-1}(\mu )$ and ${(x\to y)}_k\in f^{-1}(\mu )$, for any $x,y\in H$ and $t,k\in (0,1]$. Then, $f{(x)}_t\in \mu$ and $f{(x\to y)}_k\in \mu$. Since $\mu$ is an $(\in ,\in \vee q)$-fuzzy filter of H, we have $f{(y)}_{min\{t,k\}}\in \vee q\mu$. Hence, $y_{min\{t,k\}}\in \vee q{f}^{-1}(\mu )$. Therefore, $f^{-1}(\mu )$ is an $(\in ,\in \vee q)$-fuzzy filter of H.

$(ii)$ Let $a\in K$ and $t\in (0,1]$ be such that $a_t\in f(\lambda )$. Then, $(f(\lambda ))(a)\ge t$. By assumption, there exists $x\in f^{-1}(a)$ such that $\lambda (x)=su{p}_{z\in f^{-1}(a)}\lambda (z)$. Then, $x_t\in \lambda$. Since $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, we have $1_t\in \lambda$. Now, $1\in f^{-1}(1)$, so $(f(\lambda ))(1)\ge \lambda (1)$, then $(f(\lambda ))(1)\ge t$ or $(f(\lambda ))(1)+t>1$. Thus, $1_t\in \vee qf(\lambda )$. In a similar way, let $a,a\to b\in K$ and $t,k\in (0,1]$ be such that $a_t\in f(\lambda )$ and ${(a\to b)}_k\in f(\lambda )$. Then, $(f(\lambda ))(a)\ge t$ and $(f(\lambda ))(a\to b)\ge k$. By assumption, there exist $x\in f^{-1}(a)$ and $x\to y\in f^{-1}(a\to b)$ such that $\lambda (x)=su{p}_{z\in f^{-1}(a)}\lambda (z)$ and $\lambda (x\to y)=su{p}_{w\in f^{-1}(a\to b)}\lambda (w)$. Then, $x_t\in \lambda$ and ${(x\to y)}_k\in \lambda$. Since $\lambda$ is an $(\in ,\in \vee q)$-fuzzy filter of H, we have $y_{min\{t,k\}}\in \lambda$. Now, $y\in f^{-1}(y)$, so $(f(\lambda ))(y)\ge \lambda (y)$, then $(f(\lambda ))(y)\ge min\{t,k\}$ or $(f(\lambda ))(y)+min\{t,k\}>1$. Thus, $y_{min\{t,k\}}\in \vee qf(\lambda )$. □

Theorem 15.

Let λ be an $(\in ,\in \vee q)$-fuzzy filter of H such that:

$$\begin{array}{c}\hfill |\{\lambda (x)\mid \lambda (x)<0.5\}|\ge 2.\end{array}$$

Then, there exist two $(\in ,\in \vee q)$-fuzzy filters μ and ν of H such that:

(i)

$\lambda =\mu \cup \nu$.

(ii)

$\mathrm{Im}(\mu )$ and $\mathrm{Im}(\nu )$ have at least two elements.

(iii)

μ and ν do not have the same family of $\in \vee q$-level filters.

Proof. 

Let $\{\lambda (x)\mid \lambda (x)<0.5\}=\{t_1,t_2,\dots ,t_r\}$ where $t_1>t_2>\cdots >t_r$ and $r\ge 2$. Then, the chain of $\in \vee q$-level filters of $\lambda$ is:

$$\begin{array}{c}\hfill {\lambda }_{\in \vee q}^{0.5}\subseteq {\lambda }_{\in \vee q}^{t_1}\subseteq {\lambda }_{\in \vee q}^{t_2}\subseteq \cdots \subseteq {\lambda }_{\in \vee q}^{t_r}=H.\end{array}$$

Define two fuzzy sets $\mu$ and $\nu$ in H by:

$$\begin{array}{c}\hfill \mu (x)=\left\{\begin{array}{c}{t}_1\mathrm{if}x\in {\lambda }_{\in \vee q}^{t_1},\hfill \\ t_n\mathrm{if}x\in {\lambda }_{\in \vee q}^{t_n}\setminus {\lambda }_{\in \vee q}^{t_{n-1}}\mathrm{for}n=2,3,\cdots ,r,\hfill \end{array}\right.\end{array}$$

and:

$$\begin{array}{c}\hfill \nu (x)=\left\{\begin{array}{c}\lambda (x)\mathrm{if}x\in {\lambda }_{\in \vee q}^{0.5},\hfill \\ k\mathrm{if}x\in {\lambda }_{\in \vee q}^{t_2}\setminus {\lambda }_{\in \vee q}^{0.5},\hfill \\ t_n\mathrm{if}x\in {\lambda }_{\in \vee q}^{t_n}\setminus {\lambda }_{\in \vee q}^{t_{n-1}}\mathrm{for}n=3,4,\cdots ,r,\hfill \end{array}\right.\end{array}$$

respectively, where $k\in (t_3,t_2)$. Then, $\mu$ and $\nu$ are $(\in ,\in \vee q)$-fuzzy filters of H, and $\mu \subseteq \lambda$ and $\nu \subseteq \lambda$. The chains of $\in \vee q$-level filters of $\mu$ and $\nu$ are given by:

$$\begin{array}{c}\hfill {\mu }_{\in \vee q}^{t_1}\subseteq {\mu }_{\in \vee q}^{t_2}\subseteq \cdots \subseteq {\mu }_{\in \vee q}^{t_r}\mathrm{and}{\nu }_{\in \vee q}^{0.5}\subseteq {\nu }_{\in \vee q}^{t_2}\subseteq \cdots \subseteq {\nu }_{\in \vee q}^{t_r},\end{array}$$

respectively. It is clear that $\mu \cup \nu =\lambda$. This completes the proof.

 □

4. Conclusions

Our aim was to define the concepts of $(\in ,\in )$-fuzzy filters and $(\in ,\in \vee q)$-fuzzy filters of hoops, and we discussed some properties and found some equivalent definitions of them. Then, we defined a congruence relation on the hoop by an $(\in ,\in )$-fuzzy filter of the hoop and proved that the quotient structure of this relation is a hoop. For future works, we will introduce $(\alpha ,\beta )$-fuzzy (positive) implicative filters for $(\alpha ,\beta )\in \{(\in ,\in ),(\in ,\in \vee q)\}$ of hoops, investigate some of their properties, and try to find some equivalent definitions of them. Furthermore, we study the relation between them. Moreover, we can investigate the corresponding quotients.