Similarity Measures for Fractional Orthotriple Fuzzy Sets Using Cosine and Cotangent Functions and Their Application in Accident Emergency Response
Abstract
:1. Introduction
1.1. Literature Review
1.2. Motivation and Novelties
2. Preliminaries
3. Some SMs Using the Cosine and Cotangent Functions for FOFSs
3.1. Cosine SMs for FOFSs
- If then and
- 1.
- then
- 2.
- , then
- 3.
- then
- 4.
- If then
- 1.
- 2.
- 3.
- ○
- We put then reduced to i.e., Equation (13) reduced to Equation (10).
- ○
- We put and then reduced to i.e., Equation (13) reduced to Equation (7).
3.2. SMs for FOFSs Using the Cosine Function
- 1.
- 2.
- 3.
- 4.
- If then and
- The first result is obvious because the value of the cosine function is within closed-interval and also the SM based on the cosine function is within closed-interval Hence,
- The proof is straightforward.
- To prove the third result, for two FOFNs ℑ and ℜ on X, if then and for Therefore, and Hence,
- If then and for Then,Thus, we haveHence, and Therefore, the cosine function is a decreasing function with the interval
- 1.
- 2.
- 3.
3.3. SMs for FOFSs Using the Cotangent Function
- 1.
- 2.
- 3.
- 4.
- If then and
- The first result is obvious because the value of the cotangent function is within closed interval and also the SM based on the cotangent function is within closed interval Hence,
- The proof is straightforward.
- To prove the third result, for two FOFNs ℑ and ℜ on X, if then and for Therefore, , and Hence,
- If then , and for Then,Thus, we haveHence, and Therefore, the cotangent function is a decreasing function with the interval
- 1.
- 2.
- 3.
4. Decision Making Algorithm
- In this step, we take the classes about the known and unknown information in the form of fractional orthotriple fuzzy numbers.
- In this step, we compute some SM of each known fractional orthotriple fuzzy numbers with unknown fractional orthotriple fuzzy numbers by using the similarity measures , , , , and .
- In this step, we compute some weighted similarity measure of each known fractional orthotriple fuzzy numbers with unknown fractional orthotriple fuzzy numbers by using the similarity measures , , , , and .
- In this step, we classify the unknown alternative based on ranking.
Application
- : Control the crowds: the police team control the crowd so that no more casualties will happen and rescue steps can take place.
- : To organized the rescue injured: when the accident occurred the first step is to save the lives of the injured. However, the other people should be shifted to a safe place.
- : Quick observation of the situation: when the situation seemed to be going bad the rescue team immediately took steps.
- : Removal of dead and injured bodies: the emergency team remove the dead bodies as well as the injured for treatment from the Mosque.
- : To remove the crane and wash the floor of the Mosque.
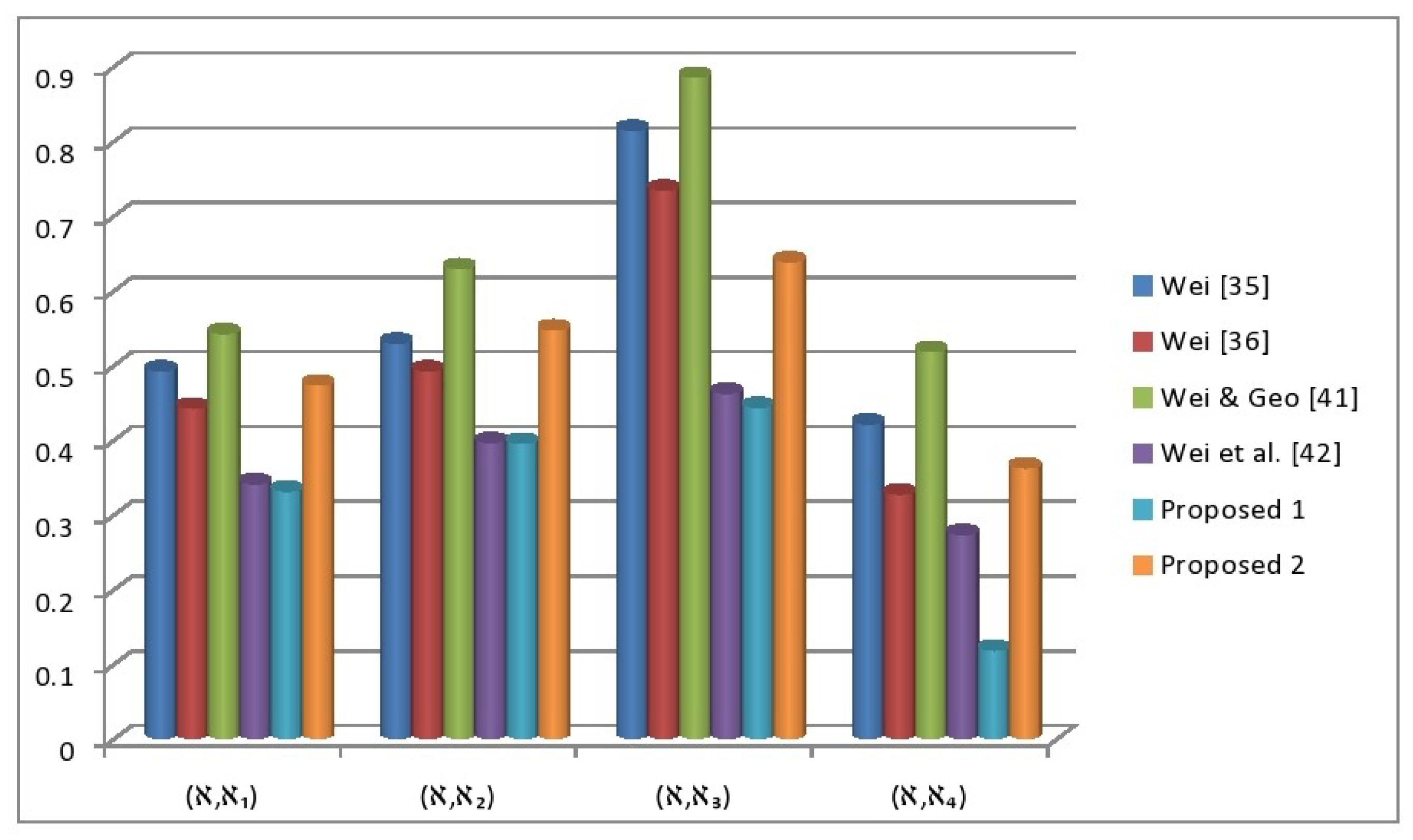
5. Comparative Study
Sensitivity Analysis
- ○
- We put then Equation (14) reduced to WSM of SFS such as;
- ○
- We put and then Equation (14) reduces to WSM of PyFS such as;
- ○
- We put then Equation (14) reduces to WSM of PFS such as:
- ○
- We put and then Equation (14) reduces to WSM of IFS such as:
- ○
- We put then Equation (17) reduces to WSM of SFS such that
- ○
- We put and then Equation (17) reduces to WSM of PyFS such that
- ○
- We put then Equation (17) reduces to WSM of PFS such that
- ○
- We put and then Equation (17) reduces to WSM of IFS such that
- ○
- We put then Equation (22) reduces to WSM of SFS such that
- ○
- We put and then Equation (22) reduces to WSM of PyFS such that
- ○
- ∘ We put then Equation (17) reduces to WSM of PFS such that
- ○
- We put and then Equation (22) reduces to WSM of IFS such that
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean fuzzy subsets. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24–28 June 2013; pp. 57–61. [Google Scholar]
- Yager, R.R.; Abbasov, A.M. Pythagorean membership grades, complex numbers and decision making. Int. J. Intell. Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- Asiain, M.J.; Bustince, H.; Mesiar, R.; Kolesárová, A.; Takáč, Z. Negations with respect to admissible orders in the interval-valued fuzzy set theory. IEEE Trans. Fuzzy Syst. 2018, 26, 556–568. [Google Scholar] [CrossRef]
- Mahmood, T.; Liu, P.; Ye, J.; Khan, Q. Several hybrid aggregation operators for triangular intuitionistic fuzzy set and their application in multi-criteria decision making. Granul. Comput. 2018, 3, 153–168. [Google Scholar] [CrossRef]
- Li, H. 3D distances of intuitionistic fuzzy sets based on hesitating index. In Proceedings of the Chinese Control and Decision Conference (CCDC), Liaoning, China, 9–11 June 2018; pp. 2514–2518. [Google Scholar]
- Peng, X.; Yang, Y. Some results for Pythagorean fuzzy sets. Int. J. Intell. Syst. 2015, 30, 1133–1160. [Google Scholar] [CrossRef]
- Garg, H. A new generalized Pythagorean fuzzy information aggregation using Einstein operations and its application to decision making. Int. J. Intell. Syst. 2016, 31, 886–920. [Google Scholar] [CrossRef]
- Wei, G.; Lu, M. Pythagorean fuzzy Maclaurin symmetric mean operators in multiple attribute decision making. Int. J. Intell. Syst. 2018, 33, 1043–1070. [Google Scholar] [CrossRef]
- Wei, G.; Lu, M. Pythagorean Hesitant Fuzzy Hamacher Aggregation Operators in Multiple-Attribute Decision Making. J. Intell. Syst. 2017, 28, 756–776. [Google Scholar] [CrossRef]
- Lu, M.; Wei, G.; Alsaadi, F.E.; Hayat, T.; Alsaedi, A. Hesitant Pythagorean fuzzy hamacher aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2017, 33, 1105–1117. [Google Scholar] [CrossRef]
- Cuong, B.C. Picture fuzzy sets. J. Comput. Sci. Cybern. 2014, 30, 409. [Google Scholar]
- Akram, M.; Bashir, A.; Garg, H. Decision-making model under complex picture fuzzy Hamacher aggregation operators. Comput. Appl. Math. 2020, 39, 1–38. [Google Scholar] [CrossRef]
- Khalil, A.M.; Li, S.G.; Garg, H.; Li, H.; Ma, S. New operations on interval-valued picture fuzzy set, interval-valued picture fuzzy soft set and their applications. IEEE Access 2019, 7, 51236–51253. [Google Scholar] [CrossRef]
- Garg, H. Some picture fuzzy aggregation operators and their applications to multicriteria decision-making. Arab. J. Sci. Eng. 2017, 42, 5275–5290. [Google Scholar] [CrossRef]
- Lin, M.; Huang, C.; Xu, Z. MULTIMOORA based MCDM model for site selection of car sharing station under picture fuzzy environment. Sustain. Cities Soc. 2020, 53, 101873. [Google Scholar] [CrossRef]
- Liu, P.; Munir, M.; Mahmood, T.; Ullah, K. Some similarity measures for interval-valued picture fuzzy sets and their applications in decision making. Information 2019, 10, 369. [Google Scholar] [CrossRef] [Green Version]
- Wei, G. Picture fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. Fundam. Inform. 2018, 157, 271–320. [Google Scholar] [CrossRef]
- Singh, P. Correlation coefficients for picture fuzzy sets. J. Intell. Fuzzy Syst. 2015, 28, 591–604. [Google Scholar] [CrossRef]
- Mahmood, T.; Ullah, K.; Khan, Q.; Jan, N. An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 2019, 31, 7041–7053. [Google Scholar] [CrossRef]
- Peng, Y.F.; Chiu, C.H.; Tsai, W.R.; Chou, M.H. Design of an omni-directional spherical robot: Using fuzzy control. In Proceedings of the International Multiconference of Engineers and Computer Scientists, Hong Kong, China, 13–15 March 2019; Volume 1, pp. 18–20. [Google Scholar]
- Ashraf, S.; Abdullah, S.; Aslam, M.; Qiyas, M.; Kutbi, M.A. Spherical fuzzy sets and its representation of spherical fuzzy t-norms and t-conorms. J. Intell. Fuzzy Syst. 2019, 36, 6089–6102. [Google Scholar] [CrossRef]
- Zeng, S.; Hussain, A.; Mahmood, T.; Irfan Ali, M.; Ashraf, S.; Munir, M. Covering-Based Spherical Fuzzy Rough Set Model Hybrid with TOPSIS for Multi-Attribute Decision-Making. Symmetry 2019, 11, 547. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Khan, Q.; Mahmood, T.; Hassan, N. T-spherical fuzzy power Muirhead mean operator based on novel operational laws and their application in multi-attribute group decision making. IEEE Access 2019, 7, 22613–22632. [Google Scholar] [CrossRef]
- Ullah, K.; Hassan, N.; Mahmood, T.; Jan, N.; Hassan, M. Evaluation of investment policy based on multi-attribute decision-making using interval valued T-spherical fuzzy aggregation operators. Symmetry 2019, 11, 357. [Google Scholar] [CrossRef] [Green Version]
- Zeng, S.; Garg, H.; Munir, M.; Mahmood, T.; Hussain, A. A Multi-Attribute Decision Making Process with Immediate Probabilistic Interactive Averaging Aggregation Operators of TSpherical Fuzzy Sets and Its Application in the Selection of Solar Cells. Energies 2019, 12, 4436. [Google Scholar] [CrossRef] [Green Version]
- Garg, H.; Munir, M.; Ullah, K.; Mahmood, T.; Jan, N. Algorithm for T-spherical fuzzy multiattribute decision making based on improved interactive aggregation operators. Symmetry 2018, 10, 670. [Google Scholar] [CrossRef] [Green Version]
- Dengfeng, L.; Chuntian, C. New SMs of intuitionistic fuzzy sets and application to pattern recognitions. Pattern Recognit. Lett. 2002, 23, 221–225. [Google Scholar] [CrossRef]
- Hung, W.L.; Yang, M.S. SMs of intuitionistic fuzzy sets based on Hausdorff distance. Pattern Recognit. Lett. 2004, 25, 1603–1611. [Google Scholar] [CrossRef]
- Vlachos, I.K.; Sergiadis, G.D. Intuitionistic fuzzy information–applications to pattern recognition. Pattern Recognit. Lett. 2007, 28, 197–206. [Google Scholar] [CrossRef]
- Son, L.H.; Phong, P.H. On the performance evaluation of intuitionistic vector SMs for medical diagnosis 1. J. Intell. Fuzzy Syst. 2016, 31, 1597–1608. [Google Scholar] [CrossRef]
- Miaoying, T. A new fuzzy SM based on cotangent function for medical diagnosis. Adv. Model. Optim. 2013, 15, 151–156. [Google Scholar]
- Xia, M.; Xu, Z. Some new SMs for intuitionistic fuzzy values and their application in group decision making. J. Syst. Syst. Eng. 2010, 19, 430–452. [Google Scholar] [CrossRef]
- Yang, M.S.; Lin, D.C. On similarity and inclusion measures between type-2 fuzzy sets with an application to clustering. Comput. Math. Appl. 2009, 57, 896–907. [Google Scholar] [CrossRef] [Green Version]
- Ye, J. Cosine SMs for intuitionistic fuzzy sets and their applications. Math. Comput. Model. 2011, 53, 91–97. [Google Scholar] [CrossRef]
- Rajarajeswari, P.; Uma, N. Intuitionistic fuzzy multi SM based on cotangent function. Int. J. Eng. Res. Technol. 2013, 2, 1323–1329. [Google Scholar]
- Ye, J. SMs of intuitionistic fuzzy sets based on cosine function for the decision making of mechanical design schemes. J. Intell. Fuzzy Syst. 2016, 30, 151–158. [Google Scholar] [CrossRef]
- Wei, G. Some SMs for picture fuzzy sets and their applications. Iran. J. Fuzzy Syst. 2018, 15, 77–89. [Google Scholar]
- Wei, G. Some cosine SMs for picture fuzzy sets and their applications to strategic decision making. Informatica 2017, 28, 547–564. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, Z.; Mahmood, T.; Saad, M.; Jan, N.; Ullah, K. SMs for picture hesitant fuzzy sets and their applications in pattern recognition. J. Prime Res. Math. 2019, 15, 81–100. [Google Scholar]
- Wei, G.; Wei, Y. SMs of Pythagorean fuzzy sets based on the cosine function and their applications. Int. J. Intell. Syst. 2018, 33, 634–652. [Google Scholar] [CrossRef]
- Ullah, K.; Mahmood, T.; Jan, N. SMs for T-spherical fuzzy sets with applications in pattern recognition. Symmetry 2018, 10, 193. [Google Scholar] [CrossRef] [Green Version]
- Abosuliman, S.S.; Abdullah, S.; Qiyas, M. Three-Way Decisions Making Using Covering Based Fractional Orthotriple Fuzzy Rough Set Model. Mathematics 2020, 8, 1121. [Google Scholar] [CrossRef]
- Wei, G.; Wang, J.; Lu, M.; Wu, J.; Wei, C. Similarity measures of spherical fuzzy sets based on cosine function and their applications. IEEE Access 2019, 7, 159069–159080. [Google Scholar] [CrossRef]
- Wei, G.; Gao, H. The generalized Dice similarity measures for picture fuzzy sets and their applications. Informatica 2018, 29, 107–124. [Google Scholar] [CrossRef] [Green Version]

| ℵ | |||||
|---|---|---|---|---|---|
| SMs | ||||
|---|---|---|---|---|
| WSMs | ||||
|---|---|---|---|---|
| ℵ | |||||
|---|---|---|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naeem, M.; Qiyas, M.; Al-Shomrani, M.M.; Abdullah, S. Similarity Measures for Fractional Orthotriple Fuzzy Sets Using Cosine and Cotangent Functions and Their Application in Accident Emergency Response. Mathematics 2020, 8, 1653. https://doi.org/10.3390/math8101653
Naeem M, Qiyas M, Al-Shomrani MM, Abdullah S. Similarity Measures for Fractional Orthotriple Fuzzy Sets Using Cosine and Cotangent Functions and Their Application in Accident Emergency Response. Mathematics. 2020; 8(10):1653. https://doi.org/10.3390/math8101653
Chicago/Turabian StyleNaeem, Muhammad, Muhammad Qiyas, Mohammed M. Al-Shomrani, and Saleem Abdullah. 2020. "Similarity Measures for Fractional Orthotriple Fuzzy Sets Using Cosine and Cotangent Functions and Their Application in Accident Emergency Response" Mathematics 8, no. 10: 1653. https://doi.org/10.3390/math8101653





