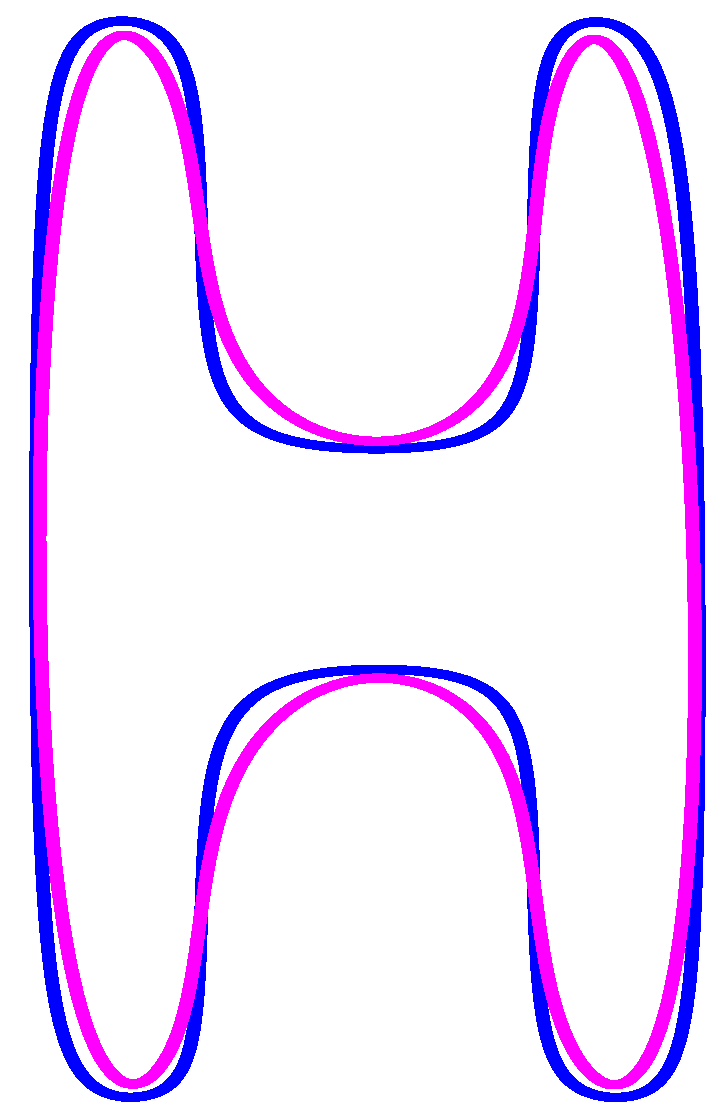Geometric Modeling Using New Cubic Trigonometric B-Spline Functions with Shape Parameter

Abstract

Trigonometric B-spline curves with shape parameters are equally important and useful for modeling in Computer-Aided Geometric Design (CAGD) like classical B-spline curves. This paper introduces the cubic polynomial and rational cubic B-spline curves using new cubic basis functions with shape parameter $\xi \in [0,4]$. All geometric characteristics of the proposed Trigonometric B-spline curves are similar to the classical B-spline, but the shape-adjustable is additional quality that the classical B-spline curves does not hold. The properties of these bases are similar to classical B-spline basis and have been delineated. Furthermore, uniform and non-uniform rational B-spline basis are also presented. $C^3$ and $C^5$ continuities for trigonometric B-spline basis and $C^3$ continuities for rational basis are derived. In order to legitimize our proposed scheme for both basis, floating and periodic curves are constructed. $2D$ and $3D$ models are also constructed using proposed curves.

1. Introduction

Splines are a kind of curve, initially evolved in the days prior to computer modeling. Geometric modeling refers to a set of techniques concerned mainly with developing efficient representations of geometric aspects of design. Therefore, geometric modeling is a fundamental part of all CAD (computer-aided design) tools. The basic geometric modeling approaches available to designers on the CAD system are: (1) Wireframe modeling, (2) curve modeling, (3) surface modeling, and (4) solid modeling.

In curve modeling, we deal with trigonometric Bézier-like [1,2,3,4,5], Q-Bézier [6], H-Bézier [7], Ball Bézier-like [8], S-$\lambda$ Bézier-like [9], classical Bézier, B-spline, and NURBS curve, etc. Schoenberg introduced the trigonometric spline interpolation, spline interpolation of higher derivatives, interpolating spline as limit of polynomials, and Spline interpolation and best quadrature formulae in [10,11,12,13]. Lyche and Winther [14] proved a stable recurrence relation for trigonometric B-splines. Walz [15] constructed some identities for trigonometric B-splines with an application to curve design. The term B-spline (Basis spline) introduced is in [16,17,18]. The curves swarmed the area of Computer Aided Geometric Design (CAGD) in the middle of 1980s. In CAGD, trigonometric polynomials have also procured the great attention for $2D$ and $3D$ modeling, for example [19] proposed $C^n$ continuous trigonometric spline curves for data interpolation. The trigonometric Bézier-like curve with shape parameters based on new trigonometric basis function is proposed by [20]. Majeed and Faiza [21] proposed the curves and bases based on trigonometric B-spline for geometric modeling.

The quadratic trigonometric polynomial curve with $C^1$ continuity is introduced by [22]. It holds the basic properties of classical B-spline curves. Han [23] added cubic trigonometric B-spline curves on uniform and non-uniform knots with shape parameters to the literature. The application of the B-spline curve in Bio-modeling is given in [24]. Chouby and Ojha [25] introduced the quadratic spline curve with variable shape parameters. Pagani and Scott [26] proposed the sampling method for the reconstruction of curves and surfaces. Surface reconstruction by parallel curves is proposed by [27] with the application of fracture reconstruction.

Hu et al. [28] proposed a scheme based on $\lambda \mu$-B-spline for the construction of rotational surface. Rational Bézier curves is proposed by [29] for the construction of frontal bone fracture. Yan and Liang [30] proposed algebraic-trigonometric blended spline curve (xyB curves). In the proposed curve, x and y are shape parameters to control the curve. Troll [31] proposed cubic trigonometric Bézier curves. A generation of convex polygon triangulation based on planted trivalent binary tree and ballot notation was proposed by [32]. SARACEVIC and SELİMİ [33] proposed the method for Catalan number decomposition in the expressions of the form $(2+ı)$. The authors in [34] have discussed the geometric effect of shape parameter introduced in [22,23]. The trigonometric cubic Bézier curve is proposed by [35] with shape parameters. Gang and Guo-Zhao [36] introduced interpolating $\alpha$-B-spline build on the new B-splines possessing global and local shape parameters.

This paper presents new trigonometric cubic B-spline basis functions acquiring shape parameter $\xi$. The proposed basis and curves satisfy the basic properties and are $C^5$ continuous. Rational basis functions and curves are also derived at uniform and non-uniform knots. $C^3$ continuous rational curves are also derived in this paper. Validity and applicability of the proposed curves are checked by modeling the floating and periodic curves. In the end, the proposed curves are also used for $2D$ and $3D$ modeling. The objectives of the proposed research are:

• To derive new trigonometric B-spline basis functions with shape parameter $\xi$;
• To derive trigonometric rational B-spline and NURBS curves;
• To derive different continuities for basis and curve on uniform and non-uniform knots;
• To apply the derived curves for $2D$ and $3D$ modeling.

The rest of the paper is organized as follow. In Section 2, trigonometric B-spine bases have been constructed. Section 3, presents the modeling of cubic trigonometric B-spline curves with its application. Section 4 explains the construction of rational trigonometric B-spline and NURBS bases. The construction of rational trigonometric B-spline curves and geometric modeling with concluding remarks is explained in Section 5.

2. The Construction of Trigonometric B-Spline Basis

The proposed trigonometric cubic B-spline with $\xi \in [0,4]$ as shape parameter on knot vector N$(n_0<n_1<n_2<...<n_{i+4})$ is defined as:

$$F_j(n)=\left\{\begin{array}{c}{a}_j(l_3(t_j))n\in [n_j,n_{j+1}),\hfill \\ \sum _{k=0}^3{c}_{j+1,k}(l_k)(t_{j+1})n\in [n_{j+1},n_{j+2}),\hfill \\ \sum _{k=0}^3{b}_{j+2,k}(l_k)(t_{j+2})n\in [n_{j+2},n_{j+3}),\hfill \\ d_{j+3}(l_0(t_{j+3}))n\in [n_{j+3},n_{j+4}),\hfill \\ 0otherwise.\hfill \end{array}\right.$$

(1)

Here, $t_j(n)=\frac{\pi }{2}(\frac{n-n_j}{n_{j+1}-n_j})$ and $j\in [0,4]$. For uniform knots $q_j=q_{j-1}=q_{j-2}$. The functions used in Equation (1) are:

$$\begin{array}{c}{\displaystyle a_j=\frac{2{\alpha }_{j-1}{\beta }_{j-2}{q}_j^3}{{\psi }_{j-2}},b_{j,0}=[1-({\xi }^2-3\xi -1)d_{j+1}]{\gamma }_{j+1}(q_{j-1}-q_j),}\hfill \\ {\displaystyle b_{j,1}=\frac{3{\gamma }_{j+1}{q}_{j-1}^2{\alpha }_j}{2{\varphi }_{j-3}},}\hfill \\ {\displaystyle b_{j,2}=\frac{(1-2\xi ){\beta }_{j-1}{q}_{j-1}{b}_{j,0}}{{\varphi }_{j+1}},}\hfill \\ {\displaystyle b_{j,3}=4\xi [q_{j+1}-q_j]{\gamma }_j,}\hfill \\ {\displaystyle d_j=\frac{{\alpha }_{j+2}{q}_j}{2{\beta }_{j+1}{\psi }_{j+2}},}\hfill \\ {\displaystyle c_{j,3}=-3{\beta }_{j-1}(q_{j+2}-q_{j-1})[{\gamma }_{j+2}{q}_{j+1}+{\alpha }_{j+1}{q}_j]a_{j+2},}\hfill \\ {\displaystyle c_{j,2}=\frac{4{\varphi }_{j-1}}{3{\gamma }_{j+1}{q}_{j+1}},}\hfill \\ {\displaystyle c_{j,1}=\frac{12{\gamma }_j{\alpha }_{j+1}{q}_j^3{\psi }_{j-1}{c}_{j,0}}{{\varphi }_{j+1}^2},}\hfill \\ {\displaystyle c_{j,0}=(q_{j+2}-q_{j+1}){\alpha }_{j+1}{d}_{j-1},}\hfill \end{array}$$

(2)

where:

$$\begin{array}{c}{q}_j=n_{j+1}-n_j,{\alpha }_j=\frac{1}{q_{j+1}+q_j},{\beta }_j=\frac{1}{q_{j-1}+q_{j-2}}\hfill \\ {\gamma }_j=\frac{2}{q_{j-1}+q_j+q_{j+1}},{\varphi }_j=\frac{{\psi }_{j-2}(q_{j+1}+1)}{2({\beta }_{j-1}{q}_{j-1}^3+{\alpha }_j{q}_{j+1}^2)},\hfill \\ {\psi }_j=6{\xi }^2{\alpha }_{j-1}{q}_{j-1}^2-3\xi q_j+10{\beta }_{j+1}{q}_{j+1}^2.\hfill \end{array}$$

(3)

The proposed cubic trigonometric B-spline functions possessing $\xi$ are defined as:

$$\begin{array}{c}{l}_0(t)={(1-sint)}^2({\xi }^2-\xi +1-sint),\hfill \\ l_1(t)={(1+cost)}^2({\xi }^2-\xi +1+cost),\hfill \\ l_2(t)={(1+sint)}^2({\xi }^2-\xi +1+sint),\hfill \\ l_3(t)={(1-cost)}^2({\xi }^2-\xi +1-cost).\hfill \end{array}$$

(4)

The basis functions can be defined on $n\in [n_j,n_{j+1})$ by replacing j by $j-3,j-2,j-1,j$ in Equation (1). The basis of the functions are:

$$\begin{array}{c}{F}_0(n)=d_j(l_0(t_j)),\hfill \\ F_1(n)=\sum _{k=0}^3{b}_{j,k}(l_k)(t_j),\hfill \\ F_2(n)=\sum _{k=0}^3{c}_{j,k}(l_k)(t_j),\hfill \\ F_3(n)=a_j(l_3(t_j)).\hfill \end{array}$$

(5)

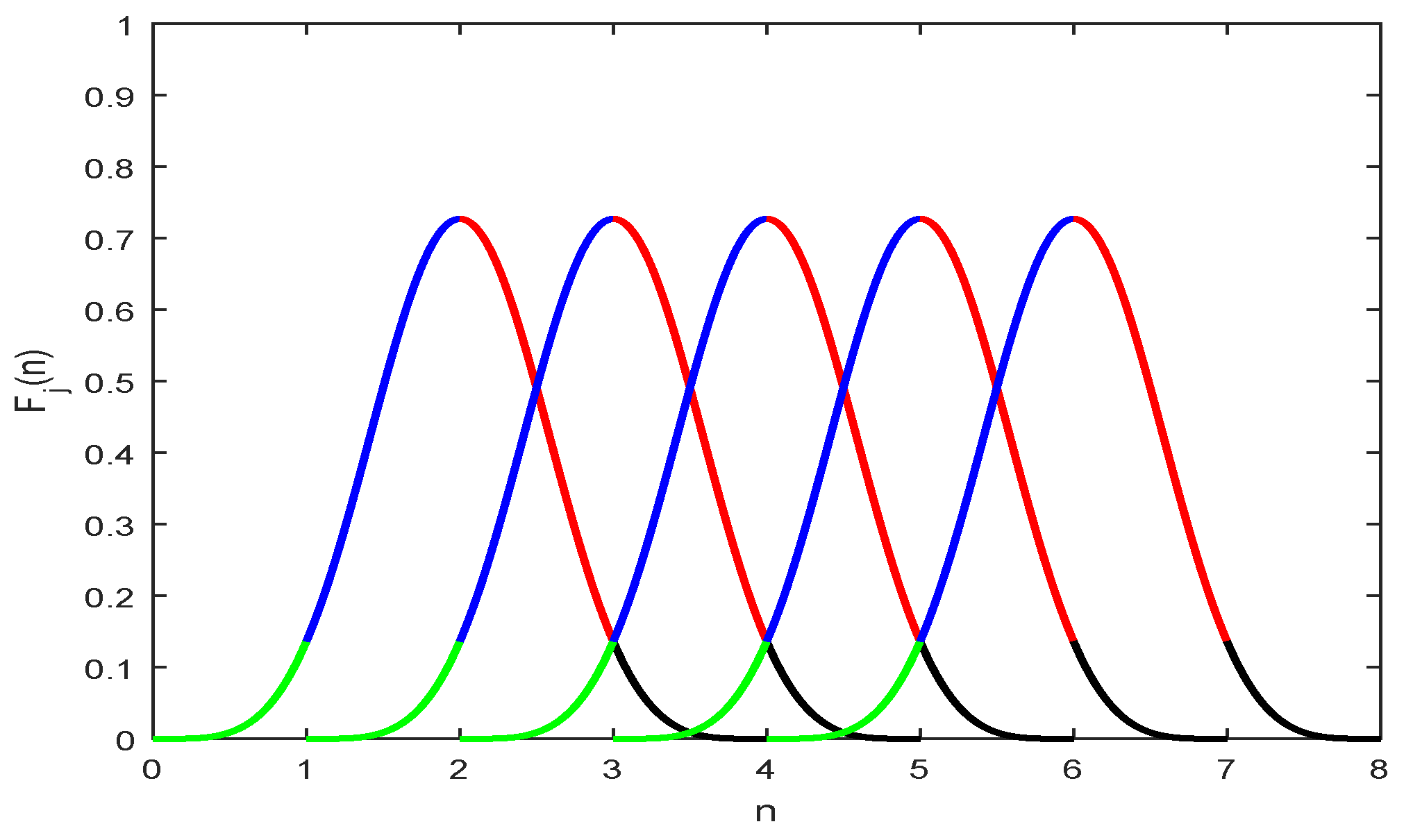
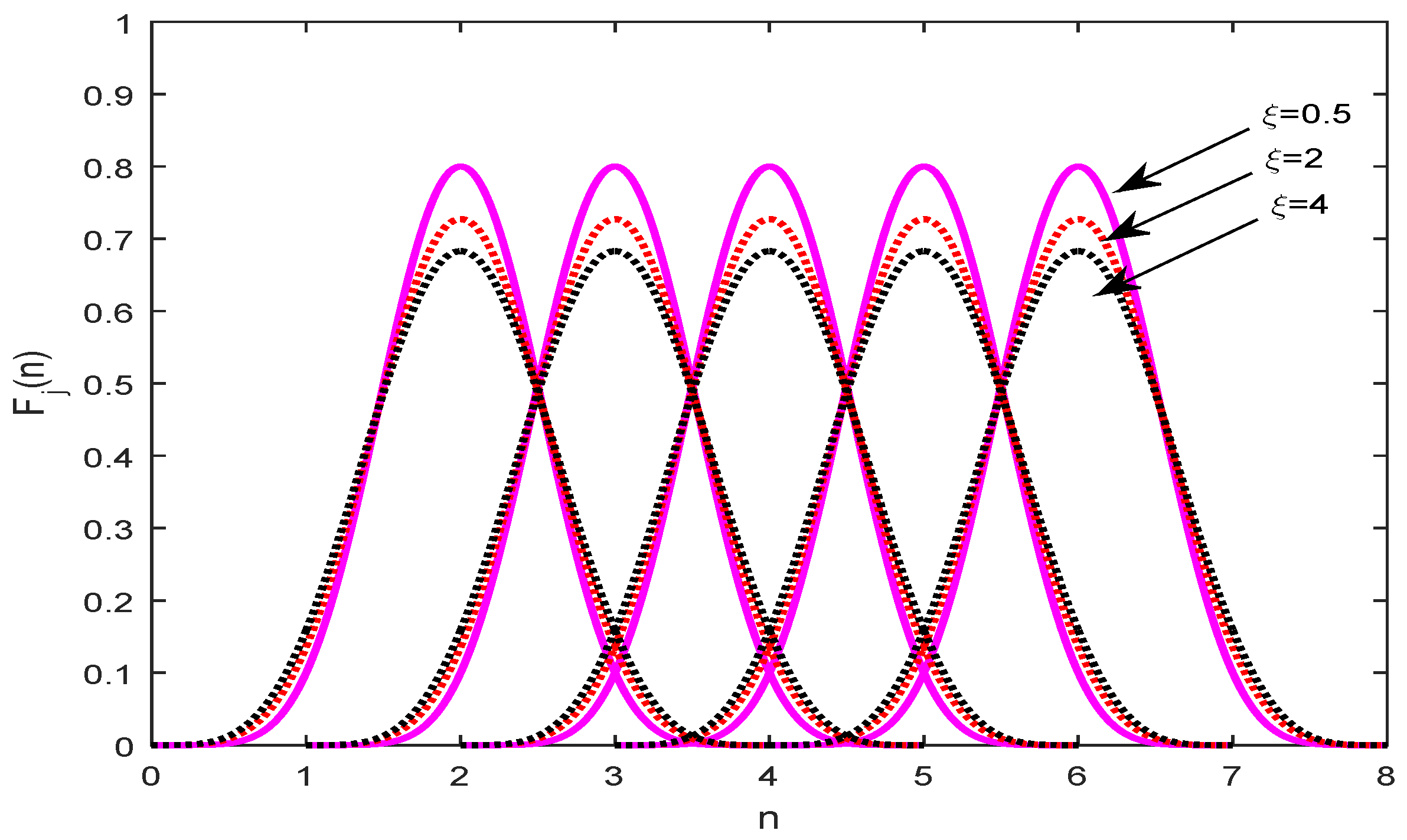
Figure 1 represents the graphical behavior of spline functions, where the effect of shape parameter $\xi$ is represented in Figure 2.

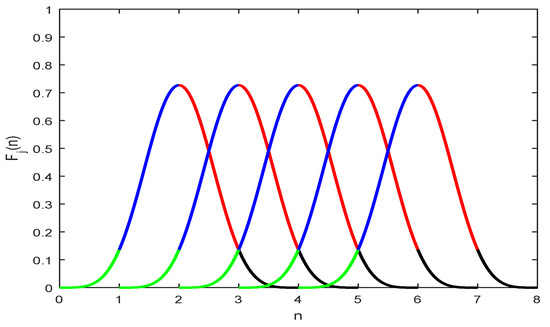
Figure 1. Graphical behavior of the proposed trigonometric functions.

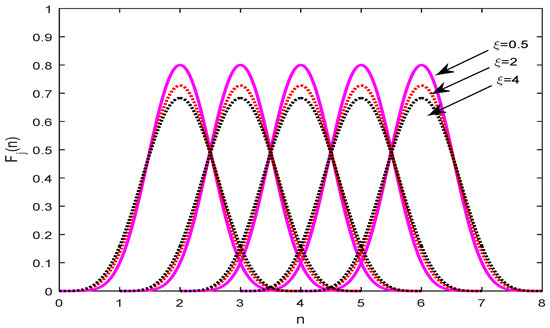
Figure 2. The effect of shape parameter $\xi$.

Properties of the Cubic Trigonometric Spline Functions

The following properties are satisfied by the proposed basis.

Theorem 1.

The proposed cubic trigonometric B-spline basis function satisfy the partition of unity property:

$$\sum _{j=0}^3{F}_j(n)=1.$$

Proof of Theorem 1.

See Appendix A □

Theorem 2.

The cubic trigonometric B-spline basis holds non-negativity property i.e., $F_j(n)>0$.

Proof of Theorem 2.

See Appendix B □

Theorem 3.

The derived basis are $C^3$ and $C^5$ continuous for non-uniform knots.

Proof of Theorem 3.

See Appendix C □

3. Modeling of Cubic Trigonometric B-Spline Curves

Definition 1.

Let $F_j(n)$ be the basis functions defined in Equation (5) above and $S_j\in R^2$ for $j=[0,3]$ are control points in plane. The cubic trigonometric B-spline curve is defined as:

$$G(n)=\sum _{j=0}^3{F}_j(n)S_j,$$

(6)

where,

$$\begin{array}{c}{F}_0(n)=d_j(l_0(t_j)),\hfill \\ F_1(n)=\sum _{k=0}^3{b}_{j,k}(l_k)(t_j),\hfill \\ F_2(n)=\sum _{k=0}^3{c}_{j,k}(l_k)(t_j),\hfill \\ F_3(n)=a_j(l_3(t_j)).\hfill \end{array}$$

and

$$t_j(n)=\frac{\pi }{2}(\frac{n-n_j}{n_{j+1}-n_j}).$$

3.1. Properties of Cubic Trigonometric B-Spline Curves

The following properties are obeyed by proposed curves.

3.1.1. Convex Hull Property

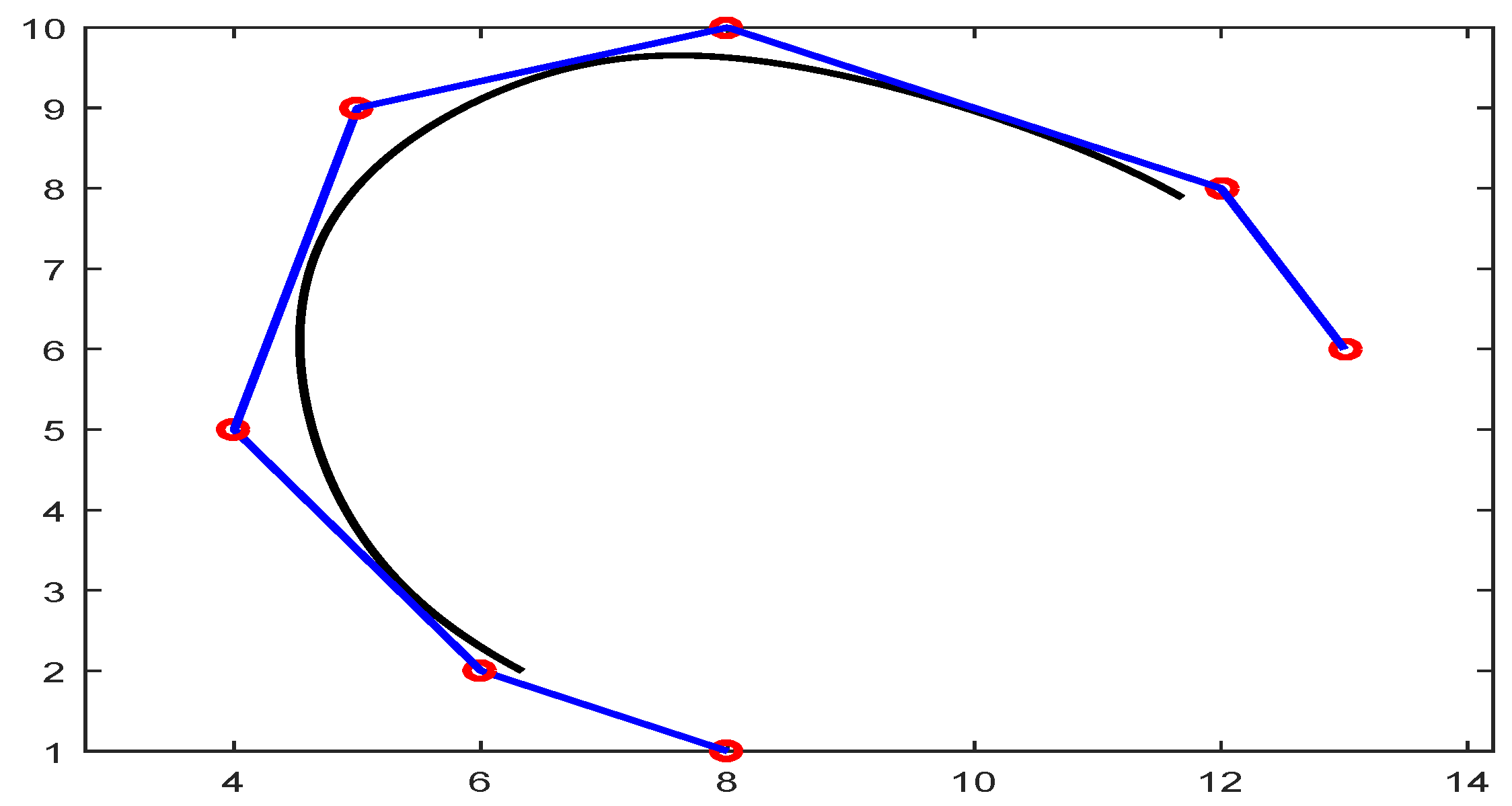
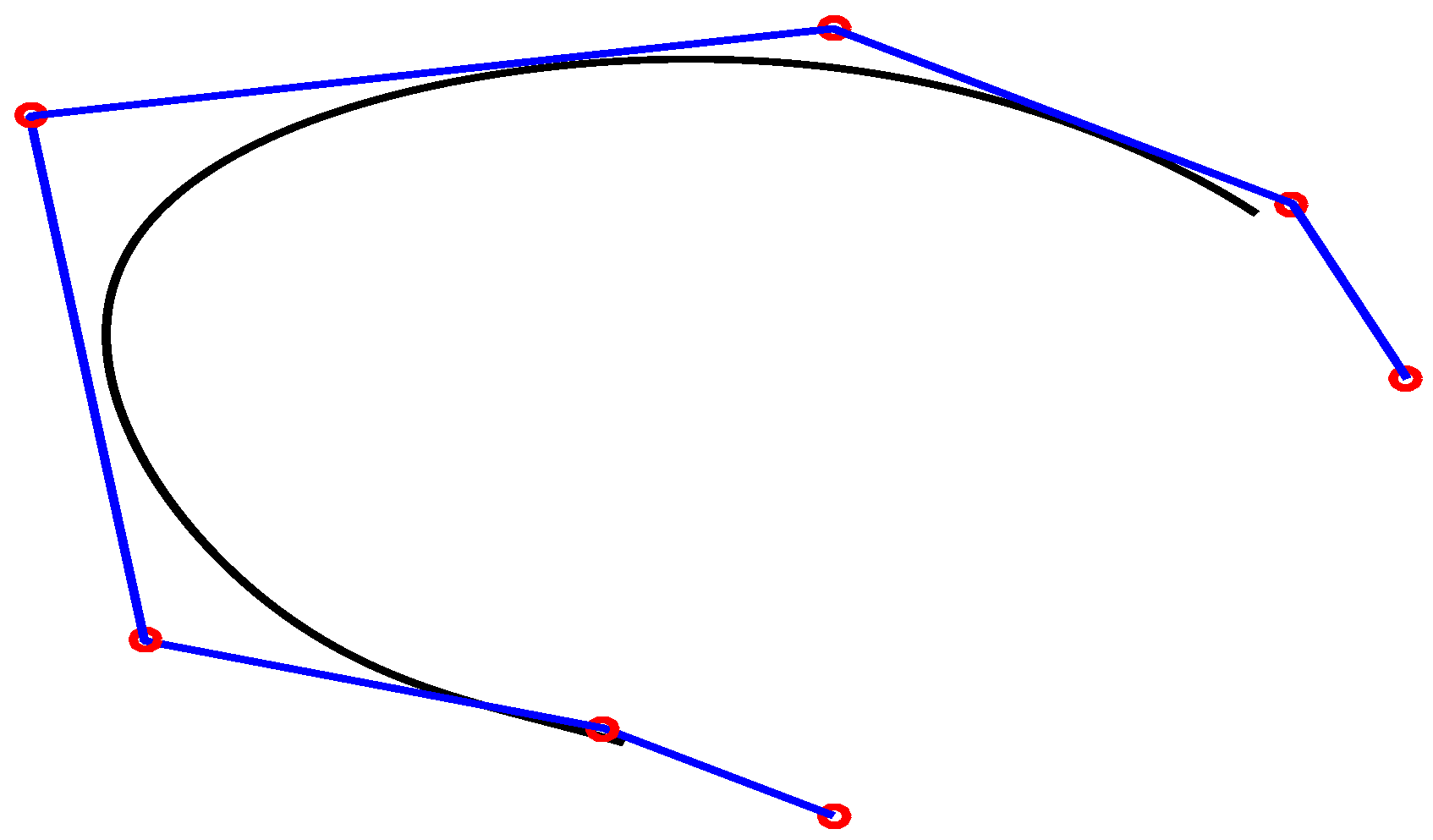
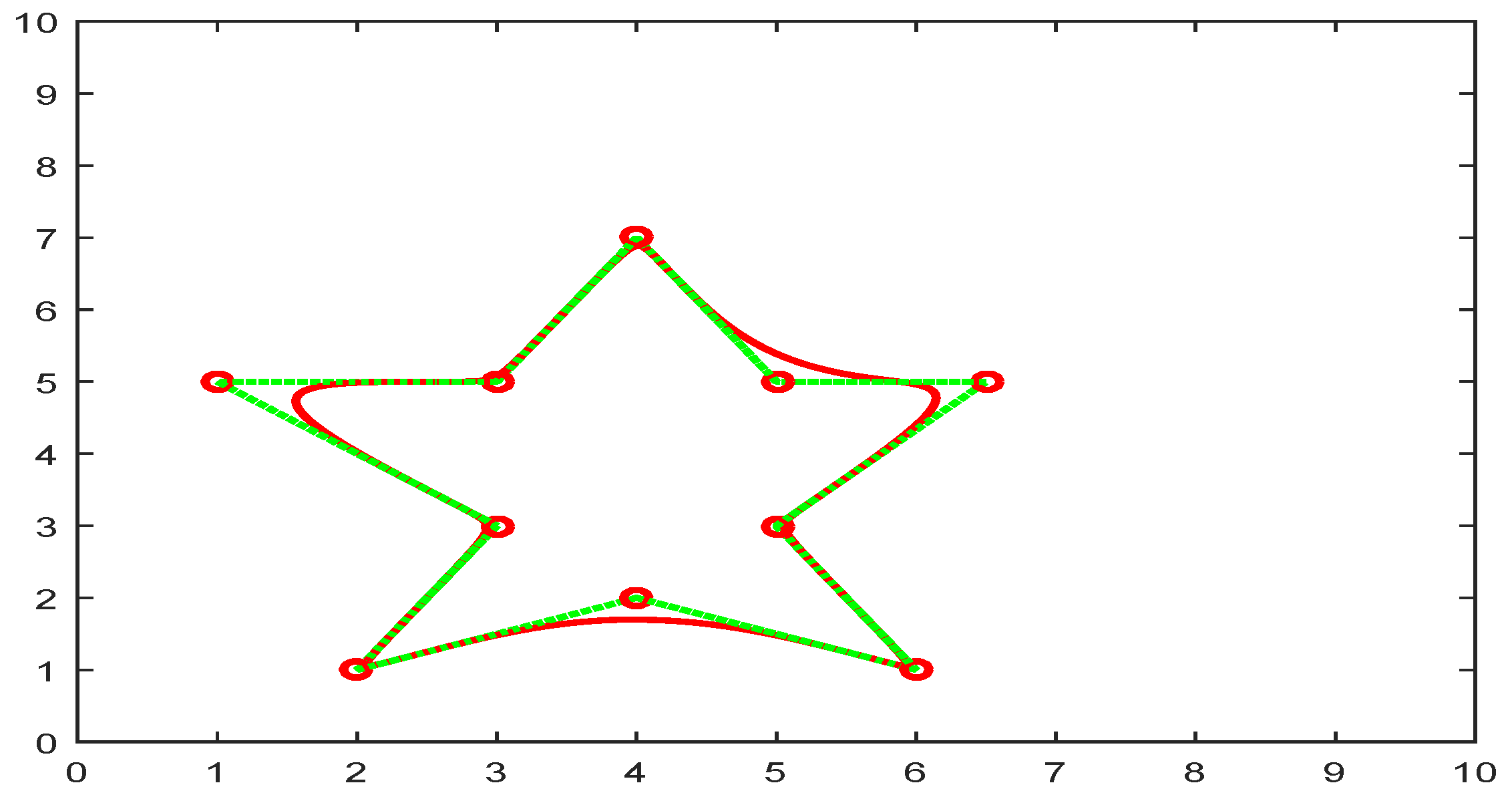
The constructed curves always lies within the convex hull of the control polygon as shown in Figure 3.

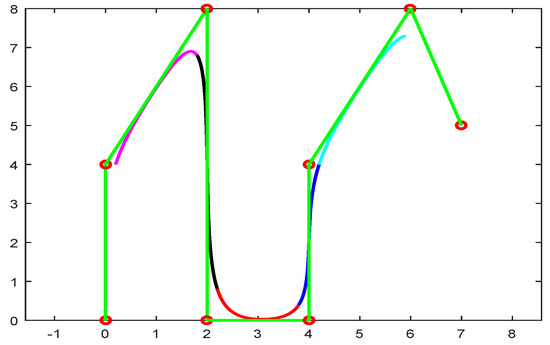
Figure 3. Convex hull property.

3.1.2. Affine Transformation

The transformation may be of rotation, scaling, reflection, and translation. Let L be the transformation then:

$$L(\sum _{j=0}^n{S}_j{F}_j(n))=\sum _{j=0}^{n}L(S_j)F_j(n).$$

Theorem 4.

The proposed curve possesses $C^3$ and $C^5$ continuity for $\xi \ne 1$. For multiple knots, the curve has $C^{3-k}$ continuity here $k=[0,3]$.

Proof of Theorem 4.

See Appendix D □

3.2. Floating and Periodic Curves Using Proposed Trigonometric Basis Functions

3.2.1. Floating Cubic B-Spline Curve

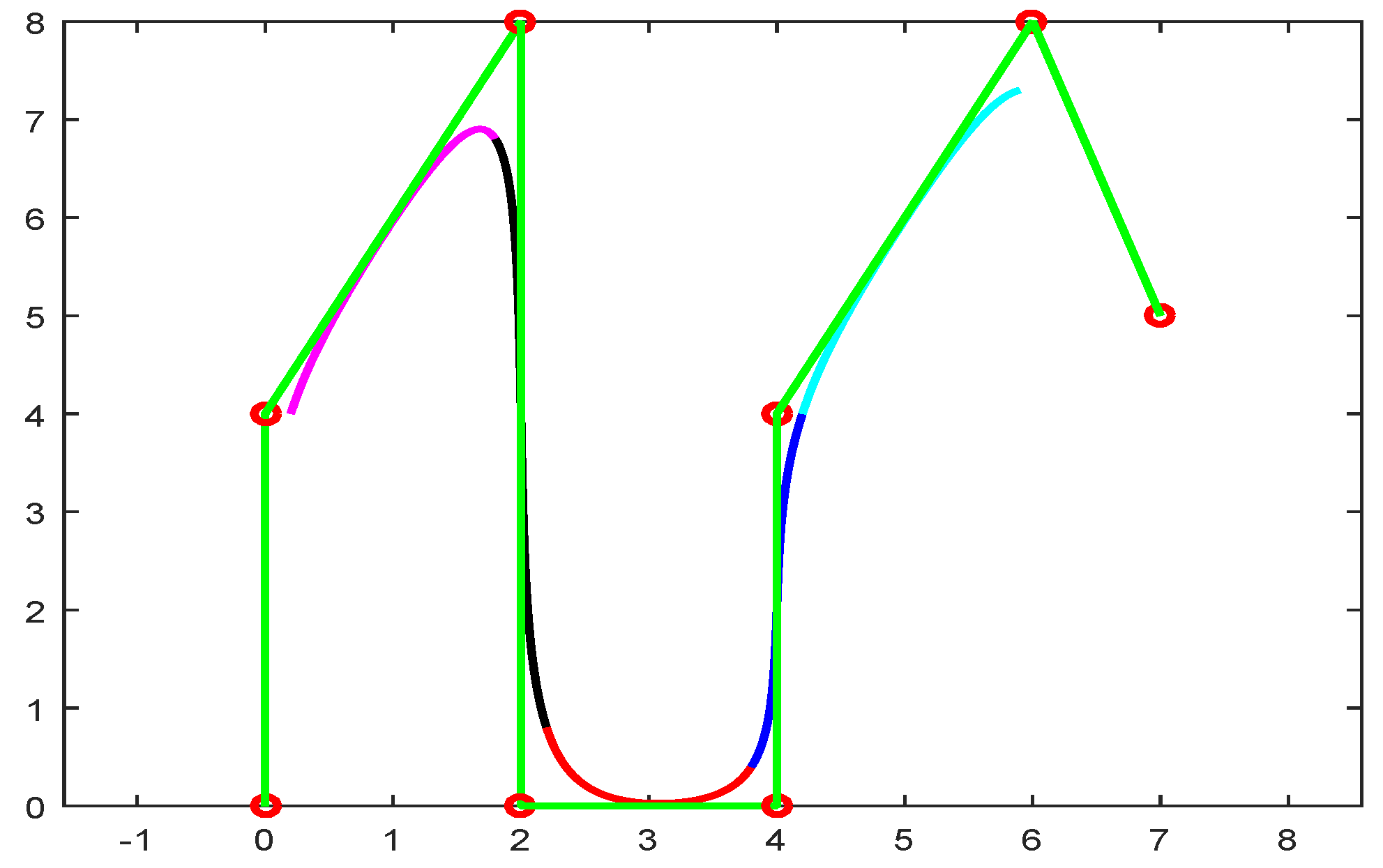
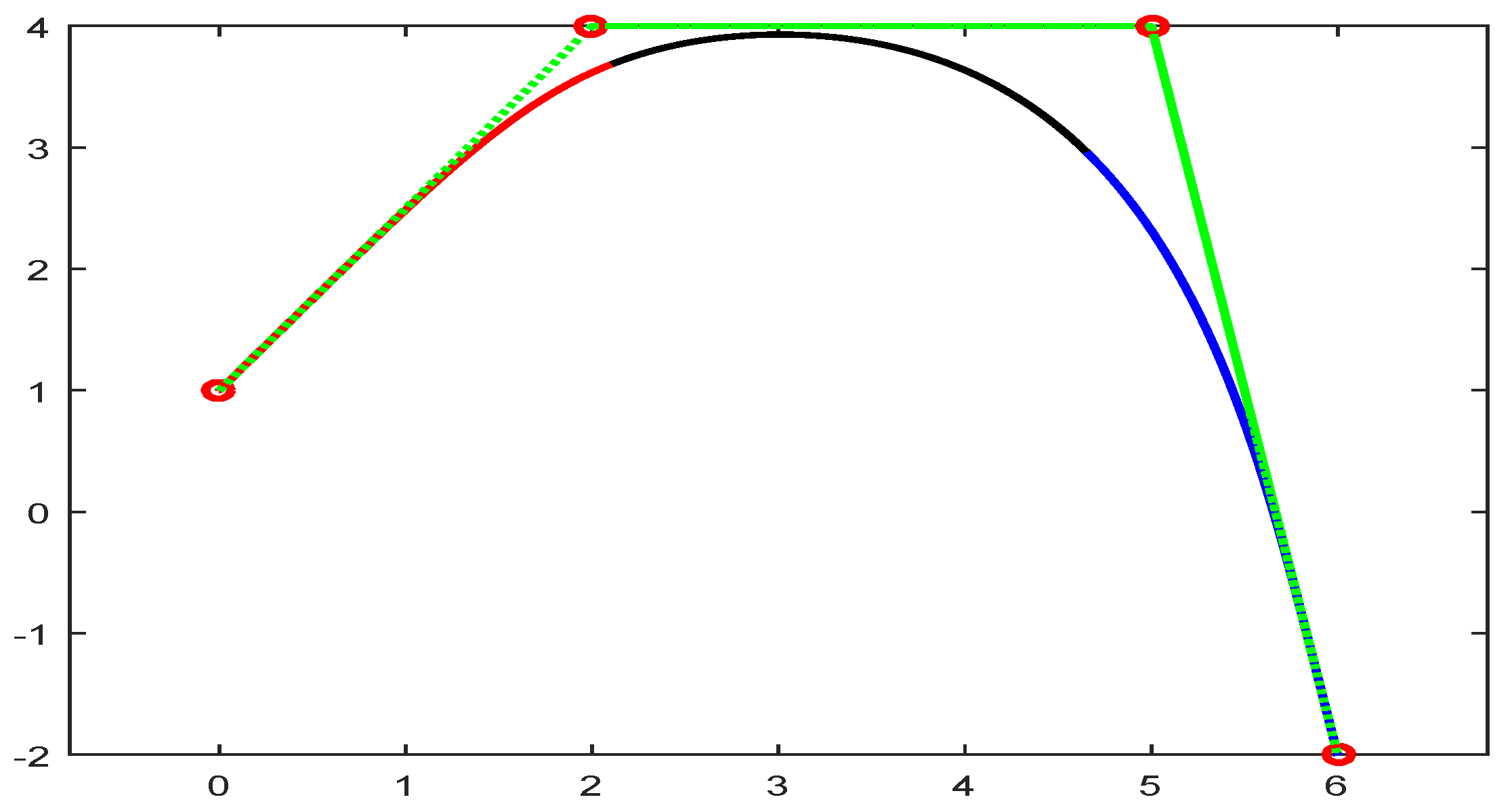
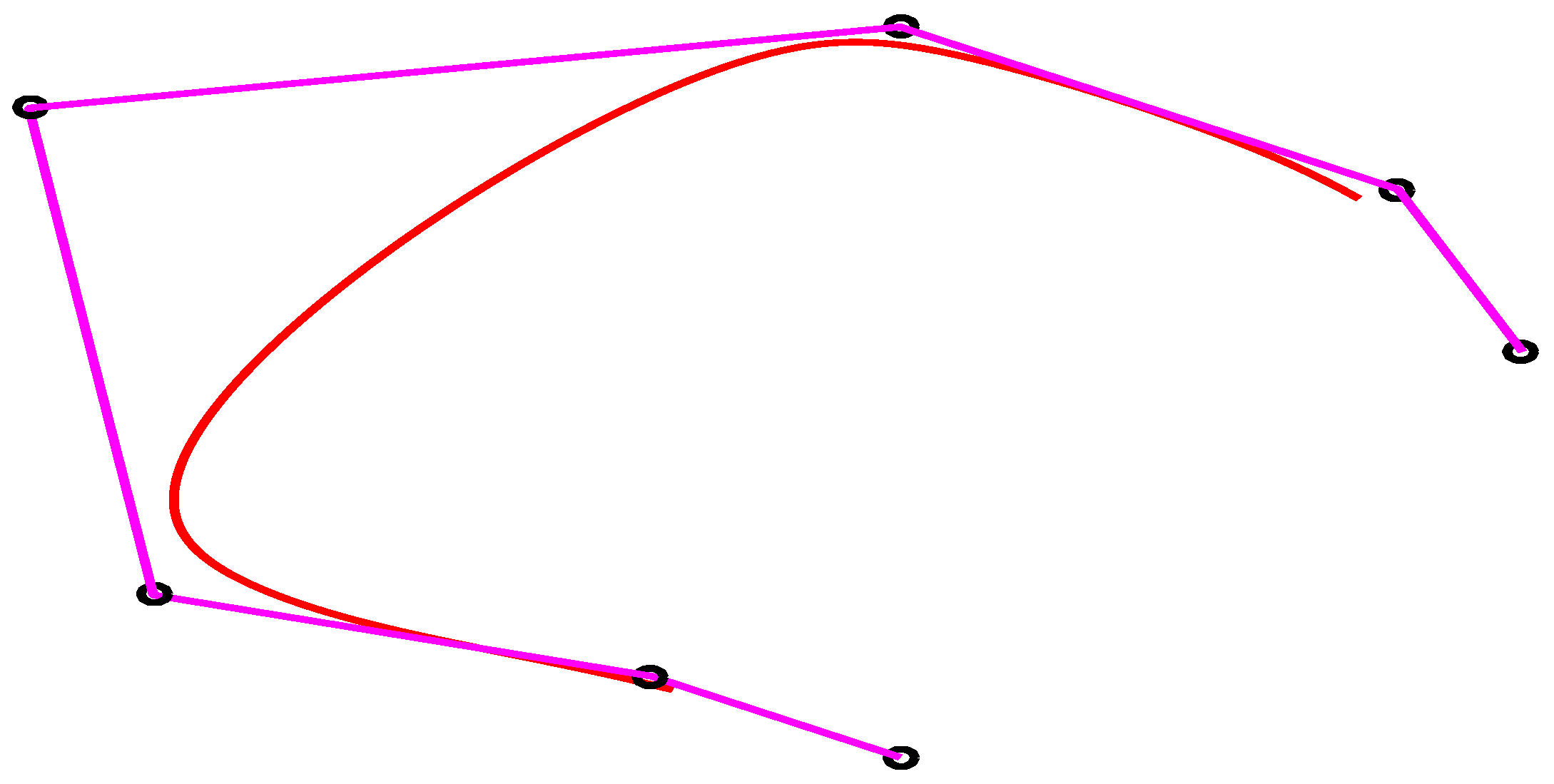
The cubic trigonometric basis are used to construct the floating curves with $\xi =4$ and 1 as shown in Figure 4.

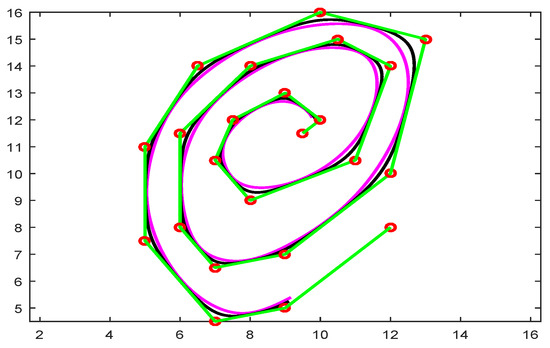
Figure 4. Floating curve using $\xi =4$ (magenta) and $\xi =1$ (black) color curve.

3.2.2. Periodic Trigonometric B-Spline Curves

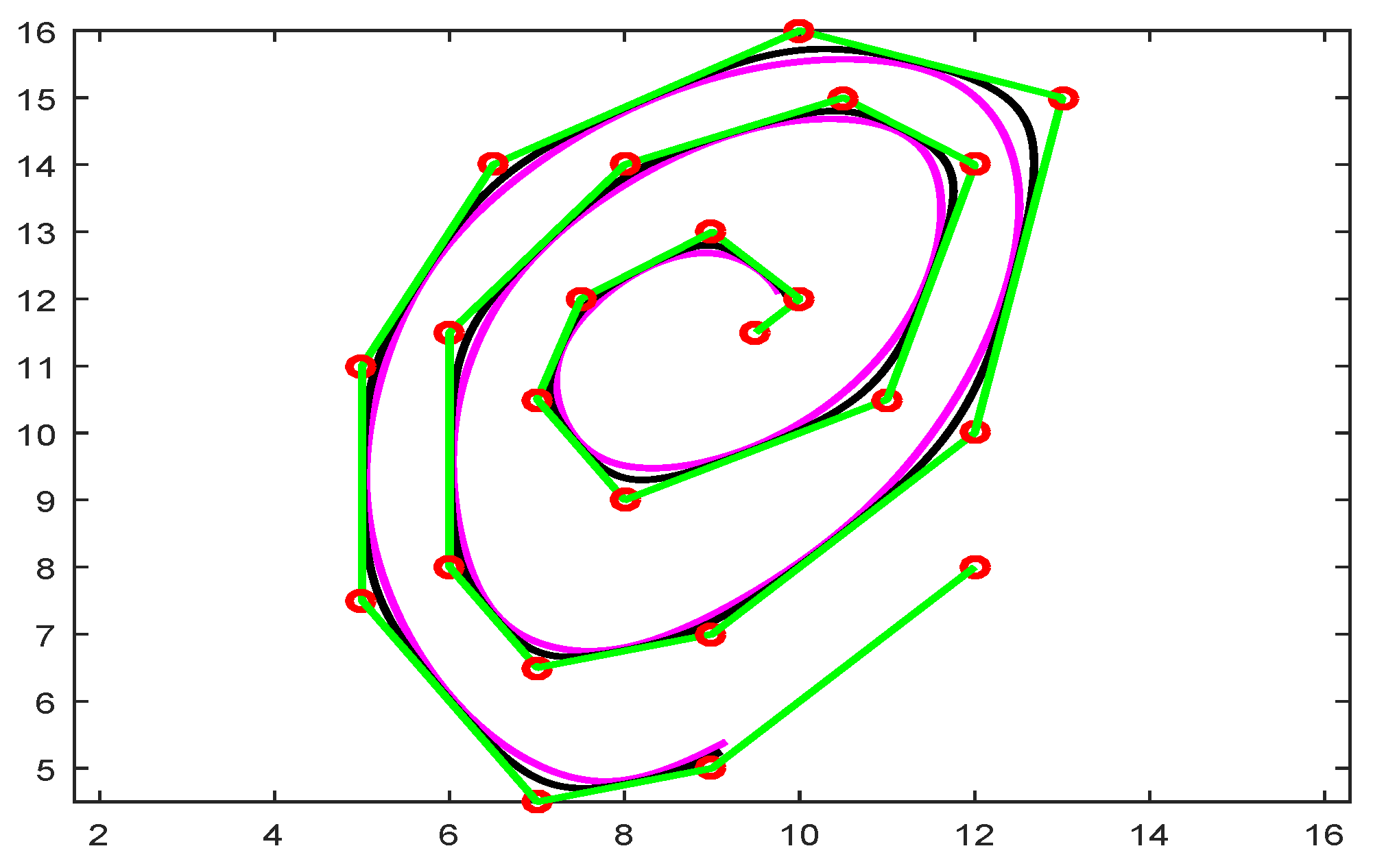
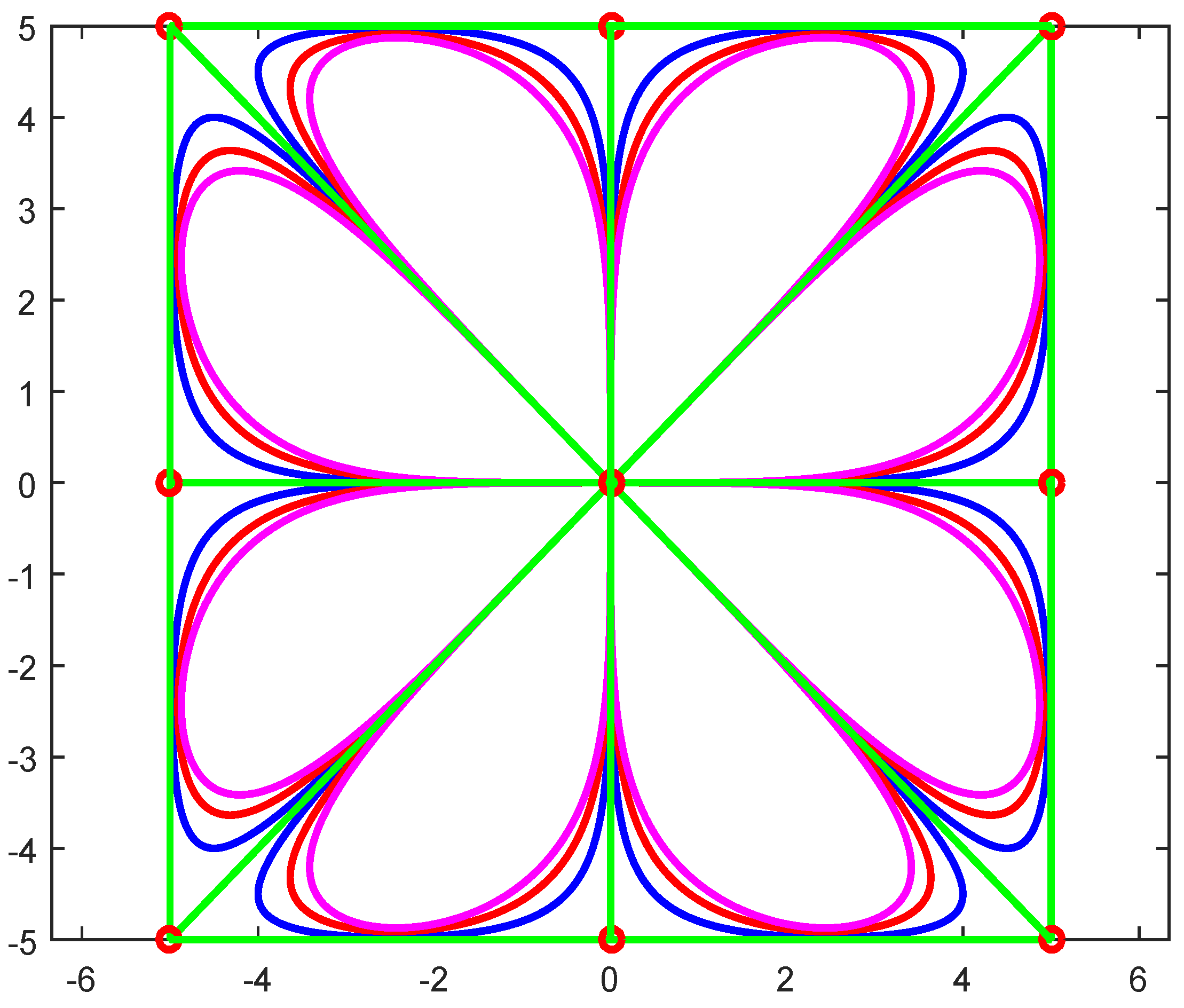
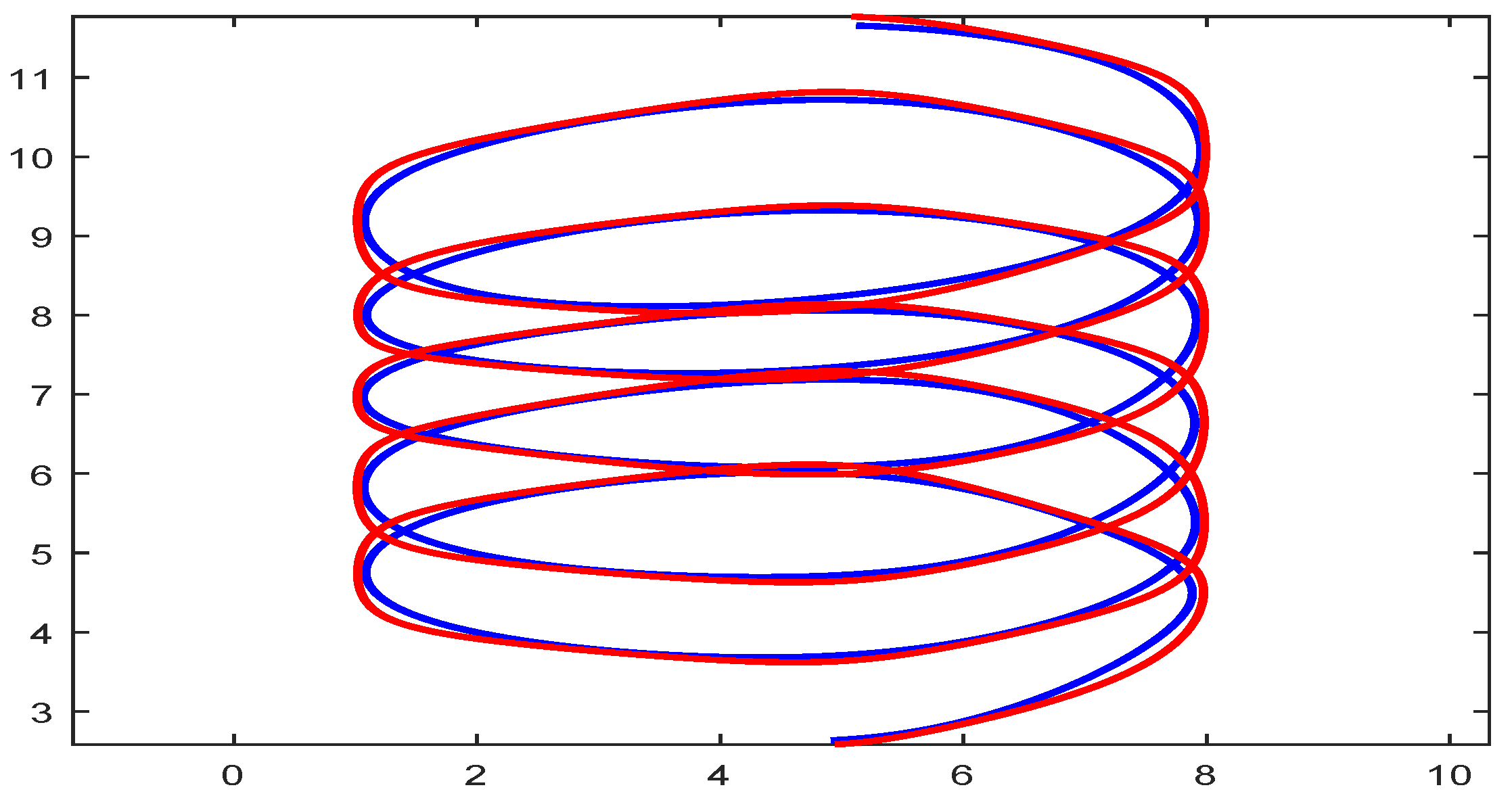
Periodic curve is drawn using cubic trigonometric B-spline basis functions as shown in Figure 5. Periodic curves can be drawn in blue, red, and magenta colors with $\xi =0,2$, and 4 respectively these shape parameters provide more flexibility than classical B-spline curves.

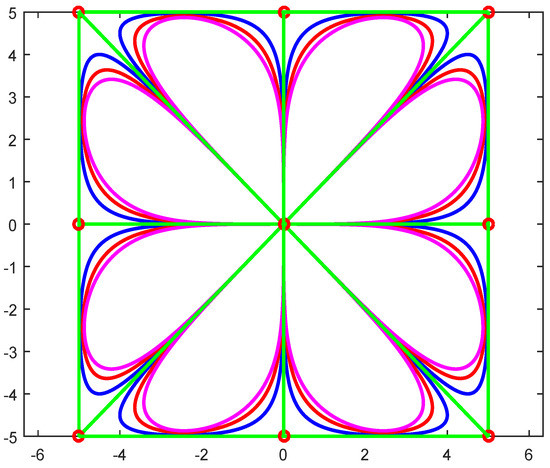
Figure 5. Periodic curve with $\xi =0$ (Blue), $\xi =2$ (Red), and $\xi =4$ (Magenta).

From Figure 4 and Figure 5, it is observed that the proposed cubic trigonometric B-spline curves work well for both floating and periodic curves. It is also observed that shape parameter $\xi$ has a significant effect on the curve.

4. Rational Trigonometric B-Spline and NURBS

Definition 2.

Rational trigonometric B-spline and NURBS are a generalization of B-spline basis. It enhances the flexibility of the curve. It is generally expressed as:

$$Y(n)=\frac{{\sum }_{j=0}^n(w_j{F}_{j,d}(n))}{{\sum }_{j=0}^n(w_j{F}_{j,d}(n))}.$$

Here d is the degree of trigonometric B-spline basis. $w_{j}s$ are positive weights. $F_{j,d}(n)$ are the trigonometric B-spline basis. Simply, we can write it as:

$$Y(n)=\sum _{j=0}^n{Q}_{j,d}(n),$$

where,

$$Q_{j,d}(n)=\frac{(w_j{F}_{j,d}(n))}{{\sum }_{j=0}^n(w_j{F}_{j,d}(n))}.$$

The expression for the rational trigonometric B-spline and NURBS becomes:

$$Y(n)=\frac{{\sum }_{j=0}^3(w_j{F}_j(n))}{{\sum }_{j=0}^3(w_j{F}_j(n))},$$

or

$$Y(n)=\sum _{j=0}^3{Q}_j(n),$$

where

$$Q_j(n)=\frac{(w_j{F}_j(n))}{{\sum }_{j=0}^3(w_j{F}_j(n))}.$$

Remark 1.

In the above equations if B-spline basis $F_j(n)$ are defined over uniform knots then the basis becomes Rational trigonometric B-spline otherwise NURBS.

Properties of the Rational Trigonometric B-Spline and NURBS

The proposed rational trigonometric B-spline and NURBS basis possess the following properties.

Theorem 5.

For all $w_j=1$, then $Q_j(n)=F_j(n)$.

Proof of Theorem 5.

We prove this by taking:

$$Q_j(n)=\frac{w_j{F}_j(n)}{{\sum }_{j=0}^3(w_j{F}_j(n))}.$$

Put, $w_j=1$ then above equation becomes:

$$Q_j(n)=\frac{F_j(n)}{(F_0(n)+F_1(n)+F_2(n)+F_3(n))}.$$

Here $F_0(n),F_1(n),F_2(n),F_3(n),$ are defined in Equation (5). Since, we have proved earlier that:

$$\sum _{j=0}^3{F}_j(n)=1.$$

Thus, we get:

$$Q_j(n)=(F_j(n)).$$

□

Theorem 6.

The rational cubic trigonometric B-spline basis function satisfies the partition of unity property i.e.

$$Y(n)=\sum _{j=0}^3{Q}_j(n)=1.$$

Proof of Theorem 6.

Since,

$$Q_j(n)=\frac{(w_j{F}_j(n))}{{\sum }_{j=0}^3(w_j{F}_j(n))},$$

or simply:

$$Q_j(n)=\frac{(w_j{F}_j(n))}{w_0{F}_0(n)+w_1{F}_1(n)+w_2{F}_2(n)+w_3{F}_3(n)}.$$

Now,

$$Y(n)=\sum _{j=0}^3{Q}_j(n),$$

$$Y(n)=Q_0(n)+Q_1(n)+Q_2(n)+Q_3(n).$$

$$\begin{array}{ccc}\hfill Y(n)& =& \frac{w_0{F}_0(n)}{w_0{F}_0(n)+w_1{F}_1(n)+w_2{F}_2(n)+w_3{F}_3(n)}\hfill \\ & & +\frac{w_1{F}_1(n)}{w_0{F}_0(n)+w_1{F}_1(n)+w_2{F}_2(n)+w_3{F}_3(n)}\hfill \\ & & +\frac{w_2{F}_2(n)}{w_0{F}_0(n)+w_1{F}_1(n)+w_2{F}_2(n)+w_3{F}_3(n)}\hfill \\ & & +\frac{w_3{F}_3(n)}{w_0{F}_0(n)+w_1{F}_1(n)+w_2{F}_2(n)+w_3{F}_3(n)}.\hfill \\ & =& \frac{w_0{F}_0(n)+w_1{F}_1(n)+w_2{F}_2(n)+w_3{F}_3(n)}{w_0{F}_0(n)+w_1{F}_1(n)+w_2{F}_2(n)+w_3{F}_3(n)}\hfill \\ & =& 1\hfill \end{array}$$

(7)

Hence, partition of unity holds. □

5. Rational Trigonometric B-Spline and NURBS Curve

Definition 3.

Rational trigonometric B-spline and NURBS curve possessing shape parameter ξ is expressed generally as:

$$Z(n)=\frac{{\sum }_{j=0}^3(w_j{H}_j{F}_j(n))}{{\sum }_{j=0}^3(w_j{F}_j(n))},$$

or

$$Z(n)=\sum _{j=0}^3{H}_j{Q}_j(n),$$

where $H_j=H_0,...,H_n$ are control points, $w_{j}s$ are non-negative weights, and $F_j(n)$ are trigonometric B-spline basis.

5.1. Properties of Rational Trigonometric B-Spline and NURBS Curve

5.1.1. Convex Hull Property

Rational trigonometric B-spline and NURBS curves always lie inside the convex hull of control polygon as shown in Figure 6 and Figure 7, respectively.

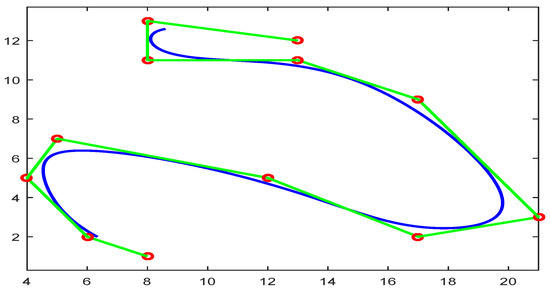
Figure 6. Convex hull of rational trigonometric curve.

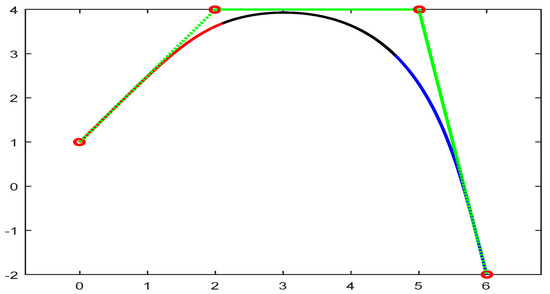
Figure 7. Convex hull of NURBS curve.

5.1.2. Affine Transformation

Let T be an affine transformation, then:

$$T(\frac{{\sum }_{j=0}^n(w_j{H}_j{F}_{j,d}(n))}{{\sum }_{j=0}^n(w_j{F}_{j,d}(n))})=\frac{{\sum }_{j=0}^n(w_{j}T(H_j)F_{j,d}(n))}{{\sum }_{j=0}^n(w_j{F}_{j,d}(n))}.$$

5.1.3. Local Approximation

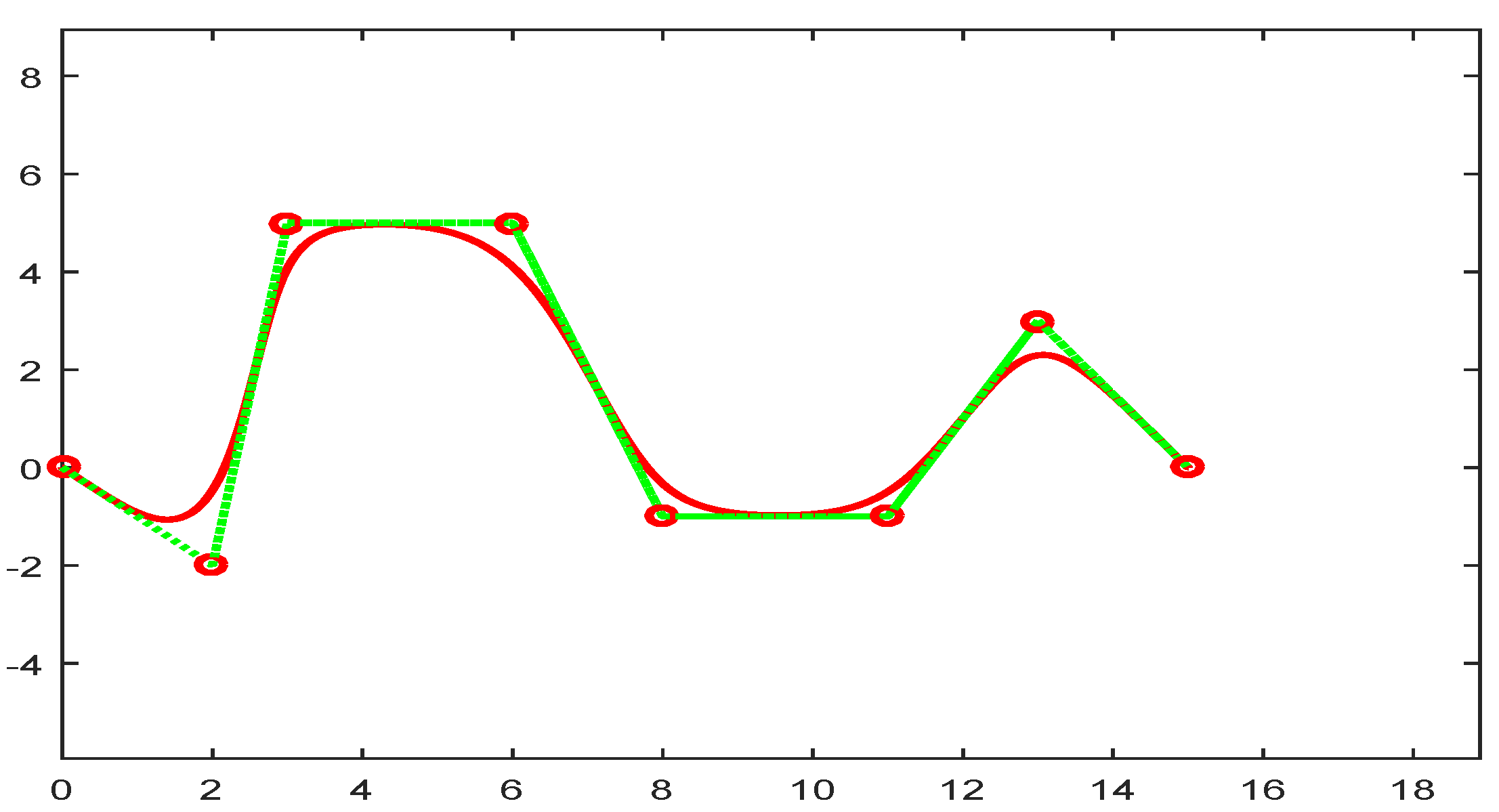
The shape of the curve can be distorted, either by changing the control points or weights. In Figure 8, the curve is without any change of control point and weight. Figure 9 explains that the change of control points affect the curve locally. Similarly, in Figure 10, a change of weight can be seen clearly.

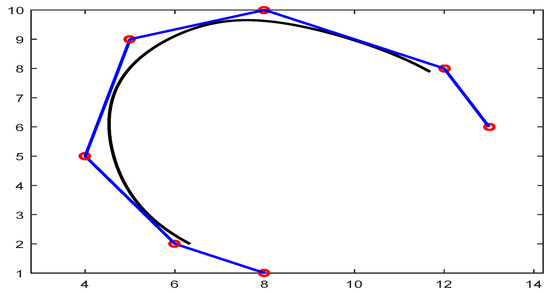
Figure 8. Without changing the weight and control point.

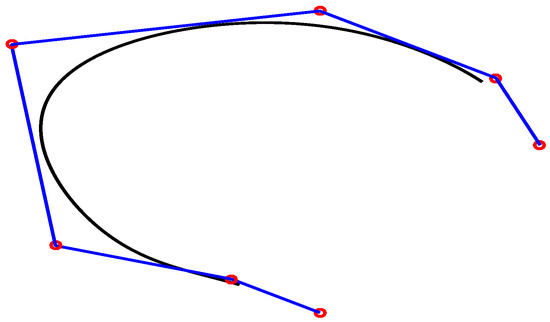
Figure 9. The effect of changing the control point.

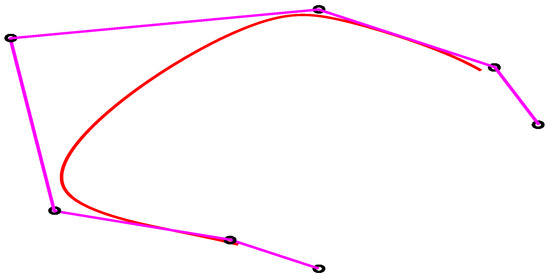
Figure 10. The effect of changing the weight.

5.1.4. Continuity

Theorem 7.

The rational trigonometric B-spline and NURBS curve has $C^3$ continuity. These curve have $C^{3-k}$ continuity, $k=[0,4]$. The curve becomes discontinuous at $k=4$.

Proof of Theorem 7.

See Appendix E □

5.2. Floating and Periodic Rational Trigonometric B-Spline and NURBS Curve

5.2.1. Floating Rational and NURBS Curve

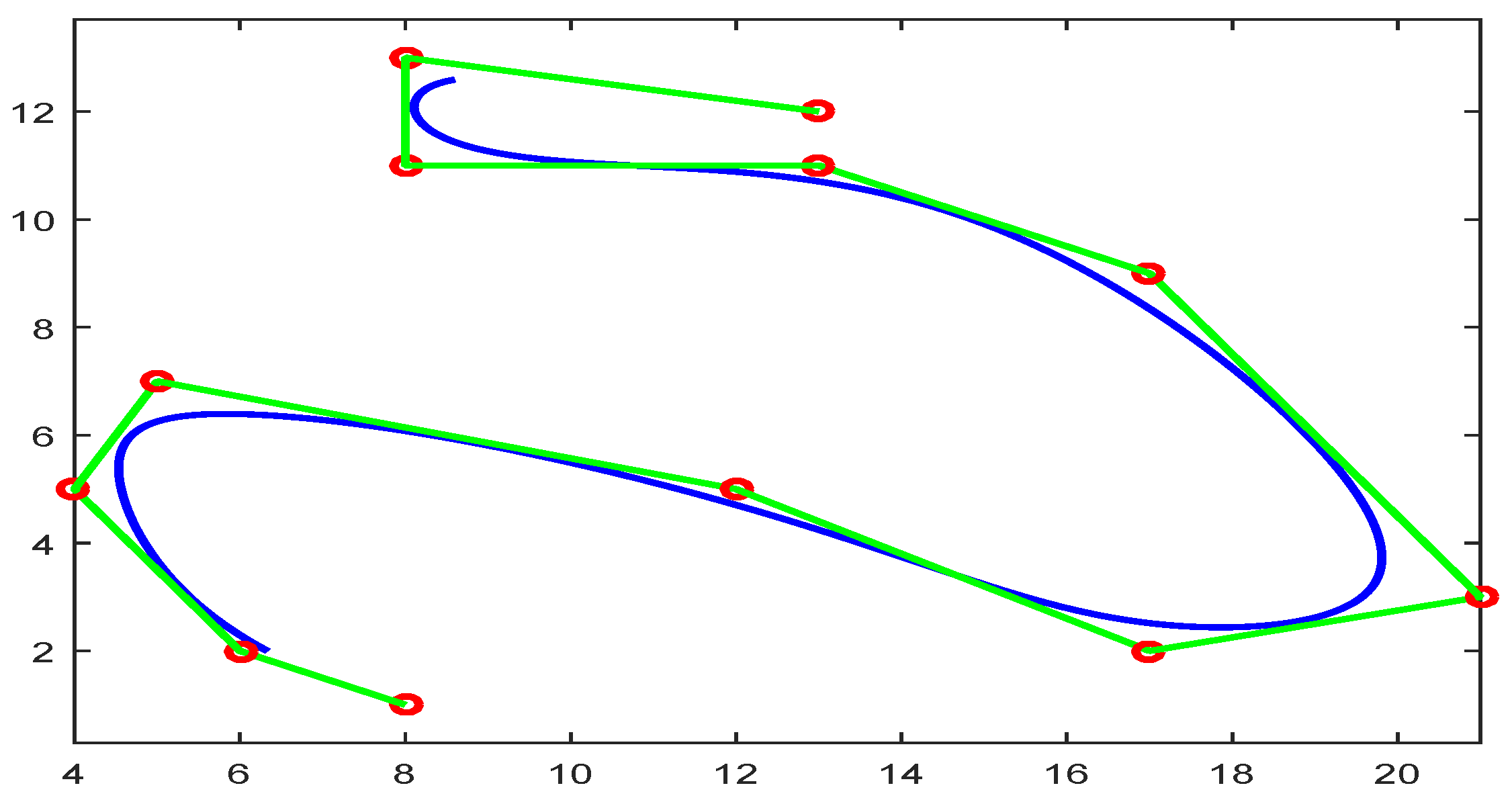
A floating curve is also known as an open curve, such curves whose first and last point does not meet. Figure 11 and Figure 12 show the floating rational trigonometric B-spline and NURBS curve, respectively. A total of 36 control points are used to construct rational trigonometric curve possessing $\xi =3,0$ for the blue and red color, respectively. The control polygon of NURBS is formed possessing $\xi =3$ see Figure 12.

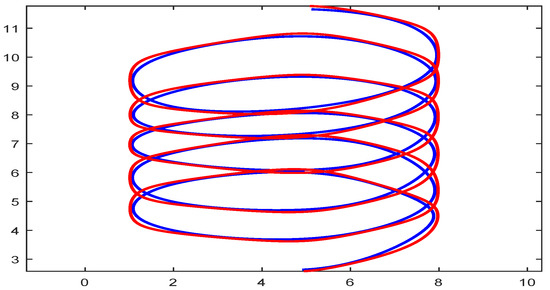
Figure 11. Floating rational trigonometric curve with different $\xi$.

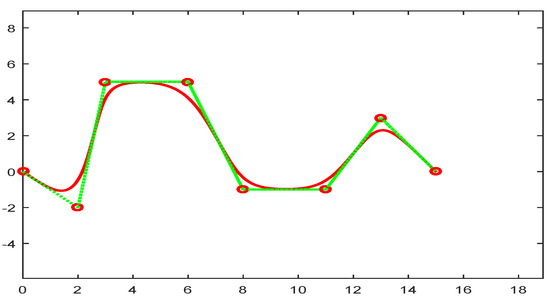
Figure 12. Floating NURBS curve with $\xi =3$.

5.2.2. Periodic Rational and NURBS Curve

In Figure 13 and Figure 14 the periodic rational trigonometric B-spline and NURBS curve is constructed. The generated rational trigonometric curve consists of 12 control points.

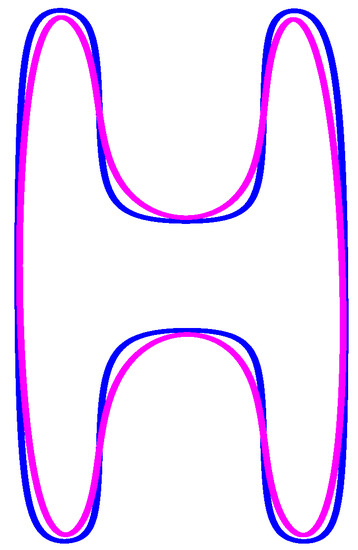
Figure 13. Periodic rational curve with different $\xi$.

Figure 14. Periodic NURBS curve with $\xi =3$.

The shape parameter and weight make the designing of the Rational and NURBS curve more smooth and accurate.

5.3. Application of B-Spline and Uniform Rational Trigonometric B-Spline Curve

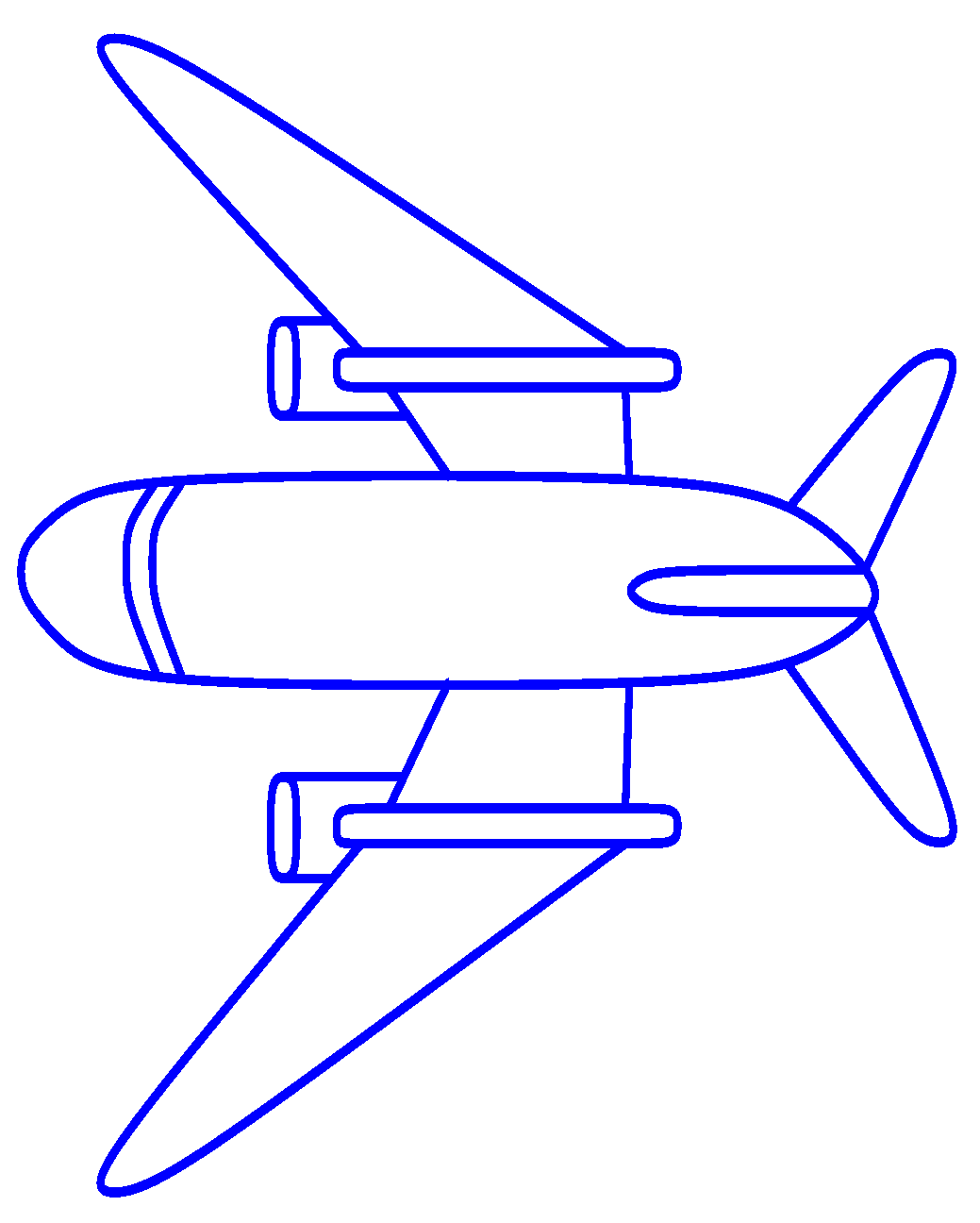
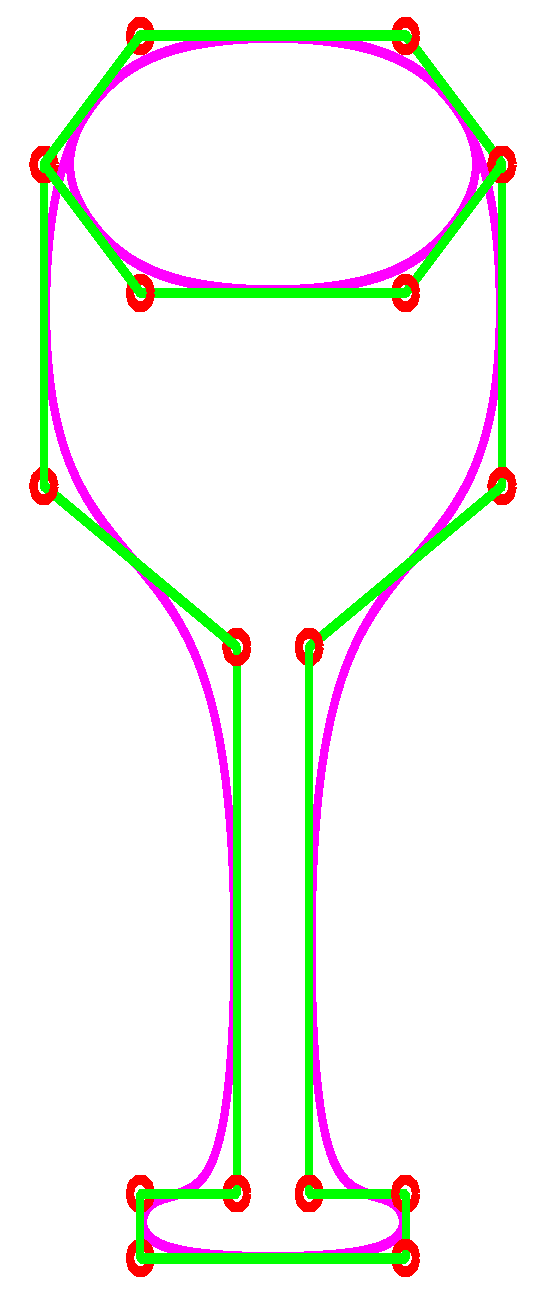
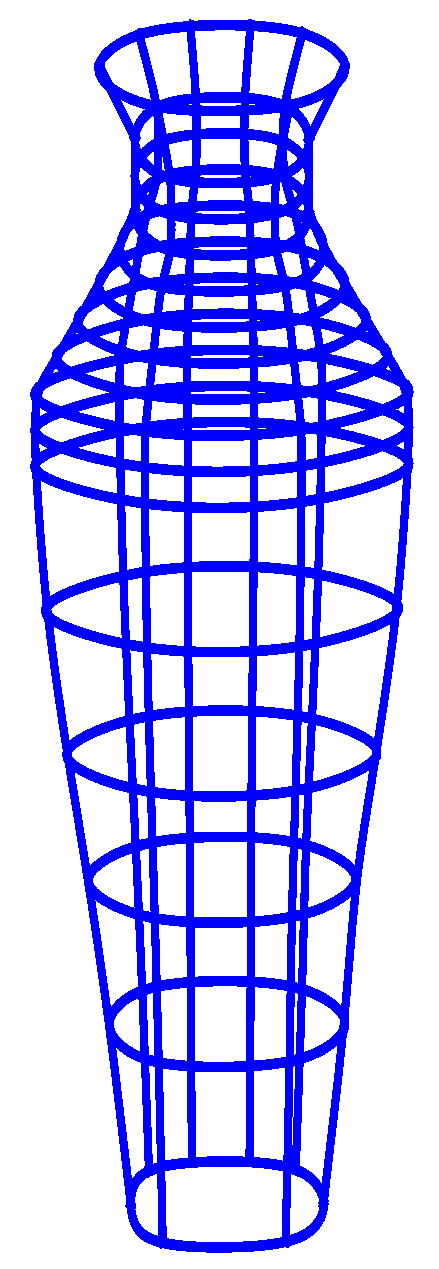
Proposed cubic trigonometric curves have been used for $2D$ and $3D$ modeling like in Figure 15, and we have designed an aeroplane with 107 control points with the shape parameter $\xi =0.4$. The execution time for this model is 0.578 s. In Figure 16, glass has been designed using 25 control points and $\xi =2$. The CPU time recorded for this model is 0.209 s. An apple has been designed in a $2D$ form using the proposed method as shown in Figure 17. Different control points with $\xi =3$ is used for this model. Lastly, proposed curves have been used to design a vase in $3D$ form as shown in Figure 18. The shape parameter $\xi =2$ is used in this model. The execution time for this model is 0.593 s.

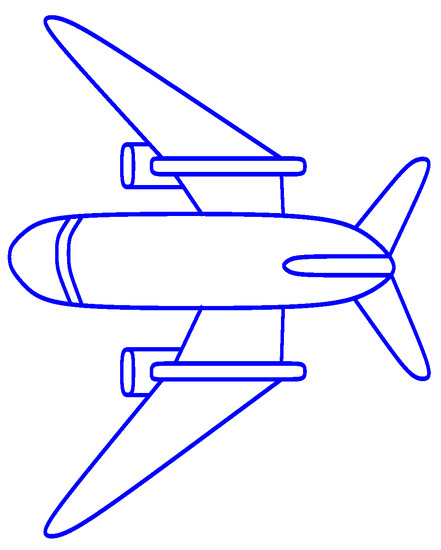
Figure 15. Aeroplane design using cubic trigonometric B-spline curves.

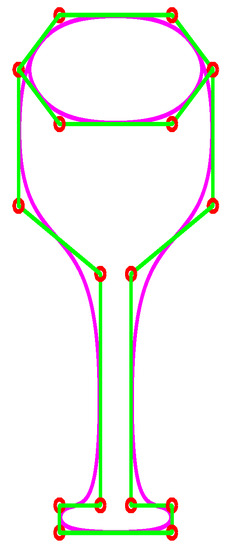
Figure 16. Glass design using cubic trigonometric B-spline curve.

Figure 17. Apple designing using rational B-spline curve.

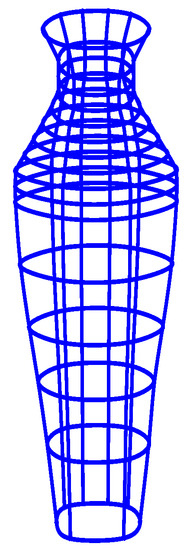
Figure 18. $3D$ vase mesh design using cubic trigonometric B-spline curves.

5.4. Conclusions

Cubic trigonometric and rational cubic trigonometric B-spline basis functions and curves with shape parameter $\xi$ were derived in this paper. The cubic trigonometric B-spline curves were $C^3$ and $C^5$ continuous at uniform and non-uniform knots and were derived. Rational cubic trigonometric B-spline curves were $C^3$ continuous for both uniform and non-uniform knots. Both cubic polynomial and cubic rational basis and curves obeyed the basic properties and were derived in this paper. The rendering of floating and periodic curves reflected the flexibility and applicability of the proposed method. Different $2D$ and $3D$ models were designed using the proposed curves successfully. This curve was more flexible, easy to use, and had a larger parametric range than the existing scheme. This work can be extended by adding shape parameter, using higher degree in functions, and by constructing the surface using proposed curves.