A Novel Technique to Control the Accuracy of a Nonlinear Fractional Order Model of COVID-19: Application of the CESTAC Method and the CADNA Library
Abstract
:1. Introduction
2. Preliminaries
3. Nonlinear Fractional Order Model of COVID-19
4. Existence of Solution
5. Special Solution via Iteration Approach
Fixed Point Theorem for Stability Analysis of the Iteration Method
6. Application of the HATM to Solve the Model
7. CESTAC Method with CADNA Library
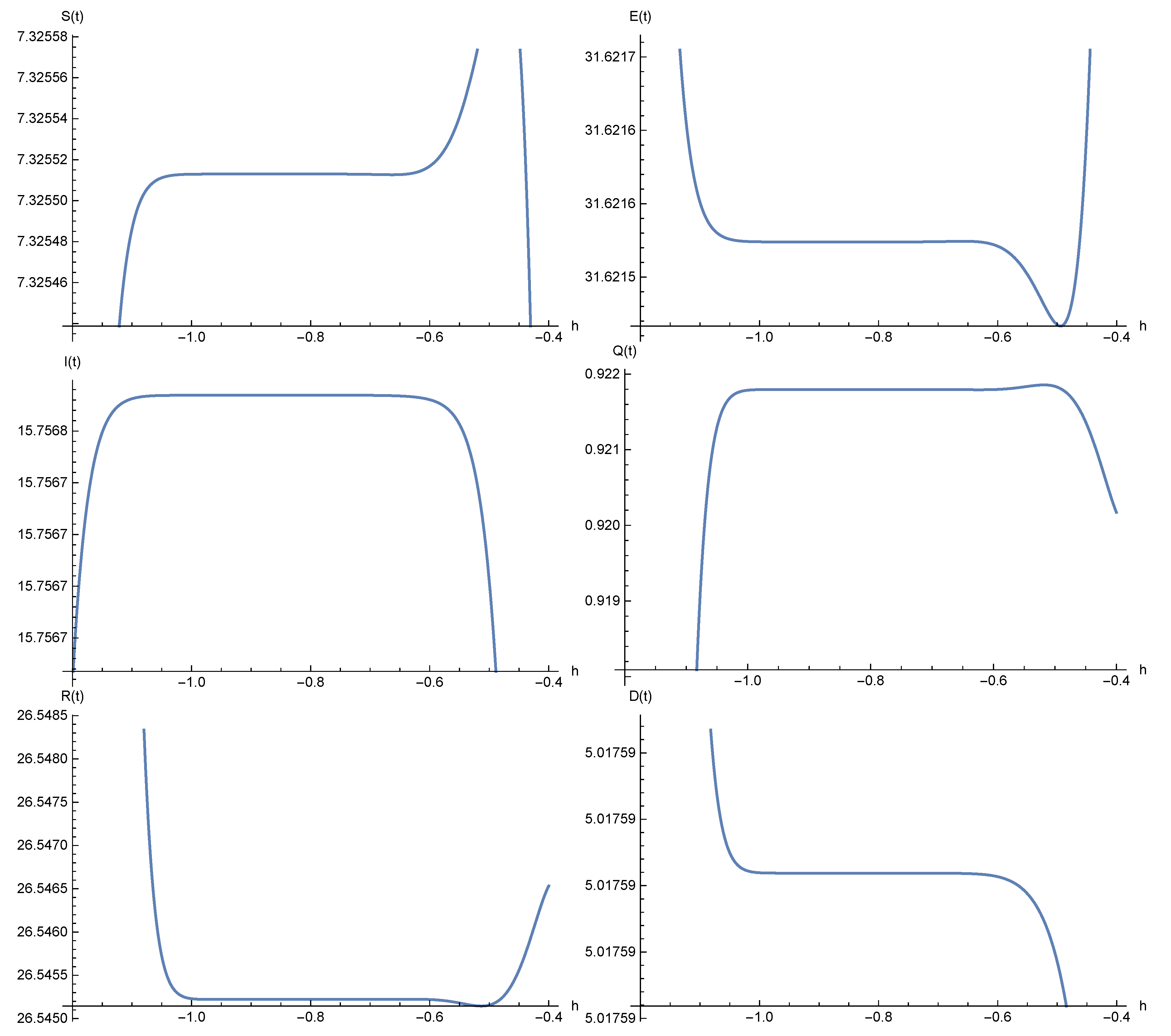
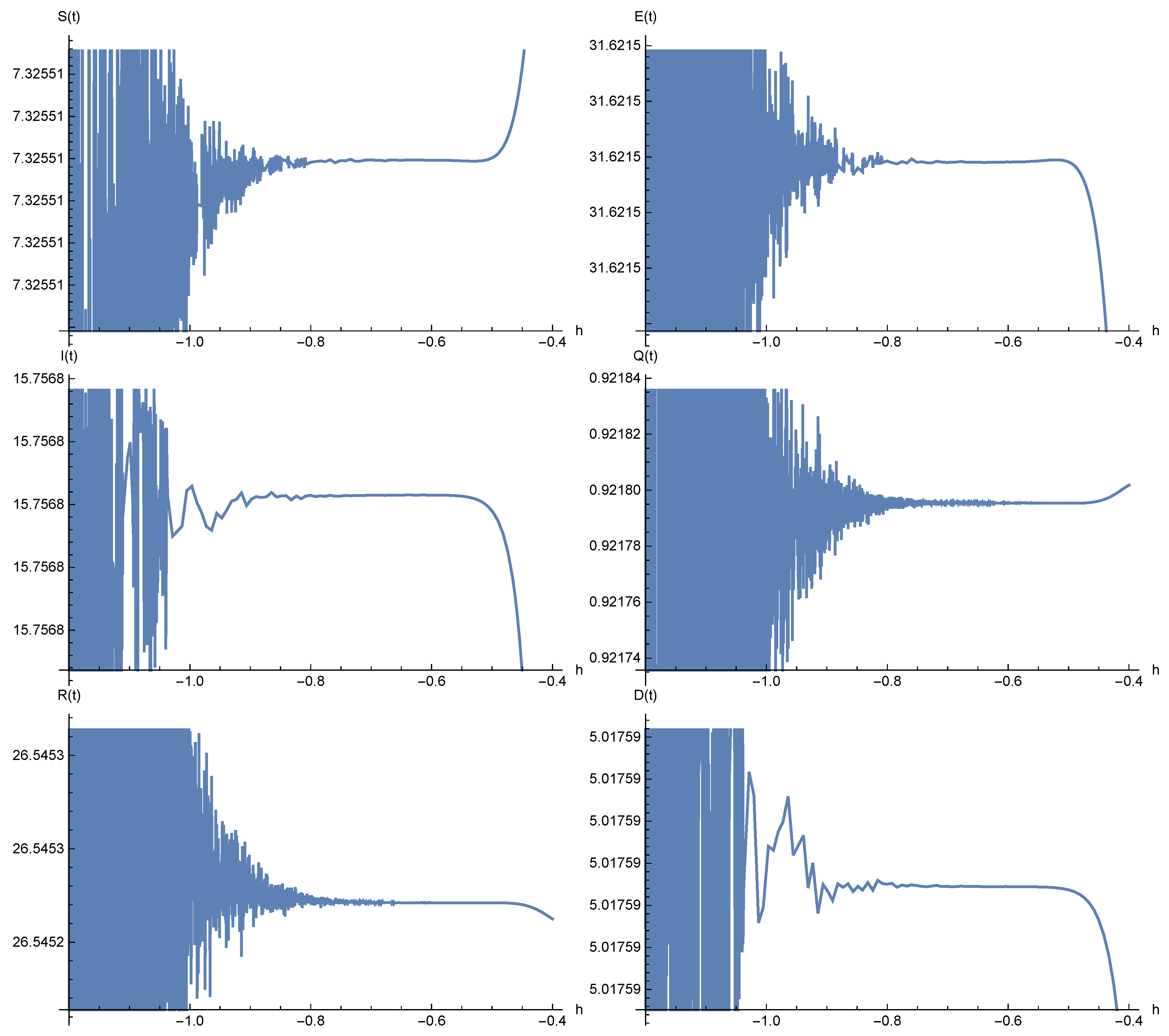
8. Numerical Results
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Coronavirus Disease (COVID-19) Pandemic. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019# (accessed on 2 March 2021).
- Srivastava, H.M.; Area, I.; Nieto, J.J. Power-series solutions of compartmental epidemiological models. Math. Biosci. Eng. 2021, 18. [Google Scholar] [CrossRef]
- Ndaïrou, F.; Area, I.; Nieto, J.J.; Silva, C.J.; Torres, D.F.M. Fractional model of COVID-19 applied to Galicia, Spain and Portugal. Chaos Solitons Fractals 2021, 144, 110652. [Google Scholar] [CrossRef]
- Bushnaq, S.; Saeed, T.; Torres, D.F.M.; Zeb, A. Control of COVID-19 dynamics through a fractional-order model. Alex. Eng. J. 2021, 60, 3587–3592. [Google Scholar] [CrossRef]
- Hu, F.; Huang, M.; Sun, J.; Zhang, X.; Liu, J. An analysis model of diagnosis and treatment for COVID-19 pandemic based on medical information fusion. Inf. Fusion 2021, 73, 11–21. [Google Scholar] [CrossRef]
- Gebremeskel, A.A.; Berhe, H.W.; Atsbaha, H.A. Mathematical modeling and analysis of COVID-19 epidemic and predicting its future situation in Ethiopia. Results Phys. 2021, 22, 103853. [Google Scholar] [CrossRef]
- Inc, M.; Acay, B.; Berhe, H.W.; Yusuf, A.; Khan, A.; Yao, S.-W. Analysis of novel fractional COVID-19 model with real-life data application. Results Phys. 2021, 23, 103968. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, C.; Bi, Y.; Yuan, L.; Jiang, Y.; Hasi, C.; Zhang, X.; Kong, X. Analysis of COVID-19 epidemic and clinical risk factors of patients under epidemiological Markov model. Results Phys. 2021, 22, 103881. [Google Scholar] [CrossRef]
- Galanis, G.; Hanieh, A. Incorporating Social Determinants of Health into Modelling of COVID-19 and other Infectious Diseases: A Baseline Socioeconomic Compartmental Model. Soc. Sci. Med. 2021, 274, 113794. [Google Scholar] [CrossRef]
- Panwar, V.S.; Sheik Uduman, P.S.; Gómez-Aguilar, J.F. Mathematical modeling of coronavirus disease COVID-19 dynamics using CF and ABC non-singular fractional derivatives. Chaos Solitons Fractals 2021, 145, 110757. [Google Scholar] [CrossRef]
- Naik, P.A.; Zu, J.; Owolabi, K.M. Modeling the mechanics of viral kinetics under immune control during primary infection of HIV-1 with treatment in fractional order. Phys. A Stat. Mech. Appl. 2020, 545, 123816. [Google Scholar] [CrossRef]
- Ghanbari, B.; Günerhan, H.; Srivastava, H.M. An application of the Atangana–Baleanu fractional derivative in mathematical biology: A three-species predator-prey model. Chaos Solitons Fractals 2020, 138, 109910. [Google Scholar] [CrossRef]
- Günerhan, H.; Dutta, H.; Dokuyucu, M.A.; Adel, W. Analysis of a fractional HIV model with Caputo and constant proportional Caputo operators. Chaos Solitons Fractals 2020, 139, 110053. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Sidorov, D. Caputo–Fabrizio Fractional Derivative to Solve the Fractional Model of Energy Supply-Demand System. Math. Model. Eng. Probl. 2020, 7, 359–367. [Google Scholar] [CrossRef]
- Naik, P.A.; Yavuz, M.; Zu, J. The role of prostitution on HIV transmission with memory: A modeling approach. Alex. Eng. J. 2020, 59, 2513–2531. [Google Scholar] [CrossRef]
- Naik, P.A.; Zu, J.; Owolabi, K.M. Global dynamics of a fractional order model for the transmission of HIV epidemic with optimal control. Chaos Solitons Fractals 2020, 138, 109826. [Google Scholar] [CrossRef]
- Suleman, M.; Lu, D.; He, J.H.; Farooq, U.; Noeiaghdam, S.; Chandio, F.A. Elzaki Projected Differential Transform method for Fractional order System of Linear and Nonlinear Fractional Partial Differential Equation. Fractals 2018, 26, 1850041. [Google Scholar]
- Noeiaghdam, S. A novel technique to solve the modified epidemiological model of computer viruses. SeMA J. 2019, 76, 97–108. [Google Scholar] [CrossRef]
- Hattaf, K.; Mohsen, A.A.; Harraq, J.; Achtaich, N. Modeling the dynamics of COVID-19 with carrier effect and environmental contamination. Int. J. Model. Simul. Sci. Comput. 2021. [Google Scholar] [CrossRef]
- Abboubakar, H.; Kumar, P.; Rangaig, N.A.; Kumar, S. A malaria model with Caputo–Fabrizio and Atangana–Baleanu derivatives. Int. J. Model. Simul. Sci. Comput. 2021, 2021 12, 2150013. [Google Scholar] [CrossRef]
- Liao, S.J. Beyond Perturbation: Introduction to Homotopy Analysis Method; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Liao, S.J. Homotopy Analysis Method in Nonlinear Differential Equations; Higher Education Press: Beijing, China; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Liao, S.J. The Proposed Homotopy Analysis Techniques for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Noeiaghdam, S.; Fariborzi Araghi, M.A. A novel approach to find optimal parameter in the homotopy-regularization method for solving integral equations. Appl. Math. Inf. Sci. 2020, 14, 1–8. [Google Scholar]
- Noeiaghdam, S.; Fariborzi Araghi, M.A.; Abbasbandy, S. Finding optimal convergence control parameter in the homotopy analysis method to solve integral equations based on the stochastic arithmetic. Numer. Algorithms 2019, 81, 237. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Fariborzi Araghi, M.A. Homotopy regularization method to solve the singular Volterra integral equations of the first kind. Jordan J. Math. Stat. 2018, 11, 1–12. [Google Scholar]
- Fariborzi Araghi, M.A.; Noeiaghdam, S. A novel technique based on the homotopy analysis method to solve the first kind Cauchy integral equations arising in the theory of airfoils. J. Interpolat. Approx. Sci. Comput. 2016, 2016, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Noeiaghdam, S.; Suleman, M.; Budak, H. Solving a modified non-linear epidemiological model of computer viruses by homotopy analysis method. Math. Sci. 2018, 12, 211–222. [Google Scholar] [CrossRef] [Green Version]
- Vignes, J. A stochastic arithmetic for reliable scientific computation. Math. Comput. Simul. 1993, 35, 233–261. [Google Scholar] [CrossRef]
- Laboratoire d’Informatique de Paris 6. Available online: https://www-pequan.lip6.fr/ (accessed on 10 December 2020).
- Chesneaux, J.M. CADNA, an ADA tool for round–off error analysis and for numerical debugging. In Proceedings of the Congress on ADA, Aerospace, Barcelona, Spain, 20–25 May 1990. [Google Scholar]
- Chesneaux, J.M.; Jézéquel, F. Dynamical control of computations using the Trapezoidal and Simpson’s rules. J. Univers. Comput. Sci. 1998, 4, 2–10. [Google Scholar]
- Graillat, S.; Jézéquel, F.; Wang, S.; Zhu, Y. Stochastic arithmetic in multi precision. Math. Comput. Sci. 2011, 5, 359–375. [Google Scholar] [CrossRef]
- Graillat, S.; Jézéquel, F.; Picot, R. Numerical Validation of Compensated Summation Algorithms with Stochastic Arithmetic. Electron. Notes Theor. Comput. Sci. 2015, 317, 55–69. [Google Scholar] [CrossRef]
- Jézéquel, F.; Mecanique, C.R. A dynamical strategy for approximation methods. Comptes Rendus Mec. 2006, 334, 362–367. [Google Scholar] [CrossRef] [Green Version]
- Noeiaghdam, S.; Sidorov, D.; Wazwaz, A.M.; Sidorov, N.; Sizikov, V. The numerical validation of the Adomian decomposition method for solving Volterra integral equation with discontinuous kernel using the CESTAC method. Mathematics 2021, 9, 260. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Sidorov, D.; Zamyshlyaeva, A.; Tynda, A.; Dreglea, A. A valid dynamical control on the reverse osmosis system using the CESTAC method. Mathematics 2021, 9, 48. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Fariborzi Araghi, M.A. A novel algorithm to evaluate definite integrals by the Gauss-Legendre integration rule based on the stochastic arithmetic: Application in the model of osmosis system. Math. Model. Eng. Probl. 2020, 7, 577–586. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Dreglea, A.; He, J.H.; Avazzadeh, Z.; Suleman, M.; Fariborzi Araghi, M.A.; Sidorov, D.; Sidorov, N. Error estimation of the homotopy perturbation method to solve second kind Volterra integral equations with piecewise smooth kernels: Application of the CADNA library. Symmetry 2020, 12, 1730. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Sidorov, D.; Sizikov, V.; Sidorov, N. Control of accuracy on Taylor-collocation method to solve the weakly regular Volterra integral equations of the first kind by using the CESTAC method. Appl. Comput. Math. Int. J. 2020, 19, 81. [Google Scholar]
- Noeiaghdam, S.; Fariborzi Araghi, M.A. Valid implementation of the Sinc-collocation method to solve the linear integral equations by CADNA library. J. Math. Model. 2019, 7, 63–84. [Google Scholar]
- Noeiaghdam, S.; Sidorov, D.; Muftahov, D.I.; Zhukov, A.V. Control of Accuracy on Taylor-Collocation Method for Load Leveling Problem. Bull. Irkutsk State Univ. Ser. Math. 2019, 30, 59–72. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Losada, J.; Nieto, J.J. Properties of the new fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Abdeljawad, T.; Baleanu, D. On fractional derivatives with exponential kernel and their discrete versions. Rep. Math. Phys. 2017, 80, 11–27. [Google Scholar] [CrossRef] [Green Version]
- Belgacem, F.B.M.; Karaballi, A.A.; Kalla, S.L. Analytical investigations of the Sumudu transform and applications to integral production equations. Math. Probl. Eng. 2003, 3, 103–118. [Google Scholar] [CrossRef] [Green Version]
- Bodkhe, D.S.; Panchal, S.K. On Sumudu transform of fractional derivatives and its applications to fractional differential equations. Asian J. Math. Comput. Res. 2016, 11, 69–77. [Google Scholar]
- Shah, K.; Junaid, N.A.M. Extraction of Laplace, Sumudu, Fourier and Mellin transform from the natural transform. J. Appl. Environ. Biol. Sci. 2015, 5, 1–10. [Google Scholar]
- Watugala, G.K. Sumudu transform: A new integral transform to solve differential equations and control engineering problems. Int. J. Math. Educ. Sci. Technol. 1993, 24, 35–43. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Y.; Medved, M. Picard and weakly Picard operators technique for nonlinear differential equations in Banach spaces. J. Math. Anal. Appl. 2012, 389, 261–274. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, K.; Chatterjee, K.; Kumar, A.; Shankar, S. Healthcare impact of COVID-19 epidemic in India: A stochastic mathematical model. Med. J. Armed Forces India 2020, 76, 147–155. [Google Scholar] [CrossRef]
- Sarkar, K.; Khajanchi, S.; Nieto, J.J. Modeling and forecasting the COVID-19 pandemic in India. Chaos Solitons Fractals 2020, 139, 110049. [Google Scholar] [CrossRef]
- Vignes, J. Discrete Stochastic Arithmetic for Validating Results of Numerical Software. Spec. Issue Numer. Algorithms 2004, 7, 377–390. [Google Scholar] [CrossRef]
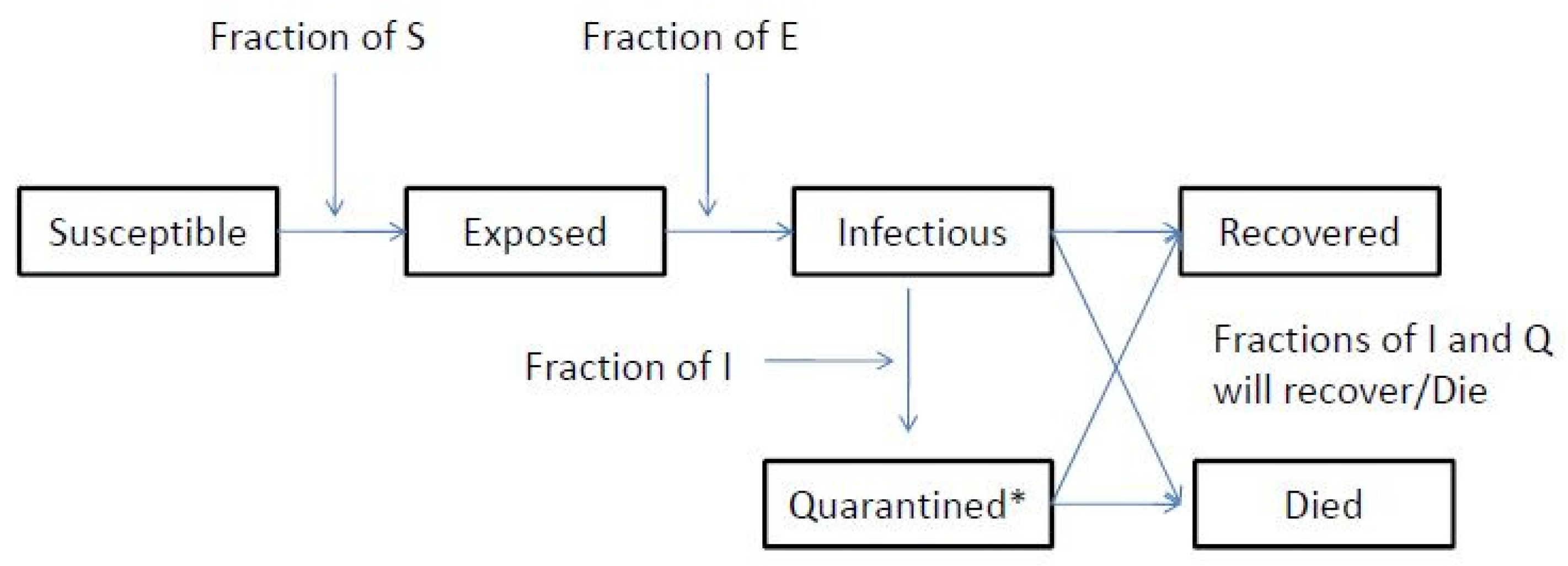

| Parameters | Values |
|---|---|
| Incubation Period | Mean= 5.1 days |
| Infectious Period | Mean= 7 days |
| Basic Reproduction Number | Mean= 2.28 |
| Mean Death Rate | |
| Active Cases Quarantined q | 0.01 |
| Period Quarantined | 14 days |
| Quarantined Cases | 20 |
| Recovered Cases | 12 |
| Deaths | 5 |
| Exposed Cases | 20 |
| Infected Cases | 15 |
| Quarantined Cases | 15 |
| m | Approximate Solutions | Difference between Two Iterations |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 91948 | ||
| m | Approximate Solutions | Difference between Two Iterations |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 30397 | ||
| 4 | ||
| 5 | ||
| Small Values | 0.5 | Large Values | ||||
|---|---|---|---|---|---|---|
| m | 9 | 5 | 3 | 1 | 1 |
| m | Approximate Solutions | Difference between Two Iterations |
|---|---|---|
| 1 | 0.6416038 | 0.6416040 |
| 35.75721 | 35.75721 | |
| 14.30519 | 14.30519 | |
| 21.33839 | 21.33840 | |
| 47.63999 | 47.63999 | |
| 5.294120 | 5.294120 | |
| 2 | 8.290508 | 1.87447 |
| 30.37535 | 5.38186 | |
| 14.48619 | 0.18099 | |
| 34.01543 | 12.67704 | |
| 5.92429 | 41.757 | |
| 5.18415 | 0.10996 | |
| 3 | 7.42754 | 0.86296 |
| 31.0735 | 0.69816 | |
| 14.44400 | ||
| 34.8834 | ||
| 60.98040 | ||
| 5.373754 | 0.18960 | |
| ⋮ | ⋮ | ⋮ |
| 9 | 7.61575 | |
| 30.7691 | ||
| 14.42713 | ||
| 19.1588 | ||
| 45.76194 | ||
| 5.33333 | ||
| 10 | 7.61582 | |
| 30.76886 | @.0 | |
| 14.4270 | ||
| 19.16541 | ||
| 45.76194 | @.0 | |
| 5.28554 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noeiaghdam, S.; Micula, S.; Nieto, J.J. A Novel Technique to Control the Accuracy of a Nonlinear Fractional Order Model of COVID-19: Application of the CESTAC Method and the CADNA Library. Mathematics 2021, 9, 1321. https://doi.org/10.3390/math9121321
Noeiaghdam S, Micula S, Nieto JJ. A Novel Technique to Control the Accuracy of a Nonlinear Fractional Order Model of COVID-19: Application of the CESTAC Method and the CADNA Library. Mathematics. 2021; 9(12):1321. https://doi.org/10.3390/math9121321
Chicago/Turabian StyleNoeiaghdam, Samad, Sanda Micula, and Juan J. Nieto. 2021. "A Novel Technique to Control the Accuracy of a Nonlinear Fractional Order Model of COVID-19: Application of the CESTAC Method and the CADNA Library" Mathematics 9, no. 12: 1321. https://doi.org/10.3390/math9121321
APA StyleNoeiaghdam, S., Micula, S., & Nieto, J. J. (2021). A Novel Technique to Control the Accuracy of a Nonlinear Fractional Order Model of COVID-19: Application of the CESTAC Method and the CADNA Library. Mathematics, 9(12), 1321. https://doi.org/10.3390/math9121321








