Bearing Fault Diagnosis Using a Grad-CAM-Based Convolutional Neuro-Fuzzy Network
Abstract
:1. Introduction
- (1)
- A novel SBDS was developed to diagnose the health of bearing.
- (2)
- A high-precision GC-CNFN model with fewer parameters is proposed to identify bearing faults.
- (3)
- The proposed GC-CNFN can automatically perform feature extraction from and modeling with the original raw vibration signal without the need for expert experience and knowledge.
- (4)
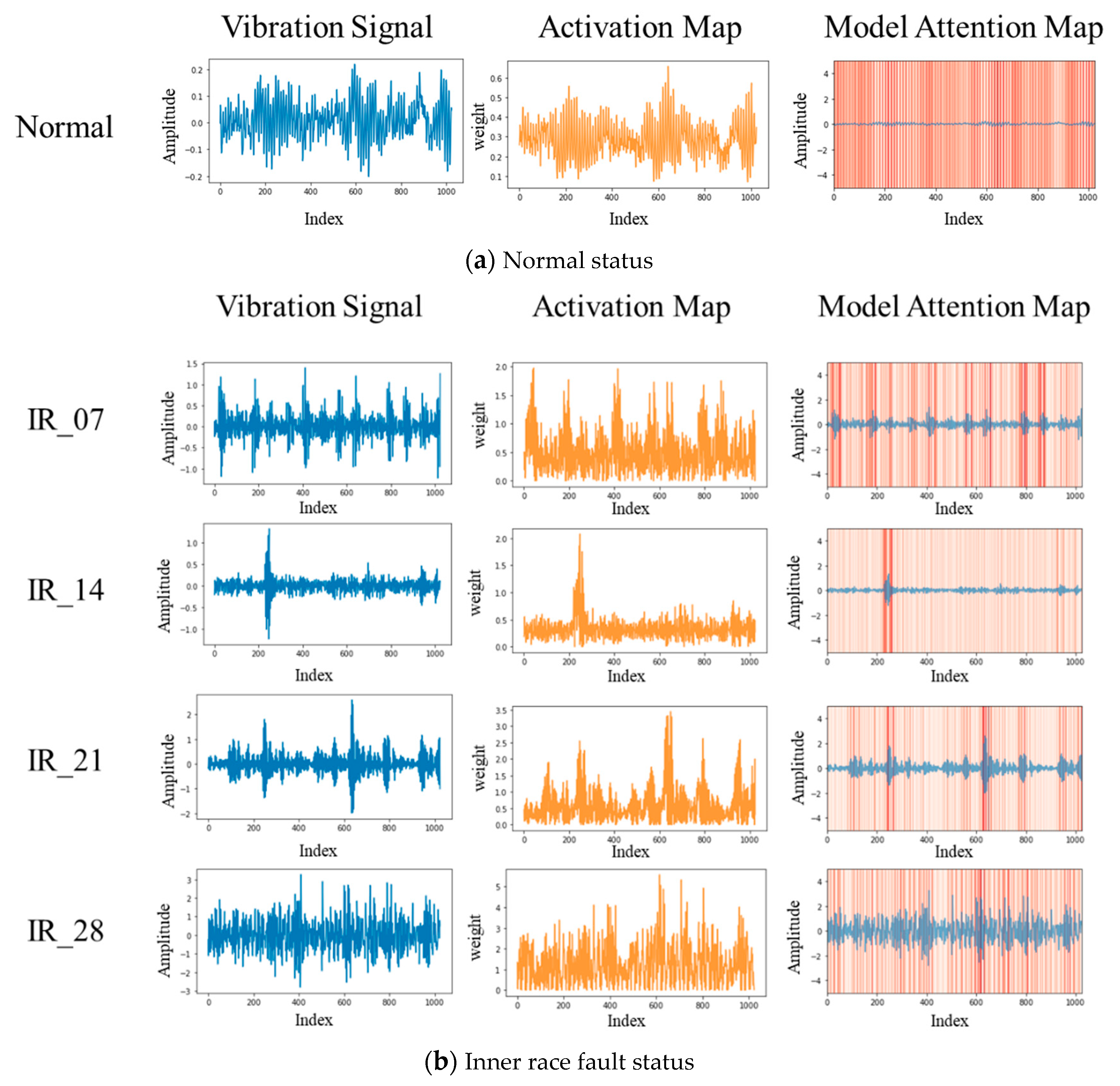
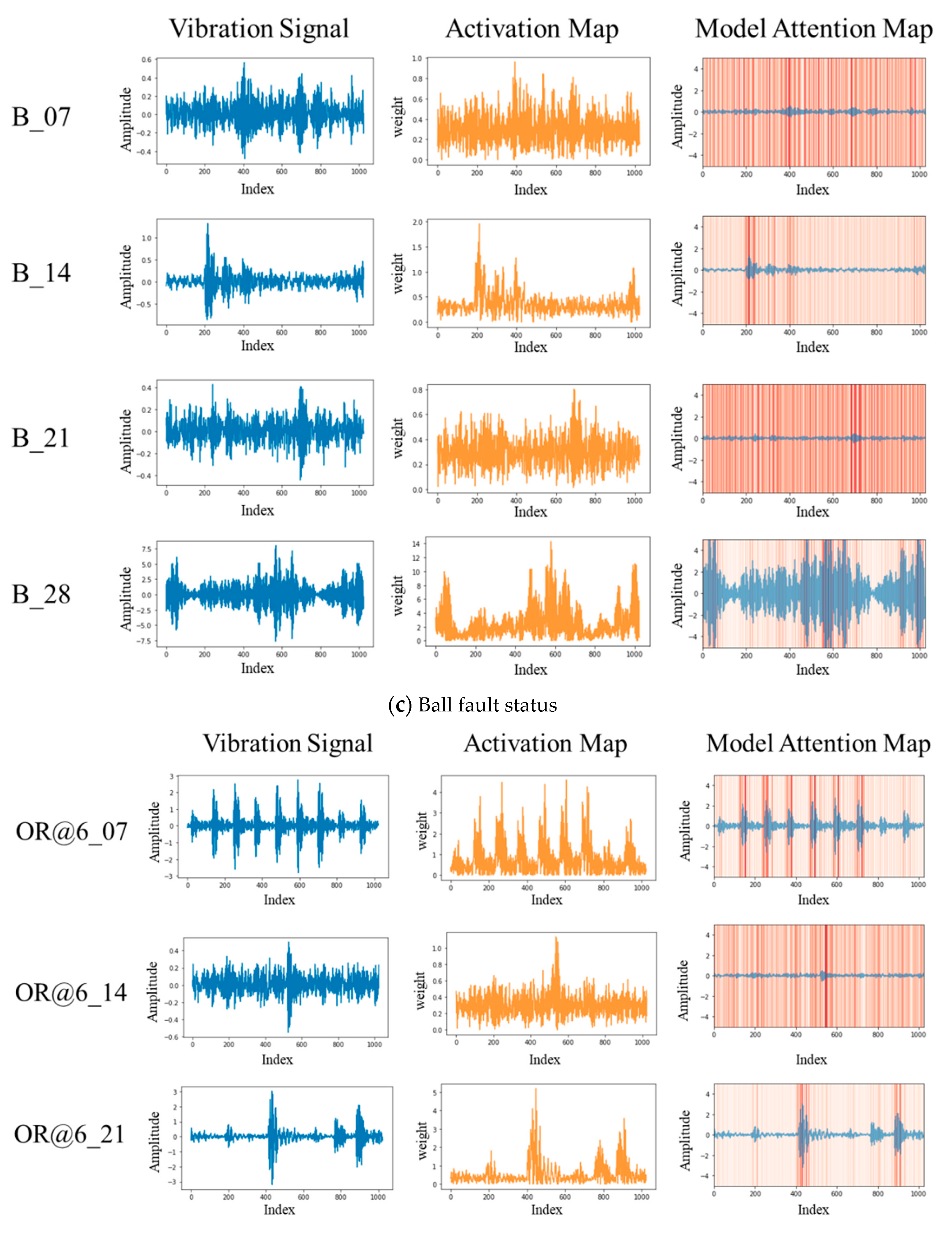
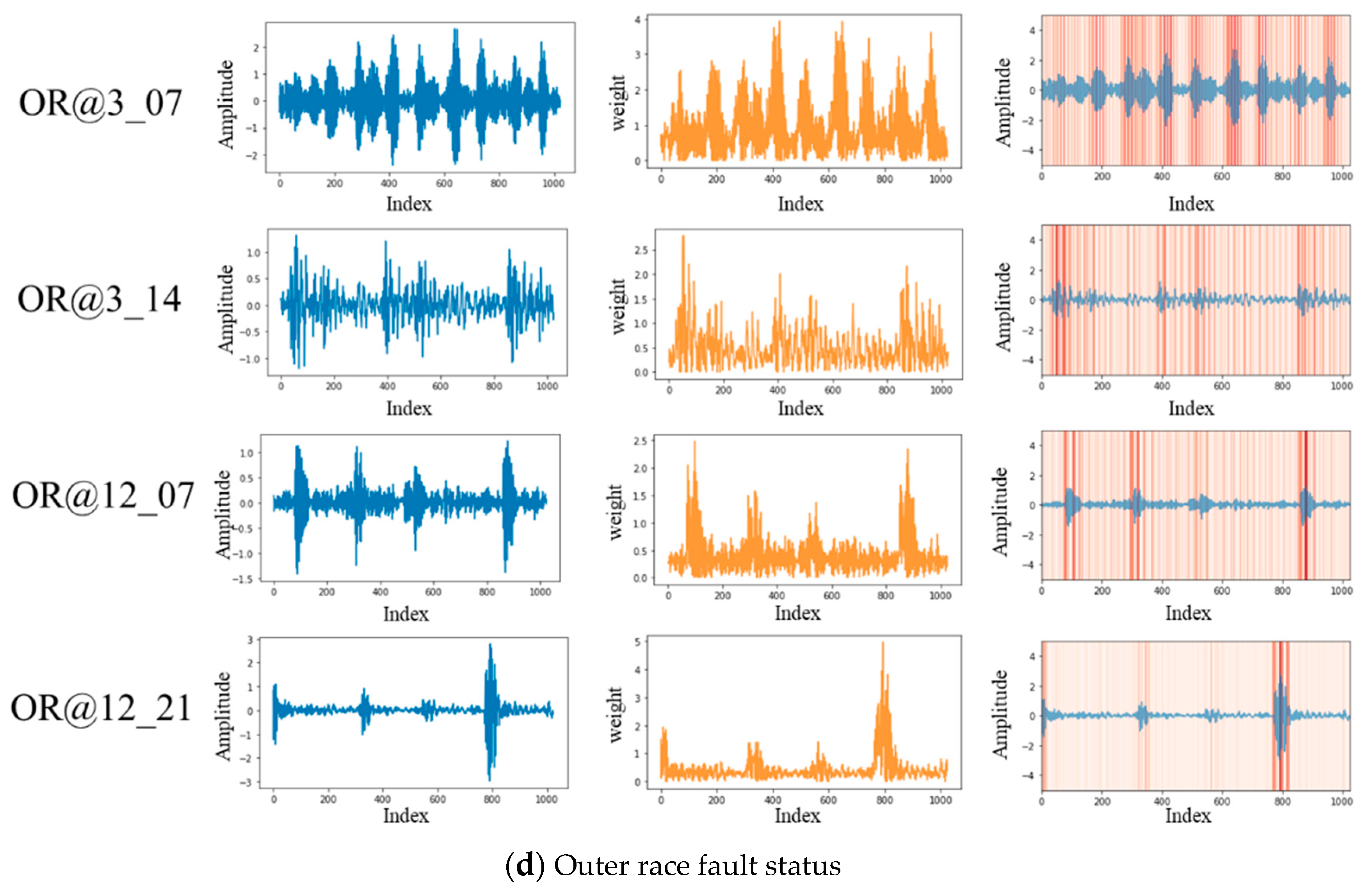
- By referring to the model attention maps generated by the GC-CNFN, users can determine the region in which the model focuses on the vibration signal and understand the basis of the model’s classification.
2. Related Work
2.1. Convolutional Neural Network (CNN)
- Convolution layer
- Pooling layer
- Flatten layer
2.2. Gradient-Weighted Class Activation Mapping (Grad-CAM)
3. Problem Definition
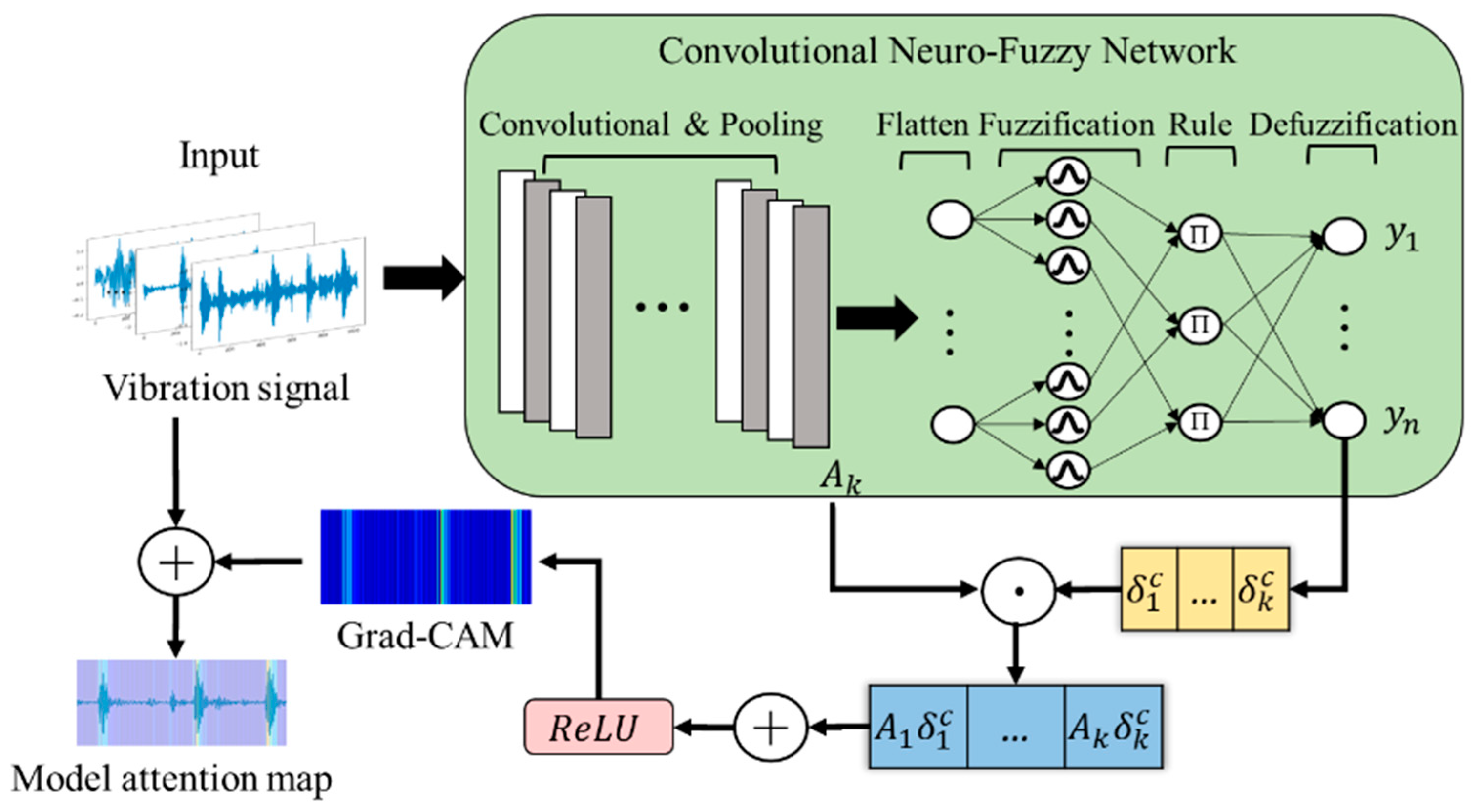
3.1. Structure of the GC-CNFN
- Convolutional layer
- Pooling layer
- Flatten layer
- Fuzzification layer
- Rule layer
- Defuzzification layer
3.2. Parameter Learning Phase
4. Experimental Results
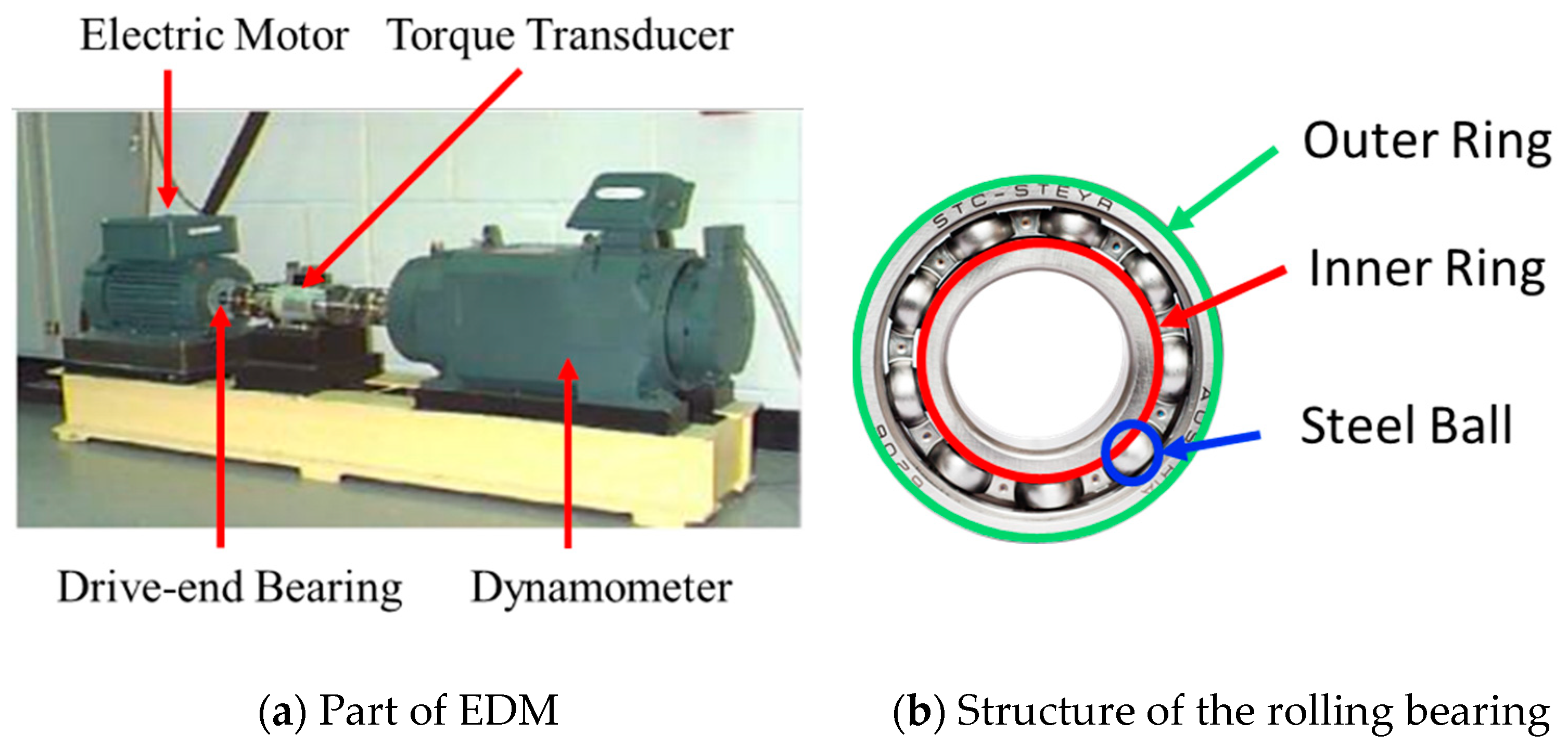
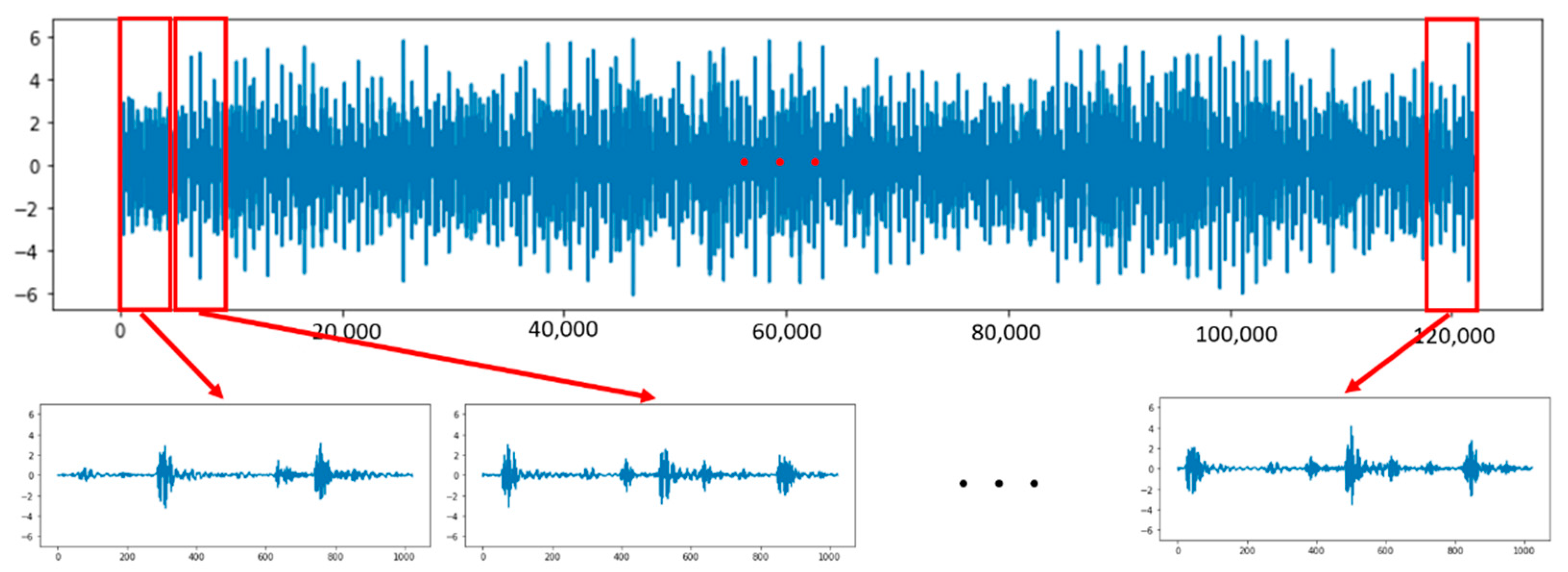
4.1. Data Preprocessing
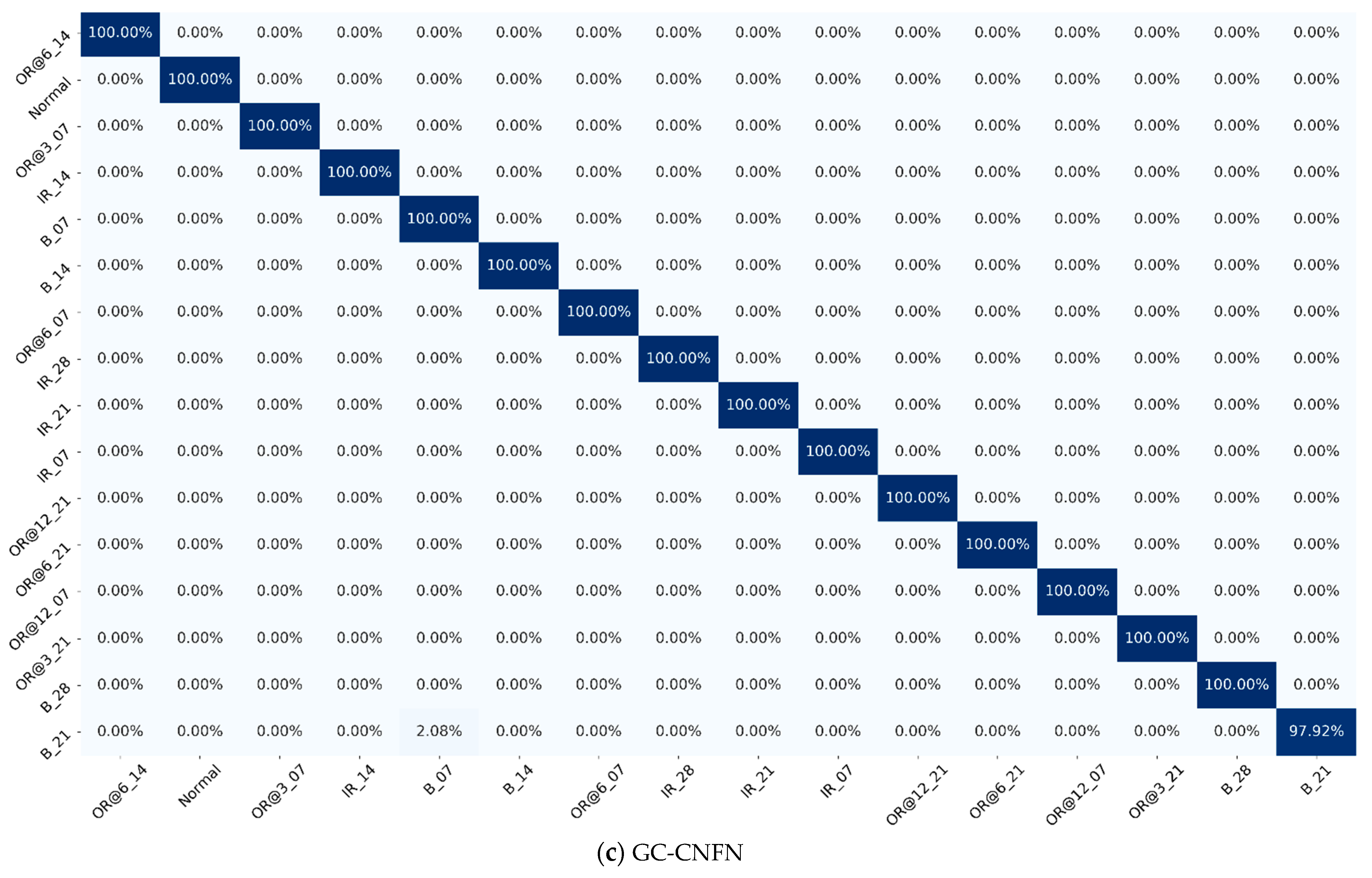
4.2. Bearing Fault Diagnosis and Evaluation for CWRU Dataset
4.3. Model Attention Map for Vibration Signals
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- On Recommended Interval of Updating Induction Motors; JEMA: Tokyo, Japan, 2000. (In Japanese)
- Motor Reliability Working Group. Report of large motor reliability survey of industrial and commercial installations, Part, I. IEEE Trans. Ind. Appl. 1985, IA-21, 853–864. [Google Scholar] [CrossRef]
- Motor Reliability Working Group. Report of large motor reliability survey of industrial and commercial installations, Part II. IEEE Trans. Ind. Appl. 1985, IA-21, 865–872. [Google Scholar] [CrossRef]
- Motor Reliability Working Group. Report of large motor reliability survey of industrial and commercial installations: Part 3. IEEE Trans. Ind. Appl. 1987, IA-23, 153–158. [Google Scholar] [CrossRef]
- Akyurt, I.; Kuvvetli, Y.; Deveci, M. Enterprise Resource Planning in The Age of Industry 4.0 A General Overview; CRC Press: Boca Raton, FL, USA, 2020; pp. 178–185. [Google Scholar]
- Afshari, N.; Loparo, K.A. A Model-Based Technique for the Fault Detection of Rolling Element Bearings Using Detection Filter Design and Sliding Mode Technique. In Proceedings of the 37th IEEE Conference on Decision and Control, Tampa, FL, USA, 18 December 1998. [Google Scholar]
- White, J.; Speyer, J. Detection filter design: Spectral theory and algorithms. IEEE Trans. Autom. Control. 1987, 32, 593–603. [Google Scholar] [CrossRef]
- Slotine, J.E.; Hedrick, J.K.; Misawa, E.A. On Sliding Observers for Nonlinear Systems. In Proceedings of the 1986 American Control Conference, Seattle, WA, USA, 18–20 June 1986. [Google Scholar]
- Adams, M.L. Analysis of Rolling Element Bearing Faults in Rotating Machinery: Experiments, Modeling, Fault Detection and Diagnosis; Case Western Reserve University: Cleveland, OH, USA, 2001. [Google Scholar]
- Forst, W.; Hoffmann, D. Optimization—Theory and Practice; Springer: New York, NY, USA, 2010. [Google Scholar]
- Jalan, A.K.; Mohanty, A.R. Model based fault diagnosis of a rotor–bearing system for misalignment and unbalance under steady-state condition. J. Sound Vib. 2009, 327, 604–622. [Google Scholar] [CrossRef]
- Simani, S.; Fantuzzi, C.; Patton, R. Model-Based Fault Diagnosis in Dynamic Systems Using Identification Techniques; Springer: London, UK, 2003. [Google Scholar]
- Nikolaou, N.G.; Antoniadis, I.A. Rolling element bearing fault diagnosis using wavelet packets. NDT E Int. 2002, 35, 197–205. [Google Scholar] [CrossRef]
- Cocconcelli, M.; Zimroz, R.; Rubini, R.; Bartelmus, W. STFT Based Approach for Ball Bearing Fault Detection in a Varying Speed Motor. In Condition Monitoring of Machinery in Non-Stationary Operations; Fakhfakh, T., Bartelmus, W., Chaari, F., Zimroz, R., Haddar, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 41–50. [Google Scholar]
- Van, M.; Kang, H.-J.; Shin, K.-S. Rolling element bearing fault diagnosis based on non-local means de-noising and empirical mode decomposition. IET Sci. Meas. Technol. 2014, 8, 571–578. [Google Scholar] [CrossRef]
- Ville, D.V.D.; Kocher, M. Sure-based non-local means. IEEE Signal Process. Lett. 2009, 16, 973–976. [Google Scholar] [CrossRef] [Green Version]
- Tracey, B.H.; Miller, E.L. Nonlocal means denoising of ECG signals. IEEE Trans. Biomed. Eng. 2012, 59, 2383–2386. [Google Scholar] [CrossRef]
- Junsheng, C.; Dejie, Y.; Yu, Y. A fault diagnosis approach for roller bearings based on EMD method and AR model. Mech. Syst. Signal Process. 2006, 20, 350–362. [Google Scholar] [CrossRef]
- Fu, S.; Liu, K.; Xu, Y.G.; Liu, Y. Rolling Bearing Diagnosing Method Based on Time Domain Analysis and Adaptive Fuzzy C-Means Clustering. Shock. Vib. 2016, 2016, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Yuwono, M.; Qin, Y.; Zhou, J.; Guo, Y.; Celler, B.G.; Su, S.W. Automatic bearing fault diagnosis using particle swarm clustering and Hidden Markov Model. Eng. Appl. Artif. Intell. 2016, 47, 88–100. [Google Scholar] [CrossRef]
- Ben Ali, J.; Fnaiech, N.; Saidi, L.; Chebel-Morello, B.; Fnaiech, F. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals. Appl. Acoust. 2015, 89, 16–27. [Google Scholar] [CrossRef]
- Ertunc, H.M.; Ocak, H.; Aliustaoglu, C. ANN- and ANFIS-based multi-staged decision algorithm for the detection and diagnosis of bearing faults. Neural Comput. Appl. 2013, 22, 435–446. [Google Scholar] [CrossRef]
- Jang, J.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Deveci, M.; Pekaslan, D.; Canıtez, F. The assessment of smart city projects using zSlice type-2 fuzzy sets based interval agreement method. Sustain. Cities Soc. 2020, 53, 101889. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A new convolutional neural network-based data-driven fault diagnosis method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Tax, D.; Ypma, A.; Duin, R. Pump Failure Detection Using Support Vector Data Descriptions; Springer: Heidelberg/Berlin, Germany, 1999; Volume 1642, pp. 415–426. [Google Scholar]
- Lei, Y.; Jia, F.; Lin, J.; Xing, S.; Ding, S.X. An intelligent fault diagnosis method using unsupervised feature learning towards mechanical big data. IEEE Trans. Ind. Electron. 2016, 63, 3137–3147. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Zhang, X.; Niu, M. Rolling bearing fault diagnosis using an optimization deep belief network. Meas. Sci. Technol. 2015, 26, 115002. [Google Scholar] [CrossRef]
- Xie, S.; Ren, G.; Zhu, J. Application of a new one-dimensional deep convolutional neural network for intelligent fault diagnosis of rolling bearings. Sci. Prog. 2020, 103, 0036850420951394. [Google Scholar] [CrossRef]
- Wan, L.; Chen, Y.; Li, H.; Li, C. Rolling-element bearing fault diagnosis using improved lenet-5 network. Sensors 2020, 20, 1693. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. In The Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, USA, 1998; pp. 255–258. [Google Scholar]
- Dolz, J.; Desrosiers, C.; Ben Ayed, I. 3D fully convolutional networks for subcortical segmentation in MRI: A large-scale study. NeuroImage 2018, 170, 456–470. [Google Scholar] [CrossRef] [Green Version]
- Ji, S.; Xu, W.; Yang, M.; Yu, K. 3D convolutional neural networks for human action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 221–231. [Google Scholar] [CrossRef] [Green Version]
- Scherer, D.; Müller, A.; Behnke, S. Evaluation of Pooling Operations in Convolutional Architectures for Object Recognition; Springer: Heidelberg/Berlin, Germany, 2010; pp. 92–101. [Google Scholar]
- Yu, D.; Wang, H.; Chen, P.; Wei, Z. Mixed Pooling for Convolutional Neural Networks; Springer: Cham, Swizerland, 2014; pp. 364–375. [Google Scholar]
- Thiyagalingam, J.; Beckmann, O.; Kelly, P.H.J. An Exhaustive Evaluation of Row-Major, Column-Major and Morton Layouts for Large Two-Dimensional Arrays. In Performance Engineering: 19th Annual UK Performance Engineering Workshop; Jarvis, S.A., Ed.; University of Warwick: Coventry, UK, 2003; pp. 340–351. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning Deep Features for Discriminative Localization. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar]
- Lin, M.; Chen, Q.; Yan, S. Network in Network. arXiv 2013, arXiv:1312.4400. [Google Scholar]
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnostics using the case western reserve university data: A benchmark study. Mech. Syst. Sig. Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]






| Fault Diameter | Motor Load | Motor Speed | Normal | Inner Race | Ball | Outer Race (Fault Position) | ||
|---|---|---|---|---|---|---|---|---|
| @6 | @3 | @12 | ||||||
| 0 | 0 | 1797 | Normal | — | — | — | — | — |
| 1 | 1772 | |||||||
| 2 | 1750 | |||||||
| 3 | 1730 | |||||||
| 0.007 | 0 | 1797 | — | IR_07 | B_07 | OR@6_07 | OR@3_07 | OR@12_07 |
| 1 | 1772 | |||||||
| 2 | 1750 | |||||||
| 3 | 1730 | |||||||
| 0.014 | 0 | 1797 | — | IR_14 | B_14 | OR@6_14 | OR@3_14 | — |
| 1 | 1772 | |||||||
| 2 | 1750 | |||||||
| 3 | 1730 | |||||||
| 0.021 | 0 | 1797 | — | IR_21 | B_21 | OR@6_21 | — | OR@12_21 |
| 1 | 1772 | |||||||
| 2 | 1750 | |||||||
| 3 | 1730 | |||||||
| 0.028 | 0 | 1797 | — | IR_28 | B_28 | — | — | — |
| 1 | 1772 | |||||||
| 2 | 1750 | |||||||
| 3 | 1730 | |||||||
| Fault Diameter | Normal | Inner Race | Ball | Outer Race (Fault Position) | ||
|---|---|---|---|---|---|---|
| @6 | @3 | @12 | ||||
| 0 | 1657 | — | — | — | — | — |
| 0.007 | — | 476 | 473 | 475 | 474 | 476 |
| 0.014 | — | 472 | 475 | 474 | 475 | — |
| 0.021 | — | 474 | 475 | 476 | — | 474 |
| 0.028 | — | 471 | 471 | — | — | — |
| Layer | Parameter |
|---|---|
| Input | 1024 1 |
| Conv1D (size, channel) | 32 1, 5 |
| Conv1D (size, channel) | 16 1, 3 |
| Max-pooling (size, stride) | 10 1, 1 |
| Fuzzy (rule) | 32 |
| Defuzzifier (Output) | 16 |
| Model | ODCNN | I1DLeNet | |
|---|---|---|---|
| Layer | |||
| Convolutional 1 (size, channel) | 10 × 1, 50 | 6 × 64, 50 | |
| Pooling 1 (size, stride, mode) | 2 × 1, A | 8 × 1, 8, M | |
| Convolutional 2 (size, channel) | 20 50, 5 | 16 × 1, 16 | |
| Pooling 2 (size, stride, mode) | 2 × 1, A | 2 × 1, 1, M | |
| Convolutional 3 (size, channel) | — | 32 × 1, 8 | |
| Pooling 3 (size, stride, mode) | — | 2 × 1, 1, M | |
| Convolutional 4 (size, channel) | — | 32 × 1, 4 | |
| Pooling 4 (size, stride, mode) | — | 2 × 1, 1, M | |
| Fully connected (neuron) | 200 | 120 | |
| Fully connected (neuron) | 200 | 84 | |
| Output | 16 | 16 | |
| Model | ODCNN [28] | I1DLeNet [29] | GC-CNFN | |
|---|---|---|---|---|
| Evaluation Item | ||||
| Training | Best accuracy | 0.9962 | 0.9949 | 0.9975 |
| Worst accuracy | 0.9922 | 0.9913 | 0.9924 | |
| Average accuracy | 0.9947 | 0.9835 | 0.9955 | |
| Standard deviation | 0.0028 | 0.0040 | 0.0019 | |
| Total parameters | 1,078,146 | 375,122 | 20,248 | |
| Average training time (s) | 217.6 | 141.5 | 117.7 | |
| Testing accuracy | 0.9931 | 0.9874 | 0.9988 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-J.; Jhang, J.-Y. Bearing Fault Diagnosis Using a Grad-CAM-Based Convolutional Neuro-Fuzzy Network. Mathematics 2021, 9, 1502. https://doi.org/10.3390/math9131502
Lin C-J, Jhang J-Y. Bearing Fault Diagnosis Using a Grad-CAM-Based Convolutional Neuro-Fuzzy Network. Mathematics. 2021; 9(13):1502. https://doi.org/10.3390/math9131502
Chicago/Turabian StyleLin, Cheng-Jian, and Jyun-Yu Jhang. 2021. "Bearing Fault Diagnosis Using a Grad-CAM-Based Convolutional Neuro-Fuzzy Network" Mathematics 9, no. 13: 1502. https://doi.org/10.3390/math9131502
APA StyleLin, C.-J., & Jhang, J.-Y. (2021). Bearing Fault Diagnosis Using a Grad-CAM-Based Convolutional Neuro-Fuzzy Network. Mathematics, 9(13), 1502. https://doi.org/10.3390/math9131502






