A Solution of Richards’ Equation by Generalized Finite Differences for Stationary Flow in a Dam
Abstract
:1. Introduction
2. Materials and Methods
2.1. Richards’ Equation
2.2. Finite Difference Formulation
- If the grid is regular, for instance, an actual rectangular grid, the matrix coefficient in Equation (9) will be equal for all the inner grid nodes. Additionally, if the right-hand side of that equation is constant, which is the case in several important equations (v.gr. Poisson equation), the coefficients will be the same for all the inner grid nodes. This implies that in specific modeling applications, the calculation of the coefficients can be very efficient.
- Furthermore, if the positions of the neighbors are symmetrical to the central node and the differential operator is self-adjoint, the number of different coefficients required decreases (v.gr. four nodes is the discretization of the Poisson equation). This is precisely the case of the standard differences in rectangular grids. However, the analogous case occurs in other regular structures, such as those used in [39].
2.3. Case of Study
2.3.1. Problem Domain and Boundary Conditions
2.3.2. Grid Independence
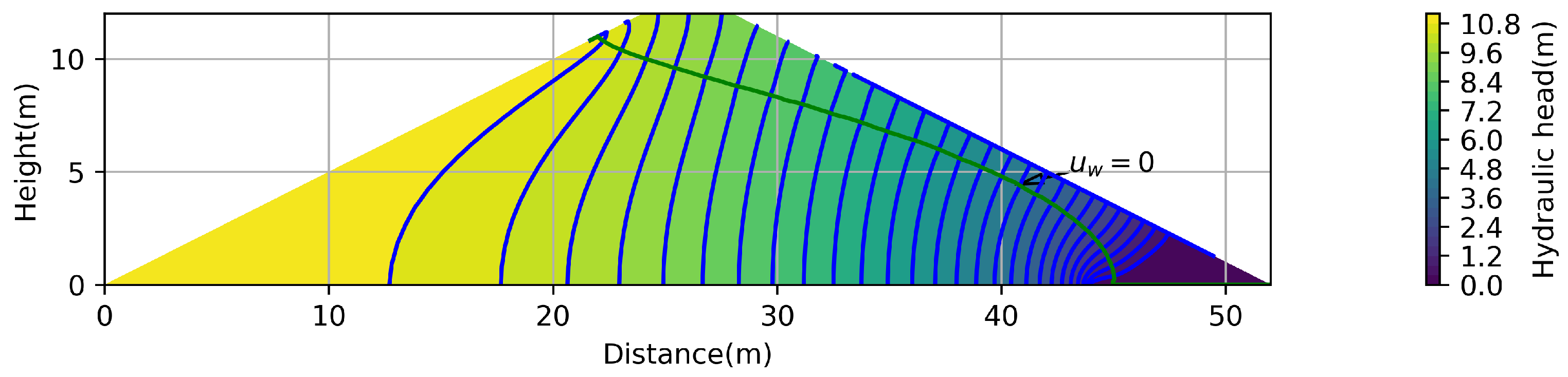
2.3.3. Stationary Flow in a Dam
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kaufmann, J.E. Catastrophic Sinkhole Collapse in Missouri. 2007. Available online: https://pubs.usgs.gov/fs/2007/3060/ (accessed on 4 May 2021).
- Voight, B.; Faust, C. Frictional heat and strength loss in some rapid landslides: Error correction and affirmation of mechanism for the Vaiont landslide. Geotechnique 1992, 42, 641–643. [Google Scholar] [CrossRef]
- Kilburn, C.R.; Petley, D.N. Forecasting giant, catastrophic slope collapse: Lessons from Vajont, Northern Italy. Geomorphology 2003, 54, 21–32. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Zha, Y.; Yang, J.; Zeng, J.; Tso, C.H.M.; Zeng, W.; Shi, L. Review of numerical solution of Richardson—Richards equation for variably saturated flow in soils. WIREs Water 2019, 6, 1–23. [Google Scholar] [CrossRef]
- Farthing, M.W.; Ogden, F.L. Numerical Solution of Richards’ Equation: A Review of Advances and Challenges. Oil Sci. Soc. Am. J. 2018, 81, 1257–1269. [Google Scholar] [CrossRef] [Green Version]
- List, F.; Radu, F. A study on iterative methods for solving Richards’ equation. Comput. Geosci. 2016, 20, 341–353. [Google Scholar] [CrossRef] [Green Version]
- Celia, M.; Bouloutas, E.T.; Zarba, R.L. A general mass-conservative numerical solution for the unsaturated flow equation. Water Resour. Res. 1990, 26, 1483–1496. [Google Scholar] [CrossRef]
- Howington, S.E.; Berger, R.C.; Hallberg, J.P.; Peters, J.F.; Stagg, A.K.; Jenkins, E.W.; Kelley, C.T. A Model to Simulate the Interaction between Groundwater and Surface Water; Technical Report; US Army Engineering Research and Development Center: Vicksburg, MS, USA, 1999. [Google Scholar]
- Simunek, J.; van Genuchten, M.; Sejna, M. Development and applications of the HYDRUS and STANMOD software packages and related codes. Vadose Zone J. 2008, 7, 587–600. [Google Scholar] [CrossRef] [Green Version]
- Trefry, M.G.; Muffels, C. Feflow: A finite-element ground water flow and transport modeling tool. Ground Water 2007, 45, 525–528. [Google Scholar] [CrossRef]
- Camporese, M.; Paniconi, C.; Putti, M.; Orlandini, S. Surface-subsurface flow modeling with path-based runoff routing, boundary condition-based coupling, and assimilation of multisource observation data. Water Resour. Res. 2010, 46, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Yeh, G.T.; Shih, D.S.; Cheng, J.R.C. An integrated media, integrated processes watershed model. Comput. Fluids 2011, 45, 2–13. [Google Scholar] [CrossRef]
- Solin, P.; Kuraz, M. Solving the nonstationary Richards equation with adaptive hp-FEM. Adv. Water Resour. 2011, 34, 1062–1081. [Google Scholar] [CrossRef]
- Ngo-Cong, D.; Mai-Duy, N.; Antille, D.L.; van Genuchten, M.T. A control volume scheme using compact integrated radial basis function stencils for solving the Richards equation. J. Hydrol. 2020, 580, 1–10. [Google Scholar] [CrossRef]
- Eymard, R.; Gutnic, M.; Hilhorst, D. The finite volume method for Richards equation. Comput. Geosci. 1999, 3, 259–294. [Google Scholar] [CrossRef]
- Manzini, G.; Ferraris, S. Mass-conservative finite volume methods on 2-D unstructured grids for the Richards’ equation. Adv. Water Resour. 2004, 27, 1199–1215. [Google Scholar] [CrossRef]
- Caviedes-Voullième, D.; García-Navarro, P.; Murillo, J. Verification, conservation, stability and efficiency of a finite volume method for the 1D Richards equation. J. Hydrol. 2013, 480, 69–84. [Google Scholar] [CrossRef]
- Casulli, V.; Zanolli, P. A nested Newton-type algorithm for finite volume methods solving Richards’ equation in mixed form. SIAM J. Sci. Comput. 2010, 32, 2255–2273. [Google Scholar] [CrossRef]
- Aravena, J.E.; Dussaillant, A. Storm-water infiltration and focused recharge modeling with finite-volume two-dimensional Richards equation: Application to an experimental rain garden. J. Hydraul. Eng. 2009, 135, 1072–1080. [Google Scholar] [CrossRef] [Green Version]
- Esmaeilzadeh, M.; Barron, R.; Balachandar, R. Numerical Solution of Partial Differential Equations in Arbitrary Shaped Domains Using Cartesian Cut-Stencil Finite Difference Method. Part I: Concepts and Fundamentals. Numer. Math. Theor. Meth. Appl. 2020, 13, 881–907. [Google Scholar] [CrossRef]
- Fayer, M.H.; Jones, T.L. UNSAT-H Version 2. 0: Unsaturated Soil Water and Heat Flow Model (No. PNL-6779); Technical Report; Pacific Northwest National Laboratory: Richland, WA, USA, 1990. [Google Scholar]
- Flerchinger, G.N. The Simultaneous Heat and Water (SHAW) Model: Technical Documentation; Technical Report; USDA Agricultural Research Service: Boise, ID, USA, 2000. [Google Scholar]
- van Dam, J.C.; Feddes, R.A. Numerical simulation of infiltration, evaporation, and shallow groundwater levels with the Richards’ equation. J. Hydrol. 2000, 233, 72–85. [Google Scholar] [CrossRef]
- Jansson, P.E.; Karlberg, L. Coupled Heat and Mass Transfer Model for Soil-Plant-Atmosphere Systems; Technical Report; Royal Institute of Technology: Stockholm, Sweden, 2010. [Google Scholar]
- Hsieh, P.A.; Wingle, W.; Healy, R.W. VS2DI—A Graphical Software Package for Simulating Fluid Flow and Solute or Energy Transport in Variably Saturated Porous Media; Technical Report; U.S. Geological Survey: Lakewood, CO, USA, 2000.
- Domínguez-Mota, F.J.; Mendoza-Armenta, S.; Tinoco-Guerrero, G.; Tinoco-Ruiz, J.G. Finite difference schemes satisfying an optimality condition for the unsteady heat equation. Math. Comput. Simul. 2014, 106, 76–83. [Google Scholar] [CrossRef]
- Chávez-Negrete, C.; Domínguez-Mota, F.J.; Santana-Quinteros, D. Numerical solution of Richards’ equation of water flow by generalized finite differences. Comput. Geotech. 2018, 101, 168–175. [Google Scholar] [CrossRef]
- Jensen, P. Finite difference techniques for variable grids. Comput. Struct. 1972, 2, 17–29. [Google Scholar] [CrossRef]
- Liszka, T.; Orkisz, J. The finite difference method at arbitrary irregular grids and its application in applied mechanics. Comput. Struct. 1980, II, 83–95. [Google Scholar] [CrossRef]
- Benito, J.J.; Ureña, F.; Gavete, L. Influence of several factors in the generalized finite difference method. Appl. Math. Model. 2001, 25, 1039–1053. [Google Scholar] [CrossRef]
- Ureña-Prieto, F.; Muñoz, J.J.B.; Gavete-Corvinos, L.A.; Alonso, B. Application of the Generalized Finite Difference Method to Solve the Advection-diffusion Equation. Comput. Appl. Math. 2011, 235, 1849–1855. [Google Scholar] [CrossRef] [Green Version]
- Milewski, S. Meshless Finite Difference Method with Higher Order Approximation—Applications in Mechanics. Arch. Comput. Methods Eng. 2012, 19, 1–49. [Google Scholar] [CrossRef]
- Li, T.S.; Wong, S.M. Solving the singular Motz problem using Radial Basis functions. In Proceedings of the 9th International Conference on Computational Methods (ICCM2018), Rome, Italy, 6–10 August 2018. [Google Scholar]
- Fredlund, D.G.; Rahardjo, H.; Fredlund, M.D. Unsaturated Soil Mechanics in Engineering Practice; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Genuchten, M.T.V. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Jefferies, A.; Kuhnert, J.; Aschenbrenner, L.; Giffhorn, U. Finite pointset method for the simulation of a vehicle travelling through a body of water. In Meshfree Methods for Partial Differential Equations VII; Springer: Berlin/Heidelberg, Germany, 2015; pp. 205–221. [Google Scholar]
- Kellogg, R.B. Difference equations on a mesh arising from a general triangulation. Math. Comput. 1964, 18, 203–210. [Google Scholar] [CrossRef]
- Lyness, J.F.; Owen, D.R.J.; Zienkiewicz, O.C. The finite element analysis of engineering systems governed by a non-linear quasi-harmonic equation. Comput. Struct. 1975, 5, 65–79. [Google Scholar] [CrossRef]
- George, P. Automatic Mesh Generation: Application to Finite Element Method; Wiley Publishers: Hoboken, NJ, USA, 1991. [Google Scholar]
Short Biography of Author
 | Carlos Chávez-Negrete is a professor of in the Civil Engineering School of the Universidad Michoacana de San Nicolás de Hidalgo (UMSNH) in Morelia, Mexico. He holds a Ph.D. in Geotechnical Engineering from Universitat Politècnica de Catalunya, in Spain. His research interest includes laboratory characterization of soils and rocks, slope stability analysis, pavement analysis, and design, the development of numerical methods for geotechnical engineering, and unsaturated soil mechanics. |
 | Francisco Domínguez-Mota completed a B.Sc. in Physics and Mathematics at the Universidad Michoacana in México. He obtained a Master degree in Applied Mathematics from the Center of Research in Mathematics in Guanajuato, Mexico, and a Ph.D in Mathematics at the Universidad Nacional Autónoma de México. He is a member of the National System of Researchers (SNI) in México, and is a researcher in Applied Mathematics at the Universidad Michoacana. His areas of research include numerical solution of differential equations and applications in engineering, numerical generation of structured grids and applications of optimization in large scale problems. |
 | Daniel Santana-Quinteros is a M.Sc. student at the Centro de ciencias matemáticas UNAM campus Morelia. He completed a B.Sc. in Physics and Mathematic at the Universidad Michoacana in México. He has been a math teacher since 2018. His areas of research include numerical solution of differential equations, flow in porous media, biomathematics and systems biology. |










| Mesh | A | B |
|---|---|---|
| Mesh 0 | 0.03572126729978147 | 0.09399951295707337 |
| Mesh 1 | 0.00629495397038204 | 0.01468723574184271 |
| Mesh 2 | 0.00213435762711308 | 0.00213435762711308 |
| Parameter | Value |
|---|---|
| 0.05 | |
| 0.5 | |
| (1/kPa) | 0.86 |
| n | 1.57 |
| ks (m/s) |
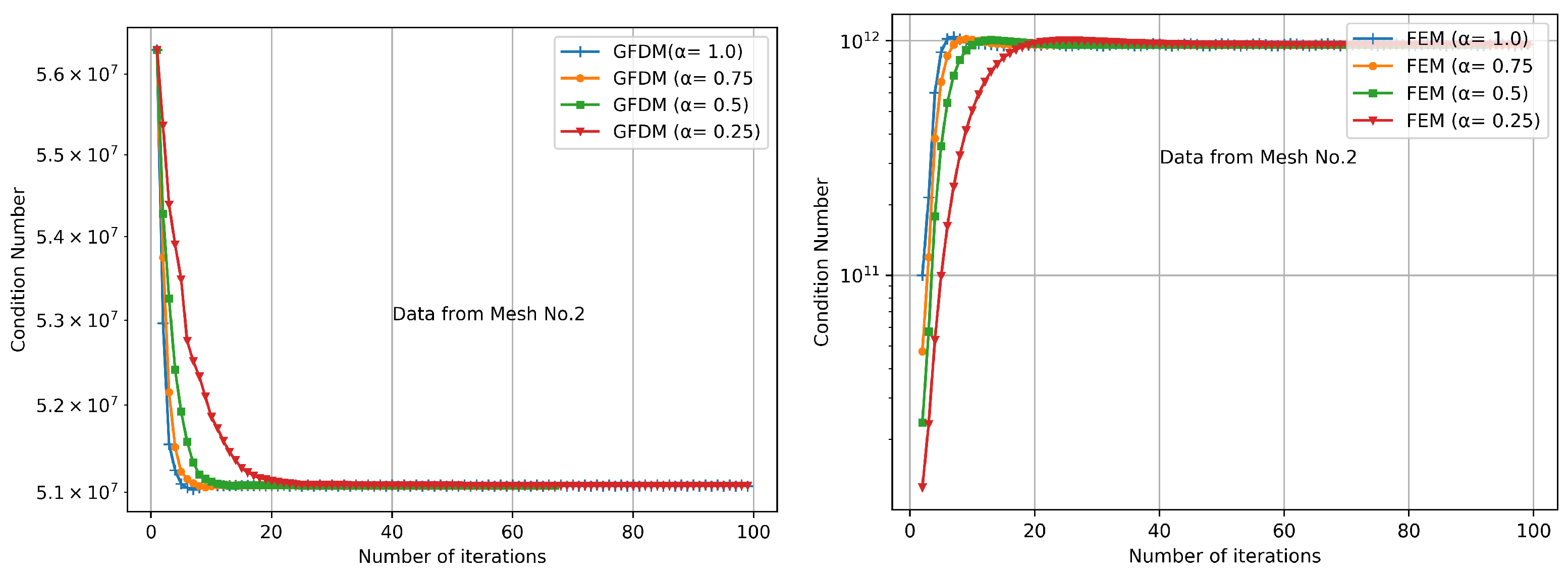
| Method | Mesh | LS Slope | Order | |
|---|---|---|---|---|
| GFDM | 1 | 0.25 | −0.0211 | 0.9843 |
| GFDM | 1 | 0.50 | −0.0341 | 0.9947 |
| GFDM | 1 | 0.75 | −0.0486 | 0.9974 |
| GFDM | 1 | 1.00 | −0.0642 | 0.9989 |
| FEM | 1 | 0.25 | −0.1017 | 1.0203 |
| FEM | 1 | 0.50 | −0.2147 | 1.0041 |
| FEM | 1 | 0.75 | −0.2172 | −1.0301 |
| FEM | 1 | 1.00 | −0.1505 | 0.1884 |
| GFDM | 2 | 0.25 | −0.1374 | 0.9978 |
| GFDM | 2 | 0.50 | −0.2772 | 0.9952 |
| GFDM | 2 | 0.75 | −0.4542 | 2.6186 |
| GFDM | 2 | 1.00 | 0.0000 | −1.3084 |
| FEM | 2 | 0.25 | −0.1180 | 0.9987 |
| FEM | 2 | 0.50 | −0.2076 | 2.2392 |
| FEM | 2 | 0.75 | −0.1362 | −2.6338 |
| FEM | 2 | 1.00 | −0.0001 | −3.2192 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chávez-Negrete, C.; Santana-Quinteros, D.; Domínguez-Mota, F. A Solution of Richards’ Equation by Generalized Finite Differences for Stationary Flow in a Dam. Mathematics 2021, 9, 1604. https://doi.org/10.3390/math9141604
Chávez-Negrete C, Santana-Quinteros D, Domínguez-Mota F. A Solution of Richards’ Equation by Generalized Finite Differences for Stationary Flow in a Dam. Mathematics. 2021; 9(14):1604. https://doi.org/10.3390/math9141604
Chicago/Turabian StyleChávez-Negrete, Carlos, Daniel Santana-Quinteros, and Francisco Domínguez-Mota. 2021. "A Solution of Richards’ Equation by Generalized Finite Differences for Stationary Flow in a Dam" Mathematics 9, no. 14: 1604. https://doi.org/10.3390/math9141604
APA StyleChávez-Negrete, C., Santana-Quinteros, D., & Domínguez-Mota, F. (2021). A Solution of Richards’ Equation by Generalized Finite Differences for Stationary Flow in a Dam. Mathematics, 9(14), 1604. https://doi.org/10.3390/math9141604






