Mathematical Modelling of Turbulent Combustion of Two-Phase Mixtures of Gas and Solid Particles with a Eulerian–Eulerian Approach: The Case of Hydrogen Combustion in the Presence of Graphite Particles
Abstract
:1. Introduction
2. Mathematical Equations of the Model
2.1. A Two-Phase Flow Model for Mixtures of Gases and Solid Particles
Closure Equations for the Interphase Transport
2.2. Model of the Chemical Kinetics
2.3. A Detailed Turbulence Model
2.4. The Turbulent Combustion Model
3. Numerical Methods
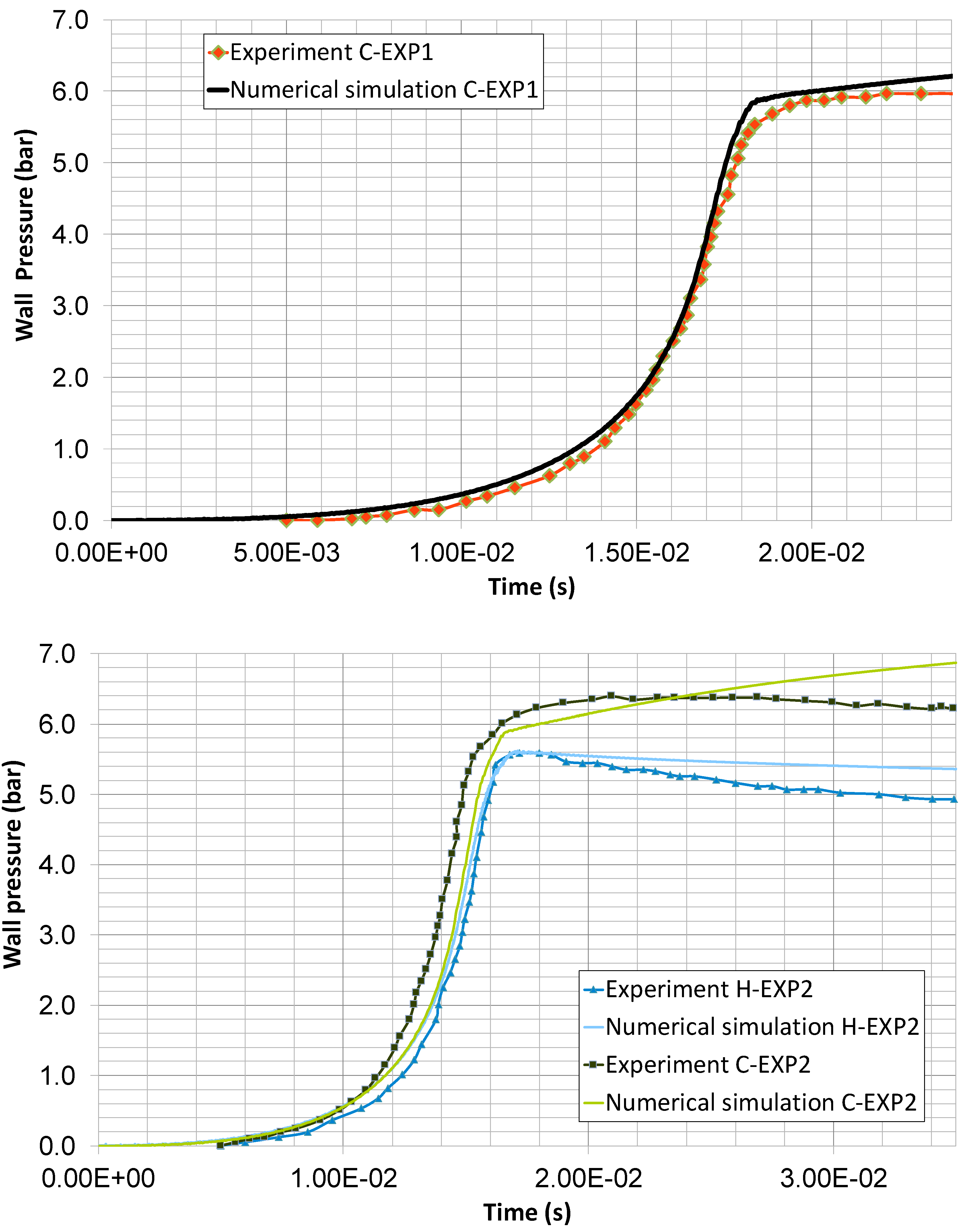
4. Results and Discussion
- Experiment 1 (C-EXP1): N2/O2 3.76 and 20% H2. Graphite powder concentration C(solid) = 94.1 g/m3;
- Experiment 2 (C-EXP2): N2/O2 2.33 and 20% H2. Graphite powder concentration C(solid) = 96.6 g/m3.
5. Conclusions
- In case of highly diluted mixtures of H2–air and graphite particles, the benchmarked results showed that LES with a detailed chemistry model were found to be an appropriate engineering approach for analysing premixed turbulent combustion of graphite–H2 mixtures.
- The validation against the experimental data show that the two-phase approach used in the present model based on the Eulerian–Eulerian approach seems to be accurate enough to afford this type of combustion sequences with highly diluted mixtures.
- Under the conditions studied, the model captured well the key tendencies linked to the presence of carbon particles of the microns order. In this sense, the model was able to predict that the presence of a low concentration of carbon particles (of the order of 96 g/m3) accelerated the combustion sequence, obtaining smaller combustion times than in the absence of particles and larger maximum wall pressure levels (of the order of 15%).
- Classical graphite and hydrogen detailed oxidation mechanisms [30,31,33] coupled with a Eulerian–Eulerian model provided good results in the prediction of combustion products under turbulent combustion conditions. Regarding graphite combustion, the porous oxidation model provided results closer to the experiments than the nonporous model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Representative area of a particle. | |
| Drag coefficient of particles. | |
| Proportional constant of the turbulent model. | |
| Specific heat capacity of phase m. | |
| Mean diameter of particles. | |
| Diffusion coefficient of species k. | |
| Activation energy for reaction i. | |
| Total energy of the gas phase. | |
| Total energy of the solid phase. | |
| Efficiency function accounting for turbulent flame wrinkling. | |
| Factor decreasing the reaction rate for the TFM. | |
| Drag force over particles. | |
| Enthalpy of gas. | |
| All-ones vector. | |
| Kinetic coefficient of reaction i. | |
| Turbulent kinetic energy at the subgrid scale. | |
| Mass of a particle. | |
| Nusselt number. | |
| Pressure. | |
| Partial pressure of reagent j. | |
| Prandtl number. | |
| Heat flux vector. | |
| Interphase heat transfer rate. | |
| Heat released to the gas phase by chemical reactions. | |
| Heat released to the solid phase by chemical reactions. | |
| Reynolds number based on particle diameter . | |
| Mass reaction rate of reaction i. | |
| Large-scale strain-rate tensor. | |
| Laminar flame speed. | |
| t | Time. |
| Grid-scale or FAVRE-filtered velocity. | |
| Velocity vector of the gas phase. | |
| Velocity vector of the solid phase. | |
| . | |
| V | . |
| Mass fraction of species k in phase m. | |
| Greek Letters | |
| Void fraction. | |
| Temperature exponent in reaction i. | |
| Combustion mass source term. | |
| Laminar flame thickness. | |
| Formation enthalpy of species k in phase m. | |
| Viscosity. | |
| Eddy viscosity. | |
| Density of the gas phase. | |
| Density of the solid phase. | |
| Concentration of particles. | |
| Friction stress tensor. | |
| Subgrid-scale turbulent stress tensor component i,j. | |
| Mass reaction rate for species k in phase m. | |
References
- Farid, M.M.; Jeong, H.J.; Kim, K.H.; Lee, J.; Kim, D.; Hwang, J. Numerical investigation of particle transport hydrodynamics and coal combustion in an industrialscale circulating fluidized bed combustor: Effects of coal feeder positions and coal feeding rates. Fuel 2017, 192, 187–200. [Google Scholar] [CrossRef]
- Adamczyk, W.P.; Weçel, G.; Klajny, M.; Kozołub, P.; Klimanek, A.; Białecki, R.A. Modeling of particle transport and combustion phenomena in a large-scale circulating fluidized bed boiler using a hybrid Euler-Lagrange approach. Particuology 2014, 16, 29–40. [Google Scholar] [CrossRef]
- Alattab, K.A.; Zainal, Z.A. Syngas production and combustion characteristics in a biomass fixed bed gasifier with cyclone combustor. Appl. Therm. Eng. 2017, 113, 714–721. [Google Scholar] [CrossRef]
- Yang, B.; Wang, L.; Ning, L.; Zeng, K. Effects of pilot injection timing on the combustion noise and particle emissions of a diesel/natural gas dualfuel engine at low load. Appl. Therm. Eng. 2016, 102, 822–828. [Google Scholar] [CrossRef]
- Goix, S.; Lévêque, T.; Xiong, T.; Schreck, E.; Baeza-Squiban, A.; Geret, F.; Uzug, G.; Austruy, A.; Dumat, C. Environmental and health impacts of fine and ultrafine metallic particles: Assessment of threat scores. Environ. Res. 2014, 133, 185–194. [Google Scholar] [CrossRef] [PubMed]
- Benajes, J.; García, A.; Monsalve-Serrano, J.; Boronat, V. Gaseous emissions and particle size distribution of dualmode dualfuel dieselgasoline concept from low to full load. Appl. Therm. Eng. 2017, 120, 138–149. [Google Scholar] [CrossRef]
- Otón-Martínez, R.A.; Monreal-González, G.; García-Cascales, J.R.; Vera-García, F.; Velasco, F.J.S.; Ramírez-Fernández, F.J. An approach formulated in terms of conserved variables for the characterisation of propellant combus-tion in internal ballistics. Int. J. Numer. Meth. Fluids 2015, 79, 394–415. [Google Scholar] [CrossRef]
- Monreal-González, G.; Otón-Martínez, R.A.; Velasco, F.J.S.; García-Cascáles, J.R.; Ramírez-Fernández, F.J. One-Dimensional Modelling of Internal Ballistics. J. Energetic Mater. 2017, 35, 397–420. [Google Scholar] [CrossRef]
- Kuo, K.K.; Summerfield, M. Fundamentals of Solid-Propellant Combustion, 90th ed.; American Institute of Aeronautics and Astronautics: New York, NY, USA, 1984. [Google Scholar]
- Hamdan, M.; Qubbaj, A. Inhibition effect of inert compounds on oil shale dust explosion. Appl. Therm. Eng. 1998, 18, 221–229. [Google Scholar] [CrossRef]
- Peng, W.; Chen, T.; Sun, Q.; Wang, J.; Yu, S. Preliminary experiment design of graphite dust emission measurement under accident conditions for HTGR. Nucl. Eng. Des. 2017, 316, 218–227. [Google Scholar] [CrossRef]
- Herranz, L.; Del Prá, C.L.; Velasco, F.S. Preliminary steps toward assessing aerosol retention in the break stage of a dry steam generator during severe accident SGTR sequences. Nucl. Eng. Des. 2008, 238, 1392–1399. [Google Scholar] [CrossRef]
- Raimond, E.; Clément, B.; Denis, J.; Guigueno, Y.; Vola, D. Use of Phébus FP and other FP programs for atmospheric radioactive release assessment in case of a severe accident in a PWR (deterministic and probabilistic approaches developed at IRSN). Ann. Nucl. Energy 2013, 61, 190–198. [Google Scholar] [CrossRef]
- García-Cascales, J.R.; Otón-Martínez, R.A.; Sánchez-Velasco, F.J.; Vera-García, F.; Bentaiby, A.; Meynet, N. Advances in the characterisation of reactive gas and solid mixtures under low pressure conditions. Comput. Fluids 2014, 101, 64–87. [Google Scholar] [CrossRef]
- Topilski, L.; Reyes, S. Accident Analysis Report—Vol. iii: Hypothetical Event Analysis; Technical Report ITER-D-2E2XAMv4.1, ITER Project; France, 2009. [Google Scholar]
- García-Cascales, J.R.; Velasco, F.J.S.; Otón-Martínez, R.A.; Espín-Tolosa, S.; Bentaib, A.; Meynet, N.; Bleyer, A. Characterisation of metal combustion with DUST code. Fusion Eng. Des. 2015, 98–99, 2142–2146. [Google Scholar] [CrossRef]
- Velasco, F.J.S.; Otón-Martínez, R.A.; García-Cascales, J.R.; Espín, S.; Meynet, N.; Bentaib, A. Modelling detonation of H2-O2-N2 mixtures in presence of solid particles in 3D scenarios. Int. J. Hydrog. Energy 2016, 41, 17154–17168. [Google Scholar] [CrossRef]
- Pitsch, H. Large-eddy simulation of turbulent combustion. Annu. Rev. Fluid Mech. 2006, 38, 453–482. [Google Scholar] [CrossRef] [Green Version]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A Fluid Dyn. 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Chai, X.; Mahesh, K. Dynamic k-equation model for large eddy simulations of compressible flows. J. Fluid Mech. 2012, 699, 385–413. [Google Scholar] [CrossRef]
- Nicolás-Pérez, F.; Velasco, F.J.S.; García-Cascales, J.R.; Otón-Martínez, R.A.; López-Belchí, A.; Moratilla, D.; Rey, F.; Laso, A. On the accuracy of RANS, DES and LES turbulence models for predicting drag reduction with Base Bleed technology. Aerospace Sci. Technol. 2017, 67, 126–140. [Google Scholar] [CrossRef]
- Emami, S.; Mazaheri, K.; Shamooni, A.; Mahmoudi, Y. LES of flame acceleration and DDT in hydrogen–air mixture using artificially thickened flame approach and detailed chemical kinetics. Int. J. Hydrog. Energy 2015, 40, 7395–7408. [Google Scholar] [CrossRef]
- Sánchez, A.L.; Williams, F.A. Recent advances in understanding of flammability characteristics of hydrogen. Prog. Energy Combust. Sci. 2014, 41, 1–55. [Google Scholar] [CrossRef]
- Williams, F.A. Detailed and reduced chemistry for hydrogen autoignition. J. Loss Prev. Process. Ind. 2008, 21, 131–135. [Google Scholar] [CrossRef]
- Saxena, P.; Williams, F.A. Testing a small detailed chemical-kinetic mechanism for the combustion of hydrogen and carbon monoxide. Combust. Flame 2006, 145, 316–323. [Google Scholar] [CrossRef]
- Gibeling, H.; Buggeln, R. Reacting Flow Models for Navier-Stokes Analysis of Projectile Base Combustión; AIAA Paper No. 91-2077; AIAA: Reston, VA, USA, 1991. [Google Scholar]
- Zhuo, C.; Feng, F.; Wu, X.; Liu, Q.; Ma, H. Numerical simulation of the muzzle flows with base bleed projectile based on dynamic overlapped grids. Comput. Fluids 2014, 105, 307–320. [Google Scholar] [CrossRef]
- Bournot, H.; Daniel, E.; Cayzac, R. Improvements of the base bleed effect using reactive particles. Int. J. Therm. Sci. 2006, 45, 1052–1065. [Google Scholar] [CrossRef]
- Chelliah, H. The influence of heterogeneous kinetics and thermal radiation on the oxidation of graphite particles. Combust. Flame 1996, 104, 81–94. [Google Scholar] [CrossRef]
- Chelliah, H.K.; Makino, A.; Kato, I.; Araki, N.; Law, C.K. Modeling of graphite oxidation in a stagnation-point flow field using detailed homogeneous and semiglobal heterogeneous mechanisms with comparisons to experiments. Combust. Flame 1996, 104, 469–480. [Google Scholar] [CrossRef]
- Bradley, D.; Dixon-Lewis, G.; Habik, S.E.; Mushi, E.M.J. Twentieth Symposium (International) on Combustion; The Combustion Institute: Pittsburgh, PA, USA, 1984; pp. 931–940. [Google Scholar]
- Yetter, R.A.; Dryer, F.L.; Rabitz, H. A Comprehensive Reaction Mechanism For Carbon Monoxide/Hydrogen/Oxygen Kinetics. Combust. Sci. Technol. 1991, 79, 97–128. [Google Scholar] [CrossRef]
- Druzhinin, O.A.; Elghobashi, S. On the decay rate of isotropic turbulence laden with micropaticles. Phys. Fluids 1999, 11, 602–610. [Google Scholar] [CrossRef]
- Shotorban, B.; Balachandar, S. A Eulerian model for large-eddy simulation of concentration of particles with small Stokes numbers. Phys. Fluids 2007, 19, 118107. [Google Scholar] [CrossRef]
- Yeh, F.; Lei, U. On the motion of small particles in a homogeneous isotropic turbulent flow. Phys. Fluids A Fluid Dyn. 1991, 3, 2571–2586. [Google Scholar] [CrossRef]
- Simonin, O.; Deutsch, E.; Minier, J.P. Eulerian prediction of the fluid/particle correlated motion in turbulent two-phase flows. Flow Turbul. Combust. 1993, 51, 275–283. [Google Scholar] [CrossRef]
- Wang, Q.; Squires, K. Large eddy simulation of particle-laden turbulent channel flow. Phys. Fluids 1996, 8, 1207–1223. [Google Scholar] [CrossRef]
- Boivin, M.; Simonin, O.; Squires, K. On the prediction of gas–solid flows with two-way coupling using large eddy simulation. Phys. Fluids 2000, 12, 2080. [Google Scholar] [CrossRef]
- Apte, S.; Mahesh, K.; Moin, P.; Oefelein, J. Largeeddy simulation of swirling particle-laden flows in a coaxialjet combustor. Int. J. Multiphase Flow 2003, 29, 1311–1331. [Google Scholar] [CrossRef]
- Denkevits, A.; Dorofeev, S. Dust explosion hazard in ITER: Explosion indices of fine graphite and tungsten dusts and their mixtures. Fusion Eng. Des. 2005, 75–79, 1135–1139. [Google Scholar] [CrossRef]
- Favre, A. Statistical equations of turbulent gases. In Problems of Hydrodynamic and Continuum Mechanics; SIAM: Philadelphia, PA, USA, 1969; pp. 231–266. [Google Scholar]
- McBride, B.J.; Gordon, S.; Reno, M.A. Coefficients for Calculating Thermodynamic and Transport Properties of Individual Species; NASA: Washington, DC, USA, 1983. [Google Scholar]
- Lii, W.S. The viscosity of gases and molecular force. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1893, 36, 507–531. [Google Scholar] [CrossRef] [Green Version]
- Crowe, C.T.; Schwarzkopf, J.D.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- García-Cascales, J.R.; Vera-García, F.; Zueco-Jordán, J.; Bentaïb, A.; Meynet, N.; Vendel, J.; Perrault, D. Development of a IRSN code for dust mobilisation problems in ITER. Fusion Eng. Des. 2010, 85, 2274–2281. [Google Scholar] [CrossRef]
- Otterman, B.; Levine, A.S. Analysis of Gas-Solid Particle Flows in Shock Tubes. AIAA J. 1974, 12, 579–580. [Google Scholar] [CrossRef]
- Miura, H.; Glass, I.I. On dusty-gas shock tube. Proc. R. Soc. Lond. 1982, 382, 373–388. [Google Scholar]
- Knudsen, J.G.; Katz, D.L.; Street, R.E. Fluid Dynamics and Heat Transfer. Phys. Today 1959, 12, 40–44. [Google Scholar] [CrossRef]
- Laurendeau, N.M. Heterogeneous kinetics of coal char gasification and combustión. Prog. Energy Combust. Sci. 1978, 4, 221–270. [Google Scholar] [CrossRef]
- Tabor, G.; Weller, H.G. Large Eddy Simulation of Premixed Turbulent Combustion Using Ξ Flame Surface Wrinkling Model. Flow Turbul. Combust. 2004, 72, 1–28. [Google Scholar] [CrossRef]
- Poinsot, D.V.T. Theoretical and Numerical Combustion, 3rd ed.; RT Edwards, Inc.: West Bundaberg, Australia, 2012. [Google Scholar]
- Charlette, F.; Meneveau, C.; Veynante, D. A power-law flame wrinkling model for LES of premixed turbulent combustion Part I: Non-dynamic formulation and initial tests. Combust. Flame 2002, 131, 159–180. [Google Scholar] [CrossRef]
- Wang, G.; Boileau, M.; Veynante, D. Implementation of a dynamic thickened flame model for large eddy simulations of turbulent premixed combustion. Combust. Flame 2011, 158, 2199–2213. [Google Scholar] [CrossRef]
- Liou, M.-S. A sequel to AUSM, Part II: AUSM+-up for all speeds. J. Comput. Phys. 2006, 214, 137–170. [Google Scholar] [CrossRef]
- Liou, M.-S. A Sequel to AUSM: AUSM+. J. Comput. Phys. 1996, 129, 364–382. [Google Scholar] [CrossRef]
- Koop, A.H. Numerical Simulation of Unsteady Three Dimensional Sheet Cavitation. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2009. [Google Scholar] [CrossRef] [Green Version]
- Rusanov, V. Calculation of interaction of non-steady shock waves with obstacles. J. Comput. Math. Phys. 1962, 1, 267–279. [Google Scholar]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics; Springer: Berlin, Germany, 1997. [Google Scholar]
- Pope, S. Computationally efficient implementation of combustion chemistry using in situ adaptive tabulation. Combust. Theory Model. 1997, 1, 41–63. [Google Scholar] [CrossRef]
- Lu, L.; Pope, S.B. An improved algorithm for in situ adaptive tabulation. J. Comput. Phys. 2009, 228, 361–386. [Google Scholar] [CrossRef]
- Hiremath, V.; Ren, Z.; Pope, S.B. Combined dimension reduction and tabulation strategy using ISAT–RCCE–GALI for the efficient implementation of combustion chemistry. Combust. Flame 2011, 158, 2113–2127. [Google Scholar] [CrossRef]
- Nicolás-Pérez, F.; Velasco, F.J.S.; García-Cascales, J.R.; Otón-Martínez, R.A.; Bentaib, A.; Chaumeix, N. Evaluation of dif-ferent models for turbulent combustion of hydrogen-air mixtures. Large Eddy Simulation of a LOVA sequence with hy-drogen deflagration in ITER Vacuum Vessel. Fusion Eng. Des. 2020, 161, 111901. [Google Scholar] [CrossRef]
- Hedengren, J.D.; Edgar, T.F. In Situ Adaptive Tabulation for Real-Time Control. Ind. Eng. Chem. Res. 2005, 44, 2716–2724. [Google Scholar] [CrossRef] [Green Version]
- Sabard, J.; Chaumeix, N.; Bentaib, A. Hydrogen explosion in ITER: Effect of oxygen content on flame propagation of H2/O2/N2 mixtures. Fusion Eng. Des. 2013, 88, 2669–2673. [Google Scholar] [CrossRef]
- Sabard, J. Etude de L’explosion de Mélanges Diphasiques: Hydrogène et Poussières. Ph.D. Thesis, Université d’Orléans, Orléans, France, 2013; pp. 185–221. [Google Scholar]
- Sabard, J.; Goulier, J.; Chaumeix, N.; Mevel, R.; Studer, E.; Bentaib, A. Determination of explosion combustion parameters of H2/O2/N2 mixtures. In Proceedings of the International Symposium on Hazard, Prevention and Mitigation of Industrial Explosions (ISHPMIE), Cracov, Poland, 22–27 July 2012. [Google Scholar]
- Jiménez, M.A.; Martín-Valdepeñas, J.M.; Martín-Fuertes, F.; Fernández, J.A. A detailed chemistry model for transient hy-drogen and carbon monoxide catalytic recombination on parallel flat Pt surfaces implemented in an integral code. Nucl. Eng. Des. 2007, 237, 460–472. [Google Scholar] [CrossRef] [Green Version]
- Nuclear Energy Agency, Committee on the Safety of Nuclear Installations. Carbon Monoxide—Hydrogen Combustion Characteritics in Containment Conditions; Final Report, NEA/CSNI/R(2000)10; Nuclear Energy Agency: Paris, France, 2000. [Google Scholar]

| (a) | |||||
| Reaction | i | Ai (1) | Ei (J/kmol) | (kg/m2/s) | |
| C+OHCO+H | 1 | 3.56 × 10−3 | −0.5 | 0.0 | |
| C+OCO | 2 | 6.56 × 10−3 | −0.5 | 0.0 | |
| C+H2OCO+H2 | 3 | 4.74 | 0.0 | 2.878592 × 108 | |
| C+CO22CO | 4 | 8.88 × 10−2 | 0.0 | 2.849304 × 108 | |
| C+(1/2)O2CO | 5 | 2.37 × 10−2 | 0.0 | 1.255200 × 108 | where |
| 6 | 2.10 × 10−4 | 0.0 | −1.715440 × 107 | ||
| 7 | 5.28 × 10−4 | 0.0 | 6.359680 × 107 | ||
| 8 | 1.79 × 102 | 0.0 | 4.058480 × 108 | ||
| (b) | |||||
| Reaction | i | Bi (1) | i | Ei (J/kmol) | |
| C+OHCO+H | 9 | 1.65 | 0.5 | 0.0 | |
| C+OCO | 10 | 3.41 | 0.5 | 0.0 | |
| C+H2OCO+H2 | 11 | 6.00 × 107 | 0.0 | 2.690312 × 108 | |
| C+CO22CO | 12 | 6.0 × 107 | 0.0 | 2.690312 × 108 | |
| 2C+O22CO | 13 | 2.2 × 106 | 0.0 | 1.799120 × 108 | |
| Step | Reaction | Bi (b) | αi (b) | Ei (J/kmol) |
|---|---|---|---|---|
| 1 | H + O2 = OH + O | 1.91 × 1014 | 0.0 | 68,784,960 |
| 2 | H2 + O = OH + H | 5.13 × 104 | 2.67 | 26,317,360 |
| 3 | H2 + OH = H2O + H | 2.14 × 108 | 1.51 | 14,351,120 |
| 4 | OH + OH = O+H2O | k = 5.46 × 1011 | x | exp (0.00149·T) |
| 5 | H2 + M = H + H+M(a) | 4.57 × 1019 | −1.4 | 436,725,920 |
| 6 | O + O+M = O2 + M(a) | 6.17 × 1015 | −0.5 | 0 |
| 7 | H + O+M = OH + M(a) | 4.68 × 1018 | −1.0 | 0 |
| 8 | H + OH + M = H2O + M(a) | 2.24 × 1022 | −2.0 | 0 |
| 9 | H + O2 + M = HO2 + M(a) | 4.76 × 1019 | −1.42 | 0 |
| 10 | HO2 + H = H2 + O2 | 6.61 × 1013 | 0.0 | 8,911,920 |
| 11 | HO2 + H = OH + OH | 17.0 × 1014 | 0.0 | 3,640,080 |
| 12 | HO2 + O = OH + O2 | 1.74 × 1013 | 0.0 | −1,673,600 |
| 13 | HO2 + OH = H2O + O2 | 1.45 × 1016 | −1.0 | 0 |
| 14 | HO2 + HO2 = H2O2 + O2 | 3.02 × 1012 | 0.0 | 5,815,760 |
| 15 | H2O2 + M = OH + OH + M(a) | 1.20 × 1017 | 0.0 | 190,372,000 |
| 16 | H2O2 + H = H2O + OH | 1.00 × 1013 | 0.0 | 15,020,560 |
| 17 | H2O2 + H = HO2 + H2 | 4.79 × 1013 | 0.0 | 33,262,800 |
| 18 | H2O2 + O = HO2 + OH | 9.55 × 106 | 2.0 | 16,610,480 |
| 19 | H2O2 + OH = H2O + HO2 | 7.08 × 1012 | 0.0 | 5,983,120 |
| 20 | CO + O+M = CO2 + M(a) | 2.51 × 1013 | 0.0 | −18,995,360 |
| 21 | CO + O2 = CO2 + H | 2.51 × 1012 | 0.0 | 199,534,960 |
| 22 | CO + OH = CO2 + O | K = 6.75 × 1010 | x | exp(0.000907·T) |
| 23 | CO + HO2 = CO2 + OH | 6.03 × 1013 | 0.0 | 96,022,800 |
| 24 | HCO + M = CO + H+M(a) | 1.86 × 1017 | −1.0 | 71,128,000 |
| 25 | HCO + H = CO + H2 | 7.24 × 1013 | 0.0 | 0 |
| 26 | HCO + O = CO + OH | 3.02 × 1013 | 0.0 | 0 |
| 27 | HCO + OH = CO + H2O | 3.02 × 1013 | 0.0 | 0 |
| 28 | HCO + O2 = CO + HO2 | 4.17 × 1012 | 0.0 | 0 |
| Experiment 1 | Experimental | Two-phase Model | Experiment 2 | Experimental | Two-phase Model |
|---|---|---|---|---|---|
| Pmax (bar) | 6.0 | 6.2 | Pmax (bar) | 6.4 | 6.9 |
| Error, Pmax (%) | - | 3.3 | Error, Pmax (%) | - | 7.8 |
| trise (ms) | 24.0 | 19.0 | trise (ms) | 20.9 | 17.1 |
| Error, trise (%) | - | 20.8 | Error, trise (%) | - | 18.2 |
| Experiment and Combustion Product Considered | COSILAB Numerical Prediction of the Combustion Products Considered (%mol) [66] | Experimental Measurements of the Combustion Products (%mol) [66] | Present Study: Two-Phase Model with the Porous Approach; (%mol) Prediction in Combustion Products | Present Study: Two-Phase Model with the Nonporous Approach; (%mol) Prediction in Combustion Products |
|---|---|---|---|---|
| Experiment 1, CO | 15.44% | 0% | 0.22% | <0.0001% |
| Experiment 2, CO | 11.57% | 0% | 1.46% | - |
| Experiment 1, H2O | 10.76% | 22.26% | 20.77% | 21.98% |
| Experiment 2, H2O | 16.49% | 22.29% | 19.26% | - |
| Experiment 1, CO2 | 3.16% | 4.34% | 3.48% | 0.012% |
| Experiment 2, CO2 | 8.23% | 6.08% | 5.26% | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicolás-Pérez, F.; Velasco, F.J.S.; Otón-Martínez, R.A.; García-Cascales, J.R.; Bentaib, A.; Chaumeix, N. Mathematical Modelling of Turbulent Combustion of Two-Phase Mixtures of Gas and Solid Particles with a Eulerian–Eulerian Approach: The Case of Hydrogen Combustion in the Presence of Graphite Particles. Mathematics 2021, 9, 2017. https://doi.org/10.3390/math9172017
Nicolás-Pérez F, Velasco FJS, Otón-Martínez RA, García-Cascales JR, Bentaib A, Chaumeix N. Mathematical Modelling of Turbulent Combustion of Two-Phase Mixtures of Gas and Solid Particles with a Eulerian–Eulerian Approach: The Case of Hydrogen Combustion in the Presence of Graphite Particles. Mathematics. 2021; 9(17):2017. https://doi.org/10.3390/math9172017
Chicago/Turabian StyleNicolás-Pérez, Francisco, F.J.S. Velasco, Ramón A. Otón-Martínez, José R. García-Cascales, Ahmed Bentaib, and Nabiha Chaumeix. 2021. "Mathematical Modelling of Turbulent Combustion of Two-Phase Mixtures of Gas and Solid Particles with a Eulerian–Eulerian Approach: The Case of Hydrogen Combustion in the Presence of Graphite Particles" Mathematics 9, no. 17: 2017. https://doi.org/10.3390/math9172017






