Abstract
Denote the least number that every system of n cubes with total volume 1 in d-dimensional (Euclidean) space can be packed parallelly into some rectangular parallelepiped of volume . New results , , , , , , can be found in the paper.
PACS:
52C17
1. Introduction
In 1966, L. Moser [1] raised the following problem: Determine the smallest number A so that any system of squares of total area 1 can be packed parallelly into some rectangle of area A. This problem can also be found in [2,3,4,5,6]. The problem has been extended to higher dimensions and has been studied for a specific number of squares (cubes). To distinguish the number of dimensions and cubes we denoted the least number that every system of n cubes with total volume 1 in d-dimensional (Euclidean) space can be packed parallelly into some rectangular parallelepiped of volume . denotes the maximum of all , .
Some results are known in 2-dimensional space. Kleitman and Krieger [7] proved that every finite system of squares with total area 1, can be packed into the rectangle with sides of lengths and , so . After twenty years Novotný [8] showed that and . The exact results are known also for , Novotný [9] proved and in Novotný [10] proved . The estimate of was improved by Novotný [11] . Later, this result was improved by Hurgady [12] .
In 3-dimensional space, the estimate of was gradually improved. Meir and Moser [13] proved and later Novotný [14] proved . The exact results are known for : Novotný [15], , Novotný [16], and in Novotný [14] proved .
The results for and are known too: , Bálint and Adamko in [17]; , Bálint and Adamko in [18]; , Sedliačková in [19].
Adamko and Bálint proved for in [20]. Theorem holds also for .
2. Main Results
The main part of this section is the proof of . We use the same method as [17,18]. At the end of the section, we offer (without proof) the values of for .
Theorem 1.
.
Outline of the proof
- 1.
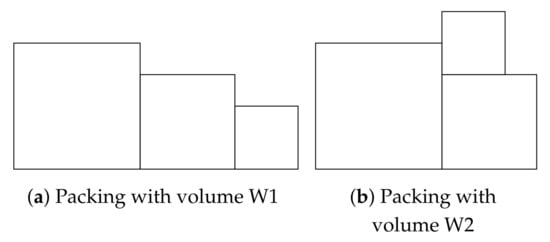
- We show, that there are only two important packing configurations. Their volumes are and , see Figure 1. Firstly, we need to find , for each . The maximum from is the final result, we denote it ;
- 2.
- Cubes with sides , , and have . We prove that this volume is sufficient for packing any three cubes with a total volume of 1 in dimension 5;
- 3.
- We obtain an estimation of the side size of the largest cube: ;
- 4.
- Using and , we obtain constraints and ;
- 5.
- 6.
- We clarify:
- (a)
- holds for . Therefore, , ;
- (b)
- holds for . Therefore, , ;
- 7.
- We show that the asked maximum is on curve C;
- (a)
- We use critical points for region ;
- (b)
- We were unable to use critical points on the whole , so we gradually numerically exclude subregions. We start with comparison of maximum of subregions and 1.8 (packing with exists).
Proof.
Consider three cubes with edge lengths in the 5-dimensional Euclidean space, where and the total volume .
We are looking for the smallest volume of a parallelepiped containing all three cubes. Therefore, from several ways of packing, we can ignore the packing that leads in any circumstances to a larger volume.
Let denote the cubes (sorted from the largest). We attach cubes X and Y to each other, for example, in the direction of the fifth dimension. Parallelepiped containing cubes X and Y has volume .
If we place the cube Z to the cube X in the direction of the fifth dimension, we receive volume . We obtain volume for other four directions.
If we place the cube Z to the cube Y in the direction of the fifth dimension, we receive again . We obtain (after appropriate shifting of the cube Y) volume for other four directions.
Because , we can ignore packings that lead to the volume .
If we start with cubes X and Z, or Z and Y, the same results are obtained.
Therefore, it is sufficient to consider only two cases of packing three cubes, see Figure 1a,b. In the first case, the volume is sufficient for packing, in the second case, the volume is sufficient.
We need to find under the conditions , and .
For three cubes with edge lengths a volume is necessary. Thus, .
If than we can pack the cubes, as shown in Figure 1b, and volume is sufficient, for cubes with edge lengths and .
Let us consider only the case that . From we find and, therefore, . Then, and, therefore, . We attain the upper bound for . and , therefore, and . This implies that we can consider only , i.e., .
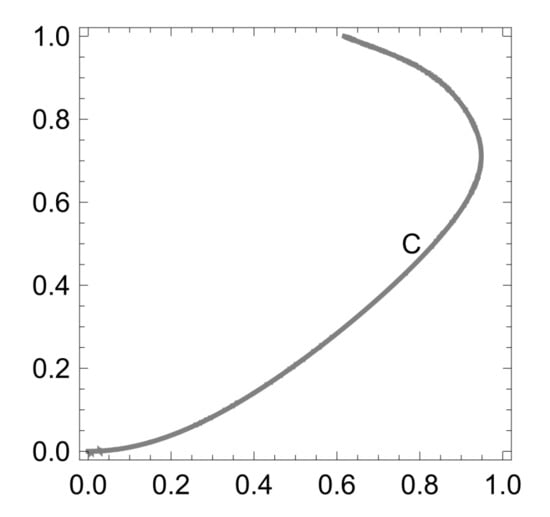
Equality holds if, and only if, . In this case, and . When we substitute into we find the curve (Figure 2).
The interval for x can be reduced. If we choose , then . If then and, therefore, . The function has the greatest value if , i.e., . For , we find .
Denote .
The inequality is valid for the intervals: , , , , , , , hence for the asked maximum holds .
Therefore, we have shown that the asked will be attained for .
From the assumption follows that and also .
Consider the closed region M determined by inequalities , . The curve C divides the region M into two open regions (Figure 3).
We are looking for when . From the condition we find
Let denote the closure of the set . The functions are continuous on M and the equality holds just in the points of the curve C.
Take the point . The inequality holds in every point , because of . Therefore, for the asked maximum holds .
Take the point . The inequality holds in every point because of . Therefore, for the asked maximum holds .
On the compact set the function (1) has its maximum in some point B.
It holds . The equality holds if but the points of the curve do not belong to the region . For every point holds Therefore, the point B must lie on the curve C.
For every point , the inequality holds, and so , .
Denote
Examine the region .
For , is . For , is . For and, step by step, for , , is always .
For and, step by step, for , , is always .
For , and, step by step, for , , , is always .
For and, step by step, for , , , , , , , is always .
For and, step by step, for , , , , , , , , , , , , , , , , , , , , , , is always .
For and, step by step, for , , , , , , , , , , , is always .
We do not exclude the region , in this way, it is not effective.
We have
From (2): and .
and , therefore, for every point , we have two inequalities:
and
Denote
For and is and, therefore, .
For and is also and, therefore, .
Therefore, the asked maximum cannot be achieved for .
For and, step by step, for , , , , , , , , is always .
We do not exclude the region , in this way, it is not effective.
For and is and, therefore, .
For and is and, therefore, .
For and is and, therefore, .
This implies that the asked maximum cannot be achieved for .
For and, step by step, for , , , , , , , , , is always .
We do not exclude the region , in this way, it is not effective.
For and is and, therefore, .
For and is and, therefore, .
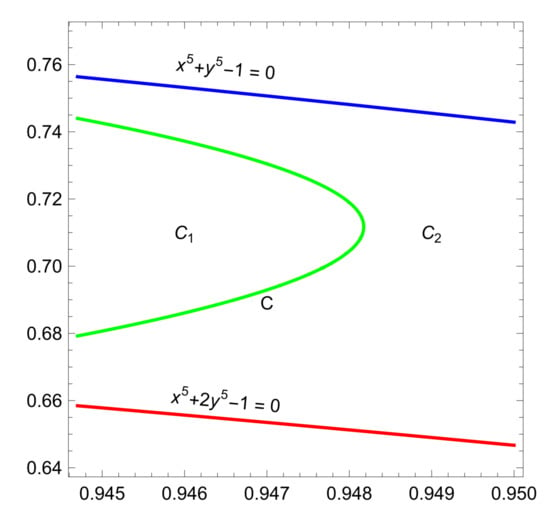
This implies that the asked maximum cannot be achieved for , see Figure 4.
For and, step by step, for , , , is always .
For and is and, therefore, .
For and is and, therefore, .
For and, step by step, for , , is always .
So function (2) on the compact set must achieve its maximum in some point of the curve C. It is the same point B as above.
We ask constrained maximum of the function
on the curve C
for .
System of equations and has the form
The solution is and then . □
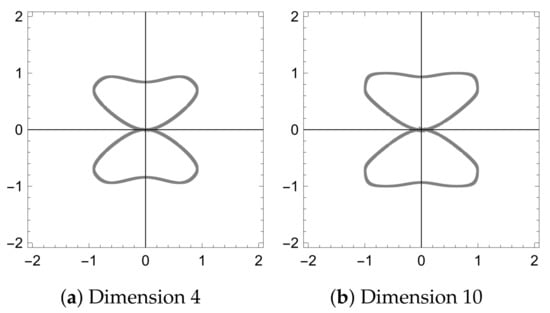
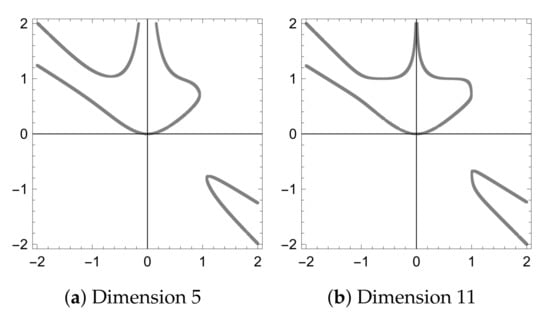
If we generalize considerations from the proof, we will achieve the curve , where d is dimension. The graph of the curve C depends on the parity of d, see Figure 5 and Figure 6. Considering only the values , the shape of the curve C is similar, regardless of parity, see Figure 2.
For the asked maximum is achieved on the curve C. For dimensions 7, 9 and 10 the resultsare:
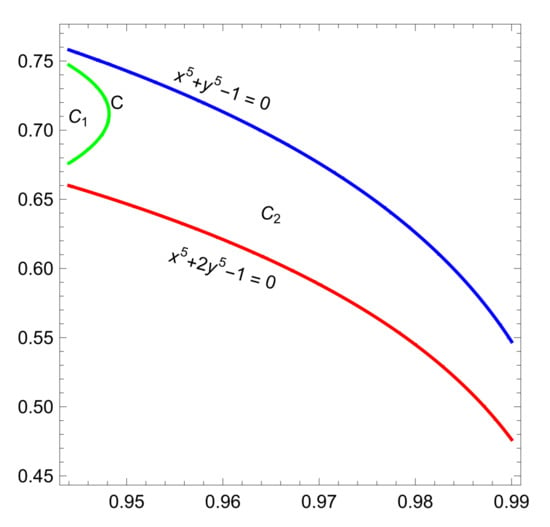
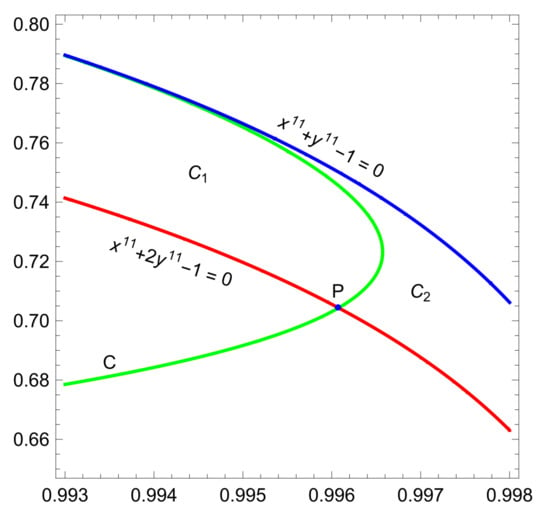
Let P is intersection the constraint curve and the curve C. If , then the constrained extreme on the curve C does not meet the required assumption . Therefore, the asked maximum must be on the constraint curve to the left of point P or on the curve C above P, see Figure 7. The same situation occurs for and .
and , .
and , ,
and , .
3. Conclusions
The issue of packing squares is an old problem and even though there are multiple partial results, it remains unresolved. We investigated a modified problem: packing three cubes in 5-dimensional space. We also calculated results for dimensions .
Considering the previous results by [17,18,19], we can say that solution is located on the curve C for dimensions . It means, that there are two (different) packings that give (the same) the largest volume.
There seems to be only a single maximal packing for dimensions greater than 10. In this packing, two smallest cubes are the same. However, the paper confirms it only for dimensions 11, 12, 13.
There is a space for several improvements in our work: Is it possible to find a without long numerical calculations? Is it true that two different maximum packings exist only for dimensions less than 11?
Author Contributions
Conceptualization, Z.S. and P.A.; methodology, Z.S. and P.A; software, P.A.; validation, P.A. and Z.S.; formal analysis, Z.S. and P.A; writing—original draft preparation, Z.S.; writing—review and editing, P.A.; visualization, Z.S.; supervision, Z.S.; project administration, Z.S.; funding acquisition, Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Slovak Grant Agency KEGA through the project No. 027ŽU-4/2020.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moser, L. Poorly Formulated Unsolved Problems of Combinatorial Geometry, Mimeographed List. 1966. Available online: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwjNi_6E2MvyAhVQ82EKHXwkDswQFnoECAgQAQ&url=https%3A%2F%2Farxiv.org%2Fpdf%2F2104.09324&usg=AOvVaw04NiNvduVgpLb0NhXT63Zw (accessed on 8 July 2021).
- Brass, P.; Moser, W.O.J.; Pach, J. Research Problems in Discrete Geometry; Springer: New York, NY, USA, 2005. [Google Scholar]
- Croft, H.T.; Falconer, K.J.; Guy, R.K. Unsolved Problems in Geometry; Springer: New York, NY, USA, 1991. [Google Scholar]
- Moon, J.W.; Moser, L. Some packing and covering theorems. Colloq. Math. 1967, 17, 103–110. [Google Scholar] [CrossRef]
- Moser, W. Problems, problems, problems. Discret. Appl. Math. 1991, 31, 201–225. [Google Scholar] [CrossRef][Green Version]
- Moser, W.; Pach, J. Research Problems in Discrete Geometry; McGill University: Montreal, QC, Canada, 1994. [Google Scholar]
- Kleitman, D.J.; Krieger, M.M. An optimal bound for two dimensional bin packing. In Proceedings of the 16th Annual Symposium on Foundations of Computer Science, Berkeley, CA, USA, 13–15 October 1975; pp. 163–168. [Google Scholar]
- Novotný, P. A note on a packing of squares. Stud. Univ. Transp. Commun. Žilina Math.-Phys. Ser. 1995, 10, 35–39. [Google Scholar]
- Novotný, P. On packing of four and five squares into a rectangle. Note Mat. 1999, 19, 199–206. [Google Scholar]
- Novotný, P. Využitie počítača pri riešení ukladacieho problému. In Proceedings of the Symposium on Computational Geometry, Kočovce, Slovak Republic, 9–11 October 2002; pp. 60–62. (In Slovak). [Google Scholar]
- Novotný, P. On packing of squares into a rectangle. Arch. Math. 1996, 32, 75–83. [Google Scholar]
- Hougardy, S. On packing squares into a rectangle. Comput. Geom. 2011, 44, 456–463. [Google Scholar] [CrossRef]
- Meir, A.; Moser, L. On packing of squares and cubes. J. Comb. Theory 1968, 5, 126–134. [Google Scholar] [CrossRef][Green Version]
- Novotný, P. Ukladanie kociek do kvádra. In Proceedings of the Symposium on Computational Geometry, Kočovce, Slovak Republic, 19–21 October 2011; pp. 100–103. (In Slovak). [Google Scholar]
- Novotný, P. Pakovanie troch kociek. In Proceedings of the Symposium on Computational Geometry, Kočovce, Slovak Republic, 27–29 September 2006; pp. 117–119. (In Slovak). [Google Scholar]
- Novotný, P. Najhoršie pakovateľné štyri kocky. In Proceedings of the Symposium on Computational Geometry, Kočovce, Slovak Republic, 24–26 October 2007; pp. 78–81. (In Slovak). [Google Scholar]
- Bálint, V.; Adamko, P. Minimalizácia objemu kvádra pre uloženie troch kociek v dimenzii 4. Slov. Pre Geom. Graf. 2015, 12, 5–16. (In Slovak) [Google Scholar]
- Bálint, V.; Adamko, P. Minimization of the parallelepiped for packing of three cubes in dimension 6. In Proceedings of the Aplimat: 15th Conference on Applied Mathematics, Bratislava, Slovak Republic, 2–4 February 2016; pp. 44–55. [Google Scholar]
- Sedliačková, Z. Packing Three Cubes in 8-Dimensional Space. J. Geom. Graph. 2018, 22, 217–223. [Google Scholar]
- Adamko, P.; Bálint, V. Universal asymptotical results on packing of cubes. Stud. Univ. Žilina Math. Ser. 2016, 28, 1–4. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).