A Note on the Paired-Domination Subdivision Number of Trees

Abstract

For a graph G with no isolated vertex, let ${\gamma }_{pr}\left(G\right)$ and ${\mathrm{sd}}_{{\gamma }_{pr}}\left(G\right)$ denote the paired-domination and paired-domination subdivision numbers, respectively. In this note, we show that if T is a tree of order $n\ge 4$ different from a healthy spider (subdivided star), then ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le min\{\frac{{\gamma }_{pr}\left(T\right)}{2}+1,\frac{n}{2}\},$ improving the $(n-1)$-upper bound that was recently proven.

1. Introduction

Throughout the paper, $G=(V,E)$ is a simple connected graph with vertex set $V=V\left(G\right)$ of order $n=\left|V\right|$ and edge set $E\left(G\right)=E$. For every vertex $v\in V\left(G\right)$, the open neighborhood of v is the set $N_G\left(v\right)=\{u\in V\left(G\right)|uv\in E(G\left)\right\}$ and the closed neighborhood of v is the set $N_G\left[v\right]=N_G\left(v\right)\cup \left\{v\right\}$. The degree of a vertex v is ${deg}_G\left(v\right)=\left|N_G\left(v\right)\right|$. When no confusion arises, we will delete the subscript G in $N_G$ and ${deg}_G.$ A vertex of degree one is called a leaf and its neighbor is called a stem. A stem is said to be strong if it is adjacent to at least two leaves. A healthy spider $S{}_q$ for $q\ge 2$ is obtained from a star $K_{1,q}$ by subdividing each edge by exactly one vertex. The center vertex of a healthy spider will be called a head. Let $P_n$ and $C_n$ be the path and cycle of order n. The diameter of G, denoted by $diam\left(G\right)$, is the maximum value among minimum distances between all pairs of distinct vertices of G. A matching in a graph G is a set of pairwise non-intersecting edges, while a perfect matching in G is a matching that covers each vertex.

A dominating set of G is a subset S of V such that every vertex in $V-S$ has at least one neighbor in $S.$ A subset S of V is a paired-dominating set of $G,$ abbreviated PD-set, if S is a dominating set and the subgraph induced by the vertices of S contains a perfect matching. The paired-domination number ${\gamma }_{pr}\left(G\right)$ is the minimum cardinality of a PD-set of G. If S is a PD-set with a perfect matching M, then two vertices u and v are said to be partners (or paired) in S if the edge $uv\in M$. We call a PD-set of minimum cardinality a ${\gamma }_{pr}\left(G\right)$-set. Note that every graph G without isolated vertices has a PD-set since the endvertices of any maximal matching in G form such a set. Paired-domination was introduced by Haynes and Slater [1] and is studied, for example, in [2,3,4,5,6,7]. For more details on paired-domination, we refer the reader to the recent book chapter [8].

As an application, in the design of networks for example, it is essential to study the effect that some modifications on the graph that have on the graph parameters. These modifications can be deletion or addition of vertices, deletion or addition of edges. We refer the reader to chapter 7 of [9] when the graph parameter is the domination number. Fink et al. [10], were the first to study the bondage number of G defined to be the minimum number of edges whose removal increases the domination number of G, while Kok and Mynhardt [11] were the first to study the reinforcement number of G defined to be the minimum number of edges which must be added to G in order to decrease the domination number of G. In [12], Velammal studied another kind of modification where the goal is find the minimum number of edges to be subdivided (each edge in G is subdivided at most once) in order to increase the domination number. For more details, see [13,14,15,16,17].

Our main purpose in this paper is to study of the paired-domination subdivision number of trees. This parameter was introduced by Favaron et al. in [18] and defined as follows. The paired-domination subdivision number ${\mathrm{sd}}_{{\gamma }_{pr}}\left(G\right)$ of a graph G is the minimum number of edges that must be subdivided (where each edge in G can be subdivided at most once) in order to increase the paired-domination number of G. Observe that since the paired-domination subdivision number of the complete graph $K_2$ remains unchanged when its only edge is subdivided, we will assume that the graph G has order at least 3. It is worth noting that it has recently been shown by Amjadi and Chellali [19] that the problem of computing the paired-domination subdivision number is NP-hard for bipartite graphs. The paired-domination subdivision number has been further studied by several authors (see [20,21,22]).

In [18], Favaron et al. have given some conditions for a graph (including trees) to have a small paired-domination subdivision number that we summarize by the following results.

Proposition 1

([18]). For every graph G of order $n\ge 3$, if ${\gamma }_{pr}\left(G\right)=2$, then $1\le {\mathrm{sd}}_{{\gamma }_{pr}}\left(G\right)\le 3$.

Proposition 2

([18]). If G contains either a strong stem or adjacent stems, then ${\mathrm{sd}}_{{\gamma }_{pr}}\left(G\right)\le 2$.

Proposition 3

([18]). If a connected graph G contains a path $v_1{v}_2{v}_3{v}_4{v}_5$ in which $deg\left(v_i\right)=2$ for $i=2,3,4$, then ${\mathrm{sd}}_{{\gamma }_{pr}}\left(G\right)\le 4$.

It should also be noted that Favaron et al. [18] conjectured that ${\mathrm{sd}}_{{\gamma }_{pr}}\left(G\right)\le n-1$ for all connected graphs of order $n.$ In connection with this conjecture, Egawa et al. [20] proved that for every connected graph G of order $n\ge 4,$ ${\mathrm{sd}}_{{\gamma }_{pr}}\left(G\right)\le 2n-5.$ Moreover, if further G has an edge $uv$ such that u and v are not partners in any ${\gamma }_{pr}\left(G\right)$-set, then ${\mathrm{sd}}_{{\gamma }_{pr}}\left(G\right)\le n-1.$ The conjecture has recently been settled in the affirmative in [22]. Restricted to the class of trees, we observe that for healthy spiders $S_q$ with $q\ge 2$ or paths $P_3,$${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)=n-1.$

In this note, we improve the $(n-1)$-upper bound on the paired-domination subdivision number for all trees T of order $n\ge 4$ different from a healthy spider by providing an upper bound on it in terms of the paired-domination number. More precisely, we will mainly show the following.

Theorem 1.

Let T be a tree of order $n\ge 4$ different from a healthy spider. Then ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le \frac{{\gamma }_{pr}\left(T\right)}{2}+1$.

In addition, we will also show that if T is a tree of order $n\ge 4$ different from a healthy spider, then its paired-domination subdivision number is at most $\frac{n}{2}.$ Before giving the proof of our results, it is necessary to recall the following two useful results.

Proposition 4

([18]). Let G be a connected graph of order $n\ge 3$ and $e=uv\in E\left(G\right)$. If $G^{\prime }$ is obtained from G by subdividing the edge e, then ${\gamma }_{pr}\left(G^{\prime }\right)\ge {\gamma }_{pr}\left(G\right)$.

Proposition 5

([18]). For $n\ge 3$,

$${\mathrm{sd}}_{{\gamma }_{pr}}\left(P_n\right)={\mathrm{sd}}_{{\gamma }_{pr}}\left(C_n\right)=\left\{\begin{array}{ccc}1& \mathrm{if}& n\equiv 0(mod4)\\ 4& \mathrm{if}& n\equiv 1(mod4)\\ 3& \mathrm{if}& n\equiv 2(mod4)\\ 2& \mathrm{if}& n\equiv 3(mod4).\end{array}\right.$$

We close this section by mentioning that the paired-domination number of a path $P_n$ of order $n\ge 2$ is $2⌈\frac{n}{4}⌉$ (see [8]).

2. Proof of Theorem 1

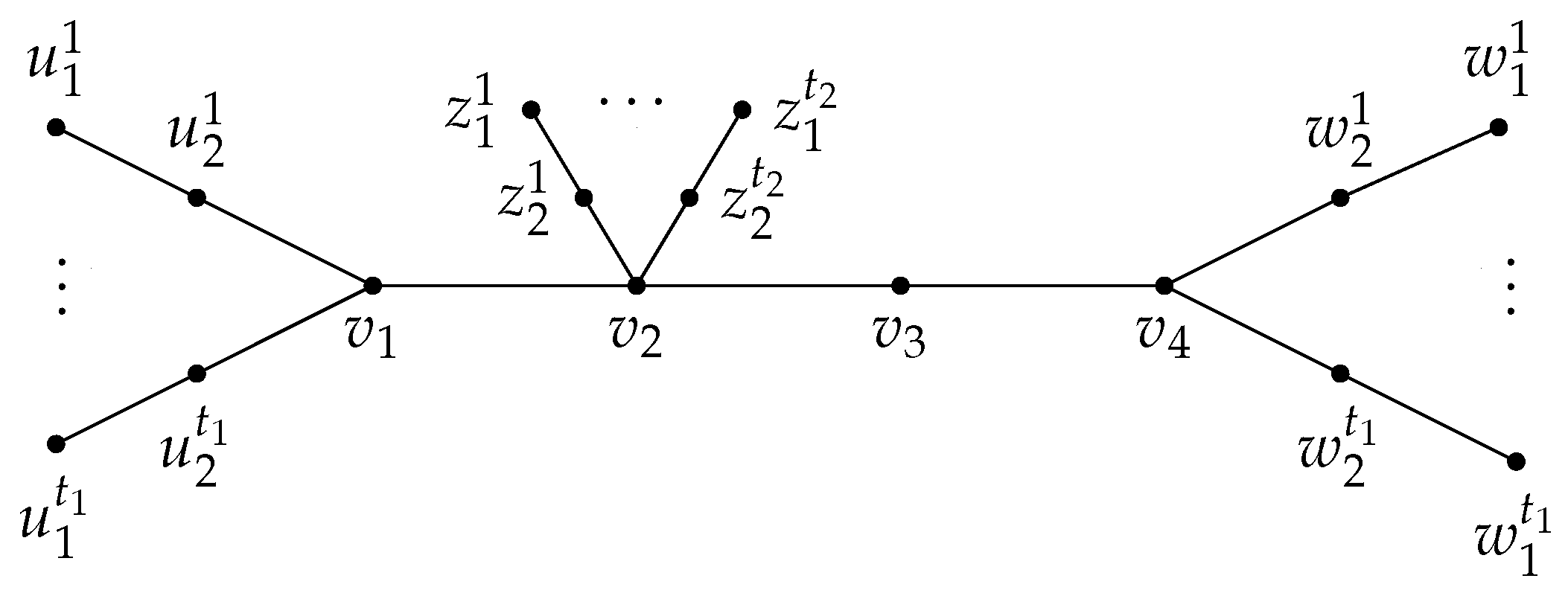
For non-negative integers $t_1,t_2$ where $t_1\ge 1$, let $F_{t_1,t_2}$ be the tree obtained from a path $v_1{v}_2{v}_3{v}_4$ by adding $t_1$ pendant paths $v_1{u}_2^i{u}_1^i$, $t_1$ pendant paths $v_4{w}_2^i{w}_1^i$, and $t_2$ pendant paths $v_2{z}_2^i{z}_1^i$ (see Figure 1). Let $\mathcal{F}$ be the family of all trees $F_{t_1,t_2}$. The set $P=\{v_1,u_2^1,v_4,w_2^1\}\cup \{u_1^i,u_2^i,w_1^i,w_2^i\mid 2\le i\le t_1\}\cup \{z_1^i,z_2^i\mid 1\le i\le t_2\}$ is a PD-set of $F_{t_1,t_2}$ and so ${\gamma }_{pr}\left(F_{t_1,t_2}\right)\le 4t_1+2t_2.$ One the other hand, if D is a ${\gamma }_{pr}\left(F_{t_1,t_2}\right)$-set, then to paired-dominate the leaves of $F_{t_1,t_2}$, we must have $|D\cap \{v_1,u_1^i,u_2^i\mid 1\le i\le t_1\}|\ge 2t_1$, $|D\cap \{v_4,w_1^i,w_2^i\mid 1\le i\le t_1\}|\ge 2t_1$ and $|D\cap \{v_2,z_1^i,z_2^i\mid 1\le i\le t_2\}|\ge 2t_2$ implying that ${\gamma }_{pr}\left(F_{t_1,t_2}\right)\ge 4t_1+2t_2.$ Thus ${\gamma }_{pr}\left(F_{t_1,t_2}\right)=4t_1+2t_2.$

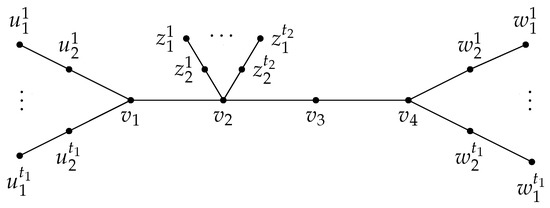
Figure 1. The graph $F_{t_1,t_2}$.

Lemma 1.

If $T\in \mathcal{F}$, then ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le \frac{n\left(T\right)-2}{2}=1+\frac{{\gamma }_{pr}\left(T\right)}{2}$.

Proof. 

Let $T=F_{t_1,t_2}$, and let $T^{\prime }$ be the tree obtained from T by subdividing the edge $v_2{v}_1$ with new vertex x, the edges $v_1{u}_2^i,u_2^i{u}_1^i$ with new vertices $x_i,y_i$ respectively, for each i, and the edge $v_2{z}_2^j$ with new vertex $a_j$ for each j, if $t_2\ge 1$. Clearly the number of subdivided edges is $2t_1+t_2+1=\frac{n\left(T\right)-2}{2}$. Let $D^{\prime }$ be a ${\gamma }_{pr}\left(T^{\prime }\right)$-set. To paired-dominate each leaf $u_1^j$, we must have $|D^{\prime }\cap \{u_1^j,u_2^j,y_j\}|\ge 2$ for each $1\le j\le t_1$; to paired-dominate each leaf $z_1^j$ we must have $|D^{\prime }\cap \{z_1^j,z_2^j,a_j\}|\ge 2$ for each $1\le j\le t_2$; and to paired-dominate the leaves $w_1^1,\dots ,w_1^{t_1}$ we may assume that $v_4,w_2^1,w_2^2,\dots ,w_2^{t_1},w_1^2,\dots ,w_1^{t_1}\in D^{\prime }$. Moreover, to paired-dominate the vertex $v_1$, we must have $|D^{\prime }\cap \{x_1,\dots ,x_{t_1},v_1,v_2,x\}|\ge 2$. Therefore ${\gamma }_{pr}\left(T^{\prime }\right)=\left|D^{\prime }\right|\ge 4t_1+2t_2+2>{\gamma }_{pr}\left(T\right)$. Hence ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le \frac{n\left(T\right)-2}{2}=1+\frac{{\gamma }_{pr}\left(T\right)}{2}$. □

Now we are ready to start the proof of Theorem 1.

Proof of Theorem 1.

If $\mathrm{diam}\left(T\right)\le 3$, then clearly ${\gamma }_{pr}\left(T\right)=2$ and by Proposition 2 we have ${\mathrm{sd}}_{{\gamma }_{pr}}\left(G\right)\le 2=\frac{{\gamma }_{pr}\left(T\right)}{2}+1$. Hence, let $\mathrm{diam}\left(T\right)\ge 4$. Note that ${\gamma }_{pr}\left(T\right)\ge 4.$ If T has a strong stem or adjacent stems, then the result follows from Proposition 2. Hence, we can assume that T has no strong stem or adjacent stems. If $\mathrm{diam}\left(T\right)=4$ and $v_1{v}_2{v}_3{v}_4{v}_5$ is a diametral path in T, then since T is not a subdivided star, we must have ${deg}_T\left(v_3\right)\ge 3$ and $v_3$ is a stem, which is a contradiction. Hence, we can assume that $\mathrm{diam}\left(T\right)\ge 5$. Let $v_1{v}_2{v}_3\dots v_k$ be a diametral path in T such that ${deg}_T\left(v_3\right)$ is as small as possible. We consider two cases.

Case 1.$\mathrm{diam}\left(T\right)\in \{5,6\}$. Root T at $v_4$, and consider the following subcases.

Subcase 1.1.$v_4$ is not a stem and ${deg}_T\left(v_3\right)=2$.

By the choice of the diametral path, we deduce that for each child w of $v_4$, the maximal subtree rooted at w is a either path $P_2,P_3$ or a healthy spider (if $\mathrm{diam}\left(T\right)=6$). Let H be the forest of $T-v_4$ where each of its components is a healthy spider. Since $de{g}_T\left(v3\right)=2$, note that H is empty if $\mathrm{diam}\left(T\right)=5.$ Now, let $v_4{u}_i^1{u}_i^2{u}_i^3$ be the (pendant) paths in T such that ${deg}_T\left(u_i^1\right)={deg}_T\left(u_i^2\right)=2$ and ${deg}_T\left(u_i^3\right)=1$ for each $i\in \{1,\cdots ,r\}$, and let $v_4{z}_i^1{z}_i^2$ be the paths in T (if any) such that ${deg}_T\left(z_i^1\right)=2$ and ${deg}_T\left(z_i^2\right)=1$ for each $i\in \{1,\cdots ,s\}$. Assume, without loss of generality, that $u_1^1=v_3$. Let $T^{\prime }$ be the tree obtained from T by subdividing the edges $v_4{v}_3,v_3{v}_2$ with new vertices $x,y$, respectively, the edge $v_4{u}_i^1$ with a new vertex ${u^{\prime }}_i^1$ for each $2\le i\le r$ and the edge $v_4{z}_j^1$ with a new vertex ${z^{\prime }}_j^1$ for each $j\in \{1,\cdots ,s\}$. Let D be a ${\gamma }_{pr}\left(T^{\prime }\right)$-set. To paired-dominate each leaf $u_i^3$ in $T^{\prime }$, we must have that $|D\cap \{u_i^1,u_i^2,u_i^3\left\}\right|\ge 2$ for each $i\in \{2,\cdots ,r\}$, to paired-dominate $u_1^3=v_1$ we must have $|D\cap \{u_1^2,u_1^3,y\left\}\right|\ge 2$, and to paired-dominate each leaf $z_j^2$ in $T^{\prime }$ we must have $|D\cap \{z_j^1,z_j^2,{z^{\prime }}_j^1\left\}\right|\ge 2$ for each $j.$ Also, to paired-dominate vertex x, we may assume that $v_4$ and x are partners in $D^{\prime }$. It follows that ${\gamma }_{pr}\left(T^{\prime }\right)\ge {\gamma }_{pr}\left(H\right)+2r+2s+2$. A similar argument shows that ${\gamma }_{pr}\left(T\right)\ge {\gamma }_{pr}\left(H\right)+2r+2s$. Moreover, the equality in the last inequality is attained since each PD-set of H can be extended to a PD-set of T by adding the set $\{z_j^1,z_j^2\mid 1\le j\le s\}\cup \{u_i^1,u_i^2\mid 1\le i\le r\}$. Thus ${\gamma }_{pr}\left(T\right)={\gamma }_{pr}\left(H\right)+2r+2s$, and therefore ${\gamma }_{pr}\left(T^{\prime }\right)>{\gamma }_{pr}\left(T\right)$. It follows that ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le r+s+1$, and hence ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le r+s+1\le \frac{{\gamma }_{pr}\left(T\right)}{2}+1$.

Subcase 1.2.$v_4$ is not a stem and ${deg}_T\left(v_3\right)\ge 3$.

By assumption, for each child w of $v_4$, the maximal subtree rooted at w is either a healthy spider or a path $P_2$. Let $w_1,\dots ,w_r$ be the children of $v_4$ such that $T_{w_i}$ is a healthy spider with head $w_i$, and let $w_i^1,\dots ,w_i^{{\ell }_i}$ be the children of $w_i$ and let $y_i^j$ be the leaf neighbor of $w_i^j$ for each $i,j$. Also, let $v_4{z}_i^1{z}_i^2$ be the paths in T (if any) such that ${deg}_T\left(z_i^1\right)=2$ and ${deg}_T\left(z_i^2\right)=1$ for each $i\in \{1,\cdots ,t\}.$ Without loss of generality, let $w_1=v_3$. Let $T^{\prime }$ be the tree obtained from T by subdividing the edge $v_4{v}_3$ with vertex x, the edges $w_i{w}_i^1,\dots ,w_i{w}_i^{{\ell }_i}$ with vertices ${w^{\prime }}_i^1,\dots ,{w^{\prime }}_i^{{\ell }_i}$, respectively, and the edge $v_4{z}_j^1$ with vertex ${z^{\prime }}_j^1$ for each j. Let D be a ${\gamma }_{pr}\left(T^{\prime }\right)$-set. To paired-dominate each leaf $y_i^j$ in $T^{\prime }$, we must have $|D\cap \{w_i^j,y_i^j,{w^{\prime }}_i^j\left\}\right|\ge 2$ for each $i,j$; to paired dominate each leaf $z_j^2$ we must have $|D\cap \{z_j^1,z_j^2,{z^{\prime }}_j^1\}\ge 2$ for each $j\in \{1,\cdots ,t\}$ and to paired dominate vertex x we may assume that $v_4$ and x are partners in $D.$ Hence ${\gamma }_{pr}\left(T^{\prime }\right)\ge {\sum }_{i=1}^{r}2{\ell }_i+2t+2$. A similar argument as above shows that ${\gamma }_{pr}\left(T\right)\ge {\sum }_{i=1}^{r}2{\ell }_i+2t.$ Moreover, the equality in the last inequality is attained since $\{v_3,v_2\}\cup \{z_j^1,z_j^2\mid 1\le j\le t\}\cup \left({\cup }_{i=2}^r\{w_i^j,y_i^j\mid 1\le j\le {\ell }_i\}\right)\cup \{w_1^j,y_1^j\mid 2\le j\le {\ell }_1\}$ is a PD-set of $T.$ Thus ${\gamma }_{pr}\left(T\right)={\sum }_{i=1}^{r}2{\ell }_i+2t$, and therefore ${\gamma }_{pr}\left(T^{\prime }\right)>{\gamma }_{pr}\left(T\right)$. It follows that ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le {\sum }_{i=1}^r{\ell }_i+t+1,$ and hence ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le \frac{{\gamma }_{pr}\left(T\right)}{2}+1$.

Subcase 1.3.$v_4$ is a stem.

Let w be a leaf neighbor of $v_4$. By assumption, w is the unique leaf adjacent to $v_4$ and $v_4$ is not adjacent to any stem. Hence, T has diameter 6. First let there be a path $v_4{u}_3{u}_2{u}_1$ in T such that ${deg}_T\left(u_2\right)={deg}_T\left(u_3\right)=2$ and ${deg}_T\left(u_1\right)=1$. Without loss of generality, we may assume that $u_3=v_3.$ Let $T^{\prime }$ be the tree obtained from T by subdividing the edges $v_{4}w,v_4{v}_3,v_3{v}_2,v_2{v}_1$ with new vertices $u,x,y,z,$ respectively, and let $D^{\prime }$ be a PD-set of $T^{\prime }$. It is easy to see that $|D^{\prime }\cap \{v_4,v_3,v_2,v_1,u,w,x,y,z\}|\ge 6$. If $v_4\notin D^{\prime }$ or $v_4\in D^{\prime }$ and its partner belongs to $\{u,x\}$, then $(D^{\prime }\setminus \{v_4,v_3,v_2,v_1,u,w,x,y,z\})\cup \{v_2,v_3,w,v_4\}$ is a PD-set of T smaller than $D^{\prime }$. If $v_4\in D^{\prime }$ and its partner does not belong to $\{u,x\}$, then $(D^{\prime }\setminus \{v_3,v_2,v_1,u,w,x,y,z\})\cup \{v_2,v_3\}$ is a PD-set of T smaller than $D^{\prime }$. Hence, ${\gamma }_{pr}\left(T^{\prime }\right)>{\gamma }_{pr}\left(T\right),$ and thus ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le 4$. Now let D be a ${\gamma }_{pr}\left(T\right)$-set. To paired-dominate $v_1$ and $v_7$, we must have $|D\cap \{v_1,v_2,v_3\left\}\right|\ge 2$ and $|D\cap \{v_6,v_5,v_7\left\}\right|\ge 2$, respectively. Moreover, to paired-dominate w, we have $|D\cap \{w,v_4\left\}\right|\ge 1$. Since ${\gamma }_{pr}\left(T\right)$ is even, we have ${\gamma }_{pr}\left(T\right)\ge 6$. Consequently, ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le 4\le \frac{{\gamma }_{pr}\left(T\right)}{2}+1$ as desired. Therefore, we can assume that T has no such a path $v_4{u}_3{u}_2{u}_1$ in T such that ${deg}_T\left(u_2\right)={deg}_T\left(u_3\right)=2$ and ${deg}_T\left(u_1\right)=1$. Thus for any child $v\ne w$ of $v_4$, the maximal subtree $T_v$ is a healthy spider. Since $\mathrm{diam}\left(T\right)=6$, we deduce that $v_4$ has at least two children whose maximal subtrees are healthy spiders. Let $v_3=w_1,\dots ,w_r$ be the children of $v_4$ such that $T_{w_i}$ is a healthy spider with head $w_i$. Suppose that $v_2=w_1^1,\dots ,w_1^{\ell }$ are the children of $w_1$ and $y_1^j$ is the leaf adjacent to $w_1^j$. Let $T^{\prime }$ be the tree obtained from T by subdividing the edges $v_{4}w,v_4{v}_3$ with new vertices $x,y$, respectively, the edges $w_1{w}_1^j,y_1^j{w}_1^j$ with new vertices $x_j$ and $y_j$, respectively for each $j\in \{1,\cdots ,\ell \}$. Clearly the number of subdivided edges is $2{deg}_T\left(w_1\right)$. Let $D^{\prime }$ be a ${\gamma }_{pr}\left(T^{\prime }\right)$-set. To paired-dominate $y_1^1,\dots ,y_1^{\ell }$, we may assume that $w_1^1,\dots ,w_1^{\ell },y_1,\cdots ,y_{\ell }\in D^{\prime }$. Also to paired-dominate the vertices $w,v_3$, we must have $|D^{\prime }\cap \{w,x,v_4,y,v_3,x_1,\dots ,x_{\ell }\}|\ge 4$. Now, if $v_4\notin D^{\prime }$ or $v_4\in D^{\prime }$ and its partner belongs to $\{x,y\}$, then $(D^{\prime }\setminus \{w,x,v_4,y,v_3,x_1,\dots ,x_{\ell },y_1,\cdots ,y_{\ell }\})\cup \{y_1^1,\cdots ,y_{\ell }^1,v_4,v_3\}$ is a PD-set of T smaller than $D^{\prime }$. If $v_4\in D^{\prime }$ and its partner does not belong to $\{x,y\}$, then $(D^{\prime }\setminus \{w,x,y,v_3,x_1,\dots ,x_{\ell },y_1,\cdots ,y_{\ell }\})\cup \{y_1^1,\cdots ,y_{\ell }^1\}$ is a PD-set of T smaller than $D^{\prime }$. In either case, we deduce that ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le 2{deg}_T\left(w_1\right).$ Now let D be a ${\gamma }_{pr}\left(T\right)$-set and let $T_{w_1},T_{w_2}$ be the components of $T-\{v_4{w}_1,v_4{w}_2\}$ containing $w_1$ and $w_2$, respectively. To paired-dominate the leaves of $T_{w_1}$ and $T_{w_2}$ we must have $|D\cap V\left(T_{w_1}\right)|\ge 2{deg}_T\left(w_1\right)-2$ and $|D\cap V\left(T_{w_2}\right)|\ge 2{deg}_T\left(w_2\right)-2\ge 2{deg}_T\left(w_1\right)-2$. Also to paired-dominate w we must have $|D\cap \{w,v_4\left\}\right|\ge 1$. Since $\left|D\right|$ is even, we deduce that $\left|D\right|\ge 4{deg}_T\left(w_1\right)-2$. This implies that ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le 2{deg}_T\left(w_1\right)\le \frac{{\gamma }_{pr}\left(T\right)}{2}+1$.

Case 2.$\mathrm{diam}\left(T\right)\ge 7$. We consider two subcases.

Subcase 2.1${deg}_T\left(v_3\right)=2$.

If T is a path, then the result follows from Proposition 5 and the exact value of the paired-domination number of a path given at the end of Section 1. Hence, we assume that T is not a path, and thus ${\gamma }_{pr}\left(T\right)>4$. If ${deg}_T\left(v_4\right)=2$, then $v_5{v}_4{v}_3{v}_2{v}_1$ is a path in T such that $deg\left(v_2\right)=deg\left(v_3\right)=deg\left(v_4\right)=2$ and the result follows from Proposition 3. Hence, assume that ${deg}_T\left(v_4\right)\ge 3$. If $v_4$ is a stem, then using an argument similar to that described in Subcase 1.3, we can see that ${\mathrm{sd}}_{{\gamma }_{pr}}\left(G\right)\le 4\le \frac{{\gamma }_{pr}\left(T\right)}{2}+1$. Thus, we assume that $v_4$ is not a stem. Hence, each component of $T-v_4$ is of order at least 2. Moreover, since $\mathrm{diam}\left(T\right)\ge 7$, one component of $T-v_4$ different from the one containing $v_3$, must have order at least four and diameter at least three. Root T at $v_4$ and let $w_1,\dots ,w_r$ be the children of $v_4$ with depth at least three, $u_1,\dots ,u_s$ be the children of $v_4$ with depth two, and $z_1,\cdots ,z_t$ be the children of $v_4$ with depth one, if any. We can assume, without loss of generality, that $v_3=u_1$ and $v_5=w_1.$ Let $T^{\prime }$ be the tree obtained from T by subdividing the edges $v_4{v}_3,v_3{v}_2,v_2{v}_1$ with new vertices $x,y,z,$ respectively, the edge $v_4{u}_i$ with new vertex $x_i$ for each $i\in \{2,\cdots ,s\}$, the edge $v_4{z}_i$ with new vertex $a_i$ for each $i\in \{1,\cdots ,t\}$ and each edge $v_4{w}_i$ with new vertex $y_i$ for all $i\in \{1,\cdots ,r\}$. We note that all edges incident to $v_4$ are subdivided and the number of subdivided edges is ${deg}_T\left(v_4\right)+2$. Let $D^{\prime }$ be a PD-set of $T^{\prime }$ and F the set of all edges in $\{v_4{u}_2,,\dots ,v_4{u}_s,v_4{w}_1,\dots ,v_4{w}_r\}$ whose subdivision vertices belong to $D^{\prime }$. Let $T_1$ be the tree obtained from T by subdividing only the edges in $F.$ Clearly, to paired-dominate vertices $v_1,v_2,v_3,x,y,z$ in $T^{\prime }$, we must have $|D^{\prime }\cap \{v_1,v_2,v_3,v_4,x,y,z\}|\ge 4$. Now, if $v_4\notin D^{\prime }$ or $v_4\in D^{\prime }$ and its partner is not x, then $(D^{\prime }-\{v_1,v_2,v_3,x,y,z\})\cup \{v_3,v_2\}$ is a PD-set of $T_1$ smaller than $D^{\prime }$ and thus ${\gamma }_{pr}\left(T^{\prime }\right)>{\gamma }_{pr}\left(T_1\right)\ge {\gamma }_{pr}\left(T\right)$. If $v_4\in D^{\prime }$ and its partner is x, then $(D^{\prime }-\{v_1,v_2,v_3,v_4,x,y,z\})\cup \{v_3,v_2\}$ is a PD-set of $T_1$ smaller than $D^{\prime }$ and thus ${\gamma }_{pr}\left(T^{\prime }\right)>{\gamma }_{pr}\left(T_1\right)\ge {\gamma }_{pr}\left(T\right)$. We deduce that ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le {deg}_T\left(v_4\right)+2.$ Now let D be a ${\gamma }_{pr}\left(T\right)$-set. To paired-dominate the leaves in each $T_{w_i},T_{u_j},T_{z_{\ell }}$ we must have $|D\cap V(T_{w_i}\left)\right|\ge 2$ and $|D\cap V(T_{u_j}\left)\right|\ge 2$ for each $i,j$, and $|D\cap (\left\{v_4\right\}\cup \left({\cup }_{m=1}^{t}V\left(T_{z_m}\right)\right)|\ge 2t$. Assume that $\mathrm{diam}\left(T\right)\ge 9$. Then to paired-dominate $v_{k-4}$, we must have $|D\cap N(v_{k-4}\left)\right|\ge 1$. Hence, $\left|D\right|\ge 2{deg}_T\left(v_4\right)+1$. But since $\left|D\right|$ is even, it follows that $\left|D\right|\ge 2{deg}_T\left(v_4\right)+2$. Therefore, ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le {deg}_T\left(v_4\right)+2\le \frac{{\gamma }_{pr}\left(T\right)}{2}+1$. Hence, we can assume in the sequel that $\mathrm{diam}\left(T\right)\in \{7,8\}.$ Now, consider the following situations.

(2.1.1) 

$v_4$ has a child $w_i$ with depth 2 and degree at least three.

Then we must have $|D\cap V(T_{w_i}\left)\right|\ge 4,$ implying that $\left|D\right|\ge 2{deg}_T\left(v_4\right)+2$, and the desired result is obtained as above.

(2.1.2) 

${deg}_T\left(v_5\right)\ge 3$.

Let w be a neighbor of $v_5$ such that $w\notin \{v_4,v_6\}$. To paired-dominate w, we must have $|D\cap N[w\left]\right|\ge 1$, and thus $\left|D\right|\ge 2{deg}_T\left(v_4\right)+1.$ Since $\left|D\right|$ is even, we have $\left|D\right|\ge 2{deg}_T\left(v_4\right)+2$, and the result follows as above.

(2.1.3) 

${deg}_T\left(v_{k-2}\right)\ge 3$. Then we have $|D\cap V(T_{v_{k-2}}\left)\right|\ge 4$ implying that $\left|D\right|\ge 2{deg}_T\left(v_4\right)+2$, and the result follows as above.

(2.1.4) 

$\mathrm{diam}\left(T\right)=8$.

If ${deg}_T\left(v_6\right)\ge 3$ and w is a neighbor of $v_6$ such that $w\notin \{v_5,v_7\}$, then the result follows as in item 2. Hence, assume that ${deg}_T\left(v_6\right)=2$. By above item we can assume that ${deg}_T\left(v_5\right)=2$. Since T is not a path, we must have ${deg}_T\left(v_4\right)\ge 3$. By item (2.1.3), we may assume that ${deg}_T\left(v_3\right)={deg}_T\left(v_7\right)=2$. In this case, one can see that ${\gamma }_{pr}\left(T\right)\ge 6$ and ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le 4$ (Proposition 3), and thus the desired result is obtained.

(2.1.5) 

$\mathrm{diam}\left(T\right)=7$.

By items 2 and 3, we may assume that ${deg}_T\left(v_5\right)={deg}_T\left(v_6\right)=2$ and the result follows as item (2.1.4).

Subcase 2.2.$deg\left(v_3\right)\ge 3$.

By the choice of diametral path in which $deg\left(v_3\right)$ is as small as possible, there is no path $v_4{u}_1{u}_2{u}_3$ in T such that $deg\left(u_1\right)=deg\left(u_2\right)=2$ and $deg\left(u_3\right)=1$. Thus the component of $T-v_3{v}_4$ containing $v_3$ is a healthy spider with head $v_3$. Similarly we may assume that the component of $T-v_{k-2}{v}_{k-3}$ containing $v_{k-2}$ is a healthy spider with head $v_{k-2}$. By the choice of the diametral path, $deg\left(v_3\right)$ is as small as possible and we have ${deg}_T\left(v_3\right)\le {deg}_T\left(v_{k-2}\right)$. Let $N_T\left(v_3\right)\setminus \left\{v_4\right\}=\{u_1=v_2,\dots ,u_s\}$ and let $u_i^{\prime }$ be the leaf neighbor of $u_i$ for each i. Suppose first that $v_4$ is a stem and let w be the leaf neighbor of $v_4$. Let $T^{\prime }$ be the tree obtained from T by subdividing the edges $v_{4}w,v_4{v}_3$ with new vertices $x,y$, respectively, and the edges $v_3{u}_i,u_i{u}_i^{\prime }$ with new vertices $x_i,y_i$, respectively, for each $i\in \{1,\cdots ,s\}$. Clearly the number of subdivided edges is $2{deg}_T\left(v_3\right)$. Let $D^{\prime }$ be a PD-set of $T^{\prime }$. Without loss of generality, we can assume that $u_1,\dots ,u_s,y_1,\dots ,y_s\in D^{\prime }$, where each $u_i$ is paired with $y_i$. Moreover, to paired-dominate the vertices $w,v_3$, we must have $|D^{\prime }\cap \{w,x,v_4,y,v_3,x_1,\dots ,x_s\}|\ge 4$. Let S be the set of all subdivision vertices. If $v_4\notin D^{\prime }$ or $v_4\in D^{\prime }$ and the partner of $v_4$ is in $\{x,y\}$, then $(D^{\prime }\setminus (S\cup \left\{w\right\}))\cup \{v_3,v_4,u_1^{\prime },\dots ,u_s^{\prime }\}$ is a PD-set of T smaller than $D^{\prime }$. If $v_4\in D^{\prime }$ and the partner of $v_4$ is not in $\{x,y\}$, then $(D^{\prime }\setminus (S\cup \{w,v_3\}))\cup \{u_1^{\prime },\dots ,u_s^{\prime }\}$ is a PD-set of T smaller than $D^{\prime }$. In either case, we obtain ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le 2{deg}_T\left(v_3\right).$ Now let D be a ${\gamma }_{pr}\left(T\right)$-set and let $T_{v_3}$ and $T_{v_{k-2}}$ be the components of $T-\{v_3{v}_4,v_{k-2}{v}_{k-3}\}$ containing $v_3$ and $v_{k-2}$, respectively. To paired-dominate the leaves of $T_{v_3}$ and $T_{v_{k-2}}$ we must have $|D\cap V\left(T_{v_3}\right)|\ge 2{deg}_T\left(v_3\right)-2$ and $|D\cap V\left(T_{v_{k-2}}\right)|\ge 2deg\left(v_{k-2}\right)-2$. Also to paired-dominate w we must have $|D\cap \{w,v_4\left\}\right|\ge 1$. Since $\left|D\right|$ is even, we have $\left|D\right|\ge 4{deg}_T\left(v_3\right)-2$. Therefore, ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le 2{deg}_T\left(v_3\right)\le \frac{{\gamma }_{pr}\left(T\right)}{2}+1,$ as desired.

Suppose now that $v_4$ is not a stem. Then each component of $T-v_4$ is of order at least two. If $T\in \mathcal{F}$, then the result follows from Lemma 1. Hence, we assume that $T\notin \mathcal{F}$. Since $\mathrm{diam}\left(T\right)\ge 7$ and ${deg}_T\left(v_3\right)\le {deg}_T\left(v_{k-2}\right)$, we deduce that $|V\left(T_{v_{k-3}}\right)|\ge |V\left(T_{v_3}\right)|+1$. On the other hand, since $T\notin \mathcal{F}$, either one of the components of $T-v_4$ that does not contain neither $v_3$ nor $v_5$ has order at least three or $|V\left(T_{v_{k-3}}\right)|\ge |V\left(T_{v_3}\right)|+2$. Let $N\left(v_4\right)=\{w_1=v_3,w_2\dots ,w_r\}$. Let $T^{\prime }$ be the tree obtained from T by subdividing the edges $v_4{w}_i$ with vertices $z_i$ for $1\le i\le r$, the edges $v_3{u}_i,u_i{u}_i^{\prime }$ with vertices $x_i,y_i$, respectively, for each $1\le i\le s$. Note that the number of subdivided edges is ${deg}_T\left(v_4\right)+2{deg}_T\left(v_3\right)-2$. Let $D^{\prime }$ be a PD-set of $T^{\prime }$ and let F be the set of all edges incident with $v_4$ whose subdivision vertices belong to $D^{\prime }$. Let $T_2$ be the tree obtained from T by subdividing only the edges in $F.$ Without loss of generality, assume that $u_1,\dots ,u_s,y_1,\dots ,y_s\in D$, where each $u_i$ is paired with $y_i$. Also, to paired-dominate vertex $v_3$, we must have $|D^{\prime }\cap \{v_4,z_1,v_3,x_1,\dots ,x_s\}|\ge 2$. Let $W=\{z_1,x_1,\dots ,x_s,y_1,\dots ,y_s\}$. If $v_4\notin D^{\prime }$ or $v_4\in D^{\prime }$ and its partner is $z_1$, then $(D^{\prime }\setminus (W\cup \{v_4,v_3\}))\cup \{v_3,u_2^{\prime },\dots ,u_s^{\prime }\}$ is a PD-set of $T_2$ smaller than $D^{\prime }$ and so ${\gamma }_p\left(T^{\prime }\right)>{\gamma }_p\left(T_2\right)\ge {\gamma }_p\left(T\right)$. If $v_4\in D^{\prime }$ and its partner is not $z_1$, then $(D^{\prime }\setminus (W\cup \left\{v_3\right\}))\cup \{u_1^{\prime },u_2^{\prime },\dots ,u_s^{\prime }\}$ is a PD-set of $T_2$ smaller than $D^{\prime }$ and again ${\gamma }_p\left(T^{\prime }\right)>{\gamma }_p\left(T_2\right)\ge {\gamma }_p\left(T\right)$. Consequently, ${\mathrm{sd}}_{{\gamma }_{pr}}\left(G\right)\le {deg}_T\left(v_4\right)+2{deg}_T\left(v_3\right)-2$. Now let D be a ${\gamma }_{pr}\left(T\right)$-set. As seen above, we can see that for each child $w_i$ of $v_4$ with depth two we have $|D\cap V\left(T_{w_i}\right)|\ge 2{deg}_T\left(w_i\right)-2.$ In particular, $|D\cap V\left(T_{v_3}\right)|\ge 2{deg}_T\left(v_3\right)-2.$ Similarly, $|D\cap V\left(T_{v_{k-2}}\right)|\ge 2{deg}_T\left(v_{k-2}\right)-2\ge 2{deg}_T\left(v_3\right)-2$. Moreover, if $q_1,...,q_t$ are the children of $v_4$ with depth one (if any), then to paired-dominate the leaf neighbors of $q_1,...,q_t,$ we must have $|D\cap (\left\{v_4\right\}\cup \left({\cup }_{i=1}^{t}V\left(T_{q_i}\right)\right)|\ge 2t$.

Assume that $\mathrm{diam}\left(T\right)\ge 9$. Then to paired-dominate $v_{k-4}$, we must have $|D\cap N(v_{k-4}\left)\right|\ge 1$. Hence $\left|D\right|\ge 4{deg}_T\left(v_3\right)-4+2({deg}_T\left(v_4\right)-2)+1=4{deg}_T\left(v_3\right)+2{deg}_T\left(v_4\right)$$-7$. But since $\left|D\right|$ is even, it follows that $\left|D\right|\ge 4{deg}_T\left(v_3\right)+2{deg}_T\left(v_4\right)-6$. Therefore, ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le {deg}_T\left(v_4\right)+2{deg}_T\left(v_3\right)-2\le \frac{{\gamma }_{pr}\left(T\right)}{2}+1$. Hence, we can assume in the sequel that $\mathrm{diam}\left(T\right)\in \{7,8\}.$ Now, consider the following situations.

(2.2.1) 

$v_4$ has a child $w_i\ne v_3$ with depth 2 and degree at least three.

Then we must have $|D\cap V(T_{w_i}\left)\right|\ge 4,$ implying that $\left|D\right|\ge 4{deg}_T\left(v_3\right)+2{deg}_T\left(v_4\right)-6$, and the desired result is obtained as above.

(2.2.2) 

${deg}_T\left(v_5\right)\ge 3$.

Let w be a neighbor of $v_5$ such that $w\notin \{v_4,v_6\}$. To paired-dominate w, we must have $|D\cap N[w\left]\right|\ge 1$, and thus $\left|D\right|\ge 4{deg}_T\left(v_3\right)+2{deg}_T\left(v_4\right)-7.$ Since $\left|D\right|$ is even, we have $\left|D\right|\ge 4{deg}_T\left(v_3\right)+2{deg}_T\left(v_4\right)-6$, and the result follows as above.

(2.2.3) 

${deg}_T\left(v_3\right)<{deg}_T\left(v_{k-2}\right)$. Then we have $|D\cap V\left(T_{v_{k-2}}\right)|\ge 2{deg}_T\left(v_{k-2}\right)-2\ge 2deg\left(v_3\right)$ implying that $\left|D\right|\ge 4{deg}_T\left(v_3\right)+2{deg}_T\left(v_4\right)-6$, and the result follows as above.

(2.2.4) 

$\mathrm{diam}\left(T\right)=8$.

If ${deg}_T\left(v_6\right)\ge 3$ and w is a neighbor of $v_6$ such that $w\notin \{v_5,v_7\}$, then the result follows as in item 2. Hence, assume that ${deg}_T\left(v_6\right)=2$. By above item we can assume that ${deg}_T\left(v_5\right)=2$. If ${deg}_T\left(v_4\right)=2$, then the result follows from Proposition 3. Thus, let ${deg}_T\left(v_4\right)\ge 3$. Note that since $v_4$ is not a stem and according to the first item and the choice of diametral path, every subtree rooted at a child of $v_4$ different from $v_3$ and $v_5$ is a path $P_2$. Moreover, by the third item we may assume that ${deg}_T\left(v_3\right)={deg}_T\left(v_7\right)$. In this case, one can see that ${\gamma }_{pr}\left(T\right)\ge 10$ and ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le 4$ (for instance we can subdivide edges $v_4{v}_5,v_5{v}_6,$ $v_6{v}_7$ and one edge incident with $v_4$ different from $v_3{v}_4$ and $v_4{v}_5$). Therefore, the desired result is obtained.

(2.2.5) 

$\mathrm{diam}\left(T\right)=7$.

Since $T\notin \mathcal{F}$, we must have ${deg}_T\left(v_3\right)<{deg}_T\left(v_6\right)$ or ${deg}_T\left(v_5\right)\ge 3$. In either case, the result follows by above items.

This completes the proof. □

The following upper bound on the paired domination number of a tree has been presented by Chellali and Haynes in [2].

Theorem 2

([2]). If T is a tree of order $n\ge 3$ with s stems, then ${\gamma }_{pr}\left(T\right)\le \frac{n+2s-1}{2}.$

According to Theorems 1 and 2, we obtain the following upper bound on the paired-domination subdivision number of a tree.

Corollary 1.

If T is a tree of order $n\ge 4$ with s stems different from a healthy spider, then ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le \frac{n+2s+3}{4}$.

Applying Theorem 1 and Corollary 1, we get the following result.

Corollary 2

([20]). If T is a tree of order $n\ge 4$ different from a healthy spider, then ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T\right)\le \frac{n}{2}.$

Proof. 

We first observe that if T has a strong stem, then by Proposition 2, $\mathrm{sd}$${}_{{\gamma }_{pr}}\left(T\right)\le 2\le n/2.$ Hence we assume that T has no strong stem. Let s be the number of stems in T and let t be the number of vertices that are neither leaves nor stems. Note that $t\ne 1$ since T is different from a healthy spider. Now, if $t=0,$ then $s=n/2$ and thus T has adjacent stems. By Proposition 2, $\mathrm{sd}$${}_{{\gamma }_{pr}}\left(T\right)\le 2\le n/2.$ Hence we can assume that $t\ge 2.$ Clearly, $s=\frac{n-t}{2}.$ If $t\ge 3,$ then $s\le \frac{n-3}{2},$ and by Corollary 1, we obtain $\mathrm{sd}$${}_{{\gamma }_{pr}}\left(T\right)\le n/2.$ Therefore, let $t=2$. Thus $n\ge 6$ and is even. Let x and y be the two vertices of T that are neither leaves nor stems. Then $V\left(T\right)-\{x,y\}$ in which each stem is paired with its unique leaf neighbor, is a PD-set of D and so ${\gamma }_{pr}\left(T\right)\le n-2$. It follows from Theorem 1 that $\mathrm{sd}$${}_{{\gamma }_{pr}}\left(T\right)\le \frac{{\gamma }_{pr}\left(T\right)}{2}+1\le n/2$ and the proof is complete. □

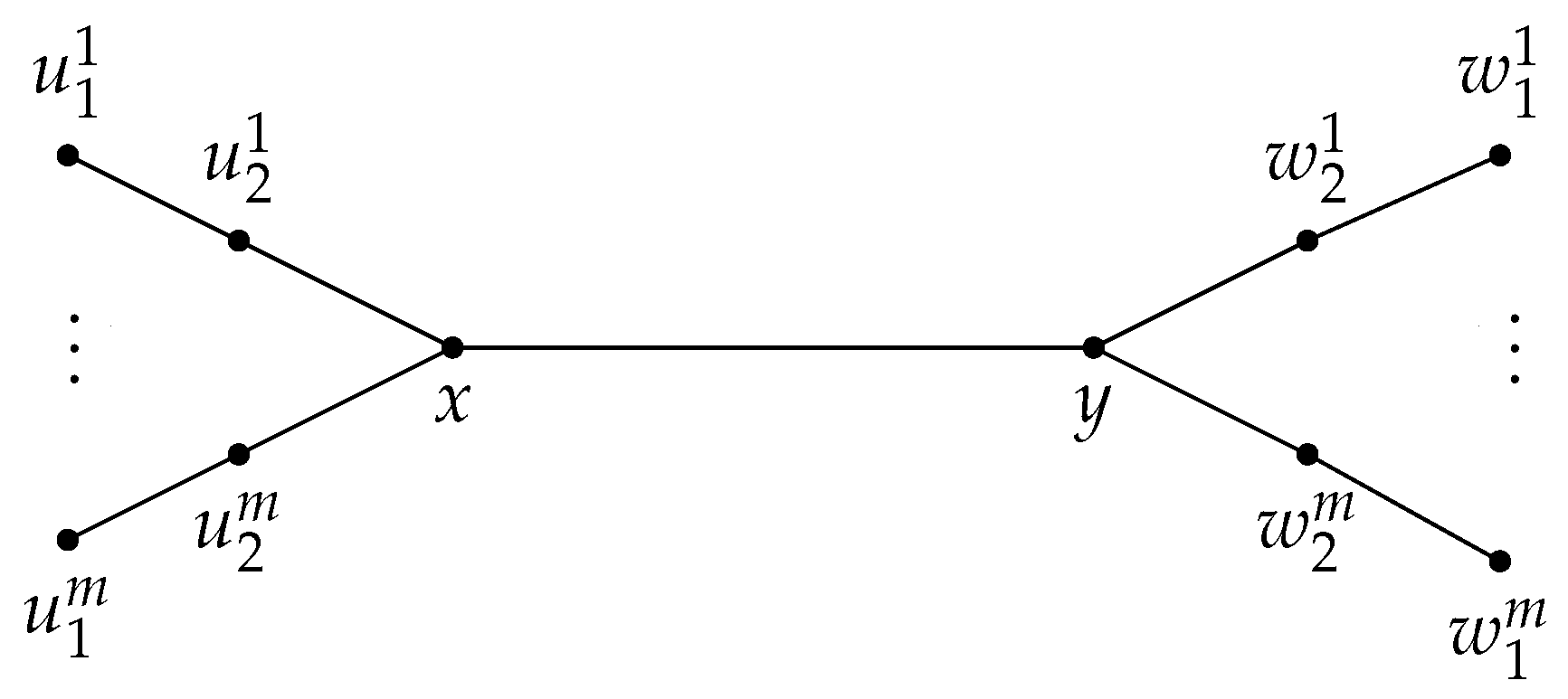
Let $H_1=S_m$ and $H_2=S_m$ be two healthy spiders with $m\ge 2$ feet each and centers x and y, respectively. Let $T_m$ be the tree obtained from $H_1$ and $H_2$ by adding the edge $xy$ (see Figure 2). It is not hard to see that $n\left(T_m\right)=4m+2$, ${\gamma }_{pr}\left(T_m\right)=4m$ and ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T_m\right)=2m+1$. Therefore the bounds of Theorem 1 and Proposition 2 are sharp.

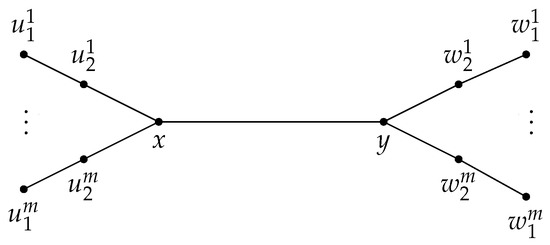
Figure 2. A tree $T_m$ with ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T_m\right)=\frac{{\gamma }_{pr}\left(T_m\right)}{2}+1=n\left(T_m\right)/2$.

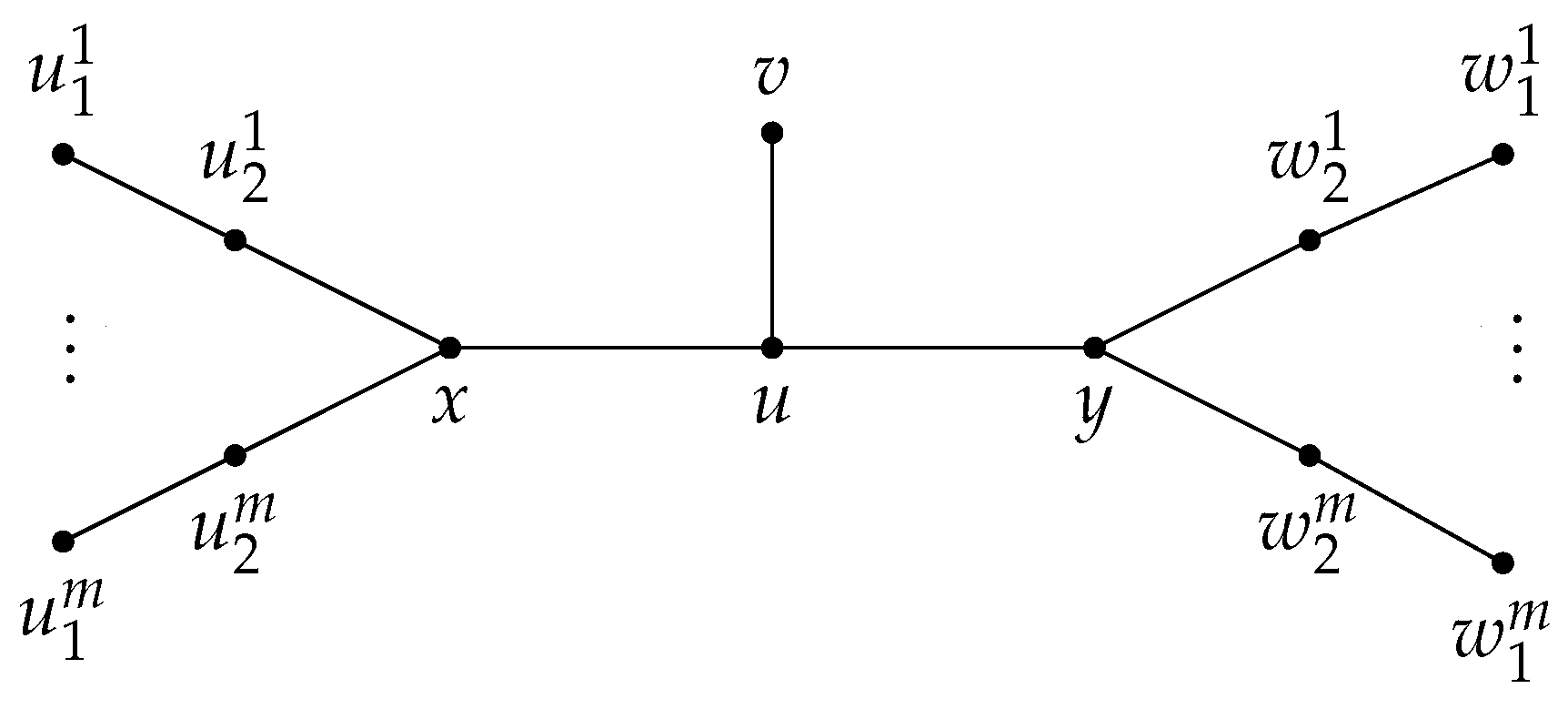
Let $T_m^{\prime }$ be the tree obtained from $T_m$ by subdividing the edge $xy$ with a subdivision vertex u and adding a new vertex v and a new edge $uv$ (see Figure 3). It is not hard to see that $n\left(T_m^{\prime }\right)=4m+4$, ${\gamma }_{pr}\left(T_m^{\prime }\right)=4m+2$ and ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T_m^{\prime }\right)=2m+2$. Therefore the bounds of Theorem 1 and Proposition 2 are sharp for any tree in the family $\mathcal{T}=\{T_m,T_m^{\prime }\mid m\ge 2\}$.

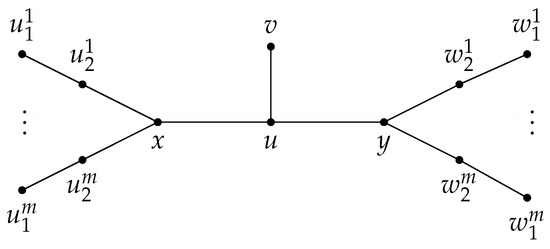
Figure 3. A tree $T_m^{\prime }$ with ${\mathrm{sd}}_{{\gamma }_{pr}}\left(T_m^{\prime }\right)=\frac{{\gamma }_{pr}\left(T_m^{\prime }\right)}{2}+1=n\left(T_m^{\prime }\right)/2$.

We conclude this paper with two conjectures.

Conjecture 1.

For any connected graph G of order $n\ge 4$ different from a healthy spider, ${\mathrm{sd}}_{{\gamma }_{pr}}\left(G\right)\le \frac{{\gamma }_{pr}\left(G\right)}{2}+2$.

Conjecture 2.

For any connected graph G of order $n\ge 7$ different from a healthy spider, ${\mathrm{sd}}_{{\gamma }_{pr}}\left(G\right)\le \frac{n}{2}$.

If G is the graph obtained from $C_5$ by adding a pendant edge at one vertex, then we have ${\mathrm{sd}}_{{\gamma }_{pr}}\left(C_5\right)={\mathrm{sd}}_{{\gamma }_{pr}}\left(G\right)=4$. Therefore, the condition $n\ge 7$ is necessary to establish the second conjecture.