Combination Synchronization of Fractional Systems Involving the Caputo–Hadamard Derivative
Abstract
:1. Introduction
2. Preliminaries
- (i)
- .
- (ii)
- .
3. Combination Synchronization of Fractional-Order Systems
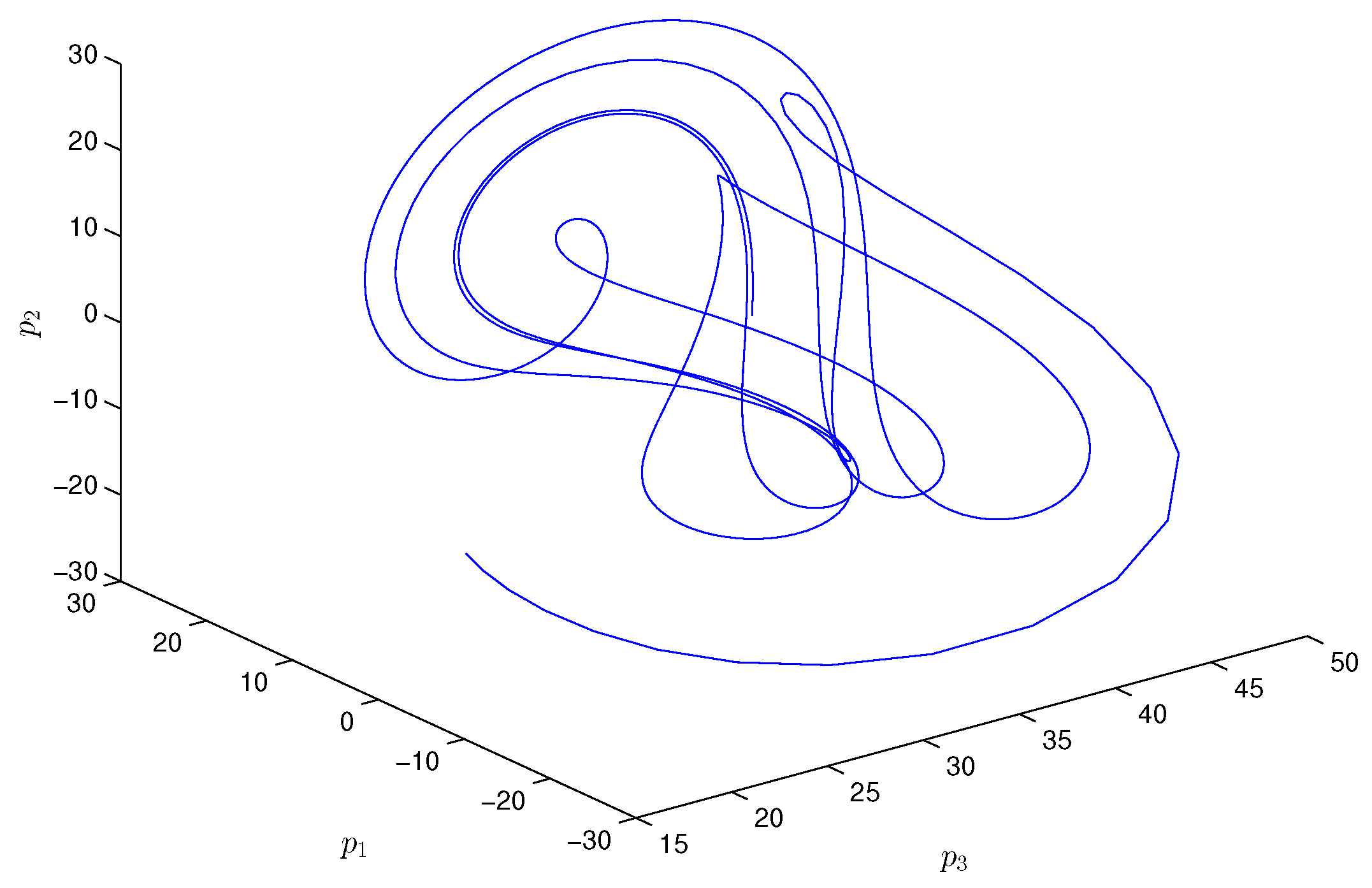
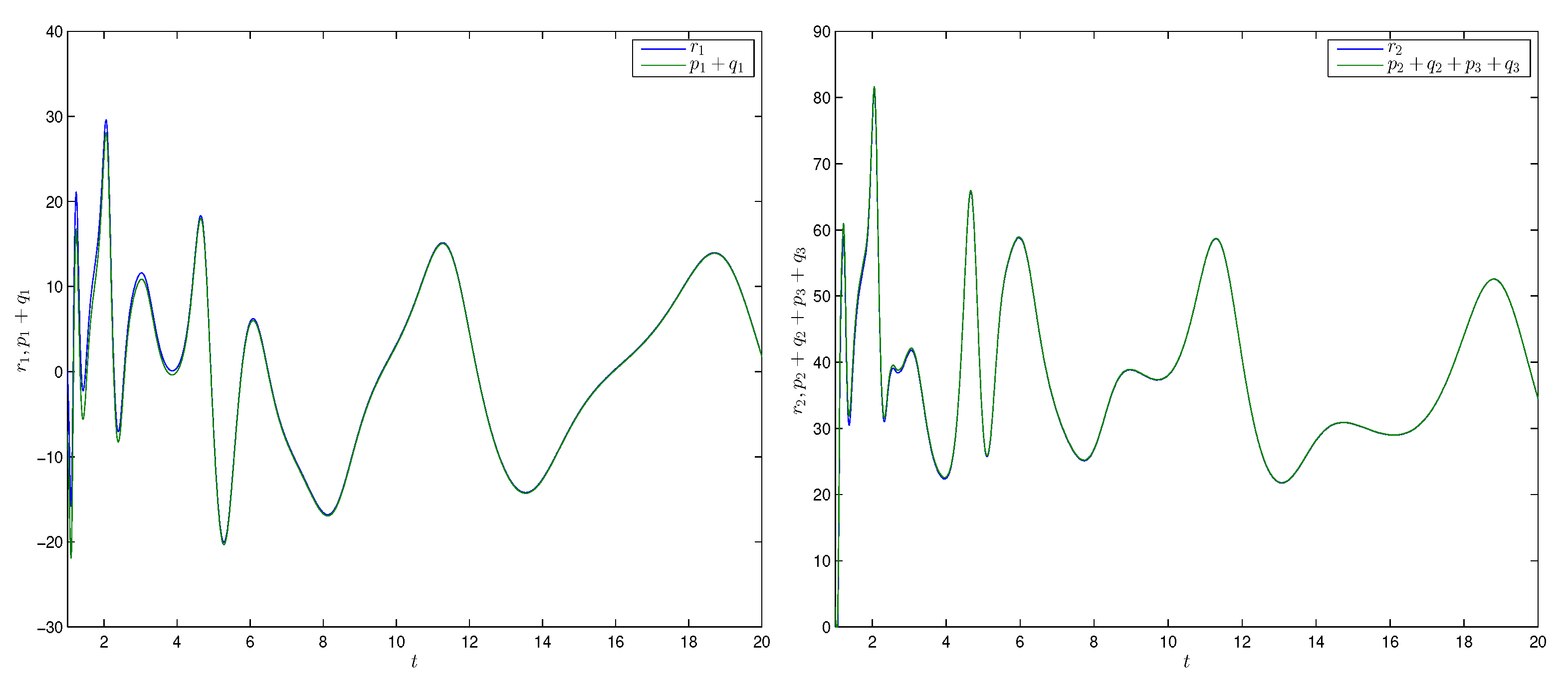
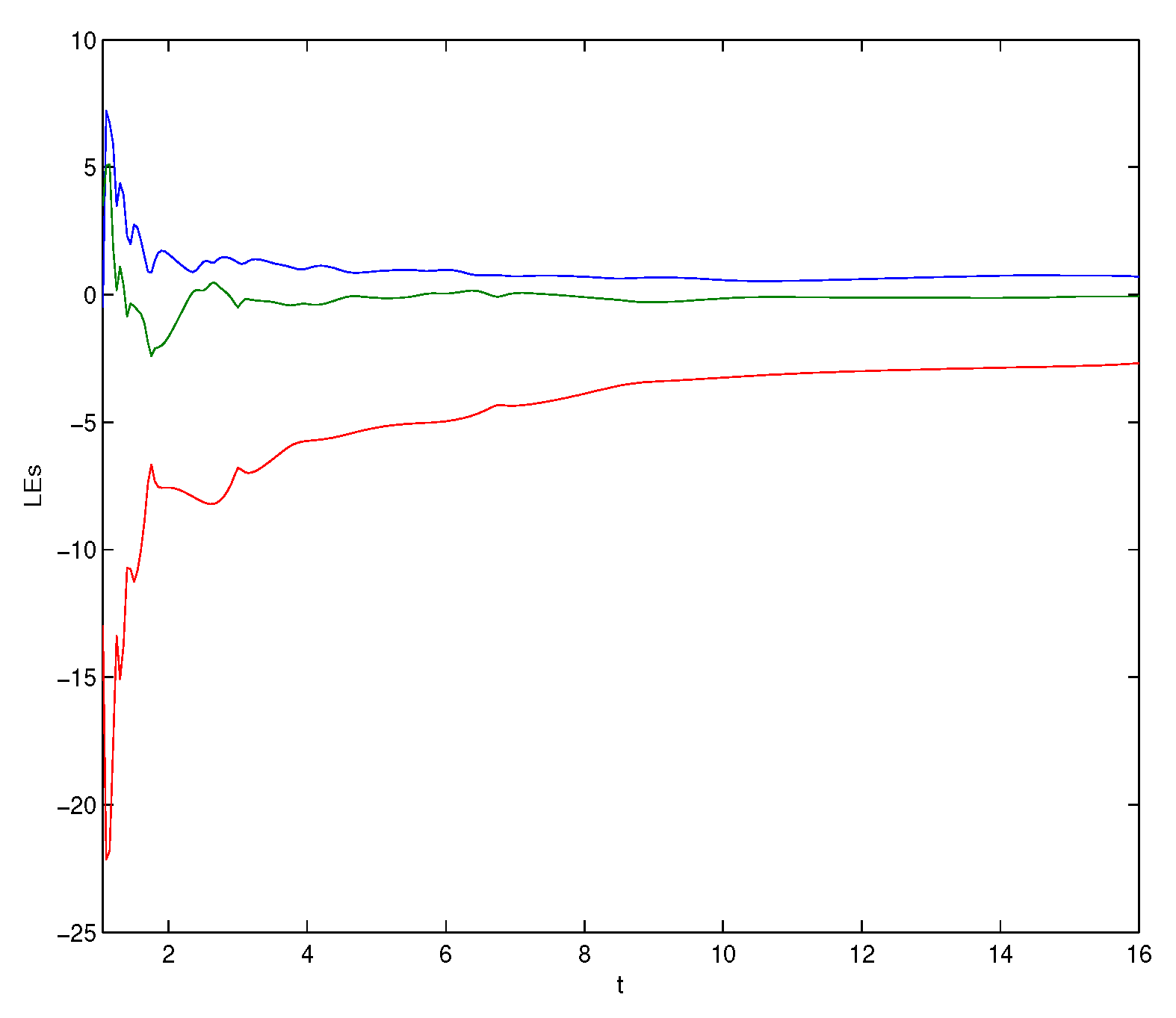
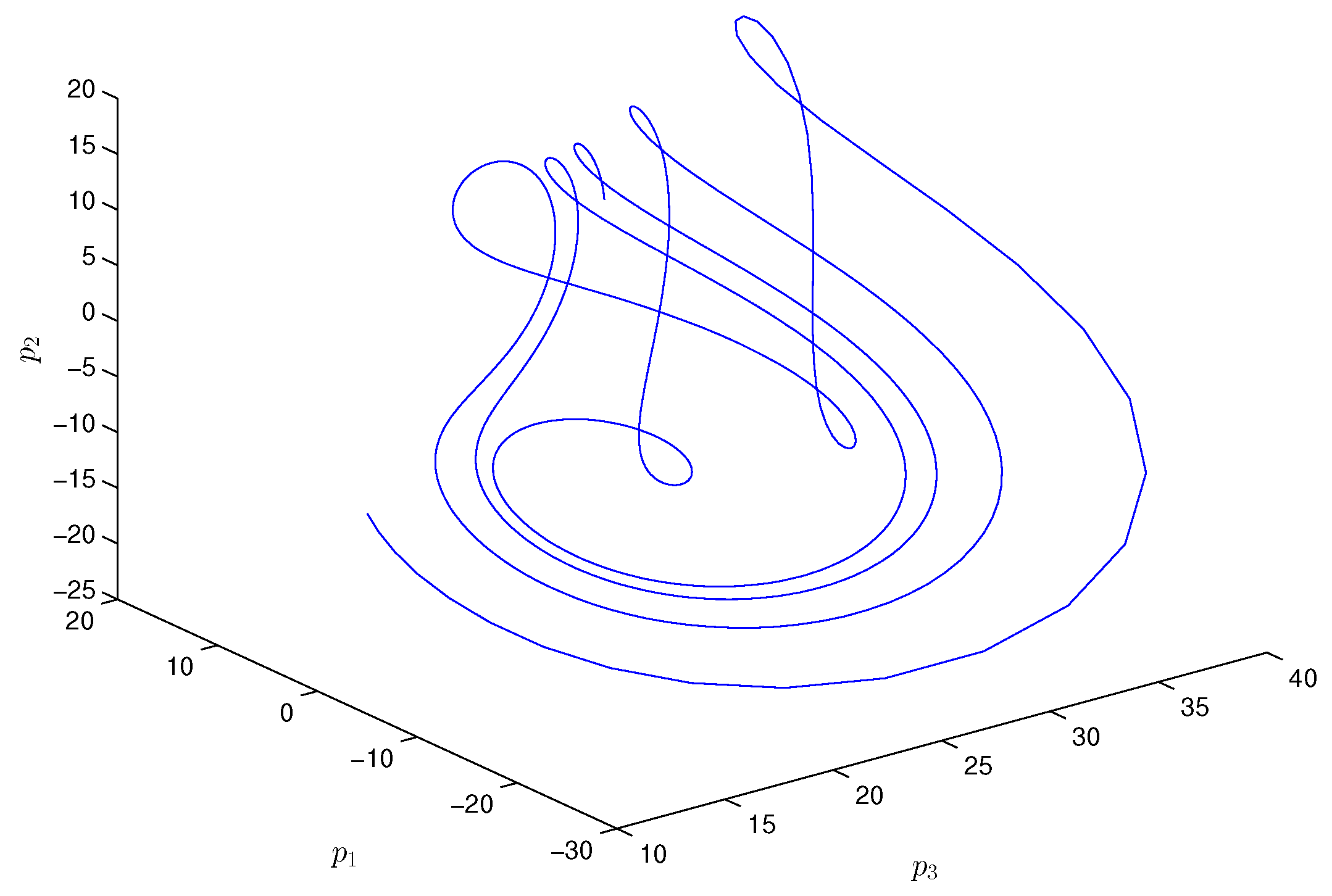
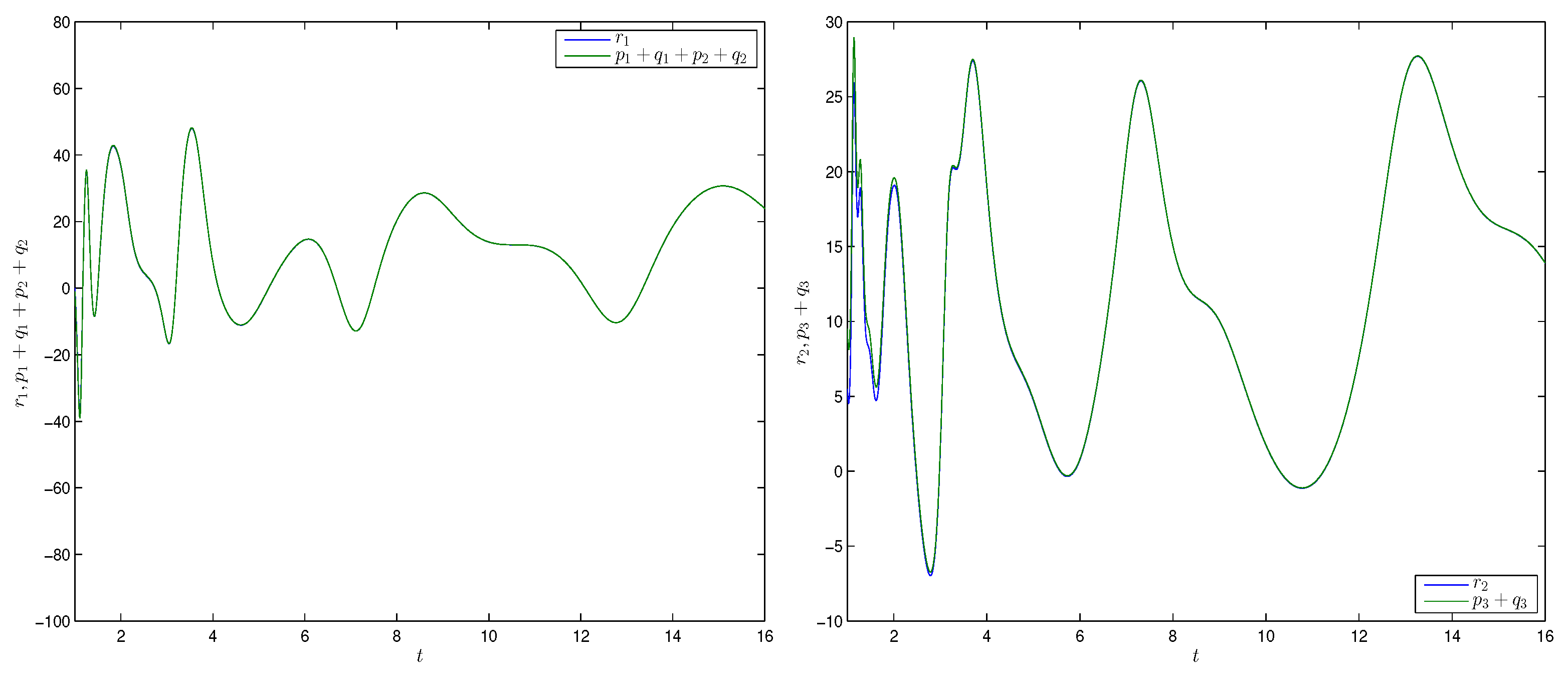
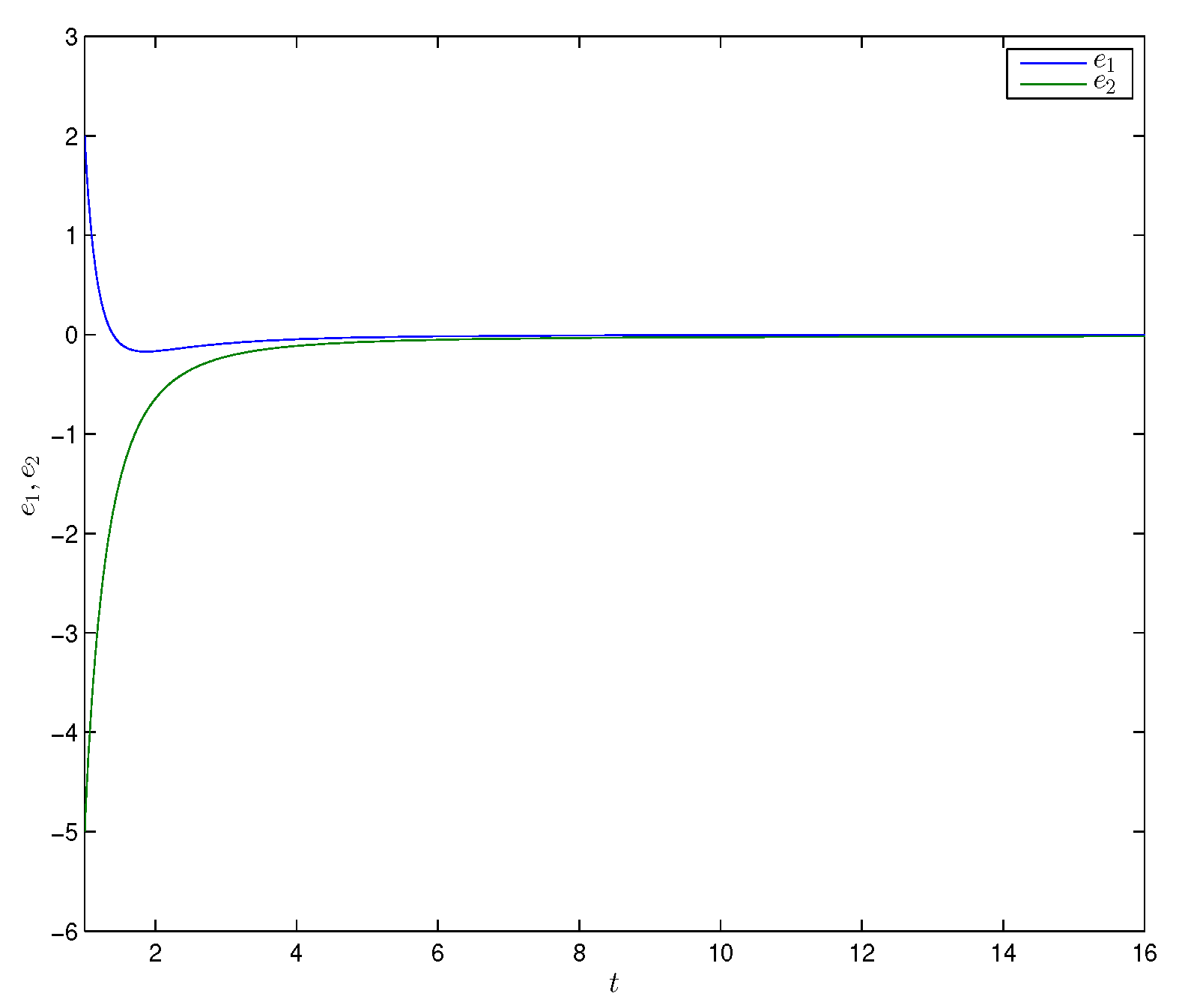
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Ahmadova, A.; Mahmudov, N.I. Langevin differential equations with general fractional orders and their applications to electric circuit theory. J. Comput. Appl. Math. 2021, 388, 113299. [Google Scholar] [CrossRef]
- Patel, V.K.; Bahuguna, D. An efficient matrix approach for the numerical solutions of electromagnetic wave model based on fractional partial derivative. Appl. Numer. Math. 2021, 169, 1–20. [Google Scholar] [CrossRef]
- Sunarto, A.; Agarwal, P.; Sulaiman, J.; Chew, J.V.L.; Aruchunan, E. Iterative method for solving one-dimensional fractional mathematical physics model via quarter-sweep and PAOR. Adv. Differ. Equ. 2021, 2021, 147. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Khan, I.; Nisar, K.S.; Singh, J. MHD flow of a generalized Casson fluid with Newtonian heating: A fractional model with Mittag–Leffler memory. Alex. Eng. J. 2020, 59, 3049–3059. [Google Scholar] [CrossRef]
- Xi, H.; Lia, Y.; Huanga, X. Adaptive function projective combination synchronization of three different fractional-order chaotic systems. Optik 2015, 126, 5346–5349. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, Switzerland, 2006. [Google Scholar]
- Katugampola, U.N. A new approach to generalized fractional derivative. Bull. Math. Anal. Appl. 2014, 6, 1–15. [Google Scholar]
- Adjabi, Y.; Jarad, F.; Baleanu, D.; Abdeljawad, T. On Cauchy problems with Caputo Hadamard fractional derivatives. J. Comput. Anal. Appl. 2016, 21, 661–681. [Google Scholar]
- Jarad, F.; Abdeljawad, T.; Baleanu, D. Caputo-type modification of the Hadamard fractional derivatives. Adv. Differ. Equ. 2012, 2012, 142. [Google Scholar] [CrossRef] [Green Version]
- Nain, A.; Vats, R.; Kumar, A. Coupled fractional differential equations involving Caputo-Hadamard derivative with nonlocal boundary conditions. Math. Meth. Appl. Sci. 2021, 44, 4192–4204. [Google Scholar] [CrossRef]
- Amara, A.; Etemad, S.; Rezapour, S. Topological degree theory and Caputo–Hadamard fractional boundary value problems. Adv. Differ. Equ. 2020, 2020, 369. [Google Scholar] [CrossRef]
- Etemad, S.; Rezapour, S.; Samei, M.E. On a fractional Caputo–Hadamard inclusion problem with sum boundary value conditions by using approximate endpoint property. Math Meth Appl Sci. 2020, 43, 9719–9734. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Jiao, L.; Wu, J.; Wang, X. Projective synchronization with different scale factors in driven-response complex network and its application to image encryption. Nonlinear Anal. 2010, 11, 3045–3058. [Google Scholar] [CrossRef]
- Hong-Yan, Z.; Le-Quan, M.; Geng, Z.; Guan-Rong, C. Generalized chaos synchronization of bidirectional arrays of discrete systems. Chin. Phys. Lett. 2013, 30, 040502. [Google Scholar]
- Kareem, S.O.; Ojo, K.S.; Njah, A.N. Function projective synchronization of identical and non-identical modified finance and Shimizu-Morioka systems. Pramana 2012, 79, 71–79. [Google Scholar] [CrossRef]
- Li, G.H. Modified projective synchronization of chaotic system. Chaos Solitons Fractals 2007, 32, 1786–1790. [Google Scholar] [CrossRef]
- Runiz, L.; Zhengmin, W. Adaptive function projective synchronization of unified chaotic systems with uncertain parameters. Chaos Solitons Fractals 2009, 42, 1266–1272. [Google Scholar] [CrossRef]
- Runzi, L.; Yinglan, W.; Shucheng, D. Combination synchronization of three classic chaotic systems using active backstepping design. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 043114. [Google Scholar] [CrossRef]
- Vincent, U.E.; Saseyi, A.O.; McClintock, P.V. Multiswitching combination synchronization of chaotic systems. Nonlinear Dyn. 2015, 80, 845–854. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.B.; Wang, X.Y.; Wang, X.Y.; Zhou, Y.F. Adaptive generalized combination complex synchronization of uncertain real and complex nonlinear systems. AIP Adv. 2016, 6, 045011. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.K.; Vijay, K.Y.; Das, S. Dual combination synchronization of the fractional order complex chaotic systems. J. Comput. Nonlinear Dyn. 2017, 12, 011017. [Google Scholar] [CrossRef]
- Vijay, K.Y.; Prasad, G.; Srivastava, M.; Das, S. Combinationcombination phase synchronization among non-identical fractional order complex chaotic systems via nonlinear control. Int. J. Dynam. Control 2018, 7, 330–340. [Google Scholar]
- Zerimeche, H.; Houmor, T.; Berkane, A. Combination synchronization of different dimensions fractional-order non-autonomous chaotic systems using scaling matrix. Int. J. Dyn. Control 2021, 9, 788–796. [Google Scholar] [CrossRef]
- Almeida, R. Caputo–Hadamard fractional derivatives of variable order. Numer. Funct. Anal. Optim. 2017, 38, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Cong, N.D.; Doan, T.S.; Tuan, H.T. Asymptotic stability of linear fractional systems with constant coefficients and small time dependent perturbations. Vietnam. J. Math. 2018, 46, 665–680. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Zhang, R.; Chen, D. Stability of nonlinear fractionalorder time varying systems. ASME J. Comput. Nonlinear Dyn. 2016, 11, 031007. [Google Scholar] [CrossRef]
- Xu, Z. Dynamics of a class of fractional-order nonautonomous Lorenz-type systems. Chaos 2017, 27, 041104. [Google Scholar]
- Lei, Y.; Xu, W.; Xu, Y.; Fang, T. Chaos control by harmonic excitation with propoer random phase. Chaos Solitons Fractals 2004, 21, 1175–1181. [Google Scholar] [CrossRef]
- Gohar, M.; Li, C.; Li, Z. Finite difference methods for caputo–hadamard fractional differential equations. Mediterr. J. Math. 2020, 17, 194. [Google Scholar] [CrossRef]
- Danca, M.F.; Kuznetsov, N. Matlab Code for Lyapunov Exponents of Fractional-Order Systems. Int. J. Bifurc. Chaos 2018, 25, 1850067. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.R.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Hayden, K.; Olson, E.; Titi, E.S. Discrete data assimilation in the Lorenz and 2D Navier–Stokes equations. Phys. D 2011, 240, 1416–1425. [Google Scholar] [CrossRef] [Green Version]
- Ku, Y.H.; Sun, X. Chaos in Van der Pol’s equation. J. Franklin Inst. 1990, 327, 197–207. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagy, A.M.; Makhlouf, A.B.; Alsenafi, A.; Alazemi, F. Combination Synchronization of Fractional Systems Involving the Caputo–Hadamard Derivative. Mathematics 2021, 9, 2781. https://doi.org/10.3390/math9212781
Nagy AM, Makhlouf AB, Alsenafi A, Alazemi F. Combination Synchronization of Fractional Systems Involving the Caputo–Hadamard Derivative. Mathematics. 2021; 9(21):2781. https://doi.org/10.3390/math9212781
Chicago/Turabian StyleNagy, Abdelhameed M., Abdellatif Ben Makhlouf, Abdulaziz Alsenafi, and Fares Alazemi. 2021. "Combination Synchronization of Fractional Systems Involving the Caputo–Hadamard Derivative" Mathematics 9, no. 21: 2781. https://doi.org/10.3390/math9212781





