Finite Element Analysis of Thermal-Diffusions Problem for Unbounded Elastic Medium Containing Spherical Cavity under DPL Model
Abstract
:1. Introduction
2. Mathematical Model
- (i)
- (DPLD) refers to the dual phase lag thermo-diffusion model
- (ii)
- (LSD) refers to the Lord and Shulman thermo-diffusion model
- (iii)
- (CTD) refers to the classical thermo-diffusion model
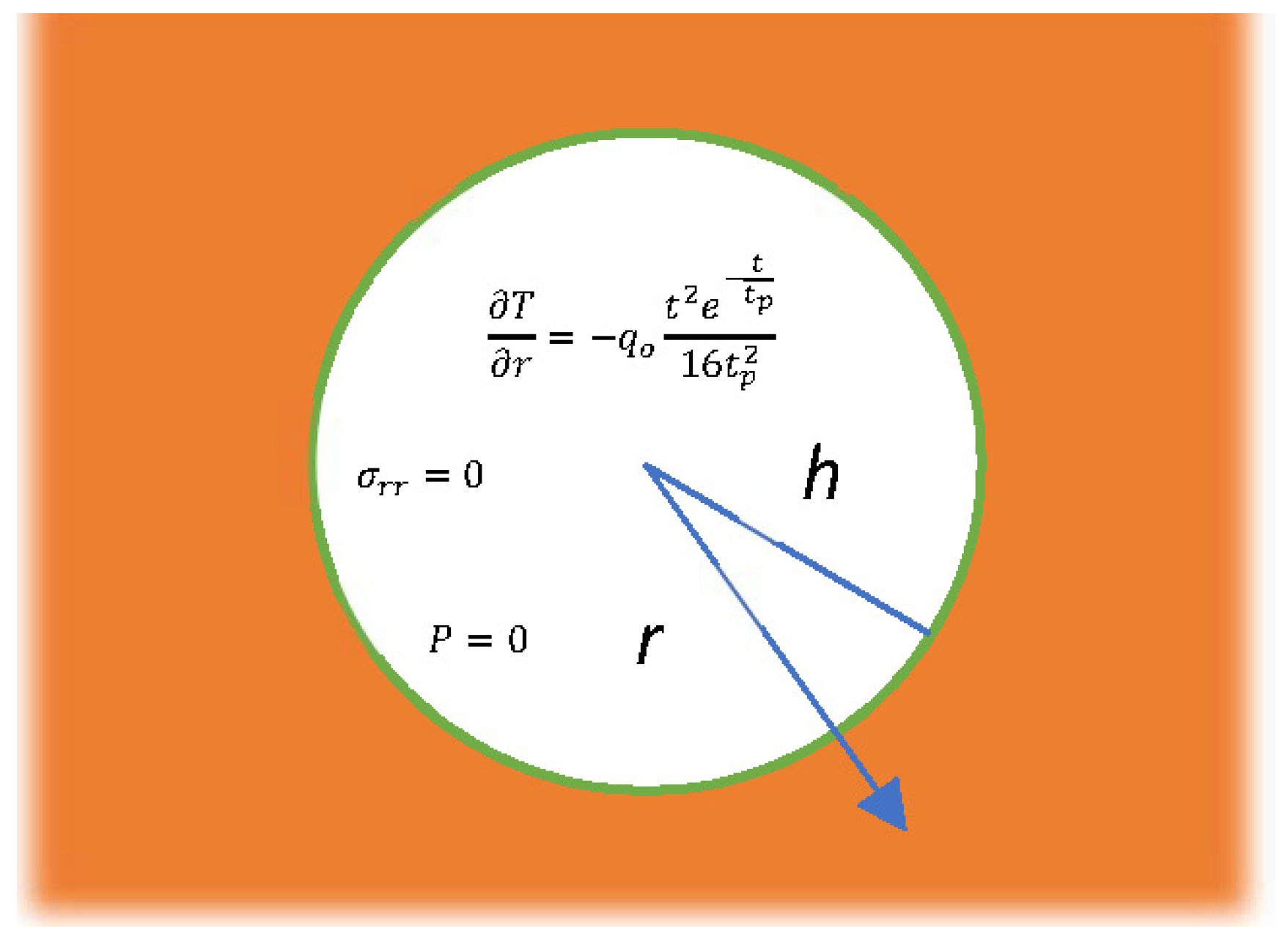
3. Initial and Boundary Conditions
4. Numerical Scheme
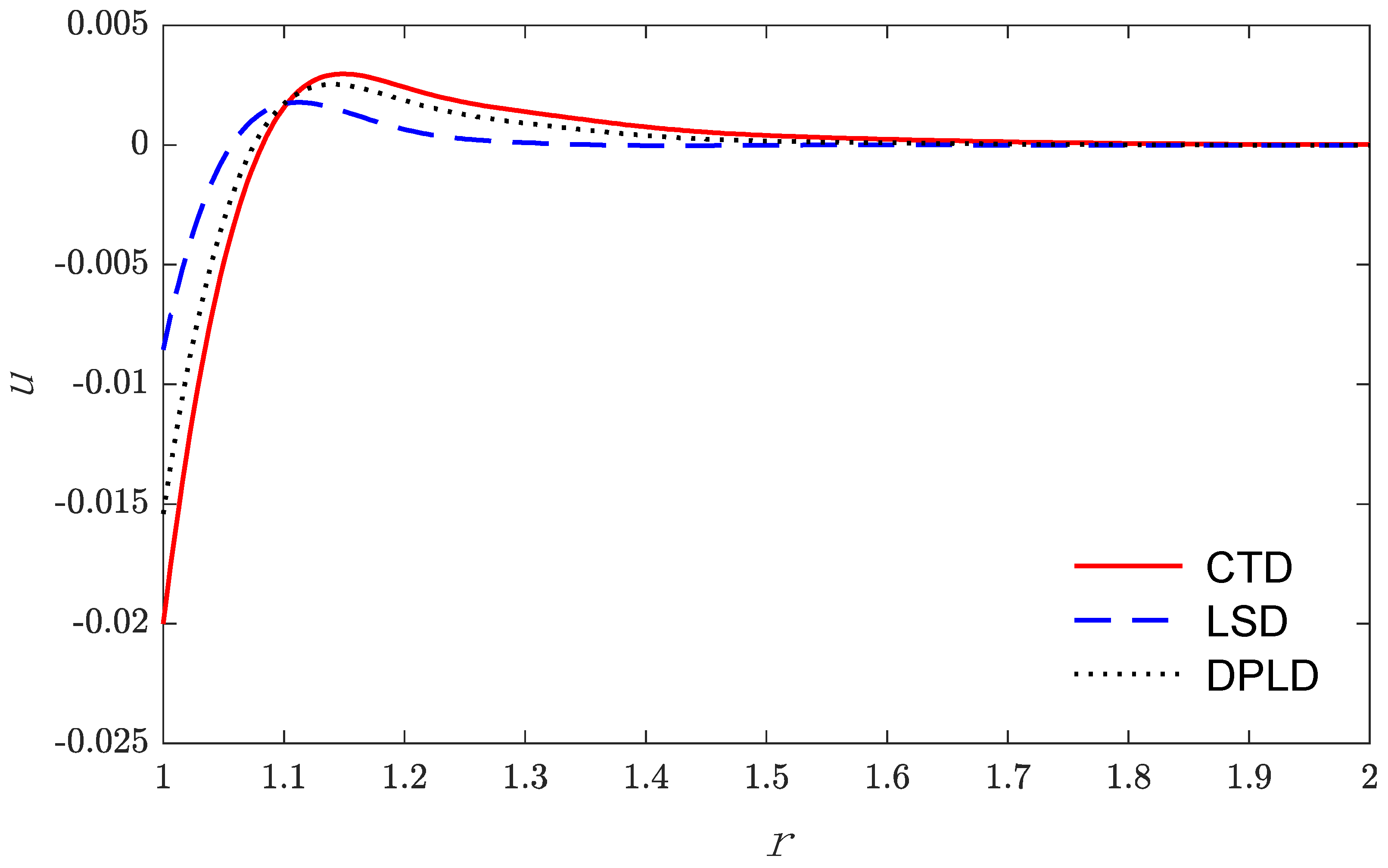
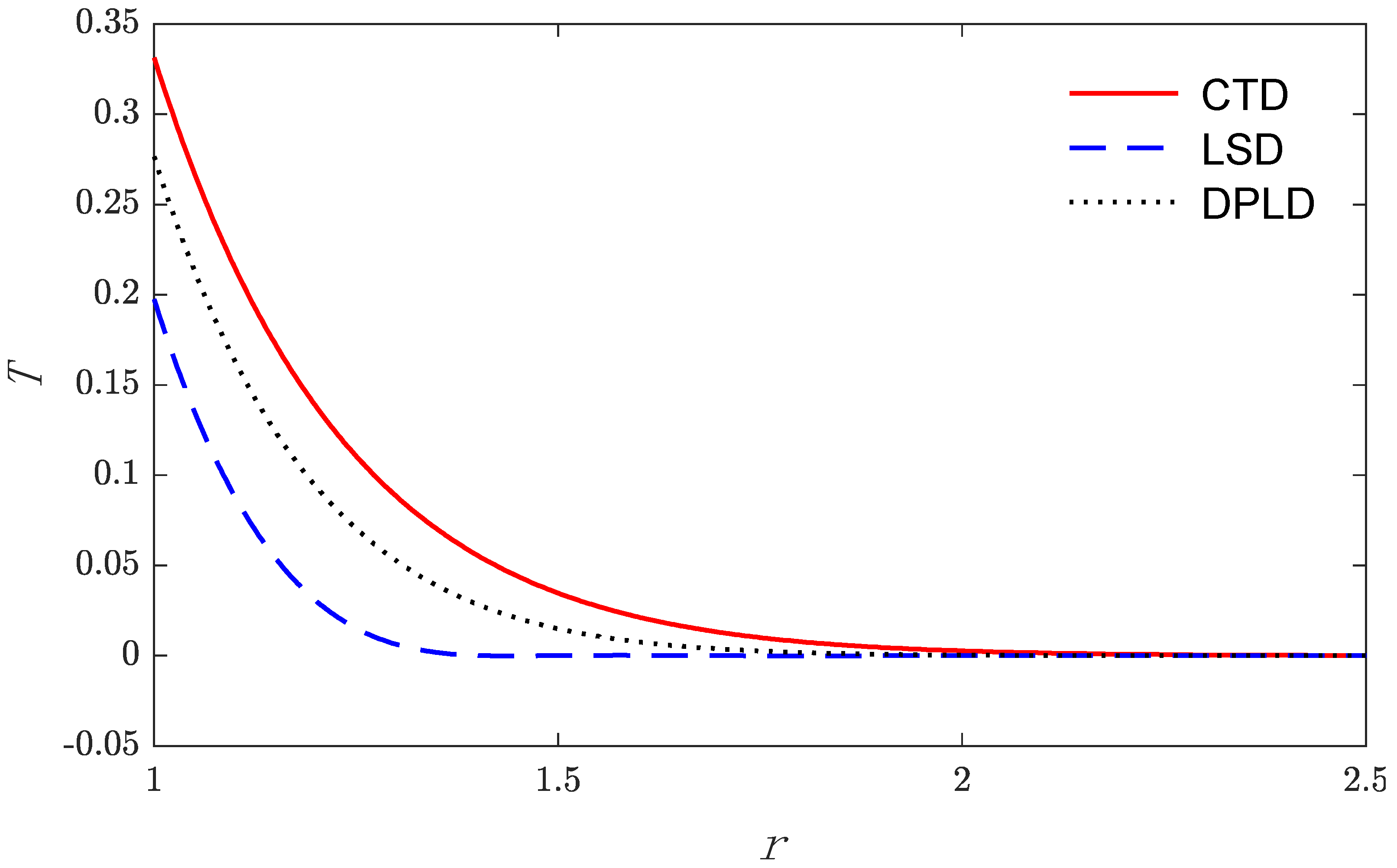
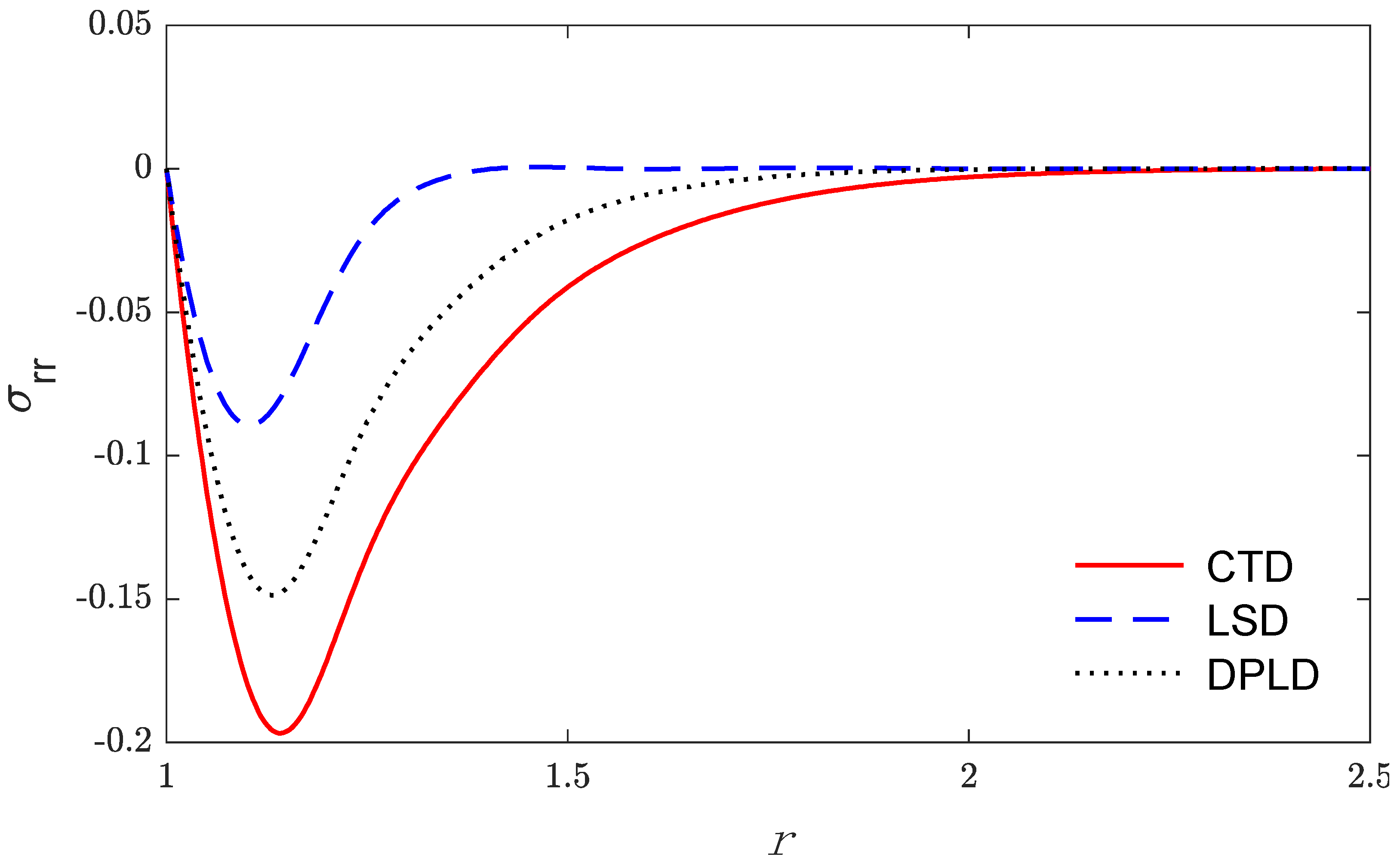
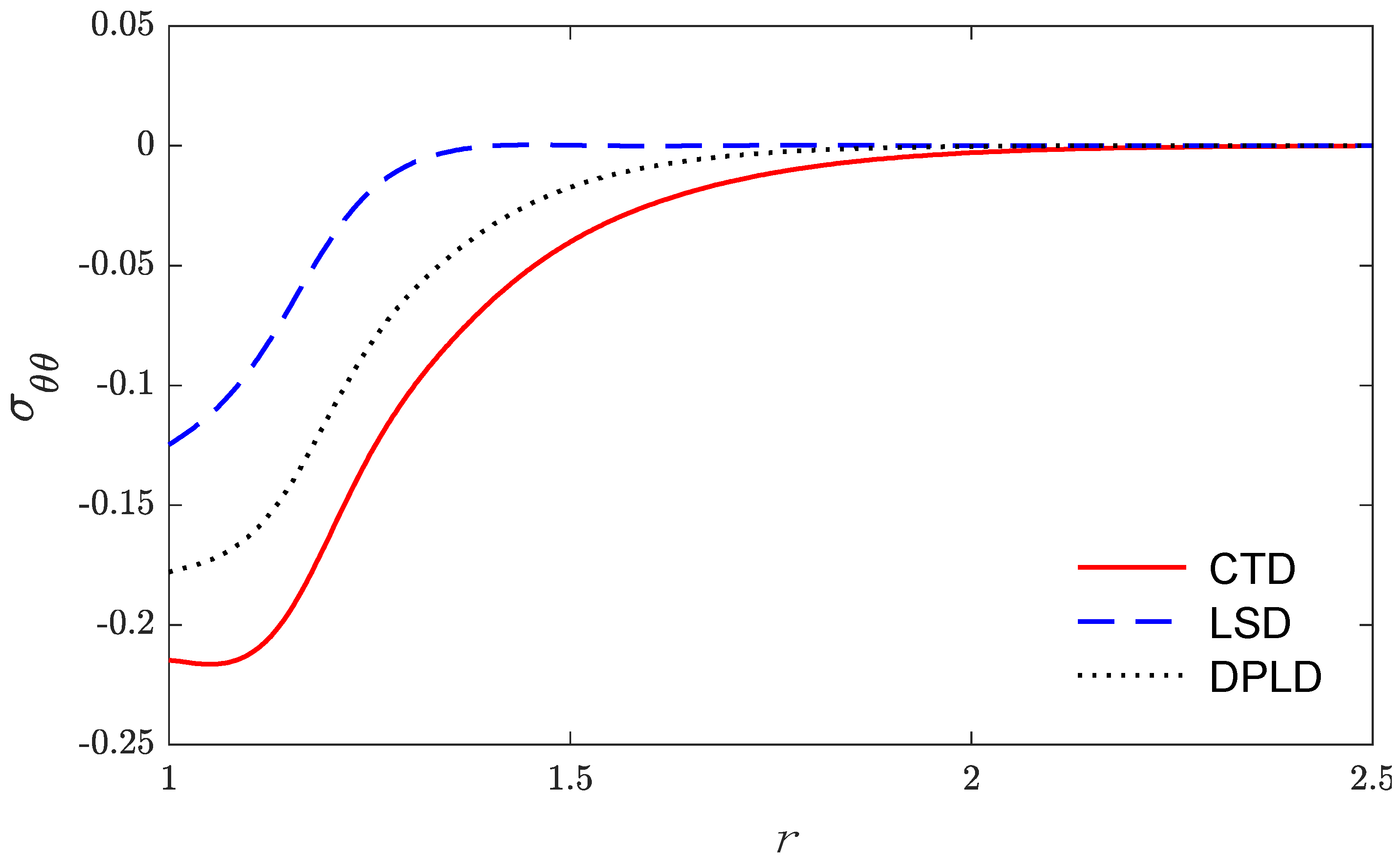
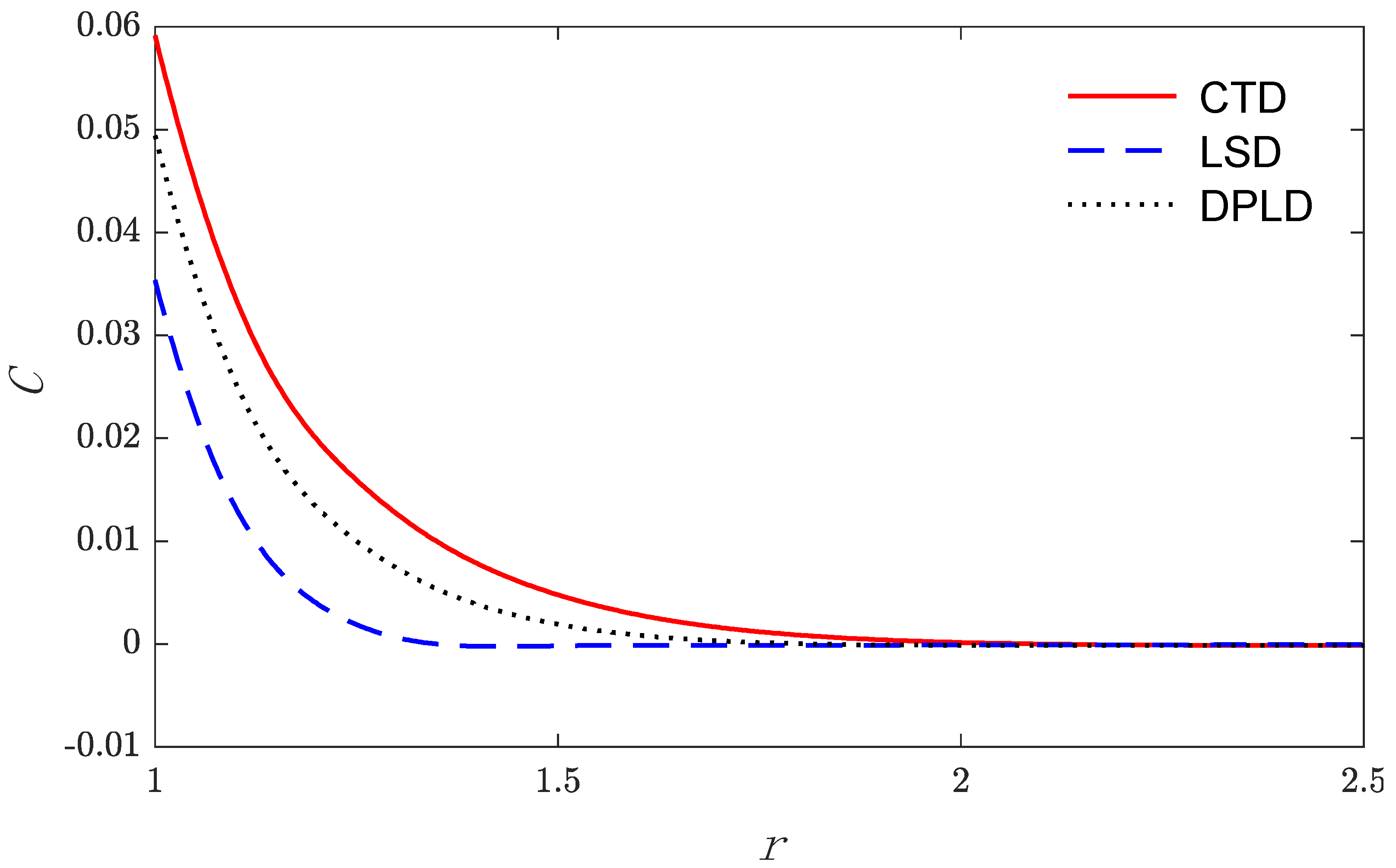
5. Numerical Result and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nowacki, W. Dynamic Problems of Thermoelasticity; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1975. [Google Scholar]
- Biot, M.A. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Nowacki, W. Dynamic problems of diffusion in solids. Eng. Fract. Mech. 1976, 8, 261–266. [Google Scholar] [CrossRef]
- Nowacki, W. Thermodiffusion in Solids. Mech. Teor. I Stosow. 1975, 13, 143–158. [Google Scholar]
- Nowacki, W. Dynamical problem of thermodiffusion in solids 1. Bull. Acad. Pol. Sci. Ser. Sci. Tech. 1974, 22, 55–64. [Google Scholar]
- Sherief, H.H.; Hamza, F.A.; Saleh, H.A. The theory of generalized thermoelastic diffusion. Int. J. Eng. Sci. 2004, 42, 591–608. [Google Scholar] [CrossRef]
- Tzou, D.Y. Macro- to Micro-Scale Heat Transfer: The Lagging Behavior; Taylor & Francis: Washington, DC, USA, 1996. [Google Scholar]
- Abbas, I.A.; Singh, B. Finite Element Analysis in a Rotating Thermoelastic Half-Space with Diffusion. J. Comput. Theor. Nanosci. 2014, 11, 2276–2282. [Google Scholar] [CrossRef]
- Villani, A.; Busso, E.P.; Ammar, K.; Forest, S.; Geers, M.G.D. A fully coupled diffusional-mechanical formulation: Numerical implementation, analytical validation, and effects of plasticity on equilibrium. Arch. Appl. Mech. 2014, 84, 1647–1664. [Google Scholar] [CrossRef] [Green Version]
- Abbas, I.A.; Kumar, R.; Chawla, V. Response of thermal source in a transversely isotropic thermoelastic half-space with mass diffusion by using a finite element method. Chin. Phys. B 2012, 21, 084601. [Google Scholar] [CrossRef]
- Sharma, J.N.; Kumari, N.; Sharma, K.K. Diffusion in a generalized thermoelastic solid in an infinite body with a cylindrical cavity. J. Appl. Mech. Tech. Phys. 2013, 54, 819–831. [Google Scholar] [CrossRef]
- Abbas, I.A.; Marin, M. Analytical Solutions of a Two-Dimensional Generalized Thermoelastic Diffusions Problem Due to Laser Pulse. Iran. J. Sci. Technol. Trans. Mech. Eng. 2018, 42, 57–71. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Elhagary, M.A.; Soleiman, A.; Khalil, K.M. Generalized thermoelastic-diffusion model with higher-order fractional time-derivatives and four-phase-lags. Mech. Based Des. Struct. Mach. 2020, 1–18. [Google Scholar] [CrossRef]
- Sobhy, M. Hygrothermal vibration of orthotropic double-layered graphene sheets embedded in an elastic medium using the two-variable plate theory. Appl. Math. Model. 2016, 40, 85–99. [Google Scholar] [CrossRef]
- Othman, M.I.; Eraki, E.E. Generalized magneto-thermoelastic half-space with diffusion under initial stress using three-phase-lag model. Mech. Based Des. Struct. Mach. 2017, 45, 145–159. [Google Scholar] [CrossRef]
- Lotfy, K. Effect of variable thermal conductivity during the photothermal diffusion process of semiconductor medium. Silicon 2019, 11, 1863–1873. [Google Scholar] [CrossRef]
- Kumar, R.; Sharma, N.; Lata, P. Effects of thermal and diffusion phase-lags in a plate with axisymmetric heat supply. Multidiscip. Model. Mater. Struct. 2016, 12, 275–290. [Google Scholar] [CrossRef]
- Abbas, I.A.; Kumar, R. Deformation due to thermal source in micropolar generalized thermoelastic half-space by finite element method. J. Comput. Theor. Nanosci. 2014, 11, 185–190. [Google Scholar] [CrossRef]
- Bezzina, S.; Zenkour, A.M. Thermoelastic diffusion of a solid cylinder in the context of modified Green–Naghdi models. Waves Random Complex Media 2021, 1–12. [Google Scholar] [CrossRef]
- Madureira, R.L.R.; Rincon, M.A.; Aouadi, M. Numerical analysis for a thermoelastic diffusion problem in moving boundary. Math. Comput. Simul. 2021, 187, 630–655. [Google Scholar] [CrossRef]
- Zenkour, A.M. Thermal diffusion of an unbounded solid with a spherical cavity via refined three-phase-lag Green–Naghdi models. Indian J. Phys. 2021, 1–18. [Google Scholar] [CrossRef]
- Singh, B.; Yadav, A.K. The Effect of Diffusion on Propagation and Reflection of Waves in a Thermo-Microstretch Solid Half-Space. Comput. Math. Model. 2021, 32, 221–234. [Google Scholar] [CrossRef]
- Elhagary, M.A. Fractional thermoelastic diffusion problem for an infinitely long hollow cylinder using the Caputo–Fabrizio definition. J. Therm. Stresses 2021, 44, 281–294. [Google Scholar]
- Molla, M.A.K.; Mallik, S.H. Variational principle, uniqueness and reciprocity theorems for higher order time-fractional four-phase-lag generalized thermoelastic diffusion model. Mech. Based Des. Struct. Mach. 2021, 1–16. [Google Scholar] [CrossRef]
- Eremeyev, V.A.; Pietraszkiewicz, W. Nonlinear resultant theory of shells accounting for thermodiffusion. Contin. Mech. Thermodyn. 2021, 33, 893–909. [Google Scholar] [CrossRef]
- Abbas, I.A. A dual phase lag model on thermoelastic interaction in an infinite fiber-reinforced anisotropic medium with a circular hole. Mech. Based Des. Struc. Mach. 2015, 43, 501–513. [Google Scholar] [CrossRef]
- Saeed, T.; Abbas, I.; Marin, M. A GL Model on Thermo-Elastic Interaction in a Poroelastic Material Using Finite Element Method. Symmetry 2020, 12, 488. [Google Scholar] [CrossRef] [Green Version]
- Marin, M.; Othman, M.I.A.; Seadawy, A.R.; Carstea, C. A domain of influence in the Moore–Gibson–Thompson theory of dipolar bodies. J. Taibah Univ. Sci. 2020, 14, 653–660. [Google Scholar] [CrossRef]
- Marin, M. Some estimates on vibrations in thermoelasticity of dipolar bodies. JVC/J. Vib. Control. 2010, 16, 33–47. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, X.M.; Zheng, H.W. Analysis on sintering driving force of unequal-sized particles in generalized thermoelastic diffusion. Fenmo Yejin Jishu/Powder Metall. Technol. 2019, 37, 259–263. [Google Scholar]
- Shaw, S.; Othman, M.I.A. Computational analysis on the influence of damping in solid body deformation during thermoelastic mass diffusion. Waves Random Complex Media 2020, 1–21. [Google Scholar] [CrossRef]
- Abo-dahab, S.M.; Abd-alla, A.M. Dual-phase-lag model on magneto-thermoelastic rotating medium with voids and diffusion under the effect of initial stress and gravity. Heat Transf. 2020, 49, 2131–2166. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Hilal, M.I.M.; Elmaklizi, Y.D. The effect of gravity and diffusion on micropolar thermoelasticity with temperature–dependent elastic medium under G–N theory. Mech. Mech. Eng. 2017, 21, 657–677. [Google Scholar]
- Sharma, D.K.; Thakur, D.; Walia, V.; Sarkar, N. Free vibration analysis of a nonlocal thermoelastic hollow cylinder with diffusion. J. Therm. Stresses 2020, 43, 981–997. [Google Scholar] [CrossRef]
- Alzahrani, F.S.; Abbas, I.A. Generalized thermoelastic diffusion in a nanoscale beam using eigenvalue approach. Acta Mech. 2016, 227, 955–968. [Google Scholar] [CrossRef]
- Bajpai, A.; Sharma, P.K.; Kumar, R. Modeling of thermoelastic diffusion plate under two temperature, fractional-order, and temperature-dependent material properties. ZAMM Z. Fur Angew. Math. Und Mech. 2021, e202000321. [Google Scholar] [CrossRef]
- Abbas, I.; Hobiny, A.D. Analytical-numerical solutions of photo-thermal interactions in semiconductor materials. Inf. Sci. Lett. 2021, 10, 189–196. [Google Scholar]
- Bassiouny, E. Mathematical Model for Hyperbolic Two Temperature Fractional-Order Thermoelastic Materials Subjected to Thermal Loading. Appl. Math. Inf. Sci. 2021, 15, 23–29. [Google Scholar]
- Abo-Dahab, S.M.; Abd-Alla, A.M.; Mahmoud, E.E. Thermal stresses in thermoelastic half-space without energy dissipation subjected to rotation and magnetic field. Appl. Math. Inf. Sci. 2017, 11, 1637–1647. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abouelregal, A.E. Effect of temperature dependency on constrained orthotropic unbounded body with a cylindrical cavity due to pulse heat flux. J. Therm. Sci. Technol. 2015, 10, JTST0019. [Google Scholar] [CrossRef] [Green Version]
- Abbas, I.A.; Youssef, H.M. A Nonlinear Generalized Thermoelasticity Model of Temperature-Dependent Materials Using Finite Element Method. Int. J. Thermophys. 2012, 33, 1302–1313. [Google Scholar] [CrossRef]
- Abbas, I.A.; Othman, M.I.A. Generalized thermoelasticity of the thermal shock problem in an isotropic hollow cylinder and temperature dependent elastic moduli. Chin. Phys. B 2012, 21, 014601. [Google Scholar] [CrossRef]
- Kumar, R.; Abbas, I.A. Deformation due to thermal source in micropolar thermoelastic media with thermal and conductive temperatures. J. Comput. Theor. Nanosci. 2013, 10, 2241–2247. [Google Scholar] [CrossRef]
- Abbas, I.A.; Youssef, H.M. Finite element analysis of two-temperature generalized magneto-thermoelasticity. Arch. Appl. Mech. 2009, 79, 917–925. [Google Scholar] [CrossRef]
- Sherief, H.H.; Saleh, H.A. A half-space problem in the theory of generalized thermoelastic diffusion. Int. J. Solids Struct. 2005, 42, 4484–4493. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hobiny, A.D.; Abbas, I.A. Finite Element Analysis of Thermal-Diffusions Problem for Unbounded Elastic Medium Containing Spherical Cavity under DPL Model. Mathematics 2021, 9, 2782. https://doi.org/10.3390/math9212782
Hobiny AD, Abbas IA. Finite Element Analysis of Thermal-Diffusions Problem for Unbounded Elastic Medium Containing Spherical Cavity under DPL Model. Mathematics. 2021; 9(21):2782. https://doi.org/10.3390/math9212782
Chicago/Turabian StyleHobiny, Aatef D., and Ibrahim A. Abbas. 2021. "Finite Element Analysis of Thermal-Diffusions Problem for Unbounded Elastic Medium Containing Spherical Cavity under DPL Model" Mathematics 9, no. 21: 2782. https://doi.org/10.3390/math9212782





