Geometric Thinking of Future Teachers for Primary Education—An Exploratory Study in Slovakia

Abstract

Various studies show that the level of knowledge achieved by pupils is influenced by the level of knowledge of their teachers. In this article, we focus on geometric thinking and the solutions for geometric tasks through a study of future teachers of primary education. The research sample consisted of 59 master’s students from the Teacher Training for Primary Education (TTPE) program. To determine the level of geometric thinking of TTPE students, the van Hiele geometric test was used. Two geometric multi-item tasks were proposed and the students’ solutions to these tasks were quantitatively and qualitatively evaluated. The main goal was to analyze students’ misconceptions while solving tasks and to compare and reveal the connections between their solutions and their achieved level of geometric thinking. A statistical implicative analysis was used for a deeper analysis, namely the statistical software C.H.I.C. The research findings show that more than 40% of TTPE students in the research sample did not reach the required level of geometric thinking. The achieved level of the geometric thinking of students is also influenced by the type of high school education. We observed problems with understanding the concept of the triangle and square in TTPE students. The connections between the solutions of two geometric tasks and the achieved level of geometric thinking were also revealed.

1. Introduction

Geometry is an essential part of the mathematical education of pupils and students at all levels of education, and it is considered a basic mathematical skill [1,2]. Geometry supports the development of spatial imagination, deductive thinking, and forms the basis of various mathematical and non-mathematical areas, playing a key role in them [3]. Usiskin [4], and many other authors, argue that many pupils cannot comprehend basic geometric concepts and take geometry lessons without mastering the fundamental knowledge and terminology. Pupils in Slovakia also face this problem, as demonstrated by the results of national tests, in which pupils achieved the lowest success in solving geometric problems [5]. Therefore, it was necessary to pay attention to the basics of geometry in the first years of education and, as Denton and West [6] argued, it was also necessary to ensure its quality teaching. The basic factors influencing pupils’ learning of mathematics, and particularly geometry, include the competence of mathematics teachers, the characteristics of the teacher, the use of the correct teaching methods and strategies, the connection of teaching with real life and, finally, the readiness of mathematics teachers [1,7,8]. Various studies [9,10,11] show that the level of knowledge achieved by pupils is influenced by the level of knowledge of their teachers. Moreover, in order to develop pupils’ geometric thinking, it is vital that mathematics teachers attain a higher level of geometric thinking than their potential pupils [1]. Therefore, geometry has become an integral part of the preparation for the teaching profession. In this article, we focus on geometric thinking and the solutions to geometric problems, via the study of future teachers of primary education and students of the Constantine the Philosopher University in Nitra, Slovakia. This was an exploratory study in which we aimed to compare the level of geometric thinking of our students with students in other countries. We also aimed to explore their ability to solve geometric problems.

2. Theoretical Framework

As in the past, geometry remains a problematic subject for modern pupils and students. Teachers are constantly trying to experiment with a variety of new methods in order to comprehend and resolve students’ misunderstandings in this area. Pierre van Hiele and Dina van Hiele-Geldof first addressed the issue of geometric thinking in the 1950s. As a teacher, they observed how their pupils learned geometry and, based on their observations, determined the levels of the cognitive process of learning geometry. This resulted in the creation of the van Hiele theory of geometric thinking in 1957.

The van Hiele theory consists of five hierarchical levels and draws on gestalt (form) psychology. Part of the theory is a supportive educational model that functions the learning of geometry and aids the progression through the various levels of geometric thinking. At present, the van Hiele theory is the most commonly used starting point in creating the geometry curriculum. The application of the theory can be seen, for example, in the Principles and Standards for School Mathematics [1]. The van Hiele model of geometric thinking forms the basis of educational content in various countries, such as the United States, Russia, the Netherlands, Taiwan and South Africa.

2.1. Model of Levels of Geometric Thinking

According to the van Hiele model of geometric thinking, the cognitive process in geometry consists of five levels (Visualization, Analysis, Informal Deduction, Formal Deduction, Rigor). The individual levels are numbered 0 to 4 (introduced by van Hiele) or numbered 1 to 5 (introduced by the American educators, Clements and Battista [12]). Therefore, we present a brief description of the various levels of geometric thinking [9,13,14,15]:

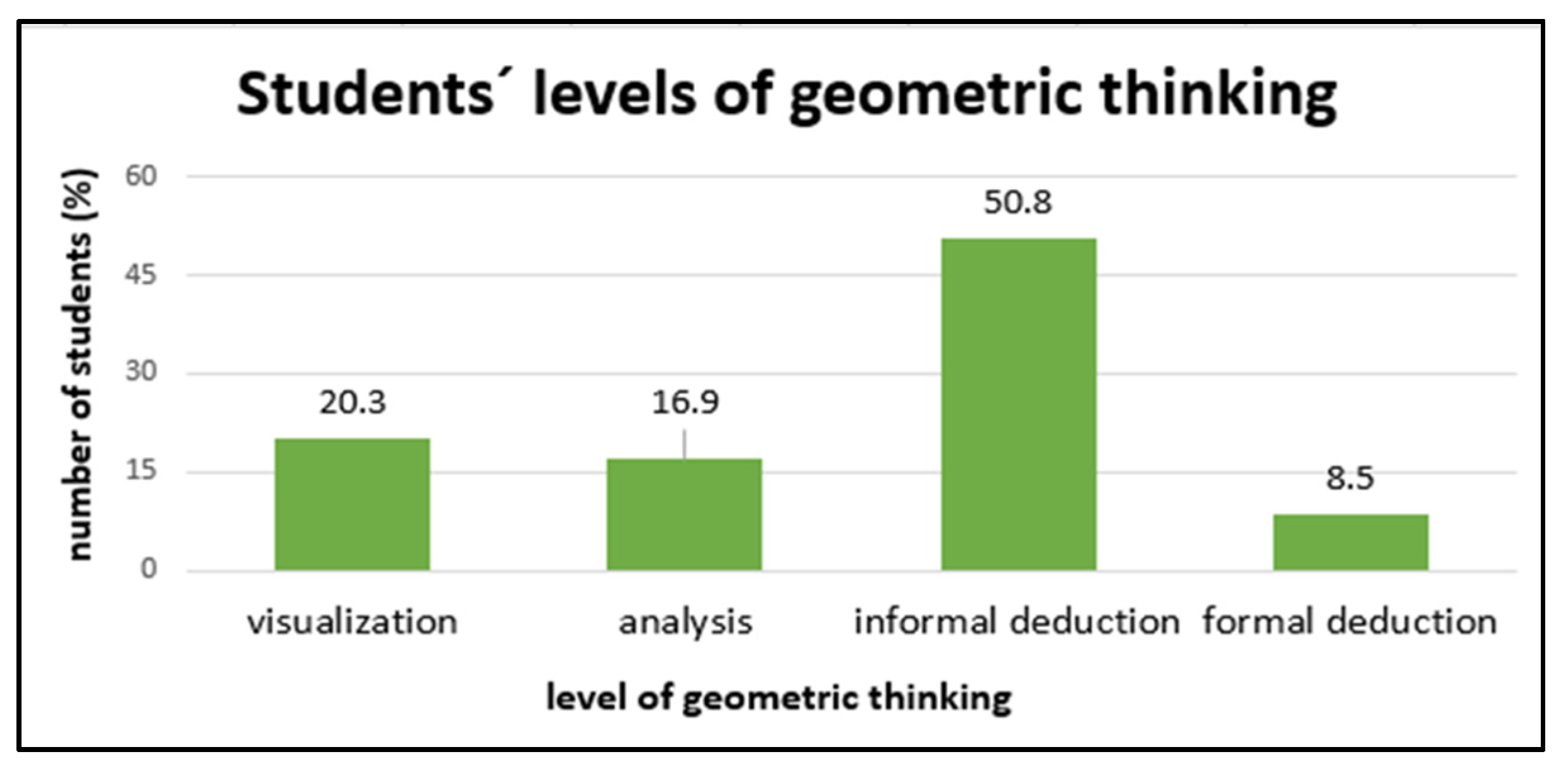
• Level 1—Visualization: In the first level, students recognize geometric shapes on the basis of their complex visual perception, while the orientation of the shapes is dominant.
• Level 2—Analysis: Students already know the properties of geometric shapes, but they do not yet perceive the relationships between individual properties. They define geometric shapes by listing all of their properties, even those that are unnecessary.
• Level 3—Informal Deduction: Students are aware of the relationships between the properties of shapes, they know that the individual properties are arranged and interconnected. They formulate the correct abstract definitions and begin to use implication, deduction and abstraction regarding statements in their thinking.
• Level 4—Formal Deduction: Students are aware of the need for a logical system of geometry and the meanings of deduction, position and tasks of axioms, as well as sentences and definitions. They are aware of the need to prove claims and can provide simple evidence at the secondary school level.
• Level 5—Rigor: Students can compare axiomatic systems and describe the effect of adding or removing axioms in a given geometric system. They understand the formal aspects of deduction and they are able to use all types of proofs.

The individual levels of geometric thinking are usually not discrete, and students do not have to be constrained to a certain level. The level of geometric thinking may vary depending on the task or the context. According to van Hiele [16], it is necessary to follow the five phases of the teaching process to progress to the next level of geometric thinking: information, guided orientation, explication, free orientation, and integration. Regarding the gradual transition through the individual phases, the teacher effectively helps the students to move to a higher level of geometric thinking and to better their knowledge of geometry [15].

The development of geometric thinking helps in solving various geometric problems, which, in turn, aid the teaching of geometry: to show students how to think logically and mathematically about spaces, shapes, and relationships between shapes using mathematical measures for size, angle, direction, orientation and position [17].

2.2. Empirical Research on the Van Hiele Theory

Since the publication of the van Hiele theory [18], many studies have been conducted to determine the level of geometric thinking of different age categories. After numerous studies, Wirzup [19] introduced the van Hiele theory in the United States. Usiskin [4] validated the existence of the first four levels of geometric thinking and created the van Hiele test to ascertain the level of geometric thinking. Clements and Battista [12] suggested using a pre-level of geometric thinking.

Research in the field of geometric thinking provides teachers with an overview of how pupils and students learn geometry at different levels of education—primary school, secondary school and university. In addition, many studies focus on defining the level of geometric thinking of mathematics teachers themselves.

For example, Halat [20]; Ma, Lee, Lin, and Wu [21]; MdYunus, Ayub, and Hock [22]; Andini, Fitriana, and Buldiyono [23]; and Hardianti, Priatna, and Priatna [24] found that primary school students are at the levels of visualization and analysis. Halat [20] research shows that gender does not affect the level of geometric thinking or the motivation of students to learn geometry. Nevertheless, Ma, Lee, Lin, and Wu [21] showed differences in the geometric thinking of boys and girls in higher levels. The results of the research of MdYunus, Ayub, and Hock [22] confirm that students taught on the basis of the van Hiele theory, together with the use of Google SketchUp, achieve better results in geometry. Based on their study, Hardianti, Piatna, and Piatna [24] designed the POGIL model, which enhanced the level of geometric thinking of students.

Usiskin [4], as well as Haviger and Vojkůvková [25,26], addressed the level of geometric thinking in students at secondary schools. Research shows that high school students are at the levels of visualization, analysis, and informal deduction. The study by Haviger and Vojkůvková [25] confirmed that gender did not have a substantial effect on the level of geometric thinking in students. Their research in secondary schools with a different geometry curriculum also proved that geometric experiences affect students’ geometric thinking.

Research conducted by Knight [27] with students at the University of Maine; by Jupri [28] with elementary school students in Indonesia; by Yilmaz and Koporan [29], and Halat [30] with students in Turkey; Arman, Cofie and Okpoti [31] with students in Ghana; and by Patkin and Burkai [32] with students in Israel shows that teachers of primary education, as well as students of primary education, do not reach the required level of geometric thinking, i.e., the levels of informal deduction, formal deduction, or rigor.

3. Research Design

Research on geometric thinking consists of two parts: determining the levels of geometric thinking and analyzing errors in solving geometric tasks. Based on the performed studies, we focused on determining the levels of geometric thinking in students from the Teacher Training for Primary Education program. The levels of students’ geometric thinking were determined using the van Hiele geometric test. The test was applied with the consent of Professor Zelman Usiskin, and we listed “Copyright © 1980 by the University of Chicago” on each copy of the test. In the evaluation part, we addressed the interrelationships between the level of geometric thinking in students and the success of solving geometric tasks. We also analyzed which correctly solved items of the van Hiele geometric test affect the achieved level of geometric thinking and the correct solution to geometric tasks.

3.1. Research Goals

The following research goals have been stated:

• To determine the level of geometric thinking of students of the Teacher Training for Primary Education (TTPE) program.
• To design geometric tasks and quantitatively evaluate the solution to these tasks.
• To qualitatively evaluate and analyze students’ misconceptions in solving these tasks.
• To compare and reveal the connections between the solution to two geometric tasks with the attained level of geometric thinking according to the Van Hiele theory.

3.2. Research Sample

The research was conducted in February 2019 and the research sample consisted of 59 master’s students of TTPE at Constantine the Philosopher University in Nitra. The students finished their secondary school studies at the various types of schools with various mathematics curricula, and thus had different geometrical skills. There were 32% of students who graduated from grammar schools, 29% studied at secondary vocational schools, and 39% of students graduated from pedagogic high schools. Grammar schools in Slovakia provide a general education to prepare students for higher education, especially universities. Secondary vocational schools consist of general education and vocational training to learn practical skills in a given profession. Most students from the research sample attended business academies. Pedagogic high schools prepare students for teaching in kindergartens. Students passed an exam in geometry during their university studies, and thus revised the fundamental knowledge of geometric shapes and their properties.

3.3. Research Tools

3.3.1. The van Hiele Geometric Test

The van Hiele geometric test was created in 1980 by Professor Zelman Usiskin of the University of Chicago. The test was created based on the van Hiele model of geometric thinking and was designed as part of the CDASSG project to validate the van Hiele theory. The test contains five items for each of the five levels of geometric thinking. The test tasks were created so that the group of items corresponded to the knowledge and skills of students at different levels, according to van Hiele model [27].

As the van Hiele theory states, the switch to a higher level is conditioned by mastering a lower level. If a student at a certain level N did not answer a sufficient number of items correctly, but was able to answer a sufficient number of items at a level higher than N, the test could be evaluated in two ways:

• Classic case: the student does not meet the criteria; he/she is not assigned to any level of geometric thinking.
• Modified case: the student is at the level of N-1 geometric thinking [33].

For example: If the student correctly answers the allotted number of questions in the first two blocks as well as the allotted number of questions in the fourth and/or fifth block, then the student is identified as not fitting the criterion in the classic case. However, in the modified case, the student is identified as having an understanding at level 2 [27].

When evaluating the test, it is crucial to specify the criteria and method of evaluation. In our research, we use the criterion of three correct items from five tasks and a modified way of assessing the level of geometric thinking in students.

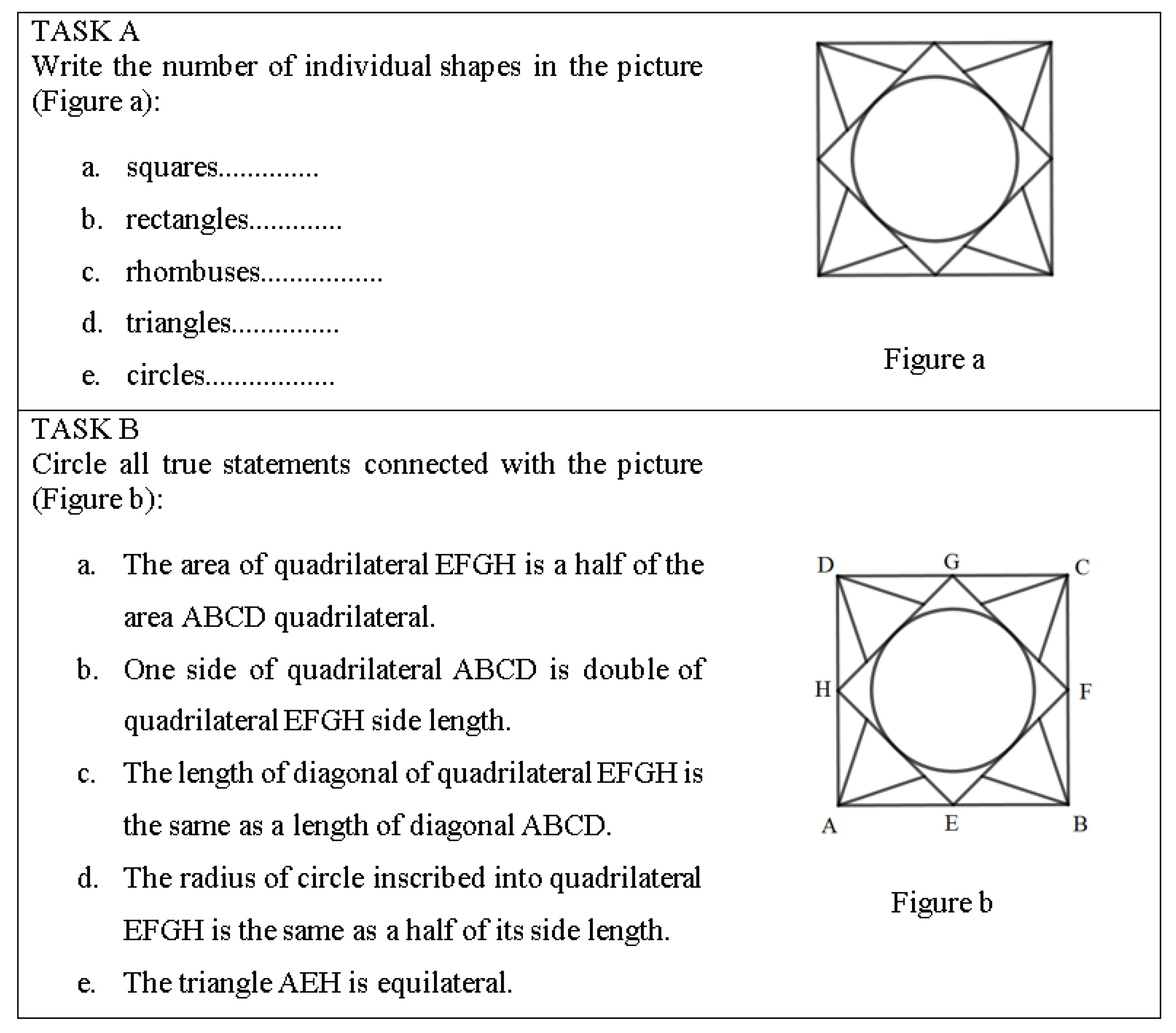
3.3.2. Two Geometric Tasks

Both research tasks were related to the geometric patterns shown in Figure 1 and were focused on the competencies of students to interpret this picture. The first task was created with a focus on the ability of students to correctly identify geometric shapes in a composite geometric figure and identify them correctly. The second task was designed to determine the ability of students to connect the properties of different geometric shapes related to the picture.

The following tasks were designed, analyzed and evaluated (Figure 1):

3.4. Statistical Implicative Analysis Methods

In addition to the standard quantitative evaluation, the methods of implicit statistical analysis were used for a deeper analysis of the dependencies and relationships between the mentioned didactic variables. The implicative analysis is indeed a powerful tool, and was originally designed for research purposes in mathematics [34]. This data analysis method created by Régis Gras also had a significant impact on a variety of areas ranging from pedagogical and psychological research to data mining. This method allows for the examination of the quasi-implications among variables, also called association rules. In the data analysis we used the software, C.H.I.C. (Classification Hiérarchique Implicative et Cohésitive), which enabled the implementation of a Statistical Implicative Analysis by offering an effective interface that was easy to use [35]. This software allows a clear visualization of the relationships of the similarities and implications between variables, or classes of variables, in a situational problem through the use of graphs.

The following didactic variables were presented in the a priori analysis:

• Type L—level of geometrical thinking of the students.
  • L1—the student reaches the visualization level;
  • L2—the student reaches the analysis level;
  • L3—the student reaches the informal deductive level;
  • L4—the student reaches the formal deductive level.
• Type VH—the student’s solution to the van Hiele test.
  • VH 1–VH 20—the student correctly solves items 1–20 of the van Hiele geometry test.
• Type A—the student’s solution to Task A.
  • Aa—the student correctly determines the number of squares;
  • Ab—the student correctly determines the number of rectangles;
  • Ac—the student correctly determines the number of rhombuses;
  • Ad—the student correctly determines the number of triangles;
  • Ae—the student correctly determines the number of circles;
  • TA—the student correctly determines the number of all geometric shapes.
• Type B—the student’s solution to Task B.
  • Ba—the student marks the statement a;
  • Bb—the student marks the statement b;
  • Bc—the student marks the statement c;
  • Bd—the student marks the statement d;
  • Be—the student marks the statement e;
  • TB—the student marks all of the statements correctly;
  • T_A_B—the student solves the whole task, A and B, correctly.

4. Data Analyses and Interpretation of Results

4.1. The Van Hiele Geometric Test results

The teachers of TTPE should achieve a higher level of geometric thinking than their potential pupils, as they should be able to help their pupils move to a higher level of geometric thinking. According to Mc Anelly [36], who stated that the separated levels of geometric thinking in the age category, pupils in the first stage of primary school should be at the levels of visualization or analysis. For this reason, we assumed that future primary school teachers should achieve at least the level of informal deduction.

The same level of geometric thinking for future primary school teachers was assumed by Knight [27]. Halat and Şahin [30], in their article, wrote that high school students should be able to prove theorems, in other words, they should at least achieve the informal deduction level. Patkin and Barkai [32] also expected that TTPE students should reach the informal deduction level at the end of their studies. According to Balut [37] the third level of geometric thinking (informal deduction) is insufficient for these students and that it would be appropriate for them to reach at least the formal deduction level.

Figure 2 shows the percentage representation of students at each level of geometric thinking. As can be observed, only 59.3% of students achieved the required informal deductive level or a higher level of geometric thinking.

Figure 3 shows the percentage representation of each level of geometric thinking for students from grammar schools, pedagogical and social academies, and secondary vocational schools. The excellent results at the level of visualization and analysis were achieved by the students from grammar schools and secondary vocational schools. We observed the biggest difference in the achieved level of geometric thinking in students of pedagogical and social academies. Figure 3 also shows that the level of analysis that was achieved by 60% of students of pedagogical and social academies and only 40% of them reached the informal deductive level.

4.2. Two Geometric Tasks Results

Figure 4 shows the achievements of students in solving individual tasks. The most demanding task for the students was to determine the total number of triangles in the picture—the subtask Ad. Only 47% of the students identified the correct number of triangles. A deeper analysis of students’ solutions to subtask Ad was made in the conference paper [38], and there was a further mistake. Thirteen percent of students considered a square that was rotated 45 degrees as a rhombus. In the Slovak geometry curriculum, we distinguish between two shapes: a rhombus and a square. A square is a parallelogram with equal and perpendicular sides; a rhombus is a parallelogram with equal and non-perpendicular sides. The least success in Task B was observed in subtask Ba, which focused on shapes with the same area. The decision that the area of the quadrilateral EFGH was half the area of quadrilateral ABCD was based on spatial skills, and students could solve the task even without special geometric knowledge.

4.3. The Relationship between the Level of Geometric Thinking and the Solutions to Two Geometric Tasks

Using the statistical program, C.H.I.C, we revealed the connections between the solution to two geometric tasks and the achieved level of geometric thinking according to van Hiele theory. Based on the mentioned didactic variables, Similarity graphs, implicative trees, and an implicative graph were produced in this software.

Figure 5 shows a similarity graph for all didactic variables Type A and B. As we can see, there is a considerable similarity between the variables Ad and Ba, which both proved to be the most challenging subtasks for students. This means that students shared similar answers, both correct and incorrect, for each of these tasks simultaneously.

As can be deduced from Figure 6, the implication tree represents the implications between some didactic variables in the a priori analysis. As we can see, it is important to observe the Ad and Ba variables, as well as the graph of similarities (Figure 5). The graph in Figure 6 shows the statistical dependencies between the correct solution to the subtasks (Ad, Ba) and the correct solution to the entire task A or task B. The strongest hierarchy (first level) is between the variables: Ad, TA (cohesion = 1). A student who determines the correct total number of triangles can correctly identify the total number of geometric shapes in the picture. The success of task B was influenced by the correct solution to the most demanding subtask Ba, in which the students had to calculate the relationship between the area of the square as well as the area of the square inscribed within this square. The second level of the hierarchy consists of a set of variables TB, Ba and Ad, TA (cohesion = 0.82). If a student correctly identifies all the properties of the geometric shapes, then they can correctly determine the number of triangles and the number of all geometric shapes in the picture.

A significant similarity (similarity = 0.86) between the didactic variables, TB and L3, can be seen in Figure 7. This means that achieving the level of informal deductions is related to the ability of students to link the properties of different geometric shapes related to the picture. This is also in accordance with characterization of this level in the van Hiele theory.

Figure 8 presents a hierarchical tree of the significant implications between the correct solution to the van Hiele geometric test items, levels of geometric thinking, and the correct solution to both geometric tasks. The implicative tree confirms the statistical dependence, mainly between the items at the level of analysis and informal deduction, the achieved level of informal deduction, and the overall success of solving geometric tasks. This fact is proved by the created group of implications, which contains the following variables: T_A_B, L3, VH8, VH10, VH14, VH18. An important finding from our research is that there is an implication between the correct solutions to both geometric tasks and the level of formal deduction in the van Hiele test; the variable T_A_B implies the variable L3 (cohesion = 0.82). We can state that our two geometric tasks can be used as a suitable test for university students who are set to be future primary school teachers, to find out if they reach the required level of geometric thinking according to the van Hiele theory, i.e., the level of informal deduction.

The implicative graph allows us to observe the software-generated dependencies of over 80% between the following groups of variables. Only the relationships between variables above 80% are of interest for the research results. There is a graph that contains all didactic variables, which vary in color according to their strength and is shown in Figure 9. According to the conditions specified in the C.H.I.C software, the intensity of implication is indicated by red (99%), blue (95%), green (90%), and gray (80%).

The graph in Figure 9 represents the implication: if the student correctly circles all the statements in Task B, then he/she correctly adds all the geometric shapes in Task A (implication = 0.85). It also confirms that if the student solves Task A correctly, then he/she correctly answers items 3 and 5 in the van Hiele geometric test. These tasks aim to define parallelograms and rectangles. An interesting finding is confirmed by the implication of Ad → VH15 (90%). Based on this implication, we know that if the student correctly adds all of the triangles in the Figure 1, he/she correctly answers the item included at the level of informal deduction, which focuses on the relationship between rectangles and parallelograms. The implication L1 → Bb (90%) shows that at the level of visualization, the student is able to determine the relationship between the length of the squares’ sides and the length of squares’ sides inscribed within it.

5. Conclusions

The exploratory study was focused on determining the level of geometric thinking and solving two geometric tasks by by TTPE students of the Constantine the Philosopher University in Nitra, Slovakia. Various studies [11,27,28] show that teachers in primary education have significant thinking difficulties at higher levels of geometric thinking. Additionally, TTPE students often have only a formal knowledge and problem-solving skills regarding geometric tasks. The results of Ndlovu’s research [39] also showed that teachers’ geometric knowledge was weaker than expected. We can observe similar problems with TTPE students.

Our findings show that more than 40% of TTPE students in the research sample do not reach the required level of geometric thinking. Similarly, Knight [27], in their research, state that, after completion of the course required by the Elementary Education program at the University of Maine, students did not achieve higher than Level 3 (informal deduction), the level of understanding expected of students completing grade 8. More than 90% of students have significant problems with deductive thinking, as well as mathematical calculations in geometry. Jupri’s research [28] also demonstrated that half of the future teachers in their research sample lacked skills in deductive thinking and in solving problems with geometric calculations.

The van Hiele theory, as opposed to Piaget’s theory, proclaims that development is a product of experience and the quality of instruction rather than age [40]. The analysis of our research data shows that the level of geometric thinking of students, according to the van Hiele theory, is also influenced by the type of high school from which they graduated. The lowest level of geometric thinking was achieved by students from pedagogical and social academies, while up to 60% of these students did not reach at least the required level of informal deduction. Our results are in line with the research statement of Haviger and Vojkůvková [26], who claim that the low results of students from different secondary schools are caused by the school’s focus; algebra is prioritized over geometry in some schools.

We observed problems with understanding the concept of the triangle and square in TTPE students. The students considered the shape with three vertices to be a triangle, even though its sides were rounded. A square that was rotated 45° was considered by the students to be a rhombus. Similar problems are mentioned in the study of Žilková et al. [41], where the authors claim that students do not have solid and stable conceptions of elementary geometrical shapes and their properties, even at the lowest cognitive levels, or if they do have conceptions, they are often wrong. Fujita and Jones [42] describe the same problem in Scotland, as well as Çontay and Paksu [43] in Turkey. Additionally, Rahaju et al. [44] state that, despite the fact that the topics related to triangles have been studied since preschool age, there are still preschool teachers who do not understand the concept of the triangle.

From the analysis of Task A, we found that determining the correct number of triangles in the picture had the most significant effect on identifying the total correct number of geometric shapes in it. Similarly, the graphs of the results of task B show that if the students understood the properties of geometric shapes in the picture, then they could use the picture to correctly identify all the triangles and count the other geometric shapes without difficulty.

The connections between the solutions to two geometric tasks and the achieved levels of geometric thinking according to the van Hiele theory were also revealed. From the similarity graph, it can be concluded that the correct solution to Task A or Task B, the content of which does not exceed the scope of the elementary school curriculum, is related to the level of formal deduction or level of informal deduction. The implication analysis also showed that if the students correctly solved both geometric tasks, which were at the level of the analysis of geometric thinking, then they reached the level of informal deduction in the van Hiele test.

Our findings, in line with the results of other researchers, showed that increased attention must be given to teaching geometry, in order to prepare future teachers for primary education. One of the ways to improve geometry knowledge for teaching is to use the van Hiele theory-based instructional activities in their preparation [45,46]. As future teachers, they should master the basic knowledge of geometry so that they can teach it effectively. University students should master basic geometric concepts, as explained in the previous study and should also understand the properties of geometric shapes. As we can see in our practice, incorporating van Hiele theory into geometric and didactic subjects at university is useful. Based on the test results, students become more aware of their shortcomings at the beginning of their studies and work more effectively together to eliminate their mistakes from the perspective of the future primary school teacher.

In Slovakia, the teaching of geometry is not based on the van Hiele theory, but certain principles can be considered as generally valid. The brief recommendation at the end of our study is to respect the basic principles of the cognitive process, the gradual transition from concrete to abstract, the use of appropriate mathematical language in teaching geometry, to build geometric ideas on the basis of a constructivist approach. Geometric concepts should be better connected with the use of models, their manipulation, and the search for real objects in the world around us. Modern digital technologies should be integrated into teaching in an appropriate way, especially in terms of motivating students and connecting the real world with the virtual world.