Attraction Basins in Metaheuristics: A Systematic Mapping Study
Abstract
1. Introduction
- optimisation problem types where attraction basins have been used,
- topics and contexts within attraction basins have been used,
- definitions of attraction basins,
- algorithms to compute attraction basins, and
- trends.
2. Related Work
2.1. Systematic Review
- A Systematic Literature Review: Very specific research goals with emphasis on quality assessment, usually done by experienced researchers, closely defined by research questions [54].
2.2. Metaheuristics
3. Method
- Defining research questions.
- Conducting a search for studies (constructing a seed set).
- Full-text screening based on inclusion/exclusion criteria.
- Iterative snowballing (each study is full-text screened prior to the next iteration).
- Classifying the studies.
- Data extraction and aggregation.
3.1. Research Questions
- RQ1: What terms (synonyms) have been used for attraction basins?
- RQ2: For which problem types (discrete, real-valued, static, dynamic, single-objective, and multi-objective) have attraction basins been used? Which search spaces are investigated on the topic better?
- RQ3: Which definitions have been used for attraction basins?
- RQ4: Which algorithms have been developed to compute attraction basins?
- RQ5: For what topics have attraction basins been used? What is the most popular topic?
- RQ6: Which journals and conferences publish the papers on the topic, and how often? Which authors investigate attraction basins more in-depth and which type of problems?
3.2. Search, Screening Criteria, and Classification
- the study is in the field of Computer Science and related to metaheuristics,
- the study deals with attraction basins, and
- the study is published in a journal or conference.
- The study is not presented in English.
- The study is not in a final publication stage.
- The study is not accessible in full-text.
- The study is a duplicate of another study.
- The study only mentions attraction basins without any further elaboration.
- ISI Web of science: TS = (“attraction basin*” OR “basin* of attraction”) AND TS = (“optimi*ation” OR “metaheuristic*” OR “heuristic*” OR “evolutionary algorithm*” OR “evolutionary computation” OR “genetic algorithm*” OR “swarm intelligence” OR “swarm algorithm*” OR “search algorithm*” OR “local search”), and then refined by RESEARCH DOMAINS: (SCIENCE TECHNOLOGY) AND DOCUMENT TYPES: (ARTICLE) AND LANGUAGES: (ENGLISH) AND RESEARCH AREAS: (COMPUTER SCIENCE), and
- Scopus: TITLE-ABS-KEY (“attraction basin*” OR “basin* of attraction”) AND TITLE-ABS-KEY (“optimi*ation” OR “metaheuristic*” OR “heuristic*” OR “evolutionary algorithm*” OR “evolutionary computation” OR “genetic algorithm*” OR “swarm intelligence” OR “swarm algorithm*” OR “search algorithm*” OR “local search”) AND LANGUAGE (english) AND (LIMIT-TO(PUBSTAGE, “final”)) AND (LIMIT-TO(SUBJAREA, “COMP”)) AND (LIMIT-TO(DOCTYPE, “cp”) OR LIMIT-TO(DOCTYPE, “ar”))
4. Results and Discussion
4.1. RQ1: Attraction Basin Synonyms
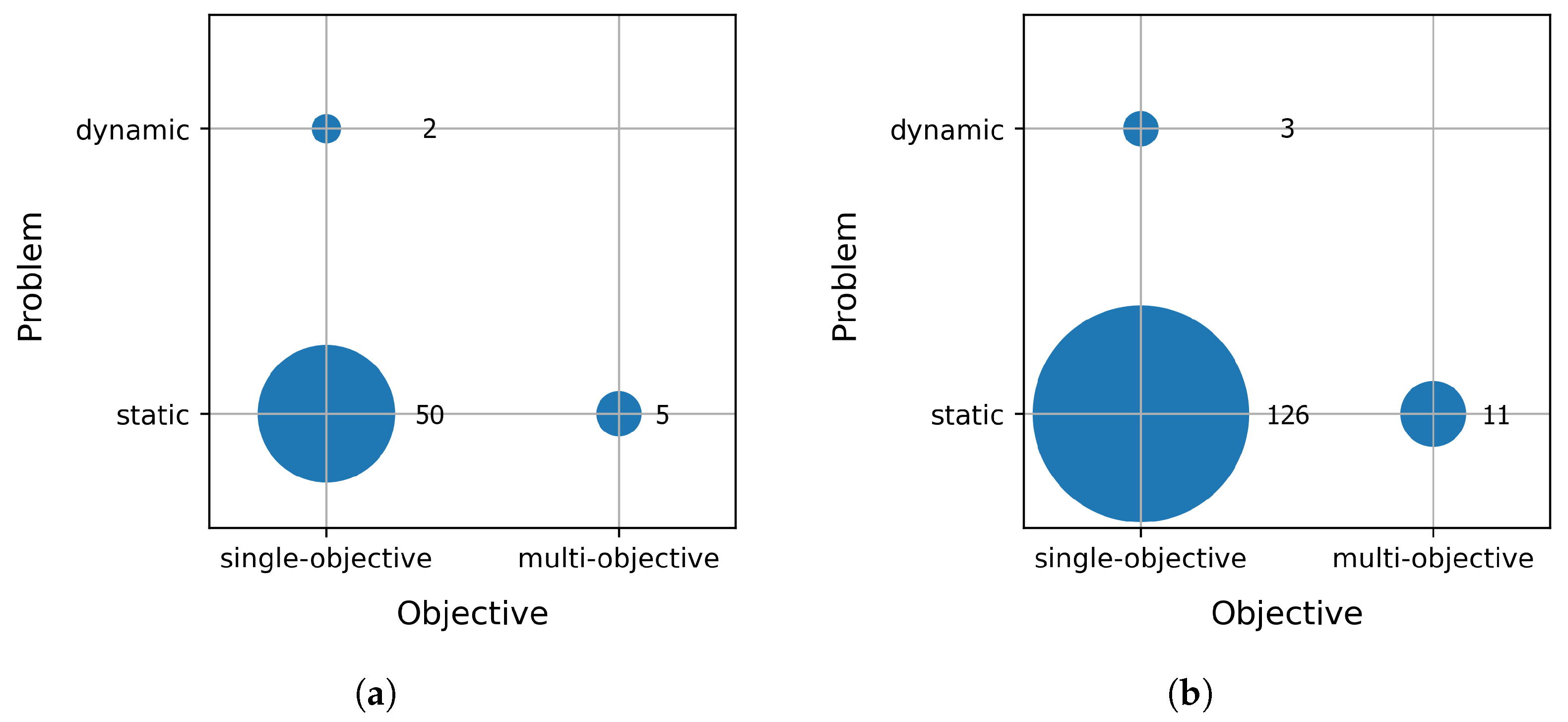
4.2. RQ2: Problem Types
4.3. RQ3: Definitions Used for Attraction Basins
- Ref. [79]: “A local optimum’s region of attraction is the set of all points in S [search space] which are primarily attracted to it. Regions of attraction may overlap. A local optimum’s strict region of attraction is the set of all points in S which are primarily attracted to it, and are not primarily attracted to any other local optimum. Strict regions of attraction do not overlap.”
- Ref. [80]: “Goldberg (1991) formally defines basins of attraction to a point as all points x such that a given hillclimber has a non-zero probability of climbing to within some ε of if started within some δ-neigbhorhood of x.”
- Ref. [81]: “A basin of attraction of a vertex is the set of vertices ”, where is the set of vertices, is the neighbourhood obtained by operator , and is the objective function to be optimised.
- Ref. [82]: “The attraction basin of a local optimum is the set of points of the search space such that a steepest ascent algorithm starting from ends at the local optimum .”
- The previous definition is generalised, i.e., the steepest ascent algorithm is replaced with the so-called pivot rule (any algorithm can be used, including a stochastic one) [83],
- Ref. [84]: “[Attraction basin] … the set of points that can reach the target via neutral or positive mutations.”
- Ref. [85]: “Given a deterministic algorithm A, the basin of attraction of a point s, is defined as the set of states that, taken as initial states, give origin to trajectories that include point s.”
- Ref. [86]: “The basin of attraction of the local minima are the set of configurations where the cost of flipping a backbone variable is less than the penalty caused by disrupting the associated block cost and cross-linking cost.”
- Ref. [87]: “The basin of attraction of a local minimum is the set of initial conditions which lead, after optimisation, to that minimum.”
- Ref. [88]: “The basin of attraction of a local optimum i is the set .”
- Ref. [32]: “An attraction basin is a region in which there is a single locally optimal point and all other points have their shortest path to reach the locally optimal point.”
- Ref. [89]: “The basin of attraction of the local optimum i is the set .”, where is the probability that s will end up in i.
- Ref. [29]: “Simply put, they are the areas around the optima that lead directly to the optimum when going downhill (assuming a minimisation problem).”—authors distinguish strong (points that lead exclusively to a single optimum), and weak attraction basins (points that can lead to many optima).
- Ref. [90]: “The attraction basin is defined as the biggest hyper-sphere that contains no valleys around a seed.”
- Ref. [91]: “The basin of attraction of a local optimum is the set of solution candidates from which the focal local optimum can be reached using a number of local search steps (no diversification steps are allowed).”
- Ref. [14]: “An attractor associated with an optimisation algorithm is the ultimate optimal point found by the iterative procedure. When the algorithm converges to an answer, the attractor of the algorithm is a single fixed-point, the simplest type of attractors. Otherwise, it is not a fixed-point attractor. The union of all orbits which converge towards an attractor is called its basin of attraction.”
- Ref. [92]: “Each point in an attraction basin has a monotonic path of increasing (for maxima) or decreasing (for minima) fitness to its local optima.”
- the domain they cover (discrete, real-valued or both),
- the number of objectives in the optimisation problem (single-objective, multi-objective, or both),
- the attraction mechanism they use (steepest ascent, local search, hill-climbing, stochastic algorithm, deterministic algorithm, monotonic increasing/decreasing, any optimisation algorithm, shortest path, etc.),
- the distinguishing between different types of basins (weak or strong, strict or non-strict), or
- the degree of generality.
4.4. RQ4: Algorithms Used for Attraction Basins
4.5. RQ5: Most Popular Topics for Attraction Basins
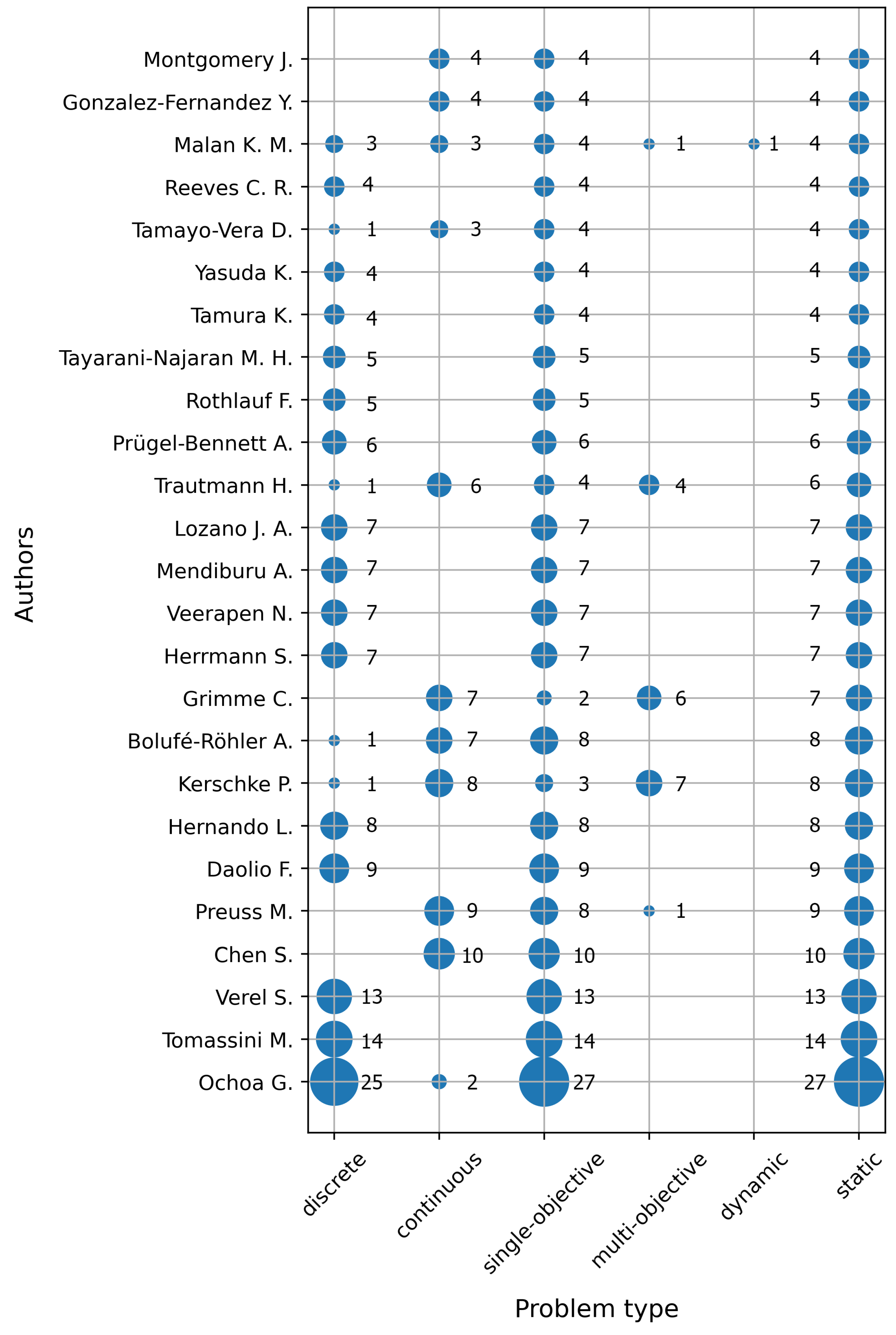
4.6. RQ6: Demographic Data of SMS
4.7. Necessity of Snowballing
5. Conclusions
- Discrete domains were investigated far better than continuous.
- Single-objective static problems dominated. Multi-objective problems were investigated better within the continuous domain, although still very weakly.
- Different definitions of attraction basins were used, while the most frequent one was based on a local search. Within the continuous domain researchers often use clusters or niches as approximated attraction basins. There is a lack of a general framework of attraction basins in the field of metaheuristics.
- Only a few “exact” algorithms were found, exhaustive enumeration with local search, reverse hillclimbing, and the primary attraction algorithm. No parallel and scalable algorithm was found to compute attraction basins.
- Attraction basins were used for many purposes, such as fitness landscape analysis, clustering and niching, comparison of metaheuristics, exploration and exploitation, and analysis of metaheuristics, to enhance the search, problem generation, filled functions, etc. Local Optima Network is the topic that received the most attention in the area regarding the attraction basins.
- The notion of attraction basins first appeared in the 1970s.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Algorithm A1 Local Search Algorithms: Best Improvement and First Improvement |
|
| Algorithm A2 Reverse hill climbing |
|
| Algorithm A3 Primary attraction to local/global optima |
|
| Algorithm A4 Algorithm to compute attraction basins in real-valued domains |
|
References
- Ellison, G. Basins of Attraction, Long-Run Stochastic Stability, and the Speed of Step- by-Step Evolution. Rev. Econ. Stud. 2000, 67, 17–45. [Google Scholar] [CrossRef]
- Page, F.H.; Wooders, M.H. Strategic Basins of Attraction, the Farsighted Core, and Network Formation Games; Technical Report; University of Warwick—Department of Economics: Coventry, UK, 2005. [Google Scholar]
- Vicario, E. Imitation and Local Interactions: Long Run Equilibrium Selection. Games 2021, 12, 30. [Google Scholar] [CrossRef]
- Scott, M.; Neta, B.; Chun, C. Basin attractors for various methods. Appl. Math. Comput. 2011, 218, 2584–2599. [Google Scholar] [CrossRef]
- Cordero, A.; Soleymani, F.; Torregrosa, J.; Shateyi, S. Basins of Attraction for Various Steffensen-Type Methods. J. Appl. Math. 2014, 2014, 539707. [Google Scholar] [CrossRef]
- Zotos, E.; Sanam Suraj, M.; Mittal, A.; Aggarwal, R. Comparing the Geometry of the Basins of Attraction, the Speed and the Efficiency of Several Numerical Methods. Int. J. Appl. Comput. Math. 2018, 4, 105. [Google Scholar] [CrossRef][Green Version]
- Demongeot, J.; Goles, E.; Morvan, M.; Noual, M.; Sené, S. Attraction Basins as Gauges of Robustness against Boundary Conditions in Biological Complex Systems. PLoS ONE 2010, 5, e0011793. [Google Scholar] [CrossRef] [PubMed]
- Gardiner, J. Evolutionary basins of attraction and convergence in plants and animals. Commun. Integr. Biol. 2013, 6, e26760. [Google Scholar] [CrossRef]
- Conforte, A.J.; Alves, L.; Coelho, F.C.; Carels, N.; Da Silva, F.A.B. Modeling Basins of Attraction for Breast Cancer Using Hopfield Networks. Front. Genet. 2020, 11, 314. [Google Scholar] [CrossRef] [PubMed]
- Isomäki, H.M.; Von Boehm, J.; Räty, R. Fractal basin boundaries of an impacting particle. Phys. Lett. A 1988, 126, 484–490. [Google Scholar] [CrossRef]
- Xu, N.; Frenkel, D.; Liu, A.J. Direct Determination of the Size of Basins of Attraction of Jammed Solids. Phys. Rev. Lett. 2011, 106, 245502. [Google Scholar] [CrossRef]
- Guseva, K.; Feudel, U.; Tél, T. Influence of the history force on inertial particle advection: Gravitational effects and horizontal diffusion. Phys. Rev. E 2013, 88, 042909. [Google Scholar] [CrossRef]
- Pitzer, E.; Affenzeller, M.; Beham, A. A closer look down the basins of attraction. In Proceedings of the 2010 UK Workshop on Computational Intelligence, Colchester, UK, 8–10 September 2010; pp. 1–6. [Google Scholar]
- Tsang, K.K. Basin of Attraction as a measure of robustness of an optimization algorithm. In Proceedings of the 2018 14th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery, Huangshan, China, 28–30 July 2018; pp. 133–137. [Google Scholar]
- Drugan, M.M. Estimating the number of basins of attraction of multi-objective combinatorial problems. J. Comb. Optim. 2019, 37, 1367–1407. [Google Scholar] [CrossRef]
- Gogna, A.; Tayal, A. Metaheuristics: Review and application. J. Exp. Theor. Artif. Intell. 2013, 25, 503–526. [Google Scholar] [CrossRef]
- Back, T.; Fogel, D.B.; Michalewicz, Z. Handbook of Evolutionary Computation, 1st ed.; Institute of Physics Publishing: Bristol, UK, 1997. [Google Scholar]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Cai, X.; Hu, Z.; Zhao, P.; Zhang, W.; Chen, J. A hybrid recommendation system with many-objective evolutionary algorithm. Expert Syst. Appl. 2020, 159, 113648. [Google Scholar] [CrossRef]
- Li, J.Y.; Zhan, Z.H.; Wang, C.; Jin, H.; Zhang, J. Boosting Data-Driven Evolutionary Algorithm with Localized Data Generation. IEEE Trans. Evol. Comput. 2020, 24, 923–937. [Google Scholar] [CrossRef]
- Einakian, S.; Newman, T.S. An examination of color theories in map-based information visualization. J. Comput. Lang. 2019, 51, 143–153. [Google Scholar] [CrossRef]
- Jerebic, J.; Mernik, M.; Liu, S.H.; Ravber, M.; Baketarić, M.; Mernik, L.; Črepinšek, M. A novel direct measure of exploration and exploitation based on attraction basins. Expert Syst. Appl. 2021, 167, 114353. [Google Scholar] [CrossRef]
- Caamaño, P.; Prieto, A.; Becerra, J.A.; Bellas, F.; Duro, R.J. Real-Valued Multimodal Fitness Landscape Characterization for Evolution. In Neural Information Processing. Theory and Algorithms; Wong, K.W., Mendis, B.S.U., Bouzerdoum, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 567–574. [Google Scholar]
- Malan, K.M.; Engelbrecht, A.P. A Survey of Techniques for Characterising Fitness Landscapes and Some Possible Ways Forward. Inf. Sci. 2013, 241, 148–163. [Google Scholar] [CrossRef]
- Chen, S.; Bolufé-Röhler, A.; Montgomery, J.; Hendtlass, T. An Analysis on the Effect of Selection on Exploration in Particle Swarm Optimization and Differential Evolution. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 3037–3044. [Google Scholar]
- Wright, S. The Roles of Mutation Inbreeding, Crossbreeding and Selection in Evolution. In Proceedings of the Sixth International Congress on Genetics, Ithaca, NY, USA, 24–31 August 1932; Brooklyn Botanic Garden: New York, NY, USA, 1932; Volume 1. [Google Scholar]
- Mersmann, O.; Preuss, M.; Trautmann, H. Benchmarking Evolutionary Algorithms: Towards Exploratory Landscape Analysis. In Parallel Problem Solving from Nature, PPSN XI; Schaefer, R., Cotta, C., Kołodziej, J., Rudolph, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 73–82. [Google Scholar]
- Muñoz, M.A.; Kirley, M.; Halgamuge, S.K. Landscape characterization of numerical optimization problems using biased scattered data. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Pitzer, E.; Affenzeller, M. A Comprehensive Survey on Fitness Landscape Analysis. In Recent Advances in Intelligent Engineering Systems; Springer: Berlin/Heidelberg, Germany, 2012; pp. 161–191. [Google Scholar]
- Tayarani-N, M.H.; Prügel-Bennett, A. An Analysis of the Fitness Landscape of Travelling Salesman Problem. Evol. Comput. 2016, 24, 347–384. [Google Scholar] [CrossRef] [PubMed]
- Merz, P. Advanced Fitness Landscape Analysis and the Performance of Memetic Algorithms. Evol. Comput. 2004, 12, 303–325. [Google Scholar] [CrossRef] [PubMed]
- Xin, B.; Chen, J.; Pan, F. Problem Difficulty Analysis for Particle Swarm Optimization: Deception and Modality. In Proceedings of the First ACM/SIGEVO Summit on Genetic and Evolutionary Computation, Shanghai, China, 12–14 June 2009; Association for Computing Machinery: New York, NY, USA, 2009; pp. 623–630. [Google Scholar]
- Mersmann, O.; Bischl, B.; Trautmann, H.; Preuss, M.; Weihs, C.; Rudolph, G. Exploratory Landscape Analysis. In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, Dublin, Ireland, 12–16 July 2011; Association for Computing Machinery: New York, NY, USA, 2011; pp. 829–836. [Google Scholar]
- Rodriguez-Maya, N.E.; Graff, M.; Flores, J.J. Performance Classification of Genetic Algorithms on Continuous Optimization Problems. In Nature-Inspired Computation and Machine Learning; Gelbukh, A., Espinoza, F.C., Galicia-Haro, S.N., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 1–12. [Google Scholar]
- Kerschke, P.; Hoos, H.H.; Neumann, F.; Trautmann, H. Automated Algorithm Selection: Survey and Perspectives. Evol. Comput. 2019, 27, 3–45. [Google Scholar] [CrossRef] [PubMed]
- Liefooghe, A.; Verel, S.; Lacroix, B.; Zăvoianu, A.C.; McCall, J. Landscape Features and Automated Algorithm Selection for Multi-Objective Interpolated Continuous Optimisation Problems. In Proceedings of the Genetic and Evolutionary Computation Conference, Lille, France, 10–14 July 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 421–429. [Google Scholar]
- Eiben, A.E.; Schippers, C.A. On Evolutionary Exploration and Exploitation. Fundam. Inform. 1998, 35, 35–50. [Google Scholar] [CrossRef]
- Ollion, C.; Doncieux, S. Why and How to Measure Exploration in Behavioral Space. In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, Dublin, Ireland, 12–16 July 2011; Association for Computing Machinery: New York, NY, USA, 2011; pp. 267–274. [Google Scholar]
- Črepinšek, M.; Liu, S.H.; Mernik, M. Exploration and Exploitation in Evolutionary Algorithms: A Survey. ACM Comput. Surv. 2013, 45, 1–33. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, J. Exploration-exploitation tradeoffs in metaheuristics: Survey and analysis. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 8633–8638. [Google Scholar]
- Squillero, G.; Tonda, A. Divergence of character and premature convergence: A survey of methodologies for promoting diversity in evolutionary optimization. Inf. Sci. 2016, 329, 782–799. [Google Scholar] [CrossRef]
- Kitchenham, B.; Pretorius, R.; Budgen, D.; Pearl Brereton, O.; Turner, M.; Niazi, M.; Linkman, S. Systematic literature reviews in software engineering—A tertiary study. Inf. Softw. Technol. 2010, 52, 792–805. [Google Scholar] [CrossRef]
- Petersen, K.; Vakkalanka, S.; Kuzniarz, L. Guidelines for conducting systematic mapping studies in software engineering: An update. Inf. Softw. Technol. 2015, 64, 1–18. [Google Scholar] [CrossRef]
- Kosar, T.; Bohra, S.; Mernik, M. Domain-Specific Languages: A Systematic Mapping Study. Inf. Softw. Technol. 2016, 71, 77–91. [Google Scholar] [CrossRef]
- Kitchenham, B.A.; Dyba, T.; Jorgensen, M. Evidence-Based Software Engineering. In Proceedings of the 26th International Conference on Software Engineering, Edinburgh, UK, 28–28 May 2004; IEEE Computer Society: Washington, DC, USA, 2004; pp. 273–281. [Google Scholar]
- Dyba, T.; Kitchenham, B.; Jorgensen, M. Evidence-based software engineering for practitioners. IEEE Softw. 2005, 22, 58–65. [Google Scholar] [CrossRef]
- Jorgensen, M.; Dyba, T.; Kitchenham, B. Teaching evidence-based software engineering to university students. In Proceedings of the 11th IEEE International Software Metrics Symposium, Washington, DC, USA, 19–22 September 2005; Volume 2005, p. 24. [Google Scholar]
- Choraś, M.; Demestichas, K.; Giełczyk, A.; Herrero, A.; Ksieniewicz, P.; Remoundou, K.; Urda, D.; Woźniak, M. Advanced Machine Learning techniques for fake news (online disinformation) detection: A systematic mapping study. Appl. Soft Comput. 2021, 101, 107050. [Google Scholar] [CrossRef]
- Houssein, E.H.; Gad, A.G.; Wazery, Y.M.; Suganthan, P.N. Task Scheduling in Cloud Computing based on Meta-heuristics: Review, Taxonomy, Open Challenges, and Future Trends. Swarm Evol. Comput. 2021, 62, 100841. [Google Scholar] [CrossRef]
- Ferranti, N.; Rosário Furtado Soares, S.S.; De Souza, J.F. Metaheuristics-based ontology meta-matching approaches. Expert Syst. Appl. 2021, 173, 114578. [Google Scholar] [CrossRef]
- Dragoi, E.N.; Dafinescu, V. Review of Metaheuristics Inspired from the Animal Kingdom. Mathematics 2021, 9, 2335. [Google Scholar] [CrossRef]
- Kitchenham, B.; Brereton, P.; Budgen, D. The Educational Value of Mapping Studies of Software Engineering Literature. In Proceedings of the 32nd ACM/IEEE International Conference on Software Engineering, Cape Town, South Africa, 1–8 May 2010; Association for Computing Machinery: New York, NY, USA, 2010; pp. 589–598. [Google Scholar]
- Felizardo, K.R.; De Souza, E.F.; Napoleão, B.M.; Vijaykumar, N.L.; Baldassarre, M.T. Secondary studies in the academic context: A systematic mapping and survey. J. Syst. Softw. 2020, 170, 110734. [Google Scholar] [CrossRef]
- Kitchenham, B.A.; Budgen, D.; Brereton, O.P. The Value of Mapping Studies: A Participant observer Case Study. In Proceedings of the 14th International Conference on Evaluation and Assessment in Software Engineering, London, UK, 13–14 May 2014; BCS Learning & Development Ltd.: Swindon, UK, 2010; pp. 25–33. [Google Scholar]
- Wohlin, C.; Runeson, P.; Da Mota Silveira Neto, P.A.; Engström, E.; Do Carmo Machado, I.; De Almeida, E.S. On the reliability of mapping studies in software engineering. J. Syst. Softw. 2013, 86, 2594–2610. [Google Scholar] [CrossRef]
- Kosar, T.; Bohra, S.; Mernik, M. A Systematic Mapping Study driven by the margin of error. J. Syst. Softw. 2018, 144, 439–449. [Google Scholar] [CrossRef]
- Wohlin, C. Guidelines for Snowballing in Systematic Literature Studies and a Replication in Software Engineering. In Proceedings of the 18th International Conference on Evaluation and Assessment in Software Engineering, London, UK, 13–14 May 2014; Association for Computing Machinery: New York, NY, USA, 2014; pp. 1–10. [Google Scholar]
- Mourão, E.; Pimentel, J.F.; Murta, L.; Kalinowski, M.; Mendes, E.; Wohlin, C. On the performance of hybrid search strategies for systematic literature reviews in software engineering. Inf. Softw. Technol. 2020, 123, 106294. [Google Scholar] [CrossRef]
- Dieste, O.; Padua, A.G. Developing Search Strategies for Detecting Relevant Experiments for Systematic Reviews. In Proceedings of the First International Symposium on Empirical Software Engineering and Measurement, Madrid, Spain, 20–21 September 2007; pp. 215–224. [Google Scholar]
- Kitchenham, B.; Charters, S. Guidelines for Performing Systematic Literature Reviews in Software Engineering; Technical Report, Keele University and Durham University Joint Report; EBSE: Goyang, Korea, 2007. [Google Scholar]
- Petersen, K.; Feldt, R.; Mujtaba, S.; Mattsson, M. Systematic Mapping Studies in Software Engineering. In Proceedings of the 12th International Conference on Evaluation and Assessment in Software Engineering, Bari, Italy, 26–27 June 2008; BCS Learning & Development Ltd.: Swindon, UK, 2008; pp. 68–77. [Google Scholar]
- Rožanc, I.; Mernik, M. The screening phase in systematic reviews: Can we speed up the process? In Advances in Computers; Hurson, A.R., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; Volume 123, pp. 115–191. [Google Scholar] [CrossRef]
- Garousi, V.; Felderer, M.; Mäntylä, M.V. Guidelines for including grey literature and conducting multivocal literature reviews in software engineering. Inf. Softw. Technol. 2019, 106, 101–121. [Google Scholar] [CrossRef]
- Kamei, F.; Wiese, I.; Lima, C.; Polato, I.; Nepomuceno, V.; Ferreira, W.; Ribeiro, M.; Pena, C.; Cartaxo, B.; Pinto, G.; et al. Grey Literature in Software Engineering: A critical review. Inf. Softw. Technol. 2021, 138. [Google Scholar] [CrossRef]
- Nepomuceno, V.; Soares, S. On the need to update systematic literature reviews. Inf. Softw. Technol. 2019, 109, 40–42. [Google Scholar] [CrossRef]
- Osman, I.H.; Kelly, J.P. Meta-Heuristics: An Overview. In Meta-Heuristics: Theory and Applications; Springer US: Boston, MA, USA, 1996; pp. 1–21. [Google Scholar]
- Črepinšek, M.; Mernik, M.; Javed, F.; Bryant, B.R.; Sprague, A. Extracting Grammar from Programs: Evolutionary Approach. ACM SIGPLAN Not. 2005, 40, 39–46. [Google Scholar] [CrossRef]
- Kovačević, Ž.; Mernik, M.; Ravber, M.; Črepinšek, M. From Grammar Inference to Semantic Inference—An Evolutionary Approach. Mathematics 2020, 8, 816. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stützle, T. Ant Colony Optimization: Artificial Ants as a Computational Intelligence Technique. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Dasgupta, D.; Michalewicz, Z. Evolutionary Algorithms—An Overview. In Evolutionary Algorithms in Engineering Applications; Dasgupta, D., Michalewicz, Z., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 3–28. [Google Scholar]
- Wolpert, D.; Macready, W. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Tangherloni, A.; Spolaor, S.; Cazzaniga, P.; Besozzi, D.; Rundo, L.; Mauri, G.; Nobile, M. Biochemical parameter estimation vs. benchmark functions: A comparative study of optimization performance and representation design. Appl. Soft Comput. J. 2019, 81, 105494. [Google Scholar] [CrossRef]
- Malan, K.M. A Survey of Advances in Landscape Analysis for Optimisation. Algorithms 2021, 14, 40. [Google Scholar] [CrossRef]
- Hernando, L.; Mendiburu, A.; Lozano, J.A. Anatomy of the Attraction Basins: Breaking with the Intuition. Evol. Comput. 2019, 27, 435–466. [Google Scholar] [CrossRef]
- Bolufé-Röhler, A.; Tamayo-Vera, D.; Chen, S. An LaF-CMAES hybrid for optimization in multi-modal search spaces. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation, San Sebastian, Spain, 5–8 June 2017; pp. 757–764. [Google Scholar]
- Gonzalez-Fernandez, Y.; Chen, S. Identifying and Exploiting the Scale of a Search Space in Particle Swarm Optimization. In Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation, Vancouver, BC, Canada, 12–16 July 2014; Association for Computing Machinery: New York, NY, USA, 2014; pp. 17–24. [Google Scholar]
- Kerschke, P.; Grimme, C. An Expedition to Multimodal Multi-objective Optimization Landscapes. In Evolutionary Multi-Criterion Optimization; Trautmann, H., Rudolph, G., Klamroth, K., Schütze, O., Wiecek, M., Jin, Y., Grimme, C., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 329–343. [Google Scholar]
- Mahfoud, S.W. Simple Analytical Models of Genetic Algorithms for Multimodal Function Optimization. In Proceedings of the 5th International Conference on Genetic Algorithms, Urbana, IL, USA, 17–21 July 1993; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993; p. 643. [Google Scholar]
- Horn, J.; Goldberg, D.E. Genetic Algorithm Difficulty and the Modality of Fitness Landscapes. In Foundations of Genetic Algorithms; Whitley, L.D., Vose, M.D., Eds.; Elsevier: Amsterdam, The Netherlands, 1995; Volume 3, pp. 243–269. [Google Scholar]
- Vassilev, V.K.; Fogarty, T.C.; Miller, J.F. Information Characteristics and the Structure of Landscapes. Evol. Comput. 2000, 8, 31–60. [Google Scholar] [CrossRef] [PubMed]
- Garnier, J.; Kallel, L. How to Detect all Maxima of a Function. In Theoretical Aspects of Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2001; pp. 343–370. [Google Scholar]
- Anderson, E.J. Markov chain modelling of the solution surface in local search. J. Oper. Res. Soc. 2002, 53, 630–636. [Google Scholar] [CrossRef]
- Wiles, J.; Tonkes, B. Mapping the Royal Road and Other Hierarchical Functions. Evol. Comput. 2003, 11, 129–149. [Google Scholar] [CrossRef]
- Prestwich, S.; Roli, A. Symmetry Breaking and Local Search Spaces. In Proceedings of the Second International Conference on Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems, Prague, Czech Republic, 31 May–1 June 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 273–287. [Google Scholar]
- Prügel-Bennett, A. Finding Critical Backbone Structures with Genetic Algorithms. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation, London, UK, 7–11 July 2007; Association for Computing Machinery: New York, NY, USA, 2007; pp. 1343–1348. [Google Scholar]
- Van Turnhout, M.; Bociort, F. Predictability and unpredictability in optical system optimization. In Current Developments in Lens Design and Optical Engineering VIII; Mouroulis, P.Z., Smith, W.J., Johnson, R.B., Eds.; SPIE: Bellingham, WA, USA, 2007; Volume 6667, pp. 63–70. [Google Scholar]
- Ochoa, G.; Tomassini, M.; Vérel, S.; Darabos, C. A Study of NK Landscapes’ Basins and Local Optima Networks. In Proceedings of the 10th Annual Conference on Genetic and Evolutionary Computation, Atlanta, GA, USA, 12–16 July 2008; Association for Computing Machinery: New York, NY, USA, 2008; pp. 555–562. [Google Scholar]
- Ochoa, G.; Verel, S.; Tomassini, M. First-Improvement vs. Best-Improvement Local Optima Networks of NK Landscapes. In Parallel Problem Solving from Nature; Schaefer, R., Cotta, C., Kołodziej, J., Rudolph, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 104–113. [Google Scholar]
- Xu, Z.; Polojärvi, M.; Yamamoto, M.; Furukawa, M. Attraction basin estimating GA: An adaptive and efficient technique for multimodal optimization. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 333–340. [Google Scholar]
- Herrmann, S.; Rothlauf, F. Predicting Heuristic Search Performance with PageRank Centrality in Local Optima Networks. In Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, Spain, 11–15 July 2015; Association for Computing Machinery: New York, NY, USA, 2015; pp. 401–408. [Google Scholar]
- Bolufé-Röhler, A.; Chen, S.; Tamayo-Vera, D. An Analysis of Minimum Population Search on Large Scale Global Optimization. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 1228–1235. [Google Scholar]
- Jones, T.; Rawlins, G. Reverse Hillclimbing, Genetic Algorithms and the Busy Beaver Problem. In Proceedings of the Fifth International Conference on Genetic Algorithms, Urbana, IL, USA, 17–21 July 1993; pp. 70–75. [Google Scholar]
- Preuss, M.; Stoean, C.; Stoean, R. Niching Foundations: Basin Identification on Fixed-Property Generated Landscapes. In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, Dublin, Ireland, 12–16 July 2011; Association for Computing Machinery: New York, NY, USA, 2011; pp. 837–844. [Google Scholar]
- Gajda-Zagórska, E. Recognizing sets in evolutionary multiobjective optimization. J. Telecommun. Inf. Technol. 2012, 2012, 74–82. [Google Scholar]
- Lin, Y.; Zhong, J.H.; Zhang, J. Parallel Exploitation in Estimated Basins of Attraction: A New Derivative-Free Optimization Algorithm. In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, Dublin, Ireland, 12–16 July 2011; Association for Computing Machinery: New York, NY, USA, 2011; pp. 133–138. [Google Scholar]
- Urselmann, M.; Barkmann, S.; Sand, G.; Engell, S. A Memetic Algorithm for Global Optimization in Chemical Process Synthesis Problems. IEEE Trans. Evol. Comput. 2011, 15, 659–683. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Jenkinson, I.; Yang, Z. Solving dynamic optimisation problems by combining evolutionary algorithms with KD-tree. In Proceedings of the 2013 International Conference on Soft Computing and Pattern Recognition, Hanoi, Vietnam, 15–18 December 2013; pp. 247–252. [Google Scholar]
- Drezewski, R. Co-Evolutionary Multi-Agent System with Speciation and Resource Sharing Mechanisms. Comput. Inform. 2006, 25, 305–331. [Google Scholar]
- Schaefer, R.; Adamska, K.; Telega, H. Clustered genetic search in continuous landscape exploration. Eng. Appl. Artif. Intell. 2004, 17, 407–416. [Google Scholar] [CrossRef]
- Ochiai, H.; Tamura, K.; Yasuda, K. Combinatorial Optimization Method Based on Hierarchical Structure in Solution Space. In Proceedings of the 2013 IEEE International Conference on Systems, Man, and Cybernetics, Manchester, UK, 13–16 October 2013; pp. 3543–3548. [Google Scholar]
- Xu, Z.; Iizuka, H.; Yamamoto, M. Attraction Basin Sphere Estimating Genetic Algorithm for Neuroevolution Problems. Artif. Life Robot. 2014, 19, 317–327. [Google Scholar] [CrossRef]
- Najaran, M.; Prügel-Bennett, A. Quadratic assignment problem: A landscape analysis. Evol. Intell. 2015, 8, 165–184. [Google Scholar] [CrossRef]
- Alyahya, K.; Rowe, J.E. Landscape Analysis of a Class of NP-Hard Binary Packing Problems. Evol. Comput. 2019, 27, 47–73. [Google Scholar] [CrossRef]
- Reeves, C.R. Fitness Landscapes and Evolutionary Algorithms. In Artificial Evolution; Fonlupt, C., Hao, J.K., Lutton, E., Schoenauer, M., Ronald, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 3–20. [Google Scholar]
- Hernando, L.; Mendiburu, A.; Lozano, J.A. A Tunable Generator of Instances of Permutation-Based Combinatorial Optimization Problems. IEEE Trans. Evol. Comput. 2016, 20, 165–179. [Google Scholar] [CrossRef]
- Wiles, J.; Tonkes, B. Visualisation of hierarchical cost surfaces for evolutionary computing. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; Volume 1, pp. 157–162. [Google Scholar]
- Schäpermeier, L.; Grimme, C.; Kerschke, P. To Boldly Show What No One Has Seen Before: A Dashboard for Visualizing Multi-objective Landscapes. In Evolutionary Multi-Criterion Optimization; Ishibuchi, H., Zhang, Q., Cheng, R., Li, K., Li, H., Wang, H., Zhou, A., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 632–644. [Google Scholar]
- Brimberg, J.; Hansen, P.; Mladenović, N. Attraction probabilities in variable neighborhood search. 4OR-A Q. J. Oper. Res. 2010, 8, 181–194. [Google Scholar] [CrossRef]
- Stoean, C.; Preuss, M.; Stoean, R.; Dumitrescu, D. Multimodal Optimization by Means of a Topological Species Conservation Algorithm. IEEE Trans. Evol. Comput. 2010, 14, 842–864. [Google Scholar] [CrossRef]
- Daolio, F.; Verel, S.; Ochoa, G.; Tomassini, M. Local Optima Networks of the Quadratic Assignment Problem. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Fieldsend, J.E. Computationally Efficient Local Optima Network Construction. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Kyoto, Japan, 15–19 July 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 1481–1488. [Google Scholar]
- Ochoa, G.; Verel, S.; Daolio, F.; Tomassini, M. Local Optima Networks: A New Model of Combinatorial Fitness Landscapes. In Recent Advances in the Theory and Application of Fitness Landscapes; Richter, H., Engelbrecht, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 233–262. [Google Scholar]
- Chen, S.; Montgomery, J.; Bolufé-Röhler, A.; Gonzalez-Fernandez, Y. A Review of Thresheld Convergence. GECONTEC Rev. Int. GestióN Conoc. Tecnol. 2015, 3, 1–13. [Google Scholar]
- Vérel, S.; Daolio, F.; Ochoa, G.; Tomassini, M. Local Optima Networks with Escape Edges. In Artificial Evolution; Hao, J.K., Legrand, P., Collet, P., Monmarché, N., Lutton, E., Schoenauer, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 49–60. [Google Scholar]
- Xu, Z.; Huang, H.X.; Pardalos, P.M.; Xu, C.X. Filled functions for unconstrained global optimization. J. Glob. Optim. 2001, 20, 49–65. [Google Scholar] [CrossRef]
- Bruck, J.; Dolev, D.; Ho, C.T.; Roşu, M.C.; Strong, R. Efficient Message Passing Interface (MPI) for Parallel Computing on Clusters of Workstations. J. Parallel Distrib. Comput. 1997, 40, 19–34. [Google Scholar] [CrossRef]
- Rao, C.M.; Shyamala, K. Analysis and Implementation of a Parallel Computing Cluster for Solving Computational Problems in Data Analytics. In Proceedings of the 2020 5th International Conference on Computing, Communication and Security, Patna, India, 14–16 October 2020; pp. 1–5. [Google Scholar]
- Byma, S.; Dhasade, A.; Altenhoff, A.; Dessimoz, C.; Larus, J.R. Parallel and Scalable Precise Clustering. In Proceedings of the ACM International Conference on Parallel Architectures and Compilation Techniques, Virtual Event, GA, USA, 3–7 October 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 217–228. [Google Scholar]
- Pieper, R.; Löff, J.; Hoffmann, R.B.; Griebler, D.; Fernandes, L.G. High-level and efficient structured stream parallelism for rust on multi-cores. J. Comput. Lang. 2021, 65, 101054. [Google Scholar] [CrossRef]
- Hentrich, D.; Oruklu, E.; Saniie, J. Program diagramming and fundamental programming patterns for a polymorphic computing dataflow processor. J. Comput. Lang. 2021, 65, 101052. [Google Scholar] [CrossRef]











| Databases | Total Number of Publications | Full-Text Screening |
|---|---|---|
| Web of Science | 105 | 18 |
| Scopus | 201 | 50 |
| Total | 306 | 68 |
| After removing duplicates | 57 | |
| Iterative forward and backward snowballing | 80 | |
| Total = 137 | ||
| Fitness landscape analysis, problem difficulty | e.g., [28,32,105] |
| Clustering, niching associated with attraction basins | e.g., [94,99,100] |
| Exploration, exploitation, diversification, intensification | e.g., [22,76,77] |
| Problem generation | [106] |
| Problem visualisation | e.g., [78,107,108] |
| Comparison, performance, analysis of metaheuristics | e.g., [31,79,109] |
| Basins within the metaheuristic to enhance the search | e.g., [96,97,110] |
| Local Optima Networks | e.g., [88,111,112] |
| Automated Algorithm Selection | [35] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baketarić, M.; Mernik, M.; Kosar, T. Attraction Basins in Metaheuristics: A Systematic Mapping Study. Mathematics 2021, 9, 3036. https://doi.org/10.3390/math9233036
Baketarić M, Mernik M, Kosar T. Attraction Basins in Metaheuristics: A Systematic Mapping Study. Mathematics. 2021; 9(23):3036. https://doi.org/10.3390/math9233036
Chicago/Turabian StyleBaketarić, Mihael, Marjan Mernik, and Tomaž Kosar. 2021. "Attraction Basins in Metaheuristics: A Systematic Mapping Study" Mathematics 9, no. 23: 3036. https://doi.org/10.3390/math9233036
APA StyleBaketarić, M., Mernik, M., & Kosar, T. (2021). Attraction Basins in Metaheuristics: A Systematic Mapping Study. Mathematics, 9(23), 3036. https://doi.org/10.3390/math9233036







