A Parallel Approach of the Enhanced Craig–Bampton Method
Abstract
:1. Introduction
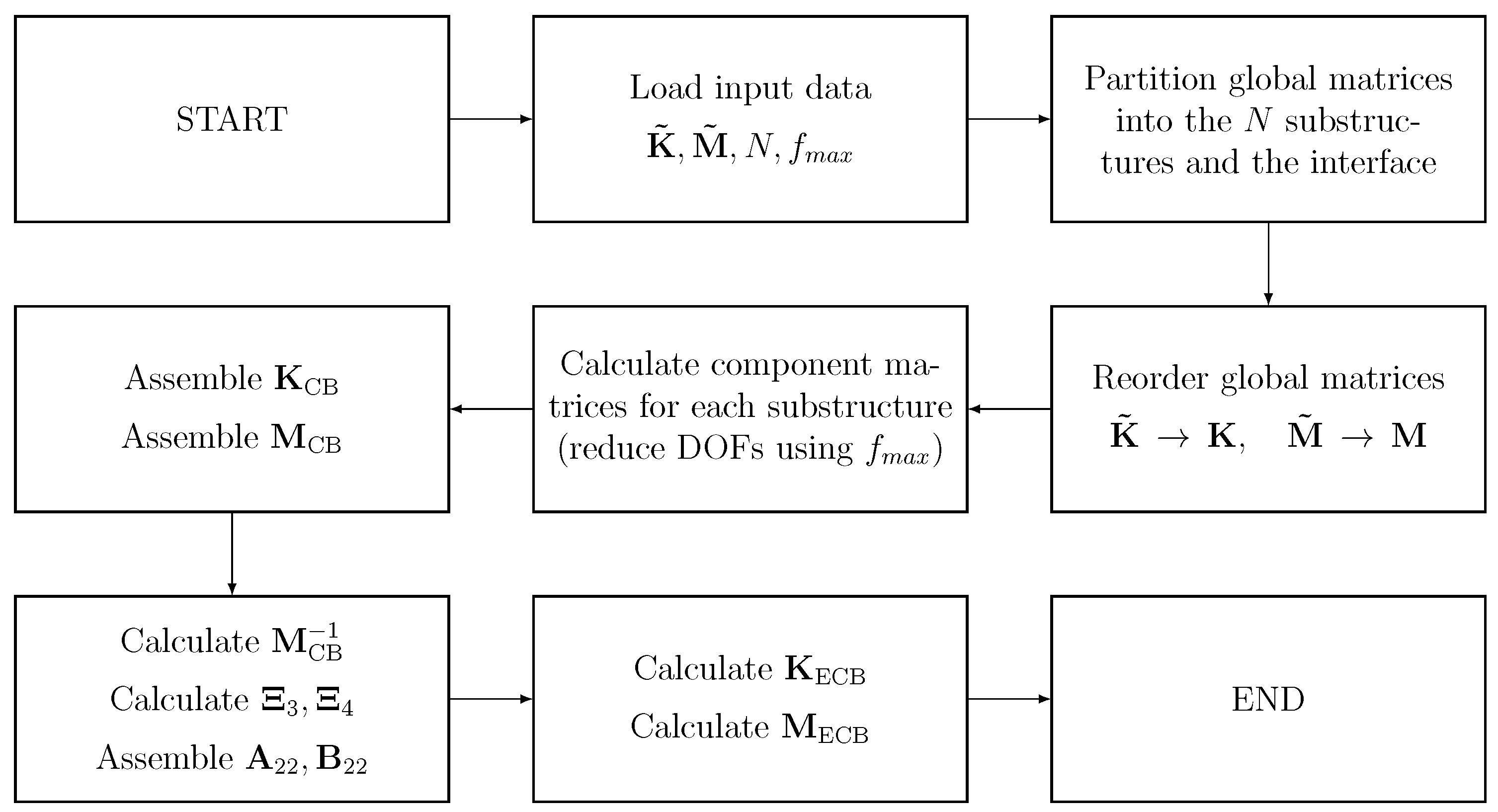
2. The Enhanced Craig–Bampton Method
3. Parallel Implementation of the ECB Method
- All independent parts of the algorithm are executed in parallel (e.g., component matrices computation).
- All ‘inner’ matrix operations (e.g., matrix-matrix multiplication) are explicitly parallelized and/or vectorized over matrix rows or columns.
- At the lowest level, the code is optimized and auto-parallelized by the compiler. Library functions provided by METIS and Intel MKL are also optimized and parallelized.
3.1. Reduction Algorithm
3.1.1. Partitioning
3.1.2. Reduction
3.1.3. Enhanced Reduction
4. Numerical Examples
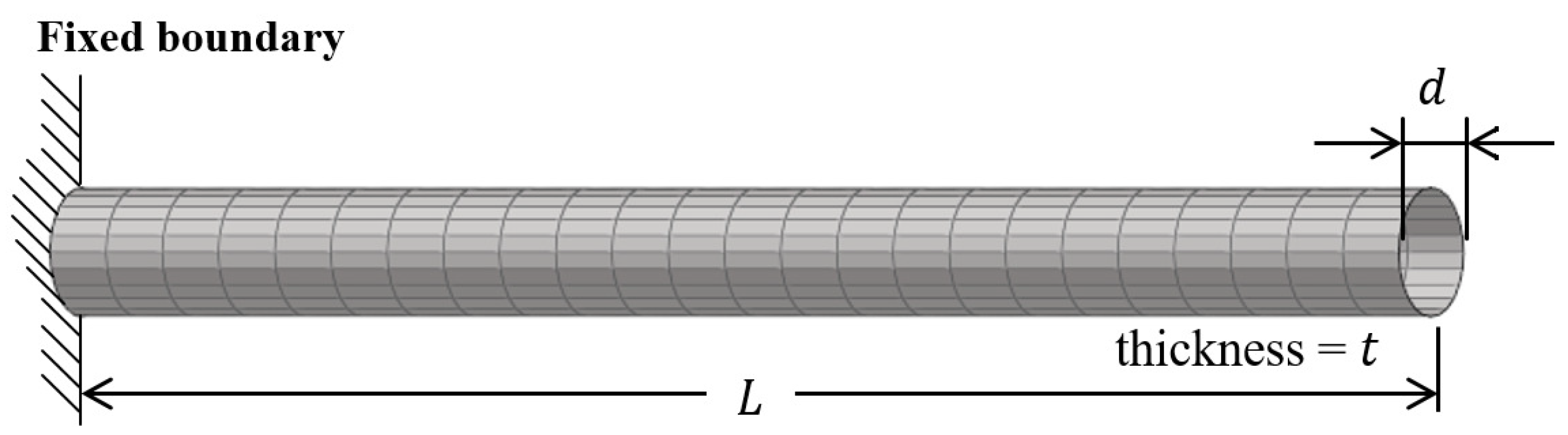
4.1. Cylindrical Shell
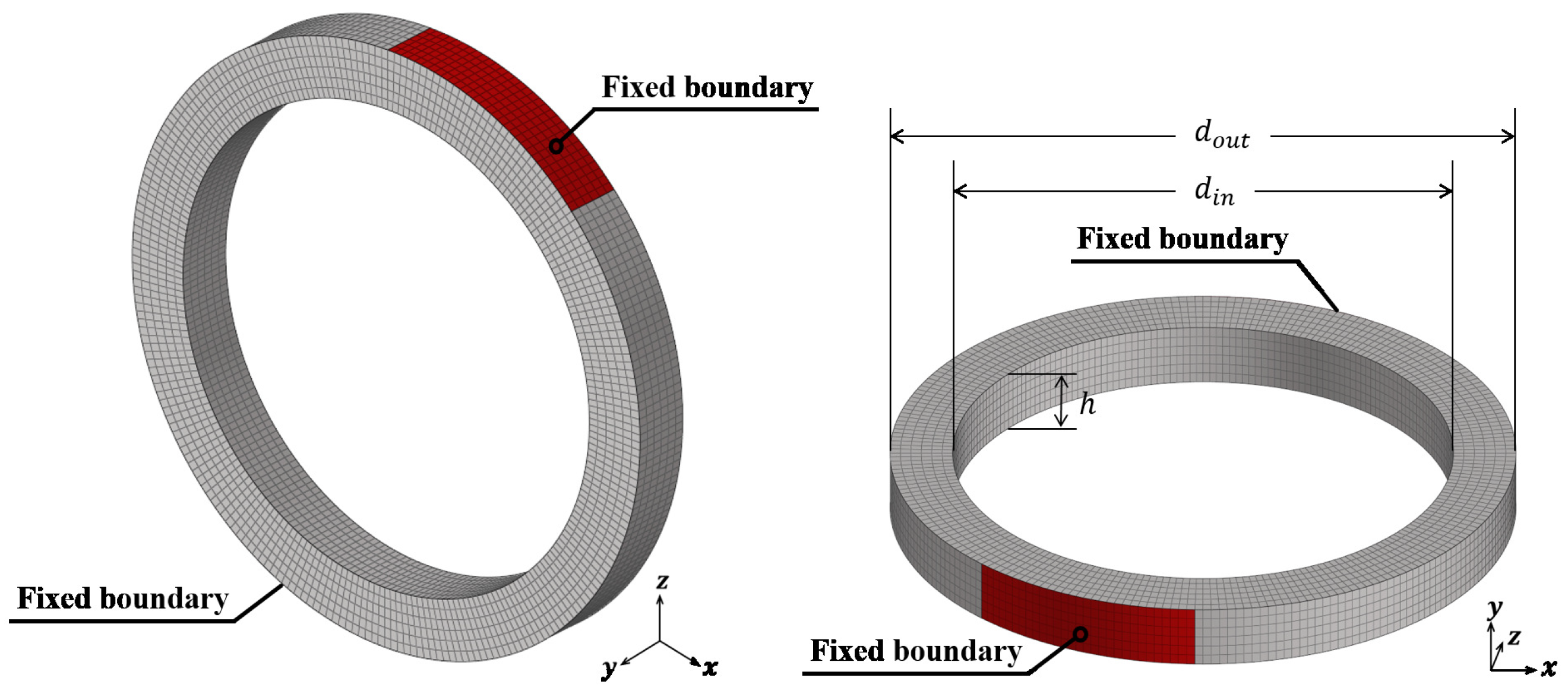
4.2. Solid Ring
4.3. Shaft Assembly
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Craig, R.R.; Bampton, B.C.C. Coupling of substructures for dynamic analysis. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef] [Green Version]
- Shabana, A.A. Dynamics of Multibody Systems; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Kim, J.G.; Han, J.B.; Lee, H.; Kim, S.S. Flexible multibody dynamics using coordinate reduction improved by dynamic correction. Multibody Syst. Dyn. 2018, 42, 411–429. [Google Scholar] [CrossRef]
- FunctionBay, Inc. Recurdyn V9R3 User Manual; FunctionBay, Inc.: Seongnam-si, Korea, 2019. [Google Scholar]
- Cammarata, A.; Pappalardo, C.M. On the use of component mode synthesis methods for the model reduction of flexible multibody systems within the floating frame of reference formulation. Mech. Syst. Signal Process. 2020, 142, 106745. [Google Scholar] [CrossRef]
- Sarsri, D.; Azrar, L.; Jebbouri, A.; El Hami, A. Component mode synthesis and polynomial chaos expansions for stochastic frequency functions of large linear FE models. Comput. Struct. 2011, 89, 346–356. [Google Scholar] [CrossRef]
- Jensen, H.A.; Millas, E.; Kusanovic, D.; Papadimitriou, C. Model-reduction techniques for Bayesian finite element model updating using dynamic response data. Comput. Methods Appl. Mech. Eng. 2014, 279, 301–324. [Google Scholar] [CrossRef]
- Yotov, V. Stochastic Finite Element Method for Vibroacoustic Loads Prediction. Ph.D. Thesis, University of Surrey, Guildford, UK, 2020. [Google Scholar]
- Nachtergaele, P.; Rixen, D.J.; Steenhoek, A.M. Efficient weakly coupled projection basis for the reduction of thermomechanical models. J. Comput. Appl. Math. 2010, 234, 2272–2278. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.M.; Kim, J.G.; Chae, S.W.; Park, K.C. A strongly coupled model reduction of vibro-acoustic interaction. Comput. Methods Appl. Mech. Eng. 2019, 347, 495–516. [Google Scholar] [CrossRef]
- Wang, X.; Wang, D.; Liu, B. Efficient Acoustic Topology Optimization Using Vibro-Acoustic Coupled Craig–Bampton Mode Synthesis. Acoust. Aust. 2020, 48, 407–418. [Google Scholar] [CrossRef]
- Kammer, D.C.; Triller, M.J. Selection of Component Modes for Craig–Bampton Substructure Representations. J. Vib. Acoust. 1996, 118, 264–270. [Google Scholar] [CrossRef]
- Bai, Z.; Liao, B.S. Towards an Optimal Substructuring Method for Model Reduction. In PARA 2004: Applied Parallel Computing. State of the Art in Scientific Computing; Springer: New York, NY, USA, 2004; pp. 276–285. [Google Scholar]
- Kim, S.M.; Kim, J.G.; Park, K.C.; Chae, S.W. A Component Mode Selection Method Based on a Consistent Perturbation Expansion of Interface Displacement. Comput. Methods Appl. Mech. Eng. 2018, 330, 578–597. [Google Scholar] [CrossRef]
- Kim, S.M.; Kim, J.G.; Chae, S.W.; Park, K.C. Evaluating Mode Selection Methods for Component Mode Synthesis. AIAA J. 2016, 54, 2852–2863. [Google Scholar] [CrossRef]
- Park, K.C.; Park, Y.H. Partitioned component mode synthesis via a flexibility approach. AIAA J. 2004, 42, 1236–1245. [Google Scholar] [CrossRef]
- Rixen, D.J. A dual Craig–Bampton method for dynamic substructuring. J. Comput. Appl. Math. 2004, 168, 383–391. [Google Scholar] [CrossRef]
- Kim, J.G.; Markovic, D. High-fidelity flexibility based CMS method with interface degrees of freedom reduction. AIAA J. 2016, 54, 3619–3631. [Google Scholar] [CrossRef]
- Kim, J.G.; Lee, P.S. An enhanced Craig–Bampton method. Int. J. Numer. Methods Eng. 2015, 103, 79–93. [Google Scholar] [CrossRef]
- Boo, S.H.; Kim, J.H.; Lee, P.S. Towards improving the enhanced Craig–Bampton method. Comput. Struct. 2018, 196, 63–75. [Google Scholar] [CrossRef]
- Tian, W.; Weng, S.; Xia, Y.; Zhu, H.; Gao, F.; Sun, Y.; Li, J. An iterative reduced-order substructuring approach to the calculation of eigensolutions and eigensensitivities. Mech. Syst. Signal Process. 2019, 130, 361–377. [Google Scholar] [CrossRef]
- Go, M.S.; Lim, J.H.; Kim, J.G.; Hwang, K.R. A family of Craig–Bampton methods considering residual mode compensation. Appl. Math. Comput. 2020, 369, 124822. [Google Scholar] [CrossRef]
- Jensen, H.A.; Muñoz, A.; Papadimitriou, C.; Vergara, C. An enhanced substructure coupling technique for dynamic re-analyses: Application to simulation-based problems. Comput. Methods Appl. Mech. Eng. 2016, 307, 215–234. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.G.; Yun, G.; Lee, P.S.; Kim, D.N. Toward modular analysis of supramolecular protein assemblies. J. Chem. Theory Comput. 2015, 11, 4260–4272. [Google Scholar] [CrossRef]
- Krattiger, D.; Hussein, M.I. Generalized Bloch mode synthesis for accelerated calculation of elastic band structures. J. Comput. Phys. 2018, 357, 183–205. [Google Scholar] [CrossRef]
- Kim, J.G.; Boo, S.H.; Lee, P.S. An enhanced AMLS method and its performance. Comput. Methods Appl. Mech. Eng. 2015, 287, 90–111. [Google Scholar] [CrossRef]
- Kim, J.G.; Park, Y.J.; Lee, G.H.; Kim, D.N. A general model reduction with primal assembly in structural dynamics. Comput. Methods Appl. Mech. Eng. 2017, 324, 1–28. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. A fast and highly quality multilevel scheme for partitioning irregular graphs. SIAM J. Sci. Comput. 1999, 20, 359–392. [Google Scholar] [CrossRef]
- Wang, E.; Zhang, Q.; Shen, B.; Zhang, G.; Lu, X.; Wu, Q.; Wang, Y. Intel Math Kernel Library. In High-Performance Computing on the Intel® Xeon PhiTM; Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Kim, J.-G.; Seo, J.; Lim, J.H. Novel modal methods for transient analysis with a reduced order model based on enhanced Craig–Bampton formulation. Appl. Math. Comput. 2019, 344, 30–45. [Google Scholar] [CrossRef]
- Dagum, L.; Menon, R. OpenMP: An industry standard API for shared-memory programming. Comput. Sci. Eng. 1998, 1, 46–55. [Google Scholar] [CrossRef] [Green Version]
- Cui, J.; Xing, J.; Wang, X.; Wang, Y.; Zhu, S.; Zheng, G. A simultaneous iterative scheme for the Craig–Bampton reduction based substructuring. In Dynamics of Coupled Structures; Springer: Cham, Switzerland, 2017; Volume 4, pp. 103–114. [Google Scholar]
- Chung, I.S.; Kim, J.G.; Chae, S.W.; Park, K.C. An iterative scheme of flexibility-based component mode synthesis with higher-order residual modal compensation. Int. J. Numer. Methods Eng. 2021, 122, 3171–3190. [Google Scholar] [CrossRef]





| Step of Algorithm | Operation Time [s] | ||||
|---|---|---|---|---|---|
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 2.5 | 0.9 | 0.5 | 0.4 | 0.6 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 0.2 | 0.6 | 1.8 | 2.9 | 8.4 | |
| 0.0 | 0.6 | 2.2 | 4.1 | 12.6 | |
| 1.1 | 2.2 | 3.7 | 5.3 | 9.2 | |
| N | ||||||
|---|---|---|---|---|---|---|
| 2 | 1320 | 1440 | 120 | 613 | 0.1 | 0.1 |
| 4 | 550 | 610 | 550 | 920 | 0.1 | 0.1 |
| 8 | 185 | 295 | 925 | 1195 | 0.2 | 0.1 |
| 16 | 60 | 135 | 1190 | 1397 | 0.3 | 0.2 |
| 32 | 10 | 65 | 1684 | 1795 | 0.6 | 0.5 |
| Step of Algorithm | Operation Time [s] | ||||
|---|---|---|---|---|---|
| 1.6 | 1.6 | 1.6 | 1.6 | 1.6 | |
| 0.1 | 0.1 | 0.1 | 0.2 | 0.2 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 7148.2 | 1377.7 | 474.2 | 412.6 | 645.0 | |
| 0.0 | 0.1 | 0.1 | 0.2 | 0.4 | |
| 35.3 | 104.5 | 316.4 | 782.2 | 5299.4 | |
| 3.5 | 22.6 | 234.1 | 1255.4 | 8414.1 | |
| 56.8 | 74.9 | 105.8 | 176.8 | 388.3 | |
| N | ||||||
|---|---|---|---|---|---|---|
| 2 | 16,785 | 16,785 | 492 | 4696 | 217.1 | 120.8 |
| 4 | 8223 | 8247 | 1137 | 5228 | 86.3 | 26.4 |
| 8 | 3924 | 3990 | 2367 | 6240 | 65.0 | 18.9 |
| 16 | 1803 | 1962 | 4644 | 8088 | 82.1 | 43.8 |
| 32 | 720 | 883 | 9425 | 11,994 | 365.1 | 245.8 |
| 64 | 180 | 364 | 17,982 | 19,113 | 1698.0 | 1288.2 |
| 128 | 18 | 198 | 22,030 | 22,721 | 2989.0 | 2382.0 |
| Step of Algorithm | Operation Time [s] | ||||
|---|---|---|---|---|---|
| 3.1 | 3.0 | 3.2 | 3.1 | 3.1 | |
| 0.1 | 0.2 | 0.3 | 0.3 | 0.5 | |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| 56,310.5 | 17,074.7 | 8282.5 | 6210.4 | 6494.7 | |
| 0.1 | 0.2 | 0.4 | 0.9 | 1.5 | |
| 174.7 | 1108.5 | 8680.3 | 26,534.1 | 61,743.2 | |
| 92.8 | 1893.8 | 14,163.9 | 43,361.5 | 104,813.5 | |
| 72.4 | 195.2 | 483.8 | 936.4 | 1539.2 | |
| N | ||||||
|---|---|---|---|---|---|---|
| 2 | 30,894 | 31,212 | 1980 | 5330 | 2556.3 | 944.2 |
| 4 | 14,052 | 15,201 | 5586 | 8573 | 1018.3 | 337.9 |
| 8 | 5964 | 7416 | 11,412 | 13,723 | 1204.1 | 526.9 |
| 16 | 2517 | 3618 | 16,998 | 18,746 | 2017.0 | 1284.1 |
| 32 | 1071 | 1677 | 22,912 | 24,186 | 3835.1 | 2909.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pařík, P.; Kim, J.-G.; Isoz, M.; Ahn, C.-u. A Parallel Approach of the Enhanced Craig–Bampton Method. Mathematics 2021, 9, 3278. https://doi.org/10.3390/math9243278
Pařík P, Kim J-G, Isoz M, Ahn C-u. A Parallel Approach of the Enhanced Craig–Bampton Method. Mathematics. 2021; 9(24):3278. https://doi.org/10.3390/math9243278
Chicago/Turabian StylePařík, Petr, Jin-Gyun Kim, Martin Isoz, and Chang-uk Ahn. 2021. "A Parallel Approach of the Enhanced Craig–Bampton Method" Mathematics 9, no. 24: 3278. https://doi.org/10.3390/math9243278
APA StylePařík, P., Kim, J.-G., Isoz, M., & Ahn, C.-u. (2021). A Parallel Approach of the Enhanced Craig–Bampton Method. Mathematics, 9(24), 3278. https://doi.org/10.3390/math9243278







