Abstract
Industrial processes seek to improve their quality control, including new technologies and satisfying requirements for globalised markets. In this paper, we present an innovative method based on Multivariate Pattern Recognition (MVPR) and process monitoring in a real-world study case. By identifying a distinctive out-of-control multivariate pattern using the Support Vector Machines (SVM) and the Mahalanobis Distance it is possible to infer the variables that disturbed the process; hence, possible faults can be predicted knowing the state of the process. The method is based on our previous work, and in this paper we present the method application for an automated process, namely, the robotic Gas Metal Arc Welding (GMAW). Results from the application indicate an overall accuracy up to , which demonstrates the effectiveness of the method, which can also be used in other MVPR tasks.
1. Introduction
The purpose of a production process is to manufacture a product to the desired specifications and quality. Quality is essential to satisfy customer needs and to improve the product’s competitiveness. To specify the quality of a product, measurements of its quality characteristics are needed to obtain variability data between different units of the finished product. The variability of the measurements is the result of the variation of each element that makes up the process and it is necessary to investigate the causes that produce this variation. The importance of the measurements for product analysis lies on obtaining information of the product itself, its relationship with the operation of the elements of the process, and the correction of the process parameters as well as the acceptance or rejection of the batch of production. Therefore, it is necessary to examine the measurements with techniques that inspect their variability.
The Statistical Process Control (SPC) is widely used to improve the performance of a process to reduce the variations that affects the quality and to maintain stability. Control charts (CCs), both univariate and multivariate, are the main techniques in SPC. Its purpose is to analyse the behaviour of the variables over time using control limits that indicate a stable state or the presence of possible failures, providing the possibility of deciding when to intervene in the process and modify an undesired effect. However, they have certain drawbacks, such as not specifying the causes that led to out-of-control signals. It is required to satisfy statistical conditions such as normality; they also depend on human judgement [2,3]. Based on the above, different authors have proposed solving this problem by analysing the variations of the univariate patterns in the control tables [4,5]. In our approach, process measurements are considered to be affected by variations associated with the assignable causes that originated them in order to eliminate the problem in the process, which is our ultimate goal.
The automotive industry is one of the most demanding industrial sectors regarding its quality, where one of the most relevant processes is the robotic welding process, specifically the Gas Metal Arc Welding (GMAW). The robotic GMAW allows welding in all positions, producing minimal slag and generating continuous welding seams. These advantages make the process ideal for automated welding applications and high-volume production and for this reason, this process was proposed as a study case to implement our recently published method [1]. In this paper quality characteristics such as bead geometry, observed as its measured width and height depend on the monitoring of different parameters from the process, such as the welding current and the speed of the welding torch along the welding joint. Our aim is to identify main process parameters, perturb those parameters in order to generate a response from our system, identify near-to-natural multivariate behaviour so that the Mahalanobis distances can be obtained and the type of multivariate pattern can be recognised using SVM, and then from this pattern the type of failure can be inferred.
In this paper, the practical application of the method to the automated GMAW is presented and the manuscript is organised as follows. After this brief introduction that includes the related work and contribution, in Section 2 the SVM and the Mahalanobis distance are introduced. In Section 3, the Multivariate Pattern Recognition (MVPR) is formally presented and the results are given in Section 4. Finally, Section 5 provides the conclusions and envisaged future work.
1.1. Related Work
The incorporation of techniques such as Artificial Neural Networks (ANNs) in the recognition of univariate patterns in control charts has been proposed to automatically examine patterns and improve efficiency. Several researchers have found this area of work interesting. An area of opportunity has been found to extend the scope of MVPR in terms of the location of the variables or group of variables that originated the out-of-control state.
Ali et al. present a synthesis of several techniques used in the SPC for quality assurance in the manufacturing and service industries. In that synthesis, they analyse different works under different approaches such as continuous and discrete data. In both approaches, they present different types of graphics used and their distribution types [6]. Awad et al. generate a methodology focused on the faults detection for a multivariate process integrating a backpropagation ANN and Hotelling statistic [7]. The methodology consists of the process data collection, the features selection through correlation and PCA, and finally the Backpropagation model. Based on the weight and bias parameters of Backpropagation, a mean vector and the covariance matrix are calculated for statistic. Finally, they calculate the statistic and graph it to determine the existence of faults. In research conducted by Zaman et al., they expose a way to analyse the special causes that affect the quality of products generated by manufacturing industries [8]. Pastuizaca et al. presented in their work an approach where the theory of fuzzy logic was incorporated with the multivariate CC , with the purpose of analysing the quality characteristics correlating their control status and influence through triangular membership functions (linguistic way) [9]. The analysed characteristics belong to a food processing industry, where three characteristics of “appearance”, “colour”, and “taste” were analysed. Alfaro et al. proposed a methodology to determine changes in the vectors corresponding to the Hotelling statistic. In the experiments, different vectors of the statistic were simulated where there was correlation between two variables and they applied mean changes of in one or both variables. The performance of different Linear Discriminant Analysis, Classification Trees, Boosting and Multy-Layer-Perceptron neural net techniques in the classification of simulated statistic vectors were examined [10]. They determined that the Boosting technique presented better results.
Researchers have been working on ANNs, especially within the area of Artificial Intelligence in which the main results have been reported. Zhou et al. developed a model composed of SVM and a genetic algorithm in conjunction with a hybrid function composed of a polynomial and a Gaussian function, with which they analysed, with a multiclass approach, the observed patterns [11]. In a similar way, Guan and Cheng generated a framework using the Monte Carlo method and a combination of “one against all” and “one against one” classifiers to analyse the simulated multivariate data [12]. Zheng and Yu demonstrated in an experimental analysis that a hybrid system performed better than separate techniques. This was done by integrating the characteristics extracted by two CNNs and which were used to train the SVM classifier [13]. Addeh et al. used an RBF ANN for the classification stage in conjunction with a learning algorithm based on the bee algorithm. The method was tested with a data set of 1600 samples of which 200 samples were from each pattern [14]. Sohaimi et al. presented a method that through a network of multilayer perceptrons identify nine categories of bivariate SPC patterns, which they use to monitor and diagnose the mean and/or variance of a bivariate process [15].
Although CNNs techniques have evolved a lot, they have to address many other issues inherited by the BP algorithm, they certainly have a solid foundation for the SPC, as some authors have recently demonstrated thanks to the increase in computing power, reconfigurable hardware and new graphics processing units (GPU). Some examples can be observed in works by Miao and Yang using the extraction of characteristics in graphical control patterns and analysis by deep learning with CNN using the Montecarlo method [16]. Yu et al. on the other hand, they used what they called the Stacked Denoising Autoencoder (SDAE) to learn the discriminatory characteristics of the signal. In this study they show a cross validation between the main techniques such as BPN, SVM, K nearest neighbour, decision trees (DT), and LVQ. The results showed that SDAE, BPN, and SVM were the best techniques [17].
1.2. Original Contribution
Quality’s characteristics such as the weld bead geometry (width and height) depends on reliably monitoring different parameters from the process, such as the welding current and the torch’s travel speed, among others. The welding current affects the depth penetration and the size of the weld bead. In the same way, an increment or decrement in torch’s travel speed modifies the depth penetration, bead width, height, and its geometric shape. In addition, the diameter of the electrode and its composition determine the correct amperage range [18]. Welding defects are present due to a low current value or an excessive travel speed which may generate lack of penetration, which results in a reduction in the welding joint strength [18]. For a continuous robotic welding process, it is essential to monitor and modify online the robot’s behaviour to improve the welding bead. In the event of any malfunction measured by the change of the geometric characteristics of the beam, the proposed approach can be used to know their causes and act accordingly in a timely manner. The idea is to apply the proposed method to monitor a real-world study case, to control its process status and to have the necessary information to determine the causes of variation that affected the process without depending on univariate analysis, human judgement, or graphics that assume data normality. To the best knowledge of the authors, this is the first time these techniques have been used for MVPR in robotic GMAW.
2. The Product, SVM, and D2
The experimental welding set up considers the weldment of a metal plate, henceforth the product. The process parameters of the GMAW to be analysed in this work are the Current () and Travel speed (), On the other hand, the quality characteristics of the product are the Width () and Height () of the welding bead as shown in Figure 1, so that the Multivariate Variable is composed by .
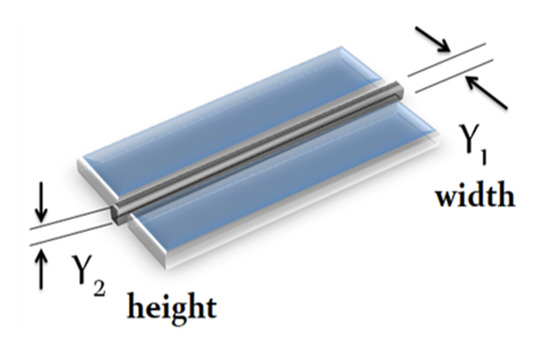
Figure 1.
Multivariate Variable Y, =
The study considers relevant aspects, since in a situation out-of-control, faults can be located in one or in various quality characteristics using information from the multivariate pattern in Y. Furthermore, the relationship or association between the multivariate patterns and the nature of the faults in the welding process parameters may be inferred. The multivariate pattern recognition is performed using the Mahalanobis distance of the weld beads using SVM.
SVM were designed to solve binary classification problems. SVM are used to solve various types of classification, learning, regression problems, among others. The idea is to select a hyperplane that is equidistant from each class, in order to achieve a maximum margin on each side of this hyperplane [19].
For a linearly separable data set labeled for two classes, the following linear hyperplane is defined , where determines the optimal hyperplane and vector w establish the hyperplane slope. An adequate classification of data is obtained through the decision function .
In real processes, data cannot always be classified linearly. To solve the classification of this type of data, we apply a nonlinear mapping of the data in a space of greater dimension where they are separable. This space is defined the feature space. In this new space, the separation hyperplane must be found. The data mapping is generated by a kernel function that allows data separation. Polynomial, Radial, and Sigmoidal kernels were used for experimentation in this work. It was found that the Sigmoid was the best kernel function [1]. The used parameters were , , and .
Although SVM was designed to deal with binary classification problems, there are approaches for applying SVM for multiple classes. The approach used for this experimentation is “one against all”, where k classifiers—SVM are generated to each class from the others. The classifier is trained with data of class i and value 1; the rest of data for other classes is defined as .
The Mahalanois distance, , allows us to determine the multivariate information providing a measurement of similarity between variables comparing their centroids. The proposed method requires the calculation of a reference value which corresponds to the variable with natural behaviour represented by in this paper. is calculated considering two cases as follows:
where and in Equation (1) are the mean vector and covariance matrix from . and in Equation (2) are the mean vector and covariance matrix calculated from the multivariate variable . The reader is referred to [1] for full theoretical details.
3. MVPR in GMAW Process Using SVM and D2
The method for MVPR in the welding process involves the following steps:
- 1)
- Define the welding process parameters .
- 2)
- Disturb the welding process behaviour with known univariate pattern signals .
- 3)
- Generate several multivariate patterns .
- 4)
- Choose the multivariate variable with near-to-natural behaviour and label it as , where .
- 5)
- 6)
- Select vectors to form training and testing databases.
- 7)
- Classify multivariate patterns in with Multiclass SVM.
- 8)
- Determine the relationship between univariate patterns and multivariate patterns in .
- 9)
- Establish possible causes that led to the formation of out-of-control signals an possible solutions.
3.1. Patterns in the Welding Process
To generate the perturbation patterns in the welding process, the process parameters data for and was generated according to Equation (3).
where:
- = process mean
- = natural variation at sampling time t
- = disturbance at time t ( = 0 when the pattern is natural).
During welding experiments, the current and the robot’s end-effector travel speed were affected by the most typical special patterns such as Increasing Trend (IT), Decreasing Trend (DT), Upward Shift (US), Downward Shift (DS), Cycle (Cy) and Natural (N) as pointed out in [20]. When the process is affected by these patterns, it was found that the response variables (width and height of the weld bead) are also affected and presented similar patterns to those applied in the process. The affectation is understood as the transfer of the statistical properties of the patterns in X to Y, but in Y the random factor is added, so it becomes complex to interpret the patterns in Y and this is precisely, one of the most important contributions of our method by determining this relationship.
The natural pattern in our case refers to the process parameters value indicated in Table 1, which also includes the and values to disturb each process parameter.

Table 1.
Process parameters to disturb the sample patterns.
The values for were and and were considered as the effect of the special variation that disturbed each and parameter, respectively. These values were selected so that the patterns occur within the range of before the data surpasses the limits of Shewhart control resulting in relevant damages in the quality of the product [21,22]. The special patterns parameters used to perturb X were as indicated in Figure 2.
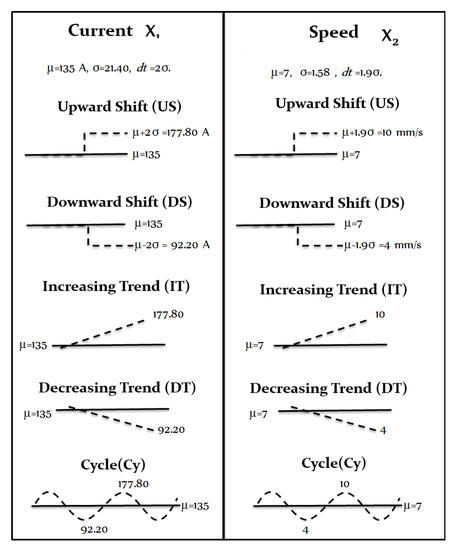
Figure 2.
Parameters to generate special patterns.
To define the appropriate values for the process and the weld bead, a visual inspection was carried out on the product as reported in [23,24]. To have an appropriate bead quality with an adequate degree of penetration as suggested by [25,26,27], the ratio , should be maintained.
Table 2 shows the 36 possible pattern compositions that perturbed the process parameters and . To determine the amount of pattern compositions, the permutation formula with repetition was applied ; where types of patterns to choose from and number of patterns that form the permutation. An experiment with a replica was performed for each special pattern composition to generate a training base and a testing base for the recognition stage. Hence, a total of 72 weld beads (products) were generated.

Table 2.
36 possible experimental patterns.
The product was made from steel SAE 1018, with dimensions 12 cm long by 5 cm wide, 0.6 cm thickness, and a weld bead length of 10 cm. As indicated earlier, the current was established as 135 A and the travel speed to 7 mm/s. The workpieces were welded and the weld bead measured using a laser beam projected onto the workpiece using an eye-in-hand CCD camera mounted onto the robot manipulator. The measurements were acquired with respect to the length of the weld bead. The measurement step was 0.5 mm, which means that one measurement was registered every 0.5 mm along the weld bead. In total, 200 measurements were obtained from a weld bead of 100 mm in length. Figure 3 shows the metal plate (product) as well as the weld bead.

Figure 3.
Metal plate with weld bead (product).
3.2. Multivariate Variables Generation Based on Measurements of Weld Beads
A total of 72 products (weld beads) were generated containing the 36 pattern behaviour shown in Table 2. The analysis of the variables of each weld bead was proposed in a multivariate manner, , with . Each element of was considered a univariate variable. Prior to the calculation of the Mahalanobis distances , normality tests were performed on the measurements of and produced in the experiments with natural patterns. It was found that and did not show normal distribution. Traditionally, a normal distribution is assumed in the CCs, which is a condition difficult to meet due to skewness distributions, commonly observed in these cases. However, this is precisely one of the advantages of using ANNs techniques since these methods neither requires control limits nor data normality [28]. Our method requires to compare and patterns looking for undisturbed behaviour of the weld bead corresponding to natural values (given in Table 1. These values were selected to form the multivariate variable C and taken as a reference to measure the from. In this way, the experimental process parameters were defined as unstable in the cases where the special patterns were applied.
3.3. Mahalanobis Distances D2 from the Weldment
A different approach was proposed for the Mahalanobis distances calculation of the 72 multivariate patterns and the mean vector and covariance matrix calculated from the multivariate variable Y, as it is shown in Equation (1). The multivariate variables Y are constituted with the information of height and width of the weld beads generated under the pattern conditions in the parameters of the process.
The vectors resulting from the distances provide the quantitative approximation measures between the observations of each multivariate pattern Y with respect to the centroid of the multivariate pattern C, as well as a representation of the multivariate patterns. For example, the multivariate variable Y was created with respect to the composition or behaviour, where the experimental parameters were affected by cyclic patterns. Similarly, the multivariate variable C was generated, in this particular case, with the behaviour where the experimental parameters were closer to the reference pattern (natural behaviour).
Figure 4a illustrates the distributions of the variables Y and C. Figure 4b shows the graphical representation of calculation between the observations of the multivariate variable Y and of the multivariate variable C. The value that the observations of multivariate variable Y differ with respect to the centroid of the multivariate variable C is shown graphically. The near-stable space is determined by the shape and orientation of the ellipse centred on the mean and the covariance .The near-stable space was defined as the multivariate variable C since it was formed by the measurements of the height and width of the weld bead generated under natural conditions in the process parameters and such measurements of the weld bead did not show normality. Seventy-two vectors of Mahalanobis distances were calculated with respect to Equation (1) using the 72 multivariate patterns corresponding to the measurements of the height and width of the weld beads.
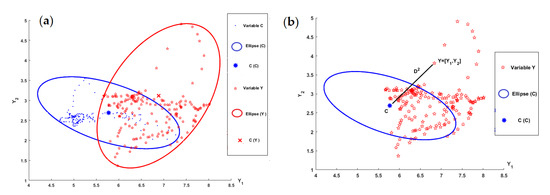
Figure 4.
Near stable (a) Distributions of the near-stable multivariate variable C and the multivariate variable Y. (b) Graphical representation of calculation between the observations of the multivariate variable Y and (, of the multivariate variable C.
3.4. Multivariate Patterns Recognition (MVPR)
In the training stage, SVM uses the training database and a vector of labels in order to learn and recognise each multivariate pattern corresponding to each .
SVM uses a vector of labels and the training database to learn and recognise each multivariate pattern corresponding to each . If the learning is correct in the next stage, the elements (C, Y) with which each one was calculated the can be inferred. In addition, the patterns present in the composition () of each multivariate variable Y corresponding to the welding beads can be known. Finally, it can be determined, according to the inferred patterns in and , if the experimental parameters (Current and Speed ) are in control or not.
In the test stage, the corresponding database is analysed by SVM. By effectively recognising each vector , we can define exactly the elements (C, Y) with which each of the distances were calculated. Likewise, the patterns present in and of each multivariate variable Y corresponding to the welding beads can be inferred. Similarly, the types of univariate patterns of the process can be defined, in addition to knowing their location in the experimental parameters of the process and the causes that originated them. It is possible to acquire and monitor all this knowledge about the process by properly recognising each pattern using the Mahalanobis distance.
4. Experimental Results
The elements that conform the GMAW robotic welding process consist of the power supply, the wire feeder, the torch (gun), argon gas, the workpiece, and a KUKA KR16 industrial robot. The robot manipulator is equipped with multiple sensors such as metal base temperature, voltage, current, and travel speed. The testbed as well as the Graphical User Interface is shown in Figure 5. Figure 6 shows a pair of welding beads that were obtained by disturbing the process parameters , i.e., varying the welding current and robot’s travel speed.

Figure 5.
Robot GMAW (a) Testbed. (b) Graphical User Interface.

Figure 6.
Weld beads resulting from disturbing the process parameters .
As mentioned earlier, in Section 3.3, a training base was formed with 36 classes of the Mahalanobis distances out of the 72 multivariate patterns and a test base with the remaining 36 patterns multivariate patterns. The experimental process parameters for the calculation of C and Y are provided in Table 3.

Table 3.
Experimental parameters for SVM and .
4.1. MVPR Using from
This experiment was carried out to determine the efficiency of multivariate pattern recognition of the 72 that were obtained with Equation (1). Table 4 shows the results.

Table 4.
Multivariate Pattern Recognition (MVPR) using different kernels and from .
The recognition percentage was using the sigmoid kernel. In other words, the SVM was able to recognise 32 multivariate patterns observed at different Mahalanobis distances and only four multivariate patterns were not correctly recognised.
4.2. MVPR Using from
As in the previous approach, three experiments were performed with their respective training and test bases for SVM. In this case, the 72 values were obtained using Equation (2). Table 5 shows the results;

Table 5.
MVPR using different kernels and from .
4.3. Out-of-Control Signal Determination
In Table 5 it can be seen that the recognition percentage was lower when using Y than when using the reference pattern C as it was shown in Table 4, which validates our method. Once C is defined, then it is easy to determine which multivariate pattern type corresponds to that particular and in consequence the univariate special patterns which this is made of. That special pattern would define the corresponding causes and the process parameters could be modified to bring the process under control. Some examples are given in Table 6.

Table 6.
Summary of special patterns and possible causes.
5. Conclusions
The main motivation for this research is focused on the development of automated online GMAW welding process monitoring, as there is a critical need for automatic and efficient analysis in multivariate processes. In this investigation, 36 multivariate patterns were observed in the 36 types of Mahalanobis distances generated by the multivariate variables of the weld beads. Characterisable forms were not visually found for each type of multivariate pattern in comparison with the particular forms of each univariate pattern of the experimental parameters of the process. The robotic welding process considered that the acquired patterns of the weld bead values do not present normal distribution in the measurements of width and height of weld beads and do not generate a normal influence on the multivariate patterns.
The existence of distinctive multivariate patterns for the behaviour of the welding robot, the calculation of the Mahalanobis distance between variables with different covariance matrices, as well as the relative validation of the association between the classes of multivariate patterns of the were presented. Using the calculated value of and the statistical parameters of the multivariate variable C, a recognition rate of up to 88.8% was obtained. The results provided by the SVM algorithm indicate the possibility of distinguishing each type of multivariate pattern present in the Mahalanobis distance. With the information of the type of multivariate pattern in the Mahalanobis distance, the patterns present in the measurements of the final product can be determined, and it is possible to know the patterns that affected each parameter of the process and the description of the real state of the final product.
The relevance of these experiments lies in the approach to the intelligent analysis of processes through the recognition of multivariate patterns in the product and the inference of the real state of the process given by the recognition. In addition, the association of the behaviour between the multivariate patterns found in the measurements of the final product (in this case the weld beads) and the univariate patterns that affected the process. When this type of special pattern is recognised, it can also be interpreted as an indicator of the type of failure and its location that will alert the operator of possible damage to the equipment and, desirably, that the robot itself automatically rectifies its parameters.
The end goal in an industrial production site is to use the MVPR method in real time, so that corrective actions can avoid additional production costs due to unnecessary rework or waste. In a real-time system, the method would require a preliminary analysis to determine the relationship of univariate patterns that affect the process parameters, the product, and the multivariate patterns observed in the product variables. In addition, at this stage the causes that originated both univariate patterns (process) and multivariate patterns (product) must be determined. In addition, a multivariate variable C is selected and the appropriate approach to the calculation of the Mahalanobis distance is defined. The initial database is formed with the information of this type of multivariate patterns and the trained SVM. In a following stage, product quality measures are taken to form the multivariate variable. The would be obtained with the current multivariate variable and the multivariate variable C. Subsequently, the vector obtained from would be examined by the SVM to recognise the multivariate pattern and choose the appropriate actions to restore the process in control. In the event that the pattern is not recognised, then specially trained personnel should include this new pattern in the database.
It should be noted that the GMAW process is a very complex process that involves several parameters, which must be adjusted for a high-quality weld. However, in this work, we only consider the main parameters to have a suitable bead geometry. Additional parameters such as stick-out distance, base metal material, shielding gas, etc. can be included to have a more complete analysis to understand the presence of cracks, voids, and the boundary of the heat affected zone. Research work in this direction has already been envisaged.
Author Contributions
P.C.-S. contributed to the design, conceptualisation and implementation, and programming in Matlab. I.L.-J. and J.A.V.-L. conceptualised the use of for multivariate pattern recognition and wrote the first draft of the article. J.L.N.-G. and A.H.-L. contributed to the experimental design and the revision of the final draft. All authors contributed to the writing of the final version of the article and accepted the published version of the manuscript.
Funding
This research was partially funded through CONACyT research grant CVU266727.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Thanks are sincerely due to K Lopez-Valadez for his valuable comments on English grammar.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SVM | Support Vector Machine |
| MVPR | Multivariate Pattern Recognition |
| Mahalanobis Distance | |
| CC | Control Charts |
| SPC | Statistical Process Control |
| ANN | Artificial Neural Networks |
| PCA | Principal Component Analysis |
References
- Chiñas-Sanchez, P.; Lopez-Juarez, I.; Vazquez-Lopez, J.A.; Kamel, A.E.; Navarro-Gonzalez, J.L. Stable and Unstable Pattern Recognition using D2 and SVM: A Multivariate Approach. Mathematics 2021, 1, 10. [Google Scholar]
- Flury, M.; Barbiero, C.A. Aplicación de técnicas de Control Multivariado en Procesos Industriales; Sextas Jornadas “Investigaciones en la Facultad” de Ciencias Económicas y Estadística; Universidad Nacional de Rosario: Rosario, Argentina, 2001. [Google Scholar]
- Chen, K.H.; Boning, D.; Welsch, R. Multivariate Statistical Process Control and Signature Analysis Using Eigenfactor Detection Methods. In Proceedings of the 33rd Symposium on the Interface of Computer Science and Statistics, Costa Mesa, CA, USA, 13–16 June 2001. [Google Scholar]
- Guh, R.S. Real-time pattern recognition in statistical process control: A hybrid neural network/decision tree-based approach. Proc. Inst. Mech. Eng. Part J. Eng. Manuf. 2005, 219, 283–298. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Ali, S.; Pievatolo, A.; Goeb, R. An Overview of Control Charts for High-quality Processes. Qual. Reliab. Eng. Int. 2016, 32, 2171–2189. [Google Scholar] [CrossRef]
- Awad, M.; AlHamaydeh, M.; Faris, A. Fault detection via nonlinear profile monitoring using artificial neural networks. Qual. Reliab. Eng. Int. 2018, 34. [Google Scholar] [CrossRef]
- Zaman, B.; Lee, M.H.; Riaz, M.; Abujiya, M. An adaptive approach to EWMA dispersion chart using Huber and Tukey functions. Qual. Reliab. Eng. Int. 2019, 35. [Google Scholar] [CrossRef]
- Fernández, M.N.P.; García, A.C.; Barzola, O.R. Multivariate multinomial T2 control chart using fuzzy approach. Int. J. Prod. Res. 2015, 53, 2225–2238. [Google Scholar] [CrossRef]
- Alfaro, E.; Alfaro, J.L.; Gámez, M.; García, N. A Comparison of Different Classification Techniques to Determine the Change Causes in Hotelling’s T2 Control Chart. Qual. Reliab. Eng. Int. 2015, 31, 1255–1263. [Google Scholar] [CrossRef]
- Zhou, X.; Jiang, P.; Wang, X. Recognition of control chart patterns using fuzzy SVM with a hybrid kernel function. J. Intell. Manuf. 2018, 29, 51–67. [Google Scholar] [CrossRef]
- Guan, F.; Cheng, L. Abnormal Quality Pattern Recognition of Industrial Process Based on Multi-Support Vector Machine. J. Softw. 2018, 13, 506–519. [Google Scholar] [CrossRef]
- Zheng, X.; Yu, J. Multivariate Process Monitoring and Fault Identification Using Convolutional Neural Networks. In Proceeding of the 24th International Conference on Industrial Engineering and Engineering Management; Springer: Singapore, 2019; pp. 197–208. [Google Scholar] [CrossRef]
- Addeh, A.; Khormali, A.; Golilarz, N.A. Control chart pattern recognition using RBF neural network with new training algorithm and practical features. ISA Trans. 2018, 79, 202–216. [Google Scholar] [CrossRef] [PubMed]
- Sohaimi, N.A.M.; Masood, I.; Nor, D.M. Bivariate SPC Chart Pattern Recognition Using Modular-Neural Network. J. Phys. Conf. Ser. 2018, 1049, 012096. [Google Scholar] [CrossRef]
- Miao, Z.; Yang, M. Control Chart Pattern Recognition Based on Convolution Neural Network. In Smart Innovations in Communication and Computational Sciences; Panigrahi, B.K., Trivedi, M.C., Mishra, K.K., Tiwari, S., Singh, P.K., Eds.; Springer: Singapore, 2019; pp. 97–104. [Google Scholar]
- Yu, J.; Zheng, X.; Wang, S. Stacked denoising autoencoder-based feature learning for out-of-control source recognition in multivariate manufacturing process. Qual. Reliab. Eng. Int. 2019, 35, 204–223. [Google Scholar] [CrossRef]
- Ramos, D.; Lopez-Juarez, I.; Perez, P. Effect of Process Parameters on Robotic GMAW Bead Area Estimation. Procedia Technol. 2013, 7, 398–405. [Google Scholar] [CrossRef]
- Morales-España, G.; Barrera-Cardenas, R.; Torres, H. Unique localization of faults in distribution systems by means of zones with SVM. Rev. Fac. Ing. 2009, 47, 187–196. [Google Scholar]
- Shewhart, W. Economic Control of Quality of Manufactured Product; Bell Telephone Laboratories Series; American Society for Quality Control; Macmillan And Co Ltd.: London, UK, 1931. [Google Scholar]
- Avellanas, C.C. Distancias Estadísticas. Estadística Española 1988, 119, 295–357. [Google Scholar]
- Salehi, M.; Kazemzadeh, R.B.; Salmasnia, A. On line detection of mean and variance shift using neural networks and support vector machine in multivariate processes. Appl. Soft Comput. 2012, 12, 2973–2984. [Google Scholar] [CrossRef]
- Flury, M.; Barbiero, C.A.; Ruggieri, M. Propuestas Para la Determinación de los Parámetros del Gráfico de Control MEWMA; “Investigaciones en la Facultad” de Ciencias Económicas y Estadística; Universidad Nacional de Rosario: Rosario, Argentina, 2004. [Google Scholar]
- Navarro, J.; Jiménez, J.; Vargas, M. Gráficos Multivariantes Aplicados al Control Estadístico de la Calidad; Netbiblo: La coruña, Spain, 2010. [Google Scholar]
- Terner, M.; BAYARSAIKHAN, T.A.; Hong, H.; Lee, J. Influence of Gas Metal Arc Welding Parameters on the Bead Properties in Automatic Cladding. J. Weld. Join. 2017, 35, 16–25. [Google Scholar] [CrossRef][Green Version]
- Deshpande, M.; Kshirsagar, J.; Dharmadhikari, D. Optimization of GMAW Process Parameters to Improve the Length of Penetration in EN 10025 S 235 Grade. J. Weld. Join. 2017, 35, 74–78. [Google Scholar] [CrossRef][Green Version]
- American National Standards Institute. Structural Welding Code-Aluminum: AWS D1.2/D1.2M; American Welding Society: Miami, FL, USA, 2013. [Google Scholar]
- Vazquez-Lopez, J.A.; Lopez-Juarez, I. SPC without Control Limits and Normality Assumption: A New Method. In Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications; Bayro-Corrochano, E., Eklundh, J.O., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 611–618. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).